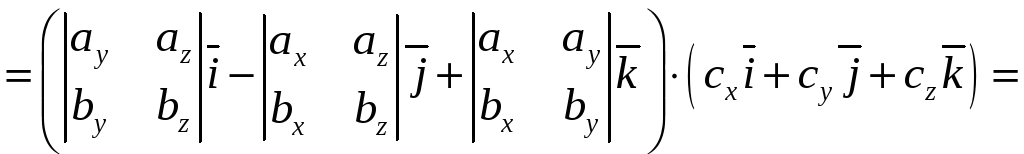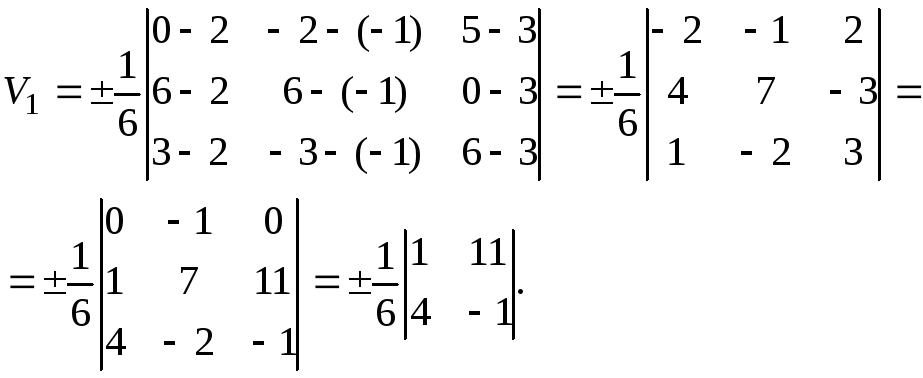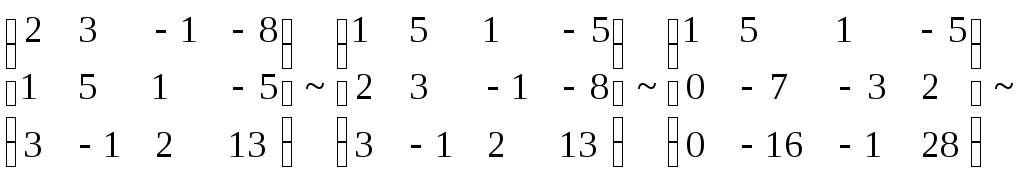Как найти высоту тетраэдра через вектора

Автор	Сообщение
	Заголовок сообщения: Высота тетраэдра Добавлено: 12 дек 2011, 22:00
Продвинутый Зарегистрирован: 13 ноя 2011, 10:48 Сообщений: 94 Cпасибо сказано: 7 Спасибо получено: 1 раз в 1 сообщении Очков репутации: 1	Даны координаты вершин тетраэдра ABCD найти его высоту DT. Подскажите пожалуйста порядок действий
Вернуться к началу

Alexdemath	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 12 дек 2011, 22:23
	Silas Если [math]A,B,C[/math] – это вершины треугольника основания тетраэдра и [math]T(x_{{}_T},y_{{}_T},z_{{}_T})[/math] точка пересечения медиан этого треугольника, то [math]T(x_{{}_T},y_{{}_T},z_{{}_T})= T!left(frac{x_{{}_A}+x_{{}_B}+x_{{}_C}}{3},,frac{y_{{}_A}+y_{{}_B}+y_{{}_C}}{3},,frac{z_{{}_A}+z_{{}_B}+z_{{}_C}}{3},right)=ldots[/math] и длина высоты есть [math]|DT|=sqrt{(x_{{}_T}-x_{{}_D})^2+(y_{{}_T}-y_{{}_D})^2+(z_{{}_T}-z_{{}_D})^2}=ldots[/math] Напишите, что получится.
Вернуться к началу

Silas	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 12 дек 2011, 22:40
	Спасибо) . Сейчас нет с собой условий задачи.Попробую позже точный ответ написать
Вернуться к началу

Silas	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 13 дек 2011, 20:05
	Нашел как можно легче сделать : 1) Найти координаты векторов АВ,АС и АD. 2) Найти объём тетраэдра, умножив эти векторы (1/6)*[AB*AC]*AD. 3) Найти S основания , умножив векторно (1/2)*AB*AC. 4) Объём пирамиды V=(1/3)*S*h, отсюда h=(3*V)/S. Или ещё проще : модуль смешанного произведения AB*AC*AD поделить на модуль векторного AB*AC
Вернуться к началу

rvelikove	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 25 фев 2012, 01:00
	Alexdemath писал(а): Silas Если [math]A,B,C[/math] – это вершины треугольника основания тетраэдра и [math]T(x_{{}_T},y_{{}_T},z_{{}_T})[/math] точка пересечения медиан этого треугольника, то [math]T(x_{{}_T},y_{{}_T},z_{{}_T})= T!left(frac{x_{{}_A}+x_{{}_B}+x_{{}_C}}{3},,frac{y_{{}_A}+y_{{}_B}+y_{{}_C}}{3},,frac{z_{{}_A}+z_{{}_B}+z_{{}_C}}{3},right)=ldots[/math] и длина высоты есть [math]|DT|=sqrt{(x_{{}_T}-x_{{}_D})^2+(y_{{}_T}-y_{{}_D})^2+(z_{{}_T}-z_{{}_D})^2}=ldots[/math] А почему точка пересечения медиан основания произвольного тетраэдра это «основание высоты»? Вроде это не так, тем более посчитав высоту через h=2*V/S и как расстояние от плоскости основания до точки D я получил другой (равный между собой) ответ Подскажите пожалуйста как найти эту точку «основания высоты»(знаю координаты всех вершин, надо найти вектор-высоту тетраэдра)? Пытался находить через коллинеарность нормали к основанию и вектора [math](x_{{}_D}-x_{{}_h},y_{{}_D}-y_{{}_h},z_{{}_D}-z_{{}_h}})[/math], но не получилось
Вернуться к началу

rvelikove	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 25 фев 2012, 11:54
	Нашёл координаты этого «основание высоты», но для этого помимо предыдущего использовал уравнение плоскости основания, но мы ещё не проходили это Подскажите, как можно без использования плоскостей это сделать?
Вернуться к началу

Как найти высоту тетраэдра формула

Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра

(h – высота тетраэдра, a – ребро тетраэдра)

Вывод формулы высоты тетраэдра

Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:

Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

• S – площадь любой грани,
• H – высота, опущенная на эту грань

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

• Все грани равны.
• Все плоские углы правильного тетраэдра равны 60°
• Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
• Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Свойства

Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h

Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2

Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2

Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)

Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8

В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4

Высоту тетраэдра через векторы

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Объем тетраэдра

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

• S – площадь любой грани,
• H – высота, опущенная на эту грань

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

• Все грани равны.
• Все плоские углы правильного тетраэдра равны 60°
• Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
• Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

[spoiler title=”источники:”]

http://yukhym.com/ru/vektory/tetraedr-treugolnaya-piramida-v-prostranstve.html

http://2mb.ru/matematika/geometriya/obem-tetraedra/

[/spoiler]

11

Лекция№6

Рассмотрим
произведение векторов
,

и
,
составленное следующим образом:
.
Здесь первые два вектора перемножаются
векторно, а их результат скалярно на
третий вектор. Такое произведение
называется векторно-скалярным, или
смешанным, произведением трех векторов.
Смешанное произведение представляет
собой некоторое число.

Выясним
геометрический смысл выражения
.

Теорема.
Смешанное произведение трех векторов
равно объему параллелепипеда, построенного
на этих векторах, взятому со знаком
«плюс», если эти векторы образуют правую
тройку, и со знаком «минус», если они
образуют левую тройку.

Доказательство..Построим
параллелепипед, ребрами которого
являются векторы
,
,

и вектор
.

Имеем:
,
,
где

– площадь параллелограмма, построенного
на векторах

и
,

для правой тройки векторов и

для левой, где

– высота параллелепипеда. Получаем:
,
т.е.
,
где

– объем параллелепипеда, образованного
векторами
,

и
.

Свойства смешанного произведения

1.
Смешанное произведение не меняется при
циклической перестановке его
сомножителей, т.е.
.

Действительно,
в этом случае не изменяется ни объем
параллелепипеда, ни ориентация его
ребер.

2.
Смешанное произведение не меняется при
перемене местами знаков векторного и
скалярного умножения, т.е.
.

Действительно,

и
.
Знак в правой части этих равенств берем
один и тот же, так как тройки векторов
,
,

и
,
,

– одной ориентации.

Следовательно,
.
Это позволяет записывать смешанное
произведение векторов

в виде

без знаков векторного, скалярного
умножения.

3.
Смешанное произведение меняет знак при
перемене мест любых двух векторов-сомножителей,
т.е.
,
,
.

Действительно,
такая перестановка равносильна
перестановке сомножителей в векторном
произведении, меняющей у произведения
знак.

4.
Смешанное произведение ненулевых
векторов
,

и

равно нулю тогда и только тогда, когда
они компланарны.

2.12. Вычисление смешанного произведения в координатной форме в ортонормированном базисе

Пусть
заданы векторы
,
,
.
Найдем их смешанное произведение,
используя выражения в координатах для
векторного и скалярного произведений:

. (10)

Полученную
формулу можно записать короче:

,

так как правая часть
равенства (10) представляет собой
разложение определителя третьего
порядка по элементам третьей строки.

Итак,
смешанное произведение векторов равно
определителю третьего порядка,
составленному из координат перемножаемых
векторов.

2.13.Некоторые приложения смешанного произведения

Определение
взаимной ориентации векторов в
пространстве

Определение
взаимной ориентации векторов
,

и

основано на следующих соображениях.
Если
,
то
,
,

– правая тройка; если
,
то
,
,

– левая тройка.

Условие
компланарности векторов

Векторы
,

и

компланарны тогда и только тогда, когда
их смешанное произведение равно нулю
(,
,
):

векторы
,
,

компланарны.

Определение
объемов параллелепипеда и треугольной
пирамиды

Нетрудно
показать, что объем параллелепипеда,
построенного на векторах
,

и

вычисляется как
,
а объем треугольной пирамиды, построенной
на этих же векторах, равен
.

Пример
1. Доказать, что векторы
,

,

компланарны.

Решение.
Найдем смешанное произведение этих
векторов по формуле:

.

. Это и означает,
что векторы

компланарны.

Пример 2.
Даны вершины тетраэдра:

(0, -2, 5),

(6, 6, 0),
(3, -3, 6),

(2, -1, 3). Найти длину его высоты, опущенной
из вершины
.

Решение.
Найдем сначала объем тетраэдра
.
По формуле получаем:

Так как
определитель равен отрицательному
числу, то в данном случае перед формулой
нужно взять знак минус. Следовательно,
.

Искомую
величину h определим
из формулы
,
где S – площадь
основания. Определим площадь S:

где

Поскольку

то

Подставляя
в формулу

значения

и
,
получим h=3.

Пример 3.
Образуют ли векторы
базис в пространстве ? Разложить вектор

по базису векторов
.

Решение. Если векторы образуют
базис в пространстве, то они не лежат в
одной плоскости, т.е. являются
некомпланарными. Найдем смешанное
произведение векторов
:
,

Следовательно,
векторы не компланарны и образуют базис
в пространстве. Если векторы образуют
базис в пространстве, то любой вектор
можно представить в виде линейной
комбинации базисных векторов, а именно
,где

координаты вектора
в
базисе векторов
.
Найдем эти координаты, составив и решив
систему уравнений

.

Решая ее
методом Гаусса, имеем

Отсюда
.
Тогда
.

Таким образом,
.

Пример
4. Вершины пирамиды находятся в точках:
,
,
,
.
Вычислить:

а)
площадь грани
;

б) объем
пирамиды
;

в)
проекцию вектора

на направление вектора
;

г) угол
;

д)
проверить, что векторы
,
,

компланарны.

Решение

а) Из
определения векторного произведения
известно, что:

.

Находим
векторы

и
,
используя формулу

;

,
.

Для
векторов, заданных своими проекциями,
векторное произведение находится по
формуле

,
где
.

Для
нашего случая

.

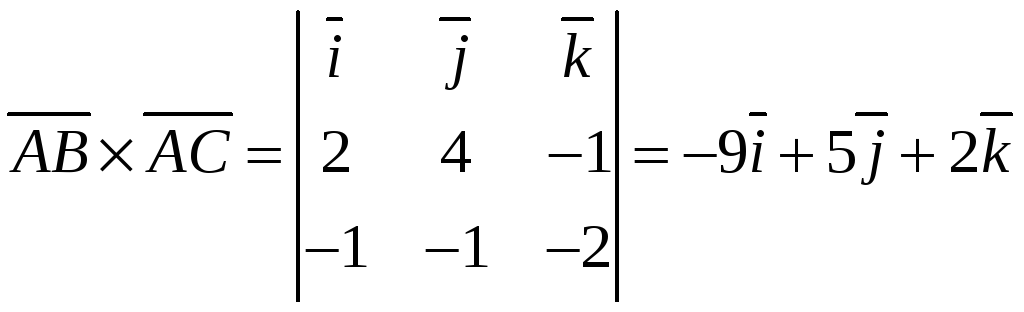
Длину
полученного вектора находим, используя
формулу

,
.

и тогда

(кв. ед.).

б)
Смешанное произведение трех векторов
по абсолютной величине равно объему
параллелепипеда, построенного на
векторах
,
,

как на ребрах.

Смешанное
произведение вычисляется по формуле:

.

Найдем
векторы
,
,
,
совпадающие с ребрами пирамиды,
сходящимися к вершине
:

,

,

.

Смешанное
произведение этих векторов

.

Так
как объем пирамиды равен

части объема параллелепипеда, построенного
на векторах
,
,
,
то

(куб. ед.).

в)
Используя формулу
,
определяющую скалярное произведение
векторов
,
,
можно записать так:

,

где

или
;

или
.

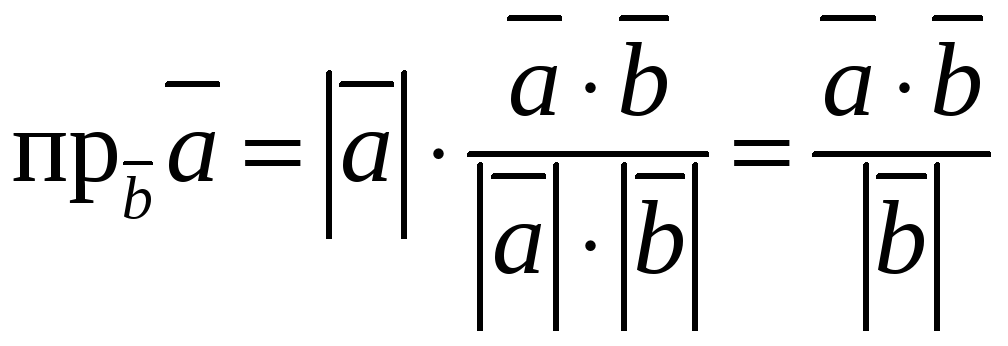
Для
нахождения проекции вектора

на направление вектора

находим координаты векторов
,
,
а затем, применяя формулу

,

получаем

.

г) Для
нахождения угла

определяем векторы
,
,
имеющие общее начало в точке
:

,

.

Затем
по формуле скалярного произведения

находим

,

.

д) Для
того чтобы три вектора

,
,

были компланарны,
необходимо и достаточно, чтобы их
смешанное произведение было равно нулю.

В нашем
случае имеем
.

Следовательно,
векторы компланарны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Высота тетраэдра, формула

Высота тетраэдра — равна корню квадратному из двух третьих, помноженному на длину ребра тетраэдра [ h = sqrt{frac{2}{3}} a ] (h – высота тетраэдра, a – ребро тетраэдра)

Вывод формулы высоты тетраэдра

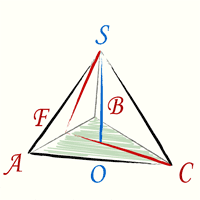
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке
красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:

[CF = FS = frac{sqrt{3}}{2}a ; CS = a ]

Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).

[p = frac{1}{2}(a + afrac{sqrt{3}}{2} + afrac{sqrt{3}}{2}) ]

[p = frac{1}{2} a (1 + sqrt{3}) ]

[h = 2 frac{ sqrt{p(p-a)(p-(afrac{sqrt{3}}{2}))(p-(afrac{sqrt{3}}{2}))}}{afrac{sqrt{3}}{2}}]

[h = 2 frac{sqrt{(frac{a}{2})^4 (sqrt{3}+1) (sqrt{3}-1)}}{afrac{sqrt{3}}{2}} = sqrt{frac{2}{3}} a ]

Вычислить, найти высоту тетраэдра по формуле(1)

Высота тетраэдра	стр. 283