Высота ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти высоту ромба по известным элементам. Для нахождения высоты ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Содержание
- Высота ромба через сторону и площадь
- Высота ромба через сторону и угол
- Высота ромба через диагонали
- Высота ромба через угол и противолежащую диагональ
- Высота ромба через угол и диагональ из данного угла
- Высота ромба через радиус вписанной в ромб окружности
1. Высота ромба через сторону и площадь
Пусть задан ромб (Рис.1).
Формула площади ромба через сторону и высоту имеет следующий вид:
Откуда легко вывести формулу высоты ромба через сторону и площадь:
2. Высота ромба через сторону и угол
Рассмотрим ромб со стороной a и углом α между сторонами (Рис.2). Выведем формулу вычисления высоты ромба через сторону и угол.
Проведем высоту AH. Для прямоугольного треугольника AHB применим теорему синусов:
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого угла. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Высота ромба через диагонали
Выведем формулу вычисления высоты ромба через диагонали. Плошадь ромба через диагонали вычисляется формулой (см. статью Площадь ромба):
а через сторону и высоту, формулой
Из формул (3) и (4) следует:
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
Применим к прямоугольному треугольнику AOB теорему Пифагора:
Откуда:
Подставим (7) в (5) и найдем h:
4. Высота ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:
Откуда получим:
С другой стороны (см. параграф 2):
Подставим (9) в (10):
Применяя формулу двойного угла для (small sin alpha, ) имеем: (small sin alpha=2 cdot sin frac{alpha}{2} cdot cos frac{alpha}{2} . ) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:
5. Высота ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Для прямоугольного треугольника AOB, имеем:
Учитывая, что ( small BO=frac{large d}{large 2}) и ( small angle ABO=frac{large alpha}{large 2}), формулу (13) можно записать так:
или
Подставим (14) в (2):
или, учитывая что (small sin alpha=2 cdot sin frac{alpha}{2} cdot cos frac{alpha}{2} , ) получим:
6. Высота ромба через радиус вписанной в ромб окружности
Покажем, что высота ромба через радиус вписанной окружности вычисляется по формуле:
В статье Площадь ромба показали, что площадь ромба через сторону и высоту вычисляется формулой
а площадь ромба через сторону и радиус вписанной окружности − формулой:
Тогда из формул (16) и (17) следует:
или:
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
-
Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
-
Через диагонали и угол между ними
- Через площадь
- Примеры задач
Нахождение высоты трапеции
Через длины сторон

Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:

Через боковую сторону и прилежащий угол

Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
![]()
Через диагонали и угол между ними

Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
![]()

Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
![]()
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b)/2.
Через площадь

Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
![]()
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:

Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см2. Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
![]()
Ромб – это фигура, являющаяся параллелограммом. Но его особенность в том, что он обладает четырьмя
одинаковыми сторонами. Имеет некоторые важные геометрические свойства, а если быть точнее:
- Два угла будут равны, если они противоположные.
- Точка пересечения делить диагонали пополам.
- Стороны, которые находятся друг напротив друга, попарно равны.
- Если сложить градусную меру соседних углов, то получится 180 градусов.
- Биссектрисами ромба являются все его диагонали
- Высота ромба через сторону и синус любого угла
- Высота ромба через длинную диагональ и синус острого
угла - Высота ромба через короткую диагональ и синус тупого
угла - Высота ромба через диагонали
- Высота ромба через диагонали и сторону
Через диагонали
Бывают случаи, когда из всех возможных данных нам известны только две диагонали: длинная и короткая,
тогда математики применяют такую формулу:
h = D * d / (√D² + d²)
где h – высота ромба, D – длинная диагональ, d – короткая диагональ.
Цифр после
запятой:
Результат в:
Пример. Имеем ромб ABCD, длинная диагональ равна 7 см, а короткая – 4 см. В условиях
сказано, что нужно найти высоту, округлив ответ до десятых. Используя предыдущую формулу,
подставляем вместо переменных следующие числа: h = 7 * 4 / (√7² + 4²) = 3.4. Ответ: 3.4 см.
Через диагонали и сторону
Когда в условиях задачи нам даны обе диагонали (и короткая, и длинная) вместо с одной из сторон, то
нужно следовать этой формуле:
h = Dd / 2a
где h – высота, D – длинная диагональ, d – короткая диагональ, a – одна из сторон
Цифр после
запятой:
Результат в:
Пример. Решим задачу. Дан ромб ABCD. Имеется две диагонали: короткая диагональ равна
3 см, а длинная 6. Сторона AB в длину составляет 8 см. Найдите высоту, ответ дайте в десятых. Режим
задачу при помощи формулы: h = 6 * 3 / 2 * 8 = 1,2 см. Ответ: 1,2 см.
Через длинную диагональ и синус острого угла
Если в задаче дан синус острого угла, а так же нам известно значение длинной диагонали, то можно
использовать данный способ:
h = D * sin α/2
где h – высота, D – длинная диагональ, sin α – синус острого угла.
Цифр после
запятой:
Результат в:
Пример. Приведём одну из возможных ситуаций. В задаче представлен ромб ABCD. Нам
неизвестны его стороны, однако мы знаем, что длинная диагональ равна 9 сантиметрам. Так же мы имеем
острый угол α в 30°. Нужно найти его высоту, ответ округляем до десятых. Для этого мы умножаем
диагональ на sin острого угла, так как он равен 30°, то его синус равен 1/2, соответственно: h = 9 * 1/2 = 2.3 сантиметра. Ответ: 2.3 см.
Через короткую диагональ и синус тупого угла
Допустим, в условиях прописано, какая длина у короткой диагонали. Так же мы знаем градус одного
тупого угла. Для решения задач подобного типа используем эту формулу:
h = d * sin β/2
где h – высота, d – короткая диагональ, β – синус тупого угла
Цифр после
запятой:
Результат в:
Пример. Решим одну из задач. Нам дан ромб ABCD. У этой фигуры короткая диагональ
равна 10 см, мы знаем, что в ромбе есть тупой угол в 150°. Найдите высоту с точностью до десятых.
Чтобы узнать необходимую величину, необходимо умножить D, что обозначает длинную диагональ на sin
150°/2, получается: h = 10 * (sin 150º / 2) = 9.8 сантиметров. Ответ: 9.8
см.
Через сторону и синус любого угла
Для того чтобы найти высоту фигуры используя сторону и любой синус, нужно обратиться к следующей
формуле:
h = a * sin α
где h является высотой, a – сторона ромба, sin α – синус любого угла, который мы решили взять
Цифр после
запятой:
Результат в:
Пример. Рассмотрим формулу на примере. Имеем ромб ABCD, где сторона CB = 5
сантиметров, а угол C равен 90°. Чтобы найти его высоту, нам необходимо умножить CB на sin угла C.
Так как синус угла 90 градусов равен 1, соответственно, получаем следующее выражение: h = 5 • 1 = 5 сантиметров составляет высота ромба ABCD. Ответ: 5 см
Если быть внимательным, то можно заметить необычные признаки ромба, по которым его легко отличить от
других:
- Если в параллелограмме есть возможность вписать окружность, то это ромб.
- Если в параллелограмме все высоты равны, то это ромб.
- Если в параллелограмме под углом в 90° пересекаются диагонали, то это ромб.
- Если в параллелограмме диагонали перпендикулярны друг друга, кроме этого ещё и делятся точкой
пересечения, то это ромб. - Если все четыре стороны параллелограмма равны, то это ромб.
Задачи на нахождение различных величин ромба встречаются во многих экзаменах, в том числе на ОГЭ и
ЕГЭ.
Порой в задачах необходимо определить высоту ромба, чтобы при её помощи узнать основную неизвестную
величину. К примеру, для того, чтобы вычислить площадь ромба, в одной из формул нам необходимо знать
высоту: , где a – это одна из сторон ромба, а h – высота. По обратной формуле можно будет найти
сторону ромба, для этого будет необходимо разделить площадь на высоту: .
Здравствуйте, уважаемые читатели. В этой статье продолжим разбор задач из 23 задания ОГЭ по математике.
Задача
Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.
К задаче построим рисунок и напишем условие
Решение
1) Так как ABCD ромб, то все стороны равны. Найдем CD
2) Рассмотрим треугольник AHD – прямоугольны. По теореме Пифагора найдем AH
Ответ 8
Вам понравился материал? Поблагодарить легко! Будем весьма признательны, если поделитесь этой статьей в социальных сетях, поставите лайк и подпишитесь на мой блог
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
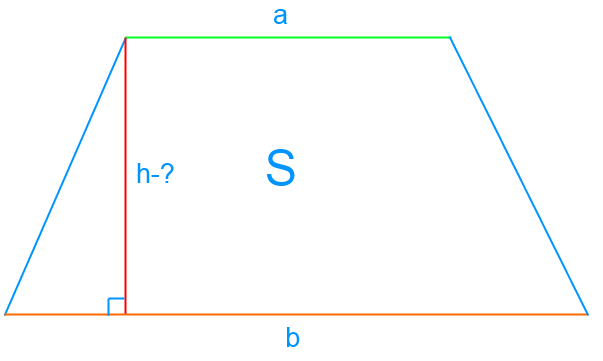
Чтобы вычислить площадь S трапеции мы используем формулу:
[S=frac{((a+b) times h)}{2}]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
[h=frac{2 times S}{(a+b)}]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
[h=frac{2 times 50}{(4+6)}=10 mathrm{~cm}]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
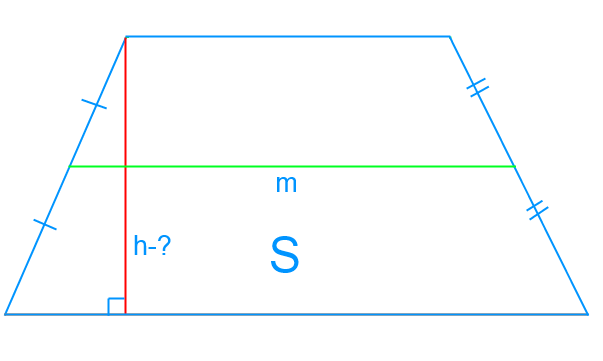
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
[h=frac{S}{m}], будет ответом.
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
[h=frac{200}{20}=10 mathrm{~cm}]
Ответ: 10 см
Высота прямоугольной трапеции
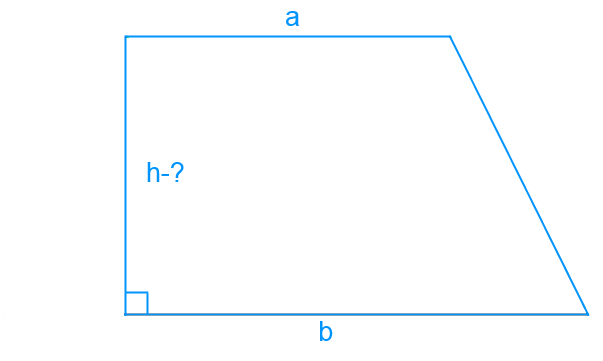
Определение
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
[A D=sqrt{left(A C^{2}-D C^{2}right)}]
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Пример 3
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
[A C^{2}=A D^{2}+D C^{2}] может быть записан
[15^{2}=14^{2}+x^{2}]
[x=sqrt{left(15^{2}-14^{2}right)}=sqrt{(225-196)}=sqrt{29} mathrm{см}]
Ответ: [sqrt{29} mathrm{см}], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Нахождение высоты через стороны
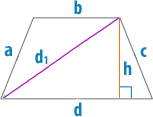
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]
Пример 4
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
[h=sqrt{2^{2}-left(frac{(4,5-2,5)^{2}+2^{2}-2 sqrt{2}^{2}}{2(4,5-2,5)}right)^{2}}=sqrt{4}=2 см]
Ответ: h=2 см.

