Как найти высоту трапеции?
Pussyca Pussyca
Ученик
(155),
закрыт
13 лет назад
Если периметр равнобедренной трапеции 32см, боковые стороны по 5см, площадь 44см (в квадрате)
Дополнен 14 лет назад
Периметр равнобедренной трапеции 32см,боковые стороны по 5 см,площадь 44см(В квадрате)
Владимир
Профи
(620)
14 лет назад
Площадь трапеции равна средней линии умноженной на высоту. Т. е если ввести обозначения:
a – нижнее основание
b – верхнее основание
с – средняя линия
d – боковая сторона
h – высота
S – площадь трапеции
P – периметр трапеции,
тогда получаем:
S=c*h, с=(a+b)/2 (средняя линия равна полусумме оснований) . Тогда получаем:
S=(a+b)*h/2
Отссюда h=2*S/(a+b)
Теперь напишем формулу для периметра:
P=a+b+2*d, отсюда
a+b=P-2*d
Подставляем эту формулу в формулу h=2*S/(a+b) и получаем:
h=2*S/(P-2*d)=2*44/(32-2*5)=4
VizuALL
Мастер
(1084)
14 лет назад
из одной из вершин большего основания опустить перендикляр, и там по теореме пифагора) но это может не сработать, я ж не знаю условие задачи)
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
-
Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
-
Через диагонали и угол между ними
- Через площадь
- Примеры задач
Нахождение высоты трапеции
Через длины сторон

Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:

Через боковую сторону и прилежащий угол

Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
![]()
Через диагонали и угол между ними

Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
![]()

Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
![]()
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b)/2.
Через площадь

Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
![]()
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:

Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см2. Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
![]()
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются – верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
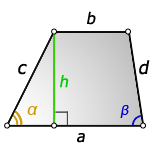
a – нижнее основание
b – верхнее основание
c , d – боковые стороны
α, β – углы трапеции
h – высота трапеции
Формулы длины высоты, (h ):
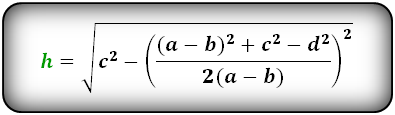
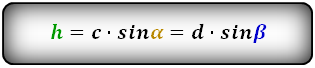
2. Формула высоты трапеции через диагонали и углы между ними
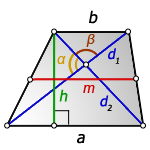
d1 , d2 – диагонали трапеции
α , β – углы между диагоналями
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
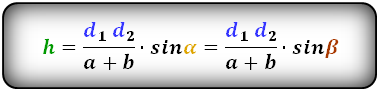
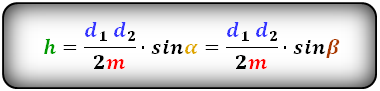
3. Формула высоты трапеции через площадь
S – площадь трапеции
a , b – основания
h – высота трапеции
m – средняя линия
Формулы длины высоты, (h ):
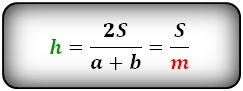
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 26 сентября 2013
-
Обновлено: 13 августа 2021
Трапецией принято называть выпуклую четырёхугольную четырехугольник с парой параллельных и двумя не
параллельными сторонами. Отрезки, которые создают параллельные прямы называются «основанием
трапеции», две других стороны играют роль «боковой стороны трапеции». Средняя линия трапеции будет
соединять два центра боковых сторон.
- Высота трапеции через боковую сторону и прилегающий угол
при основании - Высота трапеции через площадь и длины оснований
- Высота трапеции через площадь и среднию линию
- Высота трапеции через основании, диагонали и угол между
диагоналями - Высота трапеции через среднию линию, диагонали и угол между
диагоналями
Как найти высоту при помощи боковой стороны и прилегающего угла при основании
Для вычисления высоты трапеции через боковую сторону и прилегающий угол при основании нужно
воспользоваться нижеприведенной формулой:
h = a · sin α
где h — это искомая высота трапеции, a — известная боковая сторона, sin α — угол
при основании.
Цифр после
запятой:
Результат в:
Пример. Чтобы разобраться с применением формулы, давайте рассмотрим пример. Дана
некая трапеция. Нам известно, что боковая сторона равна 10 сантиметрам, а прилегающих угол
составляет 30 гр. Нам нужно найти высоту данной трапеции. Для решения у нас есть вся нужная
информация и формула выше. Подставляем значения в формулу: h = a · sin, h = 10 · sin 30, h = 10 · 1/2, h = 5 см
Как найти высоту трапецию при помощи длины основания и площади трапеции
Чтобы найти высоту трапеции через известные длины основания и площадь, нужно воспользоваться
формулой:
h = (2S) / (a + b)
где h — это искомая высота трапеции, S — известная площадь фигуры, a и b — длины
обеих оснований.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Нам известно, что в трапеции АВСD основания a и b равны
5 и 10 сантиметров. Площадь фигуры равна 30 квадратных сантиметров. Для решения нужно
воспользоваться формулой. h = (2S) / (a + b), h = (2 х 30) / (5 + 10), h = 60 /15, h = 4 см.
Высота трапеции равна 4 см.
Как найти высоту при помощи диагоналей, углу между диагоналями и средней линией трапеции
Чтобы найти высоту трапеции через среднюю линию, известные диагонали и угол между ними, нужно
прибегнуть к применению выведенной формулы:
h = ((D x d) / (2m)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, m — средняя
линия, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Дана трапеция с диагоналями 5 и 12 сантиметров.
Известно, что средняя линия фигуры равна 6 см, а угол между диагоналями – 30 градусов. Применив
формулу выше, мы сможем с легкостью найти высоту трапеции. h = ((D x d) / (2m)) x sin (α), h = ((5 x 12) / (2 х 6)) x sin (30), h = (60 /12) x 0.5, h = 2.5 см.
Высота трапеции равна 2.5 см.
Как найти высоту при помощи средней линии и площади трапеции
Чтобы найти высоту трапеции через площадь и среднюю линию воспользуемся выведенной формулой:
h = (2S) / m
где h — это искомая высота трапеции, S — известная площадь фигуры, а m — средняя
линия.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: Площадь произвольной трапеции составляет 30 квадратных
сантиметров. Средняя линия фигуры равна 5 см. Нужно найти высоту по формуле. h = (2S) / m, h = (2 х 30) / 5, h = 60 / 5, h = 12 см. 12
см – высота трапеции.
Как найти высоту при помощи известного основания, диагоналей трапеции и угла между диагоналями
Для нахождения высоты трапеции при помощи известного основания, диагонали и углу между диагоналями
используют нижеприведенную формулу:
h = ((Dd) / (a + b)) x sin (α)
где h — это искомая высота трапеции, D и d — известные диагонали, a и b — длины
обеих оснований, sin(α) — угол между диагоналями.
Цифр после
запятой:
Результат в:
Пример. Закрепим на примере: В трапеции ABCD диагонали равны 10 см каждая. Известно,
что сумма основ фигура равна 20 см. Угол, созданный между диагоналями – 30 градусов. Нужно найти
высоту. Для этого нужно воспользоваться выше предоставленной формулой. h = ((Dd) / (a+b)) x sin (α), h = ((10 х 10) / (20)) x sin (30), h = 5 x sin (30), h = 2.5 см.
Высота трапеции равна 2.5 см
Можно выделить 2 разновидности трапеции:
- Трапеция, в которой одна из боковых сторон лежит под перпендикулярным углом с обеими основами
называется прямоугольной. - Трапеции с равными боковыми сторонами называется равнобедренной.
Высотой трапеции принято называть отрезок, которой показывает самое короткое расстояние между верхним
и нижним основанием фигуры. Существует большое количество математических задач разного уровня
сложности, для решения которых активно применяют высоту. Стоит разобраться со всеми возможными
формулами, которые используются для нахождения высоты трапеции.
Трапеция представляет собой уникальную по своей простоте фигуру, состоящую из прямоугольника и двух присоединенных к нему прямоугольных треугольников. Стороной всех этих фигур внутри трапеции является высота, проведенная из углов при верхнем основании. Высота трапеции открывает множество вероятных решений для любых задач, и найти ее можно несколькими способами. Зная площадь трапеции и ее среднюю линию (или два основания, среднее арифметическое которых дает среднюю линию), можно вычислить высоту трапеции, разделив одно на другое:

Более изощренным является вычисление высоты трапеции через все ее стороны. В данном случае помимо высоты в трапеции нужно провести также диагональ, которая сформирует прямоугольный треугольник и даст возможность выразить высоты несколькими разными способами через разные треугольники.

Выразив все стороны треугольников через стороны трапеции и приведя подобные слагаемые, получается следующая формула:

