ВСЕ определения и теоремы по учебнику Атанасяна
Геометрия 7 класс
1) Смежными углами называют два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой;
2) Вертикальными угламиназываются углы если стороны одного угла являются продолжениями другого.
3) Перпендикулярными прямыминазываются две пересекающиеся прямые, если они образуют четыре прямых угла.
4) Периметром треугольниканазывается сумма длин всех сторон.
5) Первый признак треугольника:Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
6) Перпендикуляр к прямой: Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой и при том только один.
7) Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
8) Биссектрисой треугольника называетсяотрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
9) Высотой треугольника называетсяперпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
10) Замечательное свойство треугольника:В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения так же пересекаются в одной точке.
11) Равнобедренным треугольником называется треугольник, если две его стороны равны.
12) Равные стороны равнобедренного треугольниканазываются боковыми сторонами, а третья сторона – основанием.
13) Равносторонним треугольником называется треугольник, все стороны которого равны.
14) 1 свойство равнобедренного треугольника: в равнобедренном треугольнике углы при основании равны.
15) 2 свойство равнобедренного треугольника: в равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
16) Следствие 1:Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
17) Следствие 2: Медианаравнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.
18) Второй признак равенства треугольника:Если сторона, и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
19) Третий признак равенства треугольников: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
20) Параллельными прямыми называютсядве прямые, лежащие на плоскости, если они не пересекаются.
21) Признаки параллельности двух прямых: 1)Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. 2)Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 3)Если при пересечении двух прямых секущей сумма односторонних углов равна 180 градусов, то прямые параллельны.
22) Аксиомами называются исходные положения в геометрии.
23) Аксиомы: 1)Через любые две точки проходит прямая, и при том только одна. 2)На любом луче от его начала можно отложить отрезок, равный данному, и при том только один. 3)От любого луча, в заданную сторону можно отложить угол, равный данному, не развёрнутому углу, и при том только один.
24) Аксиомы параллельных прямых:Через точку, не лежащую на данной прямой проходит только одна прямая, параллельная данной.
25) Следствие 1:Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
26) Следствие 2: Если две прямые параллельны третьей прямой, то они параллельны.
27) Теорема об углах, образованных двумя параллельными прямыми и секущей:
Теорема 1:Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Следствие 1:Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
Теорема 2: Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Теорема 3: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусов.
28) Теорема о сумме углов треугольников:Сумма углов треугольников равна 180 градусов.
29) Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
30) В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой, или прямой.
31) Треугольник называется остроугольным,если все три угла острые.
32) Треугольник называется тупоугольным,если один из углов тупой.
33) Треугольник называется прямоугольным,если один из углов прямой.
34) Гипотенуза –это сторона прямоугольного треугольника, лежащая против прямого угла.
35) Катет – это другая сторона прямоугольного треугольника.
36) Теорема о соотношении между сторонами и углами треугольника: 1) В треугольнике против большей стороны лежит больший угол; 2) Против большего угла лежит большая сторона.
Следствие 1: В прямоугольном треугольнике гипотенуза больше катета.
Следствие 2: Если два угла треугольника равны, то треугольник равнобедренный.
37) Теорема «Неравенство треугольника»:
Каждая сторона треугольника меньше суммы двух других сторон
Следствие:Для любых трёх точек А, В, С не лежащих на одной прямой справедливо неравенство: АВ
Геометрия. 7 класс
Конспект урока
Медианы треугольника. Биссектрисы треугольника. Высоты треугольника
Перечень рассматриваемых вопросов:
- Понятие медианы, биссектрисы, высоты треугольника.
- Построение медианы, высоты, биссектрисы.
- Точки пересечения медианы, высоты и биссектрисы в треугольнике.
- Создание представления о замечательных точках в треугольнике.
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.
Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.
Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.
В любом треугольнике биссектрисы пересекаются в одной точке.
Введём понятие медианы треугольника.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
BM – медиана треугольника ABC.
В любом треугольнике медианы пересекаются в одной точке.
Введём понятие высоты треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
AH – высота треугольника ABC.
В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.
Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».
На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.
Докажем, что треугольники ABD и CED равны.
По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.
∠ADB = ∠CDE (по свойству вертикальных углов).
Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.
1.Нарисуем рисунок по условию задачи.
2.По условию AD и BM – биссектрисы ∆ABC.
∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°
∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°
3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.
5.∠AOB = 180° – (25° + 40°) = 115°.
Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.
В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.
1.По условию ∠СОD = 90°.
Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.
2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.
3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.
Медианы, биссектрисы и высоты треугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы продолжим рассмотрение элементов треугольника – медиан, биссектрис и высот треугольника.
Вначале дадим определение медианы треугольника и рассмотрим три медианы треугольника. Дадим определение биссектрисы треугольника и рассмотрим три биссектрисы треугольника. Дадим определение высоты треугольника и рассмотрим высоты в произвольном треугольнике и в тупом треугольнике. Далее решим ряд задач с использованием этих элементов.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
[spoiler title=”источники:”]
http://resh.edu.ru/subject/lesson/7290/conspect/
http://interneturok.ru/lesson/geometry/7-klass/treugolnikib/mediany-bissektrisy-i-vysoty-treugolnika
[/spoiler]


ГДЗ (готовое домашние задание из решебника) на Номер №488 по учебнику Геометрия 7-9 классы: учебник для общеобразовательных организаций / Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 2-е издание. Просвещение, 2014-2019г.
Условие
Найдите: а) высоту равностороннего треугольника, если его сторона равна 6 см; б) сторону равностороннего треугольника, если его высота равна 4 см.
Решение 1
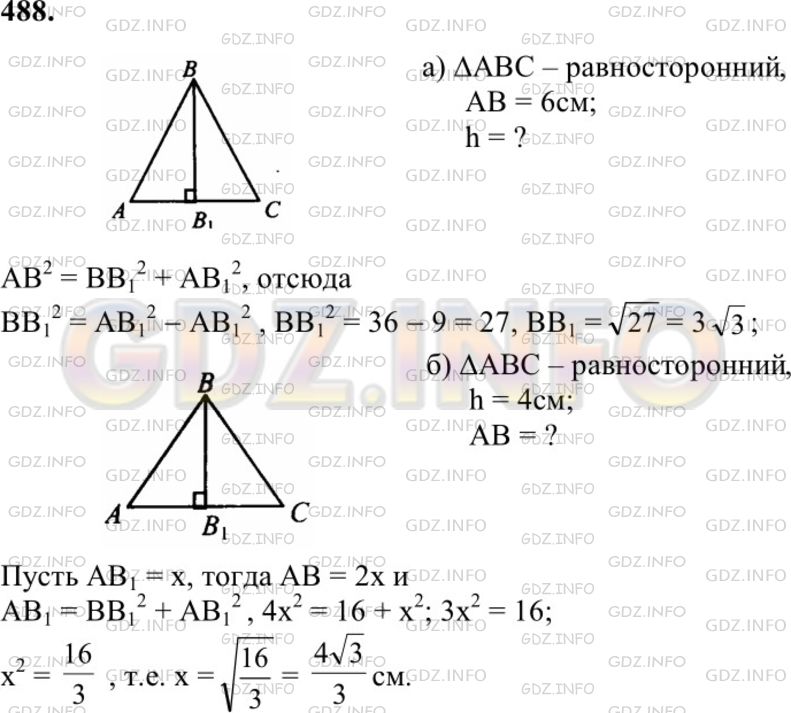
Решение 2
Подробное решение

Белый фонпереписывать в тетрадь
Цветной фонтеория и пояснения
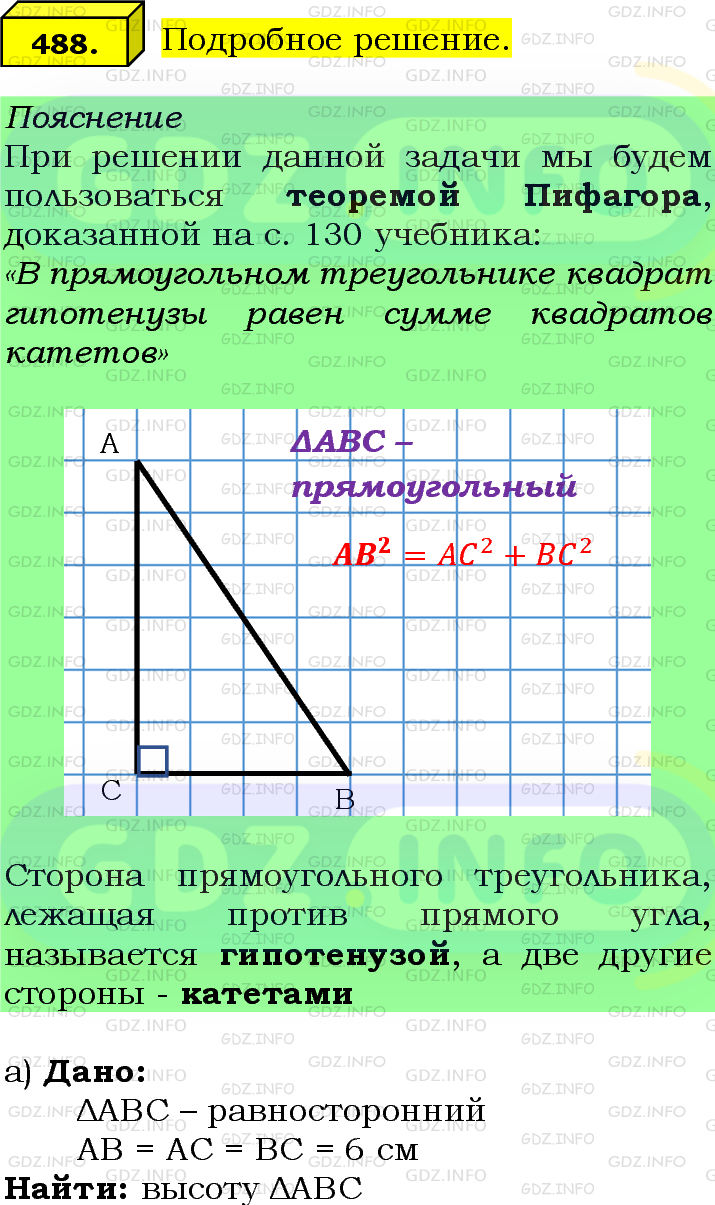
Решение 3

Решение 4

Решение 5

Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
ГДЗ и решебники
вип уровня
- ГДЗ
- 7 класс
- Геометрия
- Атанасян
- Задание 492

Условие
Найдите высоты треугольника со сторонами 10 см, 10 см и 12 см.
Решение 1
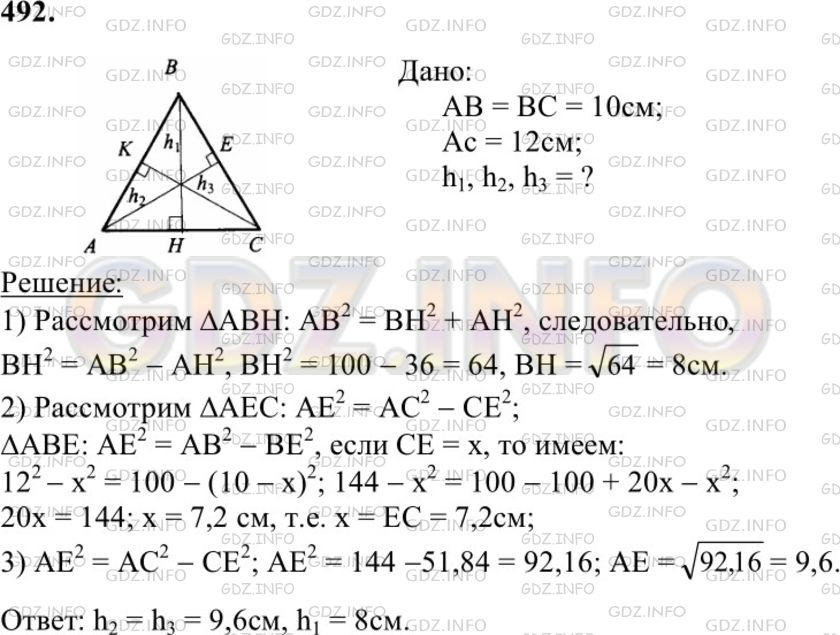
Решение 2

Решение 3

Популярные решебники
Геометрия
7 класс
Урок № 12
Медианы треугольника. Биссектрисы треугольника. Высоты треугольника
Перечень рассматриваемых вопросов:
- Понятие медианы, биссектрисы, высоты треугольника.
- Построение медианы, высоты, биссектрисы.
- Точки пересечения медианы, высоты и биссектрисы в треугольнике.
- Создание представления о замечательных точках в треугольнике.
Тезаурус:
Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.
Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Вы уже знакомы с такими понятиями как треугольник, угол, биссектриса угла.
Разберем, как построить биссектрису треугольника, а также узнаем, что такое медиана и высота треугольника.

Начнём с понятия биссектриса угла треугольника. Это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. AF – биссектриса ∠A треугольника ABC.
AA1, BB1, CC1 – биссектрисы ∆АВС

В любом треугольнике биссектрисы пересекаются в одной точке.
Введём понятие медианы треугольника.
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BM – медиана треугольника ABC.
AA1, BB1, CC1 – медианы ∆АВС.
В любом треугольнике медианы пересекаются в одной точке.

Введём понятие высоты треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

AH – высота треугольника ABC.

AH1, BH2, CH3 – высоты ∆АВС.
В любом треугольнике высоты или их продолжения пересекаются в одной точке.
Итак, сегодня мы узнали, какие отрезки называются медианой, биссектрисой, высотой треугольника, и научились их изображать с помощью чертёжных инструментов.
Рассмотрим, как можно решить задачу на доказательство, используя понятие «медиана треугольника».
На рисунке изображён треугольник ABC, при этом AD – медиана ∆ABC продолжена за сторону BC, так что AD = DE.
Докажем, что треугольники ABD и CED равны.

Дано:
АD – медиана ∆ABC.
AD = DE.
Доказать:
∆ABD = ∆CED.
Доказательство:
По условию в треугольниках ABD и CED: сторона AD равна стороне DE. Т. к. АD – медиана ∆ABC, то, по определению медианы, BD = DC.
∠ADB = ∠CDE (по свойству вертикальных углов).
Следовательно, ∆ABD = ∆CED (по первому признаку равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны).
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
Задача 1.
В треугольнике ABC проведены биссектрисы AD и BM, которые пересекаются в точке O. Найдите углы треугольника ABO, если ∠BAC = 50°, ∠ABC = 80°, а сумма углов треугольника ABO равна 180°.

Решение:
1.Нарисуем рисунок по условию задачи.
2.По условию AD и BM – биссектрисы ∆ABC.
∠BAC = 50°, ∠BAC = 2∠BAO =50° → ∠BAO = 25°
∠ABC = 80°, ∠ABC= 2∠ABO = 80°→∠ABO = 40°
3.Т. к. сумма углов треугольника ABO равна 180°, то ∠ABO + ∠BAO + ∠AOB = 180°.
4.25° + 40° + ∠AOB = 180°.
5.∠AOB = 180° – (25° + 40°) = 115°.
Ответ: ∠BAO = 25°, ∠ABO = 40°, ∠AOB = 115°.
Задача 2.
В треугольнике COD: ∠O = 90°. Найдите ∠МОВ, если ОА – биссектриса угла ∠СОM, при этом ∠COА = 20°, а ВО– биссектриса ∠МОD.

Решение:
1.По условию ∠СОD = 90°.
Кроме того, ОА – биссектриса угла ∠СОM → ∠МОА = ∠СОА = 20°.
2.ВО – биссектриса ∠МОD→∠ВОD = ∠МОВ.
3. ∠СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 20° + 20° + 2∠МОВ = 40° + 2∠МОВ = 90°.
4. 40° + 2∠МОВ = 90°.
∠МОВ = (90° – 40°):2 = 25°.
Ответ: ∠МОВ = 25°.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Высоты треугольника
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. На Рис.1 АН – высота треугольника АВС (точку Н называют основанием высоты АН).
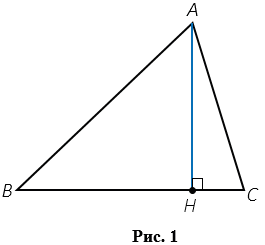
Любой треугольник имеет три высоты. На Рис.2 (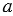 ), АН, ВМ, СК – высоты треугольника АВС (АН
), АН, ВМ, СК – высоты треугольника АВС (АН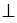 ВС, ВМ
ВС, ВМ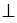 АС, СК
АС, СК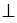 АВ).
АВ).
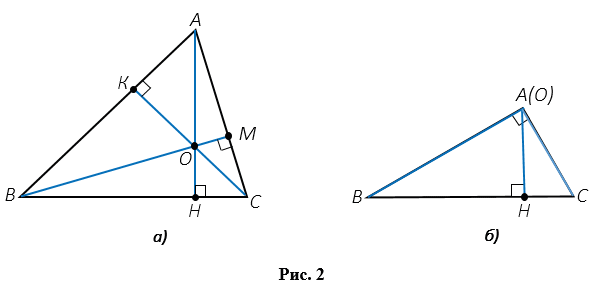
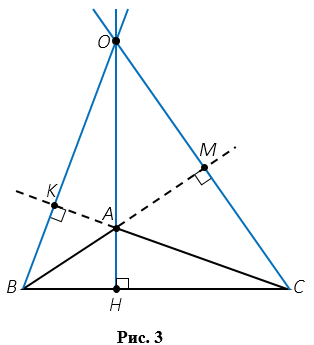
Замечательное свойство высот треугольника: в любом треугольнике высоты или их продолжения пересекаются в одной точке. На Рис.2 ( 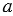 ,б ) в точке О пересекаются высоты треугольника АВС, а на Рис.3 в точке О пересекаются продолжения высот треугольника АВС.
,б ) в точке О пересекаются высоты треугольника АВС, а на Рис.3 в точке О пересекаются продолжения высот треугольника АВС.
Советуем посмотреть:
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Равнобедренный треугольник
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 530,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 577,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 706,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 715,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 864,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 910,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 932,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1006,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник



