Как найти высоту треугольника через векторы

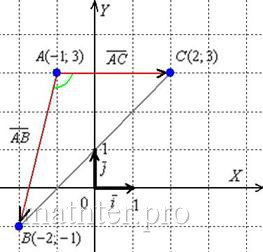
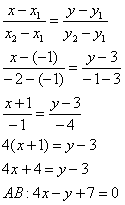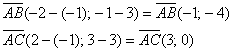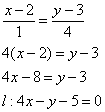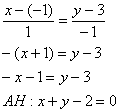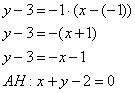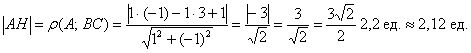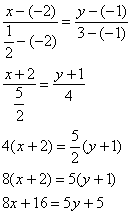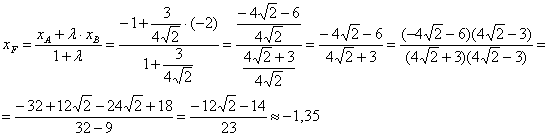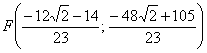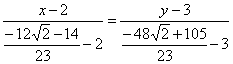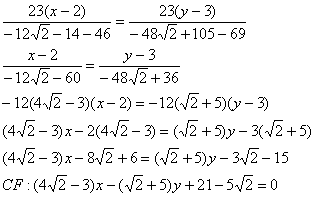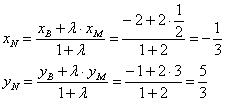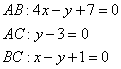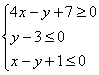Высота, проведенная к стороне АС, перпендикулярна к стороне АС по определению. Значит вектор высоты, обозначим его Х (х1,х2), должен быть перпендикулярным к вектору АС.

В качестве вектора высоты Х можно взять вектор
Х (с2-а2, -с1+а1). Чтобы проверить, что этот вектор перпендикулярен к вектору АС, надо посчитать скалярное произведение.
Получаем:
(с1-а1)*(с2-а2) + (с2-а2)*(-с1+а1) = 0
Раз скалярное произведение равно нулю, значит векторы перпендикулярны, что нам и нужно.

вектор a(2, -1, 1) вектор b (0, 4, 1)

задан 27 Янв ’14 18:40

Длины векторов легко находятся. Далее через скалярное произведение выражаем косинус угла. Зная косинус, находим синус. Через синус и длины выражаем площадь. Длина разности векторов — это противолежащая сторона. Поделив на неё удвоенную площадь, находим длину высоты.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC<2,2,2>
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

Уравнение высоты треугольника по координатам его вершин

Чтобы составить уравнение высоты треугольника по координатам его вершин нужно:

1. Составить уравнение прямой, на которой лежит высота треугольника:

Так как высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону, то угловые коэффициенты перпендикулярных прямых связаны записанной выше пропорцией.

Уравнение высоты треугольника по координатам его вершин

Составить уравнение высоты треугольника. Пример

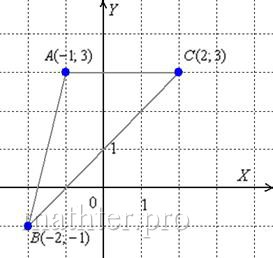
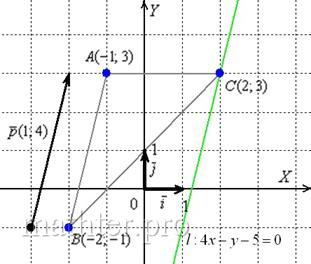
Дан треугольник АВС. Вершины треугольника имеют следующие координаты:

На сторону АС опущена высота ВН.

Составить уравнение высоты ВН.

Пример на составление уравнения высоты треугольника

Шаг 1

Составим уравнение прямой, проходящей через точки А и С.

Для этого воспользуемся уравнением прямой с угловым коэффициентом:

Подставим в это уравнение координаты точек А и С:

Уравнение стороны АС имеет вид:

Составить уравнение высоты треугольника. Шаг 1

Шаг 2

Так как прямые АС и ВН перпендикулярны, то, зная угловой коэффициент прямой АС, можем составить уравнение прямой ВН с угловым коэффициентом.

Итак, угловой коэффициент АС равен:

Отсюда, угловой коэффициент ВН будет равен:

Теперь можем записать уравнение высоты ВН:

Точка В(2,4) лежит на прямой ВН, значит, ее координаты удовлетворяют уравнению прямой ВН:

Таким образом, уравнение высоты ВН имеет вид:

Составить уравнение высоты треугольника. Шаг 2

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. источники: http://www.treugolniki.ru/uravnenie-vysoty-treugolnika/ http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Пример.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

Решение:

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

   

Таким образом, уравнение прямой BC —

   

Угловой коэффициент прямой, перпендикулярной BC,

   

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

   

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

   

Итак, уравнение высоты, проведённой к стороне BC:

   

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

   

Уравнение прямой AB:

   

Угловой коэффициент перпендикулярной ей прямой

   

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

   

Угловой коэффициент прямой, перпендикулярной AC,

   

Таким образом, уравнение перпендикулярной AC прямой имеет вид

   

Подставив в него координаты точки B(5;-3), найдём b:

   

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

   



2.9. Типовая задача с треугольником

Многие помнят из школы признаки равенства треугольников, признаки подобия треугольников и мучительное заучивание доказательств теорем. Как в

сердцАх сказал один мой одноклассник, «не понимаю, на### доказывать равенство треугольников, если и так видно, что они одинаковые». Мы тоже не

будем ничего доказывать, поскольку аналитическая геометрия рассматривает треугольник совсем с другой стороны.

Типовая задача, как правило, формулируется так: Даны три вершины треугольника. Требуется найти… много чего требуется

найти…. Повезёт, если будет пункта 3-4, но чаще всего их 5-6 и даже больше. И вам повезло – разберём всё! Или почти всё:

Задача 95

Даны вершины треугольника . Требуется:

1) составить уравнения сторон  и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить прямой , проходящей через точку  параллельно прямой ;
5) составить уравнение высоты и найти её длину;
6) вычислить площадь треугольника ;
7) составить уравнение медианы ;
8) найти точку пересечения .
и для особо опасных энтузиастов:
9) найти уравнение биссектрисы ;
10) найти центр тяжести  треугольника;
11) составить систему линейных неравенств, определяющих треугольник.

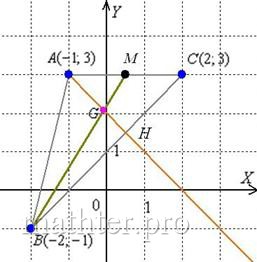
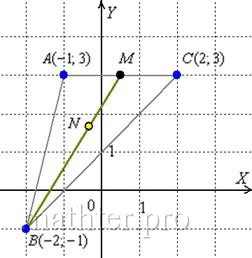
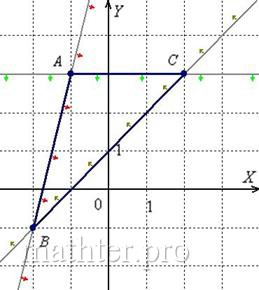
С чего начать решение? Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и

самопроверки всегда строим чертёж на черновике, не устану это рекомендовать:

Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1

см (2 тетрадные клетки). Всё хорошо видно, и расстояния удобно измерять линейкой.

Вперёд без страха и сомнений:

1) Составим уравнения сторон  и найдём их угловые

коэффициенты.
Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум

точкам.

Составим уравнение стороны  по точкам :

Для проверки мысленно либо на черновике подставляем координаты каждой точки в полученное уравнение.

Теперь

найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

Таким образом, угловой коэффициент:

Самостоятельно разбираемся со сторонами  и сверяемся, что

получилось:

2) Найдём длину стороны .  Используем соответствующую формулу для точек :

Сторону легко измерить обычной линейкой, хотя это не сильно строгая проверка 🙂

3) Найдём . Это Задача 31, повторим:

Используем формулу .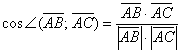
Найдём векторы:

Таким образом:
, и сам угол:
, ну что же, похоже на правду, желающие могут приложить транспортир, у кого

он есть.

Внимание! При выполнении этого пункта лучше не использовать формулы ориентированного угла

между прямыми, так как они всегда дают острый угол.

4) Составим уравнение прямой , проходящей через точку  параллельно прямой . Это стандартная задача, и мы ленимся отработать её вновь!

Из общего уравнения прямой  вытащим направляющий вектор .

Составим уравнение прямой  по точке  и направляющему вектору :

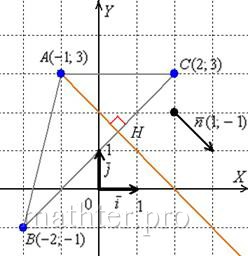
5) Составим уравнение высоты и найдём её длину.
Первую часть задания мы тоже решали:

Из уравнения стороны  снимаем вектор нормали . Уравнение высоты

 составим по точке  и направляющему вектору :

Обратите внимание, что координаты точки  нам не известны.

Иногда уравнение высоты находят из соотношения угловых коэффициентов перпендикулярных прямых: . В данном случае , тогда: . Уравнение высоты  составим по точке  и угловому коэффициенту :

Длину высоты можно найти двумя способами.

Существует окольный путь:

а) находим  – точку

пересечения высоты и стороны ;

б) находим длину отрезка  по двум

известным точкам.

Но зачем? – ведь есть удобная формула расстояния от точки  до прямой :

6) Вычислим площадь треугольника. Используем «школьную» формулу:

7) Уравнение медианы  составим в два шага:

а) Найдём точку  – середину стороны . Используем формулы координат середины отрезка.

Известны концы , и тогда середина:

б) Уравнение медианы  составим по точкам :

 – для проверки подставим координаты точек .

8) Найдём точку пересечения  высоты и медианы:
      в

Первое уравнение умножили на 5, складываем их почленно:
 – подставим в первое уравнение:

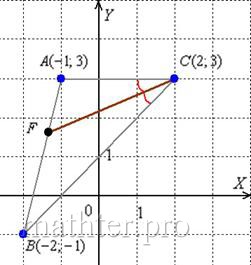
9) Биссектриса делит угол пополам:

Из свойств биссектрисы внутреннего угла следует соотношение длин следующих отрезков:

Длины сторон уже найдены в предыдущих пунктах: .

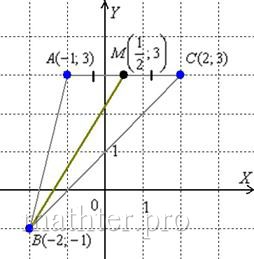
Таким образом, . Координаты точки  найдём по формулам деления отрезка в данном отношении. Да,

параметр «лямбда» получился просто сказочным, ну а кому сейчас легко? Точки  известны и понеслась нелёгкая:

Примечание: на последнем шаге я умножил числитель и знаменатель на сопряжённое выражение  – чтобы использовать формулу  и

избавиться от иррациональности в знаменателе.

Разбираемся со второй координатой:

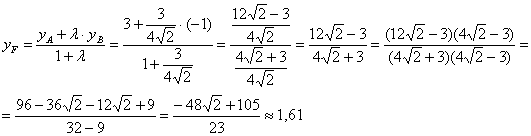
аким образом:  

И предчувствие вас не обмануло, уравнение биссектрисы  составим по точкам  по формуле :

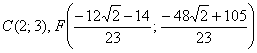
обратите внимание на технику упрощений:

Проверил, всё сходится. На практике, конечно, вычисления почти всегда будут проще. Никого не хотел запугать, так уж получилось =)

10) Найдём центр тяжести треугольника.

Но сначала поймём, что такое центр тяжести плоской фигуры. Мысленно вырежьте из тонкого однородного картона любую фигуру. …Почему-то фигура зайца

в голову пришла. Так вот: если слегка насадить данную фигуру центром тяжести (какой же я изверг =)) на вертикально расположенную иголку, то

теоретически фигура не должна свалиться.

Центром тяжести треугольника является точка пересечения его медиан. В треугольнике три медианы и пересекаются они в одной точке.

Из пункта 7 нам уже известна одна из медиан: .  Как решить задачу?

Напрашивается очевидный алгоритм: можно найти уравнение второй медианы (любой из двух оставшихся) и точку пересечения этих медиан. Но есть путь

короче! Нужно только знать полезное свойство:

Точка пересечения медиан делит каждую из медиан в

отношении , считая от вершины треугольника. Поэтому справедливо

отношение
Нам известны концы отрезка – точки  и .
По формулам деления отрезка в данном отношении:

Таким образом, центр тяжести треугольника:
И заключительный пункт задачи, для освоения которого нужно уметь решать недавно разобранные линейные

неравенства:

11) Составим систему линейных неравенств, определяющих треугольник.

Для удобства я перепишу найденные уравнения сторон:

Рассмотрим прямую . Треугольник лежит в полуплоскости, где находится

вершина . Составим вспомогательный многочлен  и вычислим его значение в точке : . Поскольку сторона  принадлежит треугольнику, то неравенство будет нестрогим:

Внимание! Если вам не понятен этот алгоритм, то обратитесь к

Задаче 90.

Рассмотрим прямую . Треугольник расположен ниже данной прямой, поэтому

очевидно неравенство .

И, наконец, для  составим многочлен , в который подставим координаты точки : .
Таким образом, получаем третье неравенство: .

Итак, треугольник  определяется следующей системой линейных

неравенств:

Готово.

Какой можно сделать вывод?

Многие задачи аналитической геометрии прозрачны и просты,
главное, не допустить вычислительных ошибок.

Следует отметить, что по настоящему трудные задачи в аналитической геометрии встречаются редко, и вы справитесь практически с любой из них!

Главное, придерживаться методики решения и проявить маломальское упорство.

Ну что, может ещё задачку? Да ладно, не надо стесняться, я же по глазам вижу, что хотите =) 

Но сейчас на очереди другая увлекательная тема, продолжаем изучать геометрию плоскости:

3.1. Алгебраическая линия и её порядок

2.8. Как научиться решать задачи по геометрии?

| Оглавление |



Автор: Aлeксaндр Eмeлин