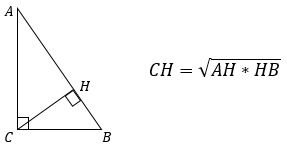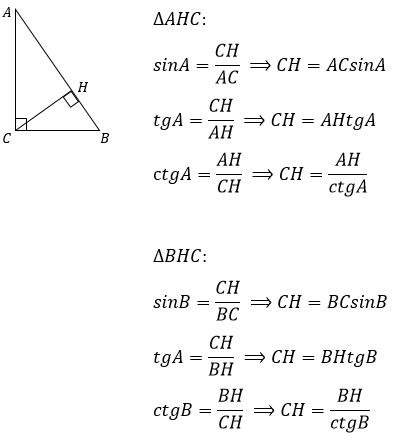Как найти высоту треугольника проведенную к гипотенузе - Сайт, где вы сможете решить свои вопросы

Высота прямоугольного треугольника, проведенная к гипотенузе

Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.

Поэтому представляю вашему вниманию основные формулы для ее нахождения.

Начну с самой важной.

1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.

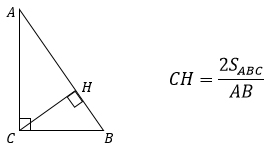
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.

Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.

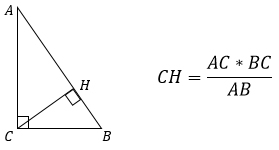
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.

Эта формула получится из второй если заменить площадь на половину произведения катетов.

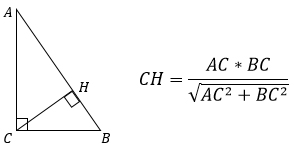
Т.к. АВ – гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:

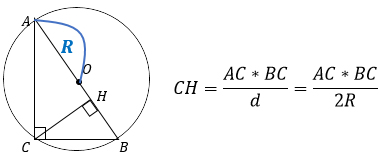
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).

Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.

5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.

Надеюсь, что данная статья оказалась полезной!)

Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.

Источник

Здравствуйте, уважаемые читатели. В этой статье продолжим разбор задач из 23 задания ОГЭ по математике.

Задача

Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведённую к гипотенузе

Построим чертеж и напишем условие для задачи

Задание №23. Найти высоту проведенную к гипотенузе.

Решение

1) Высота треугольника СН входит в формулу площади треугольника, поэтому запишем общую формулу вычисления площади треугольника и формулу вычисления площади прямоугольного треугольника:

Общая формула вычисления площади треугольника

Формула вычисления площади прямоугольного треугольника

2) Поскольку площадь треугольника при вычислении этими формулами будет одинакова, тогда приравняем эти формулы и выразим высоту СН, получаем:

3) Найдем значение АВ по теореме Пифагора:

4) Найдем значение СН

Ответ 12

Вам понравился материал? Поблагодарить легко! Будем весьма признательны, если поделитесь этой статьей в социальных сетях, поставите лайк и подпишитесь на мой блог

Источник

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла

a, b – катеты

с – гипотенуза

c₁, c₂ – отрезки полученные от деления гипотенузы, высотой

α, β – углы при гипотенузе

Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

Подробности

Опубликовано: 09 октября 2011

Обновлено: 13 августа 2021

Источник

как найти высоту проведённую к гипотенузе

Знаток

(302),
закрыт

12 лет назад

cHin-cHillo

Гений

(85865)

12 лет назад

Смотря что известно.
Если известны катеты и гипотенуза, , то высота = произведение катетов, делить на гипотенузу.
А если известны два отрезка, на которые гипотенуза делится высотой, то высота – это среднее геометрическое от этих двух отрезков.

Источник

Высота прямоугольного треугольника, проведенная к гипотенузе, может быть найдена тем или иным способом в зависимости от данных в условии задачи.

Длина высоты прямоугольного треугольника, проведенной к гипотенузе, может быть найдена по формуле

или, в другой записи,

$[A{K^2} = BK cdot KC,]$

где BK и KC — проекции катетов на гипотенузу (отрезки, на которые высота делит гипотенузу).

Высоту, проведенную к гипотенузе, можно найти через площадь прямоугольного треугольника. Если применить формулу для нахождения площади треугольника

$[S = frac{1}{2}a cdot {h_a}]$

(половина произведения стороны на высоту, проведенную к этой стороне) к гипотенузе и высоте, проведенной к гипотенузе, получим:

$[{S_{Delta ABC}} = frac{1}{2}BC cdot AK.]$

Отсюда можем найти высоту как отношение удвоенной площади треугольника к длине гипотенузы:

$[AK = frac{{2{S_{Delta ABC}}}}{{BC}}.]$

Так как площадь прямоугольного треугольника равна половине произведения катетов:

$[{S_{Delta ABC}} = frac{1}{2}AB cdot AC,]$

$[AK = frac{{2 cdot frac{1}{2}AB cdot AC}}{{BC}} = frac{{AB cdot AC}}{{BC}}.]$

То есть длина высоты, проведенной к гипотенузе, равна отношению произведения катетов к гипотенузе. Если обозначить длины катетов через a и b, длину гипотенузы — через с, формулу можно переписать в виде

$[{h_c} = frac{{ab}}{c}.]$

Так как радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы, длину высоты можно выразить через катеты и радиус описанной окружности:

$[{h_c} = frac{{ab}}{{2R}}.]$

Поскольку проведенная к гипотенузе высота образует еще два прямоугольных треугольника, ее длину можно найти через соотношения в прямоугольном треугольнике.

Из прямоугольного треугольника ABK

Из прямоугольного треугольника ACK

Длину высоты прямоугольного треугольника можно выразить через длины катетов. Так как

$[{h_c} = frac{{ab}}{c},]$

по теореме Пифагора

$[{c^2} = {a^2} + {b^2}]$

$[{h_c} = frac{{ab}}{{sqrt {{a^2} + {b^2}} }}.]$

Если возвести в квадрат обе части равенства:

$[{h_c}^2 = frac{{{a^2}{b^2}}}{{{a^2} + {b^2}}},]$

можно получить еще одну формулу для связи высоты прямоугольного треугольника с катетами:

$[frac{1}{{{h_c}^2}} = frac{{{a^2} + {b^2}}}{{{a^2}{b^2}}} = frac{{{a^2}}}{{{a^2}{b^2}}} + frac{{{b^2}}}{{{a^2}{b^2}}} = frac{1}{{{a^2}}} + frac{1}{{{b^2}}}.]$

Источник

Высота прямоугольного треугольника, проведенная к гипотенузе

Задача

как найти высоту проведённую к гипотенузе

Вам также может понравиться

Как найти телефон судебного пристава по адресу

Как найти сохранения в тотал вар

Как найти текст в microsoft word

Добавить комментарий Отменить ответ