Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы тетраэдра
Для расчёта всех основных параметров тетраэдра воспользуйтесь калькулятором.
Свойства тетраэдра
- Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед
- Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы – пополам
- Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер
Виды тетраэдров
-
Правильный тетраэдр – это такая правильная треугольная пирамида, каждая из граней которой оказывается равносторонним треугольником.
У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину - Равногранный тетраэдр – это такой тетраэдр, у которого все грани треугольники равны
- Ортоцентрический тетраэдр – это такой тетраэдр, у которого каждая высота, опущенная из вершины на противоположную грань, пересекается с остальными высотами в одной точке
- Прямоугольный тетраэдр – это такой тетраэдр, у которого каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине
-
Каркасный тетраэдр – это такой тетраэдр, который соответствует следующим условиям:
- есть сфера, которая касается каждого ребра
- суммы длин ребер, что скрещиваются равны
- суммы двугранных углов при противоположных ребрах равны
- окружности, которые вписаны в грани, попарно касаются
- каждый четырехугольник, образующийся на развертке тетраэдра — описанный
- перпендикуляры, поставленные к граням из центров окружностей, в них вписанных, пересекаются в одной точке
- Инцентрический тетраэдр – это такой тетраэдр, у которого отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке
Формула высоты тетраэдра
$$
AO = {sqrt{2 over 3}} * a
$$
Формула объёма тетраэдра
$$
V = {sqrt{2} over 12} * a^3
$$
Основные формулы для правильного тетраэдра
-
Формула площади
$$
S = a^2 * sqrt{3}
$$ -
Радиус вписанной сферы, Rвпис
$$
R_{впис} = a * {sqrt{6} over 12}
$$ -
Радиус описанной сферы, Rопис
$$
R_{опис} = a * {sqrt{6} over 4}
$$
This is equivalent to finding the distance between a point and a plane. The plane is defined by the three points comprising the base. There is a detailed explanation on determining a plane given three points and finding the minimal distance between a point and a plane.
Disclaimer: I don’t know Unity3D, so I’m kind of making up the syntax below. If something’s not clear, let me know; otherwise you’re going to have to translate into something that will compile using the Unity3D API.
The first step is to determine the equation of the plane given three points. The plane normal is given by:
n = cross(baseB-baseA, baseC-baseA);
n = n / norm(n);
Where cross returns the cross product of the two arguments, and norm returns the l2 norm (vector magnitude). The offset term in the plane equation is given by:
d = -n.x*baseA.x - n.y*baseA.y - n.z*baseA.z;
This will result in the plane equation:
n.x*X + n.y*Y + n.z*Z + d = 0
To find the distance between the top and the plane is then given by
D = dot(n, top) + d;
where dot is the dot product of the unit vector normal of the plane n and top and d is defined earlier. When D > 0 top is “above” the plane defined by the three base points where the normal points “up”. When D < 0 the top is below the plane. So, in your case, you may want to take the absolute value of D to get the distance.
Высота тетраэдра, формула
 |
Высота тетраэдра — равна корню квадратному из двух третьих, помноженному на длину ребра тетраэдра [ h = sqrt{frac{2}{3}} a ] (h – высота тетраэдра, a – ребро тетраэдра) |
Вывод формулы высоты тетраэдра
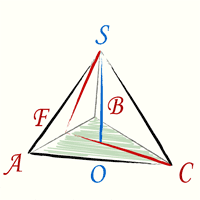
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке
красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
[CF = FS = frac{sqrt{3}}{2}a ; CS = a ]
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
[p = frac{1}{2}(a + afrac{sqrt{3}}{2} + afrac{sqrt{3}}{2}) ]
[p = frac{1}{2} a (1 + sqrt{3}) ]
[h = 2 frac{ sqrt{p(p-a)(p-(afrac{sqrt{3}}{2}))(p-(afrac{sqrt{3}}{2}))}}{afrac{sqrt{3}}{2}}]
[h = 2 frac{sqrt{(frac{a}{2})^4 (sqrt{3}+1) (sqrt{3}-1)}}{afrac{sqrt{3}}{2}} = sqrt{frac{2}{3}} a ]
Вычислить, найти высоту тетраэдра по формуле(1)
Высота тетраэдра |
стр. 283 |
|---|
можно ли найти высоту тетраэдра, зная все ребра (он не правильный)
Андрей Карельский
Мастер
(1202),
на голосовании
7 лет назад
Голосование за лучший ответ
Nazereke Bugybay
Ученик
(155)
7 лет назад
Если тетраэдр прямой, то можно найти радиус описанной окружности и дальще по пифагору высоту. Удачи!
Татьяна КозловаИскусственный Интеллект (332200)
7 лет назад
Что такое прямой тетраэдр?
Nazereke Bugybay
Ученик
(155)
То есть все ребра наклонены под одним углом к оснаванию
Татьяна Козлова
Искусственный Интеллект
(332200)
7 лет назад
Если все 6, то можно. Если только боковые, то нет.
Андрей КарельскийМастер (1202)
7 лет назад
мне известны все 6, как найти высоту? ПРИЗМА НЕ ПРАВИЛЬНАЯ И НЕ ПРЯМАЯ
Татьяна Козлова
Искусственный Интеллект
(332200)
Пардон, призма или тетраэдр?
Похожие вопросы
Высота тетраэдра, формула
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:
Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).
Свойства тетраэдра, виды и формулы
Тетраэдр в переводе с греческого означает «четырехгранник». Эта геометрическая фигура обладает четырьмя гранями, четырьмя вершинами и шестью ребрами. Грани представляют собой треугольники. По сути, тетраэдр — это треугольная пирамида. Первые упоминания о многогранниках появились еще задолго до существования Платона.
Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.
Элементы четырехгранника
 Вам будет интересно: Петрозаводский педагогический колледж: стать специалистом заочно
Вам будет интересно: Петрозаводский педагогический колледж: стать специалистом заочно
Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.
Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.
Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.
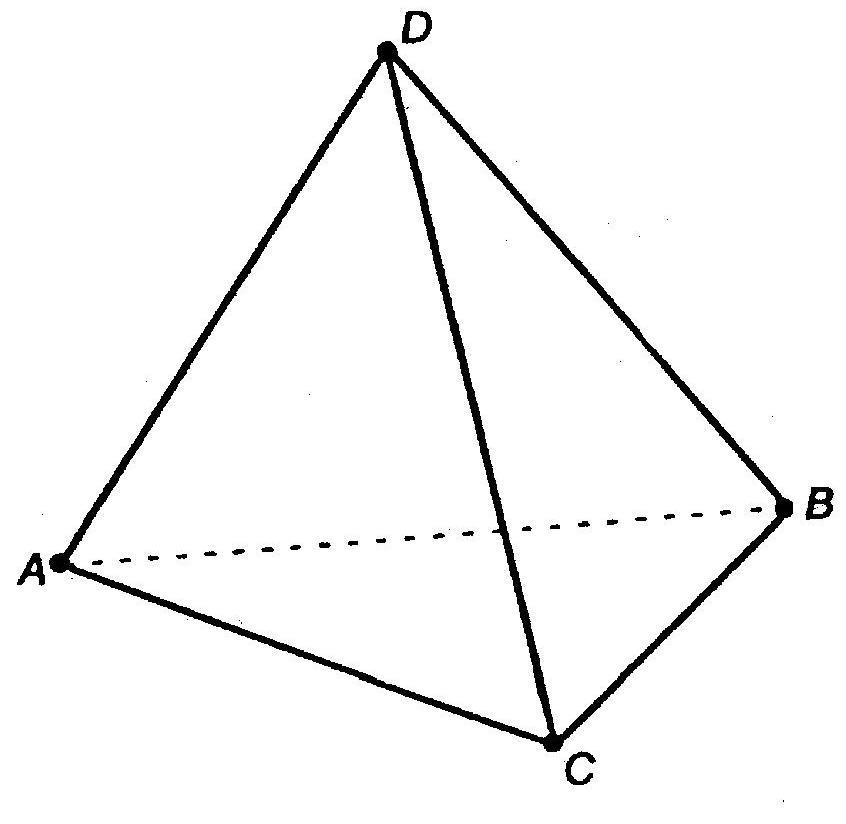
Свойства тетраэдра
1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.
2) Отличительным свойством тетраэдра является то, что медианы и бимедианы фигуры встречаются в одной точке. Важно, что последняя делит медианы в отношении 3:1, а бимедианы — пополам.
3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.
Виды тетраэдра
Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:
- правильным, то есть в основании равносторонний треугольник;
- равногранным, у которого все грани одинаковы по длине;
- ортоцентрическим, когда высоты имеют общую точку пересечения;
- прямоугольным, если плоские углы при вершине нормальные;
- соразмерным, все би высоты равны;
- каркасным, если присутствует сфера, которая касается ребер;
- инцентрическим, то есть отрезки, опущенные из вершины в центр вписанной окружности противоположной грани, имеют общую точку пересечения; эту точку именуют центром тяжести тетраэдра.
Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.
Исходя из названия, можно понять, что так он называется потому, что грани являют собой правильные треугольники. Все ребра этой фигуры конгруэнтны по длине, а грани — по площади. Правильный тетраэдр — это один из пяти аналогичных многогранников.
Формулы четырехгранника
Высота тетраэдра равна произведению корня из 2/3 и длины ребра.
Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.
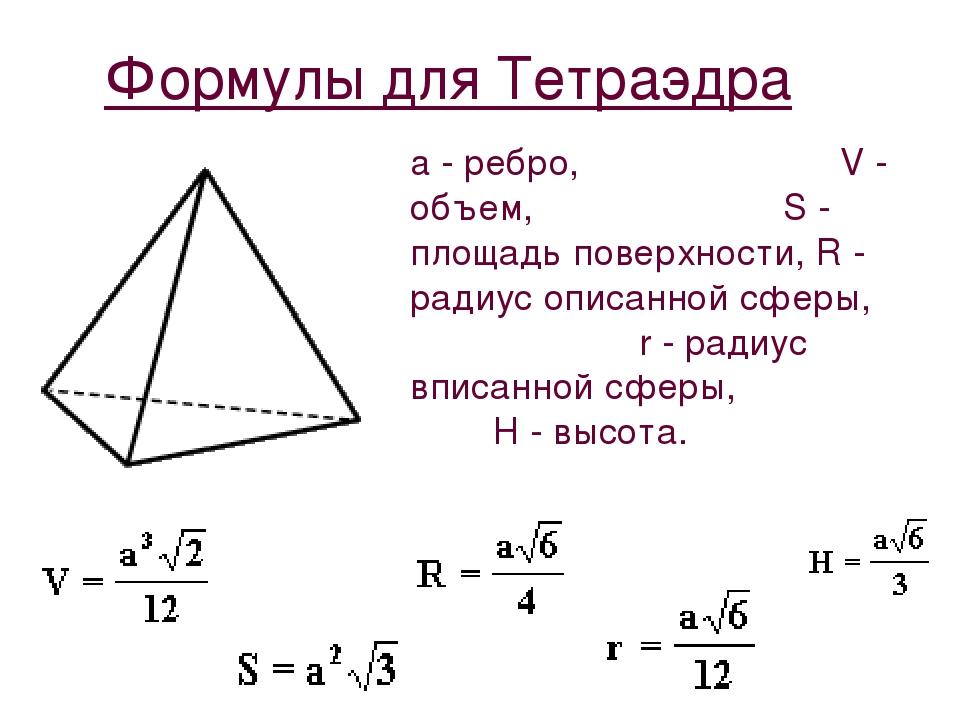
Остальные формулы для расчета площади и радиусов окружностей представлены выше.
Как найти высоту тетраэдра
Основание можно изобразить любым треугольником ABC. Центр основания изображается точкой О пересечения медиан. (Затем две из этих медиан, как не имеющие значения для решения задачи, можно стереть, оставив только точку О на медиане АЕ).
Решение. Имеем V = 1 /3 • Socн. • Н = 1 /3 • 1 /4a 2 √ 3H . Связь между а и Н найдем из треугольника AOD, где AD = a, а АО есть радиус R, круга, описанного около основания, так что a = R√ 3 .
Подставляя a 2 = 3 /2 H 2 в выражение V, получаем V = √ 3 /8 H 3 .