как найти высоту усеченного конуса. Если исвестны два радиуса оснований и образующая.
Ученик
(235),
закрыт
12 лет назад
PaulSand
Гуру
(4315)
12 лет назад
h=sqrt(l^2-(R-r)^2) (sqrt – квадратный корень из выражения в скобках, h – высота конуса, R, r – радиусы нижнего и верхнего оснований соответственно, l – образующая)
злато-серебро
Оракул
(87912)
12 лет назад
По теореме Пифагора из треугольника АВМ. , где АВ – образующая, ВМ – высота, АМ – половина разности между радиусами оснований. Представь этот усеченный конус в разрезе. Это трапеция.
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы усеченного конуса
Для расчёта всех основных параметров усеченного конуса воспользуйтесь калькулятором.
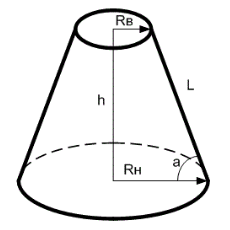
Объём усеченного конуса
$$
V = {1 over 3} * pi * h * (R_Н^2 + R_Н * R_В + R_В^2)
$$
Площадь боковой поверхности усечённого конуса
$$
S_Б = pi * (R_Н + R_В) * L
$$
Высота усеченного конуса через образующую и радиусы оснований
$$
h = sqrt{L^2 – (R_Н – R_В)^2}
$$
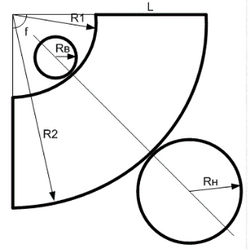
Развертка (выкройка) усеченного конуса
Длина образующей, L
$$
L = sqrt{(R_Н – R_В)^2 + h^2}
$$
$$
R_1 = {L * R_В over R_Н – R_В}
$$
$$
R_2 = L + R_1
$$
Угол ∠ f
$$
∠ f = 360° * {R_Н – R_В over L}
$$
Как найти высоту усеченного конуса
Если вблизи вершины конуса провести сечение, можно получить идентичную, но иную по форме и размерам фигуру, называемую усеченным конусом. Она имеет не один, а два радиуса, один из которых меньше другого. Как и у обычного конуса, у этой фигуры имеется высота.
Инструкция
Перед нахождением высоты усеченного конуса ознакомьтесь с его определением. Усеченным конусом называется фигура, которая образована в результате перпендикулярного сечения плоскости обыкновенного конуса, при условии, что это сечение параллельно его основанию. Данная фигура имеет три характеристики:
– r1 – наибольший радиус;
– r2 – наименьший радиус;
– h – высота.Кроме того, как и у обычного конуса, у усеченного имеется так называемая образующая, обозначаемая буквой l. Обратите внимание на внутреннее сечение конуса: оно представляет собой равнобедренную трапецию. Если ее вращать вокруг своей оси, получится усеченный конус с теми же параметрами. В данном случае, линия, делящая равнобедренную трапецию на две других, меньшего размера, совпадает с осью симметрии и с высотой конуса. Другая боковая сторона является образующей конуса.
Зная радиусы конуса и его высоту, можно найти его объем. Он вычисляется следующим образом:V=1/3πh(r1^2+r1*r2+r2^2)Если известны два радиуса конуса, а также его объем, этого достаточно, чтобы найти и высоту фигуры:h=3V/π(r1^2+r1*r2+r2^2).В том случае, если в условии задачи даны диаметры окружностей, а не радиусы, данное выражение приобретает несколько иной вид:h=12V/π(d1^2+d1*d2+d2^2).
Зная образующую конуса и угол между ней и основанием данной фигуры, также можно найти ее высоту. Для этого нужно из другой вершины трапеции провести проекцию к большему радиусу, чтобы получился небольшой прямоугольный треугольник. Проекция будет равна высоте усеченного конуса. Если известна образующая l и угол, высота определите по следующей формуле:h=l*sinα.
Если по условию задачи известна лишь площадь сечения конуса, найти высоту невозможно, если неизвестны оба его радиуса.
Источники:
- как найти высоту конуса зная диаметр
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
-
Радиус и высота усеченного конуса
Радиусы оснований усеченного конуса позволяют вычислить диаметры оснований, их периметр и площадь по стандартным формулам для окружности с учетом двух различных радиусов усеченного конуса.
d=2r
D=2R
p=2πr
P=2πR
S_r=πr^2
S_R=πR^2Поскольку нам известна высота усеченного конуса, но для дальнейших вычислений нужна также и образующая, то нужно построить трапецию во внутреннем пространстве усеченного конуса таким образом, чтобы она соединяла указанные величины через радиусы. В такой трапеции, поскольку она прямоугольная, можно построить дополнительный прямоугольный треугольник и найти в нем апофему по теореме Пифагора, а также углы при основаниях и апофеме, через тригонометрические отношения
l=√(h^2+(R-r)^2 )
tanβ=h/(R-r)
α=180°-βПлощадь боковой поверхности усеченного конуса зависит от радиусов оснований конуса и от апофемы, которую можно найти, зная высоту, по формуле приведенной выше. Площадь полной поверхности состоит из площади боковой поверхности и площади двух оснований усеченного конуса.
S_(б.п.)=πl(R+r)
S_(п.п.)=S_(б.п.)+S_r+S_R=πl(R+r)+πr^2+πR^2Найти объем усеченного конуса, зная высоту и радиусы оснований, достаточно просто, поскольку стандартная формула не предполагает других элементов расчета.
V=πh/3(R^2+rR+r^2)
Online geometry calculator which is used to find the height of a frustum of a right circular cone with the known values.
Find the Height of a Frustum of a Right Circular Cone
Online geometry calculator which is used to find the height of a frustum of a right circular cone with the known values.
Code to add this calci to your website 

Formula:

h=√(m2 – (R-r))
Where,
h = Height
m = Generatrix (Slant Height)
R = Radius (R)
r = Radius (r)
Related Calculators:
- Radius Of A Circumscribed Circle Calculator
- Total Surface Area Of A Right Circular Cylinder Calculator
- Total Surface Area Of A Right Circular Cylinder Calculator
- Scale Factor Of Frustum Of Right Circular Cone Calculator
- Lateral Surface Area Of Frustum Of Cone Calculator
- Surface Area Of A Dodecahedron Calculator