Высота правильной треугольной пирамиды.
Основание правильной пирамиды представляет собой правильный многоугольник. Так как мы имеем дело с треугольной пирамидой, то её основанием будет равносторонний треугольник.

Чтобы найти высоту пирамиды SO, достаточно вспомнить, что:
1) AO = BO = CO = R = a√3 / 3. (св-во равностороннего треугольника).
2) SB = AB. (боковое ребро равно длине стороны основания).
По теореме Пифагора высота SO равна:
SO = √(SB² – OB²) = √(a² – a²/3) = √(a²(1 – 1/3)) = √(a² * (2/3) = a√(2/3).
Итак, высота правильной треугольной пирамиды (H) равна произведению длины ребра (a) на корень из 2/3:

Высоту пирамиды также можно найти из формулы объёма:
V = 1 / 3 Sосн * H.
Так как основание пирамиды – это равносторонний треугольник, то Sосн = a² * √3 / 4.
Отсюда V = a² * √3 * H / 12 = a² * H / 4√3.
Остаётся выразить высоту:
V * 4√3 = a² * H.
H = V * (4√3 / a²).
Высота правильной треугольной пирамиды (H) равна дроби – в числителе произведение объёма пирамиды (V) на 4√3, в знаменателе – квадрат ребра (a).

Если же в условии задачи уже известна площадь основания, то высоту найти ещё проще:
H = 3 * V / Sосн.
Пример
Сторона основания правильной треугольной пирамиды равна 4 см, объём равен 10√3.
Нужно найти высоту пирамиды.
Воспользуемся вышеприведённой формулой:
H = V * (4√3 / a²) = 10√3 * 4√3 / 16 = 120 / 16 = 7,5 см.
Главная » Образование » Школа » Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
Как найти высоту в пирамиде: треугольной, четырехугольной, правильной
![]()
33774 Просмотров 0

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.
В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.
Содержание этой статьи:
- Теория
- Часто задаваемые вопросы
- Типичные ошибки на ЕГЭ
- Полезные советы
Теория
Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019
Правильная пирамида
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.
Для решения задач понадобится знать теоремы равнобедренного треугольника:
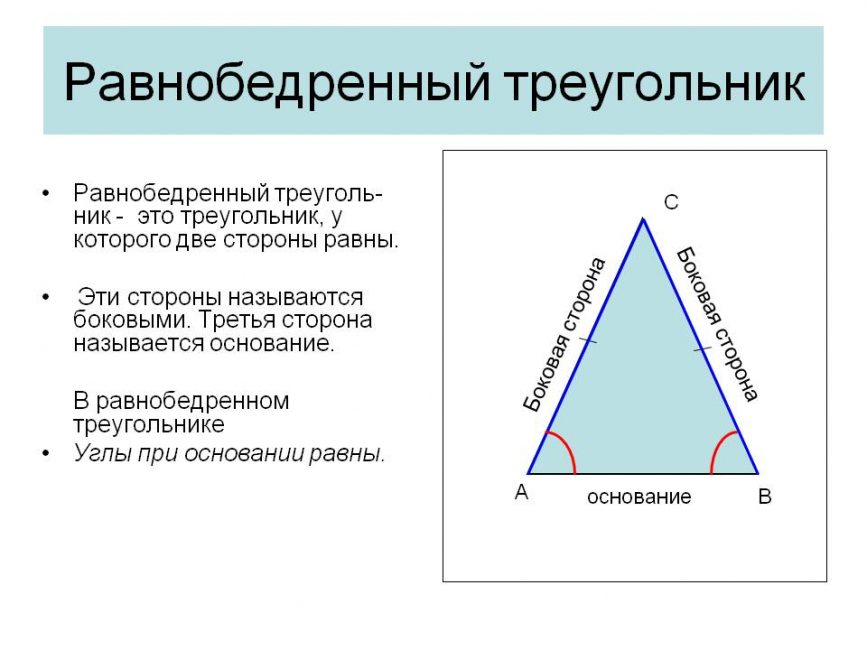
Равнобедренный треугольник
Основные свойства
1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.
2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.
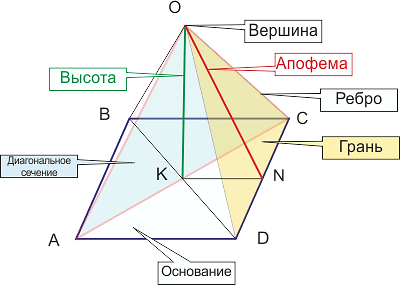
Пирамида
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Четырехугольная пирамида
Треугольная пирамида
Читайте также: Как решать задачи по математике 5 класс
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
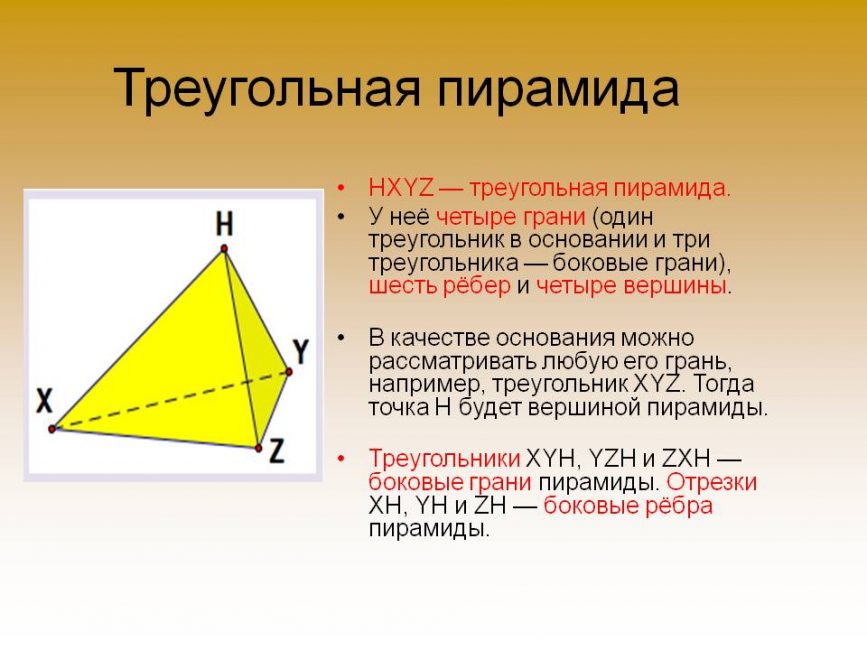
Треугольная пирамида
Необходимые знания для нахождения высоты
1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).
2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.
3Что такое правильные многоугольники: виды, свойства, формулы.
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
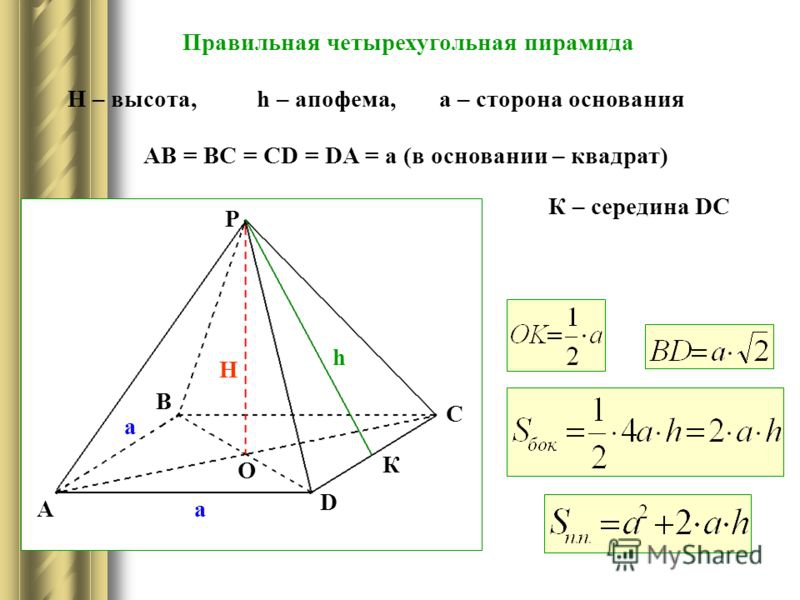
Формулы
Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:
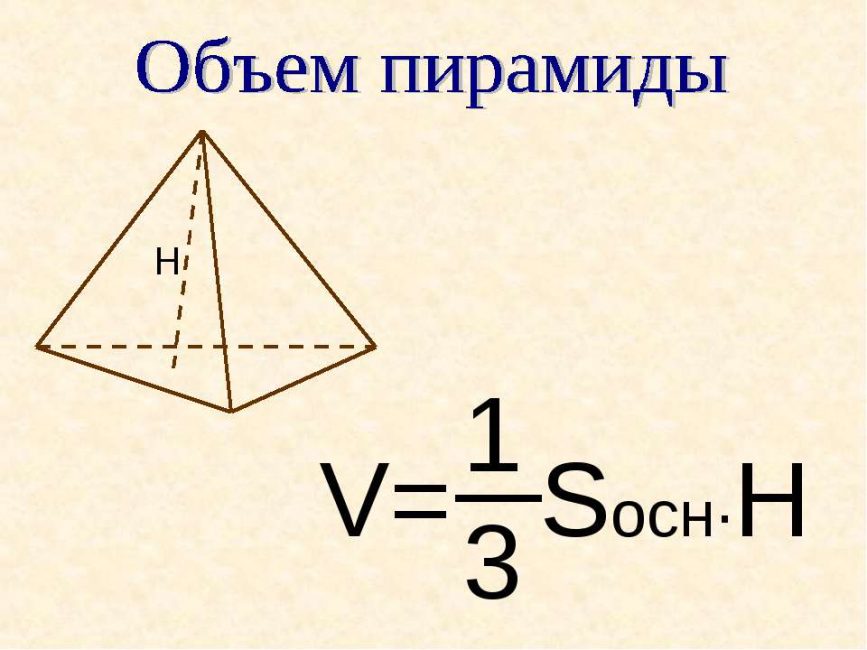
Объем пирамиды
ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида
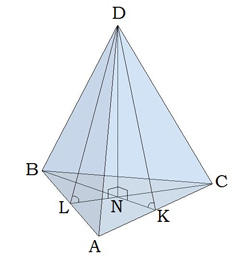
Треугольная пирамида
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Ответ: 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Ответ: 6
Четырехугольная пирамида
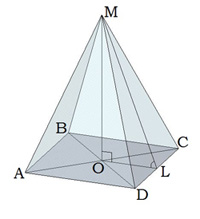
Четырехугольная пирамида
Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
OL = ½*12 = 6
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
MO = 8
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Ответ: 36
Задача 4
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.
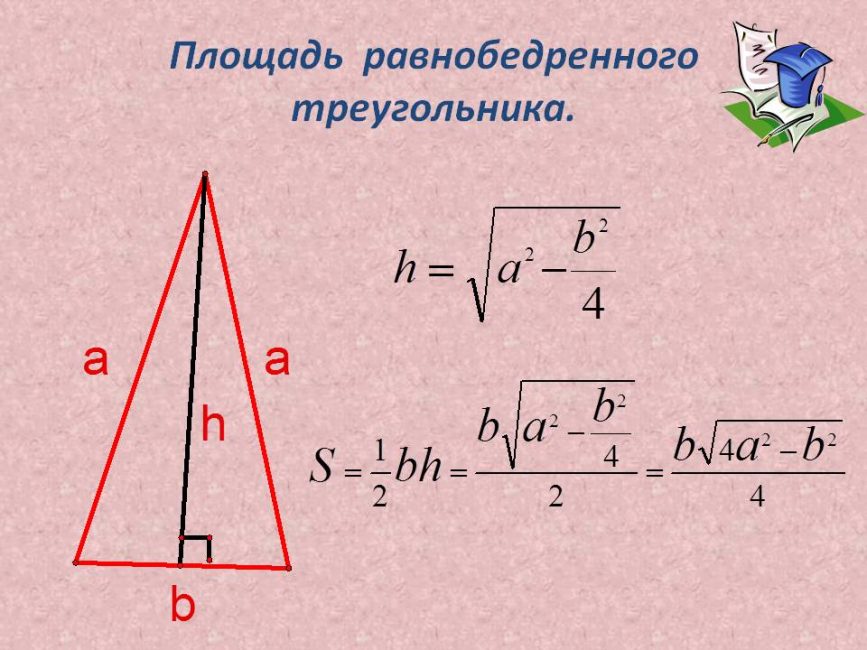
Площадь равнобедренного треугольника
36 = ½ * 4 *h
36 = 2h
H = 18
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Ответ: 12
Часто задаваемые вопросы
1Как понять, что пирамида правильная, если в условии это не указано?
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
2Могут ли быть указаны в задании лишние данные?
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.
4Как можно быстро изучить стереометрию?
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
4Как искать высоту, если известен объем?
Если выразить высоту через формулу объема, то получится следующее:
H = (3*V)/ S;
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
H = 3*70/30 = 7см
Типичные ошибки на ЕГЭ
Незнание темы
Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.
Отсутствие проверки
Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.
Задачи под копирку
Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.
Запись
Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.
Подсчеты в уме
На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается. Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.
Незнание структуры экзамена
Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно. Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.
Поспешные решения
В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Незнание степеней числа
В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
6.5 Total Score
Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи!
Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Достоверность информации
8.5
Актуальность информации
7.5
ПЛЮСЫ
- Благодаря доступной информации можно легко научиться решать задачи по геометрии
МИНУСЫ
- Необходимы знания математики
Добавить отзыв
Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.
В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.
Содержание этой статьи:
Теория
Правильная пирамида
Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.
Для решения задач понадобится знать теоремы равнобедренного треугольника:

Основные свойства

Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Треугольная пирамида
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Необходимые знания для нахождения высоты
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты

Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:

ВИДЕО: Примеры решения задач
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида

Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Четырехугольная пирамида

Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Задача 4
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

Площадь равнобедренного треугольника
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Часто задаваемые вопросы
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
Если выразить высоту через формулу объема, то получится следующее:
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
Типичные ошибки на ЕГЭ
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи! Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Пирамида. Правильная пирамида
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

Данный видеоурок поможет пользователям получить представление о теме Пирамида. Правильная пирамида. На этом занятии мы познакомимся с понятием пирамиды, дадим ей определение. Рассмотрим, что такое правильная пирамида и какими свойствами она обладает. Затем докажем теорему о боковой поверхности правильной пирамиды.
Сфера, вписанная в пирамиду

Биссекторная плоскость. Основное свойство биссекторной плоскости
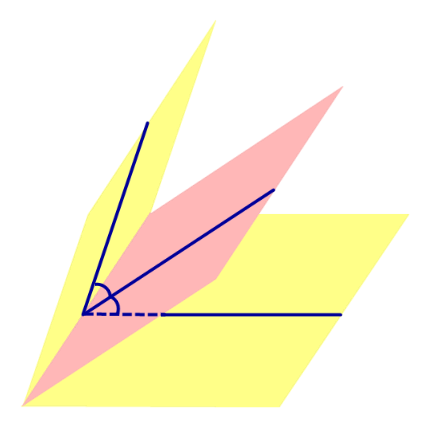
Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).
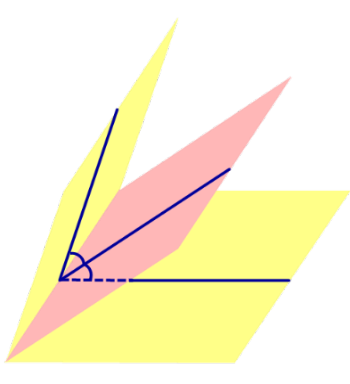
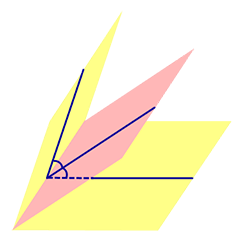
Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.
Доказательство. Рассмотрим произвольную точку O, расположенную внутри двугранного угла, и проведем через эту точку плоскость δ , перпендикулярную к ребру AB двугранного угла (рис. 2).
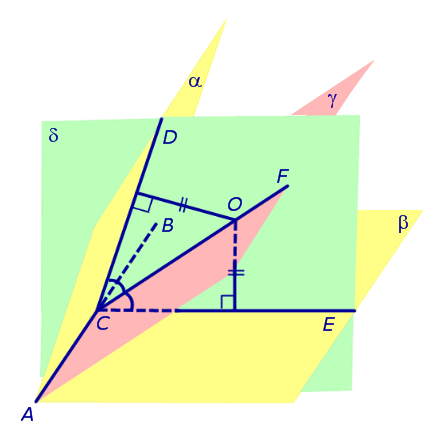
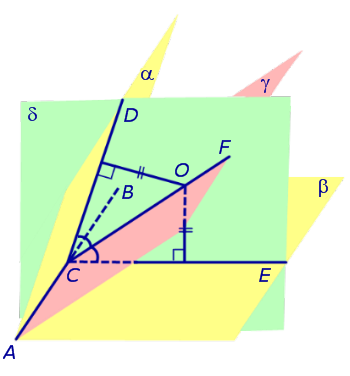
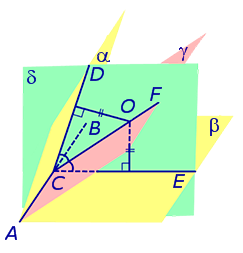
Плоскость δ пересекает ребро AB двугранного угла в точке C, а грани двугранного угла α и β по лучам CD и CE соответственно. Угол DCE является линейным углом двугранного угла. Биссекторная плоскость γ пересекает плоскость δ по биссектрисе CF линейного угла DCE .
Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.
Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).
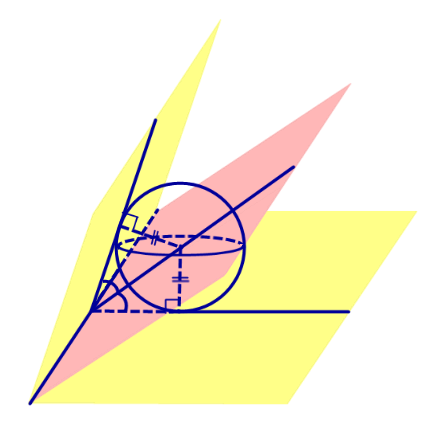
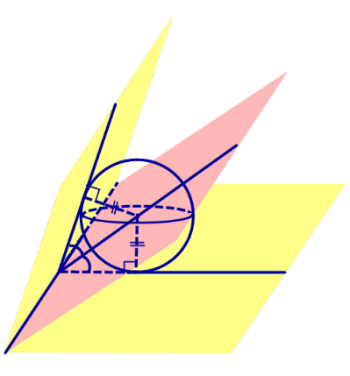

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы
Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).
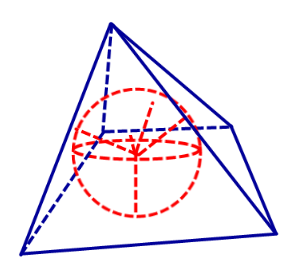

Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.
Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.
Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.
Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.
Рассмотрим несколько типов пирамид, в которые можно вписать сферу.
Утверждение 2. Если у пирамиды SA1A2 . An основание O перпендикуляра, опущенного из вершины S на плоскость основания пирамиды, лежит внутри многоугольника A1A2 . An , а все боковые грани пирамиды наклонены под одним и тем же углом к плоскости основания пирамиды, то в такую пирамиду можно вписать сферу.
Доказательство. Пусть все боковые грани пирамиды наклонены к плоскости основания под углом φ , а высота пирамиды равна h. Рассмотрим, например, боковую грань SA1A2 и проведем в ней высоту SB (рис. 5).
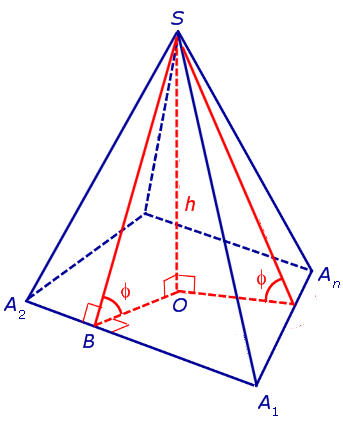
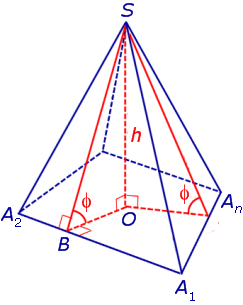
По теореме о трех перпендикулярах отрезок OB перпендикулярен ребру A1A2 . Следовательно, угол SBO является линейным углом двугранного угла между боковой гранью SA1A2 и плоскостью основания пирамиды и равен φ. Биссекторная плоскость этого двугранного угла пересекает высоту пирамиды в точке O’ (рис. 6).
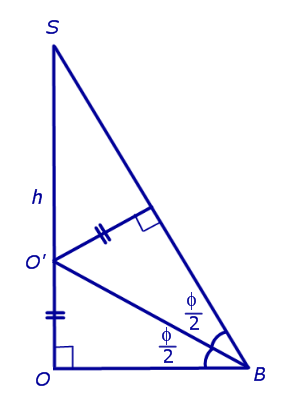
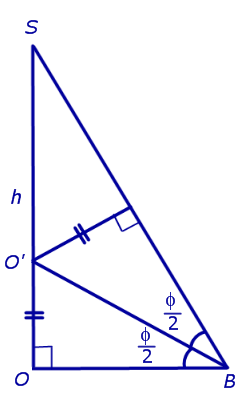
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле
Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле
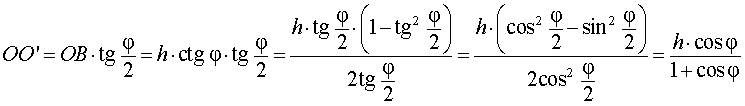
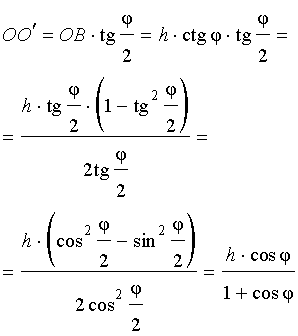
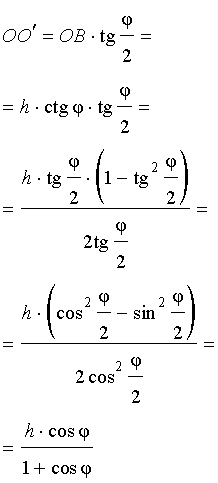
Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.
Доказательство утверждения 2 завершено.
Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо
Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле
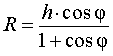 |
(1) |
Радиус сферы, вписанной в правильную n – угольную пирамиду
Решение. Рассмотрим правильную n – угольную пирамиду SA1A2 . An и обозначим символом O’ центр вписанной в пирамиду сферы, а буквой O – центр основания пирамиды. Проведем плоскость через высоту пирамиды SO и апофему SB какой-либо боковой грани (рис. 7).
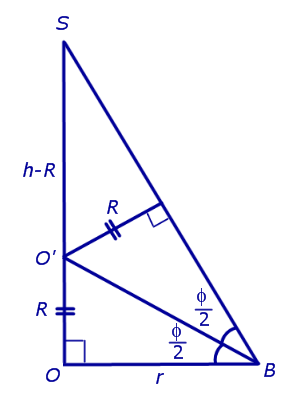
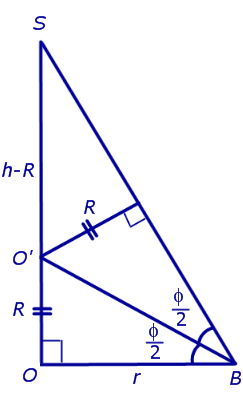
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем
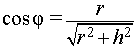 |
(2) |
В силу следствия 2 из формул (1) и (2) получаем
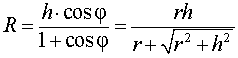
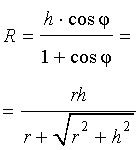
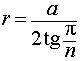
из формулы (3) получаем соотношение
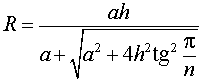
Ответ. 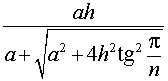
Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен
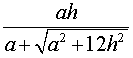
Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен
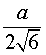
Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен
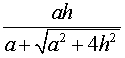
Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен
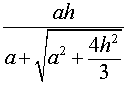
Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы
Утверждение 3. В любую треугольную пирамиду можно вписать сферу.
Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.
Действительно, пусть SABC – произвольный тетраэдр. Биссекторная плоскость внутреннего двугранного угла с ребром AC и биссекторная плоскость внутреннего двугранного угла с ребром AB пересекаются по некоторой прямой, проходящей через вершину A. Биссекторная плоскость внутреннего двугранного угла в ребром BC пересекает эту прямую в единственной точке O , которая и является центром вписанной сферы (рис. 8).
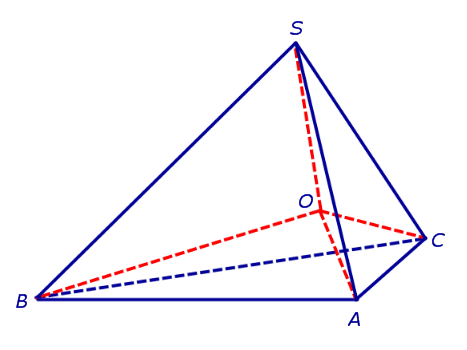
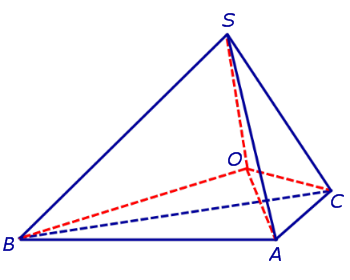
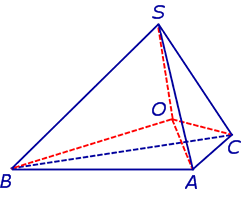
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами
а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами
то справедливы следующие равенства:
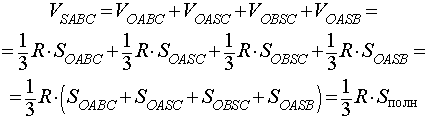
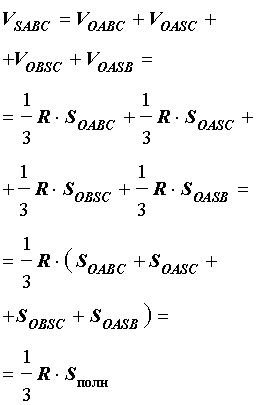
где символом Sполн обозначена площадь полной поверхности пирамиды SABC.
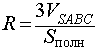
Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы
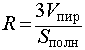
где символами Vпир и Sполн обозначены объем и площадь полной поверхности пирамиды соответственно.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/10-klass/mnogogranniki/piramida-pravilnaya-piramida
http://www.resolventa.ru/spr/stereometry/sphere_piramide.htm
[/spoiler]
Как найти высоту в правильной пирамиде
Пирамида представляет собой многогранник, в основании которого лежит многоугольник, а грани его представляют собой треугольники, обладающие общей вершиной. Для правильной пирамиды справедливо то же определение, но в основании ее лежит правильный многоугольник. Под высотой пирамиды подразумевается отрезок, который проведен от вершины пирамиды к основанию, и этот отрезок перпендикулярен ему. Найти высоту в правильной пирамиде очень легко.
Вам понадобится
- В зависимости от ситуации, знать объем пирамиды, площадь боковых граней пирамиды, длину ребра, длину диаметра многоугольника в основании.
Инструкция
Одним из способов найти высоту пирамиды, и не только правильной – это выразить ее через объем пирамиды. Формула, с помощью которой можно узнать ее объем, выглядит так:
V = (S*h)/3, где S – площадь всех боковых граней пирамиды в сумме, h – высота данной пирамиды.
Тогда из этой формулы можно вывести другую, для нахождения высоты пирамиды:
h = (3*V)/S
К примеру, известно, что площадь боковых граней пирамиды 84 см², а объем пирамиды равен 336 куб.см. Тогда найти высоту можно так:
h = (3*336)/84 = 12 см
Ответ: высота данной пирамиды 12 см
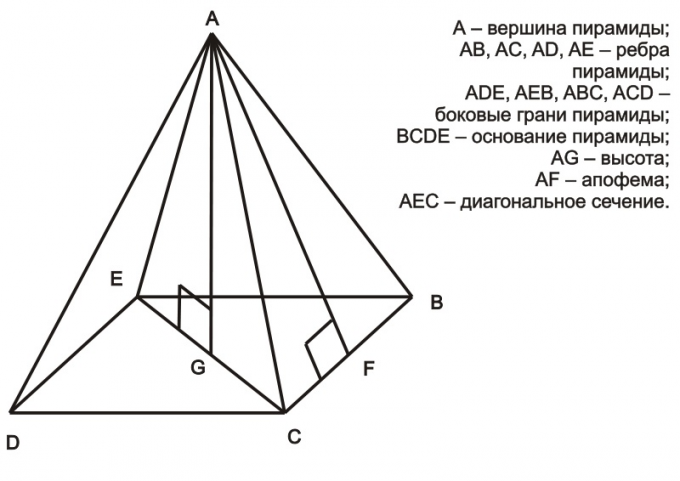
Рассматривая правильную пирамиду, в основании которой лежит правильный многоугольник, можно прийти к выводу, что треугольник, образованный высотой, половиной диагонали и одной из граней пирамиды, представляет из себя прямоугольный треугольник (например, это треугольник АEG на рисунке выше). Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов (a² = b² + c²). В случае с правильной пирамидой, гипотенуза – это грань пирамиды, один из катетов – половина диагонали многоугольника в основании, а другой катет – высота пирамиды. В таком случае, зная длину грани и диагонали, можно вычислить и высоту. В качестве примера можно рассмотреть треугольник AEG:
AE² = EG²+GA²
Отсюда высоту пирамиды GA можно выразить так:
GA = √(AE²-EG²).
Чтобы было более понятно, как находить высоту правильной пирамиды, можно рассмотреть пример: в правильной пирамиде длина грани 12 см, длина диагонали многоугольника в основании – 8 см. Исходя из этих данных, требуется найти длину высоты этой пирамиды.Решение: 12² = 4² + c², где с – неизвестный катет (высота) данной пирамиды (прямоугольного треугольника).
144 = 16 + 128
Таким образом, высота данной пирамиды √128 или, приблизительно, 11.3 см
Источники:
- правильная четырехугольная пирамида найти высоту
- Решение заданий С2 ЕГЭ по математике
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
УПРАВЛЕНИЕ
ОБРАЗОВАНИЯ
АДМИНИСТРАЦИИ ГОРОДА ХАРЦЫЗСКА
МУНИЦИПАЛЬНАЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯ
«ХАРЦЫЗСКАЯ
СРЕДНЯЯ ШКОЛА № 24»
Положение высоты в некоторых видах пирамид
11 класс
Мини – учебник по геометрии
______________________
______________________


Составитель:
учитель
математики
Заставная Н.Н.
г.
Харцызск
2020г.
|
Период: Информационно- познавательный |
Девиз: «Привет, проблема!» |
Механизм: Анализ восприятия |
Доминанта: Анализ, синтез, запоминание |
Внимательно изучи таблицу «Положение высоты в
некоторых видах пирамид». Определи, как ты воспринимаешь и владеешь полученной
информацией.
|
Полностью |
Наполовину |
Непонятно |
ПОЛОЖЕНИЕ
ВЫСОТЫ В НЕКОТОРЫХ ВИДАХ ПИРАМИД
|
|
|
Если в пирамиде Верно и обратное: |
|
|
Если в пирамиде |
|
|
Для решения используют прямоугольный |
|
|
|
|
Если в пирамиде грани Верно и обратное: |
|
|
Если в пирамиде
|
|
|
Для решения используют прямоугольный Для такого вида пирамид справедлива формула:
где |
|
|
|
|
Если в пирамиде |
|
|
Если в пирамиде |
|
|
|
|
Если в пирамиде |
|
|
|
|
Если плоскость |
|
|
|
|
Если плоскость |
|
![]()

|
|
Подумай, насколько |
|
|
Прочитай, |
Выдающийся математик – Архимед |
Великий математик, механик и инженер древности Архимед родился в 287
г. до н. э. (предположительно) в Сиракузах – богатом торговом городе Сицилии.
Отцом его был астроном Фидий, который привил сыну с детства любовь к математике,
механике и астрономии. В Александрии Египетской – научном и культурном центре
того времени – Архимед познакомился со знаменитыми александрийскими учеными,
астрономом Кононом, разносторонним ученым Эратосфеном, с которыми потом переписывался
до конца жизни. В знаменитой Александрийской библиотеке Архимед познакомился с
трудами Демокрита, Евдокса и других замечательных греческих геометров, о
которых он упоминал в своих сочинениях.
Уже при жизни Архимеда вокруг его имени создавались легенды, поводом
для которых служили его поразительные изобретения, производившие ошеломляющее
действие на современников.
Всем известен рассказ о том, как Архимед сумел определить, сделана ли
корона царя Гиерона из чистого золота. Благодаря этому случаю был открыт
основной закон гидростатики.
Другая легенда рассказывает, что построенный Гиероном в подарок
египетскому царю Птолемею роскошный корабль Сирокосия, никак не удавалось
спустить на воду. Архимед соорудил систему блоков, с помощью которых он смог проделать
это один, движением руки. Этот случай послужил поводом его крылатых слов
..Дайте мне точку опоры, и я сдвину Землю.
|
|
Архимед |
Знаменитый историк древности Полибий писал: «Такова чудесная сила
одного человека, одного дарования…римляне могли бы быстро овладеть городом, если
бы кто-либо изъял из среды сиракузян одного старца».
Архимед был убит римским солдатом после взятия Сиракуз вследствие
измены.
Плутарх сохранил нам яркий рассказ о его смерти: «К Архимеду подошел
солдат с мечом в руке, что бы убить его. Но Архимед настойчиво просил его подождать
одну минуту, чтобы задача, которой он занимался, не осталась не решенной;
солдат ,которому не было дела до его доказательства, пронзил его своим мечом»
Архимед был замечательным механиком – практиком и теоретиком, но
основным делом его жизни была математика. По словам Плутарха, Архимед был
просто одержим ею. Он забывал о пище, совершенно не заботился о себе. Его
работы относились почти ко всем областям математики того времени.
Так, он нашел все полуправильные многогранники, которые теперь носят
его имя, значительно развил учения о конических сечениях, дал геометрический
способ решения кубических уравнений вида ![]() , корни
, корни
которых он находил с помощью пересечения параболы и гиперболы Архимед провёл и
полное исследование этих уравнений.
Но главное его внимание было сосредоточено на трех типах проблем.
1.
Определение площадей криволинейных фигур или
объёмов тел. Греки до Архимеда умели находить площади прямолинейных фигур, площадь
круга, объём призмы, пирамиды цилиндра и конуса, но только Архимед нашел общий
метод, позволяющий найти любую площадь или объём. Идеи Архимеда легли в основу интегрального
исчисления. Сам Архимед определил с помощью своего метода площади и объёмы
почти всех тел, которые рассматривались в античной математике. Лучшим своим
достижением он считал определение поверхности и объёма шара. Он просил выбить
на своей могиле шар, вписанный в цилиндр.
2.
Как определить касательную в любой точке кривой.
Древние греки умели находить касательную к окружности, эллипсу, гиперболе и
параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот
метод лёг в основу дифференциального исчисления.
3.
В математике, физике и астрономии очень важно уметь
находить наибольшие и наименьшие значения изменяющихся величин – их экстремумы.
Например, как среди цилиндров, вписанных шар, найти цилиндр, имеющий наибольшей
объём? Все такие задачи могут быть решены с помощью дифференциального
исчисления. Архимед первым увидел связь этих задач с проблемами определения
касательных и показал, как с их помощью можно решать задачи на экстремумы.
Огромное значение для развития математики имело вычисленное Архимедом
отношение длины окружности к диаметру, т.е. число ![]() ,с
,с
большой степенью точности.
Идеи Архимеда почти на две тысячи лет опередили своё время. Только в XVII в. ученые смогли продолжить и развить труды великого греческого
математика. Только тогда было раскрыто их подлинное значение.
Лейбниц, один из творцов дифференциального и интегрального исчислений, писал „Внимательно читая сочинения Архимеда, перестаёшь
удивляться всем новейшим открытиям геометров”
Как Вы считаете, можем ли мы оценить Архимеда, только как учёного, зная его открытия?
Мог ли он совершить их, если бы не имел целью улучшение жизни граждан своего города?
Как Вы считаете, должен ли учёный иметь гражданскую позицию или
заниматься только наукой?
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|
Период: нормативно – регуляционный |
Девиз: «Освоим изученное!» |
Механизм: добывание, осмысление, нормирование |
Доминанта: мышление, личностная адаптация |
Тебе предстоит решить 5 задач. Выбери уровень
сложности: достаточный (средний) или высокий. Отметь, насколько понятным было
решение каждой задачи, закрась ту часть круга, которая соответствует твоему
уровню понимания решения.
|
Думай Решай Записывай |
|
|
*Достаточный уровень сложности |
**Высокий уровень сложности |
|
Задача |
|
|
Основанием пирамиды является прямоугольник со стороною |
Основанием пирамиды является равнобедренный треугольник, площадь которого |
|
Задача |
|
|
Сторона основания правильной треугольной пирамиды равна 8 |
Основание пирамиды – равнобедренный треугольник с боковой стороной |
|
Задача |
|
|
Основанием пирамиды является правильный треугольник. Одна из боковых |
Основание пирамиды – равнобедренный треугольник с боковой стороной |
|
Задача |
|
|
Основанием пирамиды |
Основание пирамиды |
|
Задача |
|
|
Основанием пирамиды является прямоугольный треугольник с гипотенузой |
В основании пирамиды лежит квадрат. Две боковые смежные грани |
|
Подведи |
|
Подчеркни, во сколько баллов ты оцениваешь свой
результат работы.
1 2 3 4 5












