Как посчитать высоту равнобедренного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать высоту равнобедренного треугольника
Чтобы посчитать чему равна высота равнобедренного треугольника просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор

Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину двух равных сторон (a) и длину основания (b)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину основания (b) и угол α
- длину основания (b) и угол β
Введите их в соответствующие поля и получите результат.
Если известны длина стороны а и основания b
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а длина основания
b =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?
Формула
h = √a2 – (b/2)2
Пример
Если сторона a = 10 см, а сторона b = 5 см, то:
h = √102 – (5/2)2 = √100 – 6.25 ≈ 9.68 см
Если известны длина стороны а и угол α
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а угол
α =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
h = a⋅sin α
Пример
Если сторона a = 5 см, а ∠α = 45°, то:
h = 5⋅sin 45 ≈ 3,53 см
Если известны длина стороны а и угол β
Чему равна высота h равнобедренного треугольника если длина сторон
a =
, а угол
β =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
h = a⋅cos β/2
Пример
Если сторона a = 5 см, а ∠β = 30°, то:
h = 5⋅cos 30/2 ≈ 4.83 см
Если известны длина стороны b и угол α
Чему равна высота h равнобедренного треугольника если длина основания
b =
, а угол
α =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?
Формула
h = b/2⋅tg α
Пример
Если сторона b = 20 см, а ∠α = 35°, то:
h = 20/2⋅tg 35 = 10⋅0.7 = 7 см
Если известны длина стороны b и угол β
Чему равна высота h равнобедренного треугольника если длина основания
b =
, а угол
β =?
Ответ:
h =
0
Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол β?
Формула
h = b/2⋅ctg β/2
Пример
Если сторона b = 15 см, а ∠β = 40°, то:
h = 15/2⋅ctg 40/2 = 7.5⋅2.7474 ≈ 20.6 см
См. также
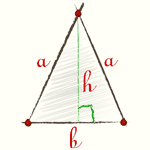
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам – это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
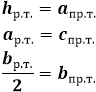
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
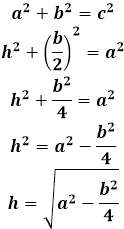
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами – например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
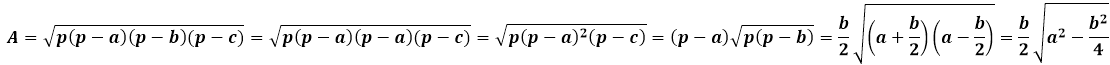
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
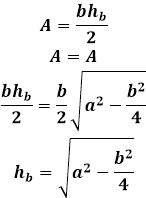
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
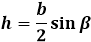
Формула через основание и угол при нем α:
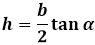
через основание и угол противолежащий ему β:
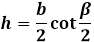
Высота равнобедренного треугольника, формула
Высота равнобедренного треугольника из теоремы Пифагора, формула
[
h^2+Big(frac{b}{2}Big)^2=a^2 \
h^2=a^2-Big(frac{b}{2}Big)^2
]
[
h=sqrt{a^2-frac{b^2}{4}}
]
Высота равнобедренного треугольника по формуле Герона, формула
[
h = frac{ 2 sqrt{p(p-a)(p-b)(p-a)}}{b}
]
где
[
p=frac{1}{2}(a+b+a)=a+frac{b}{2}
]
после подстановки коэффициента p в формулу получим
[
h = frac{ 2 sqrt{(a+frac{b}{2})(a+frac{b}{2}-a)(a+frac{b}{2}-b)(a+frac{b}{2}-a)}}{b}
]
[
h = frac{ 2 sqrt{(a+frac{b}{2})(frac{b}{2})(a-frac{b}{2})(frac{b}{2})}}{b}
]
по формулам сокращенного умножения, разность квадратов получим
[
Big(a+frac{b}{2}Big)Big(a-frac{b}{2}Big)=a^2-Big(frac{b}{2}Big)^2
]
далее вносим под корень 2 и знаменатель b
[
h = sqrt{frac{2^2(a^2-(frac{b}{2})^2)(frac{b}{2})^2}{b^2}}
]
после сокращений получим
[
h=sqrt{a^2-frac{b^2}{4}}
]
Вычислить, найти высоту равнобедренного треугольника по формуле (9)
Высота равнобедренного треугольника |
стр. 232 |
|---|
В данной публикации мы рассмотрим основные свойства высоты равнобедренного треугольника, а также разберем примеры решения задач по данной теме.
Примечание: треугольник называется равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.
-
Свойства высоты в равнобедренном треугольнике
- Свойство 1
-
Свойство 2
- Свойство 3
- Пример задачи
Свойства высоты в равнобедренном треугольнике
Свойство 1
В равнобедренном треугольнике две высоты, проведенные к боковым сторонам, равны.

AE = CD
Обратная формулировка: Если в треугольнике две высоты равны, значит он является равнобедренным.
Свойство 2
В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

- BD – высота, проведенная к основанию AC;
- BD – медиана, следовательно, AD = DC;
- BD – биссектриса, следовательно, угол α равен углу β.
- BD – серединный перпендикуляр к стороне AC.
Свойство 3
Если известны стороны/углы равнобедренного треугольника, то:
1. Длина высоты ha, опущенной на основание a, вычисляется по формуле:

- a – основание;
- b – боковая сторона.
2. Длина высоты hb, проведенной к боковой стороне b, равняется:
![]()

p – это полупериметр треугольника, рассчитывается таким образом:
![]()
3. Высоту к боковой стороне можно найти через синус угла и длину стороны треугольника:
![]()
Примечание: к равнобедренному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см. Найдите длину высоты, опущенной к основанию.
Решение
Воспользуемся первой формулой, представленной в Свойстве 3:

Задача 2
Найдите высоту, проведенную к боковой стороне равнобедренного треугольника длиной 13 см. Основание фигуры равняется 10 см.
Решение
Для начала вычислим полупериметр треугольника:
![]()
Теперь применим соответствующую формулу для нахождения высоты (представлена в Свойстве 3):
![]()
Высота равнобедренного треугольника, формула
Формулу высоты равнобедренного треугольника можно получить из теоремы Пифагора, а также по формуле Герона
Высота равнобедренного треугольника из теоремы Пифагора, формула
Высота равнобедренного треугольника по формуле Герона, формула
после подстановки коэффициента p в формулу получим
далее вносим под корень 2 и знаменатель b
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.
2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности


где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:


Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Теорема Пифагора

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
- a = √c 2 − b 2
- b = √c 2 − a 2
- c = √a 2 + b 2
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
- если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
- если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
- если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.
Записывайтесь на курсы обучения математике для школьников с 1 по 11 классы!
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a 2 + b 2 = c 2 .
Пошаговое доказательство:
- Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
- Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
- Также прямоугольная фигура ∆CBH подобна ∆ABC:
- Введем новые обозначения: BC = a, AC = b, AB = c.
- Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
- Значит a 2 = c * HB, b 2 = c * AH.
- Сложим полученные равенства:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
a 2 + b 2 = c * AB
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
- Построим прямой угол с вершиной в точке C₁.
- Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.
- Проведём отрезок A₁B₁.
- Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.
- В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
- Таким образом получится:
- Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:
- C₁A₁ = CA и C₁B₁ = CB по результату построения,
- A₁B₁ = AB по доказанному результату.
- Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
- Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
Пусть катеты a = 6 и b = 8.
По теореме Пифагора c 2 = a 2 + b 2 .
Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
- Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:
Ответ: треугольник не является прямоугольным.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/teorema-pifagora-formula
[/spoiler]
