Высота треугольника
Расстояние между вершиной треугольника и противоположной стороной называется высотой. Формально, это самый короткий отрезок между вершиной треугольника и (с возможным продлением) противоположной стороной.

Каждый треугольник имеет 3 высоты которые пересекаются в одной точке – ортоцентре. Если мы используем стандартные обозначения, в треугольнике ABC , есть три высоты: AHa, BHb, CHc . Эти три отрезка пересекаются в одной точке – ортоцентре (точка H на рисунке) треугольника. Для тупого треугольника (имеющего один угол, больше чем 90°), ортоцентр находится за пределами треугольника.
Высоты остроугольного треугольника
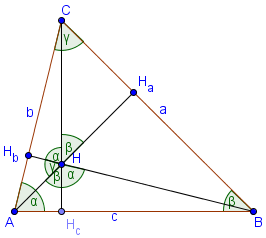
Ортоцентр – это точка внутри треугольника.
∠ AHB = 180 – γ = α + β
∠ BHC = 180 – α = β + γ
∠ AHC = 180 – β = α + γ
∠ AHHc = β, ∠ BHHc = α, ∠ BHHa = γ
Высоты тупоугольного треугольника

Ортоцентр находится вне треугольнка.
Две высоты также всегда лежат вне треугольника.
∠ AHHc = ∠ CBA = β
∠ HcHB = ∠ CAB = α
Правый треугольник

Высота AHa совпадает с AC.
Высота BHb совпадает с BC.
Ортоцентр H совпадает с C.
∠ ACHc = β, ∠ BCHc =α
Формулы
R – радиус описанной окружности
r – радиус вписанной окружности
p – полуперимерт: (a + b + c)/2
Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.
2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности


где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:


Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Способы нахождения высоты треугольника: теорема и формула
Определение высоты треугольника
Геометрия, являющаяся разделом математики, изучает структуры в пространстве и на плоскости. Одним из типов таких фигур являются геометрические фигуры. К ним можно отнести квадрат, прямоугольник, круг, пятиугольник, треугольник и другие. Из них можно делать более сложные фигуры или оставлять в первоначальном виде.
Треугольником является фигура, относящаяся к классу простых фигур, которая образована тремя точками, находящимися не на одной прямой, и соединенными между собой тремя отрезками.
Треугольники могут быть:
- разными по величине углов: прямоугольными, тупоугольными и остроугольными;
- разными по числу равных сторон: равносторонними, равнобедренными и разносторонними.
Помимо трех сторон, важными элементами треугольников являются медианы, высоты и биссектрисы.
Высотой треугольника является перпендикуляр, опущенный из угла треугольника вниз, на противоположную сторону.
В геометрии высота треугольника обозначается буквой h.
В зависимости от типа треугольника высота может:
- падать на противоположную сторону — у остроугольного треугольника;
- находиться вне треугольника — у тупоугольного треугольника;
- совпадать с одной из сторон — у прямоугольного треугольника.
Чтобы сделать высоту графически явной и понятной на рисунке, ее нередко выделяют красной линией.
Для того чтобы определить графическое начертание высоты треугольника, необходимо:
- Найти вершину фигуры.
- Опустить вниз перпендикулярную линию к противоположной стороне.
- Продлить противоположную сторону до пересечения с высотой, если требуется.
Любой треугольник имеет 3 высоты — по числу углов. Их пересечение находится в точке ортоцентра, которая, в зависимости от типа треугольника, может находиться внутри треугольника, снаружи на пересечении продолжений высот или совпадать с вершиной прямого угла.
Все три высоты треугольника обратно пропорциональны сторонам, к которым опущены. Доказательством будет соотношение:
A × H A ÷ B × H B ÷ C × H C = 1 B C ÷ 1 A C ÷ 1 A B
Выглядеть графически это будет так:
Существует множество способов нахождения высоты треугольника в зависимости от имеющихся данных.
Через площадь и длину стороны, к которой опущена высота:
где S — уже известная площадь треугольника,
Через длины всех сторон:
h = 2 p p × a p × b p × c a
где a, b и c — стороны треугольника,
p — его полупериметр.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длину прилежащей стороны и синус угла:
s i n a — синус угла прилежащей стороны.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через стороны и радиус описанной окружности.
Решать задачи с треугольником и описанной окружностью для нахождения высоты можно следующим образом:
где b, c — стороны разностороннего треугольника, к которым не опущена высота,
R — радиус описанной окружности.
Данная формула подходит только для нахождения высоты разностороннего треугольника.
Через длины отрезков, образованных на гипотенузе при проведении к ней высоты треугольника:
где C 1 и С 2 — длины отрезков, образованных на гипотенузе, проведенной к ней высотой.
Данная формула подходит только для нахождения высоты прямоугольного треугольника.
Нахождение высоты равнобедренного треугольника через основание и боковые стороны
Равнобедренным треугольником называют треугольник, имеющий одинаковые по длине катеты, которые образуют равные углы с основанием. В таком треугольнике высота будет опускаться ровно в середину основания, образуя с ним прямой угол.
Помимо высоты, проведенная линия будет являться также осью симметрии, биссектрисой вершинного угла и медианой.
Формула для нахождения высоты в этом случае:
где a — основание,
b — равные боковые стороны.
Свойства высоты в равностороннем треугольнике
Равносторонний треугольник — это треугольник, стороны которого, углы, высоты, медианы, оси симметрии и биссектрисы будут равны.
Такой треугольник является частным примером равнобедренного треугольника, но не наоборот.
Высоту в таком треугольнике можно найти с помощью следующей формулы:
где а — сторона равностороннего треугольника.
Главным свойством, которым обладает высота равностороннего треугольника, является тот факт, что она равна медиане и биссектрисе:
а — сторона правильного равностороннего треугольника.
Нахождение высоты прямоугольного треугольника через его катеты
Прямоугольным считается треугольник, у которого один из углов является прямым, то есть равным 90°. Высота, опущенная из такого угла, падает на гипотенузу треугольника и делит его на два прямоугольных треугольника, которые пропорциональны по отношению к большому треугольнику и друг к другу.
Важно отметить, что две другие высоты будут совпадать с катетами треугольника.
Найти высоту в прямоугольном треугольнике, можно через два его катета (a и b) и гипотенузу (c).
Причем гипотенуза также легко находится через катеты по теореме Пифагора:
Расчет высоты идет следующим образом:
где a, b и c — вышеупомянутые стороны треугольника.
[spoiler title=”источники:”]
http://wika.tutoronline.ru/geometriya/class/7/sposoby-nahozhdeniya-vysoty-treugolnika-teorema-i-formula
[/spoiler]
Высота треугольника, формула.
Высота треугольника это перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону, или на ее продолжение (сторона, на которую опускается перпендикуляр, в данном случае называется основанием треугольника).
В тупоугольном треугольнике
две высоты падают на продолжение сторон и лежат вне треугольника. Третья внутри треугольника.
В остроугольном треугольнике все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты служат высотами.
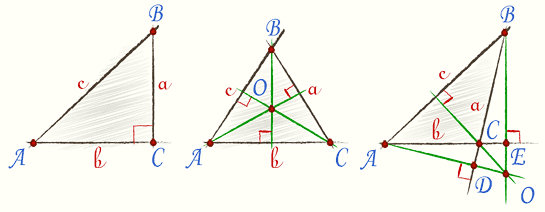
Все три высоты всегда пересекаются в одной точке, называемой Ортоцентр.
В тупоугольном треугольнике ортоцентр лежит вне треугольника. В Остроугольном – внутри треугольника. В прямоугольном треугольнике, совпадает с вершиной прямого угла.
Высота треугольника опущенная на сторону a обозначается буквой ha и через три стороны треугольника выражается формулой:
[
h_a = 2frac{sqrt{p(p-a)(p-b)(p-c)}}{a}
]
где
[
p=frac{1}{2}(a+b+c)
]
(a, b, c – стороны треугольника; ha – высота треугольника)
Вычислить, найти высоту треугольника по формуле (1).
Высота треугольника |
стр. 231 |
|---|
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
-
Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны
![]()
где S – площадь треугольника.
2. Через длины всех сторон
![]()
где p – это полупериметр треугольника, который рассчитывается так:
![]()
3. Через длину прилежащей стороны и синус угла
![]()
4. Через стороны и радиус описанной окружности
![]()

где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
![]()
2. Через стороны треугольника
![]()
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
![]()

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
![]()
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
![]()
Здесь рассмотрены все возможные способы нахождения высоты треугольников разных типов. Высота
треугольника – отрезок, проведенный из вершины треугольника перпендикулярно к противоположной
стороне. В задачах нахождение высоты часто является промежуточным звеном для поиска других значений.
Она и является катетом в треугольнике, который сама же образует, и участвует во многих формулах,
например, для нахождения площади.
- Высота разностороннего треугольника через площадь и длину
стороны - Высота разностороннего треугольника через длины всех
сторон - Высота разностороннего треугольника через длину прилежащей
стороны и синус угла - Высота разностороннего треугольника через стороны и радиус
описанной окружности - Высота равнобедренного треугольника через основание и
боковые стороны - Высота прямоугольного треугольника через длины отрезков,
образованных на гипотенузе - Высота прямоугольного треугольника через все стороны
треугольника - Высота равностороннего треугольника через сторону
треугольника
Через площадь и длину стороны разностороннего треугольника
Через площадь и длину высота находится по формуле:
h = 2S / a
где S – площадь треугольника, а – сторона треугольника.
Цифр после
запятой:
Результат в:
Согласно этой формуле высота равна удвоенной площади, деленной на длину стороны, к которой она
проведена.
Пример. Найдите высоту разностороннего треугольника, проведенную к стороне а,
площадь которого равна 27 см, а длина стороны а составляет одну треть от площади. Решение: Найдем
сторону а. Так как известно, что она составляет треть от площади, а = 27 / 3 = 9 см.
Теперь воспользуемся формулой для нахождения высоты: h = 2S / a. Подставим
известные значения. h = 2 * 27 / 9 = 6 см. Ответ: 6 см
Через длины всех сторон разностороннего треугольника
Через длины всех сторон высота разностороннего треугольника ищется по формуле:
h = (2 √(p (p-a)(p-b)(p-c))) / 2
p = (a + b + c) / 2
где h – высота, а, b, c – стороны треугольника, p – полупериметр треугольника.
Цифр после
запятой:
Результат в:
Полупериметр треугольника можно найти либо в два этапа через периметр, либо сразу по формуле. Этим
способом удобно пользоваться, когда треугольник разносторонний.
Пример. Периметр разностороннего треугольника равен 18 см. Длины сторон 6 см и 8 см. Найдите
высоту, проведенную к стороне а. Решение: P = a + b + c, значит с = P – a – b , то есть c = 18 – 8 – 6 = 4 см. Для
нахождения h будем использовать формулу h = (2 √(p (p-a)(p-b)(p-c))) / 2.
Сначала найдем полупериметр (p): p = p / 2 = 18 / 2 = 9 см. Подставим,
найденные значения в формулу высоты: h = (2 √(9 (9 — 6)(9 — 8)(9 — 4))) / 2 = √135 / 3 = 2,12 см
Через длину прилежащей стороны и синус угла разностороннего треугольника
Через длину прилежащей стороны и синус угла высота ищется по следующей формуле:
h = a * sin α
где а – длина стороны, sin α – синус прилежащей стороны.
Цифр после
запятой:
Результат в:
Пример. В разностороннем треугольнике высота проведена к стороне AB. Угол ACH равен
30˚, а длина стороны AB 12 см. Найдите длину высоты CH в треугольнике ABC. По теореме о сумме углов
в треугольнике найдем угол САН. ∠САН = 180 – (∠АСН + ∠АНС). ∠САН = 180 – 90 – 30 = 60˚ sin 60º = 1/2. СН = AB * sin ∠САН, СН = 12 * 1/2 = 6 см. Ответ:
6 см
Через стороны и радиус описанной окружности разностороннего треугольника
Через стороны и радиус описанной окружности высоту можно найти по следующей формуле:
h = bc / 2R
где r – радиус описанной около треугольника окружности, b,c – стороны треугольника
Цифр после
запятой:
Результат в:
Пример. Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из
вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см.
Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ:
5 см.
Через длины отрезков прямоугольного треугольника, образованных на гипотенузе
Через длины отрезков образованных на гипотенузе высоту можно найти по следующей формуле:
h = √(C1 * C2)
где: C1, C2 — отрезки, образованные проведением высоты к гипотенузе.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике катеты равны 4 см и 3 см. Угол BAH равен 30˚.
Найдите высоту. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике
ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол
АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС.
Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном
треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC,
значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту
(АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.
Через основание и боковые стороны равнобедренного треугольника
Через основание и боковые стороны высота равнобедренного треугольника находится по формуле:
h = √(b² — a²/4)
где а – основание треугольника, b – боковая сторона. Для равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Пример. В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к
основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию
треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН,
является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По
формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см.
Ответ: 6 см.
Высота прямоугольного треугольника через все стороны треугольника
Если известны все стороны прямоугольного треугольника, то можно найти его высоту по следующей
формуле:
h = ab / c
где a,b,c – стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚.
Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике
найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то
треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем
высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим
полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ:
3√2 см
Через сторону равностороннего треугольника
Высота равностороннего треугольника через сторону треугольника ищется по следующей формуле:
h = a√3 / 2
где a – сторона треугольника.
Цифр после
запятой:
Результат в:
Пример: Найдите высоту в равностороннем треугольнике, если известно, что его сторона
равна 4√3 см. Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ:
6 см
В зависимости от типа треугольника высота может располагаться по-разному:
- Например, в треугольнике KGM высота GH, проведённая из вершины G к стороне находится внутри
треугольника, так как треугольник является остроугольным. Кроме того, треугольник в данном
примере равнобедренный, значит, она же является биссектрисой и медианой. Знание этого пригодится
при решении задач, например таким образом можно будет найти основание.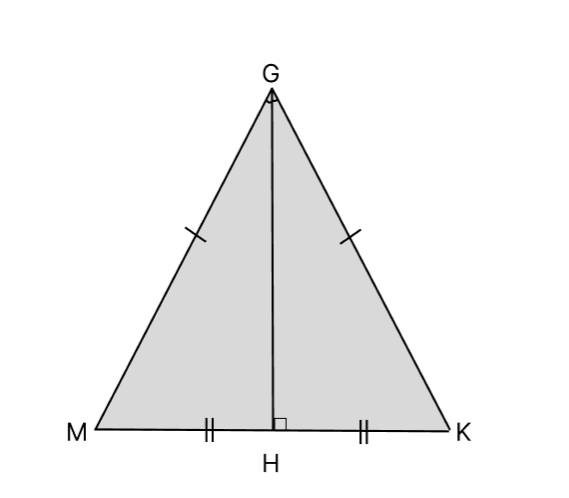
- В тупоугольном треугольнике высота будет выходить за его пределы и для того чтобы её провести
понадобится сначала продлить сторону. Например, на рисунке сторона ВС продлена до НС.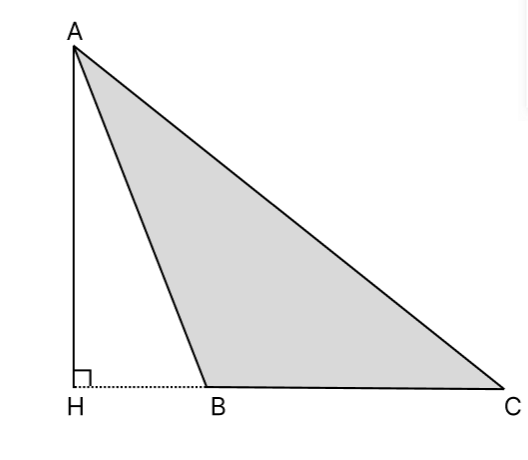
- В случае, когда треугольник имеет прямой угол – высота совпадёт с одним из катетов, либо будет
внутри треугольника (как в первом рассмотренном варианте) и проведена к гипотенузе.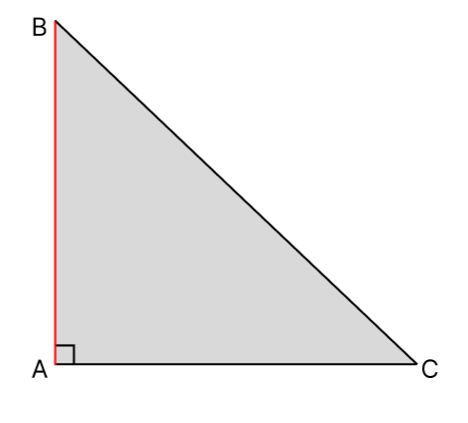
Высота треугольника — подробнее
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
На этом рисунке ( displaystyle BH) – высота.
Но иногда высота (в отличие от биссектрисы и медианы) ведёт себя, как непослушный ребенок – «выбегает» из треугольника. Это бывает в тупоугольном треугольнике.
И тогда получается так:
В общем, не нужно пугаться, если основание высоты оказалось не на стороне треугольника, а «за» треугольником, на продолжении стороны.
Как же решать задачи, в которых участвует высота?
Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.
Но попадаются задачи и похитрее, при решении которых лучше обладать дополнительными знаниями заранее, а не выводить их «с нуля». Сейчас мы обсудим некоторые из них.
Но для начала решим простенькую задачку на высоту в тупоугольном треугольнике:
В треугольнике ( displaystyle ABC) с тупым углом ( displaystyle C) проведена высота ( displaystyle BH). Найти ( displaystyle AC), если ( AB=2sqrt{10}), ( BC=sqrt{13}), ( BH=2).
Смотри: из-за того, что угол ( C) – тупой, высота ( BH) опустилась на продолжение стороны ( AC), а не на саму сторону.
Теперь давай увидим во всём этом два прямоугольных треугольника.
Смотри их целых два:
Применяем теорему Пифагора к треугольнику ( BCH):
( B{{C}^{2}}=B{{H}^{2}}+C{{H}^{2}}), то есть ( 13=4+C{{H}^{2}}); ( CH=3).
А теперь теорема Пифагора для ( Delta ABH):
( A{{B}^{2}}=A{{H}^{2}}+B{{H}^{2}}); то есть ( 40=A{{H}^{2}}+4); ( AH=6).
Теперь осталось только заметить, что ( AC=AH-CH=6-3=3).
Нашли!
А теперь давай вернемся к нашим высотам!
Остроугольный треугольник и высота
Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:
Что видим теперь? Ещё подобные треугольники!
Как от двух линий вообще могут получиться столько подобных треугольников?!
Но тем не менее…
( Delta C{{H}_{C}}Bsim Delta C{{H}_{A}}Hsim Delta A{{H}_{A}}Bsim Delta A{{H}_{C}}H)
Видишь, какое богатство? И всё это может быть использовано в задачах!
Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.
Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…
Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.
И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!
