- Математика – уроки для подготовки к экзаменам ЕГЭ ОГЭ
- Математика online
- КАК НАЙТИ ВЫСОТУ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ЕСЛИ ИЗВЕСТЕН ОБЪЕМ, ДЛИНА И ШИРИНА? Пример 5 класс

Смотреть видео:
#математикаогэ #гвэ #егэответы #репетиторпоматематике #репетитор_по_математике #огэматематика #огэответы #арифметика #ответы_огэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
- Комментарии
Нет комментариев. Ваш будет первым!
Как найти высоту, если известна длина и ширина
В основании многих геометрических фигур лежат прямоугольники и квадраты. Наиболее распространен среди них параллелепипед. Также к ним относятся куб, пирамида и усеченная пирамида. Все эти четыре фигуры имеют параметр, называемый высотой.

Инструкция
Начертите простейшую изометрическую фигуру, называемую прямоугольным параллелепипедом. Она получила свое название по той причине, что ее гранями являются прямоугольники. Основание данного параллелепипеда также является прямоугольником, имеющим ширину a и длину b.
Объем прямоугольного параллелепипеда равен произведению площади основания на высоту: V = S*h. Поскольку в основании параллелепипеда лежит прямоугольник, площадь этого основания равна S=a*b, где a – длина, b – ширина. Отсюда, объем равен V=a*b*h, где h – высота (причем, h = c, где c – ребро параллелепипеда). Если в задаче требуется найти высоту параллелепипеда, преобразуйте последнюю формулу следующим образом: h=V/a*b.
Существуют прямоугольные параллелепипеды, в основаниях которых лежат квадраты. Все его грани представляют собой прямоугольники, из которых квадратами являются два. Это означает, что его объем равен V=h*a^2, где h – высота параллелепипеда, a – длина квадрата, равная ширине. Соответственно, высоту данной фигуры найдите следующим образом: h=V/a^2.
У куба квадратами с одинаковыми параметрами являются все шесть граней. Формула для вычисления его объема выглядит так: V=a^3. Вычислять любую из его сторон, если известна другая, не требуется, поскольку все они равны между собой.
Все вышеперечисленные способы предполагают вычисление высоты через объем параллелепипеда. Однако существует и другой способ, позволяющий вычислить высоту при заданной ширине и длине. Им пользуются в том случае, если в условии задачи вместо объема приведена площадь. Площадь параллелепипеда равна S=2*a^2*b^2*c^2. Отсюда, c (высота параллелепипеда) равна с=sqrt(s/(2*a^2*b^2)).
Существуют и другие задачи по вычислению высоты при заданных длине и ширине. В некоторых из них фигурируют пирамиды. Если в задаче дан угол при плоскости основания пирамиды, а также ее длина и ширина, найдите высоту, используя теорему Пифагора и свойства углов.
Для того, чтобы найти высоту пирамиды, сначала определите диагональ основания. Из чертежа можно сделать вывод, что диагональ равна d=√a^2+b^2. Поскольку высота падает в центр основания, половину диагонали найдите следующим образом: d/2=√a^2+b^2/2. Высоту найдите, используя свойства тангенса: tgα=h/√a^2+b^2/2. Отсюда следует, что высота равна h=√a^2+b^2/2*tgα.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как и любая другая наука, математика нужна не как отдельная от реальности сущность, которую интересно изучать или обучать ей других людей.
Математика служит другим наукам, помогая решать самые разные задачи, что вы увидите в курсах физики, химии и других.
Но даже в более простых задачах, с которыми может столкнуться обычный рабочий или менеджер, математика необходима.
И сегодня как раз речь пойдет о решении задач.
Эта информация доступна зарегистрированным пользователям
Довольно часто приходится измерять те или иные предметы, начиная с мебели, заканчивая природными объектами, например, горами или реками.
Например, рассмотрим такую задачу.
Высота Эмпайр-стейт-билдинг до крыши 381 метр.
При этом на крыше установлен шпиль высотой 62 метра.
Какова общая высота сооружения?
В данном случае надо сначала понять, что спрашивается.
Вся высота сооружения – это высота от земли до самой верхней точки, в данном случае это будет верхняя точка шпиля.
Эта информация доступна зарегистрированным пользователям
Представив себе или нарисовав картинку, как показана выше, становится понятно, что для получения ответа достаточно сложить высоту до крыши и высоту шпиля, так что задача решается в одно действие.
Решение:
1) (mathbf{381+62=443}) (метра) высота сооружения
И можем записывать ответ.
Ответ: 443 метра.
Конечно, задачи зачастую бывают с большим количеством действий, рассмотрим одну из таких.
Известно, что высота Эвереста 8848 м над уровнем моря.
Высота горы Лхоцзе на 332 метра меньше высоты Эвереста.
Требуется найти высоту горы Чогори, если известно, что она на 95 метров выше Лхоцзе.
Можно решать задачу по действиям.
В таком случае первым действием необходимо найти высоту горы Лхоцзе. Для этого из высоты Эвереста необходимо вычесть 332.
1) (mathbf{8848-332=8516}) (метров) высота Лхоцзе
Вторым действием необходимо прибавить к найденному значению 95, чтобы получить высоту Чогори.
2) (mathbf{8516+95=8611}) (метров) высота Чогори
И запишем ответ.
Ответ: 8611 метров.
Но также решение можно записать одним выражением, ведь мы знаем, что сначала надо вычесть, а потом прибавить.
Тогда оно будет выглядеть так.
(mathbf{8848-332+95=8516+95=8611}) (метров) высота Чогори
Ответ, как и ожидалось, получился таким же.
Эта информация доступна зарегистрированным пользователям
Хоть скорость и является понятием физическим, довольно часто приходится решать задачи, связанные с ней как в математике, так и в реальной жизни.
Скорости измеряются в разных единицах. Наиболее популярной величиной в разговоре про транспорт являются километры в час (км/ч).
Если известно, что объект движется со скоростью 1 км/ч, это значит, что за 1 час объект преодолеет путь равный 1-му километру.
За 2 часа такой объект пройдет 2 километра и так далее.
Если, например, объект движется со скоростью 10 км/ч, это означает, что за час он пройдет 10 километров, за 2 часа 20 км, и так далее.
Запишем формулы, связывающие путь, скорость и время.
Эта информация доступна зарегистрированным пользователям
Формулы может быть сложно запоминать, поэтому можно запомнить такой треугольник, содержащий в себе те же формулы.
Эта информация доступна зарегистрированным пользователям
Попрактикуемся.
Пример 1.
Объект двигался со скоростью 3 км/ч 5 часов, какой путь он прошел?
Применим формулу для нахождения расстояния через скорость и время.
(mathbf{3cdot5=15}) (км)- длина пути.
Пример 2.
Объект проделал путь 32 км за 4 часа. С какой скоростью двигался объект, если предположить, что скорость была постоянной?
Применим формулу для нахождения скорости через время и путь.
(mathbf{32:4=8}) (км/ч)- с такой скоростью двигался объект.
Пример 3.
Объект двигался со скоростью 60 км/ч и проделал путь 180 км, сколько времени ушло на это?
Применим формулу для нахождения времени через путь и скорость.
(mathbf{180:60=3}) (ч)- столько времени занял путь.
Также иногда используются не километры в час, а метры в секунду(м/с), например, эту единицу используют для обозначения скорости ветра.
При этом все формулы остаются верны, с тем лишь учетом, что если скорость измеряется в метрах в секунду, то время должно измеряться в секундах, а путь в метрах.
Теперь, когда мы разобрались с единицами измерения и основными формулами, рассмотрим несколько задач на скорости и перемещения.
Задача 1
Допустим, ученик двигается в школу и знает несколько моментов.
Во-первых, известно, что до школы идти 5 км.
Во-вторых, скорость ученика- 4 км/ч.
До урока остается 1 час.
Вопрос, успеет ли ученик на урок? Если он не успеет, то сколько ему останется идти до школы?
Для начала нужно узнать, где окажется ученик через час.
Для этого необходимо умножить скорость ученика на его скорость.
1) (mathbf{4cdot1=4}) (км) пройдет ученик за 1 час.
Зная, что до школы ему идти 5 км, можно сделать вывод, что ученик на урок не успеет.
Тогда остается вопрос, сколько ученику останется идти?
Для этого нам надо из того, сколько ученику надо было идти в начале пути, вычесть то, сколько он уже прошел.
2) (mathbf{5-4=1}) (км) останется пройти ученику.
Вопросов в задаче была два, так что и ответ будет состоять из двух.
Ответ: нет, 1 км.
Задача 2
Туристы летели на самолете 2 часа со скоростью 150 км/ч, затем 5 часов ехали на грузовике со скоростью 40 км/ч, а после 3 часа шли пешком со скоростью 6 км/ч, вопрос, какой путь проделали туристы?
В данной задаче весь путь можно разбить на три части соответственно способу перемещения.
Далее можно посчитать путь, пройденный на каждом этапе, используя формулу нахождения пути по скорости и времени, а после сложить эти пути и получить суммарный путь.
1) (mathbf{2cdot150=300}) (км) туристы пролетели на самолете
2) (mathbf{5cdot40=200}) (км) туристы проехали на грузовике
3) (mathbf{3cdot6=18}) (км) туристы прошли пешком
Остается лишь сложить найденные величины.
4) (mathbf{300+200+18=518}) (км) общая длина пути
Ответ: 518 км.
Задача 3
Грузовой автомобиль прошел путь от одного города до другого за 8 часов, а легковой за 6 ч.
Найдите скорость легкового автомобиля, если известно, что скорость грузовика равна 60 км/ч.
Сразу найти ответ не получится, так как мы знаем только время, за которое двигался легковой автомобиль, путь же нам неизвестен.
Чтобы понять, как решать такие задачи, надо пытаться находить все, что можно, используя текущие данные.
Например, известно время, за которое двигался грузовой автомобиль, а также известна его скорость.
А значит, можно найти путь между двумя городами по формуле нахождения пути через скорость и время.
1) (mathbf{60cdot8=480}) (км)- длина пути между городами
Теперь мы можем найти скорость легкового автомобиля, так как известны два параметра: длина пути и время, за которое он этот путь преодолел.
2) (mathbf{480:6=80}) (км/ч)- скорость легкового автомобиля
Ответ: 80 км/ч.
Эта информация доступна зарегистрированным пользователям
Это довольно распространенный класс задач.
Основная их суть в том, что есть некоторый субъект, который совершает действия, будь то рабочий, производящий детали, завод, выпускающий продукцию, грузовик, перевозящий грузы и так далее.
Этот объект работает какое-то время и нам интересно, сколько за это время субъект успел сделать.
Заметим, насколько этот класс задач похож на задачи про скорость.
Рассмотрим такую задачу.
Задача 1
Рабочий производит 13 деталей в час. Сколько деталей он сделает за смену длиной в 8 часов?
В данном случае производительность рабочего можно принимать как скорость.
Время же временем и останется.
Итоговое количество деталей можно понимать как аналогию пути.
В таком случае, если для нахождения пути необходимо было умножить скорость на время, то в таких задача необходимо умножать производительность на время.
1) (mathbf{13cdot8=104}) (детали) произведет рабочий за смену.
Ответ: 104 детали
Эта информация доступна зарегистрированным пользователям
Рассмотрим еще задачи, чтобы все точно стало понятно.
Задача 2
Завод выпустил за 9 месяцев 189 927 автомобилей. Сколько автомобилей завод выпускает в месяц?
В данной задаче уже даны время и общий объем производства.
Требуется найти производительность.
Значит, необходимо разделить общий объем на время работы заводы.
1) (mathbf{189 927:9=21 103}) (автомобиля) завод производит в месяц
Ответ: 21 103 автомобиля.
Задача 3
Грузовик перевозит 4 т груза за один раз.
За месяц он совершает 15 рейсов.
Сколько груза перевозит грузовик за месяц?
В данном случае время не дано как какое-то количество месяцев, часов, секунд.
Но нам дано количество действий.
Его мы и можем использовать.
1) (mathbf{4cdot15=60}) (т) груза перевозит грузовик за месяц.
Ответ: 60 т.
Также в задачах на производительность очень часто субъект может быть не один.
То есть может встать вопрос, сколько деталей производят несколько станков, несколько рабочих и так далее.
Задача 4
Первый рабочий обслуживал 3 станка, изготавливающих по 15 деталей в час каждый.
Второй рабочий обслуживал 6 станков, изготавливающих по 10 деталей в час каждый.
Сколько всего деталей произвели два рабочих, проработав по 6 часов?
План решения задачи такой: найти, сколько деталей производит в час первый рабочий, сколько производит в час второй рабочий, из этого посчитать, сколько в час производят оба рабочих, а затем посчитать, сколько они произведут за 6 часов.
Чтобы найти, сколько производит первый рабочий в час, необходимо умножить производительность одного станка, который он обслуживает, на количество станков.
1) (mathbf{3cdot15-45}) (деталей) в час производит первый рабочий
Аналогично посчитаем для второго рабочего.
2) (mathbf{6cdot10=60}) (деталей) в час производит второй рабочий
Теперь сложим эти величины и получим, сколько в час производят оба рабочих.
3) (mathbf{45+60=105}) (деталей) в час производят оба рабочих
Известно время, известна производительность двух рабочих, остается посчитать объем производства.
4) (mathbf{105cdot6=630}) (деталей) рабочие произведут за 6 часов.
Остается записать ответ.
Ответ: 630 деталей.
Эта информация доступна зарегистрированным пользователям
Эта информация доступна зарегистрированным пользователям
Сегодня мы затронули такую тему, как производительность, и рассмотрели самый простой случай, в котором каждый субъект не зависит от других.
В реальности ситуация значительно сложнее.
Представим себе простейшую кондитерскую фабрику.
Даже там мы имеем конвейер, где все начинается с того, что должны привезти достаточное количество ингредиентов и расходных материалов, дальше идет много стадий производства, а в конце готовую продукцию должны также хорошо увезти, чтобы было место, куда складывать новую продукцию.
Конвейер очень часто может быть невидимым.
Если мы посмотрим на проекты, над которыми работают архитекторы или программисты, то увидим, что там тоже идет многоступенчатый процесс.
Проблемой таких процессов может стать то, что если случилась проблема на каком-то конкретном этапе, то встает весь конвейер, ведь на всех предыдущих этапах некуда передать результат работы, а на всех последующих этапах нечего обрабатывать.
Тут мы приходим к понятию ограничений.
Например, если станок по заморозке конфет может пропустить через себя только 500 конфет в минуту, не получится выпускать 600 конфет в час, даже если на всех остальных этапах станки будут готовы производить больше.
Это достаточно логичная мысль, но теорию управления, основанную на поиске и управлении ограничениями, разработал только в 1980-х годах израильский экономист Элияху Голдратт.
Человек был достаточно разносторонним, имел степень бакалавра по физике, магистра по философии, а работал позже менеджером в компаниях по разработке программного обеспечения, как раз занимаясь оптимизацией производства.
При желании можно найти и почитать его книги, чтобы понять, как организовывать свою работу или же работу в команде.
Задания
Версия для печати и копирования в MS Word
Тип 9 № 1976 

i
Найдите высоту прямоугольного параллелепипеда, если его объём равен 480 , длина равна 12 см, а ширина равна 5 см. Ответ дайте в сантиметрах.
Спрятать решение
Решение.
Найдем высоту параллелепипеда: 480 : 12 : 5 = 8.
Ответ: 8.
Аналоги к заданию № 1976: 2010 9518 9630 … Все
Источник: ВПР по математике 5 класс 2019 год Вариант 12
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Площадь
В школьном курсе математики 4-5 класса рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.
Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Характеристики понятия
Площадь имеет несколько характеристик:
- Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.
- Нормируемость.
На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.
Площади простых фигур
Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это латинская заглавная буква “S”. Это не правило, просто одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах площадь могут обозначать другими буквами.
Рассмотрим наиболее популярные формулы определения площадей:
- Прямоугольник. S=a*b – произведение длины на ширину.
- Треугольник. $S=<1over2>a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
- Круг. $S=pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.
Предварительно нужно убедиться в том, что параметры фигуры находятся в одинаковых единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.
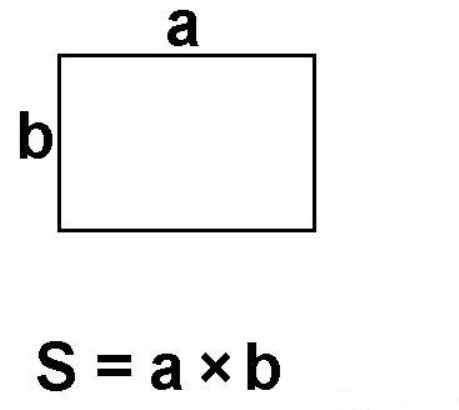
Рис. 2. Площадь прямоугольника.
Что такое площадь квадрата? Это сторона фигуры, возведенная в квадрат. Потому что квадрат это прямоугольник, длина и ширина которого равны:
Если у квадрата одна сторона равняется 100 м, то его площадь равна одному гектару. Эту единицу используют, когда необходимо оценить размеры земной поверхности при распределении сельскохозяйственных угодий:
Площади полей могут также измерять в арах, что в народе называют «соткой», потому что один ар – это квадрат, сторона которого равняется 10 м, а его площадь соответственно 100 $м^2$.
Площадь произвольной фигуры
Площадь сложной фигуры можно определить, просуммировав площади ее частей. Для этого нужно просто разделить произвольную геометрическую фигуру на простые составляющие так, чтобы можно было легко определить их квадратуры.
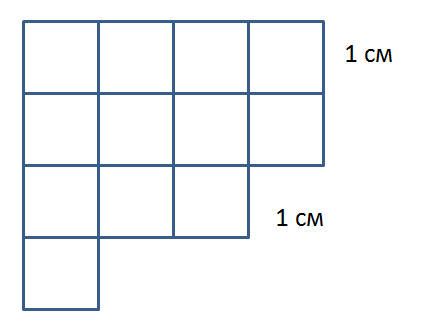
Рис. 3. Площадь сложной фигуры.
Фигуру на рисунке 3 можно разбить на 12 квадратов со сторонами 1 см. Тогда площадь каждого квадрата будет равняться $1см^2$. Получается, что площадь рассматриваемой фигуры будет $12 см^2$.
Что мы узнали?
Мы познакомились с понятием площади. Узнали, что для каждой фигуры есть свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.
Как обозначается высота h или c?

1)высота ели 19м, березы на 4 м меньше, сем ели, а высота рябины на 6 м меньше высоты березы?
1)высота ели 19м, березы на 4 м меньше, сем ели, а высота рябины на 6 м меньше высоты березы.
Объясни, что обозначают выражения.
2)составь по выражениям похожие задачи и реши их.
(40 — 8) — 7 (40 + 8) — 7

Как обозначается высота и ширина?
Как обозначается высота и ширина.

Величина рекордного прыжка кенгуру в длину была в 4 раз больше величины, обозначающей высоту прыжка этого животного?
Величина рекордного прыжка кенгуру в длину была в 4 раз больше величины, обозначающей высоту прыжка этого животного.
Какова длина прыжка, если высота прыжка равна 3м 20см?

Как обозначается корень?
Как обозначается корень.

Как обозначают доли?
Как обозначают доли?

Высота ели 19м, берёзы на 4 м меньше, чем ели, а высота рябины на 6м меньше высоты березы?
Высота ели 19м, берёзы на 4 м меньше, чем ели, а высота рябины на 6м меньше высоты березы.
Обьясни, что обозначают выражения : 19 — 4, (19 — 4) — 6.

Коробка имеет размеры : высота a см , длина b см , ширина 50 см Запишите выражение обозначающее объём коробки?
Коробка имеет размеры : высота a см , длина b см , ширина 50 см Запишите выражение обозначающее объём коробки.

Как в математике обозначаются длинна, ширина, высота?
Как в математике обозначаются длинна, ширина, высота?
Брусок поролона имеет массу 90 г.
Определите массу 1м3 поролона в килограммах.
Длинна 20 см, ширина 15 см, высота 10 см.

Помогите пожалуйста с задачей?
Помогите пожалуйста с задачей!
Высота ели 19 м, берёзы на 4 м.
Меньше, чем ели, а высота рябины на 6 м.
Меньше высоты берёзы.
Обьясни, что обозначают выражения : 19 — 4, (19 — 4) — 6.
Составь по выражениям похожие задачи и реши их.
(40 — 8) — 7 (40 + 8) — 7.

Закончи предложение целое обозначается обозначается числом?
Закончи предложение целое обозначается обозначается числом.
На этой странице сайта вы найдете ответы на вопрос Как обозначается высота h или c?, относящийся к категории Математика. Сложность вопроса соответствует базовым знаниям учеников 1 — 4 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

Я и понятия не имею как это решать.

7 * (45 — 23) = 7 * 22 = 154 9 * (38 — 17) = 9 * 21 = 189 5 * (2 * 75) = 5 * 150 = 750 6 * (4 * 4 * 5) = 6 * 40 = 480 (6 * 5) * (8 * 125) = 30 * 1000 = 30000 (9 * 3) * (2 * 50) = 27 * 100 = 2700.

45х7 — 23х7 = 154 38х9 — 9х17 = 189 2х75х5 = 750 6х4х4х5 = 480 8х6х5х125 = 30 000 9х2х50х3 = 2 700 все : ).

1)x = 10 18 — 8 = 10 2)x = 4 14 — 14 = 4 3)x = 5 11 — 6 = 5.

Первое ответ : г второе ответ : третье ответ : четвёртое ответ.

A — . Б некорректный в + . Г + д — . Е -.

А) + б) — в) + г) — д) + е) +.

7 / 15 + ( — 6 / 15) = 1 / 15 1) находим общий знаменатель. 2) решаем пример.

7 / 15 + ( — 2 / 15) = 1 / 15 Вроде так.

2) (6 — 4 8 / 15) : 2. 2 = ( 6 — 68 / 15) : 2. 2 = 22 / 15 : 2. 2 = 22 / 15 : 22 / 10 = 22 / 15 : 33 / 15 = 22 / 15 × 15 / 33 = 2 / 3.
В школьном курсе математики 4-5 класса рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.

Определение понятия
Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.
Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.
Характеристики понятия
Площадь имеет несколько характеристик:
- Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.
- Нормируемость.
На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.
Площади простых фигур
Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это латинская заглавная буква “S”. Это не правило, просто одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах площадь могут обозначать другими буквами.
Рассмотрим наиболее популярные формулы определения площадей:
- Прямоугольник. S=a*b – произведение длины на ширину.
- Треугольник. $S=<1over2>a*h$ – половина произведения основания на высоту, проведенную к этому основанию.
- Круг. $S=pi*r^2$ – отдельно нужно отметить, что окружность площади иметь не может. Только круг.

Рис. 1. Высота в произвольном треугольнике.
Предварительно нужно убедиться в том, что параметры фигуры находятся в одинаковых единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.

Рис. 2. Площадь прямоугольника.
Что такое площадь квадрата? Это сторона фигуры, возведенная в квадрат. Потому что квадрат это прямоугольник, длина и ширина которого равны:
Если у квадрата одна сторона равняется 100 м, то его площадь равна одному гектару. Эту единицу используют, когда необходимо оценить размеры земной поверхности при распределении сельскохозяйственных угодий:
Площади полей могут также измерять в арах, что в народе называют «соткой», потому что один ар – это квадрат, сторона которого равняется 10 м, а его площадь соответственно 100 $м^2$.
Площадь произвольной фигуры
Площадь сложной фигуры можно определить, просуммировав площади ее частей. Для этого нужно просто разделить произвольную геометрическую фигуру на простые составляющие так, чтобы можно было легко определить их квадратуры.

Рис. 3. Площадь сложной фигуры.
Фигуру на рисунке 3 можно разбить на 12 квадратов со сторонами 1 см. Тогда площадь каждого квадрата будет равняться $1см^2$. Получается, что площадь рассматриваемой фигуры будет $12 см^2$.
Что мы узнали?
Мы познакомились с понятием площади. Узнали, что для каждой фигуры есть свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.
