Как найти высоту параллелограмма
Как определить высоту параллелограмма, зная некоторые из его остальных параметров? Таких, как площадь, длины диагоналей и сторон, величины углов.

Вам понадобится
- калькулятор
Инструкция
В задачах по геометрии, точнее по планиметрии и тригонометрии, иногда требуется найти высоту параллелограмма, исходя из заданных значений сторон, углов, диагоналей и т.п.
Чтобы найти высоту параллелограмма, зная его площадь и длину основания, необходимо воспользоваться правилом определения площади параллелограмма. Площадь параллелограмма, как известно, равняется произведению высоты на длину основания:
S=a*h, где:
S – площадь параллелограмма,
а – длина основания параллелограмма,
h – длина опущенной на сторону а высоты, (или на ее продолжение).
Отсюда получаем, что высота параллелограмма будет равняться площади, разделенной на длину основания:
h=S/a
Например,
дано: площадь параллелограмма равняется 50 кв.см., основание – 10 см.;
найти: высоту параллелограмма.
h=50/10=5 (см).
Так как высота параллелограмма, часть основания и прилежащая к основанию сторона образуют прямоугольный треугольник, то для нахождения высоты параллелограмма можно использовать некоторые соотношения сторон и углов прямоугольных треугольников.
Если известны прилежащая к высоте h (DE) сторона параллелограмма d (AD) и противоположный высоте угол A (BAD), то расчета высоты параллелограмма нужно умножить длину прилежащей стороны на синус противоположного угла:
h=d*sinA,
например, если d=10 см, а угол А=30 градусов, то
H=10*sin(30º)=10*1/2=5 (см).
Если в условиях задачи заданы длина прилежащей к высоте h (DE) стороне параллелограмма d (AD) и длина отсекаемой высотой части основания (АЕ), то высоту параллелограмма можно найти воспользовавшись теоремой Пифагора:
|AE|^2+|ED|^2=|AD|^2, откуда определяем:
h=|ED|=√(|AD|^2-|AE|^2),
т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей стороны и отсекаемой высотой части основания.
Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 3 см, то длина высоты будет:
h=√(5^2-3^2)=4 (см).
Если известны длина прилежащей к высоте диагональ (DВ) параллелограмма и длина отсекаемой высотой части основания (ВЕ), то высоту параллелограмма можно также найти воспользовавшись теоремой Пифагора:
|ВE|^2+|ED|^2=|ВD|^2, откуда определяем:
h=|ED|=√(|ВD|^2-|ВE|^2),
т.е. высота параллелограмма равняется корню квадратному из разности квадратов длины прилежащей диагонали и отсекаемой высотой (и диагональю) части основания.
Например, если длина прилегающей стороны равняется 5 см., а длина отсекаемой части основания равна 4 см, то длина высоты будет:
h=√(5^2-4^2)=3 (см).
Видео по теме
Источники:
- что такое высота параллелограмма
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Четырёхугольник, у которого стороны, находящиеся напротив друг друга параллельны и равны друг другу,
называется параллелограммом. Отрезок перпендикулярной прямой, проходящей от любой точки прямой, на
которой лежит одна из сторон параллелограмма через прямую, на которой расположена противоположная
сторона данной фигуры, является высотой параллелограмма. Высот параллелограмма можно провести
бесконечное множество через разные точки, но они неизменно будут перпендикулярны двум сторонам
фигуры.
- Высота параллелограмма через площадь и основание
- Высота параллелограмма через боковую сторону и острый угол
при основании - Высота параллелограмма через длину отрезка, образованного
на основании и боковую сторону - Высота параллелограмма через длину отрезка, образованного
на основании и диагональ
Через площадь и основание
Высота параллелограмма равна отношению площади к основанию.
h = S / a
где h – длина высоты параллелограмма, S – площадь, a – длина основания.
Цифр после
запятой:
Результат в:
Пример. На рисунке представлены пара абсолютно одинаковых параллелограммов. На левом
обозначена длина стороны (основания) в 6 единиц и проходящие через нее в разных точках высоты в 4
единицы.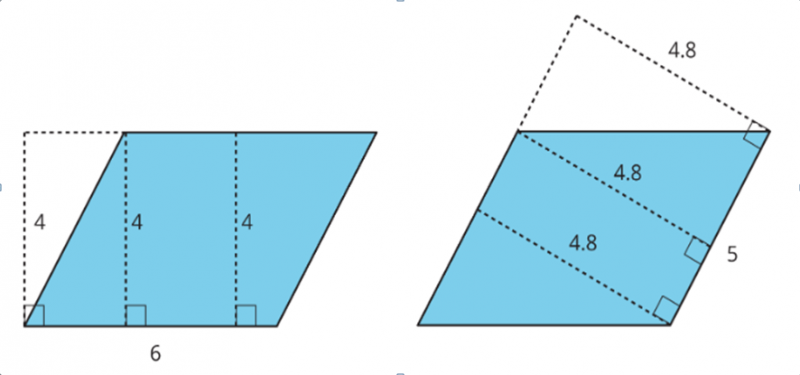 На
На
правом обозначена длина стороны (основания) в 5 единиц и проходящие через нее в разных точках высоты
в 4,8 единиц. Площадь параллелограмма можно вычислить умножением длины высоты на длину той стороны
(основания), которой эта высота перпендикулярна. Результат умножения будет одинаков для любой 2 двух
пар высота-основание. В рассматриваемом случае: 4 × 6 = 24; 4,8 × 5 = 24.
Можно визуально убедиться в этом, если разрезать фигуру и переставив части так, как показано на
рисунке.
Исходя из полученного, путем обратного подсчета можно вывести правило для определения высоты из
заданной площади и основания. В приведенном примере расчет будет выглядеть следующим образом: 24 / 6 = 4; 24 / 5 = 4,8.
Через длину отрезка, образованного на основании и диагональ
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и диагонали
производится также с использованием теоремы Пифагора. Высота в этом случае будет равна квадратному
корню из разницы диагонали и отрезка на основании.
h = √(d² — A2²)
где d — диагональ, A2 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 47 см, отрезок образованный на основании равен
34 см, тогда получим h = √(b² — A1²) = √(47² — 34²) = 32,4 см.
Через боковую сторону и острый угол при основании
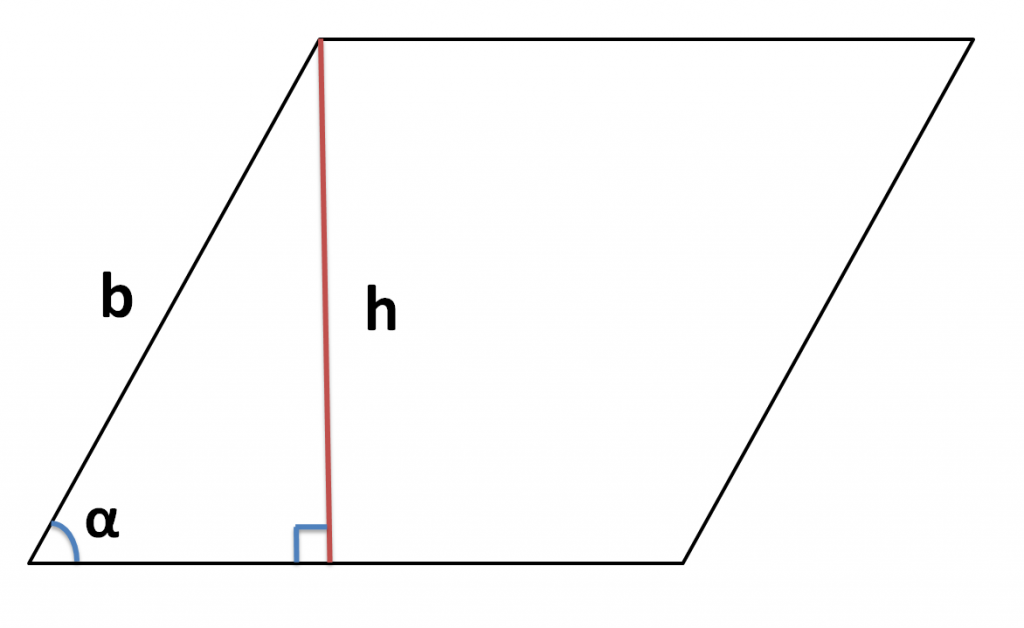
Если от тупого угла параллелограмма провести к основанию высоту, то образуется прямоугольный
треугольник, как показано на рисунке ниже. Если нам известна величина острого угла и длина боковой
стороны, то можно вычислить высоту через формулу синуса, который определяется как отношение катета к
гипотенузе. Роль катета здесь играет высота, а боковая сторона является гипотенузой. Соответственно
высота здесь будет равна произведению длины боковой стороны на синус острого угла.
h = b * sinα
где b — боковая сторона, sin α — острый угол при основании.
Цифр после
запятой:
Результат в:
Если известна величина тупого угла параллелограмма, то величину острого можно получить, отняв
величину тупого угла от 180 градусов.
Пример. Пусть боковая сторона b равна 115 см, острый угол при основании α равен 65º,
тогда получим h = b * sinα = 115 * sin 65 = 104 см.
Через длину отрезка, образованного на основании и боковую сторону
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и боковой
стороне производится с использованием теоремы Пифагора. Высота будет равна квадратному корню из
разницы квадратов боковой стороны и диагонали.
h = √(b² — A1²)
где b — боковая сторона, A1 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 39 см, отрезок образованный на основании равен
16 см, тогда получим h = √(b² — A1²) = √(39² — 16²) = 35,6 см.
Пирамида определяется как трехмерная структура – многогранник, в основе которой лежит многоугольник.
В основании пирамиды находится многоугольник. Углы многоугольника соединены линиями – боковыми
ребрами с одной точкой, которая в пирамиде именуется как вершина. Треугольники, образованные парами
соседних боковых ребер и стороной основания называются боковыми гранями.
В основании правильной пирамиды лежит правильный многоугольник (тот у которого все стороны равны
между собой). У правильной пирамиды длина боковых ребер одинаковая. Соответственно правильная
пирамида образована боковыми гранями, являющимися равными равнобедренными треугольниками,
соединенными с основанием.
Апофемами в пирамиде называют отрезки прямых, проведенных от вершины перпендикулярно к основаниям.
Также, одновременно апофемы являются высотами треугольников – боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему грани.
Установлено, что умение вычислять длину апофемы, было востребовано с древнейших времен для
строительства сооружений. Предположительно, перед возведением подобных сооружений предварительные
размеры могли быть отрегулированы древними инженерами с помощью натянутых шнуров. Расшифровка
древнеегипетских иероглифов дает перевод значения понятия землемера как «натяжителя веревок».
Умение вычислять высоту параллелограммов, было востребовано с древнейших времен для проверки
правильности измерений земельных участков. Множество древних народов тысячи лет назад воздвигали
пирамиды и курганы для различных целей. Современные измерения позволяют утверждать, что некоторые их
них точно ориентированы – как по сторонам света, так и в трехмерном измерении по созвездиям.
Вероятно, часть из этих сооружений использовалась для определения орбиты Земли относительно звезд.
Эти сведения использовались для определения времени начала различных сельскохозяйственных работ. От
этого зависела урожайность, а значит вопрос выживания народов. Таким образом, вычисление апофемы
позволяло точно ориентировать пирамиду в пространстве и спасало жизни людей.
КАК НАЙТИ ВЫСОТУ ПАРАЛЕЛОГРАММА ЕСЛИ ИЗВЕСТНО ОСНОВАНИЕ И СТОРОНА
инсаф ильдусович
Ученик
(90),
закрыт
7 лет назад
Лучший ответ
Тесты_математика
Гений
(51456)
7 лет назад
ТО есть известны все 4 стороны пар-мма-этого недостаточно-с со сторогами например-5 .10.5.10 можно построить много паралл-мов…. еще нужен.. и высота не определена
Остальные ответы
DeT_Ka G_EйMer
Ученик
(114)
7 лет назад
Что не понятно пиши, числа брала к примеру…
Похожие вопросы
Быстро вычислить высоту параллелограмма позволит этот удобный онлайн-калькулятор. С его помощью можно определить не только высоту параллелограмма, но и такие величины как площадь, биссектриса, периметр, диагональ, углы параллелограмма вместе с подробными формулами расчета.
Не забудьте добавить страницу в закладки, чтобы всегда иметь под рукой удобную шпаргалку по геометрии!
Введите данные:
Длинная сторона (a)
Короткая сторона (b)
Ключевой показатель *
Значение ключевого показателя *
Округление:
Знаков после запятой
* – обязательно заполнить

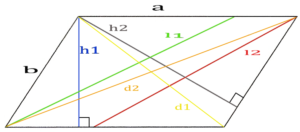
Высота – перпендикуляр исходящий из вершины угла на противоположенную сторону
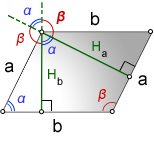 a, b – стороны параллелограмма
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
α, β – углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):


Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 13 ноября 2011
-
Обновлено: 13 августа 2021
