В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
-
Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
-
Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны
![]()
где S – площадь треугольника.
2. Через длины всех сторон
![]()
где p – это полупериметр треугольника, который рассчитывается так:
![]()
3. Через длину прилежащей стороны и синус угла
![]()
4. Через стороны и радиус описанной окружности
![]()

где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:


Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
![]()
2. Через стороны треугольника
![]()
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
![]()

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
![]()
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
![]()
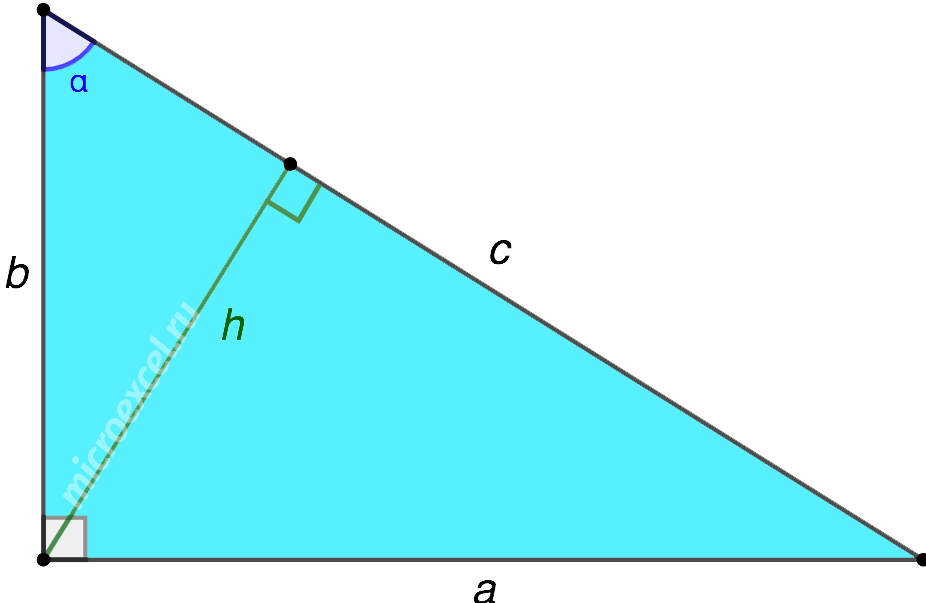
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.

H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):

Формула длины высоты через гипотенузу и острые углы, (H):

Формула длины высоты через катет и угол, (H):

Формула длины высоты через составные отрезки гипотенузы , (H):

- Подробности
-
Опубликовано: 09 октября 2011
-
Обновлено: 13 августа 2021
Все формулы высоты прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
H – высота из прямого угла
a, b – катеты
с – гипотенуза
c 1 , c 2 – отрезки полученные от деления гипотенузы, высотой
α , β – углы при гипотенузе
Формула длины высоты через стороны, ( H ):
Формула длины высоты через гипотенузу и острые углы, ( H ):
Формула длины высоты через катет и угол, ( H ):
Формула длины высоты через составные отрезки гипотенузы , ( H ):
Свойства высоты прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.
Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть
Свойства высоты в прямоугольном треугольнике
Свойство 1
В прямоугольном треугольнике две высоты (h1 и h2) совпадают с его катетами.

Третья высота (h3) опускается на гипотенузу из прямого угла.
Свойство 2
Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.
Свойство 3
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.

Аналогичным образом доказывается, что ∠ABD = ∠DAC.
Свойство 4
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:
1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:


2. Через длины сторон треугольника:

Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :



Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение
Воспользуемся первой формулой, представленной в Свойстве 4:

Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Высота в прямоугольном треугольнике
Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол равен углу .
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника в раз:
При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , — высота, , . Найдите .
Рассмотрим треугольник . В нем известны косинус угла и противолежащий катет . Зная синус угла , мы могли бы найти гипотенузу . Так давайте найдем :
(поскольку значение синуса острого угла положительно). Тогда:
Рассмотрим прямоугольный треугольник , . Поскольку
2. В треугольнике угол равен , , . Найдите высоту .
Сделайте чертеж и рассмотрите прямоугольный треугольник .
3. В треугольнике угол равен , , . К гипотенузе проведена высота . Найдите .
Это чуть более сложная задача. Ведь вам неизвестны катеты и .
Зато можно записать теорему Пифагора: .
Нам известно также, что:
Решая эту систему из двух уравнений, найдем:
Запишем площадь треугольника АВС двумя способами:
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vysota-v-pryamougolnom-treugolnike-i-ee-svojstva/
[/spoiler]
Здесь рассмотрены все возможные способы нахождения высоты треугольников разных типов. Высота
треугольника – отрезок, проведенный из вершины треугольника перпендикулярно к противоположной
стороне. В задачах нахождение высоты часто является промежуточным звеном для поиска других значений.
Она и является катетом в треугольнике, который сама же образует, и участвует во многих формулах,
например, для нахождения площади.
- Высота разностороннего треугольника через площадь и длину
стороны - Высота разностороннего треугольника через длины всех
сторон - Высота разностороннего треугольника через длину прилежащей
стороны и синус угла - Высота разностороннего треугольника через стороны и радиус
описанной окружности - Высота равнобедренного треугольника через основание и
боковые стороны - Высота прямоугольного треугольника через длины отрезков,
образованных на гипотенузе - Высота прямоугольного треугольника через все стороны
треугольника - Высота равностороннего треугольника через сторону
треугольника
Через площадь и длину стороны разностороннего треугольника
Через площадь и длину высота находится по формуле:
h = 2S / a
где S – площадь треугольника, а – сторона треугольника.
Цифр после
запятой:
Результат в:
Согласно этой формуле высота равна удвоенной площади, деленной на длину стороны, к которой она
проведена.
Пример. Найдите высоту разностороннего треугольника, проведенную к стороне а,
площадь которого равна 27 см, а длина стороны а составляет одну треть от площади. Решение: Найдем
сторону а. Так как известно, что она составляет треть от площади, а = 27 / 3 = 9 см.
Теперь воспользуемся формулой для нахождения высоты: h = 2S / a. Подставим
известные значения. h = 2 * 27 / 9 = 6 см. Ответ: 6 см
Через длины всех сторон разностороннего треугольника
Через длины всех сторон высота разностороннего треугольника ищется по формуле:
h = (2 √(p (p-a)(p-b)(p-c))) / 2
p = (a + b + c) / 2
где h – высота, а, b, c – стороны треугольника, p – полупериметр треугольника.
Цифр после
запятой:
Результат в:
Полупериметр треугольника можно найти либо в два этапа через периметр, либо сразу по формуле. Этим
способом удобно пользоваться, когда треугольник разносторонний.
Пример. Периметр разностороннего треугольника равен 18 см. Длины сторон 6 см и 8 см. Найдите
высоту, проведенную к стороне а. Решение: P = a + b + c, значит с = P – a – b , то есть c = 18 – 8 – 6 = 4 см. Для
нахождения h будем использовать формулу h = (2 √(p (p-a)(p-b)(p-c))) / 2.
Сначала найдем полупериметр (p): p = p / 2 = 18 / 2 = 9 см. Подставим,
найденные значения в формулу высоты: h = (2 √(9 (9 — 6)(9 — 8)(9 — 4))) / 2 = √135 / 3 = 2,12 см
Через длину прилежащей стороны и синус угла разностороннего треугольника
Через длину прилежащей стороны и синус угла высота ищется по следующей формуле:
h = a * sin α
где а – длина стороны, sin α – синус прилежащей стороны.
Цифр после
запятой:
Результат в:
Пример. В разностороннем треугольнике высота проведена к стороне AB. Угол ACH равен
30˚, а длина стороны AB 12 см. Найдите длину высоты CH в треугольнике ABC. По теореме о сумме углов
в треугольнике найдем угол САН. ∠САН = 180 – (∠АСН + ∠АНС). ∠САН = 180 – 90 – 30 = 60˚ sin 60º = 1/2. СН = AB * sin ∠САН, СН = 12 * 1/2 = 6 см. Ответ:
6 см
Через стороны и радиус описанной окружности разностороннего треугольника
Через стороны и радиус описанной окружности высоту можно найти по следующей формуле:
h = bc / 2R
где r – радиус описанной около треугольника окружности, b,c – стороны треугольника
Цифр после
запятой:
Результат в:
Пример. Вокруг разностороннего треугольника описана окружность с радиусом 3 см. Из
вершины между сторонами b и с проведена высота. Стороны b и с соответственно равны 5 см и 6 см.
Найдите высоту. Решение: Найдем высоту, используя формулу h = 5 * 6 / 2 * 3 = 30 / 6 = 5 см. Ответ:
5 см.
Через длины отрезков прямоугольного треугольника, образованных на гипотенузе
Через длины отрезков образованных на гипотенузе высоту можно найти по следующей формуле:
h = √(C1 * C2)
где: C1, C2 — отрезки, образованные проведением высоты к гипотенузе.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике катеты равны 4 см и 3 см. Угол BAH равен 30˚.
Найдите высоту. По теореме Пифагора найдём сторону BC, которая является гипотенузой в треугольнике
ABC. BC² = AB² = AC², BC² = 4² + 3² = 16+9 = 25 см², BC = √25 = 5 см. Угол
АНВ равен 90˚, так как АН является высотой, то есть, проведена перпендикулярно к стороне ВС.
Следовательно, треугольник АНВ – прямоугольный. Сторона ВН лежит напротив угла 30˚ в прямоугольном
треугольнике, значит, ее длина равна половине длины гипотенузы. Найдем ВН. BH = 1/2 AB. BH = 1/2 × 4 = 2 см. BC = BH + HC,
значит, HC = BC – BH, HC = 5 – 2 = 3 см. По формуле найдем высоту
(АН). АН = √(2 * 3) = √6 = 2,4 см. Ответ: 2,4 см.
Через основание и боковые стороны равнобедренного треугольника
Через основание и боковые стороны высота равнобедренного треугольника находится по формуле:
h = √(b² — a²/4)
где а – основание треугольника, b – боковая сторона. Для равнобедренного треугольника.
Цифр после
запятой:
Результат в:
Пример. В равнобедренном треугольнике АВС боковая сторона равна 8 см. Из вершины В к
основанию АС проведена высота ВН. Отрезок АН равен 5 см. Найдите высоту. Решение: Так как по условию
треугольник АВС равнобедренный по условию, то АВ = ВС = 8 см высота ВН,
является и медианой, и биссектрисой. Значит, АН = НС, а АС = НС + АН, АС = 5 + 5 = 10 см. По
формуле найдем высоту ВН = √(АВ² — АС² / 4). ВН = √(8² — 10² / 4) = √(64 — 100 / 4) = √39 = 6 см.
Ответ: 6 см.
Высота прямоугольного треугольника через все стороны треугольника
Если известны все стороны прямоугольного треугольника, то можно найти его высоту по следующей
формуле:
h = ab / c
где a,b,c – стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. В прямоугольном треугольнике угол между катетом и гипотенузой равен 45˚.
Длина стороны АС равна 6 см. Найти высоту АН. Решение: По теореме о сумме углов в треугольнике
найдем угол АСВ. ∠АСВ = 180˚ – (45˚ + 90˚) = 45˚. Так как АСВ = АСВ, то
треугольник АВС равнобедренный с основанием ВС. Таким образом, АС = АВ = 6 см. По теореме Пифагора найдем гипотенузу ВС. BC² = AB² + AC². BC² = 6² + 6² = 36 +36 = 72 см². ВС = √72 = 6√2 см. Найдем
высоту по формуле AH = AB * AC / BC. АН = 6 * 6 / 6√2= см. Домножим
полученное значение на √2: (6 * √2) / √2 * √2 = 6√2 / 2 = 3√2 см. Ответ:
3√2 см
Через сторону равностороннего треугольника
Высота равностороннего треугольника через сторону треугольника ищется по следующей формуле:
h = a√3 / 2
где a – сторона треугольника.
Цифр после
запятой:
Результат в:
Пример: Найдите высоту в равностороннем треугольнике, если известно, что его сторона
равна 4√3 см. Решение: Для нахождения высоты воспользуемся формулой h = a√3 / 2 = √3 * 4 √3 / 2 = 4 * 3 / 2 = 6 см. Ответ:
6 см
В зависимости от типа треугольника высота может располагаться по-разному:
- Например, в треугольнике KGM высота GH, проведённая из вершины G к стороне находится внутри
треугольника, так как треугольник является остроугольным. Кроме того, треугольник в данном
примере равнобедренный, значит, она же является биссектрисой и медианой. Знание этого пригодится
при решении задач, например таким образом можно будет найти основание.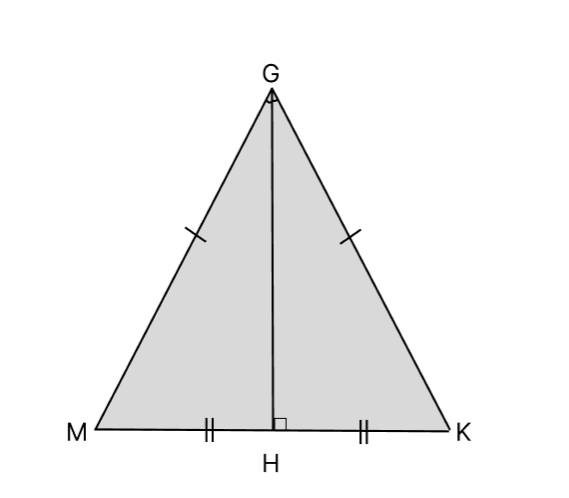
- В тупоугольном треугольнике высота будет выходить за его пределы и для того чтобы её провести
понадобится сначала продлить сторону. Например, на рисунке сторона ВС продлена до НС.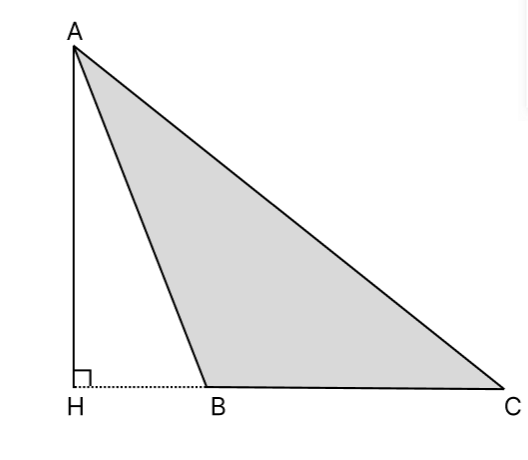
- В случае, когда треугольник имеет прямой угол – высота совпадёт с одним из катетов, либо будет
внутри треугольника (как в первом рассмотренном варианте) и проведена к гипотенузе.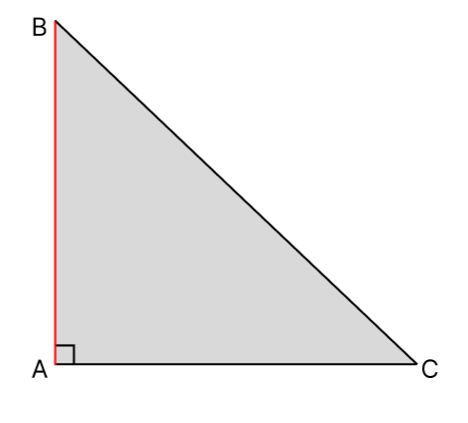
Высота, проведенная в любом треугольнике, делит его на два прямоугольных треугольника, становясь смежным катетом. Сторона, на которую опущена высота, оказывается также разделенной на две пропорциональных части. Зная все три стороны, можно собрать их по теореме Пифагора, и приравняв высоту в качестве катета в двух вышеуказанных треугольниках, получить ее формулу для любого произвольного треугольника:

С другой стороны, можно использовать сторону, прилежащую к высоте и угол α, чтобы вычислить высоту треугольника.

Известная его сторона будет гипотенузой в прямоугольном треугольнике, а сама высота – катетом, противолежащим углу α. Два этих измерения связывает синус угла, поэтому высота равна его произведению на сторону a:
h=a sinα
Высота в прямоугольном треугольнике, опущенная из прямого угла (остальные две совпадают с катетами), получает особые свойства. Так как все три получившихся прямоугольных треугольника подобны друг другу, их стороны составляют пропорцию, которая раскладывается как квадрат высоты, равный произведению проекцию катетов на гипотенузу, или проще говоря, частей гипотенузы, на которые ее делит высота.

Из этого следует, что высота равна квадратному корню из данного произведения, а это есть не что иное как среднее пропорциональное приведенного выражения.
В равностороннем треугольнике, высота делит угол, из которого она исходит, на два одинаковых угла по 30°. Высота, оказываясь катетом, прилежащим к этому углу, внутри прямоугольного треугольника, подчиняется отношению косинуса угла α, а так как  , а гипотенуза a, то формула высоты в равностороннем треугольнике будет выглядеть так:
, а гипотенуза a, то формула высоты в равностороннем треугольнике будет выглядеть так:

