Как найти высоты треугольника по формуле герона

Как найти высоты треугольника по формуле герона

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

Формула Герона для нахождения площади треугольника

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим еще один способ вычисления площади треугольника – с помощью формулы Герона. Она позволяет вычислить площадь треугольника, зная лишь его стороны, что может очень пригодиться, особенно в практических вычислениях. Мы выпишем и докажем формулу Герона, а также решим несколько задач на применение этой формулы.

[spoiler title=”источники:”]

http://mozgan.ru/Geometry/AreaTriangle

http://interneturok.ru/lesson/geometry/8-klass/ploschad/formula-gerona-dlya-nahozhdeniya-ploschadi-treugolnika

[/spoiler]

Источник

Фо́рмула Герона — формула для вычисления площади треугольника S по длинам его сторон a,b,c:

{displaystyle S={sqrt {p(p-a)(p-b)(p-c)}}},

где p — полупериметр треугольника: {displaystyle p={tfrac {1}{2}}cdot (a+b+c)}.

Формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми, такие треугольники носят название героновых, простейшим героновым треугольником является египетский треугольник.

Доказательство 1 (тригонометрическое):

Доказательство 2 (на основе теоремы Пифагора):

Треугольник со сторонами a, b, c и высотой

h, разделяющей основание

c на

d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a2 = h2 + (c − d)2 и b2 = h2 + d2 — см. рисунок справа. Вычитая из первого равенства второе, получаем a2 − b2 = c2 − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

{displaystyle d={frac {-a^{2}+b^{2}+c^{2}}{2c}}}

Для высоты h у нас было равенство h2 = b2 − d2, в которое можно подставить полученное выражение для d и применить формулы для квадратов:

{displaystyle {begin{aligned}h^{2}&=b^{2}-left({frac {-a^{2}+b^{2}+c^{2}}{2c}}right)^{2}={frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\&={frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\end{aligned}}}

Замечая, что {displaystyle b+c-a=2p-2a}, a+b+c=2p, a+b-c=2p-2c, {displaystyle a-b+c=2p-2b}, получаем:

{displaystyle {begin{aligned}h^{2}&={frac {2(p-a)cdot 2pcdot 2(p-c)cdot 2(p-b)}{4c^{2}}}={frac {4p(p-a)(p-b)(p-c)}{c^{2}}}end{aligned}}}

Используя основное равенство для площади треугольника {displaystyle S={frac {ch}{2}}} и подставляя в него полученное выражение для h, в итоге имеем:

{displaystyle {begin{aligned}S={sqrt {{frac {c^{2}}{4}}cdot {frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={sqrt {p(p-a)(p-b)(p-c)}}end{aligned}}}

ч.т.д.

Вариации и обобщения[править | править код]

  • Формулу Герона можно записать с помощью определителя в виде[1]:
    -16S^{2}={begin{vmatrix}0&a^{2}&b^{2}&1\a^{2}&0&c^{2}&1\b^{2}&c^{2}&0&1\1&1&1&0end{vmatrix}}={begin{vmatrix}a&b&c&0\b&a&0&c\c&0&a&b\0&c&b&aend{vmatrix}}
Первый определитель последней формулы является частным случаем определителя Кэли — Менгера[en] для вычисления гиперобъёма симплекса.
через длины высот h_{a}, h_{b} и h_{c} и полусумму их обратных величин H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2[3]:

S^{-1}=4{sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}};
через углы треугольника alpha , beta и gamma , полусумму их синусов {displaystyle s=(sin alpha +sin beta +sin gamma )/2} и диаметр описанной окружности {displaystyle D={tfrac {a}{sin alpha }}={tfrac {b}{sin beta }}={tfrac {c}{sin gamma }}}[4]:

S=D^{2}{sqrt {s(s-sin alpha )(s-sin beta )(s-sin gamma )}}.
  • Площадь вписанного в окружность четырёхугольника вычисляется по формуле Брахмагупты:
    S={sqrt {(p-a)(p-b)(p-c)(p-d)}},
где p={frac {a+b+c+d}{2}} — полупериметр четырёхугольника; в данном случае треугольник оказывается предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Та же формула Брахмагупты через определитель[5]:

S={frac {1}{4}}{sqrt {-{begin{vmatrix}a&b&c&-d\b&a&-d&c\c&-d&a&b\-d&c&b&aend{vmatrix}}}}
где:

{displaystyle {begin{aligned}a&={sqrt {xYZ}}\b&={sqrt {yZX}}\c&={sqrt {zXY}}\d&={sqrt {xyz}}\X&=(w-U+v),(U+v+w)\x&=(U-v+w),(v-w+U)\Y&=(u-V+w),(V+w+u)\y&=(V-w+u),(w-u+V)\Z&=(v-W+u),(W+u+v)\z&=(W-u+v),(u-v+W)end{aligned}}}.
где theta _{s}={frac {theta _{a}+theta _{b}+theta _{c}}{2}} — полупериметр.

Примечания[править | править код]

  1. ↑ Weisstein, Eric W. Heron’s Formula. Архивная копия от 5 сентября 2015 на Wayback Machine From MathWorld–A Wolfram Web Resource.
  2. ↑ Benyi, Arpad, “A Heron-type formula for the triangle, « Mathematical Gazette» 87, July 2003, 324—326.
  3. ↑ Mitchell, Douglas W., “A Heron-type formula for the reciprocal area of a triangle, ” Mathematical Gazette 89, November 2005, 494.
  4. ↑ Mitchell, Douglas W., “A Heron-type area formula in terms of sines, ” Mathematical Gazette 93, March 2009, 108—109.
  5. ↑ Стариков В. Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
  6. ↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1] Архивная копия от 27 июня 2013 на Wayback Machine, pp. 16-17.
  7. ↑ Маркелов С. Формула для объёма тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132

Литература[править | править код]

  • § 258 в А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
  • Николаев Н. О площади треугольника // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
  • Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора
Источник

Расчёт высоты треугольника по сторонам

Значащих цифр:

Определение треугольника

Треугольник это геометрическая фигура, которая состоит из трёх точек не лежащих на одной прямой и трёх отрезков попарно соединяющих эти точки. У треугольника сумма любых двух длинн сторон должна быть меньше третьей.

Определение высоты треугольника

Высота треугольника это перпендикуляр опущенный с вершины на противоположную сторону.

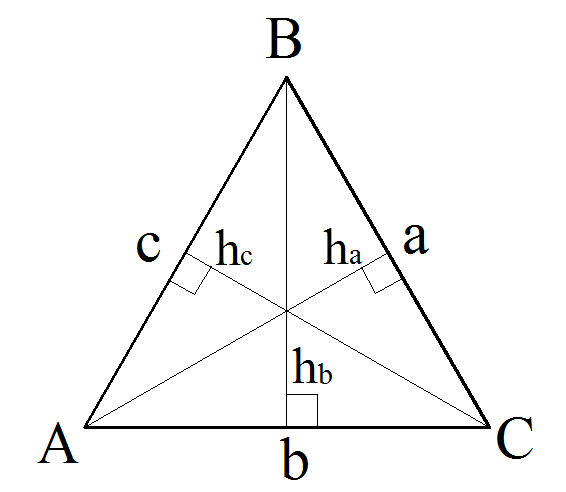
Высота треугольника по сторонам

Формулу высоты выведем из формулы Герона

color{#0000FF}{p = Large{frac{a + b + c}{2}}}

color{#0000FF}{S = sqrt{p(p-a)(p-b)(p-c)}}

Где a, b, c – длины сторон треугольника, p – полупериметр

и формулы площади треугольника

color{#0000FF}{S = Largefrac{1}{2}normalsize*b*h_b}

Выведем высоту треугольника

color{#0000FF}{Largefrac{1}{2}normalsize*b*h_b = sqrt{p(p-a)(p-b)(p-c)}}

Формулы высот треугольника

color{#0000FF}{h_b = Largefrac{2sqrt{p(p-a)(p-b)(p-c)}}{b}}

color{#0000FF}{h_a = Largefrac{2sqrt{p(p-a)(p-b)(p-c)}}{a}}

color{#0000FF}{h_c = Largefrac{2sqrt{p(p-a)(p-b)(p-c)}}{c}}

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

  • Нахождение высоты треугольника

    • Высота в разностороннем треугольнике

    • Высота в равнобедренном треугольнике

    • Высота в прямоугольном треугольнике

    • Высота в равностороннем треугольнике

  • Примеры задач

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

Высота в разностороннем треугольнике ABC

1. Через площадь и длину стороны

Формула для нахождения высоты треугольника через его площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

Формула для нахождения высоты треугольника через длины его сторон

где p – это полупериметр треугольника, который рассчитывается так:

Формула для расчета полупериметра треугольника

3. Через длину прилежащей стороны и синус угла

Формула для нахождения высоты треугольника через длину стороны и синуса угла

4. Через стороны и радиус описанной окружности

Формула для нахождения высоты треугольника через длины сторон и радиус описанной окружности

Описанная вокруг разностороннего треугольника окружность

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Формула для нахождения высоты к основанию в равнобедренном треугольнике

Опущенная на основание равнобедренного треугольника высота

Высота в прямоугольном треугольнике

Проведенная к гипотенузе высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

Формула для нахождения высоты к гипотенузе в прямоугольном треугольнике

2. Через стороны треугольника

Формула для нахождения высоты к гипотенузе в прямоугольном треугольнике через длины его сторон

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Формула для нахождения высоты в равностороннем треугольнике

Высота в равностороннем треугольнике

Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Нахождение высоты треугольника через длину стороны и синус прилежащего угла (пример)

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Нахождение основания равнобедренного треугольника через высоту и боковую сторону (пример)

Источник

Как найти высоту в треугольнике

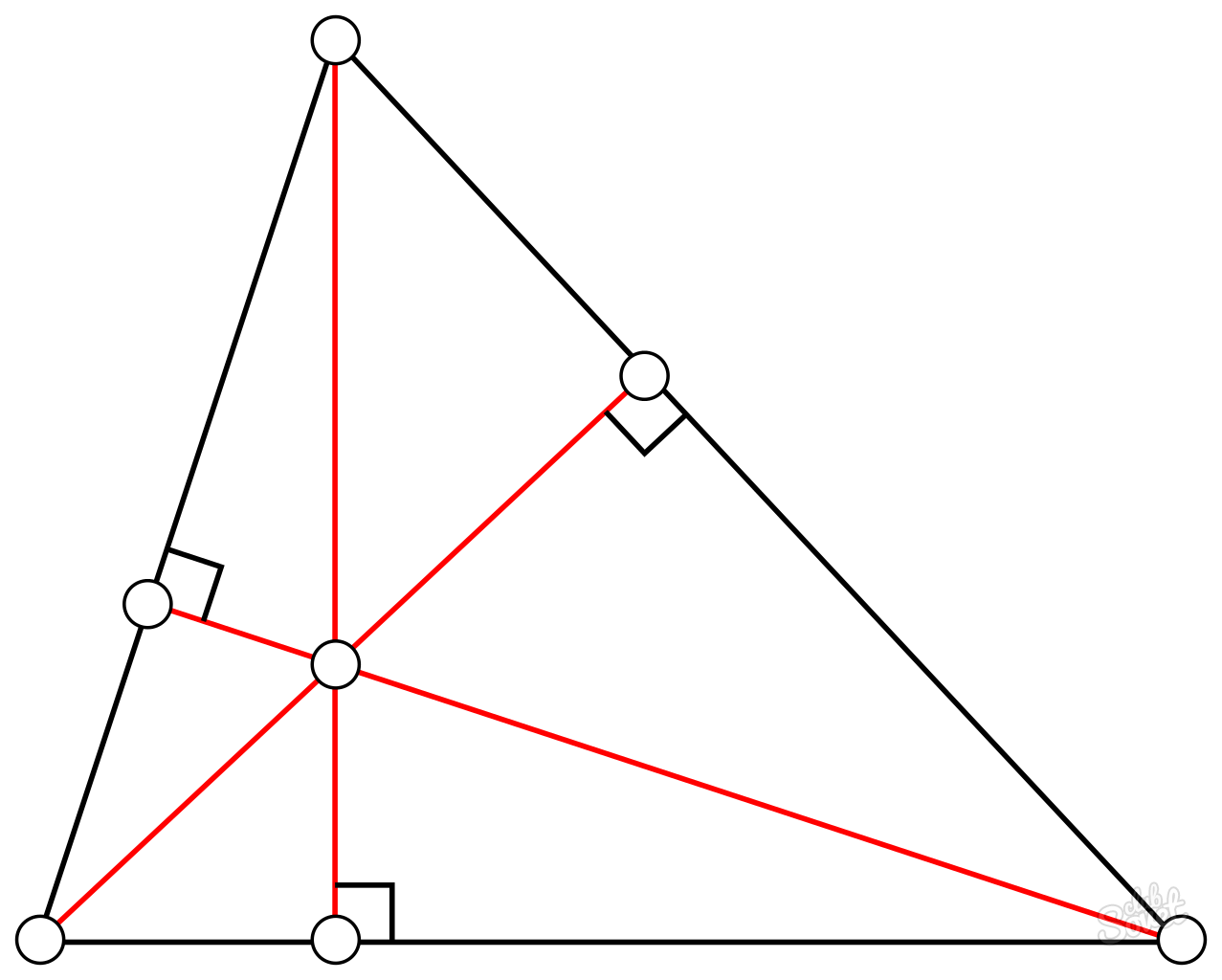
Как найти высоту в треугольнике

При решении различного рода задач, как сугубо математического, так и прикладного характера (особенно в строительстве), нередко требуется определить значение высоты определенной геометрической фигуры. Как рассчитать данную величину (высоту) в треугольнике?

Если мы попарно совместим 3 точки, расположенные не на единой прямой, то полученная фигура будет треугольником. Высота – часть прямой из любой вершины фигуры, которая при пересечении с противоположной стороной образует угол 90°.

1

 Найти высоту в разностороннем треугольнике

Определим значение высоты треугольника в случае, когда фигура имеет произвольные углы и стороны.

Формула Герона

h(a)=(2√(p(p-a)*(p-b)*(p-c)))/a, где

p – половина периметра фигуры, h(a) – отрезок к стороне a, проведенный под прямым углом к ней,
b, c – 2 другие стороны треугольника,
p=(a+b+c)/2 – расчет полупериметра.

В случае наличия площади фигуры для определения ее высоты можно воспользоваться соотношением h(a)=2S/a.

Тригонометрические функции

Для определения длины отрезка, который составляет при пересечении со стороной a прямой угол, можно воспользоваться следующими соотношениями: если известна сторона b и угол γ или сторона c и угол β, то h(a)=b*sinγ или h(a)=c*sinβ.
Где:
γ – угол между стороной b и a,
β – угол между стороной c и a.

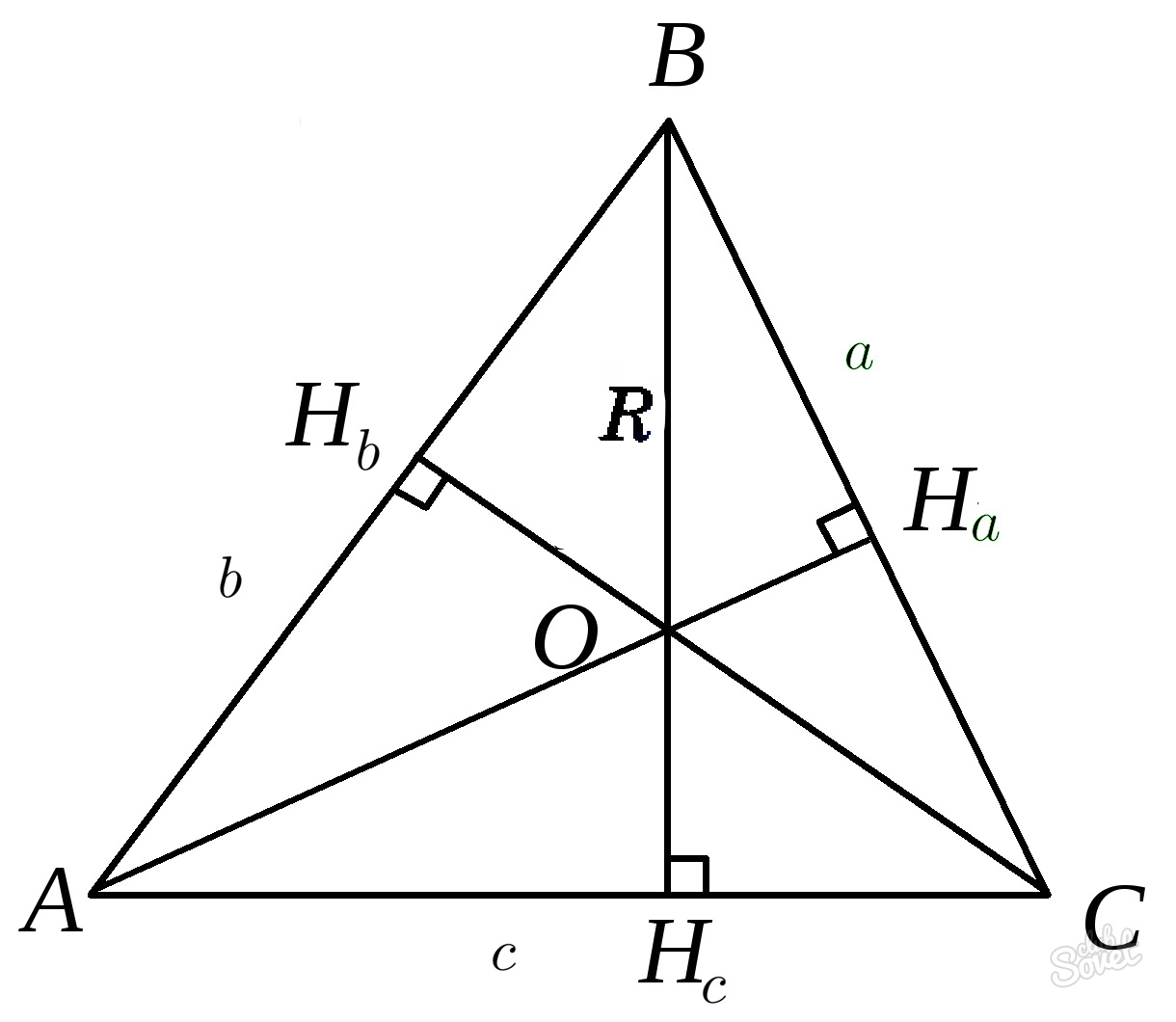
Взаимосвязь с радиусом

Если исходный треугольник вписан в окружность, для определения величины высоты можно воспользоваться радиусом такой окружности. Центр ее расположен в точке, где пересекаются все 3 высоты (из каждой вершины) – ортоцентре, а расстояние от него и до вершины (любой) – радиус.

Тогда h(a)=bc/2R, где:
b, c – 2 другие стороны треугольника,
R – радиус описывающей треугольник окружности.

2

Найти высоту в прямоугольном треугольнике

В данном виде геометрической фигуры 2 стороны при пересечении образуют прямой угол – 90°. Следовательно, если требуется определить в нем значение высоты, то необходимо вычислить либо размер одного из катетов, либо величину отрезка, образующего с гипотенузой 90°. При обозначении:
a, b – катеты,
c – гипотенуза,
h(c) – перпендикуляр на гипотенузу.
Произвести необходимые расчеты можно с помощью следующих соотношений:

  • Пифагорова теорема:

a=√(c2-b2 ),
b=√(c2-a2 ),
h(c)=2S/c,т.к. S=ab/2,то h(c)=ab/c .

  • Тригонометрические функции:

a= c*sinβ,
b=c* cosβ,
h(c)=ab/c=с* sinβ* cosβ.

3

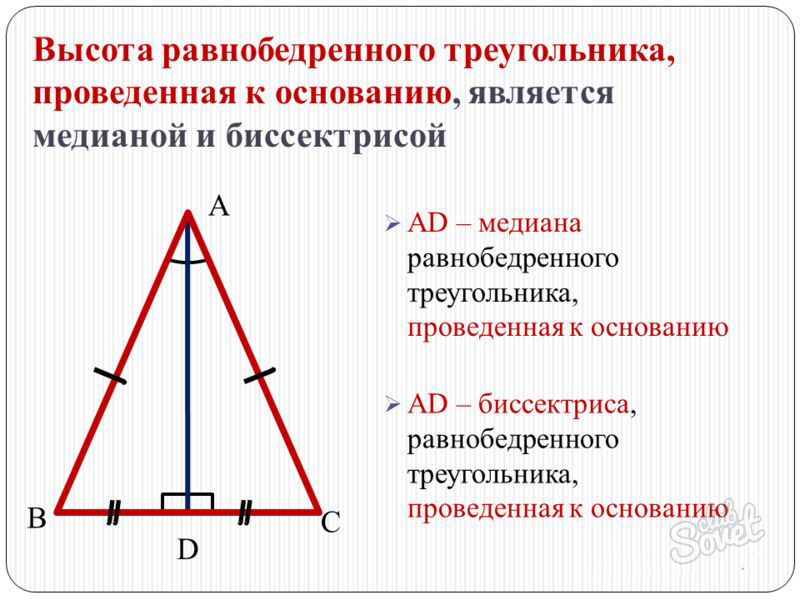
Найти высоту в равнобедренном треугольнике

Данная геометрическая фигура отличается наличием двух сторон равной величины и третьей – основанием. Для определения высоты, проведенной к третьей, отличной стороне, на помощь приходит теорема Пифагора. При обозначениях
a – боковая сторона,
c – основание,
h(c) – отрезок к c под углом 90°, то h(c)=1/2 √(4a2-c2 ).

4

Найти высоту треугольника равностороннего

В таком треугольнике отмечается равенство всех сторон, а углы составляют по 60°. Исходя из формулы для нахождения перпендикуляра на основание для равнобедренного треугольника, получаем следующее соотношение, которое справедливо для всех трех высот.

h=√3a/2 .

Источник

Добавить комментарий