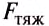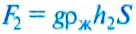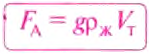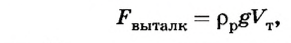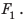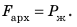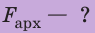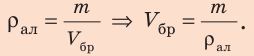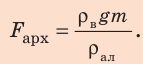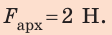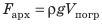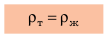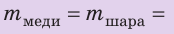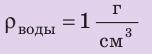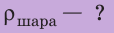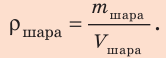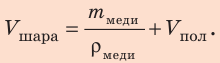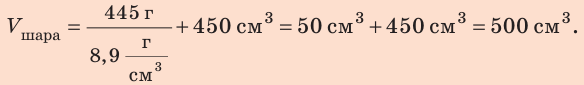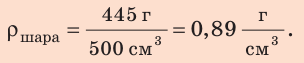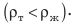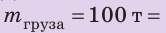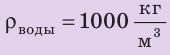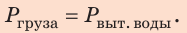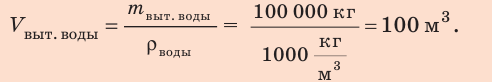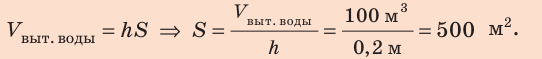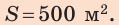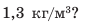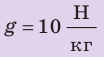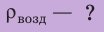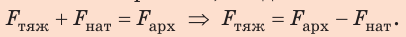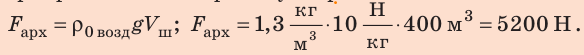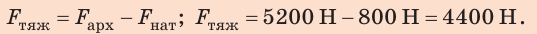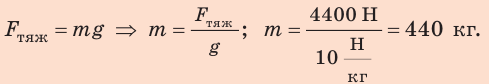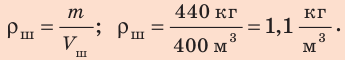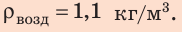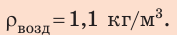Содержание:
Выталкивающая сила:
Наблюдение. Почему тяжело погрузить мяч в воду, и почему, как только мы его отпустим, он выпрыгивает из воды? Почему в море легче плавать, чем в озере? Почему в воде мы можем поднять камень, а в воздухе — нет?
Опыт 1. Подвесим к пружине тело (рис. 138). В связи с тем, что на тело действует сила тяжести 
Газы во многом подобны жидкостям. На тела, помещённые в газ, также действует выталкивающая сила. Именно под действием этой силы воздушные шары, метеорологические зонды, детские шарики, наполненные водородом, поднимаются вверх.
А от чего зависит выталкивающая сила ?
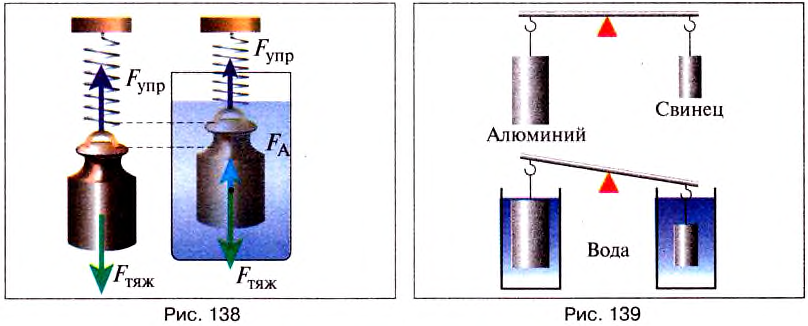
Опыт 2. Два тела разного объёма, но одинаковой массы, погрузим полностью в одну и ту же жидкость (воду). Мы видим, что тело большего объёма выталкивается из жидкости (воды) с большей силой (рис. 139).
Выталкивающая сила зависит от объёма погружённого в жидкость тела. Чем больше объём тела, тем большая выталкивающая сила действует на него.
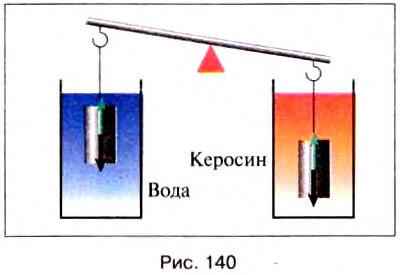
Опыт 3. Погрузим полностью два тела одинакового объёма и массы в разные жидкости, например воду и керосин (рис. 140). Нарушение равновесия в этом случае свидетельствует, что в воде на тело действует большая выталкивающая сила, это можно связать с тем, что плотность воды больше, чем плотность керосина.
Выталкивающая сила зависит от плотности жидкости, в которую погружено тело. Чем больше плотность жидкости, тем большая выталкивающая сила действует на погружённое в неё тело.
Обобщая результаты наблюдений и опытов можно сделать такой вывод.
На тело, погружённое в жидкость (газ), действует выталкивающая сила, равная по значению весу жидкости (газа), вытесненной этим телом.
Это утверждение называют законом Архимеда, древнегреческого учёного, который его открыл и, по легенде, успешно применил для решения практической задачи: определил, содержится ли в золотой короне царя Гиерона примесь серебра. Силу, которая выталкивает тело из жидкости или газа, называют еще архимедовой силой.
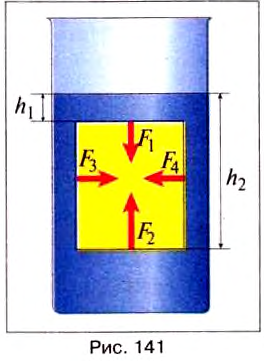
На основе закона Архимеда можно сразу написать формулу для определения выталкивающей силы, но чтобы лучше понять, вследствие чего она возникает, выполним простые расчёты. Для этого рассмотрим тело в форме прямоугольного бруска, погружённого в жидкость таким образом, чтобы его верхняя и нижняя фан и располагались параллельно поверхности жидкости (рис. 141). 
Посмотрим, каким будет результат действия сил давления на поверхность этого тела.
Согласно закону Паскаля горизонтальные силы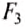 
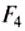
и 
действующие на симметричные боковые грани бруска, попарно равны по значению и противоположно направлены. Они не выталкивают брусок вверх, а только сжимают его с боков. Рассмотрим силы гидростатического давления на верхнюю и нижнюю грани бруска.
Пусть верхняя грань площадью S расположена на глубине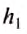 
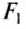
тогда сила давления 
, на неё будет равна: 
где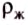 
— плотность жидкости.
Нижняя грань бруска площадью S расположена на большей глубине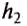 
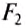
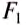
, поэтому сила давления 
на неё будет также больше, чем 
: 
Обе силы давления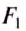 
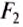
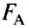
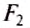
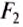
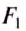
, и 
действуют вдоль вертикали, их равнодействующая и будет силой Архимеда 
, направленной вверх в сторону большей силы 
, а её значение будет равно разности сил
и : 
.
Поскольку разность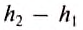 
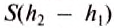
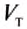
является высотой бруска, то произведение 
равно объёму тела 
, и мы окончательно получаем формулу,
являющуюся математическим выражением закона Архимеда:
Действительно, поскольку жидкость не сжимается, то объём вытесненной телом жидкости равен объёму этого тела, и произведение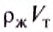 
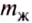
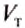
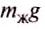
равно массе жидкости 
в объёме тела 
. В свою очередь, произведение 
является весом этой жидкости.
Из приведённого расчета наглядно видно, что выталкивающая (архимедова) сила возникает вследствие того, что значения гидростатического давления на разных глубинах неодинаковы и возрастают с глубиной.
Архимедовую силу можно определить экспериментально.
Опыт 4. Подвесим тело к динамометру (рис. 142). На тело действует сила тяжести почти 10 Н. Погрузим тело в жидкость (рис. 143).
Динамометр показывает 6 Н. Определим разность показаний динамометра. Она равняется 4 Н.
Кстати:
Однажды у императора Цао-Цао, который правил в Китае свыше 2000 лет тому назад, возникла мысль взвесить слона. Как ни суетились сановники, никто из них не мог ничего придумать, ведь нигде не было таких гигантских весов, чтобы на них можно было взвесить слона. Когда все сановники признали свою беспомощность, пришёл человек по имени Чао Чун и сказал, что он может взвесить слона. Он попросил: «Прикажите поставить слона в большую лодку, после чего обозначьте уровень погружения лодки в воду. Снимите слона, а лодку загрузите камнями так, чтобы она погрузилась до отметки. Вес камней будет равен весу слона”. Талантливый самородок, на много лет опередивший великого Архимеда, получил за своё предложение «щедрое» вознаграждение – благосклонный кивок императора Цао-Цао.
Выталкивающая сила и закон Архимеда
При взаимодействии твердых неподвижных тел, действуя друг на друга, они только деформируются. И действие каждого из этих тел на другое характеризуется силой.
Как взаимодействуют твердое тело и жидкость
Если твердое тело взаимодействует с жидкостью, то оно проникает в жидкость. Что происходит в таком случае? Ответ на этот вопрос получим из опыта.
К резиновой нити прицепим груз и измерим длину нити, которая растягивается весом груза. Если же груз после этого опустить в воду, то станет заметным сокращение длины нити. Таким образом, вес тела в воде уменьшился. Это возможно только потому, что в жидкости на погруженное тело действует выталкивающая сила. Направление этой силы противоположно направлению действия силы тяжести.
Как рассчитать значение выталкивающей силы
Опыты показывают, что значение выталкивающей силы зависит как от характеристик погруженного тела, так и от свойств жидкости.
Возьмем металлический цилиндр и стакан, объем которого равен объему цилиндра. Прицепим их к крючку динамометра и определим вес цилиндра и стакана (рис. 110). Теперь полностью погрузим цилиндр в воду. Динамометр покажет уменьшение веса. Но если стакан полностью заполнить водой, то показания динамометра восстановятся. Таким образом, выталкивающая сила равна весу воды, объем которой равен объему тела. Если воду заменить насыщенным раствором соли в воде, то выталкивающая сила будет большей, так как большим будет вес воды, объем которой равен объему тела.
Если учесть, что вес жидкости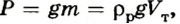 
то для расчета выталкивающей силы можно использовать формулу
где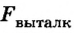 
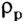
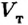
– выталкивающая сила; 
– плотность жидкости; 
– объем погруженного в жидкость тела или его части.
Зависимость, выраженная формулой для выталкивающей силы, называется законом Архимеда, сама выталкивающая сила — силой Архимеда.
От чего зависит сила Архимеда
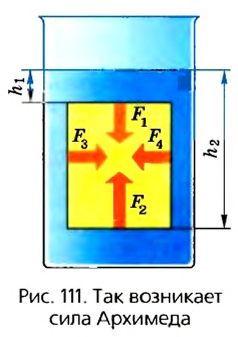
Почему действует сила Архимеда в жидкости? Представим себе, что в жидкость погружено тело в виде прямоугольного бруска (рис. 111).
На тело, погруженное в жидкость, действует выталкивающая сила, которая равна весу жидкости в объеме погруженного тела или его погруженной части.
В результате действия силы тяжести в жидкости существует давление, которое согласно закону Паскаля действует во всех направлениях. В связи с этим на верхнюю грань бруска будет действовать сила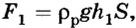 
направленная вниз.
На нижнюю грань будет действовать сила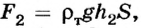 
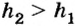
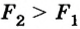
направленная вверх. Так как 
, то и 
. Равнодействующая этих сил направлена вверх. Это и будет сила Архимеда.
Действует сила Архимеда и в газах, так как в них давление тоже изменяется с высотой.
Окончательно закон Архимеда можно сформулировать так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объеме погруженной части тела.
В газах сила Архимеда значительно меньше, чем в жидкостях, поскольку плотность газа намного меньше плотности жидкости.
Выталкивающая сила в жидкостях и газах
Почему мяч, если его погрузить в воду и отпустить, выпрыгивает над поверхностью воды? Почему тяжелый камень, который на суше нельзя сдвинуть с места, можно легко поднять под водой? Почему корабль, севший на мель, самостоятельно не может всплыть? Попробуем разобраться.
Существование выталкивающей силы:
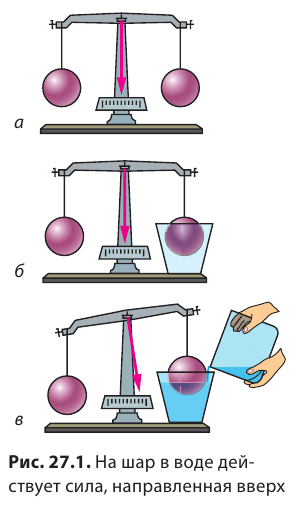
Подвесим к коромыслу весов два одинаковых шара. Массы шаров равны, значит, весы будут уравновешены (рис. 27.1, а). Подставим под правый шар пустой сосуд (рис. 27.1, б). Затем нальем в сосуд воду и увидим, что равновесие весов нарушится (рис. 27.1, в), — некая сила пытается вытолкнуть шар из воды.
Откуда берется эта сила? Чтобы разобраться, рассмотрим погруженный в жидкость кубик. На него со всех сторон действуют силы гидростатического давления жидкости (рис. 27.2). Силы гидростатического давления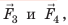 
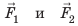
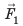
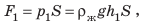
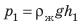
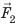
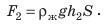
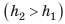
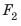
действующие на боковые грани кубика, противоположны по направлению и равны по значению, так как площади боковых граней одинаковы и эти грани расположены на одинаковой глубине. Такие силы уравновешивают друг друга. А вот силы гидростатического давления 
, соответственно действующие на верхнюю и нижнюю грани кубика, друг друга не уравновешивают. На верхнюю грань кубика действует сила давления 
: 
где 
— гидростатическое давление жидкости; S — площадь грани. Аналогично на нижнюю грань кубика действует сила давления 
: 
Нижняя грань находится на большей глубине, чем верхняя 
поэтому сила давления 
больше силы давления 
Равнодействующая этих сил равна разности значений сил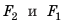 
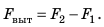
и направлена в сторону действия большей силы, то есть вертикально вверх. По вертикали вверх на кубик, погруженный в жидкость, действует сила, обусловленная разностью давлений на его нижнюю и верхнюю грани, — выталкивающая сила: 
На тело, помещенное в газ, тоже действует выталкивающая сила, но она значительно меньше выталкивающей силы, действующей на то же тело в жидкости, поскольку плотность газа намного меньше плотности жидкости. Выталкивающую силу, которая действует на тело в жидкости или газе, называют также архимедовой силой (в честь древнегреческого ученого Архимеда (рис. 27.3), который первым указал на существование этой силы и вычислил ее значение).
Расчет и вычисление силы Архимеда
Вычислим значение архимедовой (выталкивающей) силы для кубика, погруженного в жидкость (см. рис. 27.2). Вы уже знаете, что архимедова сила равна разности сил давлений жидкости на нижнюю и верхнюю грани кубика: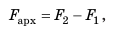 
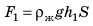
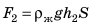
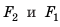
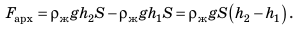
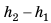
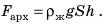
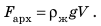
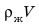
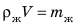
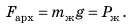
где 
— сила давления жидкости на верхнюю грань кубика; 
— сила давления жидкости на нижнюю грань кубика. Зная 
, найдем выталкивающую силу: 
Разность глубин 
, на которых находятся нижняя и верхняя грани кубика, — это высота h кубика, следовательно, 
. Произведение площади S основания кубика на его высоту h — это объем V кубика: V= Sh, значит, формула для расчета архимедовой силы: 
Здесь 
— это масса жидкости в объеме кубика, то есть масса жидкости, объем которой равен объему кубика. Так как 
, то 
Архимедова сила равна весу жидкости в объеме кубика: 
Мы рассмотрели случай с кубиком, полностью погруженным в жидкость. Однако полученный результат выполняется для тела любой формы, а также в случаях, когда тело погружено в жидкость частично (для расчетов следует брать объем погруженной в жидкость части тела). Кроме того, результат справедлив и для газов. А теперь сформулируем закон Архимеда: На тело, погруженное в жидкость или газ, действует выталкивающая сила, которая равна весу жидкости или газа в объеме погруженной части тела: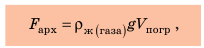 
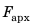
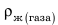
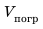
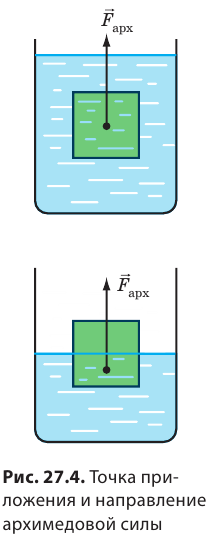
где 
— архимедова сила; 
— плотность жидкости или газа; 
— объем погруженной части тела. Архимедова сила приложена к центру погруженной части тела и направлена вертикально вверх (рис. 27.4).
Выясняем, всегда ли на тело, погруженное в жидкость, действует архимедова сила:
Подвесим к динамометру камешек на нити. Динамометр покажет вес камешка. Подставим стакан с водой так, чтобы камешек оказался полностью погруженным в воду. Показание динамометра уменьшится. Кажется, что камешек «потерял» часть своего веса. Но никакой потери веса тела в жидкости не происходит: вес перераспределяется между подвесом (нитью) и опорой (жидкостью). Даже если архимедова сила, действующая на тело, достаточна, чтобы его удержать, и подвес не будет растянут, тело все равно не находится в состоянии невесомости, ведь оно давит на опору — жидкость. Следует отметить: когда тело плавает, его вес распределяется на воду, окружающую всю поверхность тела. Поэтому во время плавания нам кажется, что мы потеряли вес. Такие комфортные условия поддержания тяжелого тела обусловили то, что в результате эволюции самые массивные существа на Земле живут в океане (рис. 27.5).
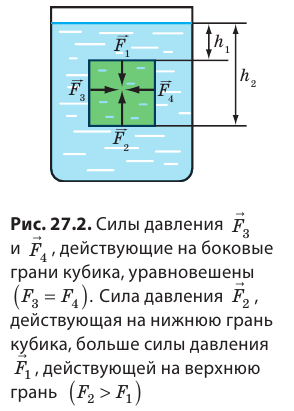
Именно архимедова сила помогает нам поднимать в воде тяжелые камни или другие предметы, ведь часть силы тяжести, действующей на эти тела, уравновешивается не силой наших рук, а выталкивающей силой.
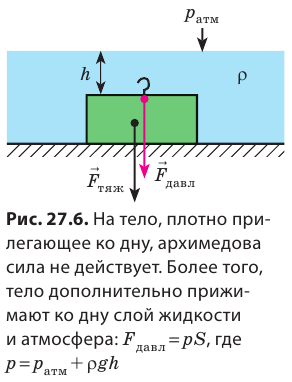
Однако случается, что вода не помогает поднять тело, а наоборот — препятствует этому. Это происходит, если тело лежит на дне и плотно к нему прилегает. Вода не может попасть под нижнюю поверхность тела и помочь своим давлением поднять его. В таком случае, чтобы оторвать тело от дна, нужно преодолеть не только силу тяжести, действующую на тело, но и силу давления воды на верхнюю поверхность тела (рис. 27.6). Данное явление может стать причиной трагедии: если подводная лодка опустится на глинистое дно и вытеснит из под себя воду, всплыть сама она не сможет.
Пример №1
Однородный алюминиевый брусок массой 540 г полностью погружен в воду и не касается дна и стенок сосуда. Определите архимедову силу, действующую на брусок. Анализ физической проблемы. Для вычисления архимедовой силы нужно знать плотность воды и объем бруска. Объем бруска определим по его массе и плотности. Плотности воды и алюминия узнаем из таблиц плотностей (с. 249). Задачу будем решать в единицах СИ.
Дано:
,
,
,
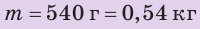
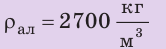
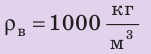
Найти:
Решение:
По закону Архимеда: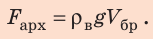 
По определению плотности: 
Подставим выражение для объема бруска в формулу для расчетов архимедовой силы:
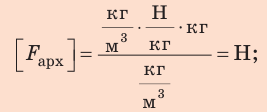
Проверим единицу, найдем значение искомой величины:
Ответ: 
Итоги:
На тело, находящееся в жидкости или газе, действует выталкивающая (архимедова) сила. Причина ее появления в том, что давление, которое оказывает жидкость или газ на верхнюю поверхность тела, отличается от давления, оказываемого на нижнюю поверхность тела. Закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, которая направлена вертикально вверх и равна весу жидкости или газа в объеме погруженной части тела:
Условия плавания тел
При приготовлении раствора соли определенной плотности хозяйки погружают в него сырое яйцо: если плотность раствора недостаточна, яйцо тонет, если достаточна — всплывает. аналогично определяют плотность сахарного сиропа при консервации.
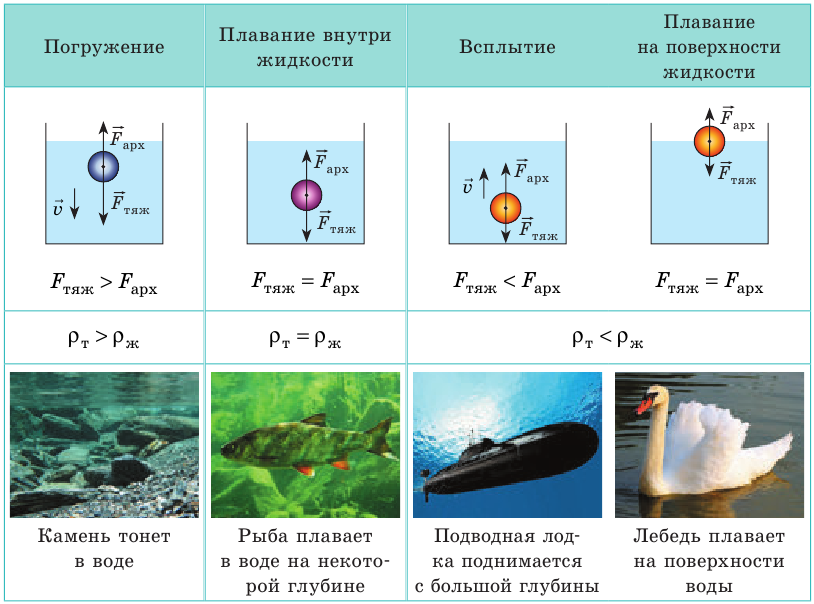
Вы наверняка можете привести множество примеров плавания тел. Плавают корабли и лодки, деревянные игрушки и воздушные шарики, плавают рыбы, дельфины, другие существа. А от чего зависит способность тела плавать? Проведем опыт. Возьмем небольшой сосуд с водой и несколько шариков, изготовленных из разных материалов. Будем поочередно погружать тела в воду, а потом отпускать их без начальной скорости. Далее в зависимости от плотности тела возможны разные варианты (см. таблицу).
Погружение
Тело начинает тонуть и в конце концов опускается на дно сосуда. Выясним, почему это происходит. На тело действуют две силы: 1) сила тяжести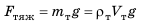 
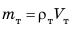
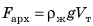
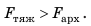
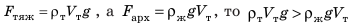
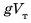
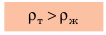
(поскольку 
), направленная вертикально вниз; 2) выталкивающая сила 
направленная вертикально вверх. Тело погружается, а это значит, что сила, направленная вниз, больше: 
Поскольку 
. После сокращения на 
имеем:
тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа. Вариант 2. Плавание внутри жидкости. Тело не тонет и не всплывает, а остается плавать внутри жидкости. Попробуйте доказать, что в данном случае плотность тела равна плотности жидкости:
тело плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа. Вариант 3. Всплытие. Тело начинает всплывать и в конце концов останавливается на поверхности жидкости, погрузившись в жидкость частично. Пока тело всплывает, архимедова сила больше силы тяжести: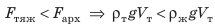 
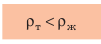
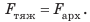
или: 
Остановка тела на поверхности жидкости означает, что архимедова сила и сила тяжести уравновешены: 
тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше, чем плотность жидкости или газа.
Плавание тел в живой природе
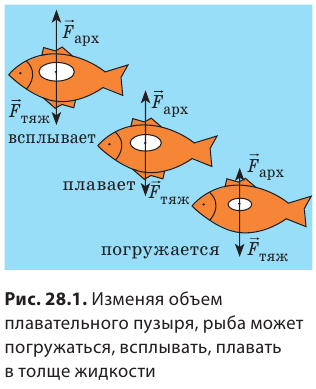
Тела обитателей морей и рек содержат в своем составе много воды, поэтому их средняя плотность близка к плотности воды. Чтобы свободно двигаться в жидкости, они должны «управлять» средней плотностью своего тела. Приведем примеры. У рыб с плавательным пузырем такое управление происходит за счет изменения объема пузыря (рис. 28.1). Моллюск наутилус (рис. 28.2), обитающий в тропических морях, может быстро всплывать и снова опускаться на дно благодаря тому, что может менять объем внутренних полостей в организме (моллюск живет в закрученной спиралью раковине). Распространенный в Европе водяной паук (рис. 28.3) несет с собой в глубину воздушную оболочку на брюшке — именно она дает ему запас плавучести и помогает вернуться на поверхность.
Пример №2
Медный шар массой 445 г имеет внутри полость объемом 450 см3. Будет ли этот шар плавать в воде? Анализ физической проблемы. Чтобы ответить на вопрос, как поведет себя шар в воде, нужно плотность шара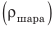 
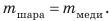
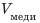
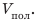
сравнить с плотностью воды 
Для вычисления плотности шара следует определить его объем и массу. Масса воздуха в шаре незначительна по сравнению с массой меди, поэтому 
Объем шара — это объем медной оболочки 
и объем полости 
Объем медной оболочки можно определить, зная массу и плотность меди. О плотностях меди и воды узнаем из таблиц плотностей (с. 249). Задачу целесообразно решать в представленных единицах.
Дано:
,
,
,
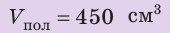
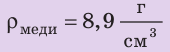
Найти:
Решение:
По определению плотности:
Объем шара: 
— объем медной оболочки.
Таким образом, 
Решим задачу по действиям. 1. Определим объем шара:
2. Зная объем и массу шара, определим его плотность:
Анализ результата: плотность шара меньше плотности воды, поэтому шар будет плавать на поверхности воды.
Ответ: да, шар будет плавать на поверхности воды.
- Заказать решение задач по физике
Итоги:
Тело тонет в жидкости или газе, если плотность тела больше, чем плотность жидкости или газа 
плавает внутри жидкости или газа, если плотность тела равна плотности жидкости или газа 
Тело всплывает в жидкости или газе либо плавает на поверхности жидкости, если плотность тела меньше плотности жидкости или газа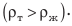 
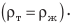
Судоходство и воздухоплавание
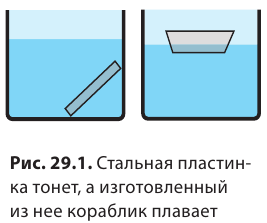
Стальной брусок в воде тонет, а стальные корабли плавают. Нейлоновая ткань падает в воздухе, а воздушные шары, изготовленные из этой ткани, поднимаются вверх сами и поднимают гондолы с пассажирами. Почему же стальные корабли плавают в воде, а воздушные шары называют аппаратами, которые легче воздуха? Получить ответы на эти вопросы вам помогут знания об основах судоходства и воздухоплавания.
Почему плавают суда
На первый взгляд, сталь непригодна для изготовления плавучего средства: плотность стали намного больше плотности воды, поэтому стальная пластинка в воде тонет. Но если из пластинки сделать кораблик и опустить его на поверхность воды, кораблик будет плавать (рис. 29.1). Почему? Дело в том, что погруженная в воду часть кораблика вытесняет воды достаточно, чтобы архимедова сила уравновесила силу тяжести, действующую на кораблик. Другими словами, средняя плотность кораблика за счет воздуха внутри него намного меньше плотности воды. Именно поэтому кораблик плавает на поверхности воды лишь немного в нее погружаясь.
Этот принцип лежит в основе конструкции всех судов. Средняя плотность судов намного меньше плотности воды, поэтому суда плавают на ее поверхности, погружаясь на относительно небольшую часть своего объема.
Характеристики судов:
Когда новое судно спускают на воду, оно начинает погружаться. Нижняя часть судна начинает вытеснять воду, вследствие чего возникает архимедова сила. Когда архимедова сила уравновешивает силу тяжести, действующую на судно, оно прекращает погружение. Глубину, на которую погружается судно, называют осадкой. Осадка судна изменяется в зависимости от загруженности судна и от того, в речной или морской воде оно находится. Разумеется, судно нельзя перегружать.
На корпус судна нанесена ватерлиния — линия, указывающая максимально допустимую осадку судна, при которой оно может безопасно плавать (рис. 29.2). Когда судно полностью нагружено, оно находится в воде вровень с ватерлинией.
Вес воды, которую вытесняет судно, погруженное в воду до ватерлинии, то есть архимедова сила, действующая на полностью нагруженное судно, называется полным водоизмещением судна. Напомним: поскольку нагруженное судно плавает на поверхности воды, то архимедова сила, которая действует на него, по значению равна силе тяжести, действующей на судно с грузом: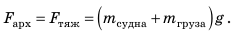 
Самые большие суда — танкеры для нефти — имеют полное водоизмещение до 5 млн кН, то есть их масса вместе с грузом достигает 500 000 т. Если из полного водоизмещения исключить вес самого судна, то получим максимальный вес груза, который может взять на борт данное судно, то есть определим грузоподъемность судна. грузоподъемность судна — максимальный вес груза, который судно может взять на борт, — это разность между полным водоизмещением судна и его весом. Украина — морское государство. В стране есть морской и речной флот, а также порты, имеющие большое экономическое значение: Одесский, Ильичевский, Южный, Николаевский, Херсонский, Бердянский, Мариупольский.
Как осуществилась мечта человека летать
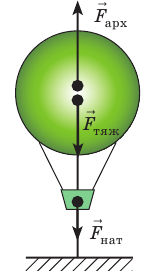
Люди уже давно используют воздушные шары (аэростаты), поднимающиеся в воздух благодаря заполнению их оболочки горячим воздухом или легким газом. На воздушный шар в воздухе действует выталкивающая сила. Средняя плотность воздушного шара меньше плотности воздуха, поэтому выталкивающая сила больше силы тяжести и шар поднимается вверх. Разность между выталкивающей (архимедовой) силой и силой тяжести представляет собой подъемную силу воздушного шара. Сейчас воздушные шары используют для метеорологических и других исследований, соревнований, перевозок пассажиров, туристических и познавательных путешествий. Воздушные шары, наполненные легким газом (в основном гелием), называют шарльерами. В последнее время распространены воздушные шары, наполненные горячим воздухом, — современные монгольфьеры (рис. 29.3). Высокую температуру воздуха внутри шара поддерживают газовые горелки, установленные в его горловине. Поскольку плотность воздуха с высотой уменьшается, воздушные шары не могут подняться на какую угодно высоту. Воздушные шары поднимаются только до той высоты, где плотность воздуха равна средней плотности шара вместе с грузом.
Пример №3
В речном порту судно взяло на борт 100 т груза. В результате осадка судна увеличилась на 0,2 м и достигла максимально допустимой. Какова площадь сечения судна на уровне ватерлинии? Анализ физической проблемы. Когда на судно взяли груз, оно увеличило осадку и дополнительно вытеснило некоторый объем воды. По закону Архимеда, вес груза равен весу дополнительно вытесненной воды: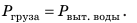 
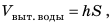
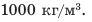
Осадка судна увеличилась всего на 20 см, значит, площадь сечения судна на уровне поверхности воды изменилась незначительно. Поэтому объем дополнительно вытесненной воды равен 
где h — увеличение осадки; S — площадь сечения судна на уровне ватерлинии (по условию судно достигло максимальной осадки). Порт речной, поэтому плотность воды равна 
Задачу следует решать в единицах СИ.
Дано:
,
,
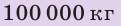
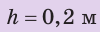
Найти:
Решение:
1. Определим массу дополнительно вытесненной воды. По закону Архимеда:
поэтому 
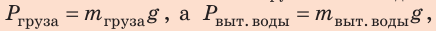
2. Определим объем дополнительно вытесненной воды:
3. Площадь S сечения судна на уровне ватерлинии найдем через объем вытесненной воды:
Ответ:
Мы решили задачу 1 по действиям. Решите эту задачу в общем виде (получите общую формулу, найдите значение искомой величины).
Пример №4
Объем воздушного шара равен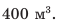 
Шар натягивает трос, которым прикреплен к причалу, с силой 800 Н. После освобождения троса шар смог подняться на некоторую высоту. Какова плотность воздуха на этой высоте, если плотность воздуха у причала 
Анализ физической проблемы. Шар прекратил подъем потому, что на этой высоте его средняя плотность равна плотности воздуха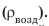 
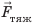
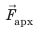
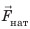
. Чтобы определить среднюю плотность шара, следует найти его массу. Массу шара найдем по силе тяжести, действующей на шар. Для определения силы тяжести выполним пояснительный рисунок и покажем все силы, действовавшие на шар на причале: 
— сила тяжести; 
— архимедова сила, 
— сила натяжения троса. Шар на причале не двигался, поэтому силы, действовавшие на него, были скомпенсированы. Задачу будем решать по действиям в единицах СИ.
Дано:
,
,
,
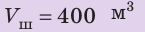
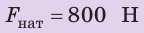
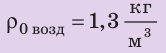
Найти:
Решение:
Силы, действовавшие на прикрепленный к причалу шар, были скомпенсированы, следовательно:
1. Найдем архимедову силу, которая действовала на прикрепленный к причалу шар:
2. Найдем силу тяжести, действующую на шар:
3. Определим массу шара:
4. По известным массе и объему шара вычислим его среднюю плотность:
5. Плотность воздуха на высоте максимального подъема шара равна средней плотности шара, потому на этой высоте
Ответ:
Итоги:
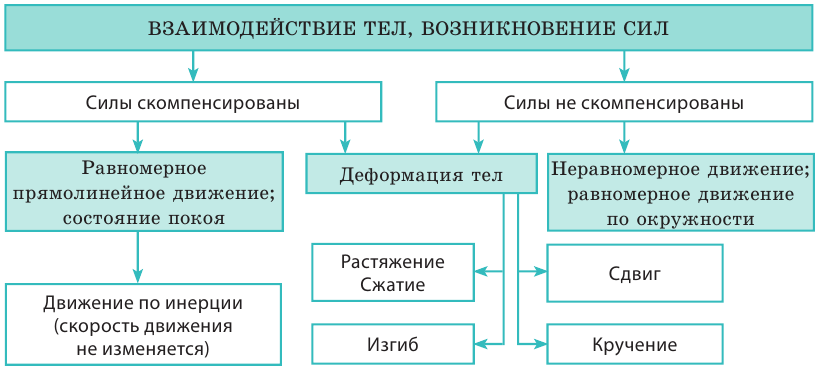
Взаимодействие тел:
Вы узнали, что причиной изменения скорости движения тел и причиной изменения формы и объема тел является взаимодействие.
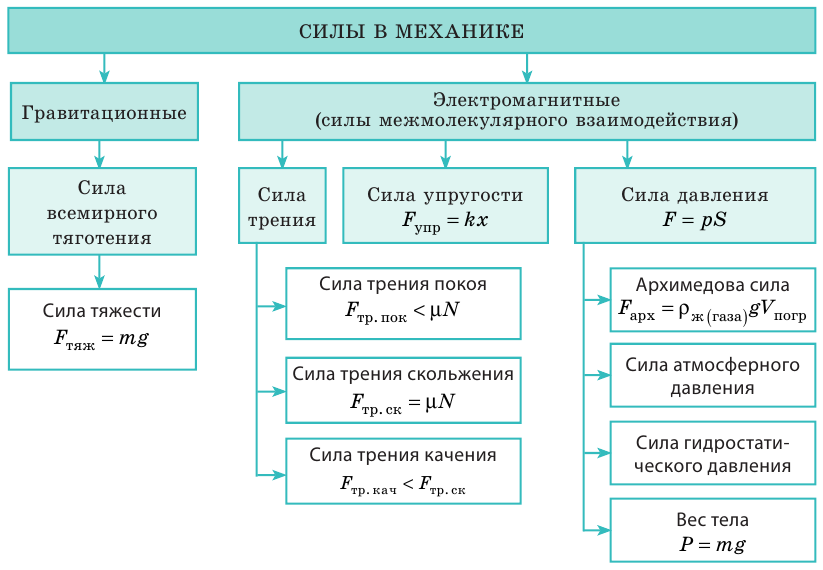
Вы ознакомились с разными силами в механике.
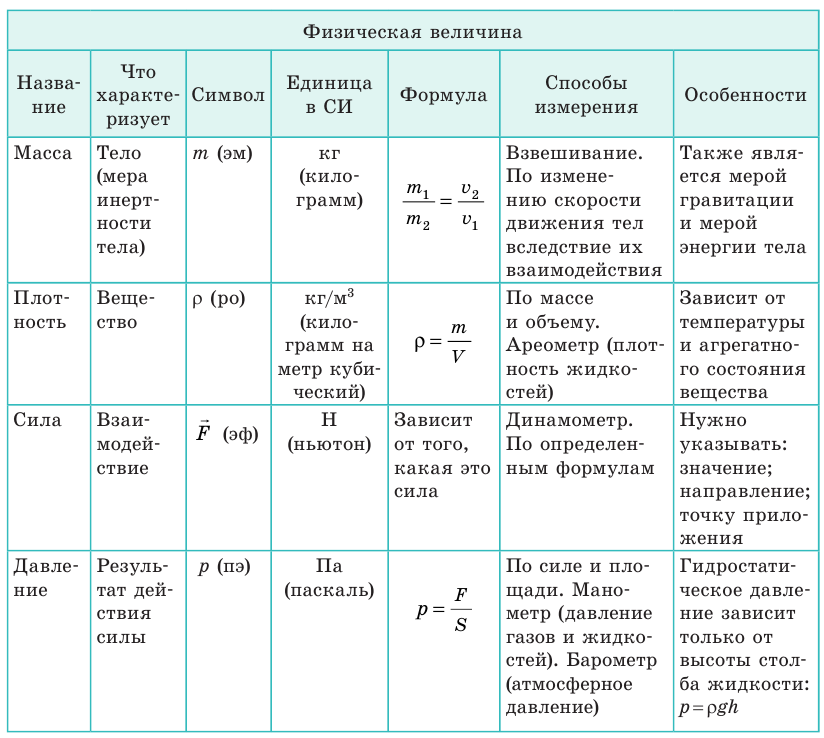
Вы продолжили знакомство с физическими телами и веществами и узнали о физических величинах, характеризующих тело, вещество, взаимодействие.
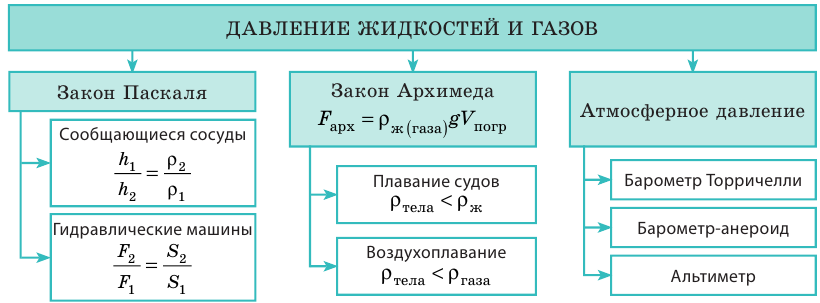
Вы узнали о давлении жидкостей и газов, ознакомились с законом Паскаля, законом Архимеда, доказали наличие атмосферного давления.
- Условия плавания тел в физике
- Гидростатическое взвешивание в физике
- Воздухоплавание в физике
- Машины и механизмы в физике
- Атмосферное давление в физике и его измерение
- Манометры в физике
- Барометры в физике
- Жидкостные насосы в физике
Определить выталкивающую силу, действующую на стекляный шар объёмом 0, 04 м3, если он на 3 / 4 погружён в воду.
Решать так Дано.
Система СИ.
Решение.
Вычисление.
Пожалуста помогите.
Вы находитесь на странице вопроса Определить выталкивающую силу, действующую на стекляный шар объёмом 0, 04 м3, если он на 3 / 4 погружён в воду? из категории Физика.
Уровень сложности вопроса рассчитан на учащихся 5 – 9 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.
urederast842
Вопрос по физике:
Определить выталкивающую силу, действующую на стекляный шар объёмом 0,04 м3, если он на 3/4 погружён в воду. решать так Дано… система СИ…. Решение…. Вычисление….
пожалуста помогите
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
prershti16
А можно я решу так:
Дано:
V₀=0,04 м³
V=(3/4)·V₀
ρ = 1000 кг/м³
g = 10 м/с²
_____________
Fa – ?
Объем шара, погруженный в жидкость:
V = (3/4)*V₀ = (3/4)*0,04 = 0,03 м³
Выталкивающая сила:
Fa = ρ*g*V = 1000*10*0,03 = 300 H
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Выталкивающая сила, действующая на объекты в жидкой среде, прикладывается вверх к жидкости и обеспечивает плавание, погружение или подъем объекта в жидкости.
Выталкивающая сила, действующая на объект, следует принципам Архимеда: задействованы несколько сущностей, таких как вес, плотность и природа жидкой среды. Используя все эти объекты, давайте научимся рассчитывать выталкивающую силу и решать задачи, связанные с выталкивающей силой.
Чтобы рассчитать выталкивающую силу, необходимо выполнить шаги, указанные ниже:
- Найдите объем погруженного тела –Поскольку на объем объекта в жидкой среде в значительной степени влияет плавучесть; поэтому нам нужно их найти.
- Найти плотность тела и текучей среды –Плотность как объекта, так и жидкости необходима, потому что плотность играет жизненно важную роль в проявлении выталкивающей силы.
- Найдите силу тяжести или направленную вниз силу –выталкивающая сила направлена вверх, поэтому ее необходимо уравновешивать силой, направленной вниз; таким образом, необходимо выяснить либо гравитацию, либо любую направленную вниз силу, действующую на объект в среде.
Формула выталкивающей силы
Поскольку мы знаем, что плотность, объем и направленная вниз сила, такая как гравитация, напрямую влияют на выталкивающую силу, используя все эти объекты, общая формула для выталкивающей силы дается выражением
Fb=V×ρ×г
Где; V — объем жидкости, ρ — плотность жидкости, g — ускорение свободного падения.
Эта формула дает выталкивающую силу жидкой среды, действующую на объект в соответствии с принципом Архимеда.
Как найти выталкивающую силу с плотностью?
Плотность — это не что иное, как масса на единицу объема вещества, поэтому плотность жидкости необходимо знать для расчета выталкивающей силы.
- Плотность жидкости находится по формуле р=м/обf
- Где ρ — плотность жидкости, m — масса, а V — объем жидкости.
- Формула может рассчитать объем жидкости; Вf=л×ш×ч; где l — длина, w — ширина, h — высота.
Подставляя значения плотности и объема, выталкивающая сила рассчитывается по формуле Fb=ρgV.
Например, тело массой 4 кг погружено в жидкую среду объемом 8 м.3 как рассчитать выталкивающую силу жидкости? Примите ускорение свободного падения равным 9.8 м/с.2.
Дано – масса объекта, m=4кг
Объем V=8м3
Плотность жидкости ρ определяется выражением
р=м/обf
р=4/8
ρ = 0.5 кг/м3
Выталкивающая сила с плотностью определяется выражением
Fb= ρgV
Подставляя значения всех заданных значений, получаем
Fb=(0.5)(8)(9.8)
Fb= 39.2N
Как рассчитать выталкивающую силу плавучего объекта?
Приведенный выше расчет, связанный с выталкивающей силой, дает величину силы, действующей на объект, чтобы вытолкнуть его из подводного состояния. Рассчитать его довольно просто, но как рассчитать выталкивающую силу плавучего объекта?
- О предмете говорят, что он плавает, если выталкивающая сила больше силы тяжести. Необходимо выполнить некоторую дополнительную работу, чтобы найти выталкивающую силу, действующую на плавучий объект. Шаги, которые необходимо выполнить для определения плавучести, приведены ниже.
- Сначала рассчитайте всю выталкивающую силу, действующую на тело в жидкости, т. е. используйте весь объем.
- Затем найдите гравитационную силу, толкающую объект вниз, по уравнению W=mg; где m — масса объекта, а g — ускорение свободного падения, также известное как вес объекта.
- Если сила плавучести и сила тяжести меньше выталкивающей силы, то объект плавает в жидкости.
Изображение кредита: Wikimedia Commons
Решенный пример может быть ясен для понимания плавучий плавучий силовой расчет.
Объект массой 12 кг и плотностью 0.58 кг/м3 опускается в жидкость. Как рассчитать выталкивающую силу, действующую на тело, чтобы оно плавало в жидкости?
Дано – масса объекта m=12кг
Плотность объекта ρ=0.58 кг/м3
Объем объекта может быть задан как
V=м/р
Подставляя значения m и ρ,
V=12/0.63
V=20.68м3
Действующая выталкивающая сила определяется выражением
Fb=ρgV
Fb=(0.58)(9.8)(20.68)
Fb= 127.67N
Вес предмета определяется
Вт=мг
Вт=(12)(9.8)
Ш=117.6Н
Поскольку значение выталкивающей силы больше значения силы тяжести, объект плавает в жидкости.
Как рассчитать выталкивающую силу в воздухе?
Выталкивающая сила в воздухе связана со смещением воздуха вместе с объектом. Расчет выталкивающей силы в воздухе сильно отличается от обычного расчета выталкивающей силы, потому что плотность воздуха намного меньше.
- Расчетная плотность воздуха примерно равна 1.3×10-3кг / м3.
- Затем рассчитать плотность объекта, плавающего в воздушной среде.
Мы знаем, что когда сила плавучести действует в направлении вверх, сила тяжести пытается тянуть объект вниз. Объект может парить в воздухе только тогда, когда выталкивающая сила больше.
В воздушной среде выталкивающая сила должна быть равна весу объекта для эффективного плавания; таким образом, мы можем писать.
Fb=м*г
Где m — масса объекта, а g — ускорение свободного падения. Но в воздухе массу можно переписать как
м=рa/п; где рa – плотность воздуха, а ρ – плотность объекта.
Подставив значение массы в уравнение выталкивающей силы, получим
Fb=pa/п*г
Задача, приведенная ниже, поможет вам лучше понять.
Как рассчитать выталкивающую силу золотой монеты плотностью 19 г в воздушной среде?
Мы знаем, что плотность золотой монеты ρg=19 г/см3
Плотность воздуха ρa=0.0013 г/см3
Выталкивающая сила, действующая на золотую монету в воздухе, определяется выражением
Fb=pa/п*г
Fb= 0.0013 / 19 * 9.8
Fb=(6.83×10-5) 9.8
Fb= 6.705 × 10-4N
Как рассчитать выталкивающую силу в воде?
Объем вытесненной воды с плотностью воды используется для расчета выталкивающей силы в воде.
- Если объект полностью погружен в воду, то для расчета следует учитывать 100% объема.
- Если объект частично погружен в воду, следует учитывать 50% объема.
- Если объект погружен только на четверть, то следует учитывать только 25% объема.
Изображение кредита: Wikimedia Commons
Остальной расчет выталкивающей силы аналогичен общему расчету плавучести.
Масса тела 15 кг, плотность 0.55 кг/м.3 частично погружен в воду. Как рассчитать выталкивающую силу, действующую на тело?
Мы знаем, что плотность объекта ρ=0.55 кг/м3
Масса объекта m = 15 кг
Объем определяется по формуле; V=m/p
V=15/0.55
V=27.27м3
Поскольку объект частично погружен в воду, его объем в воде равен половине его общего объема; таким образом, объем V=13.635 м3.
Выталкивающую силу можно определить как
Fb=ρgV
Fb=(0.55)(9.8)(13.635)
Fb= 73.492Н.
Как рассчитать выталкивающую силу воздушного шара?
Чтобы найти выталкивающую силу воздушного шара, нам нужно знать заполненный воздухом объем внутри воздушного шара, что делает расчет несколько другим.
Сам воздух, обладая малой плотностью, все же поддерживает плавание в нем определенного предмета. Некоторые воздушные шары, например гелиевые, имеют меньшую плотность, чем воздух. Таким образом, воздушные шары легко парят на них.
Когда воздушные шары наполняются газом, он приобретает форму, напоминающую сферу; таким образом, нам нужно вычислить объем выражения сферы как,
V=4/3πr3
Затем зная плотность и масса, мы можем легко вычислить выталкивающую силу.
Воздушный шар, наполненный воздухом, образует сферу радиусом 5 см и может парить в воздухе. Как рассчитать выталкивающую силу, действующую на воздушный шар при подъеме в воздух?
Дано – радиус шарика r=5см.
Объем воздушного шара определяется выражением
V=4/3πr3
V=4/3(3.14)*23
V=33.49м3.
Выталкивающая сила определяется выражением
Fb=ρgV
Плотность воздуха ρ=1.3 кг/м3.
Подставляя значения, получаем
Fb=(1.3)(9.8)(33.49)
Fb= 426.66Н.
Как рассчитать выталкивающую силу лодки?
Лодка всегда плывет по поверхности воды; плавучесть лодки следует рассчитывать, учитывая весь объем лодки.
Согласно закону Архимеда, направленная вверх сила, действующая на погруженное тело, равна весу вытесненной жидкости. И это смещение также действует в направлении вверх к центру массы смещения жидкости.
Уравнение выталкивающей силы
Fb=v*f/v=v*мг/v
Но m/v=p
Fb=ρgV
Для лодки, плывущей по воде, выталкивающая сила равна
Fb=Вт/Втa
Где; W – вес объекта в воде, Втa вес предмета в воздухе.
Как рассчитать выталкивающую силу на подводном объекте?
Для затопленного объекта объем такой же, как перемещенный объем в жидкости, и, следовательно, мы можем легко найти выталкивающую силу затопленного объекта с помощью того же уравнения.
Fb=ρgV
Для затопленного объекта необходимо найти вес вытесненной жидкости. Вес вытесненной жидкости определяется выражением
Wf=ρ×V
Как рассчитать величину выталкивающей силы?
Величина выталкивающей силы всегда равна величине его веса. Это верно только тогда, когда объект плавает. Поясним эту концепцию, рассмотрев пример плиты толщиной t и плотностью ρs, плавающей на поверхности воды с массой m.
Поскольку величина выталкивающей силы равна величине веса воды, определяемой выражением
Ww=ρwАтг; где А – площадь плиты.
Величина веса плиты определяется выражением
Ws=ρsАтг+мг
Но по закону Архимеда
Ws=Ww
ρwAtg= ρsАтг+мг
мг= рwAtg- ρsАтг
м=рwAt-ρsAt
м = А (ρwт-рst)
А=м/Pwt-Pst
Как рассчитать выталкивающую силу куба?
Когда куб погружен в жидкость, его объем равен кубическому значению каждой стороны. Используя это в качестве эталона, мы можем рассчитать выталкивающую силу, действующую на куб.
Изображение кредита: Wikimedia Commons
Например, куб со стороной 2 см погружен в масло плотностью 800 кг/мXNUMX.3. Вычислите выталкивающую силу, действующую на куб.
Длина стороны куба l=2см=0.2м.
Объем куба можно рассчитать как
V=XNUMX3= (0.2)3= 0.008 м3
Выталкивающая сила Fb=ρgV
Возьмем g=9.8 м/с2.
Подставляя значения в приведенное выше уравнение,
Fb=(800)(9.8)(0.008)
Fb= 62.72Н.
Еще несколько решенных задач
Тело массой 0.56 кг погружено в жидкость с плотностью 910 кг/мXNUMX.3. Вычислите выталкивающую силу, действующую на тело в этой жидкости. И, следовательно, вычислить вес смещения жидкости.
Решение:
Дано – масса тела, m=0.56кг.
Плотность текучей среды ρ=910кг/м3
Ускорение свободного падения g=9.8 м/с2.
Объем тела в жидкости равен
V=м/р
V=0.56/910
V = 6.153 × 10-4m3
Выталкивающая сила, действующая на тело в жидкости
Fb=ρgV
Fb=(910)(9.8)(6.153×10-4)
Fb= 5.488Н.
Плитка длиной 20 см, шириной 9 см и высотой 0.88 см плавает в жидкости с плотностью 998 кг/м.3. Рассчитайте выталкивающую силу, действующую на объект, и, следовательно, рассчитайте вес объекта, который будет плавать в жидкости. (Примите ускорение свободного падения g=10 м/с.2)
Решение:
Дано – длина данной плиты, м=20см=0.2м
Ширина плиты w=9см=0.09м
Высота плиты h=0.88см=0.0088м
Плотность текучей среды ρ=998кг/м3
Сначала нужно найти объем плиты.
V=lwh=(0.2)(0.09)(0.0088)
V = 1.58 × 10-4m3
Выталкивающая сила, действующая на плиту в жидкой среде, равна
Fb=ρgV
Fb=(998)(10)(1.58×10-4)
Fb= 1.580Н.
Шар надувают газом плотностью 0.89 кг/мXNUMX.3 и позволили парить в воздухе с плотностью 1.22 кг/м3. Воздушный шар образовал сферическую структуру радиусом 0.32 м. Рассчитайте плавучесть, приложенную к воздушному шару, и объем воздушного шара.
Решение:
Дано – плотность баллона, наполненного газом ρb=0.89 кг/м3
Плотность воздуха ρa=1.22 кг/м3
Радиус баллона r=0.32м.
Выталкивающая сила рассчитывается как
Fb=Pa/Pb*g
Fb=1.22/0.89 г
Fb= 1.32Н.
Объем баллона, наполненного газом, равен
V=4/3πr3
V=4/3(3.14)(323)
V=0.137м3.
Проверить, тонет или всплывает данное тело в жидкости плотностью 1025 кг/мXNUMX.3. Учитывая, что масса объекта 46 кг.
Решение:
Дано – плотность жидкости ρ=1025кг/м3
Масса данного тела m=46кг.
Ускорение свободного падения g=9.8 м/с2.
Объем тела в жидкости v определяется выражением
V=46/1025
V=0.044м3
Выталкивающая сила, действующая на тело в жидкости
Fb=ρgV
Fb=(1025)(9.8)(0.044)
Fb= 450.8N
Сила тяжести, действующая на тело W=mg
Вт=(46)(9.8)
W = 450.8
Так как вес тела и выталкивающая сила, действующая на тело, равны; следовательно, тело находится в состоянии нейтральной плавучести. Тело не тонет в жидкости и не поднимается в ней.
Закон Архимеда
- Выталкивание тела жидкостью при погружении
- Выталкивание тела газом при погружении
- Закон Архимеда
- Опыт с ведерком Архимеда
- Задачи
- Лабораторная работа №11. Определение плотности твердых тел и жидкостей методом гидростатического взвешивания
п.1. Выталкивание тела жидкостью при погружении
Проведем следующий опыт.
Нам понадобится: 1) динамометр; 2) груз; 3) стакан с раствором соли.
В первом случае пружина динамометра растягивается под действием силы тяжести: $$ F_text{упр1}=F_text{тяж}Rightarrow kl_1=mgRightarrow l_1=frac{mg}{k} $$
Во втором случае пружина растягивается под действием равнодействующей силы тяжести и некоторой силы, которая направлена вверх, т.е. выталкивает тело из жидкости: $$ F_text{упр2}=R=F_text{тяж}-F_text{выт}Rightarrow kl_2=mg-F_text{выт}Rightarrow l_2=frac{mg-F_text{выт}}{k} $$ Поэтому (l_2lt l_1), во втором случае пружина растягивается меньше.
Вывод:
На тело, погружённое в жидкость, действует выталкивающая сила.
 |
Действием выталкивающей силы можно объяснить, почему корабли не тонут в воде: если выталкивающая сила уравновешивает силу тяжести, то вода становится «опорой» и корабль держится на воде. |
п.2. Выталкивание тела газом при погружении
Проведем следующий опыт.
Нам понадобится: 1) весы с разновесами; 2) колба с пробкой; 3) широкий сосуд; 4) источник углекислого газа.
Получить небольшое количество углекислого газа можно при взаимодействии разбавленной соляной кислоты и карбоната кальция (мрамора): $$ mathrm{CaCO_3+2HClrightarrow CaCl_2+CO_2uparrow +H_2O} $$
Реакцию следует проводить в пробирке с газоотводной трубкой. Она будет служить источником (mathrm{CO_2}).
 |
Закрываем колбу пробкой. Помещаем колбу в широкий сосуд, подвешиваем колбу к чашке весов и уравновешиваем её с помощью разновесов. Запускаем в сосуд газоотводную трубку с углекислым газом, плотность которого больше плотности воздуха. Углекислый газ скапливается и заполняет дно сосуда, равновесие весов нарушается. На колбу начинает действовать большая выталкивающая сила, чем выталкивающая сила в воздухе: $$ rho_{mathrm{CO_2}}gt rho_text{возд}Rightarrow F_{text{выт. }mathrm{CO_2}}gt F_text{выт. возд.} $$ |
Вывод:
На тело, погружённое в газ, действует выталкивающая сила.
п.3. Закон Архимеда
В истории науки первым, кто изучал выталкивающую силу, действующую на тела в воде, был древнегреческий ученый Архимед. Поэтому эту силу также называют силой Архимеда.
| «Есть вещи, которые кажутся невероятными большинству людей, не изучавших математику».
Архимед (287-212 гг. до н.э.), |
 |
 |
Рассмотрим тело, погружённое в жидкость. Сверху на тело действует сила (F_1), которая равна давлению столба жидкости высотой (h_1) на площадь верхней поверхности тела: (F_1=rho_text{ж}gh_1S). Снизу по закону Паскаля на тело действует сила (F_2), которая равна давлению столба жидкости высотой (h_2) на площадь нижней поверхности тела: (F_2=rho_text{ж}gh_2S). |
На любом промежуточном уровне силы, действующие на боковые поверхности, равны по значению и противоположны по направлению, т.е. взаимно уравновешивают друг друга.
Равнодействующая всех сил, действующих на тело со стороны жидкости: $$ R=F_2-F-1=rho_text{ж}gS(h_2-h_1)=rho_text{ж}gSh=rho_text{ж}gV_text{т} $$
Равнодействующая направлена вверх, т.е. является выталкивающей силой.
Закон Архимеда
Выталкивающая сила направлена вертикально вверх и равна весу жидкости в объёме погружённого в неё тела: $$ F_A=rho_text{ж}V_text{т}g $$
Архимедова сила зависит от:
- плотности среды (жидкости или газа);
- объема погруженного тела (объема погруженной части тела);
- силы притяжения ((g) зависит от массы планеты и расстояния до её центра; сила Архимеда будет разной на Земле и Луне; также, сила Архимеда будет заметно отличаться на поверхности Земли и на значительной высоте от Земли).
Архимедова сила НЕ зависит от:
- плотности вещества тела;
- части объема тела, не погруженной в среду.
п.4. Опыт с ведерком Архимеда
Для опыта понадобится: 1) ведерко Архимеда; 2) небольшой камень произвольной формы; 3) широкий сосуд с отливной трубкой; 4) стакан; 5) пружина; 6) штатив.
а) Укрепим пружину на штативе и подвесим к ней пустое ведерко (его называют ведерком Архимеда), а к ведерку – небольшой камень произвольной формы.
Отметим удлинение пружины.
Нальем в широкий сосуд с отливной трубкой воду до уровня отлива.
б) Подставим пустой стакан под отлив и погрузим камень полностью в воду. Камень вытеснит объем воды, равный собственному объему.
Удлинение пружины становится меньше – на камень действует выталкивающая сила.
в) Выльем воду из стакана в ведерко.
Удлинение пружины снова становится таким, как в начале.
Значит, выталкивающая сила равна весу воды в объеме погруженного в нее тела.
Таким образом, данный опыт подтверждает закон Архимеда.
п.5. Задачи
Задача 1. Чему равна сила Архимеда, действующая на полностью погруженный в воду куб с длиной ребра 8 см? Чему равна эта сила, если куб будет погружен в воду наполовину?
Дано:
(a=8 text{см}=0,08 text{м})
(rho_{text{ж}}=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(F_A-?, F’_A-?)
1) При полном погружении объем куба в воде (V_{text{Т}}=a^3.)
Сила Архимеда begin{gather*} F_A=rho_{text{ж}}V_{text{Т}}g= rho_{text{ж}}a^3g end{gather*} Подставляем begin{gather*} F_A=1000cdot 0,08^3cdot 10=5,12 {text{Н}} end{gather*} 2) Если куб погружен наполовину, его объем в воде begin{gather*} V’_{text{Т}}=frac 12 a^3=frac 12 V_{text{Т}} end{gather*} Сила Архимеда begin{gather*} F’_A=frac 12rho_{text{ж}}V_{text{Т}}g= frac 12 F_A end{gather*} Сила уменьшается в 2 раза, т.к. объем погруженной части в 2 раза меньше. begin{gather*} F’_A=frac 12cdot 5,12=2,56 {text{Н}} end{gather*} Ответ: 1) 5,12 Н; 2) 2,56 Н
Задача 2. На полностью погруженный в воду медный шар массой 8,9 кг действует выталкивающая сила 20 Н. Сплошной ли шар или в нем есть полость? Чему равен объем полости, если она есть? Плотность меди 8900 кг/м3, g≈10 м/с2. Ответ выразите в кубических дециметрах.
Дано:
(m=8,9 text{кг})
(rho_{text{ж}}=1000 text{кг/м}^3)
(F_A=20 text{Н})
(gapprox 10 text{м/с}^2)
(rho_{text{м}}=8900 text{кг/м}^3)
__________________
(V_{text{П}}-?)
Сила Архимеда begin{gather*} F_A=rho_{text{ж}}V_{text{Т}}gRightarrow V_{text{Т}}=frac{F_A}{rho_{text{ж}}g} end{gather*} Получаем $$ V_{text{Т}}=frac{20}{1000cdot 10}=0,002 (text{м}^3) = text{объем шара} $$ С другой стороны, begin{gather*} V=frac{m}{rho_{text{м}}} end{gather*} Получаем $$ V=frac{8,9}{8900}=0,001 (text{м}^3) = text{объем вещества шара} $$ Т.к. (V_{text{Т}}gt V), в шаре есть полость.
Объем шара – это сумма объема вещества и объема полости: (V_{text{Т}}=V+V_{text{П}})
begin{gather*} V_{text{П}}=V_{text{Т}}-V\[7pt] V_{text{П}}=0,002-0,001=0,001 (text{м}^3)=1 (text{дм}^3) end{gather*} Ответ: 1 дм3
Задача 3. Силы Архимеда, действующие на одно и то же тело в воде и в керосине, отличаются на 2 Н. В какой жидкости выталкивающая сила больше? Чему равен объем тела? Ответ выразите в кубических дециметрах.
Дано:
(Delta F_A=2 text{Н})
(rho_{text{в}}=1000 text{кг/м}^3)
(rho_{text{к}}=800 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(V_{text{Т}}-?)
Сила Архимеда прямо пропорциональна плотности жидкости. Следовательно, она будет больше в воде. begin{gather*} F_{Atext{в}}=rho_{text{в}}V_{text{Т}}g,\[7pt] F_{Atext{к}}=rho_{text{к}}V_{text{Т}}g,\[7pt] Delta F_A=F_{Atext{в}}-F_{Atext{к}}=rho_{text{в}}V_{text{Т}}g -rho_{text{к}}V_{text{Т}}g=(rho_{text{в}}-rho_{text{к}})V_{text{Т}}g end{gather*} Объем тела begin{gather*} V_{text{Т}}=frac{Delta F_A}{(rho_{text{в}}-rho_{text{к}})}g end{gather*} Получаем begin{gather*} V_{text{Т}}=frac{2}{(1000-800)cdot 10}=0,001 (text{м}^3)=1 (text{дм}^3) end{gather*} Ответ: больше в воде; 1 дм3
Задача 4. Бетонная плита объёмом 2 м3 погружена в воду. Какую силу необходимо приложить, чтобы удержать её в воде; в воздухе?
Дано:
(V=2 text{м}^3)
(rho_{text{в}}=1000 text{кг/м}^3)
(rho_{text{б}}=2300 text{кг/м}^3)
__________________
(F_{text{вода}}, F_{text{воздух}}-?)
В воде на плиту действуют три силы: сила тяжести (F_{text{тяж}}=mg=rho_{text{б}}Vg), сила Архимеда (F_A=rho_{text{в}}Vg) и удерживающая сила (F_{text{вода}}), при этом: begin{gather*} F_{text{тяж}}=F_A+F_{text{вода}}Rightarrow F_{text{вода}}=F_{text{тяж}}-F_A=rho_{text{б}}Vg-rho_{text{в}}Vg\[7pt] F_{text{вода}}=(rho_{text{б}}-rho_{text{в}})Vg\[7pt] F_{text{вода}}=(2300-1000)cdot 2cdot 9,8=25480 (text{Н})approx 25,5 (text{кН}) end{gather*} В воздухе на плиту также действуют три силы, но т.к. плотность воздуха в две тысячи раз меньше плотности бетона, выталкивающей силой воздуха можно пренебречь ((F_Aapprox 0)).
Поэтому: begin{gather*} F_{text{воздух}}approx F_{text{тяж}}=rho_{text{б}}Vg\[7pt] F_{text{воздух}}=2300cdot 2cdot 9,8=45080 (text{Н})approx 45,1 (text{кН}) end{gather*} Ответ: ≈25,5 кН; ≈45,1 кН
Задача 5*. (задача Архимеда) Корона царя Гиерона в воздухе весит 20 Н, а в воде 18,75 Н. Плотность золота 20000 кг/м3. Есть ли в короне примеси?
Предполагая, что к золоту было подмешано серебро, определите массу золота и серебра в короне. Плотность серебра 10000 кг/м3.
Найдите объемные части золота и серебра в короне.
Дано:
(P=20 text{Н})
(P_{text{вода}}=18,75 text{Н})
(rho_{text{з}}=20000 text{кг/м}^3)
(rho_{text{с}}=10000 text{кг/м}^3)
__________________
(rho, m_{text{з}}, m_{text{с}}, frac{V_{text{з}}}{V}, frac{V_{text{с}}}{V}-?)
1) Сила Архимеда, выталкивающая корону из воды: begin{gather*} F_A=P-P_{text{вода}}=rho_{text{в}}VgRightarrow V=frac{P-P_{text{вода}}}{rho_{text{в}}g} end{gather*} Плотность короны: begin{gather*} rho=frac mV=frac{P}{gV}=frac Pgcdot frac{rho_{text{в}}g}{P-P_{text{вода}}}=frac{P}{P-P_{text{вода}}}rho_{text{в}}\[6pt] rho=frac{20}{20-18,75}cdot 1000=16000 left(frac{text{кг}}{text{м}^3}right)lt rho_{text{з}} end{gather*} Плотность меньше плотности золота, значит, в короне ей примеси.
2) Масса короны: begin{gather*} m=rho V=rho_{text{з}}V_{text{з}}+rho_{text{с}}V_{text{с}}=rho_{text{з}}V_{text{з}}+rho_{text{с}}(V-V_{text{з}})\[6pt] rho V-rho_{text{с}}V=rho_{text{з}}V_{text{з}} -rho_{text{с}}V_{text{з}}Rightarrow V(rho-rho_{text{с}})=V_{text{з}}(rho_{text{з}}-rho_{text{с}})Rightarrow V_{text{з}}=frac{rho-rho_{text{с}}}{rho_{text{з}}-rho_{text{с}}}V end{gather*} Масса золота: begin{gather*} m_{text{з}}=rho_{text{з}}V_{text{з}}= frac{rho-rho_{text{с}}}{rho_{text{з}}-rho_{text{с}}}rho_{text{з}}V end{gather*} Объем короны: begin{gather*} V=frac{P-P_{text{вода}}}{rho_{text{в}}g}approx frac{20-18,75}{1000cdot 10}=1,25cdot 10^{-4} (text{м}^3) end{gather*} Часть объема золота: begin{gather*} frac{V_{text{з}}}{V}=frac{rho-rho_{text{с}}}{rho_{text{з}}-rho_{text{с}}}=frac{16000-10000}{20000-10000}=0,6=60 text{%} end{gather*} Часть объема серебра: begin{gather*} frac{V_{text{с}}}{V}=100 text{%}-60 text{%}=40 text{%} end{gather*} Масса короны: begin{gather*} m=rho V=16000cdot 1,25cdot 10^{-4}=2 (text{кг}) end{gather*} Масса золота: begin{gather*} m_{text{з}}=frac{16000-10000}{20000-10000}cdot 20000cdot 1,25cdot 10^{-4}=1,5 (text{кг}) end{gather*} Масса серебра: begin{gather*} m_{text{с}}=m-m_{text{з}}=2-1,5=0,5 (text{кг}) end{gather*} Ответ: (rho=16000 frac{text{кг}}{text{м}^3}; m_{text{з}}=1,5 text{кг}; m_{text{с}}=0,5 text{кг}; frac{V_{text{з}}}{V}=60 text{%}; frac{V_{text{с}}}{V}=40 text{%})
п.6. Лабораторная работа №11. Определение плотности твердых тел и жидкостей методом гидростатического взвешивания
Цель работы
Научиться определять плотности твердых тел и жидкостей методом гидростатического взвешивания.
Теоретические сведения
1) На тело, погруженное в воду, действует выталкивающая сила $$ F_A=rho_{text{в}}V_{text{т}}g $$ где (rho_{text{в}}) – плотность воды, (V_{text{т}}) – объем тела (части тела), погруженного в жидкость, (g) – ускорение свободного падения.
Если вес твердого тела в воздухе (P=rho_{text{т}}V_{text{т}}g), его вес в воде (P=P_{text{в}}-F_A)
Отношение веса в воздухе и выталкивающей силы $$ frac{P}{F_A}=frac{rho_{text{т}}V_{text{т}}g}{rho_{text{в}}V_{text{т}}g}=frac{rho_{text{т}}}{rho_{text{в}}} $$
Плотность тела $$ rho_{text{т}}=frac{P}{F_A}rho_{text{в}} $$
Определение плотности твердого тела методом гидростатического взвешивания
Шаг 1. Измерить вес тела в воздухе (P)
Шаг 2.. Измерить вес тела в воде (P_{text{в}}).
Шаг 3.. Найти (F_A=P-P_{text{в}}).
Шаг 4.. Найти (rho_{text{т}}=frac{P}{F_A}rho_{text{в}}).
Найдем погрешность результата.
При использовании динамометра с ценой деления (d=0,1 text{Н}) абсолютная погрешность прямого измерения веса (P) и (P_{text{в}}: Delta=frac d2=0,05 text{Н}).
Абсолютная погрешность вычисления разности (F_A: Delta_{F_A}=Delta +Delta = 2Delta =d=0,1 text{Н}).
Абсолютную погрешность для табличного значения плотности воды принимаем равной (Delta_{rho_{text{в}}}=5 text{кг/м}^3).
Из формулы для плотности тела получаем относительную погрешность результата $$ delta_{rho_{text{т}}}=delta_P+ delta_{F_A}+delta_{rho_{text{в}}} $$ Где относительные погрешности в сумме вычисляются как обычно.
2) Пусть вес твердого тела в воздухе (P=rho_{text{т}}V_{text{т}}g), его вес в воде (P_{text{в}}=P-F_{text{Ав}}), а вес в другой жидкости (P_text{ж}=P-F_{text{Аж}}).
Отношение выталкивающих сил в воде и другой жидкости $$ frac{F_{text{Ав}}}{F_{text{Аж}}}=frac{rho_{text{в}}V_{text{т}}g}{rho_{text{ж}}V_{text{т}}g}=frac{rho_{text{в}}}{rho_{text{ж}}} $$
Плотность другой жидкости $$ rho_{text{ж}}=frac{F_{text{Аж}}}{F_{text{Ав}}}rho_{text{в}} $$
Определение плотности жидкости методом гидростатического взвешивания
Шаг 1. Измерить вес тела в воздухе (P)
Шаг 2.. Измерить вес тела в воде (P_{text{в}}).
Шаг 3.. Измерить вес тела в другой жидкости (P_{text{ж}}).
Шаг 4.. Найти (F_{text{Ав}}=P-P’_{text{в}}, F_{text{Аж}}=P-P’_{text{ж}}).
Шаг 5.. Найти (rho_{text{ж}}=frac{F_{text{Аж}}}{F_{text{Ав}}}rho_{text{в}}).
Найдем погрешность результата.
Абсолютная погрешность вычисления разностей (F_{text{Ав}}, F_{text{Аж}}: Delta_{F}=d=0,1 text{Н}).
Абсолютную погрешность для табличного значения плотности воды принимаем равной (Delta_{rho_{text{в}}}=5 text{кг/м}^3).
Из формулы для плотности тела получаем относительную погрешность результата $$ delta_{rho_{text{ж}}}= delta_{F_{text{Ав}}} + delta_{F_{text{Аж}}}+delta_{rho_{text{в}}} $$ Где относительные погрешности в сумме вычисляются как обычно.
Приборы и материалы
Динамометр, тело с подвесом, сосуд с водой, поваренная соль.
Ход работы
1. Измерьте вес тела в воздухе и в воде с помощью динамометра.
2. Найдите (F_A), рассчитайте плотность тела (rho_text{т}). По таблице плотностей определите, из какого вещества состоит тело.
3. Найдите относительную и абсолютную погрешность определения (rho_text{т})
4. Добавьте в воду соль из расчета примерно 0,5-0,7 столовой ложки на каждые 100 г воды.
5. Измерьте вес тела в растворе соли с помощью динамометра.
6. Найдите (F_{text{Aж}}), рассчитайте плотность раствора (rho_text{ж}). По таблице плотностей определите концентрацию (mathrm{NaCl}) в воде.
7. Найдите относительную и абсолютную погрешность определения (rho_text{ж}).
8. Сделайте выводы.
Результаты измерений и вычислений
1. Определение плотности твердого тела методом гидростатического взвешивания
Вес тела в воздухе (P=7,3 text{Н})
Вес тела в воде (P_{text{в}}=4,6 text{Н})
Сила Архимеда в воде (F_A=P-P_{text{в}}=7,3-4,6=2,7 text{Н})
Плотность тела $$ rho_{text{т}}=frac{P}{F_A}rho_{text{в}}=frac{7,3}{2,7}cdot 1000approx 2700 text{кг/м}^3 $$ Вещество: алюминий
Относительная погрешность begin{gather*} delta_{rho_{text{т}}}=delta_P+ delta_{F_A}+delta_{rho_{text{в}}}= frac{Delta}{P}+frac{2Delta}{F_A}+frac{Delta_{rho_{text{в}}}}{rho_{text{в}}}=frac{0,05}{7,3}+frac{0,1}{2,7}+frac{5}{1000}approx \[6pt] approx 0,007+0,037+0,005=0,049=4,9text{%} end{gather*} Абсолютная погрешность begin{gather*} Delta_{rho_{text{т}}}= delta_{rho_{text{т}}}cdot rho_{text{т}}=0,049cdot 2700approx 130 text{кг/м}^3\[7pt] rho_{text{т}}=(2700pm 130) text{кг/м}^3 end{gather*}
2. Определение плотности жидкости методом гидростатического взвешивания
Вес тела в воздухе (P=7,3 text{Н})
Вес тела в воде (P_{text{в}}=4,6 text{Н})
Вес тела в растворе (P_{text{ж}}=4,4 text{Н})
Сила Архимеда в воде (F_{text{Ав}}=P-P_{text{в}}=7,3-4,6=2,7 text{Н})
Сила Архимеда в растворе (F_{text{Аж}}=P-P_{text{ж}}=7,3-4,4=2,9 text{Н})
Плотность раствора $$ rho_{text{ж}}=frac{F_{text{Аж}}}{F_{text{Ав}}}rho_{text{в}}=frac{2,9}{2,7}cdot 1000approx 1130 text{кг/м}^3 $$ По таблице плотности растворов (mathrm{NaCl}) концентрация раствора (c=16text{%}).
Относительная погрешность begin{gather*} delta_{rho_{text{ж}}}= delta_{F_{text{Ав}}}+delta_{F_{text{Аж}}}+delta_{rho_{text{в}}}= frac{2Delta}{F_{text{Ав}}}+frac{2Delta}{F_{text{Аж}}}+frac{Delta_{rho_{text{в}}}}{rho_{text{в}}}=frac{0,1}{2,7}+frac{0,1}{2,9}+frac{5}{1000}approx \[6pt] approx 0,037+0,034+0,005=0,076=7,6text{%} end{gather*} Абсолютная погрешность begin{gather*} Delta_{rho_{text{ж}}}= delta_{rho_{text{ж}}}cdot rho_{text{ж}}=0,076cdot 1130approx 90 text{кг/м}^3\[7pt] rho_{text{ж}}=(1130pm 90) text{кг/м}^3 end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
При определении плотности тела методом гидростатического взвешивания получили $$ rho_{text{т}}=(2700pm 130) text{кг/м}^3 $$ Относительная погрешность результата (delta_{rho_{text{т}}}=4,9text{%})
Вещество, из которого состоит тело – алюминий.
При определении плотности раствора поваренной соли методом гидростатического взвешивания получили begin{gather*} rho_{text{ж}}=(1130pm 90) text{кг/м}^3 end{gather*} Относительная погрешность результата (delta_{rho_{text{ж}}}=7,6text{%})
По таблице плотности растворов (mathrm{NaCl}) концентрация раствора (c=16text{%}).
Таким образом, все задачи, которые были поставлены перед исследованием, успешно выполнены.
