Задачи на силу Архимеда с решениями
Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».
Название величины |
Обозначение |
Единица измерения |
Формула |
Объем тела |
V |
м3 |
Vт = FA / pg |
Плотность жидкости |
p |
кг/м3 |
pж = FA / (Vg) |
Сила Архимеда |
FA |
Н |
FA = pж Vт g |
Постоянная |
g ≈ 10 Н/кг |
Н/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Тело объемом 2 м3 погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м3, погруженный в воду на половину своего объема.

Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7.
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм3?
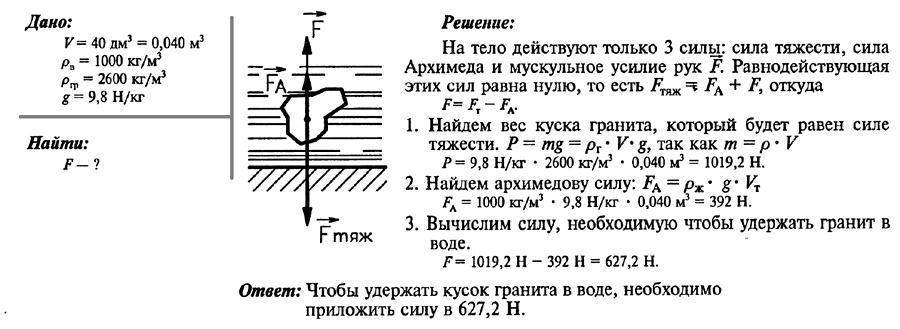
Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
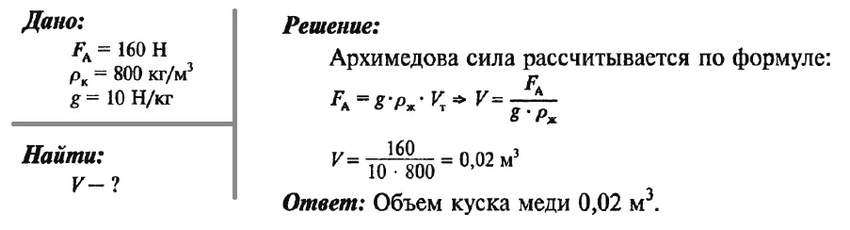
Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м3, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м3.
Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V1 – объем цилиндра, погруженного в масло (V1 = V – V2 = Sh1); h1 – высота части цилиндра, погруженной в масло; V2 – объем цилиндра, погруженного в воду после добавления масла; рв – плотность воды (1000 кг/м3); рм – плотность масла (800 кг/м3)
Найти: (h – h1) / h — ?
Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9pвgV
F1 – сила, выталкивающая цилиндр из масла F1 = pмgV1
F2 – сила, выталкивающая цилиндр из воды после добавления масла F2 = pвgV2
Баланс сил: F – F1 = F2
0,9pвgV – pмgV1 = pвgV2 V1 = V – V2 ⇒ 0,9pвV – pм(V – V2) = pвV2
V(0,9pв – pм) = V2(pв – pм) V = Sh; V1 = Sh1 ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).
Задача № 12.
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.
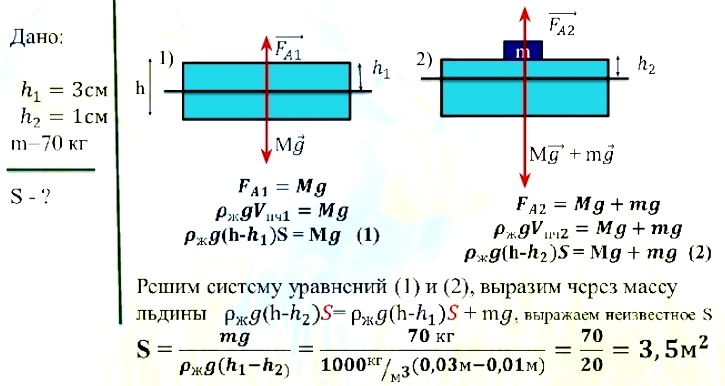
Ответ: 3,5 м3.
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».
Следующая тема: «Задачи на механическую работу».
Архимедова сила — выталкивающая сила, равная весу газа или жидкости в объёме погружённой части тела.




Опыт. Нам понадобятся ёмкость с ручкой и груз в форме цилиндра.
- Растяжение пружины динамометра отметим стрелкой на штативе (рис. (A)), она показывает вес тела в воздухе.
- Подставим сосуд, наполненный жидкостью, до уровня отливной трубки (рис. (B)) и поместим в него цилиндр.
- После погружения цилиндра вода выливается в мерный стакан. Её объём равен объёму цилиндрического груза (рис. (B)).
- Стрелка динамометра поднимается вверх, растяжение пружины уменьшается, что соответствует уменьшению веса тела в жидкости (рис. (C)). В этом случае на цилиндр действует сила тяжести и сила Архимеда, направленная вверх.
- Если в ведёрко вылить вытесненную из отливного стаканчика жидкость, то стрелка динамометра возвратится в начальное положение (рис. (D)).
Вывод: выталкивающая сила, действующая на погружённое в жидкость тело, равна весу жидкости, вытесненной этим телом.
Сила, выталкивающая тело из газа, также равна весу газа, взятого в объёме тела. Это и есть закон Архимеда.
Формулу можно записать в другом виде.
Выразим массу жидкости, вытесняемую телом, через её плотность и объём тела, погружённого в жидкость, тогда получим:
Согласно полученной формуле, на тело, погружённое в жидкость, действует выталкивающая сила (сила Архимеда), равная произведению плотности жидкости, ускорения свободного падения и объёма тела (или той его части, которая погружена в жидкость).
Эта формула позволяет рассчитать выталкивающую силу для тела, находящегося в газе. В этом случае плотность жидкости заменяют плотностью газа.
Закон Архимеда
- Выталкивание тела жидкостью при погружении
- Выталкивание тела газом при погружении
- Закон Архимеда
- Опыт с ведерком Архимеда
- Задачи
- Лабораторная работа №11. Определение плотности твердых тел и жидкостей методом гидростатического взвешивания
п.1. Выталкивание тела жидкостью при погружении
Проведем следующий опыт.
Нам понадобится: 1) динамометр; 2) груз; 3) стакан с раствором соли.
В первом случае пружина динамометра растягивается под действием силы тяжести: $$ F_text{упр1}=F_text{тяж}Rightarrow kl_1=mgRightarrow l_1=frac{mg}{k} $$
Во втором случае пружина растягивается под действием равнодействующей силы тяжести и некоторой силы, которая направлена вверх, т.е. выталкивает тело из жидкости: $$ F_text{упр2}=R=F_text{тяж}-F_text{выт}Rightarrow kl_2=mg-F_text{выт}Rightarrow l_2=frac{mg-F_text{выт}}{k} $$ Поэтому (l_2lt l_1), во втором случае пружина растягивается меньше.
Вывод:
На тело, погружённое в жидкость, действует выталкивающая сила.
 |
Действием выталкивающей силы можно объяснить, почему корабли не тонут в воде: если выталкивающая сила уравновешивает силу тяжести, то вода становится «опорой» и корабль держится на воде. |
п.2. Выталкивание тела газом при погружении
Проведем следующий опыт.
Нам понадобится: 1) весы с разновесами; 2) колба с пробкой; 3) широкий сосуд; 4) источник углекислого газа.
Получить небольшое количество углекислого газа можно при взаимодействии разбавленной соляной кислоты и карбоната кальция (мрамора): $$ mathrm{CaCO_3+2HClrightarrow CaCl_2+CO_2uparrow +H_2O} $$
Реакцию следует проводить в пробирке с газоотводной трубкой. Она будет служить источником (mathrm{CO_2}).
 |
Закрываем колбу пробкой. Помещаем колбу в широкий сосуд, подвешиваем колбу к чашке весов и уравновешиваем её с помощью разновесов. Запускаем в сосуд газоотводную трубку с углекислым газом, плотность которого больше плотности воздуха. Углекислый газ скапливается и заполняет дно сосуда, равновесие весов нарушается. На колбу начинает действовать большая выталкивающая сила, чем выталкивающая сила в воздухе: $$ rho_{mathrm{CO_2}}gt rho_text{возд}Rightarrow F_{text{выт. }mathrm{CO_2}}gt F_text{выт. возд.} $$ |
Вывод:
На тело, погружённое в газ, действует выталкивающая сила.
п.3. Закон Архимеда
В истории науки первым, кто изучал выталкивающую силу, действующую на тела в воде, был древнегреческий ученый Архимед. Поэтому эту силу также называют силой Архимеда.
| «Есть вещи, которые кажутся невероятными большинству людей, не изучавших математику».
Архимед (287-212 гг. до н.э.), |
 |
 |
Рассмотрим тело, погружённое в жидкость. Сверху на тело действует сила (F_1), которая равна давлению столба жидкости высотой (h_1) на площадь верхней поверхности тела: (F_1=rho_text{ж}gh_1S). Снизу по закону Паскаля на тело действует сила (F_2), которая равна давлению столба жидкости высотой (h_2) на площадь нижней поверхности тела: (F_2=rho_text{ж}gh_2S). |
На любом промежуточном уровне силы, действующие на боковые поверхности, равны по значению и противоположны по направлению, т.е. взаимно уравновешивают друг друга.
Равнодействующая всех сил, действующих на тело со стороны жидкости: $$ R=F_2-F-1=rho_text{ж}gS(h_2-h_1)=rho_text{ж}gSh=rho_text{ж}gV_text{т} $$
Равнодействующая направлена вверх, т.е. является выталкивающей силой.
Закон Архимеда
Выталкивающая сила направлена вертикально вверх и равна весу жидкости в объёме погружённого в неё тела: $$ F_A=rho_text{ж}V_text{т}g $$
Архимедова сила зависит от:
- плотности среды (жидкости или газа);
- объема погруженного тела (объема погруженной части тела);
- силы притяжения ((g) зависит от массы планеты и расстояния до её центра; сила Архимеда будет разной на Земле и Луне; также, сила Архимеда будет заметно отличаться на поверхности Земли и на значительной высоте от Земли).
Архимедова сила НЕ зависит от:
- плотности вещества тела;
- части объема тела, не погруженной в среду.
п.4. Опыт с ведерком Архимеда
Для опыта понадобится: 1) ведерко Архимеда; 2) небольшой камень произвольной формы; 3) широкий сосуд с отливной трубкой; 4) стакан; 5) пружина; 6) штатив.

а) Укрепим пружину на штативе и подвесим к ней пустое ведерко (его называют ведерком Архимеда), а к ведерку – небольшой камень произвольной формы.
Отметим удлинение пружины.
Нальем в широкий сосуд с отливной трубкой воду до уровня отлива.
б) Подставим пустой стакан под отлив и погрузим камень полностью в воду. Камень вытеснит объем воды, равный собственному объему.
Удлинение пружины становится меньше – на камень действует выталкивающая сила.
в) Выльем воду из стакана в ведерко.
Удлинение пружины снова становится таким, как в начале.
Значит, выталкивающая сила равна весу воды в объеме погруженного в нее тела.
Таким образом, данный опыт подтверждает закон Архимеда.
п.5. Задачи
Задача 1. Чему равна сила Архимеда, действующая на полностью погруженный в воду куб с длиной ребра 8 см? Чему равна эта сила, если куб будет погружен в воду наполовину?
Дано:
(a=8 text{см}=0,08 text{м})
(rho_{text{ж}}=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(F_A-?, F’_A-?)
1) При полном погружении объем куба в воде (V_{text{Т}}=a^3.)
Сила Архимеда begin{gather*} F_A=rho_{text{ж}}V_{text{Т}}g= rho_{text{ж}}a^3g end{gather*} Подставляем begin{gather*} F_A=1000cdot 0,08^3cdot 10=5,12 {text{Н}} end{gather*} 2) Если куб погружен наполовину, его объем в воде begin{gather*} V’_{text{Т}}=frac 12 a^3=frac 12 V_{text{Т}} end{gather*} Сила Архимеда begin{gather*} F’_A=frac 12rho_{text{ж}}V_{text{Т}}g= frac 12 F_A end{gather*} Сила уменьшается в 2 раза, т.к. объем погруженной части в 2 раза меньше. begin{gather*} F’_A=frac 12cdot 5,12=2,56 {text{Н}} end{gather*} Ответ: 1) 5,12 Н; 2) 2,56 Н
Задача 2. На полностью погруженный в воду медный шар массой 8,9 кг действует выталкивающая сила 20 Н. Сплошной ли шар или в нем есть полость? Чему равен объем полости, если она есть? Плотность меди 8900 кг/м3, g≈10 м/с2. Ответ выразите в кубических дециметрах.
Дано:
(m=8,9 text{кг})
(rho_{text{ж}}=1000 text{кг/м}^3)
(F_A=20 text{Н})
(gapprox 10 text{м/с}^2)
(rho_{text{м}}=8900 text{кг/м}^3)
__________________
(V_{text{П}}-?)
Сила Архимеда begin{gather*} F_A=rho_{text{ж}}V_{text{Т}}gRightarrow V_{text{Т}}=frac{F_A}{rho_{text{ж}}g} end{gather*} Получаем $$ V_{text{Т}}=frac{20}{1000cdot 10}=0,002 (text{м}^3) = text{объем шара} $$ С другой стороны, begin{gather*} V=frac{m}{rho_{text{м}}} end{gather*} Получаем $$ V=frac{8,9}{8900}=0,001 (text{м}^3) = text{объем вещества шара} $$ Т.к. (V_{text{Т}}gt V), в шаре есть полость.
Объем шара – это сумма объема вещества и объема полости: (V_{text{Т}}=V+V_{text{П}})
begin{gather*} V_{text{П}}=V_{text{Т}}-V\[7pt] V_{text{П}}=0,002-0,001=0,001 (text{м}^3)=1 (text{дм}^3) end{gather*} Ответ: 1 дм3
Задача 3. Силы Архимеда, действующие на одно и то же тело в воде и в керосине, отличаются на 2 Н. В какой жидкости выталкивающая сила больше? Чему равен объем тела? Ответ выразите в кубических дециметрах.
Дано:
(Delta F_A=2 text{Н})
(rho_{text{в}}=1000 text{кг/м}^3)
(rho_{text{к}}=800 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(V_{text{Т}}-?)
Сила Архимеда прямо пропорциональна плотности жидкости. Следовательно, она будет больше в воде. begin{gather*} F_{Atext{в}}=rho_{text{в}}V_{text{Т}}g,\[7pt] F_{Atext{к}}=rho_{text{к}}V_{text{Т}}g,\[7pt] Delta F_A=F_{Atext{в}}-F_{Atext{к}}=rho_{text{в}}V_{text{Т}}g -rho_{text{к}}V_{text{Т}}g=(rho_{text{в}}-rho_{text{к}})V_{text{Т}}g end{gather*} Объем тела begin{gather*} V_{text{Т}}=frac{Delta F_A}{(rho_{text{в}}-rho_{text{к}})}g end{gather*} Получаем begin{gather*} V_{text{Т}}=frac{2}{(1000-800)cdot 10}=0,001 (text{м}^3)=1 (text{дм}^3) end{gather*} Ответ: больше в воде; 1 дм3
Задача 4. Бетонная плита объёмом 2 м3 погружена в воду. Какую силу необходимо приложить, чтобы удержать её в воде; в воздухе?
Дано:
(V=2 text{м}^3)
(rho_{text{в}}=1000 text{кг/м}^3)
(rho_{text{б}}=2300 text{кг/м}^3)
__________________
(F_{text{вода}}, F_{text{воздух}}-?)

В воде на плиту действуют три силы: сила тяжести (F_{text{тяж}}=mg=rho_{text{б}}Vg), сила Архимеда (F_A=rho_{text{в}}Vg) и удерживающая сила (F_{text{вода}}), при этом: begin{gather*} F_{text{тяж}}=F_A+F_{text{вода}}Rightarrow F_{text{вода}}=F_{text{тяж}}-F_A=rho_{text{б}}Vg-rho_{text{в}}Vg\[7pt] F_{text{вода}}=(rho_{text{б}}-rho_{text{в}})Vg\[7pt] F_{text{вода}}=(2300-1000)cdot 2cdot 9,8=25480 (text{Н})approx 25,5 (text{кН}) end{gather*} В воздухе на плиту также действуют три силы, но т.к. плотность воздуха в две тысячи раз меньше плотности бетона, выталкивающей силой воздуха можно пренебречь ((F_Aapprox 0)).
Поэтому: begin{gather*} F_{text{воздух}}approx F_{text{тяж}}=rho_{text{б}}Vg\[7pt] F_{text{воздух}}=2300cdot 2cdot 9,8=45080 (text{Н})approx 45,1 (text{кН}) end{gather*} Ответ: ≈25,5 кН; ≈45,1 кН
Задача 5*. (задача Архимеда) Корона царя Гиерона в воздухе весит 20 Н, а в воде 18,75 Н. Плотность золота 20000 кг/м3. Есть ли в короне примеси?
Предполагая, что к золоту было подмешано серебро, определите массу золота и серебра в короне. Плотность серебра 10000 кг/м3.
Найдите объемные части золота и серебра в короне.
Дано:
(P=20 text{Н})
(P_{text{вода}}=18,75 text{Н})
(rho_{text{з}}=20000 text{кг/м}^3)
(rho_{text{с}}=10000 text{кг/м}^3)
__________________
(rho, m_{text{з}}, m_{text{с}}, frac{V_{text{з}}}{V}, frac{V_{text{с}}}{V}-?)
1) Сила Архимеда, выталкивающая корону из воды: begin{gather*} F_A=P-P_{text{вода}}=rho_{text{в}}VgRightarrow V=frac{P-P_{text{вода}}}{rho_{text{в}}g} end{gather*} Плотность короны: begin{gather*} rho=frac mV=frac{P}{gV}=frac Pgcdot frac{rho_{text{в}}g}{P-P_{text{вода}}}=frac{P}{P-P_{text{вода}}}rho_{text{в}}\[6pt] rho=frac{20}{20-18,75}cdot 1000=16000 left(frac{text{кг}}{text{м}^3}right)lt rho_{text{з}} end{gather*} Плотность меньше плотности золота, значит, в короне ей примеси.
2) Масса короны: begin{gather*} m=rho V=rho_{text{з}}V_{text{з}}+rho_{text{с}}V_{text{с}}=rho_{text{з}}V_{text{з}}+rho_{text{с}}(V-V_{text{з}})\[6pt] rho V-rho_{text{с}}V=rho_{text{з}}V_{text{з}} -rho_{text{с}}V_{text{з}}Rightarrow V(rho-rho_{text{с}})=V_{text{з}}(rho_{text{з}}-rho_{text{с}})Rightarrow V_{text{з}}=frac{rho-rho_{text{с}}}{rho_{text{з}}-rho_{text{с}}}V end{gather*} Масса золота: begin{gather*} m_{text{з}}=rho_{text{з}}V_{text{з}}= frac{rho-rho_{text{с}}}{rho_{text{з}}-rho_{text{с}}}rho_{text{з}}V end{gather*} Объем короны: begin{gather*} V=frac{P-P_{text{вода}}}{rho_{text{в}}g}approx frac{20-18,75}{1000cdot 10}=1,25cdot 10^{-4} (text{м}^3) end{gather*} Часть объема золота: begin{gather*} frac{V_{text{з}}}{V}=frac{rho-rho_{text{с}}}{rho_{text{з}}-rho_{text{с}}}=frac{16000-10000}{20000-10000}=0,6=60 text{%} end{gather*} Часть объема серебра: begin{gather*} frac{V_{text{с}}}{V}=100 text{%}-60 text{%}=40 text{%} end{gather*} Масса короны: begin{gather*} m=rho V=16000cdot 1,25cdot 10^{-4}=2 (text{кг}) end{gather*} Масса золота: begin{gather*} m_{text{з}}=frac{16000-10000}{20000-10000}cdot 20000cdot 1,25cdot 10^{-4}=1,5 (text{кг}) end{gather*} Масса серебра: begin{gather*} m_{text{с}}=m-m_{text{з}}=2-1,5=0,5 (text{кг}) end{gather*} Ответ: (rho=16000 frac{text{кг}}{text{м}^3}; m_{text{з}}=1,5 text{кг}; m_{text{с}}=0,5 text{кг}; frac{V_{text{з}}}{V}=60 text{%}; frac{V_{text{с}}}{V}=40 text{%})
п.6. Лабораторная работа №11. Определение плотности твердых тел и жидкостей методом гидростатического взвешивания
Цель работы
Научиться определять плотности твердых тел и жидкостей методом гидростатического взвешивания.
Теоретические сведения
1) На тело, погруженное в воду, действует выталкивающая сила $$ F_A=rho_{text{в}}V_{text{т}}g $$ где (rho_{text{в}}) – плотность воды, (V_{text{т}}) – объем тела (части тела), погруженного в жидкость, (g) – ускорение свободного падения.
Если вес твердого тела в воздухе (P=rho_{text{т}}V_{text{т}}g), его вес в воде (P=P_{text{в}}-F_A)
Отношение веса в воздухе и выталкивающей силы $$ frac{P}{F_A}=frac{rho_{text{т}}V_{text{т}}g}{rho_{text{в}}V_{text{т}}g}=frac{rho_{text{т}}}{rho_{text{в}}} $$
Плотность тела $$ rho_{text{т}}=frac{P}{F_A}rho_{text{в}} $$
Определение плотности твердого тела методом гидростатического взвешивания
Шаг 1. Измерить вес тела в воздухе (P)
Шаг 2.. Измерить вес тела в воде (P_{text{в}}).
Шаг 3.. Найти (F_A=P-P_{text{в}}).
Шаг 4.. Найти (rho_{text{т}}=frac{P}{F_A}rho_{text{в}}).
Найдем погрешность результата.
При использовании динамометра с ценой деления (d=0,1 text{Н}) абсолютная погрешность прямого измерения веса (P) и (P_{text{в}}: Delta=frac d2=0,05 text{Н}).
Абсолютная погрешность вычисления разности (F_A: Delta_{F_A}=Delta +Delta = 2Delta =d=0,1 text{Н}).
Абсолютную погрешность для табличного значения плотности воды принимаем равной (Delta_{rho_{text{в}}}=5 text{кг/м}^3).
Из формулы для плотности тела получаем относительную погрешность результата $$ delta_{rho_{text{т}}}=delta_P+ delta_{F_A}+delta_{rho_{text{в}}} $$ Где относительные погрешности в сумме вычисляются как обычно.
2) Пусть вес твердого тела в воздухе (P=rho_{text{т}}V_{text{т}}g), его вес в воде (P_{text{в}}=P-F_{text{Ав}}), а вес в другой жидкости (P_text{ж}=P-F_{text{Аж}}).
Отношение выталкивающих сил в воде и другой жидкости $$ frac{F_{text{Ав}}}{F_{text{Аж}}}=frac{rho_{text{в}}V_{text{т}}g}{rho_{text{ж}}V_{text{т}}g}=frac{rho_{text{в}}}{rho_{text{ж}}} $$
Плотность другой жидкости $$ rho_{text{ж}}=frac{F_{text{Аж}}}{F_{text{Ав}}}rho_{text{в}} $$
Определение плотности жидкости методом гидростатического взвешивания
Шаг 1. Измерить вес тела в воздухе (P)
Шаг 2.. Измерить вес тела в воде (P_{text{в}}).
Шаг 3.. Измерить вес тела в другой жидкости (P_{text{ж}}).
Шаг 4.. Найти (F_{text{Ав}}=P-P’_{text{в}}, F_{text{Аж}}=P-P’_{text{ж}}).
Шаг 5.. Найти (rho_{text{ж}}=frac{F_{text{Аж}}}{F_{text{Ав}}}rho_{text{в}}).
Найдем погрешность результата.
Абсолютная погрешность вычисления разностей (F_{text{Ав}}, F_{text{Аж}}: Delta_{F}=d=0,1 text{Н}).
Абсолютную погрешность для табличного значения плотности воды принимаем равной (Delta_{rho_{text{в}}}=5 text{кг/м}^3).
Из формулы для плотности тела получаем относительную погрешность результата $$ delta_{rho_{text{ж}}}= delta_{F_{text{Ав}}} + delta_{F_{text{Аж}}}+delta_{rho_{text{в}}} $$ Где относительные погрешности в сумме вычисляются как обычно.
Приборы и материалы
Динамометр, тело с подвесом, сосуд с водой, поваренная соль.
Ход работы
1. Измерьте вес тела в воздухе и в воде с помощью динамометра.
2. Найдите (F_A), рассчитайте плотность тела (rho_text{т}). По таблице плотностей определите, из какого вещества состоит тело.
3. Найдите относительную и абсолютную погрешность определения (rho_text{т})
4. Добавьте в воду соль из расчета примерно 0,5-0,7 столовой ложки на каждые 100 г воды.
5. Измерьте вес тела в растворе соли с помощью динамометра.
6. Найдите (F_{text{Aж}}), рассчитайте плотность раствора (rho_text{ж}). По таблице плотностей определите концентрацию (mathrm{NaCl}) в воде.
7. Найдите относительную и абсолютную погрешность определения (rho_text{ж}).
8. Сделайте выводы.
Результаты измерений и вычислений
1. Определение плотности твердого тела методом гидростатического взвешивания
Вес тела в воздухе (P=7,3 text{Н})
Вес тела в воде (P_{text{в}}=4,6 text{Н})
Сила Архимеда в воде (F_A=P-P_{text{в}}=7,3-4,6=2,7 text{Н})
Плотность тела $$ rho_{text{т}}=frac{P}{F_A}rho_{text{в}}=frac{7,3}{2,7}cdot 1000approx 2700 text{кг/м}^3 $$ Вещество: алюминий
Относительная погрешность begin{gather*} delta_{rho_{text{т}}}=delta_P+ delta_{F_A}+delta_{rho_{text{в}}}= frac{Delta}{P}+frac{2Delta}{F_A}+frac{Delta_{rho_{text{в}}}}{rho_{text{в}}}=frac{0,05}{7,3}+frac{0,1}{2,7}+frac{5}{1000}approx \[6pt] approx 0,007+0,037+0,005=0,049=4,9text{%} end{gather*} Абсолютная погрешность begin{gather*} Delta_{rho_{text{т}}}= delta_{rho_{text{т}}}cdot rho_{text{т}}=0,049cdot 2700approx 130 text{кг/м}^3\[7pt] rho_{text{т}}=(2700pm 130) text{кг/м}^3 end{gather*}
2. Определение плотности жидкости методом гидростатического взвешивания
Вес тела в воздухе (P=7,3 text{Н})
Вес тела в воде (P_{text{в}}=4,6 text{Н})
Вес тела в растворе (P_{text{ж}}=4,4 text{Н})
Сила Архимеда в воде (F_{text{Ав}}=P-P_{text{в}}=7,3-4,6=2,7 text{Н})
Сила Архимеда в растворе (F_{text{Аж}}=P-P_{text{ж}}=7,3-4,4=2,9 text{Н})
Плотность раствора $$ rho_{text{ж}}=frac{F_{text{Аж}}}{F_{text{Ав}}}rho_{text{в}}=frac{2,9}{2,7}cdot 1000approx 1130 text{кг/м}^3 $$ По таблице плотности растворов (mathrm{NaCl}) концентрация раствора (c=16text{%}).
Относительная погрешность begin{gather*} delta_{rho_{text{ж}}}= delta_{F_{text{Ав}}}+delta_{F_{text{Аж}}}+delta_{rho_{text{в}}}= frac{2Delta}{F_{text{Ав}}}+frac{2Delta}{F_{text{Аж}}}+frac{Delta_{rho_{text{в}}}}{rho_{text{в}}}=frac{0,1}{2,7}+frac{0,1}{2,9}+frac{5}{1000}approx \[6pt] approx 0,037+0,034+0,005=0,076=7,6text{%} end{gather*} Абсолютная погрешность begin{gather*} Delta_{rho_{text{ж}}}= delta_{rho_{text{ж}}}cdot rho_{text{ж}}=0,076cdot 1130approx 90 text{кг/м}^3\[7pt] rho_{text{ж}}=(1130pm 90) text{кг/м}^3 end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
При определении плотности тела методом гидростатического взвешивания получили $$ rho_{text{т}}=(2700pm 130) text{кг/м}^3 $$ Относительная погрешность результата (delta_{rho_{text{т}}}=4,9text{%})
Вещество, из которого состоит тело – алюминий.
При определении плотности раствора поваренной соли методом гидростатического взвешивания получили begin{gather*} rho_{text{ж}}=(1130pm 90) text{кг/м}^3 end{gather*} Относительная погрешность результата (delta_{rho_{text{ж}}}=7,6text{%})
По таблице плотности растворов (mathrm{NaCl}) концентрация раствора (c=16text{%}).
Таким образом, все задачи, которые были поставлены перед исследованием, успешно выполнены.


ГДЗ (готовое домашние задание из решебника) на Лабораторная работа №8 по учебнику Физика. 7 класс. : белый учебник для общеобразовательных учреждений / А. В. Перышкин. – 2-е издание: Дрофа, 2013-2019г
Цель работы:
Обнаружить на опыте выталкивающее действие жидкости на погружённое в неё тело и определить выталкивающую силу.
Приборы и материалы:
Динамометр, штатив с муфтой и лапкой, два тела разного объёма, стаканы с водой и насыщенным раствором соли в воде.
Указания к работе:
1. Повторите по учебнику § 51 “Архимедова сила”.
2. Укрепите динамометр на штативе и подвесьте к нему на нити тело. Отметьте и запишите в таблице показание динамометра. Это будет вес тела в воздухе.
3. Подставьте стакан с водой и опускайте муфту с лапкой и динамометром, пока всё тело не окажется под водой. Отметьте и запишите в таблицу показание динамометра. Это будет вес тела в воде.
4. По полученным данным вычислите выталкивающую силу, действующую на тело.
5. Вместо чистой воды возьмите насыщенный раствор соли и снова определите выталкивающую силу, действующую на то же тело.
6. Подвесьте к динамометру тело другого объёма и определите указанным способом (см. пункты 2 и 3) выталкивающую силу, действующую на него в воде.
7. Результаты запишите в таблицу 12.
На основе выполненных опытов сделайте выводы.
От каких величин зависит значение выталкивающей силы?
