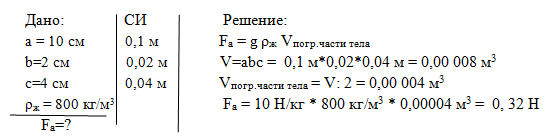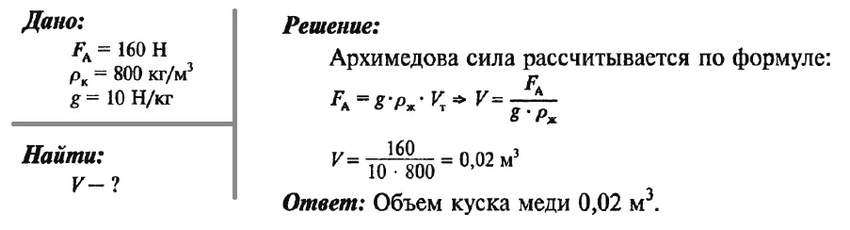Как найти выталкивающую силу плавающего тела - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

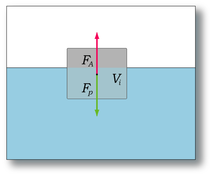
Плавучесть – это выталкивающая сила, действующая на тело, погруженное в жидкость (или газ), и направленная противоположно силе тяжести. В общих случаях выталкивающая сила может быть вычислена по формуле: F_b = V_s × D × g, где F_b – выталкивающая сила; V_s – объем части тела, погруженной в жидкость; D – плотность жидкости, в которую погружают тело; g – сила тяжести.

1
Найдите объем части тела, погруженной в жидкость (погруженный объем). Выталкивающая сила прямо пропорциональна объему части тела, погруженной в жидкость. Другими словами, чем больше погружается тело, тем больше выталкивающая сила. Это означает, что даже на тонущие тела действует выталкивающая сила. Погруженный объем должен измеряться в м³.
- У тел, которые полностью погружены в жидкость, погруженный объем равен объему тела. У тел, плавающих в жидкости, погруженный объем равен объему части тела, скрытой под поверхностью жидкости.
- В качестве примера рассмотрим шар, плавающий в воде. Если диаметр шара равен 1 м, а поверхность воды доходит до середины шара (то есть он погружен в воду наполовину), то погруженный объем шара равен его объему, деленному на 2. Объем шара вычисляется по формуле V = (4/3)π(радиус)³ = (4/3)π(0,5)³ = 0,524 м³. Погруженный объем: 0,524/2 = 0,262 м³.
2
Найдите плотность жидкости (в кг/м³), в которую погружается тело. Плотность – это отношение массы тела к занимаемому этим телом объему. Если у двух тел одинаковый объем, то масса тела с большей плотностью будет больше. Как правило, чем больше плотность жидкости, в которую погружается тело, тем больше выталкивающая сила. Плотность жидкости можно найти в интернете или в различных справочниках.
- В нашем примере шар плавает в воде. Плотность воды приблизительно равна 1000 кг/м³.
- Плотности многих других жидкостей можно найти здесь.
3
Найдите силу тяжести (или любую другую силу, действующую на тело вертикально вниз). Не важно, плавает ли тело или тонет, на него всегда действует сила тяжести. В естественных условиях сила тяжести (а точнее сила тяжести, действующая на тело массой 1 кг) приблизительно равна 9,81 Н/кг. Тем не менее, если на тело действуют и другие силы, например, центробежная сила, такие силы необходимо учесть и вычислить результирующую силу, направленную вертикально вниз.
- В нашем примере мы имеем дело с обычной стационарной системой, поэтому на шар действует только сила тяжести, равная 9,81 Н/кг.
- Однако если шар плавает в емкости с водой, которая вращается вокруг некоторой точки, то на шар будет действовать центробежная сила, которая не позволяет шару и воде выплескиваться наружу и которую необходимо учесть в расчетах.
4
Если у вас есть значения погруженного объема тела (в м³), плотность жидкости (в кг/м³) и сила тяжести (или любая другая сила, направленная вертикально вниз), то вы можете вычислить выталкивающую силу. Для этого просто перемножьте указанные выше значения, и вы найдете выталкивающую силу (в Н).
- В нашем примере: F_b = V_s × D × g. F_b = 0,262 м³ × 1000 кг/м³ × 9,81 Н/кг = 2570 Н.
5
Выясните, будет ли тело плавать или тонуть. По приведенной выше формуле можно вычислить выталкивающую силу. Но, выполнив дополнительные расчеты, вы можете определить, будет ли тело плавать или тонуть. Для этого найдите выталкивающую силу для всего тела (то есть в вычислениях используйте весь объем тела, а не погруженный объем), а затем найдите силу тяжести по формуле G = (масса тела)*(9,81 м/с²). Если выталкивающая сила больше силы тяжести, то тело будет плавать; если же сила тяжести больше выталкивающей силы, то тело будет тонуть. Если силы равны, то тело обладает «нейтральной плавучестью».
- Например, рассмотрим 20 килограммовое бревно (цилиндрической формы) с диаметром 0,75 м и высотой 1,25 м, погруженное в воду.
  - Найдите объем бревна (в нашем примере объем цилиндра) по формуле V = π(радиус)² (высота) = π(0,375)²(1,25) = 0,55 м³.
  - Далее вычислите выталкивающую силу: F_b = 0,55 м³ × 1000 кг/м³ × 9,81 Н/кг = 5395,5 Н.
  - Теперь найдите силу тяжести: G = (20 кг)(9,81 м/с²) = 196,2 Н. Это значение намного меньше значения выталкивающей силы, поэтому бревно будет плавать.
6

Используйте описанные выше вычисления для тела, погруженного в газ. Помните, что тела могут плавать не только в жидкостях, но и в газах, которые вполне могут выталкивать некоторые тела, несмотря на очень небольшую плотность газов (вспомните про шар, наполненный гелием; плотность гелия меньше плотности воздуха, поэтому шар с гелием летает (плавает) в воздухе).

Реклама

1

Поместите небольшую чашку в ведро. В этом простом эксперименте мы покажем, что на тело, погруженное в жидкость, действует выталкивающая сила, так как тело выталкивает объем жидкости, равный погруженному объему тела. Мы также продемонстрируем, как найти выталкивающую силу при помощи эксперимента. Для начала поместите небольшую чашку в ведро (или кастрюлю).
2
Наполните чашку водой (до краев). Будьте осторожны! Если вода из чашки вылилась в ведро, вылейте воду и начните заново.
- Для эксперимента предположим, что плотность воды равна 1000 кг/м³ (только если вы не используете соленую воду или другую жидкость).
- Для наполнения чашки до краев используйте пипетку.
3
Возьмите небольшой предмет, который поместится в чашке и не будет поврежден водой. Найдите массу этого тела (в килограммах; для этого взвесьте тело на весах и конвертируйте значение в граммах в килограммы). Затем медленно опустите предмет в чашку с водой (то есть погрузите тело в воду, но при этом не погружайте пальцы). Вы увидите, что некоторое количество воды вылилось из чашки в ведро.
- В этом эксперименте мы опустим в чашку с водой игрушечный автомобиль массой 0,05 кг. Объем этого автомобиля нам не нужен, чтобы вычислить выталкивающую силу.
4
При погружении тела в воду оно выталкивает некоторый объем воды (иначе тело не погрузилось бы в воду). Когда тело выталкивает воду (то есть тело действует на воду), на тело начинает действовать выталкивающая сила (то есть вода действует на тело). Вылейте воду из ведра в мерный стакан. Объем воды в мерном стакане должен быть равен объему погруженного тела.
- Другими словами, если тело плавает, то объем вытесненной жидкости равен погруженному объему тела. Если тело утонуло, то объем вытесненной жидкости равен объему всего тела.
5
Вычислите массу вытесненной воды по известным значениям объема этой воды и плотности воды. Значение объема воды, показанного шкалой мерного стакана, конвертируйте в м³ (вы можете сделать это здесь), а затем умножьте объем вытесненной воды на плотность воды (1000 кг/м³).
- В нашем примере игрушечный автомобиль утонул, вытеснив около двух столовых ложек воды (0,00003 м³). Вычислим массу вытесненной воды: 1000 кг/м³ × 0,00003 м³ = 0,03 кг.
6
Сравните массу вытесненной воды с массой погруженного тела. Если масса погруженного тела больше массы вытесненной воды, то тело утонет. Если масса вытесненной воды больше массы тела, то оно плавает. Поэтому для того, чтобы тело плавало, оно должно вытеснять количество воды с массой, превышающей массу самого тела.
- Таким образом, тела, имеющие небольшую массу, но большой объем, обладают наилучшей плавучестью. Эти два параметра характерны для полых тел. Вспомните лодку – она обладает превосходной плавучестью, потому что она полая и вытесняет много воды при небольшой массе самой лодки. Если бы лодка не была полой, она бы вообще не плавала (а тонула).
- В нашем примере масса автомобиля (0,05 кг) больше массы вытесненной воды (0,03 кг). Поэтому автомобиль и утонул.
Реклама

Советы

Используйте весы, показания которых можно сбросить до 0 перед каждым новым взвешиванием. В этом случае вы получите точные результаты.

Что вам понадобится

Маленькая чашка или миска
Большая чашка или ведро
Тело для погружения (например, резиновый мячик)
Мерный стакан

Об этой статье

Эту страницу просматривали 61 085 раз.

Была ли эта статья полезной?

Источник

Видеоурок: закон Архимеда

Зако́н Архиме́да — закон гидростатики и аэростатики: на тело, погружённое в жидкость или газ, действует выталкивающая сила, численно равная весу объема жидкости или газа, вытесненного телом. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой силой или гидростатической подъёмной силой^[1]^[2] (её не следует путать с аэро- и гидродинамической подъёмной силой, возникающей при обтекании тела потоком газа или жидкости).

Так как сила Архимеда обусловлена силой тяжести, то в невесомости она не действует.

В соответствии с законом Архимеда для выталкивающей силы выполняется^[3]:

${displaystyle F_{A}=rho gV,}$

где:

Описание[править | править код]

Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.

Плавание тела. Сила Архимеда ( $F_{A}$ ) уравновешивает вес тела ( $F_{p}$ ):

${displaystyle F_{A}=F_{p};}$
ρ_ж g V_ж = ρ_т g V_т

Например, воздушный шарик объёмом , наполненный гелием, летит вверх из-за того, что плотность гелия ( ${displaystyle rho _{He}}$ ) меньше плотности воздуха ( ${displaystyle rho _{air}}$ ):

${displaystyle F_{A}>F_{p};}$

${displaystyle rho _{air}gV>rho _{He}gV.}$

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление ( ${displaystyle P_{A}}$ ) и сила давления ( ${displaystyle F_{A}}$ ), действующие на верхнюю грань тела, равны:

${displaystyle P_{A}=rho gh_{A};}$

${displaystyle F_{A}=rho gh_{A}S,}$

где:

Давление ( ${displaystyle P_{B}}$ ) и сила давления ( ${displaystyle F_{B}}$ ), действующие на нижнюю грань тела, равны:

${displaystyle P_{B}=rho gh_{B};}$

${displaystyle F_{B}=rho gh_{B}S,}$

где:

Сила давления жидкости или газа на тело определяется разностью сил ${displaystyle F_{B}}$ и ${displaystyle F_{A}}$ :

${displaystyle F_{B}-F_{A}=rho gh_{B}S-rho gh_{A}S=rho gleft(h_{B}-h_{A}right)S=rho ghS=rho gV,}$

где:

Разница давлений:

${displaystyle P_{B}-P_{A}=rho gh_{B}-rho gh_{A}=rho gh.}$

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляцию жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.

Обобщения[править | править код]

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы[править | править код]

Вывод через мысленный эксперимент[править | править код]

Если мысленно заменить погружённое в жидкость тело той же жидкостью, мысленно размещённая в том же объёме порция воды будет находиться в равновесии и действовать на окружающую воду с силой, равной силе тяжести, действующей на порцию воды. Так как перемешивания частиц воды не происходит, можно утверждать, что окружающая вода действует на выделенный объём с той же силой, но направленной в противоположном направлении, то есть с силой, равной ^[4]^[5]^[6].

Расчёт силы[править | править код]

Гидростатическое давление на глубине , оказываемое жидкостью с плотностью rho на тело, есть . Пусть плотность жидкости ( rho ) и напряжённость гравитационного поля () — постоянные величины, а — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz , причём выберем направление оси z совпадающим с направлением вектора . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку . На неё будет действовать сила давления жидкости, направленная внутрь тела, $d{vec {F}}_{A}=-pd{vec {S}}$ . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

${displaystyle {vec {F}}_{A}=-int limits _{S}{p,d{vec {S}}}=-int limits _{S}{rho gh,d{vec {S}}}=-rho gint limits _{S}{h,d{vec {S}}}=^{*}-rho gint limits _{V}{operatorname {grad} (h),dV}=^{**}-rho gint limits _{V}{{vec {e}}_{z}dV}=-rho g{vec {e}}_{z}int limits _{V}{dV}=(rho gV)(-{vec {e}}_{z}).}$

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.

${displaystyle {}^{*}h(x,y,z)=z;}$

${displaystyle ^{**}operatorname {grad} h=nabla h={vec {e}}_{z}.}$

Получаем, что модуль силы Архимеда равен , и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Вывод через закон сохранения энергии[править | править код]

Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погружённого тела на жидкость, приводит к изменению её потенциальной энергии:

${displaystyle A=-F*(h_{1}-h_{2})=-Delta E_{p}=-m_{text{ж}}gDelta h,}$

где ${displaystyle m_{text{ж}}}$ — масса вытесненной части жидкости, Delta h — перемещение её центра масс. Отсюда модуль вытесняющей силы:

${displaystyle F=m_{text{ж}}g.}$

По третьему закону Ньютона эта сила, равна по модулю и противоположна по направлению силе Архимеда, действующей со стороны жидкости на тело. Объём вытесненной жидкости равен объёму погруженной части тела, поэтому массу вытесненной жидкости можно записать как:

${displaystyle m_{text{ж}}=rho _{text{ж}}V_{text{т}},}$

где ${displaystyle V_{text{т}}}$

— объем погружённой части тела.

Таким образом, для силы Архимеда имеем:

${displaystyle F_{A}= F=m_{text{ж}}g=rho _{text{ж}}gV_{text{т}}.}$

Условие плавания тел[править | править код]

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести ${displaystyle F_{T}}$ и силы Архимеда ${displaystyle F_{A}}$ , которые действуют на это тело. Возможны следующие три случая:

${displaystyle F_{T}>F_{A}}$ — тело тонет;
${displaystyle F_{T}=F_{A}}$ — тело плавает в жидкости или газе;
${displaystyle F_{T}<F_{A}}$ — тело всплывает до тех пор, пока не начнёт плавать.

Другая формулировка (где ${displaystyle rho _{t}}$ — плотность тела, ${displaystyle rho _{s}}$ — плотность среды, в которую тело погружено):

${displaystyle rho _{t}>rho _{s}}$ — тело тонет;
${displaystyle rho _{t}=rho _{s}}$ — тело плавает в жидкости или газе;
${displaystyle rho _{t}<rho _{s}}$ — тело всплывает до тех пор, пока не начнёт плавать.

Примечания[править | править код]

↑ Архимеда закон : [арх. 1 января 2023] // Анкилоз — Банка. — М. : Большая российская энциклопедия, 2005. — С. 331. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 2). — ISBN 5-85270-330-3.
↑ Архимеда закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 123. — 707 с. — 100 000 экз.
↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, к полю, действующему вблизи поверхности планеты).
↑ Перышкин А. , Оригинальное доказательство закона Архимеда. Дата обращения: 28 сентября 2020. Архивировано 20 июля 2020 года.
↑ Доказательство закона Архимеда для тела произвольной формы. Дата обращения: 28 сентября 2020. Архивировано 21 сентября 2020 года.
↑ Buoyancy (англ.). Архивировано 14 июля 2007 года.

Ссылки[править | править код]

Архимедов закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Закон Архимеда // Энциклопедия «Кругосвет».

Источник

Всем привет. Эта статья может показаться нудной, но без неё нельзя. Надо грамотно рассчитать плавучесть амфибии. Ранее в статье три отсека живучести я выкладывал свои мысли как и что планирую сделать, а в статье Устранение водотечности привел перечень отверстий через которые может поступать вода в автомобиль. Если багажник и салон требуют только заделки отверстий, то моторный отсек надо дополнить определённым пустотелым объёмом который необходимо рассчитаю.
Берем умную книгу и начинаем её изучать. Плавучесть – это выталкивающая сила, действующая на тело, погруженное в жидкость (или газ), и направленная противоположно силе тяжести. В общих случаях выталкивающая сила может быть вычислена по формуле: Fb = Vs × D × g, где Fb — выталкивающая сила; Vs — объем части тела, погруженной в жидкость; D – плотность жидкости, в которую погружают тело; g – сила тяжести. Ну что же формула есть, надо подставить значения.
1. Определим объём баков которые я планирую установить в моторном отсеке по формуле V = I х w х h. Их будет два, размер 45х36х28см = 0.0454м3 х 2 = 0.0907м3
2. Проще всего узнать плотность воды. Для этого смотрим справочник допустим этот Из него узнаём что плотность воды приблизительно равна 1000 кг/м3. Итак D = 1000
3. Найдём силу тяжести. Не важно, плавает ли тело или тонет, на него всегда действует сила тяжести. В естественных условиях сила тяжести (а точнее сила тяжести, действующая на тело массой 1 кг) приблизительно равна 9,81 Н/кг.
4. Считаем выталкивающую силу. Fb = Vs × D × g 0.0907 х 1000 х 9.81 = 889,767
5. Выясним, будет ли задняя часть автомобиля плавать или тонуть по формуле G = (масса задней части)*(9,81 м/с2). Если выталкивающая сила больше силы тяжести, то авто будет плавать; если же сила тяжести больше выталкивающей силы, то авто будет тонуть. Если силы равны, то авто обладает «нейтральной плавучестью». Допустим мотор, подвеска и часть кузова весят 150кг. G = 150 х 9.81 = 1471.5
Получается что сила тяжести больше выталкивающей силы. Жопа тонет. Вес мы не снизим, значит надо увеличить баки. Те два что участвовали в расчётах увеличить не смогу, нет места. Можно добавить небольшой бак под заднюю юбку с стороны моторного отсека.Там есть короб, надо сделать его герметичным. Примерный размер 15 х10 х 100см. = 0.015 добавляем этот объём к имеющимся бакам 0.0907+0.015= 0.1057 Считаем выталкивающую силу заново 0.1057 х 1000 х 9.81 = 1036.917 опять мало. Попробую добавить объём задних колёс, они ведь пустотелые и должны плавать. Не знаю как правильно их посчитать, потому нашёл объем цилиндра размером R — 30 cм h — 17см. и вычел из него объем цилиндра размером R — 22 cм. h — 17см. Получил 0.022м3 в одной шине. Считаем плавучесть с шинами. 0.1497 х 1000 х 9.81 = 1468.557 Теперь лучше, почти нулевая плавучесть.
Для интереса посчитал плавучесть кузова. Для расчёта взял следующие параметры: ш. 1.4м, д. 3.5м. Вес 1300кг. расчётная максимальная осадка (по ватерлинию) 0.8м. Сила тяжести авто 1300 х 9.81 = 12753
Выталкивающая сила 3.92 х1000 х 9.81 = 38455. На лицо троекратная плавучесть и это без тех объёмов что мы считали выше.
Подводим итог. Автомобиль имеет достаточный объём плавучести за счёт водонепроницаемого багажника и салона. И можно не добавлять баки в зад, но есть соображения, что корма будет тонуть и авто будет плавать поплавком. Что ни есть хорошо для двигателя, не эстетично и не удобно для экипажа. Потому баки в зад, ставим обязательно и будем ходить красиво.
На этом всё. До скорой встречи.

Источник

§ 1 Расчет архимедовой силы, условие плавания тел: формулы и определения

Рассмотрим решение задач на расчет архимедовой силы, условие плавания тел в жидкостях и газах.

Для решения задач нам нужно вспомнить следующие формулы и определения:

Архимедова силаравна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.

Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе: P выт.жидкости = P тела.

Морские и речные суда могут перевозить грузы. Вес груза зависит от водоизмещения судна. Водоизмещение – это вес воды, вытесненной судном, равный его весу в воздухе.

Подъемная сила аэростатовравна разности между архимедовой силы и весом оболочки, гондолы и газа, которым наполнен аэростат.

При решении задач важно верно выразить величины в системе СИ.

Архимедова сила зависит от объема тела, поэтому вспомним размерности объема:

1 дм3 = 0,001 м3;

1 см3 = 0, 000 001 м3.

§ 2 Решение задач

Задача 1:Вычислите архимедову силу, действующую на брусок размером 2х10х4 см, если он наполовину погружен в спирт.

Решение:Запишем условие задачи. Нам известны размеры бруска: длина а = 10 см, ширина b=2 см, высота c=4 см. Плотность спирта ρж = 800 кг/м3. Выразим длину, ширину и высоту в системе СИ: 0,1 м, 0,02 м, 0,04 м.

Для решения запишем формулу вычисления архимедовой силы: Fa = gρжVпогр.части тела.

Объем всего бруска прямоугольной формы равен произведению длины на ширину и на высоту: V=abc = 0,1 м*0,02*0,04 м = 0,00 008 м3.

Объем погруженной части равен половине объема: Vпогр.части тела=0,00 004 м3.

Подставим числовые значения плотности спирта, коэффициента силы тяжести, объема погруженной части тела в формулу архимедовой силы и получим: Fa = 0,32 Н.

Ответ: на брусок в спирте действует архимедова сила 0,32 Н.

Задача 2:Какую силу нужно приложить к плите массой 4 т при ее подъеме со дна водоема, если объем плиты – 2 м3?

Решение:запишем условие задачи. Масса плиты m = 4 т, выразим в СИ: 4000 кг, объем плиты V = 2 м3, плотность воды ρж = 1000 кг/м3.

На тело, погруженное в жидкость или газ, действуют две силы: сила тяжести и архимедова сила, направленные противоположно. Поэтому вес плиты в воде уменьшается: Pв воде = Pв воздухе – Fа .

Вес тела в воздухе найдем по формуле P=mg, архимедову силу определим по формуле Fa = gρжVпогр. тела.

Тогда формула веса плиты в воде запишется так: Pв воде = mg – gρжVпогр. тела.

Подставим числовые значения величин, произведем вычисления и получим ответ: вес плиты в воде равен 20 000 Н, следовательно, для поднятия плиты в воде нужно приложить силу 20 кН.

Ответ: для поднятия плиты в воде нужно приложить силу 20 кН.

Задача 3: Какой по весу груз может удержать на поверхности воды пробковый пояс объемом 6,25 дм3 и массой 2 кг, если пояс будет погружен в воду полностью?

Решение: Запишем условие задачи. Нам известны объем пояса V = 6,25 дм3, его масса m = 2 кг, плотность воды ρж = 1000 кг/м3. Выразим объем в СИ, для этого 6, 25 поделим на 1000, равно 0,00 625 м3. Найти вес груза Pгр.

Известно, что вес груза, перевозимого судами, равен разности между водоизмещением судна и его весом. Водоизмещение – это вес воды, вытесненной судном с грузом. Тогда Pгруза = Pвытесненной воды – Pсудна.

Пробковый пояс при полном погружении вытесняет воду в объеме, равном объему пояса. Вычитая из веса вытесненной воды собственный вес пояса, можем найти вес груза:

Pгруза = Pвыт.воды – Pпояса.

Определим вес вытесненной воды. Для этого массу вытесненной воды умножим на коэффициент силы тяжести, а масса воды равна произведению плотности воды на ее объем. Объем вытесненной воды равен объему спасательного пояса. Тогда вес вытесненной воды равен произведению плотности воды на объем пояса и коэффициент тяжести:

Pвыт.воды = ρводы *Vводы *g

Определим вес пояса по формуле Pпояса =mпояса·g.

Подставим числовые значения величин и вычислим вес вытесненной поясом воды и вес пояса. Тогда вес груза равен их разности.

Ответ: пробковый пояс может удерживать в воде груз весом 42,5 Н.

Задача 4:Аэростат объемом 2000 м3 наполнен водородом. Вес оболочки и гондолы 16 000 Н. Определите подъемную силу аэростата.

Решение: Запишем условие задачи. Известны объем аэростата V = 2000 м3, вес оболочки и гондолы вместе Pоб =16 000 Н, плотность водорода, которым наполнен аэростат, ρгаза = 0,09 кг/м3, плотность воздуха при нормальном атмосферном давлении ρвозд. = 1,29 кг/м3. Все данные приведены в системе СИ. Требуется найти подъемную силу Fподъемн.

На аэростат действуют сила тяжести и архимедова сила, которая поднимает его вверх. Сила тяжести действует на оболочку, гондолу и газ, которым он наполнен. Вес оболочки и гондолы известен, нужно найти вес водорода, для этого массу водорода умножим на коэффициент тяжести. Массу водорода найдем по формуле плотности. Тогда вес газа равен произведению плотности газа на объем аэростата и коэффициент тяжести: Pгаза = ρгаза *Vаэростата *g.

Архимедову силу определим по формуле Fa = gρжVаэростата.

Подставим записанные формулы в формулу подъемной силы, вынесем одинаковые множители за скобки, вычислим.

Ответ: подъемная сила аэростата равна 8000 Н = 8 кН.

§ 3 Краткие итоги по теме урока

ВАЖНО ЗАПОМНИТЬ:

При решении задач нужно помнить основные формулы и определения.

Архимедова сила равна произведению коэффициента силы тяжести на плотность жидкости и объем погруженной части тела: Fa = gρжVтела.

Тело плавает в жидкости, если вес вытесненной им жидкости равен весу этого тела в воздухе.

Водоизмещение – это вес воды, вытесненной судном с грузом, равный весу судна вместе с грузом. Вес груза, перевозимого судами или выдерживаемого спасательным поясом, плотом, льдиной, равен разности между весом вытесненной жидкости и весом самого судна, пояса, плота, льдины.

Подъемная сила аэростатов равна разности между архимедовой силы и весом аэростата (т.е. весом оболочки, гондолы и газа, которым наполнен аэростат).

Источник

Задачи на силу Архимеда с решениями

Формулы, используемые на уроках «Задачи на силу Архимеда», «Сообщающиеся сосуды».

Название величины	Обозначение	Единица измерения	Формула
Объем тела	V	м³	V_т = F_A / pg
*Плотность жидкости*	p	кг/м³	p_ж = F_A / (Vg)
*Сила Архимеда*	F_A	Н	F_A = p_ж V_т g
Постоянная	g ≈ 10 Н/кг	Н/кг

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Тело объемом 2 м³ погружено в воду. Найдите архимедову силу, действующую на тело.

Задача № 2.
Определить выталкивающую силу, действующую на деревянный плот объемом 12 м³, погруженный в воду на половину своего объема.

Задача № 3.
Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?

Задача № 4.
Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?

Задача № 5.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?

Задача № 6.
Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?

Задача № 7.
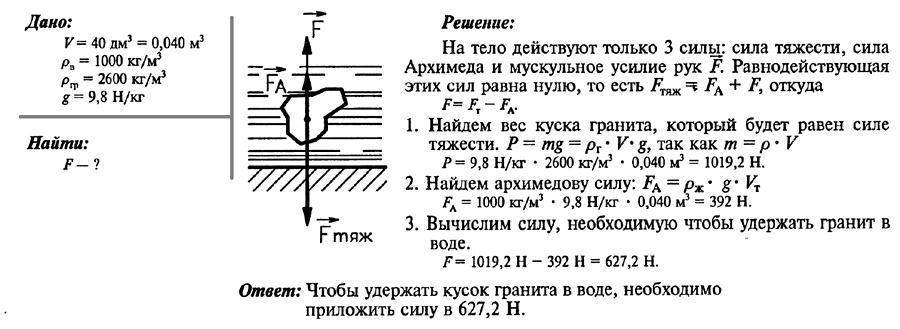
Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм³?

Задача № 8.
Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.

Задача № 9 (повышенной сложности).
Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?

Задача № 10 (повышенной сложности).
Рассчитайте, какой груз сможет поднять шар объемом 1 м³, наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)

Задача № 11.
Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м³.

Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V₁ – объем цилиндра, погруженного в масло (V₁= V – V₂ = Sh₁); h₁ – высота части цилиндра, погруженной в масло; V₂ – объем цилиндра, погруженного в воду после добавления масла; р_в – плотность воды (1000 кг/м³); р_м – плотность масла (800 кг/м³)

Найти: (h – h₁) / h — ?

Решение. F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9p_вgV
F₁ – сила, выталкивающая цилиндр из масла F₁ = p_мgV₁F₂ – сила, выталкивающая цилиндр из воды после добавления масла F₂ = p_вgV₂Баланс сил: F – F₁ = F₂0,9p_вgV – p_мgV₁ = p_вgV₂ V₁= V – V₂ ⇒ 0,9p_вV – p_м(V – V₂) = p_вV₂

V(0,9p_в – p_м) = V₂(p_в – p_м) V = Sh; V₁= Sh₁ ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).

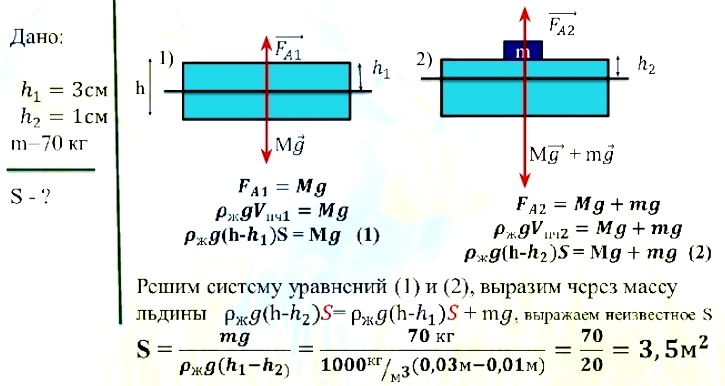
Задача № 12.
Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.

Ответ: 3,5 м³.

Теория для решения задач.

Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = р_атм + p*g*h

Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Конспект урока «Задачи на силу Архимеда с решениями».

Следующая тема: «Задачи на механическую работу».

Источник

Советы

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Описание[править | править код]

Обобщения[править | править код]

Вывод закона Архимеда для тела произвольной формы[править | править код]

Вывод через мысленный эксперимент[править | править код]

Расчёт силы[править | править код]

Вывод через закон сохранения энергии[править | править код]

Условие плавания тел[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Задачи на силу Архимеда с решениями

Название величины

Обозначение

Единица измерения

Формула

Объем тела

V

м3

Vт = FA / pg

Плотность жидкости

p

кг/м3

pж = FA / (Vg)

Сила Архимеда

FA

Н

FA = pж Vт g

Постоянная

g ≈ 10 Н/кг

Н/кг

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Теория для решения задач.

Вам также может понравиться

Как составить иск на алименты на мать

Как найти психотерапевта в москве отзывы

Как нужно составить смету

Добавить комментарий Отменить ответ

м³

V_т = F_A / pg

кг/м³

p_ж = F_A / (Vg)

F_A

F_A = p_ж V_т g