Как найти взаимно перпендикулярные векторы

Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.

Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.

Необходимое и достаточное условие перпендикулярности двух векторов

Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.

При условии значения угла между двумя ненулевыми векторами равным 90°( π2 радиан) называют перпендикулярными.

Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?

Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.

Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.

Скалярное произведение двух ненулевых векторов a→ и b→ равном нулю для выполнения равенства a→, b→=0 достаточно для их перпендикулярности.

Условие перпендикулярности на координатной плоскости

Раздел скалярного произведения в координатах демонстрирует неравенство (a→, b→)=ax·bx+ay·by, справедливое для векторов с координатами a→=(ax, ay) и b→=(bx, by), на плоскости и (a→,b→)=ax·bx+ay·by для векторов a→=(ax, ay, az) и b→=(bx, by, bz) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид ax·bx+ay·by=0, для трехмерного пространства ax·bx+ay·by+az·bz=0.

Применим на практике и рассмотрим на примерах.

Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.

Нахождение вектора, перпендикулярного данному

Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.

Нахождение вектора, перпендикулярного данному в плоскости.

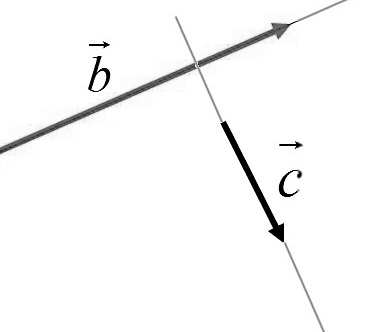
Ненулевой вектор a→ может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

Задан ненулевой вектор a→, лежащий на прямой а. Тогда заданный b→, расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным иa→. Если вектору i→ перпендикулярен вектор j→ или любой из векторов λ·j→при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b→, перпендикулярному a→=(ax, ay), сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a→=(ax, ay). Для этого необходимо записать условие перпендикулярности векторов в такой форме ax·bx+ay·by=0. Имеем bx и by , являющиеся искомыми координатами перпендикулярного вектора. Когда ax≠0, значение by является ненулевым, а bx вычислим из неравенства ax·bx+ay·by=0 ⇔bx=-ay·byax. При ax=0 и ay≠0 присваиваем bx любое значение кроме нуля, а by находим из выражения by=-ax·bxay.

Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a→=(ax, ay, az) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a→ , лежащая на прямой a. Перпендикулярную прямой a плоскость обозначаем α. В этом случае любой ненулевой вектор b→ из плоскости α перпендикулярен a→.

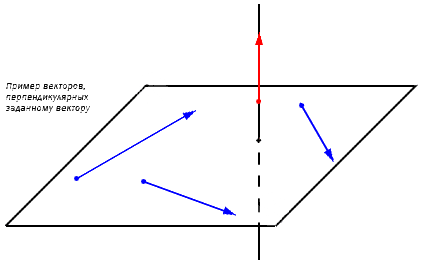
Необходимо найти координаты b→, перпендикулярного ненулевому вектору a→=(ax, ay, az).

Пусть задан b→ с координатами bx, by и bz. Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство ax·bx+ay·by+az·bz=0 должно выполняться. Из условия a→ – ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что ax≠0, ( ay≠0 или az≠0). Следовательно, имеем право разделить на эту координату все неравенство ax·bx+ay·by+az·bz=0, получим выражениеbx+ay·by+az·bzax=0⇔bx=-ay·by+az·bzax. Присваиваем координатам by и bx любое значение, вычисляем значение bx, исходя из формулы, bx=-ay·by+az·bzax. Искомый перпендикулярный вектор будет иметь значение a→=(ax, ay, az).

Рассмотрим доказательство на примере.

Нахождение координат вектора, перпендикулярного двум заданным векторам

Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторамa→(ax, ay, az) и b→=(bx, by, bz). При условии коллинеарности векторов a→ и b→ в задаче достаточно будет найти вектор, перпендикулярный a→ или b→.

При решении применяется понятие векторного произведения векторов.

Векторным произведением векторов a→ и b→ называют вектор, одновременно перпендикулярный и a→ и b→. Для решения данной задачи применяется векторное произведение a→×b→. Для трехмерного пространства имеет вид a→×b→=a→j→k→axayazbxbybz

Разберем подробнее векторное произведение на примере задачи.

Перпендикулярность векторов

Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.

Координаты вектора на плоскости, равного по модулю и перпендикулярного данному

Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.

Алгоритм получения координат перпендикулярных векторов

Вектор на плоскости xOy, перпендикулярный данному вектору получают так:

1. Поменять местами координатные числа «x» и «y».
2. Заменить знак у одной из координат на противоположный.

Графический пример

Рассмотрим небольшой графический пример (рис. 1).

Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом

На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).

[ vec{a} = left{ 4 ; 3 right} ]

[ vec{b} = left{ -3 ; 4 right} ]

Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).

Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )

Векторы, изображенные черным цветом, перпендикулярны красному вектору.

Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.

 Условие перпендикулярности векторов

Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.

Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.

Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.

[ large boxed { begin{cases} vec{a} = left{ a_{x} ; a_{y} ; a_{z} right} \ vec{b} = left{ b_{x} ; b_{y} ; b_{z} right} \ |vec{a}| ne 0  \ |vec{b}| ne 0 end{cases}}]

Запишем условие перпендикулярности векторов.

Для двумерного случая:

[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} = 0 }]

Для трехмерного случая:

[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} + a_{z} cdot b_{z} = 0 }]

Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.

При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.

Примечание:

Есть такое правило: Количество неизвестных должно равняться количеству уравнений.

Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.

Перпендикулярные векторы в физике

В физике перпендикулярность некоторых векторов достаточно важна.

Вот несколько примеров:

1. Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
2. На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
3. Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.
4. Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
5. На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).

Оценка статьи:

Загрузка…

Перпендикулярность векторов

Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.

Координаты вектора на плоскости, равного по модулю и перпендикулярного данному

Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.

Алгоритм получения координат перпендикулярных векторов

Вектор на плоскости xOy, перпендикулярный данному вектору получают так:

Графический пример

Рассмотрим небольшой графический пример (рис. 1).

На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec) и (vec).

Векторы, изображенные черным цветом, перпендикулярны красному вектору.

Условие перпендикулярности векторов

Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.

Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.

Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.

Запишем условие перпендикулярности векторов.

Для двумерного случая:

[ large boxed < a_cdot b_ + a_ cdot b_ = 0 >]

Для трехмерного случая:

[ large boxed < a_cdot b_ + a_ cdot b_ + a_ cdot b_ = 0 >]

Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.

При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.

Примечание:

Есть такое правило: Количество неизвестных должно равняться количеству уравнений.

Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.

Перпендикулярные векторы в физике

В физике перпендикулярность некоторых векторов достаточно важна.

Вот несколько примеров:

Источник

Нахождение вектора, перпендикулярного данному вектору, примеры и решения

Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.

Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.

Необходимое и достаточное условие перпендикулярности двух векторов

Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.

При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.

Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?

Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.

Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.

Вторая часть доказательства

Условие перпендикулярности на координатной плоскости

Применим на практике и рассмотрим на примерах.

Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.

Ответ: да, заданные векторы a → и b → перпендикулярны.

Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим

Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.

Нахождение вектора, перпендикулярного данному

Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.

Нахождение вектора, перпендикулярного данному в плоскости.

Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

Рассмотрим доказательство на примере.

Нахождение координат вектора, перпендикулярного двум заданным векторам

При решении применяется понятие векторного произведения векторов.

Разберем подробнее векторное произведение на примере задачи.

Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :

Источник

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Как решить?

Находим скалярное произведение данных векторов:

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

Примеры пространственных задач на ортогональность векторов

Как решить?

Находим скалярное произведение данных векторов:

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

Источник

Понятие вектора и перпендикулярности векторов

Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Для введения определения вектора один из концов отрезка назовем его началом.

Обозначение: $overline{AB}$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline{a}$ (рис. 1).

Обозначение: $overline{0}$.

Введем теперь, непосредственно, определение коллинеарных векторов.

«Как найти вектор, перпендикулярный вектору» 👇

Также введем определение скалярного произведения, которое будет нам необходимо далее.

Математически это может выглядеть следующим образом:

$overline{α}overline{β}=|overline{α}||overline{β}|cos⁡∠(overline{α},overline{β})$

Скалярное произведение также можно найти с помощью координат векторов следующим образом

$overline{α}overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$

Признак перпендикулярности через пропорциональность

Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение

Введем вначале понятие векторного произведения.

Обозначение: $overline{α}хoverline{β}$.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.

Содержание:

1. Векторы
2. Действия над векторами
3. Умножение вектора на число
4. Скалярное произведение векторов
5. Векторное произведение
6. Смешенное произведение векторов
7. Разложение вектора по базису
8. Действия над векторами, заданными своими координатами
9. Проекция вектора на ось
10. Проекции вектора на оси координат
11. Направляющие косинусы вектора
12. Разложение вектора по ортам
13. Действия над векторами, заданными в координатной форме
14. Вектор – основные определения
15. Операции над векторами и их свойства
16. Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.
17. Координаты вектора
18. Скалярное произведение векторов и его свойства
19. Векторы и их решение
20. Собственные числа и собственные векторы
21. Векторная алгебра
22. Векторы: основные определения, линейные операции
23. Линейные операции над векторами
24. Умножения вектора на скаляр
25. Основные свойства проекции вектора на ось
26. Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов
27. Скалярное, векторное, смешанное произведения векторов
28. Векторное произведение двух векторов
29. Смешанное произведение векторов, заданных в координатной форме
30. Простейшие задачи аналитической геометрии
31. Задача об определении площади треугольника
32. Задача о деление отрезка в заданном отношении

Векторы

В математике вектором называют величину, которая характеризуется только числом и направлением. Так определённые векторы ещё называют свободными векторами. Примером физических величин, которые имеют векторный характер являются скорость, сила, ускорение. Геометрически вектор — это направленный отрезок, хотя правильней говорить про целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковые длину и направление.

Векторы обозначают малыми латинскими буквами с чертой сверху , или двумя большими латинскими буквами, которые обозначают его начало и конец, например  . Длина (модуль) вектора — это длина отрезка, который отвечает данному вектору и обозначается  В зависимости от соотношения длин и направлений различают следующие виды векторов:

Действия над векторами

Рассмотрим основные действия, определённые над векторами.

1. Сложение векторов. Суммой векторов  называют вектор , который соединяет начало вектора  с концом вектора , при условии, что вектор  отложен от конца вектора . Такой способ сложения векторов называют правилом треугольника.

Учитывая, что , то найти сумму векторов  можно также по так называемым “правилом параллелограмма” (рис. 3)

Вычитание векторов сводится к сложению противоположного вектора

Запишем основные свойства действий сложения векторов:

 

Заметим, что сумма нескольких векторов находится последовательным сложением двух из них, например:

Геометрически сумма нескольких векторов находится их последовательным отложением один за одним так, чтоб начало следующего совпадало с концом предыдущего. Суммой является вектор, который будет соединять начало первого с концом последнего (рис. 4). Если такая последовательность векторов даёт замкнутую ломаную то суммой векторов является  (рис. 5).

Умножение вектора на число

Произведением вектора  на число  называют вектор , для которого выполняются условия:

а) ;

б) , причём  сонаправленные если  противоположно направленные, если . Отсюда, очевидно, что необходимым и достаточным условием коллинеарности векторов является соотношение .

Запишем основные свойства действий умножения вектора на число:

Скалярное произведение векторов

Скалярным произведением  или  векторов  и  называют выражение , где  угол, который образуют векторы. Отметим, что углом между векторами считают угол между их направлениями. Если хотя бы один из векторов равен , то их скалярное произведение считают равным нулю.

Очевидно, что скалярное произведение двух ненулевых векторов будет равно нулю тогда и только тогда когда эти вектора перпендикулярны (ортогональны). Действительно, если . Но , следовательно,

Наоборот, если  и согласно определениям

.

Например, скалярное произведение  будет равным

Запишем основные свойства действий скалярного умножения векторов:

Векторное произведение

Векторным произведением  двух векторов  и  называется вектор , который удовлетворяет условия:

1) модуль вектора  равен произведению модулей векторов   и  на синус угла между ними

 

2) вектор  перпендикулярный к плоскости, которая определяется векторами  и  (рис. 5).

3) вектор  направленный так, что кратчайший поворот вектора  к вектору  видно с конца вектора  таким, что происходит против движения стрелки (то есть вектора ,  и  образуют правую упорядоченную тройку, или правый руль).

Модуль векторного произведения равен площади параллелограмма, построенного на векторах  и . Векторное произведение выражается формулой , где  площадь параллелограмма построенного на векторах  и ,  единичный вектор направления .

Приведём основные свойства векторного произведения:

1) векторное произведение  равно нулю, если векторы   и  коллинеарные, или один из них нулевой;

2) от перестановки местами векторов-сомножителей векторное произведение меняет знак на противоположный:  (векторное произведение не имеет свойств перестановки);

3)  (распределительный закон);

4)  (соединительный закон).

Физическое содержание векторного произведения такое. Если  сила, а  радиус-вектор точки её приложения, которая имеет начало в точке , то моментом силы  относительно точки  является вектор, который равен векторному произведению  на , то есть .

Смешенное произведение векторов

Смешенным произведением векторов  называют скалярное произведение вектора  на вектор . Смешенное произведение обозначают (), поэтому по определению имеем

Как результат скалярного произведения векторов  и  смешенное произведение является скалярной величиной (числом). Геометрически смешенное произведение — это объём параллелепипеда, построенного на эти векторах, взятый со знаком плюс, если векторы  образуют правую тройку, и со знаком минус, когда эта тройка левая      (рис. 7).

 

Действительно, , где  угол между векторами  угол между векторами  и .

Объём V параллелепипеда, построенного на векторах  равный произведению площади основы S на высоту h.

Однако, знак смешенного произведения совпадает со знаком , то есть он положительный, когда угол  острый ( образуют правую тройку векторов) и отрицательный, когда угол  тупой ( образуют левую тройку векторов). Поэтому:

Из геометрического содержания смешенного произведения выходит, что 

1) смешанное произведение равно нулю тогда и только тогда, когда перемноженные вектора копланарные (условие компланарных векторов);

2) 

Учитывая коммутативность скалярного произведения и антикоммутативность векторного, для произвольных векторов  имеем

Пример 1.

Доказать, что когда М — точка АВС и О — произвольные точки пространства, то выполняется равенство: 

Решение.

Пусть  медиана треугольника АВС. По свойствам медиан треугольника  Применив к векторам  и  формулу вычитания векторов

тогда

Пример 2.

У прямоугольного параллелепипеда рёбра , имеют длину 2, 3, 5. Вычислить длины отрезков  и  и угол между прямыми  и .

Решение.

Пусть  единичные вектора направленные вдоль рёбер, которые рассматриваются. Тогда  (поскольку параллелепипед прямоугольный).

рис. 9.

Далее,

Этим закончен “перевод” условия задачи на “язык” векторов.

Теперь произведём вычисления с векторами:

Наконец “переводим” полученные вектора равенства снова на “геометрический язык”. Поскольку  аналогично .

Далее поскольку , где  угол между данными векторами то , отсюда получаем . Теперь с помощью тригонометрических таблиц находим значения угла .

Разложение вектора по базису

Базисом на площади называют упорядоченную пару неколлинеарных векторов и точку отсчёта. 

Теорема. Любой вектор  на плоскости можно разложить по двум неколлинеарным векторам  и , то есть представить в виде: .

Доказательство.

Пусть векторы  компланарные и векторы  и  неколлинеарные. От точки О отложим все три вектора и на продолжении векторов  и  построим параллелограмм  ONCM так, чтобы вектор  был его диагональю.

Тогда по правилу параллелограмма .

Но , как коллинеарные векторы. Следовательно, вектор.

Числа, которые стоят при базисных векторах в разложении вектора за двумя неколлинеарными векторами называют координатами вектора в данном базисе и обозначают .

Соответственно в пространстве базисом называется упорядоченная тройка некомпланарных векторов и точки отсчёта.  Для четырёх некомпланарных векторов справедлива следующая теорема.

Теорема. Любой вектор   в пространстве можно разложить по трём некомпланарным векторам ,  и , то есть представить в виде: .

Доказательство.

От точки О отложим векторы   и на продолжении векторов  построим параллелограмм  

в котором вектор  является диагональю. Как видим

Числа х,у,z которые стоят при базисных векторах в разложении вектора по трём некомпланарным векторам называют координатами вектора в пространстве и обозначают . Если базисные вектора взаимно перпендикулярны (их обозначают ), то вместе с точкой отсчёта они образуют декартовую систему координат, а координаты вектора в таком базисе называют декартовыми координатами. В декартовой системе координат разложение вектора будет иметь вид . Если началом вектора  является точка , а концом — точка , то координаты вектора  вычисляют как разность соответствующих координат точек А и В,

Отсюда легко установить длину вектора как расстояние между двумя точками:

Действия над векторами, заданными своими координатами

1. При сложении двух, или более векторов их соответствующие координаты складываются:

Действительно:

2. При вычитании векторов соответствующие координаты вычитаются:

Доказательство аналогично предыдущему.

3. При умножении вектора на число все координаты умножаются на это число.

Правда, для вектора  и числа  имеем:

4. Скалярное произведение двух векторов  равно сумме произведений соответствующих координат:

Правда:

Поскольку  выполняется Следовательно, мы можем записать

5. Векторное произведение векторов  заданных своими координатами вычисляется так:

6. Смешенное произведение трёх векторов  равняется:

Пример 1.

Зная координаты векторов , найти координаты векторов .

Решение:

Ответ: .

Пример 2.

Зная координаты векторов  вычислить координаты вектора .

Решение.

Ответ: .

Пример 3.

Зная координаты векторов  вычислить:

а) скалярное произведение векторов 

б) векторное произведение векторов 

в) смешенное произведение векторов .

Решение.

Ответ: 

На основании приведённых выше формул действий над векторами можно установить следующие условия и соотношения для нулевых векторов

1. Угол между векторами.

2. Условие перпендикулярности двух векторов:

(векторы перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю).

3. Условие коллинеарности двух векторов:  (векторы коллинеарные тогда и только тогда, когда соответствующие их координаты пропорциональны).

4. Условие компланарности трёх векторов.

 

(три вектора компланарны тогда и только тогда, когда их смешенное произведение равно нулю).

5. Деление отрезка АВ в заданном отношении.

Если точка  делит отрезок АВ в отношении , то координаты точки М находят по формуле:

Если точка М делит отрезок АВ на пополам то , и координаты точки находят согласно формуле:

Действия над векторами (теория)

а) Произведение вектора на число.
Определение 1. Произведением вектора  на число λ называется вектор ,
который имеет длину   и направление его совпадает с направлением вектора если λ > 0,  и противоположно ему, если λ < 0 (рис.12).

Рис. 12.

Условие                                                                            (2.6)
является условием коллинеарности двух векторов.

б) Сложение векторов.

Определение 2. Суммой двух векторов   и    называется вектор    , начало которого совпадает с началом вектора ,  а конец совпадает с концом вектора , при условии, что начало вектора   совпадает с концом вектора    (правило треугольника)  (рис.13).

Рис. 13.

Понятно, что вектор  в этом случае является диагональю параллелограмма, построенного на векторах   и    (правило параллелограмма) (рис.13).
Для векторной суммы справедливый переместительный закон

Легко убедиться, что для векторной суммы имеет место соединительный
закон   .
Исходя из определения 2, легко находим сумму, например, четырех векторов  (рис. 14).

Рис. 14.
Вектор  соединяет начало первого вектора    с концом вектора    (правило многоугольника).

в) Вычитание векторов.
Действие вычитание векторов можно рассматривать как обратное действие относительно сложения векторов.

Определение. Разностью   называется вектор  , который в сумме с вектором  дает вектор    (рис. 15), т.е. 

Рис. 15.

Как видно из рис. 15,  одна диагональ  является суммой   ,  а  вторая диагональ   является разностью векторов   и  .
Дадим еще одно определение разности векторов.

Определение. Разностью двух векторов  и   , которые имеют общее начало, называется вектор  , который соединяет концы этих векторов и направлен в сторону уменьшаемого.

Проекция вектора на ось

Пусть имеем произвольную ось l на плоскости и некоторый вектор  (рис. 16).

Рис. 16.

Опустим из начала A вектора и из конца B перпендикуляры на ось l. Основаниями перпендикуляров будут точки A₁ и B₁, которые называются проекциями точек A и B.

Величина A₁B₁ называется проекцией вектора на ось l и обозначается  , то есть .
Определение 1. Проекцией вектора   на ось l называется величина отрезка  A₁B₁, взята со знаком плюс, если направление отрезка A₁B₁  совпадает с направлением оси l, и с знаком минус, если направления противоположные.

Из точки A проведем прямую, параллельную оси l, которая пересечет отрезок  BB₁ в точке C. Вектор  образует с осью l угол φ. Величина отрезка AC равна величине отрезка  A₁B₁, а тогда из Δ ABC находим  
    или                                               (2.7)

Определение 2. Проекция вектора на любую ось равна произведению длины этого вектора на косинус угла между осью и вектором.

Если угол φ острый, то проекция   — положительное число, а если угол φ тупой, то проекция   —  отрицательное число.

Свойства проекций.

1. Если векторы   и   равны, то величины их проекций на одну и ту же ось l также равны, то есть:  .
2. Проекция суммы векторов на любую ось равна сумме проекций слагаемых на ту же ось, то есть:

3. Проекция разности двух векторов на ось l равна разности величин проекций на ту же ось, то есть:

4. Если вектор  умножен на любое число λ, то величина проекции вектора  на ось l также умножится на число λ, то есть: 

 

Проекции вектора на оси координат

Рассматривается прямоугольная система координат Oxyz в пространстве и произвольный вектор .
Пусть   
Проекции x, y, z вектора   на координатные оси называют координатами вектора и записывают .
Если заданы две точки A (x₁; y₁; z₁) и B (x₂; y₂; z₂), то координаты вектора  находятся по формулам
x = x₂ – x₁,   y = y₂ –  y₁,  z = z₂ – z₁ .

Рис. 17

Действительно, проведем через точки A и B плоскости, перпендикулярные оси Ox и обозначим точки их пересечения соответственно A₁ и B₁ (рис.17). Точки A₁ и B₁ имеют на оси Ox координаты   x₁  и  x₂ , но на основе формулы (2.1), а потому
x = x₂ – x₁ . Аналогично доказывается, что y = y₂ –  y₁,  z = z₂ – z₁ .
 

Направляющие косинусы вектора

Пусть имеем вектор   и будем считать, что он выходит из начала координат и не находится ни в одной координатной плоскости.

Рис. 18

Через точку M проведем плоскости, перпендикулярные к осям координат, и вместе с координатными плоскостями они образуют параллелепипед, диагональ которого — отрезок OM (рис.18). Через α, β, γ обозначим углы, которые образует вектор  с осями координат. Величины cos α, cos β, cos γ называются направляющими косинусами вектора . Координаты вектора .

Квадрат диагонали прямоугольного параллелепипеда равна сумме квадратов длин трех его измерений.
Поэтому
или  
                                                                     (2.8)
Формула (2.8) выражает длину вектора через его координаты. Тогда на основе формул (2.7) и (2.8) получим

Отсюда для направляющих косинусов получаем

                  (2.9)

Для направляющих косинусов справедливо равенство   (это вытекает из (2.9)).

Разложение вектора по ортам

Рассмотрим прямоугольную систему координат в пространстве и вектор, начало которого в точке O (рис.19) .

Рис. 19.

Обозначим орты осей координат Ox, Oy, Oz соответственно через  ,  причем

Спроецируем вектор   на координатные оси (через точку M проведем плоскости, перпендикулярные координатным осям). Проекциями точки M на координатные оси будут соответственно точки А, В, С (рис.19).

Из прямоугольника ODMC видно, что вектор  , но из прямоугольника AOBD получаем, что вектор  .
Тогда
                                                                          (2.10)
Вектор  , который соединяет точку O с точкой M (x, y, z) называется радиусом-вектором этой точки.
Векторы  называются составными или компонентами вектора , а их величины OA = x, OB = y, OC = z  координатами этого вектора. Компоненты вектора выразим через его координаты и единичные векторы , а именно .
Подставляя эти значения в равенство (2.10), учитывая, что  , получим
                                                                                 (2.11)

Слагаемые   являются составными или компонентами вектора  .
Тройка векторов    называется координатным базисом, а разложение (2.11) называется разложением вектора по базису .  Это основная формула векторной алгебры.

Пример 1. Построить вектор .

Рис. 20.

Решение. Компоненты вектора    являются    и  , и им 
соответствует прямоугольный параллелепипед, диагональ которого является искомый вектор (рис. 20).

Действия над векторами, заданными в координатной форме

Если векторы заданы в координатной форме, то действия сложения, вычитания, умножения вектора на число можно заменить простыми арифметическими операциями над координатами этих векторов по таким правилам.

Правило 1. При сложении векторов их одноименные координаты складываются

Пусть имеем векторы и  . Найдем  .  Запишем разложение векторов    и  .  Тогда  .
Сложив эти равенства, получим
.
Итак, координаты вектора     будут  

Правило 2. Чтобы отнять от вектора    вектор  нужно вычесть из координат вектора   соответствующие координаты вектора  , то есть

Правило 3. Чтобы умножить вектор   на число λ,  нужно каждую из его координат умножить на это число. То есть, если
   то  .
Пример 1. Найти вектор  , если   
Решение. Выполним действия последовательно и найдем

.
Значит,

Вектор – основные определения

Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.

Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Так же как и на плоскости, векторы обозначаются и т. п. и на чертеже изображаются стрелкой.

Определение 2. Длиной (или модулем) вектора называется длина отрезка а направление, определяемое лучом называется направлением вектора

Длина вектора обозначается длина вектора обозначается

Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора:

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Определение 3. Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Если ненулевые векторы и лежат на параллельных прямых (следовательно, в одной плоскости), причём лучи лежат в одной полуплоскости, границей которой является прямая то векторы и называются сонаправленными в случае же, когда эти векторы принадлежат одной прямой, они называются сонаправленными, если один из лучей или целиком содержится в другом. Нулевой вектор будем считать сонаправленным с любым вектором в пространстве.

Ясно, что сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными. Обозначения остаются обычными: (векторы и сонаправлены), (векторы и противоположно направлены).

Определение 4. Векторы и называются равными, если и (т.е. если векторы сонаправлены и их длины равны).

Теорема 1. От любой тонки пространства можно отложить вектор, равный данному, и притом только один.

Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.

Возможно вам будут полезны данные страницы:

Операции над векторами и их свойства

Операции над векторами в пространстве аналогичны соответствующим операциям на плоскости.

Пусть даны два вектора и В силу теоремы 1 от произвольной точки пространства можно отложить вектор а от точки — вектор Тогда вектор называется по определению суммой векторов и а описанное правило построения суммы двух векторов — правилом треугольника (рис. 1).

Теорема 2. Сумма векторов и не зависит от выбора точки от которой при сложении откладывается вектор (Докажите эту теорему самостоятельно.)

Правило треугольника можно сформулировать и так: для любых трёх точек пространства выполняется равенство

Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма: где — вектор, модуль которого_равен длине диагонали параллелограмма, построенного на векторах причём вектор откладывают от той же точки, что и векторы (рис. 2).

Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:

1)

2) — коммутативность (переместительный закон);

3) — ассоциативность (сочетательный закон).

Здесь — произвольные векторы в пространстве.

Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.

Вектор, противоположный данному ненулевому вектору обозначается

Определение 6. Разностью двух векторов и называется вектор такой, что его сумма с вектором равна вектору

Разность векторов и обозначается Таким образом, по определению если

Разность векторов и можно найти по формуле (рис. 3) (докажите эту формулу самостоятельно). Замечание. Так же как и на плоскости, для сложения нескольких векторов в пространстве можно использовать правило многоугольника (рис. 4), только в последнем случае этот многоугольник будет пространственным (т.е. не все векторы, его составляющие, лежат в одной плоскости).

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых.

Умножение (произведение) вектора на число и его свойства, так же как и свойства операции сложения, не претерпевают изменений и в пространстве.

Определение 7. Произведением ненулевого вектора на действительное число называется вектор длина которого равна произведению длины вектора на модуль числа причём вектор сонаправлен с вектором при и противоположно направлен вектору при

Таким образом, по определению, если причём при Ясно, что векторы коллинеарны. Если же или то

Свойства умножения вектора на число не отличаются от аналогичных свойств на плоскости:

1.   — ассоциативность (сочетательный закон);
2.   —дистрибутивность относительно сложения векторов (1-й распределительный закон);
3.   — дистрибутивность относительно сложения чисел (2-й распределительный закон).

Здесь и — произвольные векторы, — произвольные действительные числа.

Справедлива также и лемма о коллинеарных векторах: если векторы и коллинеарны и то существует такое действительное число

что (ясно, что если

Сформулируем и докажем ещё одну важную для решения некоторых задач теорему.

Теорема 3. Пусть где — некоторое действительное число, отличное от -1, тогда точки принадлежат одной прямой. Для произвольной точки пространства справедливо равенство:

Доказательство 

1. Из равенства следует, что векторы коллинеарны, и так как — общая точка прямых и эти прямые совпадают, поэтому точки принадлежат одной прямой.

2. Пусть — произвольная точка пространства. Тогда и поскольку откуда Поделив обе части последнего равенства на приходим к формуле (1). Теорема доказана.

З. Компланарные и некомпланарные векторы

Следующее понятие уже не имеет аналога в планиметрии.

Определение 8. Векторы называются компланарными, если лучи, задающие их направления, параллельны некоторой плоскости.

Замечание. Из определения 8 следует, что при откладывании от одной точки векторов, равных нескольким данным компланарным векторам, получим векторы, лежащие в одной плоскости. Таким образом, компланарные векторы лежат либо в одной плоскости, либо в параллельных плоскостях.

Очевидно, что любые два вектора компланарны и любые три вектора, два из которых коллинеарны, также являются компланарными (поясните). Рассмотрим теперь условия, при которых три вектора, из которых никакие два не коллинеарны, являются компланарными.

Теорема 4. Векторы из которых никакие два не коллинеарны, являются компланарными в том и только том случае, если существуют такие действительные числа и что

(иными словами, векторы являются компланарными в том и только том случае, если один из них можно выразить через два других, или, как говорят, разложить по двум другим).

Доказательство

1. Пусть векторы компланарны. Докажем, что для них имеет место равенство (5). Отложим от произвольной

точки векторы Векторы лежат в одной плоскости (см. замечание). Проведём через точку прямую до пересечения с прямой в точке и прямую до пересечения с прямой в точке (см. рис. 8). Так как векторы коллинеарны, по лемме о коллинеарных векторах (см. §1.2) существуют такие действительные числа и что Но по правилу параллелограмма откуда Обратно, пусть выполнено равенство (5).

Докажем, что векторы компланарны. Векторы при откладывании от одной точки определяют некоторую плоскость. Согласно правилу параллелограмма и равенству (5) вектор принадлежит той же плоскости, откуда следует, что векторы и а значит, и векторы компланарны. Теорема доказана.

Отложим от произвольной точки пространства векторы где — три данных некомпланарных вектора, и рассмотрим параллелепипед построенный на векторах (рис. 9). Тогда сумму векторов можно найти следующим образом: Это правило сложения трёх некомпланарных векторов называется правилом параллелепипеда.

Если векторы не являются компланарными и для вектора имеет место равенство где — некоторые действительные числа, то говорят, что вектор разложен по трём некомпланарным векторам

а числа называются коэффициентами разложения.

Следующая теорема, называемая теоремой о разложении вектора по трём некомпланарным векторам, является основной во всей элементарной (школьной) векторной алгебре.

Теорема 5. Любой вектор пространства можно разложить по трём данным некомпланарным векторам причём коэффициенты разложения определятся единственным образом. Доказательство. 1. Если векторы и коллинеарны, то и теорема доказана.

2. Пусть векторы и не коллинеарны. Отложим от произвольной точки пространства векторы (рис. 10). Проведём через точку прямую до пересечения с плоскостью в точке Через точку в плоскости проведём прямую до пересечения с прямой в точке (в частности, если то точка совпадает с точкой Согласно правилу многоугольника но векторы по построению коллинеарны, поэтому в силу леммы о коллинеарных векторах где — некоторые действительные числа Таким образом, учитывая, что приходим к равенству

3. Докажем теперь, что разложение вектора по данным векторам единственно. Допустим, что это не так, т.е. существует ещё одно разложение в котором хотя бы один коэффициент не равен соответствующему коэффициенту в полученном нами разложении. Пусть, например, Вычтем последнее равенство из предпоследнего.

Тогда отсюда – т. е. векторы компланарны, что противоречит условию теоремы. Значит, наше допущение о ещё одном разложении неверно, т.е. разложение вектора по данным векторам единственно. Теорема доказана.

Итак, любой вектор пространства можно разложить по трём данным некомпланарным векторам причём единственным образом. Заданную тройку некомпланарных векторов называют базисом, сами векторы — базисными векторами, а разложение вектора по векторам называют разложением по данному базису

Координаты вектора

Так же как и на плоскости, в пространстве помимо координат точки вводятся координаты вектора. Рассмотрим три попарно перпендикулярных вектора отложенных от некоторой точки пространства, таких, что (например, их можно направить по рёбрам единичного куба). Эти векторы, очевидно, не являются компланарными. Поэтому, в силу теоремы 5, любой вектор можно разложить_по векторам причём единственным образом: Введём прямоугольную систему координат с началом в точке так, чтобы направления осей совпали_с направлениями векторов соответственно. Тогда векторы называются единичными векторами осей координат, а числа — координатами вектора в системе координат (обозначения:

Свойства векторов пространства, заданных своими координатами, аналогичны соответствующим свойствам векторов на плоскости:

1. Два вектора равны в том и только том случае, если равны их координаты.
2. Координаты суммы (разности) двух векторов равны суммам (разностям) соответствующих координат этих векторов, т.е. для векторов получаем
3. При умножении вектора на число каждая его координата умножается на это число, т.е. для вектора и действительного числа получаем

Докажем, например, свойство 2. Так как то, согласно свойствам сложения векторов и умножения вектора на число, т. е. вектор имеет координаты что и требовалось доказать. Остальные свойства доказываются аналогично.

Скалярное произведение векторов и его свойства

Определение скалярного произведения векторов и в пространстве ничем не отличается от аналогичного определения для векторов на плоскости.

Определение 11. Скалярным произведением векторов называется произведение длин этих векторов на косинус угла между ними (обозначение: Таким образом, по определению,

Теорема 8. Два ненулевых вектора взаимно перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю, т. е.

Доказательство этой теоремы вытекает из формулы (9).

Определение 12. Скалярным квадратом вектора называется скалярное произведение Скалярный квадрат обозначается т.е. по определению

Так как то

Таким образом, длина вектора равна квадратному корню из его скалярного квадрата.

Замечание. Скалярное произведение есть число, поэтому грубой ошибкой явилась бы запись:

Если векторы и заданы своими координатами: то скалярное произведение может быть выражено через их координаты.

Теорема 9. Скалярное произведение векторов равно сумме произведений их соответственных координат, т. е.

Доказательство. Отложим от произвольной точки пространства векторы При этом, как мы знаем, соответствующие координаты векторов и а также и будут равны, а угол По теореме косинусов для треугольника получим

итак как имеем откуда Но

поэтому

Решение любой геометрической задачи на вычисление сводится, в сущности, к нахождению величин двух типов: расстояний и углов. Если в пространстве задан некоторый базис (в частности, прямоугольный), т. е. тройка некомпланарных векторов, то на основании теоремы 5 любой вектор пространства можно разложить по векторам этого базиса, причём единственным образом.

Если известны длины векторов, образующих базис, углы между ними и разложение некоторого вектора по векторам этого базиса, то, используя свойства скалярного произведения, можно определить длину такого вектора и угол, образуемый им с любым другим вектором, разложение которого по векторам этого базиса известно.

Таким образом, векторы позволяют находить решения довольно широкого класса геометрических задач, а умение определять разложение вектора по базисным векторам является важнейшим фактором их решения.

Для решения задач о разложении вектора по трём данным некомпланарным векторам, разумеется, необходимо, помимо теоремы 5, знание предшествующего ей материала.

Примеры с решением

Задача 1.

Основанием четырёхугольной пирамиды является параллелограмм Точки и — середины рёбер и соответственно. Найдите разложение векторов по векторам

Решение (см. рис. 14).

1. но поэтому

2. Так как — середина но (см. следствие 1 теоремы 3), поэтому

Ответ:

Заметим, что в разложении вектора по векторам коэффициент разложения при векторе равен нулю, а это означает, в силу теоремы 4, что векторы компланарны. Если заранее «увидеть», что где — середина (отсюда то разложение вектора можно было бы найти проще. Но векторный метод тем и хорош, что, даже не обладая развитым пространственным воображением, а лишь зная основные определения и теоремы, можно получить правильный ответ (пусть и не всегда самым оптимальным путём)!

Задача 2.

Пусть — точка пересечения медиан треугольника — произвольная точка пространства. Найдите разложение вектора по векторам

Решение (см. рис. 15). Пусть — середина ребра Так как — точка пересечения медиан треугольника точки принадлежат одной прямой, причём, в силу теоремы о точке пересечения медиан треугольника, Согласно следствию I теоремы 3 Тогда

Ответ:

Векторы и их решение

Вектором называется направленный отрезок. Направление отрезка показывается стрелкой. Различают начало и конец отрезка. 

Два вектора называются равными между собой, если каждый из них можно получить параллельными перенесениями другого. 

Равные векторы являются параллельными (колинеарными), имеют одно и то же направление и одинаковую длину. Длина вектора  называется абсолютной величиной или модулем вектора и обозначается 

Вектор называется нулевым (ноль- вектором), если он имеет нулевую длину, то есть его конец сходится с началом. 

Чтобы найти сумму двух векторов  и  совместим начало вектора  с концом вектора .

Суммой  векторов  и   называется вектор, начало которого сходится с началом вектора , а конец – с концом вектора  (рис. 1.1).

 Правило треугольника

 Правило параллелограмма 

Для складывания векторов имеют место такие законы: 

1) переставной (коммутативный)

2) связующий 

3) для каждого вектора  существует противоположный  такой, что 

4)

5) для некоторых двух  векторов  и   выполняются неравенства: 

Если вектор  образует угол  с осью  (рис. 1.2), то проекцию вектора  на ость называется величина 

Пусть вектор имеет начало в точке  а конец – в точке   Тогда величины   являются проекциями вектора  на оси  Проекции вектора однозначно определяют вектор. Потому имеет место равенство 

Если вектор  то проекция суммы векторов 

Произведением вектора  на число  называется вектор  длина которого равна  Умножение вектора на число имеет свойство ассоциативности и дистрибутивности, то есть для произвольных чисел  и векторов  и  справедливы равенства: 

Любой вектор  можно записать в виде

где  – единичные векторы,   называются компонентами вектора     (рис. 1.3) .

Пример 1.73  

Даны два вектора:  и  

Найти вектор 

Решение 

Признаком колинеарности двух векторов   и    является пропорциональность их координат: 

Скалярным произведением двух векторов   и    называется число  которое равно произведению их модулей на косинус угла между ними: 

Скалярное произведение можно записать в таком виде: 

Если векторы   и    заданы своими координатами, то их скалярное произведение вычисляется по формуле: 

Учитывая формулы (1.18) и (1.19), можно найти косинус угла между векторами    и  : 

Отсюда получается условие перпендикулярности двух векторов: если   и    или в координатной форме: 

Среди свойств скалярного произведения отметим так: 

Векторным произведением вектора  на вектор  называется вектор  который имеет такие свойства: 

1) длина вектора  равна произведению длин сомножителей на синус угла между ними: 

2) вектор  перпендикулярный к векторам  и 

3) из конца вектора   кратчайший поворот от   к    является таким, что происходит против часовой стрелки (рис. 1.4). 

Заметим, что  а модуль векторного произведения равен плоскости параллелограмма, построенного на векторах   и   , если у них общее начало.  

В координатной форме векторное произведение векторов  и  можно записать в виде:  

Смешанным или скалярно – векторным произведением трех векторов  называется векторное произведение векторов    и   , скалярно умноженный на вектор  то есть 

Если векторы  – компланарны, то есть расположены в одной плоскости или на параллельных плоскостях, то их смешанное произведение равно нулю. 

Если известные координаты сомножителей  то смешанное произведение вычисляется по формуле: 

Если три ненулевых  разложены в одной плоскости (компланарны), то из смешанное произведение 

Следует, в координатной форме условие компланарности трех ненулевых векторов имеет вид: 

Решение примеров:

Пример 1.74 

Заданы координатами точек   и  Найти: 

1) вектор  если 

2) угол между векторами  и 

3) координаты вектора 

4) объем пирамиды с вершинами в точках 

Решение 

1) По формуле (1.14) находим 

тогда 

2) Косинус угла между векторами  и  вычислим по формуле (1.20): 

Поскольку косинус угла отрицательный, то угол  тупой. 

3) Координаты векторного произведения находим по формуле (1.22):

4) Чтобы найти объем пирамиды, найдем сначала смешанное произведение векторов, что выходят из одной вершины пирамиды: 

Тогда объем пирамиды

Собственные числа и собственные векторы

Вектор – столбец   называется собственным вектором квадратной матрицы   – ого порядка, что соответствует собственному значению  если он удовлетворяют матричному уравнению  или 

Тут  – единичная матрица  – ого порядка, а  – нулевой вектор – столбец. При условии, что  получим характеристическое уравнение для определения собственных значений 

Координаты собственного вектора  что соответствуют собственному значению  является решением системы уравнений: 

Собственный вектор обозначаются с точностью к постоянному множителю.

Решение примеров:

Пример 1.90.

Обозначить  собственные определения и собственные векторы матрицы

Решение. Характеристические уравнения данной матрицы имеет вид (1.24): 

 или 

отсюда получается, что матрица  имеет два собственных значения  и  Собственный вектор  что соответствует  обозначаются с системой уравнений вида (1.25)

  или 

которое приводится к одному уравнению 

Возьмем  получим решение в виде 

Следует, первый собственный вектор является 

Второй вектор  что соответствует собственному значению  определяется из системы уравнений вида (1.25)

Эта система уравнений так же приводится к одному уравнению  положив  запишем ее решение в виде  Следует, второй собственный вектор: 

Таким образом, матрица  имеет два разных определения  и  и два собственных вектора, равных  и  (с точностью к постоянному множителю). 

Пример 1.91 

Найти собственные векторы и собственные значения матрицы 

Решение. Характеристическое уравнение

Раскрыв определитель получим: 

Корень  – кратный, показатель кратности  корень  – простой, 

Система уравнений для определения собственных векторов имеет вид: 

Последовательно подставим  и  в записанную систему: 

Фундаментальная система уравнений получается, если свободным переменным  последовательно дать значения 

Получили два линейно независимые собственные векторы. Вся совокупность векторов, что соответствуют собственному значению  имеет вид: 

Фундаментальная система решений получается, если взять 

Векторная алгебра

Понятие «вектор» (от лат. vector – носитель), как отрезка, имеет определенную длину и определенное направление, впервые появилось в работах по построению числовых систем в ирландского математика Уильяма Гамильтона (1805-1865). Это понятие связано с объектами, которые характеризуются величиной и направлением, например, скорость, сила, ускорение. При этом скорость можно понимать в широком смысле: скорость изменения издержек производства, доходов, спроса, потребления и предложения и др. Вектор может указывать направление наибольшего возрастания или убывания функции, описывающей различные экономические процессы. Векторы, рассмотренные в данном разделе, является частным случаем -мерных векторов: они предполагают геометрическую интерпретацию, потому что принадлежат к векторным линейных пространств размерности

Для графического изображения решения экономических задач на плоскости и в пространстве применяются средства аналитической геометрии. Аналитическая геометрия – математическая наука, объектом изучения которой являются геометрические фигуры, а предметом – установление их свойств средствами алгебры с помощью координатного метода. Теоретической базой этой науки является частично известна из школы векторная алгебра.

Основателем метода координат и, вместе с тем, аналитической геометрии является Рене Декарт (1596-1650) – французский философ, математик, физик и физиолог. Его именем и названа известная «декартова прямоугольная система координат», которая позволяет определить положение фигуры на плоскости и тела в пространстве.

После изучения данной темы вы сможете:

● использовать инструмент векторной алгебры для геометрического изображения и анализа объектов экономических процессов;
● применять уравнение прямой линии на плоскости для геометрической интерпретации зависимости между функциональному признаку и аргументом, что на нее влияет;
● применять уравнение кривых второго порядка при построении нелинейных математических моделей экономических задач;
● осуществлять геометрическую интерпретацию решений экономических задач с помощью поверхностей и плоскостей.

Векторы: основные определения, линейные операции

Выберем на произвольной прямой (в или в ) отрезок и укажем, которую из точек или считать начальной (началом отрезка), а какую – конечной (концом отрезка). Конец отрезка обозначают стрелке и говорят, что на отрезке задано направление. Отрезок с заданным на нем направлением, или коротко – направленный отрезок, называется вектором. Вектор обозначается символом или строчными буквами латинского
алфавита с чертой: и др. (Рис. 6.1). 

Рис. 6.1

В применимых задачах естественных наук существенным является обстоятельство – где, в какой точке находится начало вектора. Например, результат действия силы зависит не только от ее величины и направления действия, но и от того, в какой точке она прикладывается.

Вектор, для которого фиксированная (не фиксирована) начальная точка называется связанным (свободным). Векторы, которые применяются в экономических задачах, как правило, не являются связанными, поэтому в дальнейшем будем рассматривать преимущественно свободные векторы

Длиной, или модулем, вектора называется длина соответствующего отрезка и обозначается одним из символов: 

Нулевым вектором 0, или ноль-вектором, называется вектор, длина которого равна нулю, а направление его считается произвольным (неопределенным).

Единичным вектором называется вектор, длина которого равна единице.

Равными векторами называются векторы, которые принадлежат одной прямой или параллельным прямым, одинаково направлены и имеют равные длины.

Взаимно противоположными называются векторы, которые принадлежат одной прямой или параллельным прямым, имеют равные длины, но противоположно направлены. Вектор, противоположный вектору , обозначают символом .

Коллинеарными называют векторы, которые принадлежат одной прямой или параллельным прямым.

Компланарными называются векторы, которые принадлежат одной плоскости или параллельным плоскостям.

Линейные операции над векторами

Будем считать, что векторы принадлежат одни плоскости. Осуществляя параллельный перенос одного из векторов , совместим начало вектора с концом вектора (или наоборот) и по отрезками, соответствующие векторам, как по двум сторонам, построим треугольник (рис. 6.2 а).

1. Суммой векторов называется вектор , который определяется третьей стороной треугольника, с началом в начале вектора . Порядок построения суммы двух векторов по этому определению называют правилом треугольника.

Параллельный перенос можно осуществить и так, что объединятся начала векторов и , тогда на векторах как на сторонах построим параллелограмм (рис. 6.2 б), и придем к известному из школьного курса алгебры правилу параллелограмма.

Рис. 6.2

Правило треугольника обобщается на произвольное конечное число векторов. Если параллельным переносом расположить векторы так, что конец предыдущего вектора (начиная с первого) является началом следующего, то результирующим будет вектор, соединяющий начало первого вектора слагаемого с концом последнего (рис. 6.3):

Рис. 6.3

Соответствующее правило называют правилом многоугольника.
Свойства суммы векторов:
1) переставная, или коммутативна:

2) соединительная, или ассоциативная:

3) 

4) 

Разницу  можно рассматривать как сумму вектора с вектором, противоположным вектору 

Умножения вектора на скаляр

Пусть – некоторое действительное число . Произведением вектора со скаляром называется вектор , модуль которого равен произведению модулей , а направление совпадает с направлением , если , или противоположно направлению , если (рис. 6.4):

Рис. 6.4

При вектор превращается в ноль-вектор .
Свойства умножения вектора на скаляр:
1) переставной или коммутативных закон:

  где 

2) соединительный, или ассоциативный закон:

 где 

3) распределительный или дистрибутивный закон:

 где 

4) 

5) 

Из определения умножения вектора на скаляр следует необходимое и достаточное условие коллинеарности двух векторов: вектора и коллинеарны тогда и только тогда, когда каждый из них является произведением другого из скаляром:

Известно, что три ненулевые векторы и компланарны тогда и только тогда, когда один из них является линейной комбинацией двух других:

 компланарны 

Рассмотрим понятие, имеет очень важное значение в теории векторов – проекции вектора на ось (прямую, имеет направление; заданное направление считать положительным, противоположное направление – отрицательным).

Компонентой вектора относительно оси называют вектор, начало которого является проекцией начала вектора на ось , а конец – проекцией конца вектора на ось (рис. 6.5).

Рис. 6.5

Проекцией вектора на ось называют скаляр, равный длине компоненты вектора относительно оси со знаком , если направление компоненты совпадает с направлением оси , или со знаком , если ее направление противоположно направлению оси:

Основные свойства проекции вектора на ось

1. Проекция вектора на ось равна произведению длины вектора с косинусом угла между вектором и осью:

2. Проекция суммы двух векторов на эту ось равна сумме их проекций на эту ось:

Это свойство обобщается на любое конечное число векторов.

3. Проекция на ось произведения вектора со скаляром равна произведению со скаляром проекции самого вектора на ось:

Прямоугольная система координат в пространстве. Координатная и алгебраическая формы задания векторов

Пусть в трехмерном векторном пространстве задана прямоугольная декартова система координат , что определяется тремя взаимно перпендикулярными числовыми осями – осями, на которых указано масштаб (единицу длины) – с общей точкой – началом координат (рис. 6.6).

Рис. 6.6

Выберем в пространстве произвольную точку  и соединим ее отрезком прямой с началом координат . Вектор , началом которого является начало координат , а концом данная точка , называется радиусом-вектором точки . Отметим, что радиусы-векторы точек пространства являются связанными векторами. 

Под декартовыми прямоугольными координатами точки понимают проекции ее радиус-вектора на оси

Точка с координатами обозначается через . Вектор каждой точки пространства (кроме точки ) определяет прямоугольный параллелепипед с диагональю, что является отрезком, на котором построено вектор (рис. 6.6).

Измерениями параллелепипеда есть модули координат точки . Длина диагонали параллелепипеда определяется по формуле: 

Углы , которые образованы радиусом-вектором с координатными осями называются его направляющими углами. 

откуда:

Косинусы направляющих углов называются направляющими косинусами радиус-вектора . С (6.4) получаем свойства:
1) направляющие косинусы являются координатами единичного радиус-вектора: 

2) сумма квадратов направляющих косинусов вектора равна единице: 

Понятие «координата», «направляющие углы», «направляющие косинусы» без изменений переносятся на любые свободные векторы, потому начало каждого из них параллельным переносом можно поместить в начало , дает радиус вектор определенной точки.

Координатами любого вектора в пространстве называются его проекции на оси координат. Они обозначаются символами и пишут: или , где согласно определению координат:

Задача вектора тройкой его координат , называют координатной формой задачи.

Для единичных векторов , расположенных соответственно на осям , имеем:

Длина произвольного вектора и его направляющие косинусы вычисляются по формулам:

Найти длину и направляющие косинусы вектора 

По формулам (6.5) имеем: 

Установим связь между координатами вектора – числами – и его компонентами – векторами – с помощью единичных векторов (рис. 6.7).

Рис. 6.7

Компонентами вектора относительно координатных осей являются векторы (рис. 6.7). Согласно операции сложения векторов по правилу многоугольника получаем:

Следовательно, любой вектор в трехмерном пространстве является суммой трех его компонент относительно координатных осей:

Изображение вектора с в виде суммы произведений координат с единичными векторами (ортами) называют алгебраической формой задания вектора.

Согласно свойствами операций над векторами, алгебраическая форма задания дает возможность установить результаты действий над векторами, заданными в координатной форме.
1. При добавлении (вычитании) двух векторов с : и , их соответствующие по номеру координаты прилагаются (вычитаются):

Действительно, по свойствам ассоциативности и дистрибутивности имеем:

2. При умножении вектора на скаляр все его координаты умножаются на этот скаляр:

Действительно, согласно распределительным свойствам умножения скаляра на сумму векторов имеем:

Скалярное, векторное, смешанное произведения векторов

Скалярным произведением двух векторов и называется число (скаляр), равное произведению их модулей с косинус угла между ними и обозначается :

Вместо часто пишут или используют обозначения . Название этой операции согласуется с ее сути, а именно: скалярное произведение является скаляром, то есть числом.

Для определения угла между векторами и совмещают их начала и рассматривают угол между двумя лучами и (рис. 6.8). Если угол острый, то , если тупой, то .

Основные свойства скалярного произведения векторов вытекают из его определения (6.7).

1. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы взаимно перпендикулярны (ортогональные):

2. Скалярный квадрат вектора равен квадрату его модуля, то есть

3. Скалярное произведение подчиняется всем законам арифметики чисел относительно линейных операций:

4. Скалярное произведение двух векторов равно произведению модуля одного из них с проекцией второго на ось, направление которого определяется первым вектором:

Доказательство этого свойства основывается на определении (6.3).

Скалярное произведение векторов и , заданных в координатной форме. Пусть имеем два вектора 

1. Вычислим скалярные произведения единичных векторов По свойству Для других пар на основании свойства 1 имеем: 

2. Находим произведение , подавая векторы в алгебраической форме (6.6) и используя распределительный закон:

Раскрываем скобки и получаем:

Скалярное произведение двух векторов равно сумме произведений одноименных координат. Это полностью совпадает с определением скалярного произведения -мерных векторов.

Как следствие из (6.12) при получаем формулу (6.5) модуля вектора через его координаты:

Определим угол между двумя ненулевыми векторами и , заданные в координатной форме. Воспользуемся определением скалярного произведения (6.7) и соотношения (6.5). В результате получаем:

Следовательно, косинус угла между двумя векторами определяется формулой: 

Отсюда 

В результате с соотношением (6.13) получим критерий ортогональности двух векторов, заданных в координатной форме: 

Критерием коллинеарности векторов и , заданных в координатной форме является пропорциональность их координат:

Векторное произведение двух векторов

Пусть и – векторы пространства , определяющие некоторую плоскость . Вектор называется векторным произведением векторов и , если вектор удовлетворяет условиям: 

1) модуль его численно равен площади параллелограмма, построенного на векторах и как на сторонах;
2) он перпендикулярный плоскости параллелограмма и направленный так, что поворот вектора до совмещения с вектором кратчайшим путем наблюдается с конца вектора против часовой стрелки (рис. 6.9).

Рис. 6.9

Векторное произведение обозначается символами: , или 

Следовательно,

где наименьший из углов  что соответствует совмещению с поворотом вектора против часовой стрелки.

Основные свойства векторного произведения вытекают из его определения.
1. Векторное произведение ненулевых векторов равно ноль-вектору тогда и только тогда, когда векторы  и коллинеарны:

Еще одним критерием коллинеарности векторов является равенство нулевому вектору их векторного произведения.

2. Векторные произведения с разным порядком сомножителей являются взаимно противоположными векторами:

Это означает, что векторное произведение не подчиняется переставному (коммутативному) закону.

3. Векторное произведение подчиняется ассоциативному закону относительно скалярного множителя и дистрибутивному закону относительно сложения:

где 

Векторное произведение векторов  и , заданных в координатной форме. Пусть имеем два ненулевые векторы: 

1. Определяем векторные произведения ортов (рис. 6.10).

Векторное произведение одноименных векторов по свойству 1 дает ноль вектор:

Однако все векторные произведения разноименных единичных векторов будут давать единичные векторы:

Рис. 6.10

Рассмотрим, например, произведение . Совмещение с кратчайшим путем (указано дугой со стрелкой на рис. 6.10) происходит против часовой стрелки, если смотреть с конца вектора , следовательно, . Тогда по свойству

2. Находим произведение , подавая векторы в алгебраической форме и используя арифметические свойства (6.18) и соотношения (6.19):

Множители при  это вскрытые определители 2-го порядка, поэтому 

Коэффициенты при единичных векторах в соотношении (6.20) являются координатами вектора как векторного произведения векторов и .

Если символы в соотношении (6.20) считать элементами первой строки определителя 3-го порядка, то окончательно получим представление  в виде определителя: 

Найдем векторное произведение векторов  и 

Модуль векторного произведения  определяет площадь параллелограмма, построенного на векторах  и 

Смешанным произведением трех векторов и называется векторное произведение двух из них, умножен скалярно на третий вектор, то есть и т. д.

Смешанное произведение можно обозначать тройкой векторов , в которой первые два элемента считают связанными векторным произведением, а результат векторного произведения умножают на третий вектор скалярно, то есть – это все равно, что . Понятно, что результатом смешанного произведения является скаляр, поскольку векторное произведение  является вектором (обозначим его через ), а произведение дает скаляр.

Геометрическая интерпретация смешанного произведения. Пусть и – некомпланарные векторы. Построим на этих векторах как на ребрах параллелепипед (рис. 6.11).

Рис. 6.11

Вектор по длине численно равна площади параллелограмма, построенного на векторах и как на сторонах. Этот параллелограмм является основой параллелепипеда, построенного на векторах и . Вектор является перпендикулярным плоскости параллелограмма.

Согласно (6.11) скалярное произведение можно представить как произведение модуля и проекции вектора на ось, определяется вектором :

где , причем  является положительным числом, если угол между векторами и острый, и отрицательным, если этот угол тупой. По модулю эта проекция равна высоте параллелепипеда .

Модуль смешанного произведения трех векторов численно равен объему параллелепипеда , построенного на векторах как на ребрах:

Основные свойства смешанного произведения вытекают из его определения и геометрической интерпретации.
1. Смешанное произведение ненулевых векторов равно нулю, если по крайней мере два из трех векторов коллинеарны или все три – компланарны, и наоборот.

Необходимым и достаточным условием компланарности трех ненулевых векторов является равенство нулю их смешанного произведения:

 компланарны 

Свяжем с изображенными на плоскости векторами круг (рис. 6.12). Перечисление векторов, начиная с любого, против часовой стрелки назовем положительным, или циклическим, перестановкой векторов, в противном случае – отрицательной перестановкой.

2. Циклическая перестановка трех сомножителей смешанного произведения не меняет его величины, а отрицательное перестановки меняет его знак на противоположный:

Смешанное произведение векторов, заданных в координатной форме

Пусть имеем три ненулевые векторы  По определению смешанного произведения и представлением векторного и скалярного произведений в координатной форме имеем:

Полученная сумма произведений является расписанием определителя 3-го порядка, составленный из координат векторов, по элементам его третьей строки, то есть:

Векторы компланарны тогда и только тогда, когда определитель 3-го порядка, элементами строк которого являются координаты этих векторов равен нулю (свойство 1):

 компланарны 

С помощью смешанного произведения векторов легко определить, относятся ли четыре точки одной плоскости. Для этого следует проверить выполнение условия компланарности трех векторов с общим началом в одной из точек.

Простейшие задачи аналитической геометрии

Задача об определении длины отрезка. Найти длину отрезка , если известны координаты его концов: . Эту задачу можно рассматривать как задачу о нахождении расстояния между двумя точками.

1. Введем в рассмотрение вектор с началом и концом и радиусы-векторы (рис. 6.13).
2. Определим координаты вектора как разности векторов и :
3. Находим модуль вектора , который и равна длине отрезка :

Задача об определении площади треугольника

Найдем площадь треугольника, заданного координатами вершин: 

По аксиомой стереометрии известно, что три точки в пространстве определяют плоскость и притом только одну. Для упрощения изложения, не нарушает общего подхода к решению задачи, договоримся рассматривать треугольник , принадлежащей плоскости : и .

1. Введем в рассмотрение векторы:

и найдем их векторное произведение 

По соотношению (6.20) имеем: 

2. Вычислим модуль вектора , численно равна площади параллелограмма , построенного на векторах как на сторонах (рис. 6.14):

Тогда для площади треугольника имеем: 

Знак или берется в зависимости от того, каким будет определитель – положительным или отрицательным.

Если треугольник принадлежит не плоскости , а любой другой плоскости в пространстве, то его площадь тоже можно найти по формуле:

Найдем площадь треугольника с вершинами   

Введем в рассмотрение векторы:  и   и определим их векторное произведение:

Тогда 

 (кв. ед.)

Задача о деление отрезка в заданном отношении

Пусть в пространстве заданы две точки . Проведем через них произвольную прямую и установим на этой прямой положительное направление, согласно которому определим направление на отрезке (рис. 6.15). На прямой возьмем точку , которая может принадлежать отрезку , или его продолжению. При этом, если точка принадлежит отрезку (рис. 6.15 а), говорится, что она осуществляет внутреннее деление отрезка на части, если не принадлежит (рис. 6.15 б) – то внешний.

Рис. 6.15

Число , которое определяется формулой

называется отношением, в котором точка разделяет направленный отрезок . Если , то осуществляет внутреннее (внешнее) деление отрезка на части.

Задача о деление отрезка в заданном отношении формулируется так: найти координаты точки , что разделяет отрезок в отношении , если отрезок задан координатами начала и конца –

Пусть точкам соответствуют радиусы-векторы (рис. 6.16). Из определения (6.29) следует, что векторы и коллинеарны, то есть . Следовательно, 

С этого векторного равенства найдем вектор 

или в координатах:

Отсюда, если отрезок разделить на две равные части точкой  то координаты точки могут быть найдены следующим образом:

Можно доказать, что координаты точки пересечения медиан треугольника, заданного координатами его вершин  вычисляются по формулам: