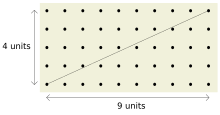
В «лесу», составленном на координатной плоскости из точек с целочисленными координатами, из начала координат «видны» только «деревья» со взаимно простыми координатами.
Взаимно простые числа — целые числа, не имеющие никаких общих делителей, кроме ±1. Равносильное определение[1]: целые числа взаимно просты, если их наибольший общий делитель (НОД) равен 1.
Например, взаимно просты числа 14 и 25, так как у них нет общих делителей; но числа 15 и 25 не взаимно просты, так как у них имеется общий делитель 5.
Для указания взаимной простоты чисел 


Это понятие было введено в книге VII «Начал» Евклида. Для определения того, являются ли два числа взаимно простыми, можно использовать алгоритм Евклида.
Понятие взаимной простоты естественным образом обобщается на любые евклидовы кольца[⇨].
Попарно взаимно простые числа[править | править код]
Если в наборе целых чисел любые два числа взаимно просты, то такие числа называются попарно взаимно простыми (или просто попарно простыми[3]). Для двух чисел понятия «взаимно простые» и «попарно простые» совпадают, для более чем двух чисел свойство попарной простоты более сильно, чем ранее определённое свойство взаимной простоты (в совокупности) — попарно простые числа будут и взаимно простыми, но обратное неверно[3]. Примеры:
- 8, 15 — не простые, но взаимно простые.
- 6, 8, 9 — взаимно простые (в совокупности) числа, но не попарно простые.
- 8, 15, 49 — попарно простые и взаимно простые (в совокупности).
Если числа 
- НОД
НОД
НОД
НОД
,
- где НОД – наибольший общий делитель.
Свойства[править | править код]
Все упомянутые в этом разделе числа подразумеваются целыми, если не оговорено иное.
- Дробь является несократимой тогда и только тогда, когда её числитель и знаменатель взаимно просты.
Таблица взаимной простоты чисел до 30[править | править код]
В каждой клетке стоит наибольший общий делитель её координат, и соответствующие взаимно-простым парам координат единицы выделены тёмным. Из описанного выше свойства следует, что средняя плотность тёмных клеток при расширении таблицы до бесконечности станет равна 
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 3 |
| 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 4 | 1 | 2 |
| 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 |
| 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 6 |
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 | 1 | 1 | 1 | 1 | 7 | 1 | 1 |
| 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 |
| 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 |
| 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 10 |
| 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 12 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 4 | 1 | 6 |
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 13 | 1 | 1 | 1 | 1 |
| 14 | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 2 | 1 | 14 | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 2 | 1 | 14 | 1 | 2 |
| 15 | 1 | 1 | 3 | 1 | 5 | 3 | 1 | 1 | 3 | 5 | 1 | 3 | 1 | 1 | 15 | 1 | 1 | 3 | 1 | 5 | 3 | 1 | 1 | 3 | 5 | 1 | 3 | 1 | 1 | 15 |
| 16 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 16 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 4 | 1 | 2 |
| 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 18 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 9 | 2 | 1 | 6 | 1 | 2 | 3 | 2 | 1 | 18 | 1 | 2 | 3 | 2 | 1 | 6 | 1 | 2 | 9 | 2 | 1 | 6 |
| 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 20 | 1 | 2 | 1 | 4 | 5 | 2 | 1 | 4 | 1 | 10 | 1 | 4 | 1 | 2 | 5 | 4 | 1 | 2 | 1 | 20 | 1 | 2 | 1 | 4 | 5 | 2 | 1 | 4 | 1 | 10 |
| 21 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 1 | 3 | 1 | 1 | 3 | 1 | 7 | 3 | 1 | 1 | 3 | 1 | 1 | 21 | 1 | 1 | 3 | 1 | 1 | 3 | 7 | 1 | 3 |
| 22 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 11 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 22 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 24 | 1 | 2 | 3 | 4 | 1 | 6 | 1 | 8 | 3 | 2 | 1 | 12 | 1 | 2 | 3 | 8 | 1 | 6 | 1 | 4 | 3 | 2 | 1 | 24 | 1 | 2 | 3 | 4 | 1 | 6 |
| 25 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 25 | 1 | 1 | 1 | 1 | 5 |
| 26 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 13 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 26 | 1 | 2 | 1 | 2 |
| 27 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 9 | 1 | 1 | 3 | 1 | 1 | 3 | 1 | 1 | 27 | 1 | 1 | 3 |
| 28 | 1 | 2 | 1 | 4 | 1 | 2 | 7 | 4 | 1 | 2 | 1 | 4 | 1 | 14 | 1 | 4 | 1 | 2 | 1 | 4 | 7 | 2 | 1 | 4 | 1 | 2 | 1 | 28 | 1 | 2 |
| 29 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 29 | 1 |
| 30 | 1 | 2 | 3 | 2 | 5 | 6 | 1 | 2 | 3 | 10 | 1 | 6 | 1 | 2 | 15 | 2 | 1 | 6 | 1 | 10 | 3 | 2 | 1 | 6 | 5 | 2 | 3 | 2 | 1 | 30 |
Вариации и обобщения[править | править код]
Понятия простого числа, наибольшего общего делителя и взаимно простых чисел естественно обобщаются на произвольные евклидовы кольца, например, на кольцо многочленов или гауссовы целые числа. Обобщением понятия простого числа является «неприводимый элемент». Данное выше определение взаимно простых чисел не годится для произвольного евклидова кольца, поскольку в кольце могут быть делители единицы; в частности, НОД определяется с точностью до умножения на делитель единицы. Поэтому определение взаимно простых чисел следует модифицировать[6].
Элементы евклидова кольца называются взаимно простыми, если множество их наибольших общих делителей содержит только делители единицы.
Равносильные формулировки[6]:
Имеет также место лемма Евклида.
Практическое применение[править | править код]
Свойство взаимной простоты не только играет важную роль в теории чисел и коммутативной алгебре, но имеет ряд важных практических приложений, в частности, число зубьев на звёздочках и число звеньев цепи в цепной передаче стремятся делать взаимно простыми, что обеспечивает равномерность износа: каждый зуб звёздочки будет поочерёдно работать со всеми звеньями цепи.
Примечания[править | править код]
- ↑ 1 2 Взаимно простые числа. // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 690.
- ↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — С. 139. — 703 с. — ISBN 5-03-001793-3.
- ↑ 1 2 Михелович, 1967, с. 28.
- ↑ Нестеренко Ю. В. Теория чисел. — М.: Издательский центр «Академия», 2008. — С. 40. — 272 с. — ISBN 9785769546464.
- ↑ Михелович, 1967, с. 64.
- ↑ 1 2 Ларин С. В. Алгебра и теория чисел. Группы, кольца и поля: учеб. пособие для академического бакалавриата. — 2-е изд. — М.: Юрайт, 2018. — С. 92—93. — 160 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-05567-2.
Литература[править | править код]
- Взаимно простые числа // Большая советская энциклопедия : в 66 т. (65 т. и 1 доп.) / гл. ред. О. Ю. Шмидт. — М. : Советская энциклопедия, 1926—1947.
- Михелович Ш. Х. Теория чисел. — 2-е изд. — М.: Высшая школа, 1967. — 336 с.
В этом статье мы расскажем о том, что такое взаимно простые числа. В первом пункте сформулируем определения для двух, трех и более взаимно простых чисел, приведем несколько примеров и покажем, в каких случаях два числа можно считать простыми по отношению друг к другу. После этого перейдем к формулировке основных свойств и их доказательствам. В последнем пункте мы поговорим о связанном понятии – попарно простых числах.
Что такое взаимно простые числа
Взаимно простыми могут быть как два целых числа, так и их большее количество. Для начала введем определение для двух чисел, для чего нам понадобится понятие их наибольшего общего делителя. Если нужно, повторите материал, посвященный ему.
Взаимно простыми будут два таких числа a и b, наибольший общий делитель которых равен 1, т.е. НОД (a, b) =1.
Из данного определения можно сделать вывод, что единственный положительный общий делитель у двух взаимно простых чисел будет равен 1. Всего два таких числа имеют два общих делителя – единицу и минус единицу.
Какие можно привести примеры взаимно простых чисел? Например, такой парой будут 5 и 11. Они имеют только один общий положительный делитель, равный 1, что является подтверждением их взаимной простоты.
Если мы возьмем два простых числа, то по отношению друг к другу они будут взаимно простыми во всех случаях, однако такие взаимные отношения образуются также и между составными числами. Возможны случаи, когда одно число в паре взаимно простых является составным, а второе простым, или же составными являются они оба.
Это утверждение иллюстрирует следующий пример: составные числа -9 и 8 образуют взаимно простую пару. Докажем это, вычислив их наибольший общий делитель. Для этого запишем все их делители (рекомендуем перечитать статью о нахождении делителей числа). У 8 это будут числа ±1, ±2, ±4, ±8, а у 9 – ±1, ±3, ±9. Выбираем из всех делителей тот, что будет общим и наибольшим – это единица. Следовательно, если НОД (8, −9)=1, то 8 и -9 будут взаимно простыми по отношению друг к другу.
Взаимно простыми числами не являются 500 и 45, поскольку у них есть еще один общий делитель – 5 (см. статью о признаках делимости на 5). Пять больше единицы и является положительным числом. Другой подобной парой могут быть -201 и 3, поскольку их оба можно разделить на 3, на что указывает соответствующий признак делимости.
На практике довольно часто приходится определять взаимную простоту двух целых чисел. Выяснение этого можно свести к поиску наибольшего общего делителя и сравнению его с единицей. Также удобно пользоваться таблицей простых чисел, чтобы не производить лишних вычислений: если одно из заданных чисел есть в этой таблице, значит, оно делится только на единицу и само на себя. Разберем решение подобной задачи.
Условие: выясните, являются ли взаимно простыми числа 275 и 84.
Решение
Оба числа явно имеют больше одного делителя, поэтому сразу назвать их взаимно простыми мы не можем.
Вычисляем наибольший общий делитель, используя алгоритм Евклида: 275=84·3+23, 84=23·3+15, 23=15·1+8, 15=8·1+7, 8=7·1+1, 7=7·1.
Ответ: поскольку НОД (84, 275) =1, то данные числа будут взаимно простыми.
Как мы уже говорили раньше, определение таких чисел можно распространить и на случаи, когда у нас есть не два числа, а больше.
Взаимно простыми целые числа a1, a2, …, ak, k>2 будут тогда, когда они имеют наибольший общий делитель, равный 1.
Иными словами, если у нас есть набор некоторых чисел с наибольшим положительным делителем, большим 1, то все эти числа не являются по отношению друг к другу взаимно обратными.
Возьмем несколько примеров. Так, целые числа −99, 17 и −27 – взаимно простые. Любое количество простых чисел будет взаимно простым по отношению ко всем членам совокупности, как, например, в последовательности 2, 3, 11, 19, 151, 293 и 667. А вот числа 12, −9, 900 и −72 взаимно простыми не будут, потому что кроме единицы у них будет еще один положительный делитель, равный 3. То же самое относится к числам 17, 85 и 187: кроме единицы, их все можно разделить на 17.
Обычно взаимная простота чисел не является очевидной с первого взгляда, этот факт нуждается в доказательстве. Чтобы выяснить, будут ли некоторые числа взаимно простыми, нужно найти их наибольший общий делитель и сделать вывод на основании его сравнения с единицей.
Условие: определите, являются ли числа 331, 463 и 733 взаимно простыми.
Решение
Сверимся с таблицей простых чисел и определим, что все три этих числа в ней есть. Тогда их общим делителем может быть только единица.
Ответ: все эти числа будут взаимно простыми по отношению друг к другу.
Условие: приведите доказательство того, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.
Решение
Начнем с выявления их наибольшего общего делителя, после чего убедимся, что он не равен 1. Поскольку у отрицательных чисел те же делители, что и у соответствующих положительных, то НОД (−14, 105, 2 107, −91) =НОД (14, 105, 2 107, 91). Согласно правилам, которые мы привели в статье о нахождении наибольшего общего делителя, в данном случае НОД будет равен семи.
Ответ: семь больше единицы, значит, взаимно простыми эти числа не являются.
Основные свойства взаимно простых чисел
Такие числа имеют некоторые практически важные свойства. Перечислим их по порядку и докажем.
Если разделить целые числа a и b на число, соответствующее их наибольшему общему делителю, мы получим взаимно простые числа. Иначе говоря, a: НОД (a, b) и b: НОД (a, b) будут взаимно простыми.
Это свойство мы уже доказывали. Доказательство можно посмотреть в статье о свойствах наибольшего общего делителя. Благодаря ему мы можем определять пары взаимно простых чисел: достаточно лишь взять два любых целых числа и выполнить деление на НОД. В итоге мы должны получить взаимно простые числа.
Необходимым и достаточным условием взаимной простоты чисел a и b является существование таких целых чисел u0 и v0, при которых равенство a·u0+b·v0=1 будет верным.
Начнем с доказательства необходимости этого условия. Допустим, у нас есть два взаимно простых числа, обозначенных a и b. Тогда по определению этого понятия их наибольший общий делитель будет равен единице. Из свойств НОД нам известно, что для целых a и b существует соотношение Безу a·u0+b·v0=НОД (a, b). Из него получим, что a·u0+b·v0=1. После этого нам надо доказать достаточность условия. Пусть равенство a·u0+b·v0=1 будет верным, в таком случае, если НОД (a, b) делит и a, и b, то он будет делить и сумму a·u0+b·v0, и единицу соответственно (это можно утверждать, исходя из свойств делимости). А такое возможно только в том случае, если НОД (a, b)=1, что доказывает взаимную простоту a и b.
В самом деле, если a и b являются взаимно простыми, то согласно предыдущему свойству, будет верным равенство a·u0+b·v0=1. Умножаем обе его части на c и получаем, что a·c·u0+b·c·v0=c. Мы можем разделить первое слагаемое a·c·u0+b·c·v0 на b, потому что это возможно для a·c, и второе слагаемое также делится на b, ведь один из множителей у нас равен b. Из этого заключаем, что всю сумму можно разделить на b, а поскольку эта сумма равна c, то c можно разделить на b.
Если два целых числа a и b являются взаимно простыми, то НОД (a·c, b)=НОД (c, b).
Докажем, что НОД (a·c, b) будет делить НОД (c, b), а после этого – что НОД (c, b) делит НОД (a·c, b), что и будет доказательством верности равенства НОД (a·c, b)=НОД (c, b).
Поскольку НОД (a·c, b) делит и a·c и b, а НОД(a·c, b) делит b, то он также будет делить и b·c. Значит, НОД (a·c, b) делит и a·c и b·c, следовательно, в силу свойств НОД он делит и НОД (a·c, b·c), который будет равен c·НОД (a, b)=c. Следовательно, НОД (a·c, b) делит и b и c, следовательно, делит и НОД (c, b).
Также можно сказать, что поскольку НОД (c, b) делит и c, и b, то он будет делить и c, и a·c. Значит, НОД (c, b) делит и a·c и b, следовательно, делит и НОД (a·c, b).
Таким образом, НОД (a·c, b) и НОД (c, b) взаимно делят друг друга, значит, они являются равными.
Если числа из последовательности a1, a2, …, ak будут взаимно простыми по отношению к числам последовательности b1, b2, …, bm (при натуральных значениях k и m), то их произведения a1·a2·…·ak и b1·b2·…·bm также являются взаимно простыми, в частности, a1=a2=…=ak=a и b1=b2=…=bm=b, то ak и bm – взаимно простые.
Согласно предыдущему свойству, мы можем записать равенства следующего вида: НОД (a1·a2·…·ak, bm) =НОД (a2·…·ak, bm) =…=НОД (ak, bm) =1. Возможность последнего перехода обеспечивается тем, что ak и bm взаимно просты по условию. Значит, НОД (a1·a2·…·ak, bm) =1.
Обозначим a1·a2·…· ak=A и получим, что НОД (b1·b2·…· bm, a1·a2·…·ak) =НОД (b1·b2·…· bm, A)= НОД (b2·…·b·bm, A)=… =НОД (bm, A) =1. Это будет справедливым в силу последнего равенства из цепочки, построенной выше. Таким образом, у нас получилось равенство НОД (b1·b2·…·bm, a1·a2·…·ak) =1, с помощью которого можно доказать взаимную простоту произведений a1·a2·…·ak и b1·b2·…·bm
Это все свойства взаимно простых чисел, о которых бы мы хотели вам рассказать.
Понятие попарно простых чисел
Зная, что из себя представляют взаимно простые числа, мы можем сформулировать определение попарно простых чисел.
Попарно простые числа – это последовательность целых чисел a1, a2, …, ak, где каждое число будет взаимно простым по отношению к остальным.
Примером последовательности попарно простых чисел может быть 14, 9, 17, и −25. Здесь все пары (14 и 9, 14 и 17, 14 и −25, 9 и 17, 9 и −25, 17 и−25) взаимно просты. Отметим, что условие взаимной простоты является обязательным для попарно простых чисел, но взаимно простые числа будут попарно простыми далеко не во всех случаях. Например, в последовательности 8, 16, 5 и 15 числа не являются таковыми, поскольку 8 и 16 не будут взаимно простыми.
Также следует остановиться на понятии совокупности некоторого количества простых чисел. Они всегда будут и взаимно, и попарно простыми. Примером может быть последовательность 71, 443, 857, 991. В случае с простыми числами понятия взаимной и попарной простоты будут совпадать.
Калькулятор взаимно простых чисел
Онлайн калькулятор определит являются ли число взаимно простыми, путем нахождения наибольшего общего делителя чисел.
Для определения взаимно простых чисел необходимо указать количество и ввести числа.
Нажмите кнопку рассчитать и калькулятор укажет как определить взаимно простые числа.
Определение взаимно простых чисел
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Ниже описано как определить являются ли числа 35 и 40 взаимно простыми.
- 1 Находим наибольший общий делитель чисел: НОД(35, 40)=5.
- 2 Наибольший общий делитель ≠ 1 следовательно числа не взаимно простые.
Пример Определить являются ли 77 и 20 взаимно простыми числами

Примеры взаимно простых чисел
Рассмотрим на примере как определить взаимно простые числа.
Пример Являются ли числа 42 и 55 взаимно простыми

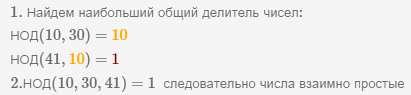
Определим что 3 числа 10, 30, 41 являются взаимно простыми.
Пример Проверить что числа 10, 30, 41 взаимно просты
Смотрите также
Другие страницы
Какие числа называют взаимно простыми
Содержание:
- Что значит взаимно простые числа
- Свойства и признаки
- Как доказать, что числа взаимно простые
- Таблица взаимно простых чисел
- Задачи
Что значит взаимно простые числа
В окружающем нас мире и на уроках в школе люди постоянно оперируют различными числами. С их помощью выражают значения физических параметров, соотносят какие-либо величины между собой, дают характеристику объектам и явлениям. К примеру, уровень знаний ученика определяют путем выставления балла по заранее заданной шкале. Подобные способы оценки применяют повсеместно.
Ярким примером применения числовой шкалы является проведение различных социальных или маркетинговых опросов. Без чисел сложно представить жизнь и науку. При этом используют не только ряд о единицы до десятки, но и различные виды значений. В зависимости от характера решаемых задач подбирают тот или иной формат представления характеристик, данных, информации.
В числе областей хозяйственной деятельности, которые не обходятся без исчислений, присутствует индустрия информационных технологий, в частности, написание программного кода. В математике существуют множества чисел. При решении задач можно встретить величины, которые имеют целые или дробные значения, или, к примеру, являются иррациональными.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если в перечисленных понятиях необходимо разбираться, то с простыми числами вопросов, как правило, не возникает. Однако термин не распространяется на все числа, с которыми человек сталкивается в повседневной жизни, ожидая трамвай нужного маршрута, проверяя таймер или баланс денежного счета. С целью исключить путаницу и подмену понятий лучше в первую очередь начать с терминологии.
Простое число представляет собой такое число, которое можно нацело поделить на единицу или на само себя.
В качестве типичного примера простого числа допустимо записать 13. Дело в том, что данное число является простым, а доказать это совершенно не сложно. Если проанализировать значение, то можно заметить возможность деления 13 на 1 или на 13. При поиске результата от частного 13 и других чисел получим результат с остатком. Из примера становится понятно, что простых чисел довольно мало, так как превалирующая часть числового множества делится на прочие числа нацело.
Важно помнить об отсутствии остатка в результате подобного деления. Когда со свойствами простого числа все стало понятнее, можно приступить к рассмотрению вопроса о взаимно простых числах. Данное определение распространяется не только на пары чисел, но и на большее количество подобных значений. Приведем ниже расшифровку термина.
Пара чисел а и b из множества целых являются взаимно простыми при равенстве их максимального общего делителя единице, то есть НОД (a, b) = 1.
Исходя из вышесказанного, стоит отметить, что взаимно простыми числами допустимо называть те, которые обладают единственным общим делителем со значением, равным единице. Подобная формулировка не менее важна, чем основная расшифровка термина, так как в распространенных случаях позволяет оперативно идентифицировать простейшие числовые значение в числовых последовательностях и совокупностях.
Свойства и признаки
Резюмируем, что при отсутствии каких-либо общих максимальных делителей у чисел, кроме единицы, такие числа допустимо считать взаимно простыми. Важно запомнить этот признак и уметь оперировать им в процессе решения задач. Однако задания на взаимно простые числа не всегда обладают очевидным способом поиска ответа.
Нередко встречаются примеры, где расчеты стоит начать со сложных математических преобразований для привидения чисел в нужных формат, который позволит выполнить сравнение или сделать вывод о том, что они взаимно простые. При этом можно упростить вычисления с помощью свойств, которыми обладают данные числа. Перечислим основные из них:
- Числа из множества натуральных, которые являются взаимно простыми с некоторым натуральным числом n, допустимо задать с помощью функции Эйлера (varphi (n).)
- Числа a и b идентифицированы как взаимно простые лишь при существовании целых х и у с условием, что ax+by=1 (соотношение Безу).
- При наличии взаимно простых чисел а и b допустимо говорить о том, что взаимно просты следующие числа (2^{a}-1 и 2^{b}-1). Данное утверждение верно и в обратную сторону.
- При наличии а в роли делителя умножения bc, являющегося взаимно простым числом для b, допустимо говорить о том, что а является делителем с.
- При условии, что d= НОД (a,b) числа (frac {a}{d} и frac {b}{d}) являются взаимно простыми.
- Дробь не представляется возможным сократить при наличии в числителе и знаменателе взаимно простых чисел.
- Когда имеется пара взаимно простых чисел а и m, сравнение (axequiv b{pmod {m}}) для любого b обладает лишь одним решением по модулю m.
- В том случае, когда пара целых чисел a и b определена как взаимно простые, справедливо следующее равенство: НОД (a⋅c, b)=НОД (c, b).
Как доказать, что числа взаимно простые
Когда в совокупности произвольная пара чисел является взаимно простой, подобные числа допустимо считать попарно взаимно простыми.
Стоит отметить, что применительно к большему количеству чисел важно помнить о взаимной простоте попарно простых чисел. Обратное утверждение уже будет неверным. В математике нередко встречаются задания на доказательство попарной и взаимной простоты каких-либо чисел. В процессе решения таких задач целесообразно использовать признаки и свойства, которые были изучены в теоретическом курсе ранее. Существуют еще важные условия, с помощью которых достаточно просто подтвердить или опровергнуть принадлежность заданных чисел к той или иной категории.
Когда числа (a_1, ldots), (a_n) являются попарно простыми, их минимальное общее кратное соответствует абсолютной величине произведения рассматриваемых чисел: (|a_{1}cdot ldots cdot a_{n}|;)
Кроме того, для произвольного b из множества целых чисел справедливо следующее математическое соотношение:
(НОД (a_{1}cdot a_{2}ldots a_{n},b)= НОД (a_{1},b) НОД(a_{2},b) … НОД(a_{n},b),)
где НОД обозначает максимальный общий делитель для рассматриваемых чисел.
Таблица взаимно простых чисел
Упростить работу с взаимно простыми числами поможет табличная форма, изображенная ниже. Подобный инструмент полезен при решении задач, когда требуется выполнить разнообразные вычисления, сравнить простые числа, доказать их взаимную или попарную простоту. Пользоваться таблицей несложно. В любой из клеток расположен максимальный общий делитель ее координат, и соответствующие взаимно простым парам координат единицы выделены темным.
Источник: ru.wikipedia.org
Задачи
Полученные знания и ценную информацию можно применять на практике. Попробуем справиться с решением нескольких типичных примеров. В процессе необходимо руководствоваться стандартным алгоритмом действий. На первом шаге полезно внимательно прочитать условия задания. После того, как сформировано представление о том, какой ответ требуется получить, можно приступать к разработке плана действий. Как правило, первоначальный анализ на возможность применения признаков, свойств или табличных значений существенно упрощает дальнейшие расчеты. В связи с этим, озвученным пунктом нельзя пренебрегать. Рассмотрим основные приемы для работы с простыми числами.
Задача 1
Имеется пара чисел 84 и 275. Необходимо подтвердить тот факт, что указанные числа взаимно простые.
Решение
В данном случае целесообразно воспользоваться табличной формой. Заметим, что в таблице указанные в условии задачи числа отсутствуют. По этой причине нужно обратиться к следующему методу доказательства, а именно, вычисления максимального общего делителя. Рассчитать искомое значение несложно с применением правила Евклида. Выполним пошаговые действия:
(275 = 84 cdot 3 + 23)
(84 = 23 cdot 3 + 15)
(23 = 15 cdot 1 + 8)
(15 = 8 cdot 1 + 7)
(8 = 7 cdot 1 + 1)
(7 = 7 cdot 1)
В результате получим, что максимальный общий делитель для пары чисел, состоящей из 84 и 275, обладает значением, равным единице. Таким образом, выполнено условие, характерное для взаимной простоты пары чисел.
Ответ: подтверждено, что 84 и 275 представляют собой пару взаимно простых чисел.
Задача 2
Дано несколько чисел: 331, 463, 733. Необходимо выяснить, допустимо ли считать перечисленные числа взаимно простыми.
Решение
Согласно информации, предоставленной в таблице простых чисел, 331, 463 и 733 представляют собой простые числа. Это позволяет сделать вывод о наличии для рассматриваемой тройки чисел лишь одного общего делителя со знаком плюс. Таким делителем является 1. В результате при выполнении перечисленных условий допустимо говорить о взаимной простоте исследуемых чисел.
Ответ: 331, 463, 733 относятся к категории взаимно простых чисел.
Задача 3
Требуется подтвердить, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.
Решение
Вычислим для рассматриваемых числовых пар максимальный общий делитель, значение которого не должно совпадать с 1. С помощью свойства делителей для отрицательных и положительных чисел сформулируем следующее равенство:
НОД (−14, 105, 2 107, −91) = НОД (14, 105, 2 107, 91)
Выполним дальнейшие вычисления:
НОД (14, 105, 2 107, 91) = 7
Ответ: представленные в условии задания числа не являются взаимно простыми, так как их общий делитель отличен от единицы.
Таким образом, путем несложных вычислений и действенных приемов удалось справиться с тремя задачами. Заметим, что решение типовых примеров достаточно компактны и не занимают много времени. Это связано с корректным составлением алгоритма действий и умением применять свойства и табличные значения, характерные для простейших чисел, в практических условиях.
- Простые множители
- Разложение на множители онлайн
- Взаимно простые числа
- Проверка онлайн на взаимно простые числа
Взаимно простые числа
Разберемся, что такое взаимно простые числа. Это такие числа, которые не имеют общих делителей, кроме 1 или -1. Можно сформулировать и по другому. У взаимно простых чисел наибольший общий делитель (НОД) равен единице.
Например, числа 5 и 4 – взаимно простые, потому что число 5 имеет делители 1 и 5, а делители четверки: 1, 2 и 4. Общий делитель у них – это единица, а значит, они взаимно просты.
По второму определению: наибольший общий делитель чисел 5 и 4 равен 1, НОД(5,4) = 1, а значит они взаимно простые.
Взаимно простые числа от 1 до 100
Приведем примеры взаимно простых чисел.
2 и 99,
15 и 16,
28 и 57,
29 и 31,
12 и 1,
59 и 97 и т. д.
Чтобы образовывать взаимно простые числа, должно быть, по крайней мере, два числа.
Как проверить, являются ли взаимно простыми числа
По определению взаимно простых чисел, если числа имеют 1 или -1 в качестве единственного общего множителя, то такие числа будут взаимно простыми.
Решим примеры.
Являются ли взаимно простыми числа:
35 и 40
Решение:
Раскладываем оба числа на простые множители.
Множители первого числа: 35 = 5 х 7.
Множители второго числа: 40 = 2 х 2 х 2 х 5.
Общий множитель данных чисел равен 5. Следовательно, 35 и 40 не являются взаимно простыми.
77 и 20
Решение:
Множители первого числа: 77= 7 х 11.
Множители второго числа: 20 = 2 х 2 х 5.
НОД чисел 77 и 20 равен единице, а значит эти числа будут взаимно простыми.
231 и 280
Решение:
При разложении обоих чисел на множители получаем:
231 = 3 х 7 х 11.
280 = 2 х 2 х 2 х 5 х 7.
Наибольший общий делитель этих чисел равен 7, а значит они не взаимно простые.
Свойства взаимно простых чисел
Свойство 1: Число 1 взаимно простое с каждым числом.
Свойство 2: Все простые числа взаимно просты между собой.
Поскольку каждое простое число имеет только два делителя: 1 и само число, единственным общим делителем двух простых чисел будет 1. Например, 11 и 17 – это два простых числа. Множители 11 равны 1, 11, а делители 17 равны 1, 17. Единственный общий делитель равен 1 и, следовательно, они взаимно просты.
Свойство 3: Любые два последовательных числа всегда взаимно просты.
Рассмотрим любые два последовательных числа, например, 2 и 3, 3 и 4 или 14 и 15. У всех этих чисел общий делитель – это единица.
Свойство 4: Сумма любых двух взаимно простых чисел всегда взаимно проста с их произведением.
2 и 3 взаимно просты. Их сумма равна 5 (2+3), а произведение – 6 (2х3). Следовательно, числа 5 и 6 взаимно просты.
Решение примеров.
Являются ли взаимно простыми числа 21 и 24
21 и 24 не являются взаимно простыми числами, потому что имеют множитель равный 3. ( 21 = 3 х 7, 24 = 2 х 2 х 2 х 3).
Являются ли взаимно простыми числа 13 и 11
13 и 11 взаимно простые числа, потому что это простые числа (свойство 2).
Являются ли взаимно простыми числа 17 и 18
17 и 18 взаимно простые числа, потому что это два последовательных числа (свойство 3).
В чем разница между простыми и взаимно простыми числами?
Простое число определяется как число, которое не имеет множителя, кроме 1 и самого себя.
Но взаимно простые числа считаются парами, и два числа взаимно просты, если их общий делитель равен только 1. Их НОД равен единице.
Таким образом, взаимно простые числа – это обязательно 2 или более чисел. Составные числа также могут быть взаимно простыми.
Пример
Числа 25 и 26 – это составные числа (25 = 5 х 5, 26 = 2 х 13). Но они взаимно просты, т.к. это последовательные числа (свойство 3).