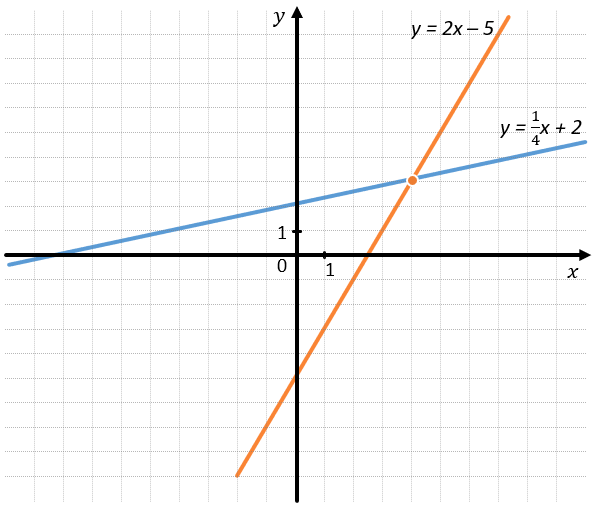1) Найти точку пересечения прямых:
y=2,5−0,5x
и
y=−5x−2
.
Для построения графика каждой линейной функции составим таблицу значений.
Для функции
y=2,5−0,5x
имеем:
| (x) | (0) | (5) |
| (y) | (2,5) | (0) |
Через полученные точки проведём прямую
l1
.
Для функции
y=−5x−2
имеем:
| (x) | (0) | (-0,4) |
| (y) | (-2) | (0) |
Через полученные точки проведём прямую
l2
.

Прямые
l1
и
l2
пересекаются в точке (А(-1;3)).
2) Определить, в какой точке пересекаются прямые:
y=2x−3
и
y=2x+1
.
Угловые коэффициенты линейных функций одинаковые (k=2), то есть прямые
y=2x−3
и
y=2x+1
параллельные, они не пересекаются.
3) Определить, в какой точке пересекаются прямые:
y=3x+11
и
y=−x+11
.
Угловые коэффициенты данных линейных функций различны:
k1=3
и
k2=−1
— прямые пересекаются в одной точке.
Можно заметить, что обе прямые проходят через точку ((0; 11)).
Значит, точка ((0;11)) и есть точка пересечения данных
прямых.
Графики
двух линейных функций представляют собой прямые, которые либо пересекаются,
либо параллельны.
ПРИМЕР:
Даны графики функций, заданных формулами:
у =
0,9х – 1,
у =
0,8х + 1
с различными коэффициентами при х.

Выясним, пересекаются ли эти графики.
Пересечение графиков означает, что они имеют общую точку. В этом случае
найдётся такое значение х, которому соответствует одно и то же значение у для
обеих функций. Чтобы найти это значение х,
надо решить уравнение
0,9х – 1 = 0,8х + 1.
Имеем:
0,9х – 0,8х = 1 + 1,
0,1х = 2,
х =
20.
При х = 20 обе
функции
у =
0,9х – 1,
у =
0,8х + 1
принимают одно и то же значение,
равное 17. Точка
(20; 17) принадлежит как одному, так и другому
графику. Такая точка только одна. Значит, прямые, являющиеся графиками функций
у =
0,9х – 1,
у =
0,8х + 1
пересекаются.
ПРИМЕР:
Даны графики функций, заданных формулами:
у =
0,5х + 1,
у =
0,5х – 2
с одинаковыми коэффициентами при х.

Чтобы выяснить, пересекаются ли графики
этих функций, надо решить уравнение
0,5х + 4 = 0,5х – 2.
Так как это уравнение не имеет корней, то
прямые, которые являются графиками функций
у =
0,5х + 1,
у =
0,5х – 2
Не имеют общих точек, т. е. они
параллельны.
Графики двух
линейных функций, заданных формулами вида
y = аx + b,
пересекаются,
если коэффициенты при х различны, и параллельны, если коэффициенты
при х одинаковы.
На
рисунке изображены прямые, которые являются графиками линейных функций,
заданных формулами вида
y = аx + b,
с
одинаковыми коэффициентами при х и различными
значениями b.

Все эти прямые параллельны и наклонены к оси х под одним и тем же углом. Этот угол зависит
от коэффициента а. Число а называют угловым
коэффициентом прямой – графика функции
y = аx + b,
используя термин угловой
коэффициент прямой, доказанное выше свойство можно
сформулировать так:
– если угловые
коэффициенты прямых, являющихся графиками двух линейных функций, различны, то
эти прямые пересекаются, а если угловые коэффициенты одинаковы, то прямые
параллельны.
Из формулы
y = аx + b,
Следует, что при х
= 0 значение
у равно b. Значит, график функции
y = аx + b пересекает ось у в точке с
координатами (0; b). На рисунке
изображены прямые, которые являются графиками функций, заданных формулами
вида y = аx + b с различными а и одним и тем же
значением b.
Все эти прямые пересекаются в одной точке, лежащей на оси у.

Задания к уроку 21
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Координатная плоскость
- Урок 2. Диаграммы
- Урок 3. Графики
- Урок 4. Множества
- Урок 5. Что такое функция ?
- Урок 6. Аналитический способ задания функции
- Урок 7. Табличный способ задания функции
- Урок 8. Графический способ задания функции
- Урок 9. Нахождение области определения и области значения функции аналитическим методом
- Урок 10. Нахождение области определения и области значения функции с помощью графика
- Урок 11. Нули функции
- Урок 12. Возрастание и убывание функции
- Урок 13. Экстремальные значения функции
- Урок 14. Симметричные функции
- Урок 15. Чётные и нечётные функции
- Урок 16. Функция, обратная данной
- Урок 17. Линейная функция
- Урок 18. График линейной функции
- Урок 19. Прямая пропорциональность
- Урок 20. График прямой пропорциональности
- Урок 22. Обратно пропорциональная зависимость
- Урок 23. График обратно пропорциональной зависимости
- Урок 24. Квадратичная функция
- Урок 25. График функции у = aх2 + b
- Урок 26. График функции у = a(х – m)2 + n
- Урок 27. График функции у = aх2 + bx + c
- Урок 28. Функция y = √͞͞͞͞͞х и её график
- Урок 29. Функция y = хn и её график
- Урок 30. Построение графиков функций методом геометрических преобразований
Взаимное расположение графиков линейной функции
График линейной функции представляет собой прямую. Если на одной координатной прямой существуют две прямые, то они, как и любые прямые на плоскости, могут пересекаться, быть параллельными друг другу или совпадать.
Рассмотрим две линейные функции:
(y = k_{1}x + b_{1 }) и (y = k_{2}x + b_{2})
И их возможные расположения на одной координатной плоскости.
СОВПАДЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций совпадают при:
(k_{1} = k_{2})
(b_{1} = b_{2})
Например:
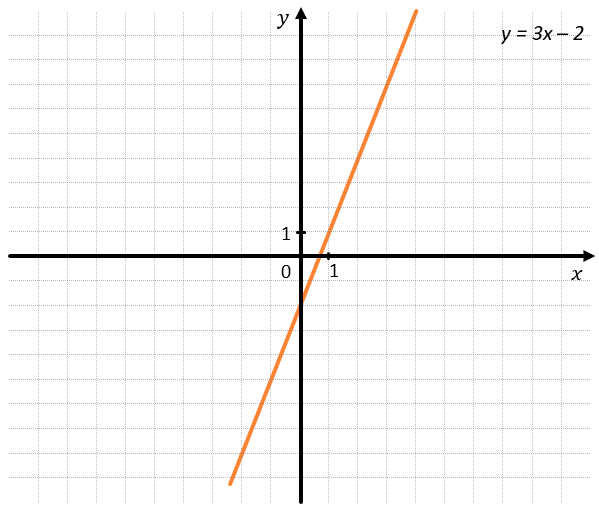
Графики функций (y = 3x–2) и (y = 3x–2) совпадают, так как
(k_{1} = k_{2} = 3 ) и ( b_{1} = b_{2} = –2)
ПАРАЛЛЕЛЬНОСТЬ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций параллельны при:
(k_{1} = k_{2})
(b_{1} neq b_{2})
Например:
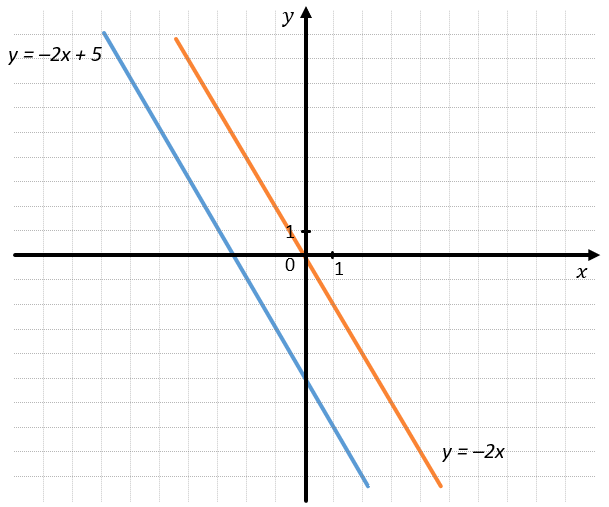
Графики функций (y = –2x) и (y = –2x + 5) параллельны, так как
(k_{1} = k_{2} = –2)
(b_{1} = 0; b_{2} = 5 Longrightarrow b_{1} neq b_{2} )
ПЕРЕСЕЧЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций пересекаются при:
(k_{1} neq k_{2} ) и ( b_{1} neq b_{2})
Например:
Графики функций (y = 2x–5) и( y = frac{1}{4}x + 2) пересекаются, так как
(k_{1} = 2, k_{2} = frac{1}{4} Longrightarrow k_{1} neq k_{2})
(и)
(b_{1} = –5, b_{2} = 2 Longrightarrow b_{1} neq b_{2})
При этом по определению пересекающихся прямых, они должны иметь одну общую точку. Эта будет такая точка с координатами ((x; y)), которая будет принадлежать как первому, так и второму графику функций.
То есть для функций:
(y_{1} = k_{1}x_{1} + b_{1})
(y_{2} = k_{2}x_{2} + b_{2})
Будут соблюдаться условия:
(k_{1} neq k_{2} ) и ( b_{1} neq b_{2})
Поэтому будет существовать точка пересечения этих графиков с координатами:
(x = x_{1} = x_{2})
(y = y_{1} = y_{2})
В таком случае, чтобы найти точку пересечения графиков функций без построения для функций (mathbf{y}_{mathbf{1}} = k_{1}x = b_{1}) нужно:
1. Приравнять (y_{1} и y_{2},) а значит приравнять( k_{1}x_{1} + b_{1} и k_{2}x_{2} + b_{2}.)
2. Так как (x_{1} = x_{2} = x), решим уравнение
(k_{1}x + b_{1} = k_{2}x + b_{2}.)
3. Подставить найденный аргумент в любую из функций и найти её значение y. Найденная пара (x; y) будет являться координатой общей точки для данных графиков функций.
Рассмотрим данный алгоритм на примере функций, заданных на графике выше.
Пример №1:
Найти без построений точку пересечения для графиков
(y = 2x – 5 ) и ( y = frac{1}{4}x + 2)
1. Игреки данных функций равны, следовательно:
(2x – 5 = frac{1}{4}x + 2)
2. Иксы в данном уравнении равны, значит можем решить уравнение:
(frac{7}{4}x = 7)
(x = 4)
3. Подставим x = 4 в первое уравнение, получим:
(y = 2x – 5)
(y = 2 bullet 4 – 5)
(y = 3)
Следовательно, точкой пересечения данных графиков является точка с координатами ((4;3)), что и подтверждает наш график выше.
ЧАСТНЫЙ СЛУЧАЙ ПЕРЕСЕЧЕНИЯ ЛИНЕЙНЫХ ФУНКЦИЙ
Графики линейных функций пересекаются под прямым углом, если
(k_{1} bullet k_{2} = –1)
(k_{1} = –frac{1}{k_{2}})
Например:
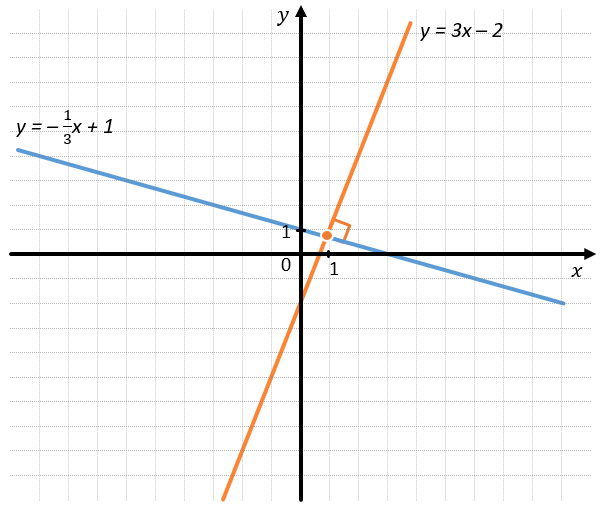
Графики функций (y = 3x–2) и (y = –frac{1}{3}x + 1) перпендикулярны друг дугу, так как
(k_{1} bullet k_{2} = 3 bullet (–frac{1}{3}) = –1)
§ 1 Взаимное расположение графиков линейных функций
Из курса геометрии мы знаем, что 2 прямые на плоскости могут совпадать, т.е. иметь бесконечно много общих точек; пересекаться, т.е. иметь одну общую точку или не пересекаться, т. е. не иметь ни одной общей точки. Такие прямые называются параллельными.
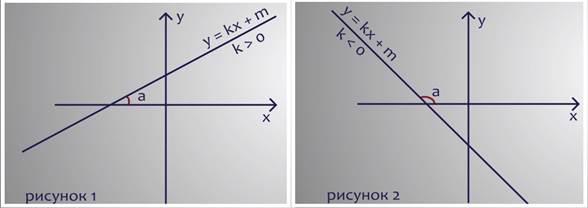
Линейная функция задаётся равенством вида у = kх + m. Коэффициент k называют угловым коэффициентом. Он «отвечает» за угол наклона прямой относительно положительного направления оси х. Если k > 0, то угол наклона острый (как на рисунке 1), если k < 0, то угол наклона тупой (как на рисунке 2).
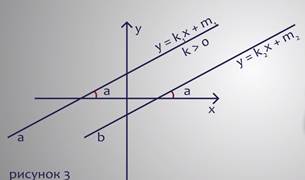
А теперь посмотрим на рисунок 3. На нём изображены 2 прямые, заданные уравнениями у = k1 + m1 и у = k2 + m2. Предположим, что k1 = k2. Это означает, что углы наклона прямой одинаковы. Это соответственные углы, а значит данные нам прямые параллельны по признаку параллельных прямых.
Таким образом, если 2 линейные функции имеют одинаковый угловой коэффициент, то их графики будут параллельны. Если же угловые коэффициенты не равны, то графики будут пересекаться.
Например, даны линейные функции, заданные формулами у = 2х – 1 и у = 2х + 3. Как будут располагаться на плоскости их графики по отношению друг к другу? Так как угловой коэффициент первой функции k1 = 2 и угловой коэффициент второй функции k2 = 2, то графики будут параллельны.
Или другая пара: у = х – 3 и у = 2х + 3. У первой функции коэффициент k1 = 1, а у второй функции коэффициент k2 = 2. Это неравные коэффициенты, поэтому графики этих функций будут пересекаться. А в каком же случае прямые будут совпадать?
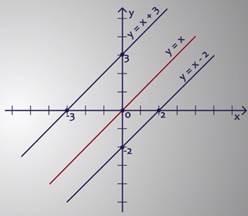
Для ответа надо сначала ответить на другой вопрос: а за что «отвечает» коэффициент m? Давайте посмотрим на рисунок, на котором изображены графики трёх функций:
у = х, у = х + 3 и у = х – 2.
У всех трёх функций угловой коэффициент k= 1, т. е. графики параллельны. Но обратите внимание: график функции у = х проходит через начало координат, здесь m = 0. График функции у = х + 3 получен сдвигом графика у = х на 3 единицы вверх, как показывает коэффициент m = 3.
График функции у = х – 2 получен сдвигом графика у = х на 2 единицы вниз, как показывает коэффициент m = –2. Иначе говоря, коэффициент m отвечает за параллельный перенос графика у = kх относительно начала координат на m единиц вдоль оси у.
Теперь можно ответить на поставленный вопрос. 2 прямые будут совпадать, если у них одинаковые угловые коэффициенты и коэффициент m1равен коэффициенту m2.
§ 2 Краткие итоги по теме урока
Графики линейных функций по отношению друг к другу на плоскости могут быть параллельны, если угловые коэффициенты k1 и k2 равны, а коэффициенты m1 и m2 различны. Могут пересекаться в случае, когда угловые коэффициенты k1 и k2 не равны. А также могут совпадать, если угловые коэффициенты k1 и k2 равны и коэффициенты m1 и m2 так же равны. График функции у = kх проходит через начало координат, т. к. коэффициент m = 0, а график функции у = kх + m проходит через точку (0; m).
Вопросы
занятия:
· рассмотреть угловой коэффициент линейной
функции;
· выяснить, как зависит взаимное расположение
графиков функций от значений угловых коэффициентов.
Материал
урока
На
прошлом уроке мы познакомились с линейной функцией:
На
этом уроке мы выясним, как зависит расположение графиков линейных функции от
значений коэффициентов k
и
b.
Рассмотрим
функции и построим их графики:
У
рассматриваемых функций коэффициенты k
равны,
а коэффициенты b
не
равны.
Все
прямые по построению параллельны, а также они наклонены к оси икс под
одинаковым углом. Этот угол зависит от значения числа k,
которое называют угловым коэффициентом графика линейной функции.
Давайте
построим графики функций:
У
данных функций угловые коэффициенты различны. При этом у первой функции
коэффициент k
отрицателен
и график этой функции образует с осью икс тупой угол. А у второй функции
угловой коэффициент положителен и график образует с осью икс острый угол.
Обратите
внимание, что в отличие от предыдущего примера, где угловые коэффициенты равны
и прямые параллельны, здесь графики функций пересекаются.
Таким
образом, можем сделать вывод.
Если
угловые коэффициенты прямых, являющихся графиками двух линейных функций,
различны, то эти прямые пересекаются, а если угловые коэффициенты одинаковы, то
прямые параллельны.
В
системе координат, в которой мы с вами строили графики функций, в качестве
координатных осей берутся прямые, которые перпендикулярны друг к другу, поэтому
её называют прямоугольной.
Такая
система координат была введена знаменитым французским учёным Рене Декартом. И в
его честь её так же называют декартовой.