Как найти взаимную тройку векторов

Как найти взаимную тройку векторов

Взаимный базис

~

1. Доказать, что для произвольных векторов ~a, b, ~c выполняется тождество

~

~

~

2

:

(1)

([b; ~c]; [~c; ~a]; [~a; b]) = (~a;

b; ~c)

Решение. Обозначим левую часть доказываемого тождества через L. По определению

~

~

смешанного произведения L = ([[b; ~c]; [~c; ~a]]; [~a; b]). Тогда по формуле двойного векторного

произведения

~

~

~

L = (~c([b; ~c]; ~a) ~a([b; ~c]; ~c); [~a; b]):

По свойствам скалярного и смешанного произведений

~

~

~

~

~

~

~

~

2

:

L = (~c(b; ~c; ~a) b(b; ~c; ~c); [~a; b]) = (b; ~c; ~a)(~c; [~a; b]) = (b; ~c; ~a)(~a; b; ~c) = (~a; b; ~c)

Пусть ~e1, ~e2, ~e3 тройка векторов. Рассмотрим такие векторы ~e1, ~e2, ~e3, что (~ei;

~ej) = ij,

где

ij

– символ

Кронекера: ij

= 1; если i = j и ij = 0; если i = j:

1

, ~e

2

, ~e

3

через векторы ~e1, ~e2

, ~e3

6

2. Выразить векторы ~e

и наоборот, выразить векторы ~e1,

~e2, ~e3 через векторы ~e1, ~e2, ~e3.

Решение. Пусть векторы ~e1; ~e2; ~e3 компланарны. Тогда, например, ~e3 = ~e1 + ~e2 и 1 =

(~e3;~e3) = (~e1; ~e3) + (~e2; ~e3) = 0: Противоречие. Значит, векторы ~e1; ~e2; ~e3 не компланарны.

Аналогично векторы ~e1; ~e2; ~e3

не компланарны. Из условий (~e1; ~e2) = (~e1;

~e3) = 0 вытекает,

что ~e1 можно записать в виде ~e1 = [~e2; ~e3]. Коэффициент находится из условия (~e1; ~e1) = 1 однозначно: = (~e1; ~e2; ~e3) 1. Аналогично находятся векторы ~e2 и ~e3 и обратно. Итак,

~e1 =

[~e2; ~e3]

;

~e2 =

[~e3; ~e1]

;

~e3 =

[~e1; ~e2]

;

(2)

(~e1; ~e2; ~e3)

(~e1; ~e2; ~e3)

(~e1; ~e2; ~e3)

~e1

=

[~e2; ~e3]

;

~e2

=

[~e3; ~e1]

;

~e3

=

[~e1; ~e2]

:

(2 b)

(~e1; ~e2; ~e3)

(~e1; ~e2; ~e3)

(~e1; ~e2; ~e3)

3. Доказать, что векторы ~e1, ~e2, ~e3, если их определить равенствами (2), некомпланарны. Решение. Достаточно показать, что смешанное произведение векторов ~e1, ~e2, ~e3 отлично

от 0. По формуле (2) и линейности смешанного произведения по всем аргументам имеем

(~e1; ~e2; ~e3) = (~e1; ~e2; ~e3) 3([~e2; ~e3]; [~e3; ~e1]; [~e1; ~e2]):

Откуда по (1) получаем, что

(~e1; ~e2; ~e3) =

1

:

(3)

(~e1

; ~e2; ~e3)

Определение. Базис e =< ~e1; ~e2; ~e3 > называется взаимным с базисом e =< ~e1; ~e2; ~e3 >

или биортогональным к базису e =< ~e1; ~e2; ~e3 >.

Замечание. 1) Из задач 2 и 3 и определения взаимного базиса вытекает, что взаимный базис определен однозначно.

2)Если исходный базис положителен, то взаимный с ним базис также положителен. Если исходный базис отрицателен, то взаимный с ним базис тоже отрицателен.

3)Если базис e является взаимным к исходному базису e, то взаимный базис к e совпадает с исходным базисом e, т.е. базис, взаимный к взаимному базису есть исходный базис.

4)Если исходный базис ортонормированный, то взаимный базис совпадает с исходным базисом.

5)Если исходный базис совпадает со взаимным, то исходный базис ортонормированный. Вопрос: Какова размерность векторов взаимного базиса e, если векторы базиса e измеря-

ются в сантиметрах?

4. Доказать, что для любого вектора ~a выполнено:

~a = (a; ~e1)~e1 + (a; ~e2)~e2 + (a; ~e3)~e3;

(4)

~a = (a; ~e1)~e1 + (a; ~e2)~e2 + (a; ~e3)~e3:

(5)

Решение. Чтобы доказать (4), умножим равенство ~a = ~e1 + ~e2 + ~e3 скалярно сначала на ~e1, затем на ~e2 и на ~e3. Мы получим = (a; ~e1), = (a; ~e2), = (a; ~e3). Равенство (5) вытекает из (4) и того, что базисы e и e взаимны друг другу.

Замечание. Числа ; ; называются контравариантными координатами вектора ~a в базисе < ~e1; ~e2;~e3 >, а числа (~a; ~e1); (~a; ~e2); (~a; ~e3) называются ковариантными координатами вектора ~a в базисе < ~e1; ~e2; ~e3 >. Таким образом равенства (4) и (5) означает, что ковариантные координаты вектора есть его контравариантные координаты во взаимном базисе и наоборот, контравариантные координаты вектора есть его ковариантные координаты во взаимном базисе. Эти равенства также доказывают, что ковариантные координаты вектора действительно координаты: они взаимно-однозначно соответствуют вектору, складываются при сложении векторов и умножаются на число при умножении вектора на это число.

~

~

Следствие. Если векторы ~a, b, ~c некомпланарны, то любой вектор d единственным образом

представим в виде

~

~

d = x~a + yb + z~c:

В координатной форме (относительно некоторого базиса) это равенство запишется в виде системы линейных уравнений Ax = d с основной невырожденной матрицей A, столбцами кото-

рой являются координатные столбцы , ~, и столбцом свободных членов координатным

~a b ~c d

~

столбцом вектора d. Из формулы (4) и представления (2) векторов взаимной тройки вытекает,

что решение системы Ax = d может быть найдено по формуле (формула Крамера)

~ ~

~

~ ~

x =

(d; b; ~c)

;

y =

(~a; d; ~c)

;

z =

(~a; b; d)

:

~

~

~

(~a; b; ~c)

(~a; b; ~c)

(~a;

b; ~c)

(~x; ~a)

(~x;

~

(~x; ~c)

b)

5. Доказать, что (~a; ~b; ~c)(~x; ~y; ~z) =

(~z; ~a)

(~z;

~b)

(~z; ~c)

:

(~y; ~a)

(~y;

~b)

(~y; ~c)

~

Решение. Если (~a; b; ~c) = 0, то тождество

очевидно: левая

часть равна 0 и правая часть

равна 0, т.к. у определителя один из столбцов является линейной комбинацией остальных.

~

Пусть теперь (~a; b; ~c) 6= 0. Рассмотрим выражение

R = (~y; ~a)

(~y; ~b)

(~y; ~c) (~a; ~b; ~c) 1:

(~x; ~a)

~

(~x; ~c)

(~x; b)

(~z; ~a)

(~z; ~b)

(~z; ~c)

По формуле (3) R можно переписать

в виде

R = (~y; ~a)

(~y; ~b)

(~y; ~c) (~a ; ~b ; ~c );

(~x; ~a)

~

(~x; ~c)

(~x; b)

(~z; ~a)

(~z; ~b)

(~z; ~c)

где ~ взаимная тройка с ~ . По (5) в определителе из по строкам стоят коор-

~a ; b ; ~c ~a; b; ~c R

~

динаты векторов ~x; ~y; ~z в базисе < ~a ; b ; ~c >. То есть R представляет собой координатную

~

запись смешанного произведения (~x; ~y; ~z) в базисе < ~a ; b ; ~c >, что доказывает тождество.

~

Следствие. Объем параллелепипеда, построенного на векторах ~a; b; ~c

v

V = u

(~a; ~a)

~

(~a; ~c)

(~a; b)

:

(6)

(~b; ~a)

(~b; ~b)

(~b; ~c)

u

(~c; ~a)

~

(~c; ~c)

(~c; b)

u

u

t

~

~

6. Решить систему: (~x;~a) = p; (~x; b) = q; (~x;~c) = r; если (~a; b;~c) 6= 0:

2

Решение. Согласно (5) имеем:

~

~

x =

p[b;~c] + q[~c;~a] + r[~a; b]

:

~

(~a; b;~c)

~

~

~

~

7. Пусть ~a = [b;~c];

b = [~c;~a];

~c = [~a; b]: Найти ~a;

b; ~c:

~

~

2

~

Решение. Из задачи (1) вытекает, что (~a; b;~c) = (~a; b;~c)

: Тогда если (~a; b;~c) = 1; то вза-

~

~

> ортонормирован-

имный к < ~a; b;~c > базис совпадает с исходным. Значит базис < ~a; b;~c

~

ный. Кроме того, он положительный (правый). Если же (~a; b;~c) = 0; то все векторы нулевые:

~

~

так как векторы компланарны, то, например, ~a = b + ~c: Тогда (~a;~a) = (~a; b) + (~a;~c) =

~

~

~

~

~

(~a;~c;~a) + (~a;~a; b) = 0: Значит j~aj = 0; значит ~a = 0: Аналогично b = 0 и ~c = 0:

Скалярное, векторное и смешанное произведения в аффинной системе координат

Определение. Метрическими коэффициентами базиса e =< ~e1; ~e2; ~e3 > называются следующие скалярные произведения:

gij = (ei; ej):

Матрицу G = (gij), составленную из этих произведений, называют матрицей Грама. Часто еe обозначают : Отметим, что gij = gji для всех i; j: Значит = T :

1

2

3

~

1

; y

2

; y

3

) заданы координатами относительно базиса e, то

Если векторы ~a(x

; x

; x

) и b(y

их скалярное произведение вычисляется по формуле:

3

3

y1

i

j

1

2

3

2

(~a; ~b) =

=1 j=1

gijx

x

= (x

; x

; x

)G

0y31

:

@y A

Xi

X

~

~

; y2; y3) во вза-

1

2

3

)

1. Найти скалярное произведение (~a; b), если ~a(x

; x

; x

в базисе e, а b(y1

имном базисе e.

Решение. Используя билинейность скалярного произведения и определение взаимного базиса, имеем:

XX

~

i

~ei;

yj~e

j

1

2

3

y3:

(~a; b) =

x

= x

y1 + x

y2 + x

2. Зная матрицу Грама G = (gij) базиса e, найти объем V параллелепипеда, построенного на векторах с координатами (x1; x2; x3), (y1; y2; y3) и (z1; z2; z3).

Решение. Из геометрического смысла смешанного произведения, заключаем, что V с точностью до знака равен

x1 x2 x3

y1 y2 y3 (~e1; ~e2; ~e3):

z1 z2 z3

p

Из (6) получаем, что с точностью до знака (~e1; ~e2; ~e3) = det G: Окончательно

V = pdet G det

0y1

y2

y3

1:

x1

x2

x3

@

A

z1

z2

z3

Замечание.

1

1

(~e1; ~e2; ~e3) =

=

p

:

(~e1; ~e2; ~e3)

det G

~

~

~ ~

~ ~

3. Доказать формулу: ([~a; b]; [~c; d]) = (~a; ~c)(b; d)

(~a; d)(b; ~c):

~

~

~

~

~

~

~

Решение. ([~a; b]; [~c; d]) =

(~a; b; [~c; d])

= (b; [~c; d];~a) =

(b; [[~c;

~

~ ~

~ ~

~

~

~

~

~

(b;~c(~a; d) d(~a;~c)) = (b; d(~a;~c) ~c(~a; d)) = (~a; ~c)(b; d)

(~a; d)(b; ~c):

~

~

~

d];~a])

= (b; [~a; [~c; d]]) =

3

4. Выразить координаты векторного произведения ~ через координаты сомножителей

[~a; b]

1 2 3 и ~ 1 2 3 и метрические коэффициенты базиса, считая базис положительным

~a( ; ; ) b( ; ; )

(правым).

Решение. Мы имеем:

[~a;~b] =

1

2

3

(e~1; e~2; e~3) = (~a; e~1) (~a; e~2)

(~a; e~3)

(~e1; ~e2;~e3) =

~e

1

~e

2

~e

3

~e1

~e2

~e3

1

2

3

~

~

~

(b; e~1) (b; e~2) (b; e~3)

~e1

~e2

~e3

=

1

(~a; e~1)

(~a; e~2)

(~a; e~3)

:

pdet G

~

~

~

(b; e~1)

(b; e~2)

(b; e~3)

Отсюда, подставляя вместо и ~ базисные векторы, можно, в частности, найти

~a b

[~e1; ~e2] =

1

g11

g12

g13 ;

pdet G

~e1

~e2

~e3

g

g

g

21

22

23

[~e2; ~e3] =

1

g21

g22

g23 ;

pdet G

~e1

~e2

~e3

g

g

g

31

32

33

[~e1; ~e3] =

~e1

~e2

~e3

:

pdet G g11

g12

g13

1

g

g

g

31

32

33

Решение вторым способом. В силу билинейности векторного произведения, достаточно выразить через метрические коэффициенты координаты векторов [~e1; ~e2], [~e2; ~e3] и [~e1; ~e3].

Пусть [~e1; ~e2] = 1~e1 + 2~e3 + 1~e3: Найдем первую координату 1. По формуле (4) и выражению (2) векторов взаимного базиса через векторы ~e1; ~e2; ~e3, имеем:

1 = ([~e1; ~e2]; ~e1) = (~e1; ~e2; ~e3) 1([~e1; ~e2]; [~e2; ~e3]):

Теперь воспользуемся формулой

~ ~ ~ ~ ~ ~ ([~a; b]; [~c; d]) = (~a; ~c)(b; d) (~a; d)(b; ~c);

откуда получаем выражение для 1:

(~e1; ~e2) (~e1; ~e3)

1 =

(~e1

; ~e2; ~e3)

= pdet G

g22

g23

:

(~e2

; ~e2) (~e2; ~e3)

1

g12

g13

Аналогично находятся координаты 2 и 3:

;

2

= pdet G

g21

g23

3 = pdet G g21

g22

:

1

g11

g13

1

g11

g12

Итак,

1

g11

g12

[~e1; ~e2] =

g13

:

pdet G

~e1

~e2

~e3

g

g

g

21

22

23

Аналогично находим, что

[~e2; ~e3] =

1

g21

g22

g23 ;

pdet G

~e1

~e2

~e3

g

g

g

31

32

33

[~e1; ~e3] =

~e1

~e2

~e3

:

pdet G g11

g12

g13

1

g

g

g

31

32

33

4

Источник

Тройкой векторов называются
три вектора, если указано, какой из них считается
первым, какой вторым и какой третьим. Тройку
векторов записывают в порядке нумерации;
например, запись
,
,

означает, что вектор
считается
первым,
– вторым,

 – третьим.

Тройка некомпланарных векторов

,
,
 называется правой, если
составляющие ее векторы, будучи приведены к
общему началу, располагаются в порядке нумерации
аналогично тому, как расположены большой,
указательный и средний пальцы правой руки. Если
векторы
,
,
 расположены
аналогично тому, как расположены большой,
указательный и средний пальцы левой руки, то
тройка этих векторов называется левой.

Смешанным произведенем трех векторов

,
,
 называется число, равное
векторному произведению
, умноженному
скалярно на вектор
, то есть

.

Имеет место тождество, ввиду чего для
обозначения смешанного произведения

употребляется более простой символ
.
Таким образом,



,
.

Смешанное произведение

равно объему параллелепипеда, построенного на
векторах
,
,
, взятого со
знаком плюс, если тройка
правая, и со
знаком минус, если эта тройка левая. Если векторы
,
,
 компланарны (и только в этом
случае), смешанное произведение
равно нулю; иначе
говоря, равенство



есть необходимое и достаточное
условие компланарности векторов
,
,
.

Если векторы
,
,

заданы своими координатами:



,
,
,

то смешанное произведение

определяется формулой



.

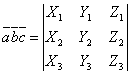
Напомним, что система координатных
осей предполагется правой (вместе с тем является
правой и тройка векторов
,
,
).

Источник

Макеты страниц

Пусть — базис в евклидовом пространстве Базис называется взаимным для базиса если выполняются соотношения

при

Символ называется символом Кронекера.

Возникает вопрос о существовании и единственности взаимного базиса. Ответ на этот вопрос утвердительный: для любого данного базиса существует единственный взаимный

базис. Для доказательства поступим следующим образом. Пусть координаты искомых векторов в базисе

Умножая скалярно обе части последних равенств на получим, используя (8.2),

Соотношения (8.4) при фиксированном можно рассматривать как квадратную систему линейных уравнений относительно неизвестных координат вектора в базисе Так как определитель системы (8.4) представляет собой определитель Грама базисных векторов он, согласно следствию из теоремы 8.1, отличен от нуля, и поэтому система (8.4) имеет единственное решение которое будет ненулевым, поскольку эта система неоднородная. Затем с помощью соотношений (8.3) строятся векторы которые, очевидно, удовлетворяют соотношениям (8.2).

Мы должны еще убедиться, что векторы образуют базис

Пусть некоторая линейная комбинация этих векторов равна нулю

Умножая скалярно последнее равенство последовательно на и используя (8.2), получим Следовательно, векторы линейно независимы, т. е. образуют базис.

Итак, взаимный базис и для базиса существует и определяется единственным образом.

Замечание 1. В силу симметрии соотношений (8.2) относительно взаимным базисом для базиса будет базис Поэтому в дальнейшем мы будем говорить о взаимных базисах

Замечание 2. Если базис ортонормированный, то взаимный базис совпадает с данным базисом. Действительно, полагая в этом случае мы убедимся, что соотношения (8.2) выполняются. Используя свойство единственности взаимного базиса, мы убедимся в справедливости замечания.

Пусть — взаимные базисы, произвольный вектор пространства. Разлагая вектор х по базисным векторам получим

Координаты вектора х в базисе называются ковариантными кооординатами вектора х, а а координаты этого вектора в базисе называются контравариантными координатами вектора х. Эти наименования будут разъяснены в следующем пункте.

Для сокращения записи формул, в которых фигурируют однотипные слагаемые (примерами таких формул могут служить соотношения (8.5)), мы будем пользоваться в дальнейшем соглашением о суммировании. Это соглашение заключается в следующем. Пусть имеется выражение, составленное из сомножителей, которые снабжены конечным числом индексов, часть из которых нижние, а другая часть — верхние. При этом договариваются все нижние индексы обозначать различными символами Верхние индексы также договариваются обозначать различными символами. Если в этом выражении встречаются два одинаковых индекса, из которых один верхний, а другой нижний, то считают, что по этим индексам производится суммирование, т. е. индексам последовательно даются значения а затем складываются полученные слагаемые.

Например,

С помощью соглашения о суммировании формулы (8.5) записываются следующим компактным образом:

Замечание 3. Верхние и нижние одинаковые индексы, о которых говорилось в соглашении о суммировании, обычно называются индексами суммирования. Ясно, что индексы суммирования могут обозначаться любыми одинаковыми символами. При этом не изменится выражение, в которых они фигурируют. Например, представляют собой одно и то же выражение.

Получим теперь явное выражение для ковариантных и контравариантных координат вектора х.

Для этого умножим скалярно первое из равенств (8.6) на , а второе на . Учитывая затем соотношения (8.2), найдем

Итак,

С помощью соотношений (8.7) запишем формулы (8.6) в следующем виде:

Соотношения (8.8) называются формулами Гиббса.

Обратимся еще раз к вопросу о построении взаимных базисов.

С помощью формул (8.8) имеем

Введем обозначения

С помощью этих обозначений перепишем соотношения (8.9) следующим образом:

Итак, для построения базиса по базису достаточно знать матрицу а для построения базиса по базису достаточно знать матрицу

Докажем, что указанные матрицы взаимно обратны Отметим, что так как элементы обратной матрицы могут быть вычислены через элементы данной матрицы, то ясно, что с помощью соотношений (8.11) решается вопрос о построении взаимных базисов

Итак, установим, что матрицы взаимно обратны.

Умножая первое из равенств (8.11) скалярно на получим Из этого соотношения, учитывая (8.2) и (8.10), найдем

Таким образом, произведение матриц представляет собой единичную матрицу Следовательно, матрицы взаимно обратны.

Источник

Добавить комментарий