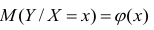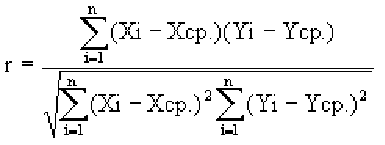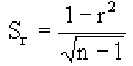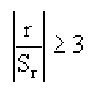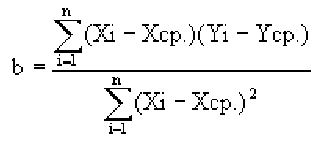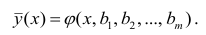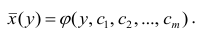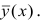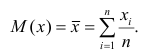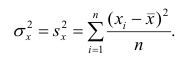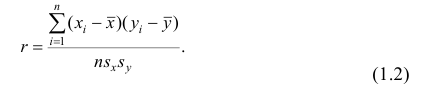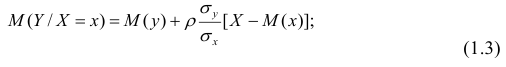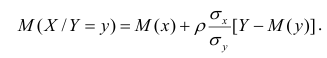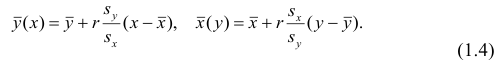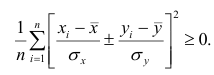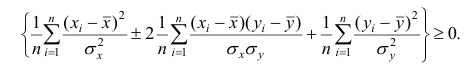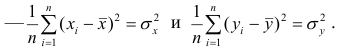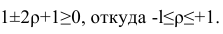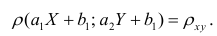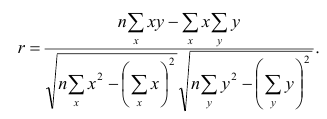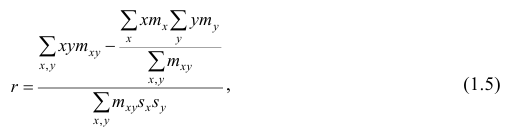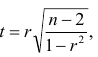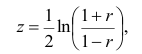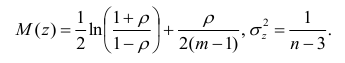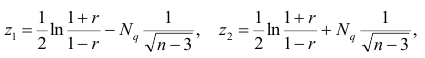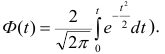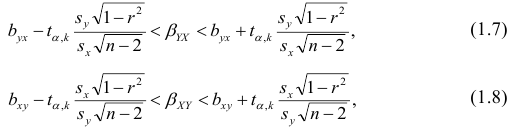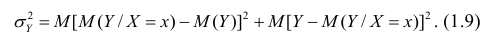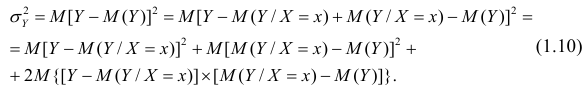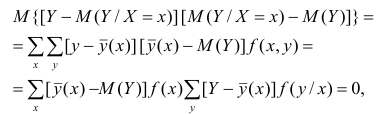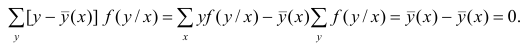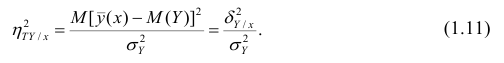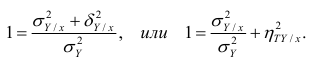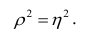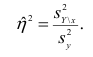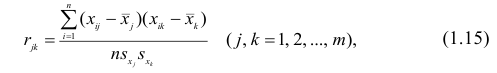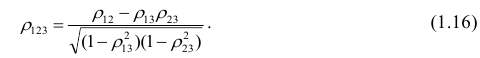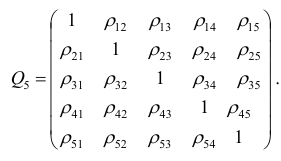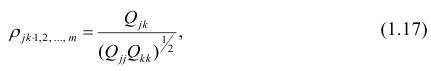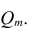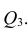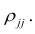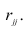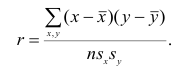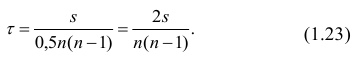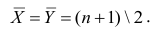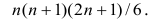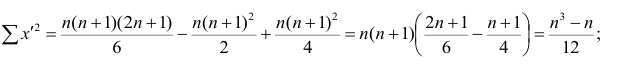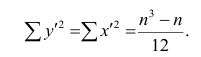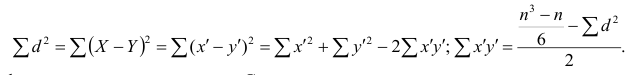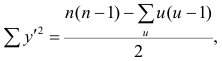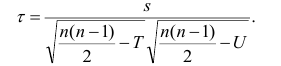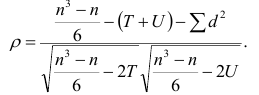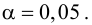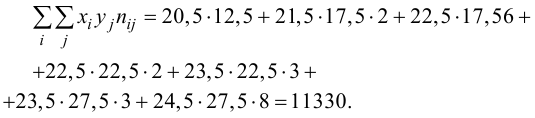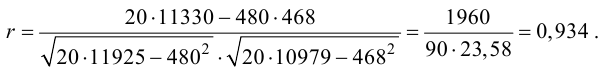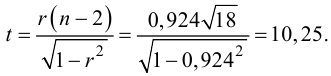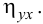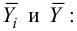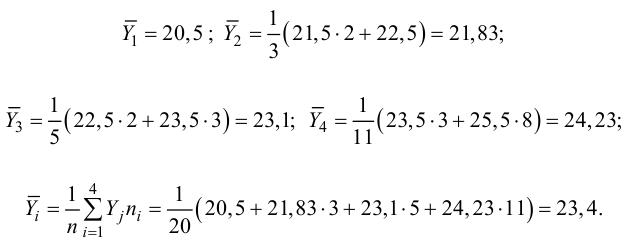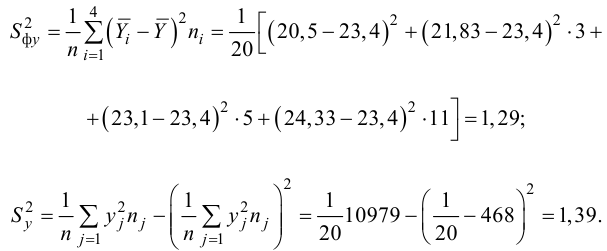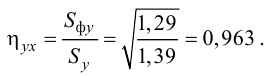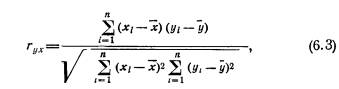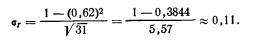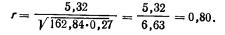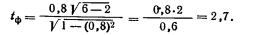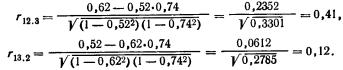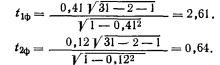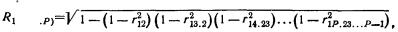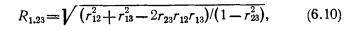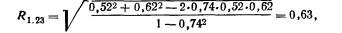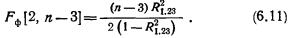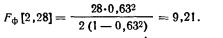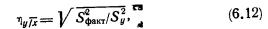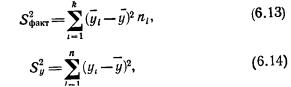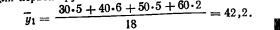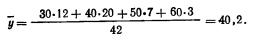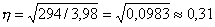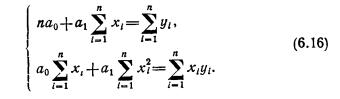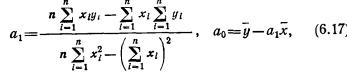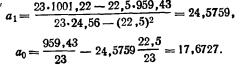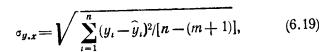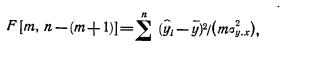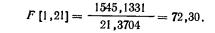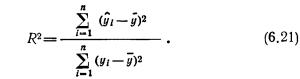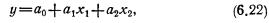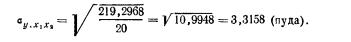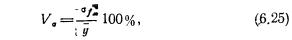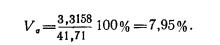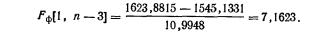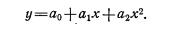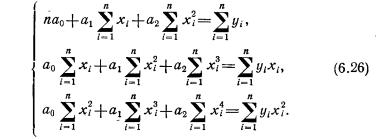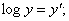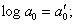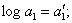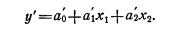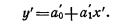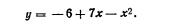Статистическое изучение взаимосвязей
1. Виды взаимосвязей и понятие
корреляционной зависимости
2. Методы выявления корреляционной
связи
3. Однофакторный корреляционно-регрессионный
анализ
4. Многофакторный корреляционно-регрессионный
анализ
5. Непараметрические показатели связи
1. Виды взаимосвязей и понятие
корреляционной зависимости
Все статистические показатели находятся
между собой в определённых связях и
соотношениях.
Задача статистического исследования
состоит в том, чтобы определить характер
данной взаимосвязи.
Существуют следующие виды взаимосвязей:
1. Факторные. В этом случае связи
проявляются в согласованной вариации
различных признаков у одной и той же
совокупности. При этом один из признаков
выступает как фактор, а другой – как
следствие. Изучение этих связей
производится методом группировок, а
также теорией корреляции.
2. Компонентные. К данному виду
относятся такие взаимосвязи, при которых
изменение какого-то сложного явления
целиком определяется изменением
компонентов, входящих в это сложное
явление как множители (X=x·f). Для
этого применяется индексный метод.
Например, с помощью системы взаимосвязанных
индексов узнают, как изменился товарооборот
за счёт изменения количества проданных
товаров и цен.
3. Балансовые. Применяются при анализе
связей и пропорций в образовании ресурсов
и их распределении. Баланс
представляет систему показателей,
которая состоит их двух сумм абсолютных
величин, связанных между собой знаком
равенства,
а + б = в + г.
Например, баланс материальных ресурсов:
остаток + поступление = расход
+ остаток
начальный конечный
Признаки (показатели) при изучении
взаимосвязей делятся на 2 вида:
Признаки, обуславливающие изменение
других, называютфакторными, или
простофакторами.
Признаки, изменяющиеся под действием
факторных признаков, являютсярезультативными.
Различают 2 вида взаимосвязей:
функциональныеистохастические.
Функциональнойназывают такую
связь, при которой определенному значению
факторного признака соответствует
только одно значение результативного
признака.
Если причинная зависимость проявляется
не в каждом случае, а в общем, среднем
при большом числе наблюдений, то такая
связь называется стохастической.
Частным случаем стохастической связи
является корреляционная связь, при
которой изменение среднего значения
результативного признака обусловлено
изменением факторного.
Особенности стохастических
(корреляционных) связей:
– обнаруживаются не в единичных случаях,
а в общем и среднем при большом числе
наблюдений;
–
неполные, они учитывают не все действующие
факторы, а только существенные;
– необратимы. Например, функциональную
связь можно превратить в
другую функциональную связь
. Если мы говорим, что урожайность
сельхозпродукции зависит от количества
внесенных удобрений, то обратное
утверждение лишено смысла.
По направлению выделяют связьпрямуюиобратную. Припрямой связи с
увеличением факторного признака
происходит увеличение результативного.
В случаеобратной связи с увеличением
факторного признака происходит уменьшение
результативного.
По аналитическому выражению выделяют
связилинейные (прямолинейные)инелинейные (криволинейные). Если
связь между явлениями выражена уравнением
прямой линии, то оналинейная. Если
связь выражена уравнением кривой линии
(параболы, гиперболы, степенной,
показательной и т.п.), то онанелинейная.
По количеству факторов, действующих
на результативный признак, различают
связиоднофакторныеимногофакторные.
Если один признак-фактор и результативный
признак, то связь – однофакторная
(парная регрессия). Если признаков-факторов
2 и более, то связь многофакторная
(множественная регрессия).
Связи различают еще по степени тесноты
связи (см. таблицу Чэддока).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Корреляционный анализ:
Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).
В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е.
Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.
Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Введение в корреляционный анализ
Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).
В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.
Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.
Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.
Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.
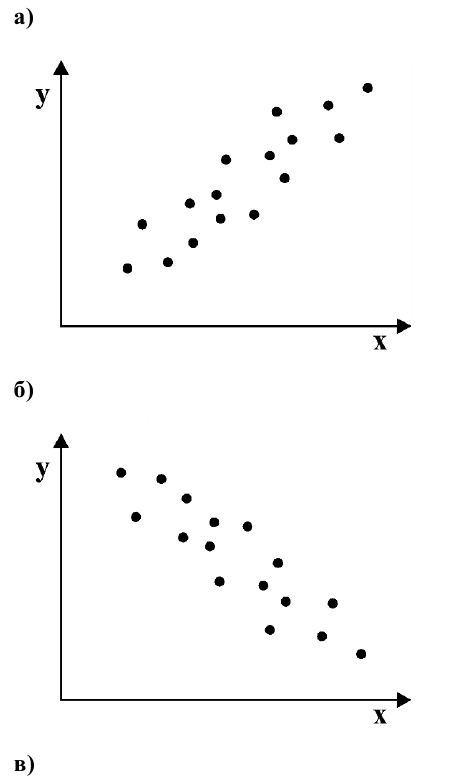
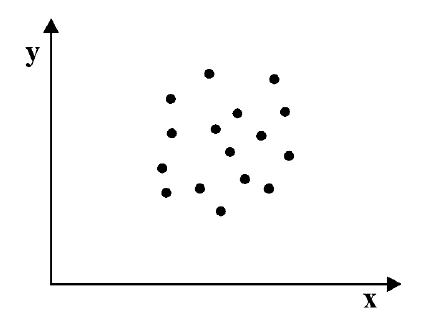
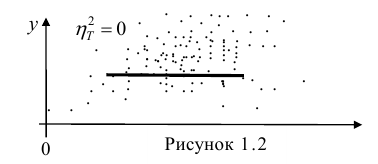
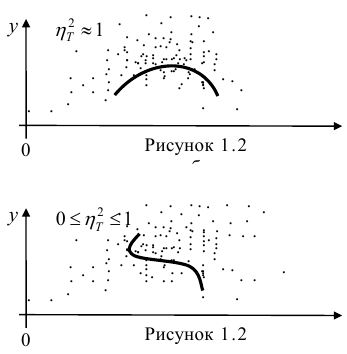
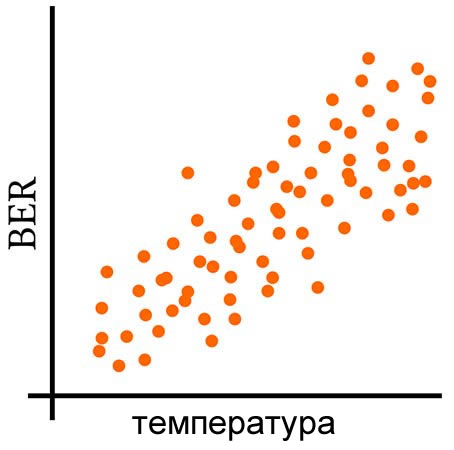
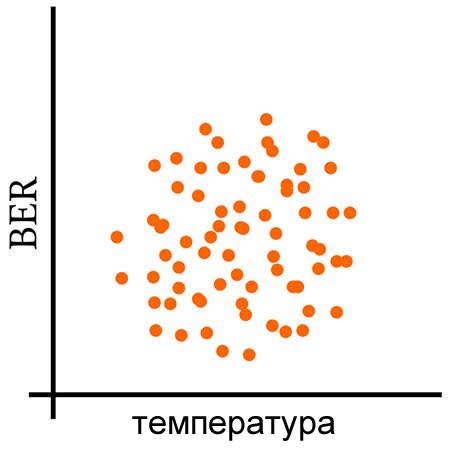
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину 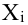
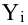
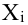
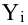
Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) – корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика – это случай в).
С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.
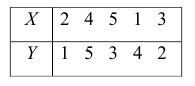
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: 
Коэффициент r мы считаем в Excel, с помощью функции 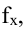
Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.
Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% – другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.
Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь – случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку:
Связь нельзя считать случайной, если:
В то время как задача корреляционного анализа – установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа – описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии 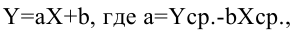
Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y – нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.
Определение формы связи. Понятие регрессии
Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).
Условное математическое ожидание 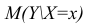
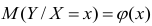
функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание
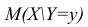
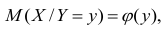
На примере, дискретного распределения найдём функцию регрессии.
Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.
Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек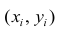
Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.
Аналогично определяется кривая регрессии X по Y (X на Y):
Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.
Возникает вопрос: почему для определения кривой регрессии
используют именно условное среднее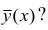
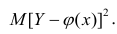
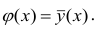
Если рассеивание вычисляется относительно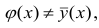
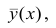
Основные положения корреляционного анализа
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.
Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.
Предпосылки корреляционного анализа следующие:
- 1) переменные величины должны быть случайными;
- 2) случайные величины должны иметь совместное нормальное распределение.
Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
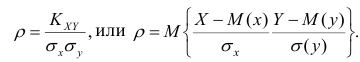
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 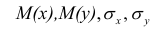
математического ожидания является среднее арифметическое, т.е.
Оценкой дисперсии служит выборочная дисперсия, т.е.
Тогда выборочный коэффициент корреляции
Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.
При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:
функция регрессии X на Y — следующий вид:
Выражения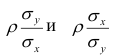
Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 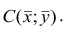
Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.
Свойства коэффициента корреляции
Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.
Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).
Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:
Возведём выражение под знаком суммы в квадрат:
Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что
Таким образом, окончательно получаем
Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных 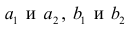
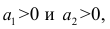
Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.
Если коэффициент корреляции 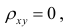
Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле
Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой
где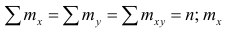
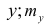
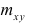
Из формулы (1.2) очевидно, что 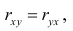
Поле корреляции. Вычисление оценок параметров двумерной модели
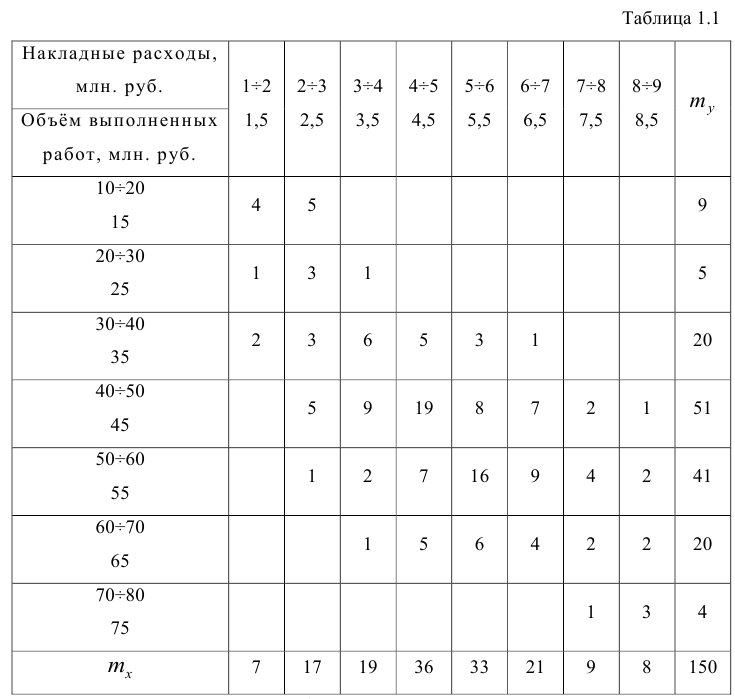
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 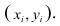
Пару случайных чисел 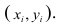
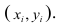
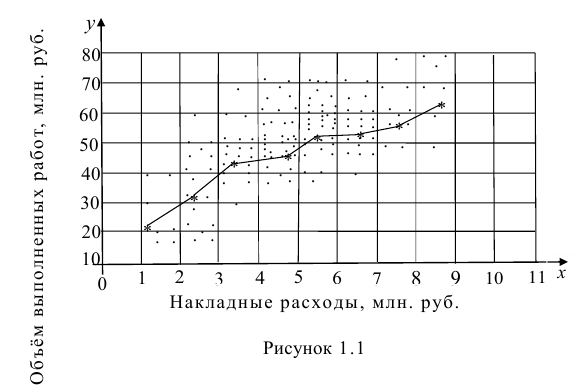
По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
Если вычислить средние значения у в каждом интервале изменения х [обозначим их 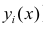
Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. Эти частоты обозначают 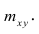
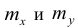
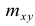
Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.
Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:
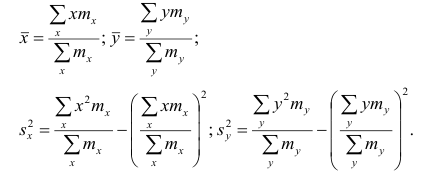
Проверка гипотезы о значимости коэффициента корреляции
На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.
Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 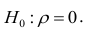
которая имеет распределение Стьюдента с k=n-2
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение 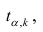
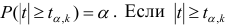
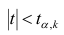
В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:
где r=thz — гиперболический тангенс от z.
Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами
В этом, случае доверительный интервал для римеетвид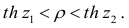
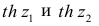
где 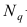
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:
где 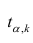
Корреляционное отношение
На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это 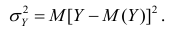
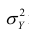
Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 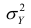
Первое слагаемое обозначим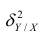
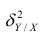
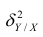
Покажем, что 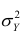
Для простоты полагаем распределение дискретным. Имеем
так как при любом х справедливо равенство
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии 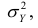
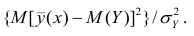
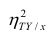
Разделив обе части равенства (1.9) на 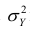
Из последней формулы имеем
Поскольку 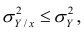
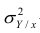
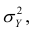
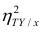
Все сделанные выводы справедливы и для 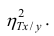
следует, что 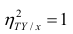
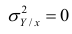
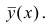
Далее, из равенства (1.12) следует, что 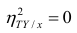
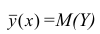
Аналогичными свойствами обладает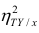
Часто используют величину
Считают, что она не может быть отрицательной. Значения величины 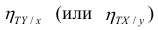
Значения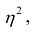
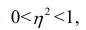
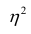
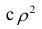
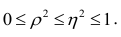
Разность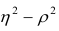
При вычислении 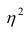
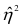
Понятие о многомерном корреляционном анализе
Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.
Пусть имеется многомерная нормальная совокупность с m признаками 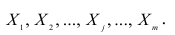
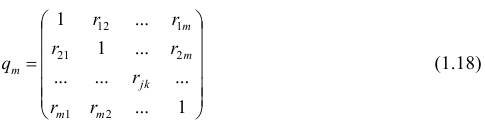
можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):
где 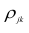
Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид
где 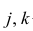
Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.
В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между 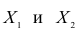
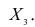
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 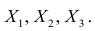
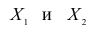
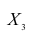
корреляции и имеет вид
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при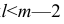
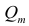
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид
Для определения частного коэффициента корреляции второго порядка, например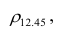
вычеркнув из исходной матрицы 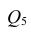
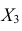
В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде
где 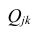
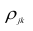
матрицы 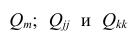
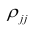
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу
Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:
Формула выборочного частного коэффициента корреляции имеет вид
где 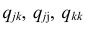
Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 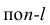
Множественный коэффициент корреляции
Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции
где 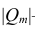
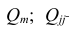
дополнение к элементу
Квадрат коэффициента множественной корреляции 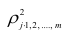
множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 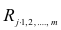
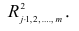
где 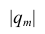
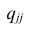
Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.
Ранговая корреляция
В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.
Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции
Пусть 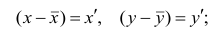
что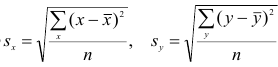
В зависимости от того, что принять за меру различия между величинами 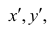
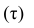
Введём следующую меру различия между объектами: будем считать 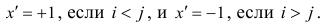
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как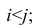
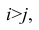
Рассмотрим формулу ( 1 .22). В нашем случае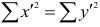
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е.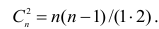
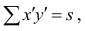
Теперь рассмотрим другую меру различия между объектами. Если обозначить через 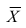
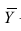
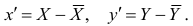
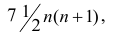
Тогда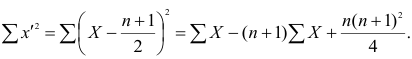
чисел натурального ряда равна
Тогда
Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину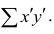
Коэффициент корреляции рангов Спирмэна
У коэффициентов 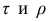
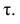
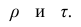
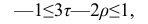
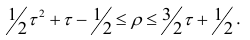
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём: одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму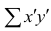
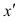
Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. Формулы коэффициентов корреляции для 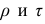
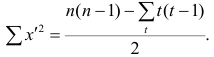
где t и u—число связанных пар в последовательностях.
Обозначая 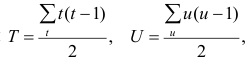
Аналогично находим выражение для р. Только в этом случае
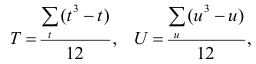
последовательностях, а
Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.
Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации
где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.
Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.
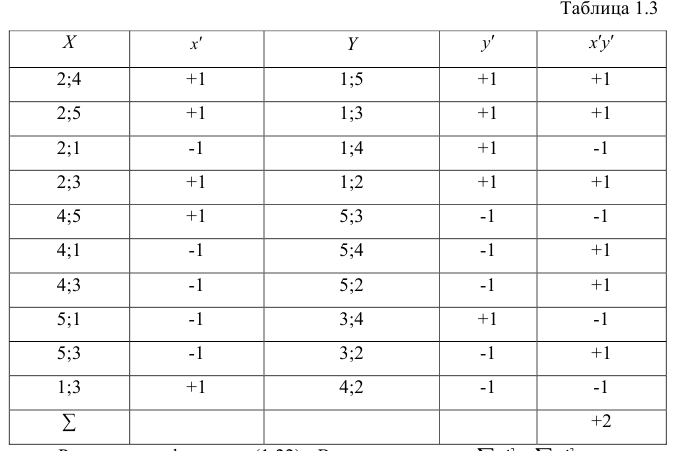
Пример:
Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне
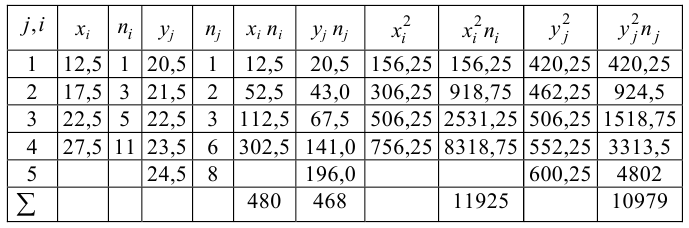
Решение. Для вычислений составим таблицу. Находим суммы
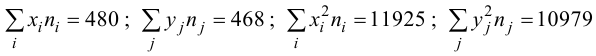
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции
Проверим значимость 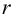
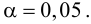
По таблице распределения П6 Стьюдента 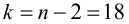
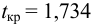
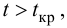
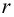
Пример:
Для данных табл. 13 найти корреляционное отношение
Для вычисления эмпирического корреляционного отношения найдем групповые средние
Тогда
Вычисляем корреляционное отношение
- Статистические решающие функции
- Случайные процессы
- Выборочный метод
- Статистическая проверка гипотез
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Проверка статистических гипотез
- Регрессионный анализ
Поиск статистических взаимосвязей: корреляция, причинно-следственная связь и ковариация
Добавлено 22 сентября 2020 в 22:54
В данной статье объясняется статистическая мера, которая помогает нам делать выводы о том, как одна переменная влияет на другую.
В этой серии статей, посвященной статистике в электротехнике, приводятся высокоуровневые определения и примеры статистических концепций, которые можно применять в процессе проектирования. Ознакомиться со статьями серии вы можете в меню с оглавлением выше, над статьей.
Корреляция и причинно-следственная связь
Допустим, у нас есть система беспроводной связи, которая доставляет нам проблемы. Частота битовых ошибок (BER) резко меняется от одного полевого теста к другому, и очевидной причины такого нестабильного поведения нет. Что еще хуже, полевые испытания даже не близки к контролируемым экспериментам, и существует довольно много факторов (тепловые и атмосферные условия, вибрация, радиочастотные помехи, электромагнитные помехи от ближайшего оборудования, ориентация, относительная скорость), которые могут влиять на производительность системы.
Один из способов справиться с этой ситуацией – выбрать факторы, которые с наибольшей вероятностью будут сильно влиять на BER, собрать данные и найти причинно-следственные связи. Поскольку доказать причинно-следственную связь часто очень сложно, наш анализ на самом деле даст количественную оценку корреляции, а затем мы можем либо предположить, что корреляция указывает на причинную связь (что рискованно), либо попытаться продемонстрировать причинность путем сбора новых данных из тщательно спланированного эксперимента.
Таким образом, поиск причинно-следственной связи начинается с поиска корреляции, а корреляция начинается с ковариации.
Переменные, которые изменяются вместе
Описательная статистическая мера, называемая дисперсией, обсуждалась в одной из предыдущих статей, которая также охватывает стандартное отклонение. Дисперсия (обозначается σ2) – это усредненная мощность (выраженная в единицах мощности) случайных отклонений в наборе данных. Мы рассчитываем дисперсию следующим образом:
[sigma^2=frac{1}{N-1}sum_{i=1}^{N}(X_i-mu)^2]
где N – количество значений в наборе данных (т.е. размер выборки), а μ – среднее значение.
Допустим, мы начинаем наше исследование с того, что отправим систему на несколько полевых испытаний и сохраним множество упорядоченных пар, состоящих из значений температуры окружающей среды и BER. Например, мы могли бы вычислить средний BER за пять минут работы, а затем связать эти данные со средней температурой за тот же интервал. Затем мы повторяем процедуру измерения в течение следующего пятиминутного интервала, следующего пятиминутного интервала и так далее.
Данные температуры и BER будут иметь свои собственные отдельные дисперсии, то есть склонность значений в заданном наборе данных отклоняться от среднего значения того же набора данных. Но мы также можем вычислить ковариацию, которая отражает склонность значений в двух наборах данных к линейному изменению вместе (или, более кратко, к линейному совместному изменению, англ. «co-vary» – отсюда и название «ковариация»).
Следующие три графика дают визуальное объяснение того, что означает совместное изменение переменных.
Расчет ковариации
Следующее математическое соотношение определяется как ковариация двух переменных X и Y:
[operatorname {cov} (X,Y)=operatorname {E} {{big [}(X-operatorname {E} [X])(Y-operatorname {E} [Y]){big ]}}]
Для дискретных данных с размером выборки N это соотношение будет следующим:
[operatorname {cov} (X,Y)=frac{1}{N-1}sum_{i=1}^{N}(X_i-operatorname {E}[X])(Y_i-operatorname {E}[Y])]
Возможно, вы не знакомы с обозначением E[X]. «E» означает «ожидаемое значение», которое равно среднему арифметическому. (Существует тонкое концептуальное различие между ожидаемым значением и средним значением, но это тема для другой статьи.) Я хотел ввести это обозначение, потому что концепция ожидаемого значения дает нам другой способ думать о среднем значении набора данных – это значение, которое мы ожидаем от следующего измерения, в том смысле, что это ожидаемое значение имеет наибольшую вероятность появления.
Формула ковариации станет интуитивно понятна, если вы поразмыслите над ней на минуту или две:
- Отклонения (как по величине, так и по полярности) в наборе данных X умножаются на отклонения в наборе данных Y.
- Соответствующие отклонения в двух наборах данных, которые являются как положительными, так и отрицательными, внесут положительный вклад в суммирование.
- Если одно отклонение положительное, а соответствующее отклонение другого набора данных отрицательное, вклад будет отрицательным.
- Когда мы делим результат суммирования на N–1, мы усредняем все эти вклады и тем самым генерируем значение, которое указывает
- склонность значений в двух наборах данных отклоняться в одном направлении (т.е.положительная ковариация),
- склонность к отклонениям в противоположные стороны (отрицательная ковариация),
- или отсутствие склонности к совместному отклонению (нулевая ковариация).
Заключение
Ковариация количественно определяет линейную корреляцию двух случайных величин. Однако значения ковариации несколько сложно интерпретировать, и в следующей статье мы обсудим две модифицированные версии ковариации, которые сделают корреляционный анализ более удобным.
Теги
BERКовариацияКорреляцияОписательная статистикаПричинность / причинно-следственная связьСтандартное отклонениеСтатистикаСтатистическая связь
Общие понятия об изучении связей
Анализ взаимосвязей, присущих изучаемым процессам и явлениям, является важнейшей задачей исторических, как впрочем и многих других, исследований. В тех случаях, когда речь идет о явлениях и процессах, обладающих сложной структурой и многообразием свойственных им связей, такой анализ представляет собой сложную задачу. Прежде всего необходимо установить наличие взаимосвязей и их характер. Вслед за этим возникает вопрос о тесноте взаимосвязей и степени воздействия различных факторов (причин) на интересующий исследователя результат. Если черты и свойства изучаемых объектов могут быть измерены и выражены количественно, то анализ взаимосвязей может вестись на основе применения математических методов. Использование этих методов позволяет проверить гипотезу о наличии или отсутствии взаимосвязей между теми или иными признаками, выдвигаемую на основе содержательного анализа. Далее, лишь посредством математических методов можно установить тесноту и характер взаимосвязей или выявить силу (степень) воздействия различных факторов на результат.
Наиболее разработанными в математической статистике методами анализа взаимосвязей являются корреляционный и регрессионный анализ. Но прежде чем переходить к их характеристике, остановимся на вопросе о характере и форме тех взаимосвязей, которые присущи объективным явлениям природы и общества.
Функциональные зависимости. Функциональная зависимость двух количественных признаков или переменных состоит в том, что каждому значению одной переменной всегда соответствует одно определенное значение другой переменной. Например, при строительстве железных дорог на километр пути приходится вполне определенное количество уложенных рельсов. Поэтому рассматривая статистические данные по таким количественным признакам: у— длина уложенного железнодорожного пути (в км), х—количество истраченного на строительстве рельсового проката (в тоннах), мы будем иметь дело с функциональной зависимостью определенного вида. Рассмотрим эту зависимость подробнее на условном примере:
Соотношение между признаками, отображенное в таблице, удобно представить в наглядной графической форме, рассматривая числовые данные как координаты точек в прямоугольной системе координат (рис. 8).
Графическим изображением анализируемой зависимости (полученным путем соединения непрерывной линией точек, соответствующих данным таблицы) служит прямая линия. Такая зависимость называется прямой пропорциональной зависимостью. Ее аналитическим выражением является уравнение y=kx, где k — коэффициент пропорциональности (в нашем случае &=100). Прямая пропорциональная зависимость представляет собой частный случай линейной зависимости, которая характеризуется уравнением
y=kx+b
Графическим изображением линейной зависимости также служит прямая линия (рис. 9).
Линейная зависимость является наиболее простой и в определенном смысле универсальной формой связи многих явлений. Ее универсальность состоит в том, что более сложные зависимости часто можно рассматривать «в первом приближении» как линейные. Здесь мы подходим к выяснению роли функциональных зависимостей в анализе стати стических связей. Непосредственно функциональные зависимости в чистом виде редко встречаются в общественных явлениях. Связи обычно носят гораздо более сложный характер. Однако их описание во всей сложности часто затруднительно, да и нецелесообразно. Поэтому их рассматривают как соответствующие тем или иным видам функциональной зависимости. Простейшей формой функциональной связи является линейная зависимость, которая широко используется в регрессионном и особенно в корреляционном анализе. Гипотеза о линейной связи между исследуемыми признаками получила широкое распространение в анализе взаимосвязей. Лишь в том случае, если результаты применения гипотезы о линейной зависимости оказываются неудачными или имеются веские основания против линейной связи, используют более сложные функциональные зависимости.
Отметим наиболее употребительные формы функциональной зависимости, применяемые в статистическом анализе.
В случае если прямая линия не соответствует характеру используемых данных, можно использовать параболу (рис. 10). Аналитическое выражение ее имеет вид:
Наличие в этом уравнении члена a2x2 является простейшей формой учета нелинейности.
В том случае, когда мы имеем дело с затуханием роста или падения, удобно использовать гиперболические либо логарифмические зависимости (рис. 11 и 12). Математические выражения для гиперболической и логарифмической зависимостей выглядят так:
y=k/x; y=a lgx
Процессы демографического и экономического роста описываются экспоненциальными зависимостями вида:
y=keλx.
Графическое изображение этой зависимости (k>0, λ>0) иллюстрируется рис. 13.
Подбор подходящей функциональной зависимости на основе графического и логического анализа является важным этапом исследования взаимосвязей, особенно в тех случаях, когда линейная связь оказалась неприемлемой.

В отличие от функциональной зависимости, когда каждому значению одного признака всегда соответствует определенное значение другого, при статистической зависимости одному и тому же значению одного признака могут соответствовать различные значения другого. Это происходит в силу того, что при статистической зависимости связь устанавливается между признаками (двумя, тремя и т. д.), которые изменяются не только в силу взаимодействия между собой, но и под воздействием множества различных неучтенных факторов. В результате множественного воздействия взаимно переплетающихся факторов связь между признаками существует и проявляется не в каждом отдельном случае, как при функциональной связи, а только в тенденции, «в среднем». Поэтому здесь установить наличие взаимосвязи и определить ее количественную меру можно не на основе единичных наблюдений, а лишь применительно к определенной совокупности объектов, т. е. в среднем по отношению к тем или иным массовым объектам или явлениям. Характеризующие эти объекты количественные показатели в источниковедении и в статистике называются массовыми данными.
Задачи анализа статистических связей. Анализ статистической, или корреляционной, связи предполагает выявление формы связи, а также оценку тесноты связи. Первая задача решается методами регрессионного анализа, вторая — методами корреляционного анализа. Регрессионный анализ сводится к описанию статистической связи с помощью подходящей функциональной зависимости. Корреляционный анализ позволяет оценивать тесноту связи посредством специальных показателей, причем выбор их зависит от вида функциональной зависимости, пригодной для адекватного описания рассматриваемой статистической взаимосвязи. Как указывалось, наиболее распространенной в изучении связей является гипотеза о линейной зависимости. Соответствующие ей методы корреляционного и регрессионного анализа наиболее полно разработаны в математической статистике. Прежде чем перейти к изложению этих методов, остановимся на двух общих вопросах, относящихся к корреляционному и регрессионному анализу.
Один из важных вопросов, возникающих в изучении связей,— установление «направления» зависимости. Пусть для простоты рассматривается связь между двумя признаками y и х. Какой из этих признаков следует считать подверженным влиянию, или результативным (зависимой переменной), какой — оказывающим влияние, или факторным (независимой переменной)?
Первостепенное значение в решении этого вопроса имеет содержательный анализ. Положим, мы рассматриваем связь между производительностью труда рабочих и стажем их работы. По-видимому, результативным признаком следует признать производительность труда, а факторным — стаж рабочего. Не всегда «направление» связи проявляется столь очевидно. Тогда при решении вопроса о выборе результативного признака на первый план выступает постановка содержательной проблемы, для исследования которой используется изучение взаимосвязей. Например, устанавливая «направление» связи между такими признаками, как доходность предприятий и их энерговооруженность, мы должны исходить из того, что же мы хотим установить в действительности: влияние внедрения новой техники и технологии на доходность предприятий или же потенциальные возможности предприятий в овладении передовой техникой и технологией. В первом случае результативным признаком естественно считать доходность, во втором — энерговооруженность.
Далее, корреляционный и регрессионный анализ могут применяться и дают вполне корректные результаты при соблюдении определенных условий. Это однородность исходных данных, независимость отдельных значений признака друг от друга и нормальность распределения изучаемых признаков. Некоторые способы проверки однородности, случайности и нормальности распределении данных указаны в гл. 9.
Условия применения корреляционного и регрессионного анализа, а также возникающие на практике нарушения условий и следствия этих нарушений рассмотрены в § 2 и 3 данной главы.
Линейная корреляция
Одной из основных мер связи в корреляционном анализе является линейный коэффициент корреляции.
Парный линейный коэффициент корреляции. С помощью парного линейного коэффициента корреляции измеряется теснота связи между двумя признаками. Линейный коэффициент корреляции чаще всего рассчитывается по формуле
где xi и yi — значения признаков х и у соответственно для i-ro объекта, i=1, .., n; n — число объектов; 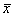
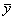
Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Равенство коэффициента нулю свидетельствует об отсутствии линейной связи. Равенство коэффициента —1 или +1 показывает наличие функциональной связи. Знак «+» указывает на связь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «—» — на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).
Пример 1. Используя данные табл. 1, рассчитаем коэффициент корреляции между доходом крестьянского хозяйства и стоимостью имеющегося в этом хозяйстве скота
Воспользуемся формулой (6.3), а промежуточные расчеты сделаем с помощью рабочей табл. 1, в которую введем необходимые для вычислений графы:
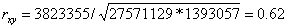
Как оценить полученное значение коэффициента корреляции? Велико оно или мало? О наличии или об отсутствии связи свидетельствует? Для ответа на эти вопросы проводят проверку значимости коэффициента.
Проверка значимости парного линейного коэффициента корреляции. Коэффициенты корреляции, как правило, рассчитываются для выборочных данных. Чтобы распространить полученные частные результаты на генеральную совокупность, приходится допустить некоторую ошибку, которую можно оценить с помощью средней квадратической ошибки. Средняя квадратическая ошибка для парного линейного коэффициента корреляции достаточно большой выборки вычисляется по формуле
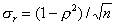
где ρ — коэффициент корреляции генеральной совокупности; n — объем выборки.
В математической статистике доказано, что если признаки х и y распределены по нормальному закону, то в достаточно больших выборках коэффициенты корреляции можно считать распределенными нормально со средним значением ρ и средним квадратическим отклонением σr (нормальное распределение рассмотрено в гл. 4). Этот факт используется для построения доверительных интервалов коэффициента корреляции в генеральной совокупности, а также для проверки значимости выборочных коэффициентов корреляции, т. е. для проверки того, могло ли данное значение r получиться в выборке из некоррелированной генеральной совокупности (ρ=0) в силу простой случайности.
Очевидно, чем больше отклонение r от ρ, тем менее вероятно, что оно случайно. Так, для нормального распределения вероятность того, что выборочное значение r отличается от ρ больше чем на 3σr, меньше 0,01, т. е. величина нормированного отклонения 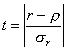
Если 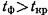
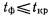
Пример 2. Выясним, является ли значимым коэффициент корреляция между доходов крестьянского хозяйства и стоимостью скота в хозяйстве.
В нашем примере, задавшись степенью достоверности Р, равной 0,99 и найдя соответствующее ей в таблице 1 приложения значение tкр=2.58, проводим сравнение. Поскольку tф=0.62/0,18=3,44 заметно превосходит табличное значение 2,58 и вероятность того, что это случайность, мала (0,01), связь между доходом крестьянского хозяйства и стоимостью имеющегося в нем скота следует признать значимой.
Поскольку вычисленный в примере 1 линейный коэффициент корреляции имеет положительный знак, то взаимосвязь между признаками прямая: чем больше скота в хозяйстве, тем больше доход, и чем меньше скота, тем доход меньше.
Заметим, что линейный коэффициент корреляции является показателем взаимной связи между признаками и не дает представления о том, какой из признаков является факторным, а какой — результативным (в формуле (6.3) признаки х и у совершенно равноправны).
Установив существенность взаимной связи между двумя признаками, можно поставить вопрос о тесноте связи. Напомним, что теснота линейной связи измеряется линейным коэффициентом корреляции, но такая оценка верна только для случая, когда расчеты проведены для генеральной совокупности. Для выборочных данных, что обычно имеет место в практике использования корреляционного анализа, необходимо выявить те границы, в пределах которых находится значение коэффициента корреляции генеральной совокупности, т. е. определить для него доверительные интервалы.
Доверительные интервалы для парного линейного коэффициента корреляции. После расчета выборочного коэффициента корреляции (r) и его средней квадратической ошибки (σr) устанавливается уровень достоверности выводов или доверительная вероятность. Для больших выборок соответственно выбранной вероятности Р по таблице нормального распределения определяется параметр t. Верхняя граница интервала получается прибавлением к выборочному коэффициенту корреляции tσr, нижняя граница—вычитанием tσr. Формула средней квадратической ошибки (6.4) содержит неизвестный на практике генеральный коэффициент корреляции. Обычно в расчетах его заменяют выборочным коэффициентом корреляции.
Пример 3. Определим доверительные интервалы для коэффициента, вычисленного в примере 1.
Полагая доверительную вероятность Р, т. е. вероятность, с которой гарантируются результаты, равной 0,98, находим в табл. 1 приложения соответствующее ей значение t, равное 2,33. Воспользовавшись формулой (6.4), где вместо ρ возьмем выборочный коэффициент корреляции r, равный 0,62, получим значение для средней квадратической ошибки
Поскольку tσr=2.33*0.11=0.26, верхняя и нижняя границы равны соответственно 0,88 и 0,36. Другими словами, с вероятностью 0,98 линейный коэффициент корреляции генеральной совокупности находится в пределах от 0,36 до 0,88.
Важнейшей предпосылкой использования корреляционного анализа является нормальность распределения признаков в генеральной совокупности. Нормальность распределения или, по крайней мере, близость распределения к нормальному необходима для корректного проведения проверки значимости связи и вычисления доверительных интервалов. Методы проверки нормальности распределения см. в гл. 9.
Проверка значимости парного линейного коэффициента корреляции для случая малой выборки. При пользовании формулами (6,4) — (6.5) необходимо учитывать два ограничения. Во-первых, они верны для коэффициента корреляции генеральной совокупности и замена последнего выборочным коэффициентом корреляции является искусственным приемом. Риск заменить генеральный коэффициент корреляции существенно отличным от него выборочным коэффициентом увеличивается с уменьшением объема выборки п. Во-вторых, при выборках небольшого объема распределение выборочного коэффициента корреляции может значительно отличаться от нормального, а нормальность распределения является важнейшим условием корректного использования доверительных интервалов и проверки значимости коэффициентов.
Таким образом, при малых объемах выборок (практически при n<50) изложенная выше методика определения доверительных интервалов и проверки значимости коэффициентов корреляции неприменима (поэтому примеры 2—3 являются в какой-то мере условными). Особенно возрастают требования к объему выборки при высоких, близких к 1, значениях показателя связи генеральной совокупности.
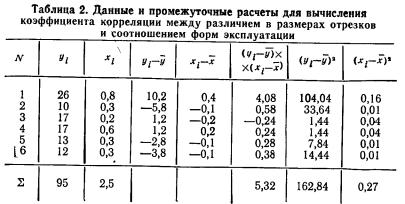
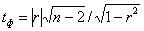
и сравнивается с табличной или критической величиной tкр, зависящей от числа k=n—2, где n—объем выборки, и от выбранной степени достоверности Р. Если , то приходят к выводу о наличии связи; если tф<tкр, то гипотеза об отсутствии связи не отклоняется.
Пример 4. В трех первых столбцах табл. 2 приведены данные, позволяющие анализировать зависимость различий в размерах отрезков, установленных реформой 1861 г. и соотношением форм эксплуатации по шести губерниям Черноземного центра. Вычислим линейный коэффициент корреляции между этими признаками и проверим его значимость (у — % отрезков, х — отношение числа оброчных крестьян к числу барщинных).
Рассчитав средние значения признаков ( 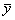
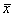
Для проверки значимости коэффициента воспользуемся формулой (6.6):
Табличное значение tкр(k) находим в табл. 2 приложения. Оно расположено на пересечении строки с номером k=n—2 и столбца с удовлетворяющей исследователя степенью достоверности результата. Для нашего примера число степеней свободы k=6—2=4. Положив степень достоверности результата Р равной 0,80, на пересечении 4-й строки и соответствующего 0,90 столбца находим tкр( k)=2,13.
Поскольку tф==2,7>t( k)==2,13, с риском ошибиться в 10 случаях из 100 отбрасываем гипотезу об отсутствии линейной связи, т. е. считаем, что связь между размером отрезков и формой эксплуатации крестьян существует.
Понятие о частной и множественной корреляции. С помощью парного линейного коэффициента корреляции выявляется связь между двумя признаками, один из которых можно рассматривать как результативный, другой — как факторный. Но в действительности на результат воздействуют несколько факторов. В связи с этим возникают два типа задач: задачи измерения комплексного влияния на результативную переменную нескольких переменных и задачи определения тесноты связи между двумя переменными при фиксированных значениях остальных переменных. Задачи первого типа решаются с помощью множественных коэффициентов корреляции, задачи второго типа — с помощью частных коэффициентов корреляции.
Частный, или чистый, коэффициент корреляции между двумя признаками при исключении влияния третьего признака (обозначим его символом r12.3) рассчитывается по формуле (Существует алгоритм, позволяющий вычислить частные коэффициенты корреляции при исключенном влиянии двух, трех и т. д. факторов. Этот рекуррентный алгоритм используется в машинном варианте (есть стандартные программы для ЭВМ).)
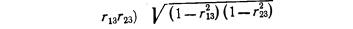
где индексы при r показывают номера признаков, связь между которыми оценивается.
Частный коэффициент корреляции первого и второго признаков при исключении влияния третьего оценивает тесноту линейной корреляционной связи между первым и вторым признаками при фиксированном значении третьего признака. Другими словами, он оценивает влияние на результативный (первый) признак изменения лишь второго признака.
Оценка влияния на результативный признак изменений третьего признака при постоянных значениях второго признака определяется по формуле
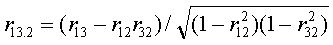
Значения частных коэффициентов корреляции заключаются в тех же пределах от —1 до +1, что и значения парных коэффициентов корреляции, и так же интерпретируются.
Пример 5. На основе данных табл. 1 оценить, какое из направлений хозяйства — скотоводческое или земледельческое — определяет доход в зажиточной группе крестьян.
Для решения этого вопроса в дополнение к рассчитанному в примере 1 коэффициенту r12, показывающему тесноту взаимосвязи между доходом хозяйства и стоимостью скота в нем, вычислим еще два парных коэффициента корреляции: r13—коэффициент связи между доходом, крестьянского хозяйства и уровнем землепользования в нем, r23 — коэффициент связи между землепользованием крестьянского двора и стоимостью всего скота.
Получим r12=0,62, r13=0,52, r23=0,74. Парные коэффициенты корреляции, показывающие тесноту связи между доходом и уровнем землепользования, между доходом и стоимостью скота, почти равны по величине. Отсюда можно сделать вывод о том, что ни та, ни другая формы хозяйствования не имеет преимущественного влияния на доход. Однако взаимосвязь между самими факторными признаками, т. е. между землепользованием и стоимостью скота (r23), оказалась довольно тесной. Наличие же связи между факторными признаками может искажать действительную тесноту связи между результативным и факторными признаками. Расчет частных коэффициентов корреляции позволяет избавляться от этих искажений. Воспользовавшись формулами (6.7) и (6.8), вычислим коэффициенты r12.3 и r13.2.
Частный коэффициент корреляции между доходом крестьянского двора и стоимостью скота при постоянном показателе землепользования меньше, чем соответствующий парный коэффициент корреляции (0,41 против 0,62). По-видимому, взаимная зависимость между величиной дохода и стоимостью скота частично опосредствовалась через воздействие уровня землепользования.
Частная корреляция между доходом и землепользованием совсем мала (0,12) при довольно большом значении парного коэффициента (0,52). Это можно объяснить тем, что взаимная зависимость дохода и землепользования в значительной степени были усилена влиянием исключенного здесь фактора — стоимости скота.
Таким образом, частные коэффициенты корреляции позволяют установить тесноту взаимосвязи между двумя признаками при исключении влияния других переменных, но для окончательных выводов необходима проверка уровня значимости частных коэффициентов корреляции.
Значимость частных коэффициентов корреляции зависит не только от величины выборочного коэффициента и объема выборки, но также и от числа введенных в исследование переменных.
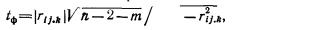
Для проверки значимости частных коэффициентов корреляции вычисляют величину по формуле
где rij.k — коэффициент корреляции между i и j признаками при исключенном влиянии k-го признака; m—количество исключенных признаков, и сравнивают ее с табличным или критическим значением, соответствующим принятому уровню значимости.
Наличие связи подтверждается, если вычисленное значение tф превосходит значение tкр.
Пример 5 (продолжение). Проверить значимость частных коэффициентов корреляции, рассчитанных выше.
Воспользовавшись формулой (6.9), вычислим величины t1ф для r12.3 и t2ф для r13.2:
Для того чтобы найти табличные значения tкр, нужно задаться степенью достоверности выводов и учесть число n—2—m, фигурирующее в формуле (6.9).
Табличное значение tкр находится по табл. 2 приложения на пересечении строки с номером (n —2—m) и столбца, соответствующего заданной степени достоверности выводов.
В нашем примере в каждом коэффициенте число признаков, от которых мы абстрагируемся, равно 1 и, следовательно, n —2—m=31—2—1==28. Задавшись степенью достоверности, равной 0,90, по табл. 2 приложения находим значение tкр, равное 1,7.
Поскольку t1ф>tкр, подтверждается наличие взаимосвязи между доходом и стоимостью скота. Для второго из рассматриваемых коэффициентов t2ф<tкр, что свидетельствует, по-видимому, об отсутствии непосредственной связи между доходом и землепользованием.
Множественный, или совокупный, коэффициент корреляции для случая трех признаков, один из которых — результативный (с номером 1) и два—факторных (с порядковыми номерами 2 и 3) рассчитывается по формуле (Для расчетов используется такая формула
пригодная для случаев, когда число признаков, совокупное влияние которых исследуется, превосходит два. Существуют стандартные программы, вычисляющие R1(23…P))
где подстрочные индексы при r показывают номера признаков, связь между которыми оценивается этим коэффициентом корреляции.
Множественный коэффициент корреляции является показателем тесноты линейной связи между результативным признаком и совокупностью факторных признаков.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1. Равенство его нулю говорит об отсутствии линейной связи, равенство единице—о функциональной связи. Указаний на то, является ли связь прямой или обратной, коэффициент не дает.
Пример 6. Рассчитать множественный коэффициент корреляции между величиной дохода крестьянского хозяйства и совокупным влиянием на него уровня землепользования и стоимости скота в хозяйстве.
Воспользуемся результатами предыдущих примеров: r12=0.62; r13=0.52; r23=0.74. По формуле (6.10);
т. е. степень тесноты связи между доходом крестьянского хозяйства и совокупностью двух факторных признаков составляет 0,63.
Вопрос о значимости множественного коэффициента корреляции решается с помощью так называемого F-критерия. Величина Fф, рассчитанная по специальной формуле, сравнивается с табличным (критическим) значением Fкр — распределения Фишера, соответствующим выбранной степени достоверности Р (или уровню значимости α=1—Р). Если Fф>Fкр, то коэффициент признается значимым на уровне а, так как вероятность того, что Fф для выборки случайно получилось больше Fкр, мала (меньше α). Для случая двух факторных признаков величина вычисляется по формуле (Формула расчетной величины F для общего случая m факторных признаков имеет вид
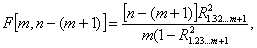
где R1.23…m+1—множественный коэффициент корреляции; n—число объектов, для которых приводятся значения признаков; m — число факторных признаков. Этот же критерий используется для проверки значимости регрессии, см. (6.20).)
Пример 6 (продолжение). Проверить значимость вычисленного в примере 6 множественного коэффициента корреляции для уровня значимости α=0,05 (P=0,95).
Воспользуемся формулой (6.11):
В табл. 4А приложения (соответствующей α=0,05) во 2-м столбце и 28-й строке (номер столбца определяется по первому числу в квадратной скобке при F, а номер строки—по второму числу) находим критическое значение –распределения. Поскольку при достоверности вывода, равной 0,95, Fкр=3,34, т. е. Fф>Fкр, совместное влияние на величину дохода уровня землепользования и стоимости скота имеет место.
Коэффициент детерминации. Линейный коэффициент корреляции оценивает тесноту взаимосвязи между признаками и показывает, является ли связь прямой или обратной. Но понятие тесноты взаимосвязи часто может быть недостаточным при содержательном анализе взаимосвязей. В частности, коэффициент корреляции не показывает степень воздействия факторного признака на результативный. Таким показателем является коэффициент детерминации (обозначим его D), для случая линейной связи представляющий собой квадрат парного линейного коэффициента корреляции (D=r2) или квадрат множественного коэффициента корреляции. Его значение определяет долю (в процентах) изменений, обусловленных влиянием факторного признака, в общей изменчивости результативного признака.
Пример 7. Рассчитать по данным примера 4 (табл. 2) коэффициент детерминации.
Коэффициент корреляции равен 0,80. Коэффициент детерминации составляет: D=0,802•100%=64%.
Таким образом, различия в размерах отрезков в губерниях Черноземного центра на 64% определялись различиями в соотношении форм эксплуатации.
Корреляционная таблица. В предыдущем изложении каждый признак был представлен рядом значений. В некоторых случаях удобна другая форма записи исходных данных, в виде корреляционной таблицы.
Корреляционная таблица имеет такое устройство: по строкам располагаются значения одного признака, по столбцам — другого признака. Число, стоящее в клетке на пересечении i-й строки и j-го столбца, показывает, как часто i-e значение первого признака встречается совместно с j-м значением второго признака.
В табл. 3 представлены сведения об уходящих в отставку дворянах (60-е годы XVIII в.). В строках дан возраст ухода в отставку, в столбцах — имущественное обложение уходящих в отставку, характеризуемое числом принадлежащих им крестьян. В клетках представлены числа, показывающие, как часто встречаются соответствующие сочетания количественных значений этих двух признаков.
Корреляционная таблица является удобной формой представления данных. Уже беглое знакомство с ней нередко позволяет судить о тесноте связи (не обязательно линейной) между признаками. Если большие значения одного признака в основном сочетаются с большими значениями другого признака, а малые—с малыми, т. е. числа концентрируются вдоль диагонали таблицы, то можно говорить о наличии прямой связи. Если малые значения одного признака в большинстве случаев встречаются совместно с большими значениями другого признака, т. е. числа сосредоточены вдоль другой диагонали, то имеется обратная связь. При этом, чем больше концентрация частот вдоль одной из диагоналей, тем теснее связь.
Корреляционное отношение. Когда изучаемая совокупность (в виде корреляционной таблицы) разбивается на группы по одному (факторному) признаку х, то для каждой из этих групп можно вычислить соответствующие групповые средние результативного признака 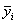
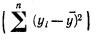
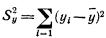
или остаточной (S2ост). Поэтому отношение
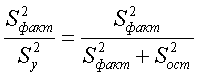
является мерой степени влияния факторного признака на результативный. Значение квадратного корня из этого отношения измеряет «направленную связь» (x→y) в общем виде и носит название корреляционного отношения (ηy/x).
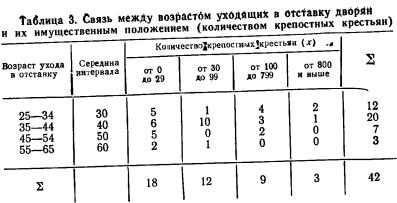
Величины Sфакт2 и Sy2 вычисляются по формулам:
где 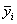
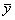
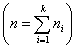
Рассмотрим вычисление корреляционного отношения, воспользовавшись данными табл. 3.
Пример 8. В источнике, содержащем данные об уходящих в отставку дворянах, имеются сведения о. причинах ухода в отставку. Как правило, в качестве причины указывалась болезнь. Являлась ли эта причина единственной? Есть основания предположить, что возраст ухода в отставку зависел также от имущественного положения находящихся на военной службе дворян: чем более они были обеспечены, тем с большей легкостью могли оставить службу. Для проверки этого предположения измерим тесноту связи между возрастом уходящих в отставку дворян и их имущественным положением по данным табл. 3.
По признаку имущественного положения совокупность разбита на 4 группы. Рассчитаем средний возраст ухода в отставку для каждой группы
Аналогично вычислим 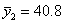
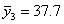
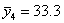
Наконец, вычислим общую среднюю арифметическую (средний возраст ухода в отставку по всем данным табл. 3). Для расчета этой средней в качестве весов возьмем числа, стоящие в последнем суммарном столбце таблицы;
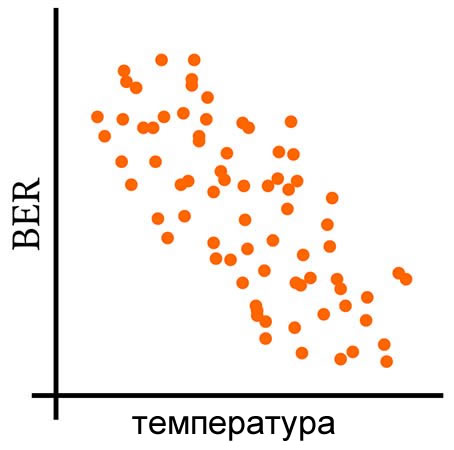
Далее, воспользовавшись последовательно формулами (6.13), (6.14) и (6 12), рассчитаем корреляционное отношение:
S2факт=(42,2-40,2)2+(40,8-40,2)2*12+37,7-40,2)2*9+(33,3-40,2)2*3=294,
S2y=(30-40.2)2*12+(40-40.2)2*20+(50-40.2)2*7+(60-40.2)2*3=3098,
Величена корреляционного отношения изменяется в пределах от 0 до 1. Близость ее к нулю говорит об отсутствии связи, близость к единице—о тесной связи.
Корреляционное отношение в отличие от линейного коэффициента корреляции не указывает, является ли связь прямой или обратной. Однако нередко уже по виду исходной таблицы можно решить этот вопрос. Промежуточные расчеты также помогают определить, является связь прямой или обратной: если с ростом факторного группировочного признака растут групповые средние результативного признака, то связь—прямая, если же с увеличением факторного признака значения групповых средних уменьшаются, то связь—обратная.
Как показатель тесноты связи корреляционное отношение имеет более универсальный характер, чем линейный коэффициент корреляции, поскольку его использование не ограничивается случаями линейной связи, а факторный признак может быть не количественным, а ранговым и даже номинальным.
Квадрат корреляционного отношения, выраженный в процентах, и коэффициент детерминации, как он определен выше, имеют одинаковый смысл, только при расчете коэффициента детерминации используется предположение о линейной связи между факторным и результативным признаками, тогда как при вычислении корреляционного отношения вопрос о форме связи не ставится.
Возвращаясь к примеру 8, оценим полученные в нем результаты. Корреляционное отношение, выражающее степень тесноты связи, оказалось равным 0,31, а квадрат корреляционного отношения в процентах (коэффициент детерминации) —9,9%.
Таким образом, возраст ухода в отставку зависит от имущественного положения, но в целом в небольшой степени: колебания имущественного положения только на 9,9% объясняют колебания возраста ухода в отставку. Причем, поскольку с увеличением количества крестьян у владельцев средний возраст ухода в отставку уменьшается, то связь между этими признаками — обратная (Вопрос оценки значимости корреляционного отношения в выборке рассмотрен в § 4 гл. 9.).
Линейный коэффициент корреляции, как уже отмечалось, является показателем взаимной связи между признаками, но не указывает, какой из них результативный, а какой — факторный. В этом отношении от него выгодно отличается корреляционное отношение, которое позволяет выявить это соотношение. Для этого вычисляются два корреляционных отношения, сравнение которых и помогает определить правильное распределение «ролей» между признаками.
Коэффициент корреляции и корреляционное отношение являются эффективным средством выявления связи между различными количественными признаками и определения ее тесноты. Коэффициент детерминации дает представление и о степени воздействия одних факторов на другие. Однако решение вопроса о тесноте связи нередко упирается в вопрос о форме связи. Кроме того, знание формы связи дает развернутое представление о влиянии различных факторов на результативный признак, а также возможность прогнозирования изменений результата при тех или иных комбинациях значений факторов.
Выявление формы связи осуществляется с помощью методов регрессионного анализа.
§ 3. Линейная регрессия

Суть метода наименьших квадратов. Рассмотрим содержание метода на конкретном примере. Пусть имеются данные о сборе хлеба на душу населения по совокупности черноземных губерний. От каких факторов зависит величина этого сбора? Вероятно, определяющее влияние на величину сбора хлеба оказывает величина посева и уровень урожайности. Рассмотрим сначала зависимость величины сбора хлеба на душу населения от размера посева на душу (столбцы 1 и 2 табл .4) Попытаемся представить интересующую нас зависимость с помощью прямой линии. Разумеется, такая линия может дать только приближенное представление о форме реальной статистической связи. Постараемся сделать это приближение наилучшим. Оно будет тем лучше, чем меньше исходные данные будут отличаться от соответствующих точек, лежащих на линии. Степень близости может быть выражена величиной суммы квадратов отклонении, реальных значений от, расположенных на прямой. Использование именно квадратов отклонений (не просто отклонений) позволяет суммировать отклонения различных знаков без их взаимного погашения и дополнительно обеспечивает сравнительно большее внимание, уделяемое большим отклонениям. Именно этот критерий (минимизация суммы квадратов отклонений) положен в основу метода наименьших квадратов.
В вычислительном аспекте метод наименьших квадратов сводится к составлению и решению системы так называемых нормальных уравнений. Исходным этапом для этого является подбор вида функции, отображающей статистическую связь.
Тип функции в каждом конкретном случае можно подобрать путем прикидки на графике исходных данных подходящей, т. е. достаточно хорошо приближающей эти данные, линии. В нашем случае связь между сбором хлеба на душу и величиной посева на душу может быть изображена с помощью прямой линии (рис. 14) и записана в виде
где у—величина сбора хлеба на душу (результативный признак или зависимая переменная); x—величина посева на душу (факторный признак или независимая переменная); ao и a1 — параметры уравнения, которые могут быть найдены методом наименьших квадратов.
Для нахождения искомых параметров нужно составить систему уравнений, которая в данном случае будет иметь вид
Полученная система может быть решена известным из школьного курса методом Гаусса. Искомые параметры системы из двух нормальных уравнений можно вычислить и непосредственно с помощью последовательного использования нижеприведенных формул:
где yi — i-e значение результативного признака; xi — i-e значение факторного признака; 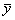
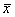
Пример 9. Найдем уравнение линейной связи между величиной сбора хлеба (у) и размером посева (х) по данным табл. 4. Проделав необходимые вычисления, получим из (6.17):
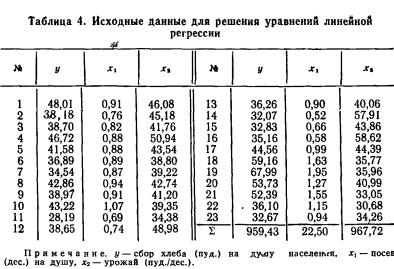
принято говорить, уравнение регрессии, выглядит следующим образом:
у = 17,6727+24,5759x.
Интерпретация коэффициента регрессии. Уравнение регрессии не только определяет форму анализируемой связи, но и показывает, в какой степени изменение одного признака сопровождается изменением другого признака.
Коэффициент при х, называемый коэффициентом регрессии, показывает, на какую величину в среднем изменяется результативный признак у при изменении факторного признака х на единицу.
В примере 9 коэффициент регрессии получился равным 24,58. Следовательно, с увеличением посева, приходящегося на душу, на одну десятину сбор хлеба на душу населения в среднем увеличивается на 24,58 пуда.
Средняя и предельная ошибки коэффициента регрессии. Поскольку уравнения регрессии рассчитываются, как правило, для выборочных данных, обязательно встают вопросы точности и надежности полученных результатов. Вычисленный коэффициент регрессии, будучи выборочным, с некоторой точностью оценивает соответствующий коэффициент регрессии генеральной совокупности. Представление об этой точности дает средняя ошибка коэффициента регрессии ( 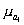
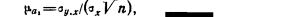
где
уi, — i-e значение результативного признака; ŷi — i-e выравненное значение, полученное из уравнения (6.15); xi—i-e значение факторного признака; σx—среднее квадратическое отклонение х; n — число значений х или, что то же самое, значений у; m—число факгорных признаков (независимых переменных).
В формуле (6.18), в частности, формализовано очевидное положение: чем больше фактические значения отклоняются от выравненных, тем большую ошибку следует ожидать; чем меньше число наблюдений, на основе которых строится уравнение, тем больше будет ошибка.
Средняя ошибка коэффициента регрессии является основой для расчета предельной ошибки. Последняя показывает, в каких пределах находится истинное значение коэффициента регрессии при заданной надежности результатов. Предельная ошибка коэффициента регрессии вычисляется аналогично предельной ошибке средней арифметической (см. гл. 5), т. е. как t 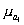
Пример 10. Найти среднюю и предельную ошибки коэффициента регрессии, полученного в примере 9.
Для расчета 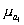
ŷi = 17,6681 +24,5762*0,91 = 40,04 и т. д.
Затем вычислим отклонения фактических значений уi, от выравненных и их квадраты
Далее, подсчитав средний по черноземным губерниям посев на душу ( =0,98), отклонения фактических значений xi от этой средней, квадраты отклонений и среднее квадратическое отклонение
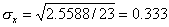
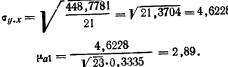
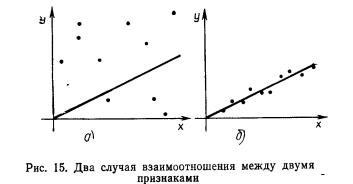
Задавшись уровнем надежности, равным 0,95, найдем по табл. 1 приложения соответствующее ему значение t=1,96, рассчитаем предельную ошибку 1,96*2,89=5,66 и пределы коэффициента регрессии для принятого уровня надежности (В случае малых выборок величина t находится из табл. 2 приложения.). Нижняя граница коэффициента регрессии равна 24,58-5,66=18,92, а верхняя граница 24,58+5,66=30,24
Средняя квадратическая ошибка линии регрессии. Уравнение регрессии представляет собой функциональную связь, при которой по любому значению х можно однозначно определить значение у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание.
На рис. 15 представлены два различных случая взаимоотношения между двумя признаками. В обоих случаях предполагаемая связь описывается одним и тем же уравнением, но во втором случае соотношение между признаками х и у достаточно четко выражено и уравнение, по-видимому, довольно хорошо описывает это соотношение, тогда как в первом случае сомнительно само наличие сколько-нибудь закономерного соотношения между признаками. И в том, и в другом случаях, несмотря на их существенное различие, метод наименьших квадратов дает одинаковое уравнение, поскольку этот метод нечувствителен к потенциальным возможностям исходного материала вписаться в ту или иную схему. Кроме того, метод наименьших квадратов применяется для расчета неизвестных параметров заранее выбранного вида функции, и вопрос о выборе наиболее подходящего для конкретных данных вида функции в рамках этого метода не ставится и не решается. Таким образом, при пользовании методом наименьших квадратов открытыми остаются два важных вопроса, а именно: существует ли связь и верен ли выбор вида функции, с помощью которой делается попытка описать форму связи.
Чтобы оценить, насколько точно уравнение регрессии описывает реальные соотношения между переменными, нужно ввести меру рассеяния фактических значений относительно вычисленных с помощью уравнения. Такой мерой служит средняя квадратическая ошибка регрессионного уравнения, вычисляемая по приведенной выше формуле (6.19).
Пример 11. Определить среднюю квадратическую ошибку уравнения, полученного в примере 9.
Промежуточные расчеты примера 10 дают нам среднюю квадратическую ошибку уравнения. Она равна 4,6 пуда.
Этот показатель аналогичен среднему квадратическому отклонению для средней. Подобно тому, как по величине среднего квадратического отклонения можно судить о представительности средней арифметической (см. гл. 5), по величине средней квадратической ошибки регрессионного уравнения можно сделать вывод о том, насколько показательна для соотношения между признаками та связь, которая выявлена уравнением. В каждом конкретном случае фактическая ошибка может оказаться либо больше, либо меньше средней. Средняя квадратическая ошибка уравнения показывает, насколько в среднем мы ошибемся, если будем пользоваться уравнением, и тем самым дает представление о точности уравнения. Чем меньше σy.x, тем точнее предсказание линии регрессии, тем лучше уравнение регрессии описывает существующую связь. Показатель σy.x позволяет различать случаи, представленные на рис. 15. В случае б) он окажется значительно меньше, чем в случае а). Величина σy.x зависит как от выбора функции, так и от степени описываемой связи.
Варьируя виды функций для выравнивания и оценивая результаты с помощью средней квадратической ошибки, можно среди рассматриваемых выбрать лучшую функцию, функцию с наименьшей средней ошибкой. Но существует ли связь? Значимо ли уравнение регрессии, используемое для отображения предполагаемой связи? На эти вопросы отвечает определяемый ниже критерий значи-мости регрессии.
Мерой значимости линии регрессии может служить следующее соотношение:
где ŷi—i-e выравненное значение; 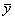
Действительно, связь тем больше, чем значительнее мера рассеяния признака, обусловленная регрессией, превосходит меру рассеяния отклонений фактических значений от выравненных.
Соотношение (6.20) позволяет решить вопрос о значимости регрессии. Регрессия значима, т. е. между признаками существует линейная связь, если для данного уровня значимости вычисленное значение Fф[m,n-(m+1)] превышает критическое значение Fкр[m,n-(m+1)], стоящее на пересечении m-го столбца и [n—(m+1)]-й строки специальной таблицы (см. табл. 4 приложения).
Пример 12. Выясним, связаны ли сбор хлеба на душу населения и посев на душу населения линейной зависимостью.
Воспользуемся F-критерием значимости регрессии. Подставив в формулу (6.20) данные табл. 4 и результат примера 10, получим
Обращаясь к таблице F-распределения для Р=0,95 (α=1—Р=0,5) и учитывая, что n=23, m =1, в табл. 4А приложения на пересечения 1-го столбца и 21-й строки находим критическое значение Fкр, равное 4,32 при степени надежности Р=0,95. Поскольку вычисленное значение Fф существенно превосходит по величине Fкр, то обнаруженная линейная связь существенна, т. е. априорная гипотеза о наличии линейной связи подтвердилась. Вывод сделан при степени надежности P=0,95. Между прочим, вывод в данном случае останется прежним, если надежность повысить до Р=0,99 (соответствующее значение Fкр=8,02 по табл. 4Б приложения для уровня значимости α=0,01).
Коэффициент детерминации. С помощью F-критерия мы Установили, что существует линейная зависимость между величиной сбора хлеба и величиной посева на душу. Следовательно, можно утверждать, что величина сбора хлеба, приходящегося на душу, линейно зависит от величины посева на душу. Теперь уместно поставить уточняющий вопрос — в какой степени величина посева на душу определяет величину сбора хлеба на душу? На этот вопрос можно ответить, рассчитав, какая часть вариации результативного признака может быть объяснена влиянием факторного признака.
Рассмотрим отношение
Оно показывает долю разброса, учитываемого регрессией, в общем разбросе результативного признака и носит название коэффициента детерминации. Этот показатель, равный отношению факторной вариации к полной вариации признака, позволяет судить о том, насколько «удачно» выбран вид функции (Отметим, что по смыслу коэффициент детерминации в регрессионном анализе соответствует квадрату корреляционного отношения для корреляционной таблицы (см. § 2).). Проведя расчеты, основанные на одних и тех же исходных данных, для нескольких типов функций, мы можем из них выбрать такую, которая дает наибольшее значение R2 и, следовательно, в большей степени, чем другие функции, объясняет вариацию результативного признака. Действительно, при расчете R2 для одних и тех же данных, но разных функций знаменатель выражения (6.21) остается неизменным, а числитель показывает ту часть вариации результативного признака, которая учитывается выбранной функцией. Чем больше R2, т. е. чем больше числитель, тем больше изменение факторного признака объясняет изменение результативного признака и тем, следовательно, лучше уравнение регрессии, лучше выбор функции.
Наконец, отметим, что введенный ранее, при изложении методов корреляционного анализа, коэффициент детерминации совпадает с определенным здесь показателем, если выравнивание производится По прямой линии. Но последний показатель (R2) имеет более широкий спектр применения и может использоваться в случае связи, отличной от линейной (см. § 4 данной главы).
Пример 13. Рассчитать коэффициент детерминации для уравнения, полученного в примере 9.
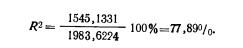
Вычислим R2, воспользовавшись формулой (6.21) и данными табл. 4:
Итак, уравнение регрессии почти на 78% объясняет колебания сбора хлеба на душу. Это немало, но, По-видимому, можно улучшить модель введением в нее еще одного фактора.
Случай двух независимых переменных. Простейший случай множественной регрессии. В предыдущем изложении регрессионного анализа мы имели дело с двумя признаками — результативным и факторным. Но на результат действует обычно не один фактор, а несколько, что необходимо учитывать для достаточно полного анализа связей.
В математической статистике разработаны методы множественной регрессии (Регрессия называется множественной, если число независимых переменных, учтенных в ней, больше или равно двум.), позволяющие анализировать влияние на результативный признак нескольких факторных. К рассмотрению этих методов мы и переходим.
Возвратимся к примеру 9. В нем была определена форма связи между величиной сбора хлеба на душу и размером посева на душу. Введем в анализ еще один фактор — уровень урожайности (см. столбец З табл. 4). Без сомнения, эта переменная влияет на сбор хлеба на душу. Но в какой степени влияет? Насколько обе независимые переменные определяют сбор хлеба на душу в черноземных губерниях? Какая из переменных — посев на душу или урожайность — оказывает определяющее влияние на сбор хлеба? Попытаемся ответить на эти вопросы.
После добавления второй независимой переменной уравнение регрессии будет выглядеть так:
где у—сбор хлеба на душу; х1—размер посева на душу; x2—урожай с десятины (в пудах); а0, а1, а2—параметры, подлежащие определению.
Для нахождения числовых значений искомых параметров, как и в случае одной независимой переменной, пользуются методом наименьших квадратов. Он сводится к составлению и решению системы нормальных уравнений, которая имеет вид
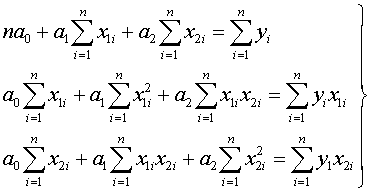
Когда система состоит из трех и более нормальных уравнений, решение ее усложняется. Существуют стандартные программы расчета неизвестных параметров регрессионного уравнения на ЭВМ. При ручном счете можно воспользоваться известным из школьного курса методом Гаусса.
Пример 14. По данным табл. 4 описанным способом найдем параметры a0, а1, а2 уравнения (6.22). Получены следующие результаты: a2=0,3288, a1=28,7536, a0=-0,2495.
Таким образом, уравнение множественной регрессии между величиной сбора хлеба на душу населения (у), размером посева на душу (x1) и уровнем урожайности (х2) имеет вид:
у=-0,2495+28,7536x1+0,3288x2.
Интерпретация коэффициентов уравнения множественной регрессии. Коэффициент при х1 в полученном уравнении отличается от аналогичного коэффициента в уравнении примера 9.
Коэффициент при независимой переменной в уравнении простой регрессии отличается от коэффициента при соответствующей переменной в уравнении множественной регрессии тем, что в последнем элиминировано влияние всех учтенных в данном уравнении признаков.
Коэффициенты уравнения множественной регрессии поэтому называются частными или чистыми коэффициентами регрессии.
Частный коэффициент множественной регрессии при х1 показывает, что с увеличением посева на душу на 1 дес. и при фиксированной урожайности сбор хлеба на душу населения вырастает в среднем на 28,8 пуда. Частный коэффициент при x2 показывает, что при фиксированном посеве на душу увеличение урожая на единицу, т. е. на 1 пуд с десятины, вызывает в среднем увеличение сбора хлеба на душу на 0,33 пуда. Отсюда можно сделать вывод, что увеличение сбора хлеба в черноземных губерниях России идет, в основном, за счет расширения посева и в значительно меньшей степени—за счет повышения урожайности, т. е. экстенсивная форма развития зернового хозяйства является господствующей.
Введение переменной х2 в уравнение позволяет уточнить коэффициент при х1. Конкретно, коэффициент оказался выше (28,8 против 24,6), когда в изучаемой связи вычленилось влияние урожайности на сбор хлеба.
Однако выводы, полученные в результате анализа коэффициентов регрессии, не являются пока корректными, поскольку, во-первых, не учтена разная масштабность факторов, во-вторых, не выяснен вопрос о значимости коэффициента a2.
Величина коэффициентов регрессии изменяется в зависимости от единиц измерения, в которых представлены переменные. Если переменные выражены в разном масштабе измерения, то соответствующие им коэффициенты становятся несравнимыми. Для достижения сопоставимости коэффициенты регрессии исходного уравнения стандартизуют, взяв вместо исходных переменных их отношения к собственным средним квадратическим отклонениям. Тогда уравнение (6.22) приобретает вид
Сравнивая полученное уравнение с уравнением (6.22), определяем стандартизованные частные коэффициенты уравнения, так называемые бета-коэффициенты, по формулам:
где β1 и β2—бета-коэффициенты; а1 и а2—коэффициенты регрессии исходного уравнения; σу, 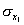
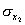
Вычислив бета-коэффициенты для уравнения, полученного в примере 14:
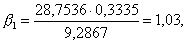
видим, что вывод о преобладании в черноземной полосе россии экстенсивной формы развития хозяйства над интенсивной остается в силе, так как β1 значительно больше, чем β2.
Оценка точности уравнения множественной регрессии.
Точность уравнения множественной регрессии, как и в случае уравнения с одной независимой переменной, оценивается средней квадратической ошибкой уравнения. Обозначим ее 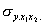
Пример 15. Оценим точность полученного в примере 14 уравнения регрессии.
Воспользовавшись формулой (6.19) и данными табл. 4, вычислим среднюю квадратическую ошибку уравнения:
Оценка полезности введения дополнительной переменной. Точность уравнения регрессии тесно связана с вопросом ценности включения дополнительных членов в это уравнение.
Сравним средние квадратические ошибки, рассчитанные для уравнения с одной переменной х1 (пример 11) и для уравнения с двумя независимыми переменными х1 и х2. Включение в уравнение новой переменной (урожайности) уменьшило среднюю квадратическую ошибку почти вдвое.
Можно провести сравнение ошибок с помощью коэффициентов вариации
где σf—средняя квадратическая ошибка регрессионного уравнения; 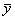
Для уравнения, содержащего одну независимую переменную:
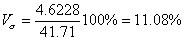
Для уравнения, содержащего две независимые переменные:
Итак, введение независимой переменной «урожайность» уменьшило среднюю квадратическую ошибку до величины порядка 7,95% среднего значения зависимой переменной.
Наконец, по формуле (6.21) рассчитаем коэффициент детерминации
Он показывает, что уравнение регрессии на 81,9% объясняет колебания сбора хлеба на душу населения. Сравнивая полученный результат (81,9%) с величиной R2 для однофакторного уравнения (77,9%), видим, что включение переменной «урожайность» заметно увеличило точность уравнения.
Таким образом, сравнение средних квадратических ошибок уравнения, коэффициентов вариации, коэффициентов детерминации, рассчитанных до и после введения независимой переменной, позволяет судить о полезности включения этой переменной в уравнение. Однако следует быть осторожными в выводах при подобных сравнениях, поскольку увеличение R2 или уменьшение σ и Vσ не всегда имеют приписываемый им здесь смысл. Так, увеличение R2 может объясняться тем фактом, что число рассматриваемых параметров в уравнении приближается к числу объектов наблюдения. Скажем, весьма сомнительными будут ссылки на увеличение R2 или уменьшение σ, если в уравнение вводится третья или четвертая независимая переменная и уравнение строится на данных по шести, семи объектам.
Полезность включения дополнительного фактора можно оценить с помощью F-критерия.
Частный F-критерий показывает степень влияния дополнительной независимой переменной на результативный признак и может использоваться при решении вопроса о добавлении в уравнение или исключении из него этой независимой переменной.
Разброс признака, объясняемый уравнением регрессии (6.22), можно разложить на два вида: 1) разброс признака, обусловленный независимой переменной х1, и 2) разброс признака, обусловленный независимой переменной x2, когда х1 уже включена в уравнение. Первой составляющей соответствует разброс признака, объясняемый уравнением (6.15), включающим только переменную х1. Разность между разбросом признака, обусловленным уравнением (6.22), и разбросом признака, обусловленным уравнением (6.15), определит ту часть разброса, которая объясняется дополнительной независимой переменной x2. Отношение указанной разности к разбросу признака, регрессией не объясняемому, представляет собой значение частного критерия. Частный F-критерий называется также последовательным, если статистические характеристики строятся при последовательном добавлении переменных в регрессионное уравнение.
Пример 16. Оценить полезность включения в уравнение регрессии дополнительной переменной «урожайность» (по данным и результатам примеров 12 и 15).
Разброс признака, объясняемый уравнением множественной регрессии и рассчитываемый как сумма квадратов разностей выравненных значений и их средней, равен 1623,8815. Разброс признака, объясняемый уравнением простой регрессии, составляет 1545,1331.
Разброс признака, регрессией не объясняемый, определяется квадратом средней квадратической ошибки уравнения и равен 10,9948 (см. пример 15).
Воспользовавшись этими характеристиками, рассчитаем частный F-критерий
С уровнем надежности 0,95 (α=0,05) табличное значение F (1,20), т. е. значение, стоящее на пересечении 1-го столбца и 20-й строки табл. 4А приложения, равно 4,35. Рассчитанное значение Fф значительно превосходит табличное, и, следовательно, включение в уравнение переменной «урожайность» имеет смысл.
Таким образом, выводы, сделанные ранее относительно коэффициентов регрессии, вполне правомерны.
Важным условием применения к обработке данных метода множественной регрессии является отсутствие сколько-нибудь значительной взаимосвязи между факторными признаками. При практическом использовании метода множественной регрессии, прежде чем включать факторы в уравнение, необходимо убедиться в том, что они независимы.
Если один из факторов зависит линейно от другого, то система нормальных уравнений, используемая для нахождения параметров уравнения, не разрешима. Содержательно этот факт можно толковать так: если факторы х1 и x2 связаны между собой, то они действуют на результативный признак у практически как один фактор, т. е. сливаются воедино и их влияние на изменение у разделить невозможно. Когда между независимыми переменными уравнения множественной регрессии имеется линейная связь, следствием которой является неразрешимость системы нормальных уравнений, то говорят о наличии мультиколлинеарности.
На практике вопрос о наличии или об отсутствии мультиколлинеарности решается с помощью показателей взаимосвязи. В случае двух факторных признаков используется парный коэффициент корреляции между ними: если этот коэффициент по абсолютной величине превышает 0,8, то признаки относят к числу мультиколлинеарных. Если число факторных признаков больше двух, то рассчитываются множественные коэффициенты корреляции. Фактор признается мультиколлинеарным, если множественный коэффициент корреляции, характеризующий совместное влияние на этот фактор остальных факторных признаков, превзойдет по величине коэффициент множественной корреляции между результативным признаком и совокупностью всех независимых переменных.
Самый естественный способ устранения мультиколлинеарности — исключение одного из двух линейно связанных факторных признаков. Этот способ прост, но не всегда приемлем, так как подлежащий исключению фактор может оказывать на зависимую переменную особое влияние. В такой ситуации применяются более сложные методы избавления от мультиколлинеарности (См.: Мот Ж. Статистические предвидения и решения на предприятии. М., 1966; Ковалева Л. Н. Многофакторное прогнозирование на основе рядов динамики. М., 1980.).
Выбор «наилучшего» уравнения регрессии. Эта проблема связана с двойственным отношением к вопросу о включении в регрессионное уравнение независимых переменных. С одной стороны, естественно стремление учесть все возможные влияния на результативный признак и, следовательно, включить в модель полный набор выявленных переменных. С другой стороны, возрастает сложность расчетов и затраты, связанные с получением максимума информации, могут оказаться неоправданными. Нельзя забывать и о том, что для построения уравнения регрессии число объектов должно в несколько раз превышать число независимых переменных. Эти противоречивые требования приводят к необходимости компромисса, результатом которого и является «наилучшее» уравнение регрессии. Существует несколько методов, приводящих к цели: метод всех возможных регрессий, метод исключения, метод включения, шаговый регрессионный и ступенчатый регрессионный методы.
Метод всех возможных регрессий заключается в переборе и сравнении всех потенциально возможных уравнений. В качестве критерия сравнения используется коэффициент детерминации R2. «Наилучшим» признается уравнение с наибольшей величиной R2. Метод весьма трудоемок и предполагает использование вычислительных машин.
Методы исключения и включения являются усовершенствованными вариантами предыдущего метода. В методе исключения в качестве исходного рассматривается регрессионное уравнение, включающее все возможные переменные. Рассчитывается частный F-критерий для каждой из переменных, как будто бы она была последней переменной, введенной в регрессионное уравнение. Минимальная величина частного F-критерия (Fmin) сравнивается с критической величиной (Fкр), основанной на заданном исследователем уровне значимости. Если Fmin>Fкр, то уравнение остается без изменения. Если Fminкр, то переменная, для которой рассчитывался этот частный F-критерий, исключается. Производится перерасчет уравнения регрессии для оставшихся переменных, и процедура повторяется для нового уравнения регрессии. Исключение из рассмотрения уравнений с незначимыми переменными уменьшает объем вычислений, что является достоинством этого метода по сравнению с предыдущим.
Метод включения состоит в том, что в уравнение включаются переменные по степени их важности до тех пор, пока уравнение не станет достаточно «хорошим». Степень важности определяется линейным коэффициентом корреляции, показывающим тесноту связи между анализируемой независимой переменной и результативным признаком: чем теснее связь, тем больше информации о результирующем признаке содержит данный факторный признак и тем важнее, следовательно, введение этого признака в уравнение.
Процедура начинается с отбора факторного признака, наиболее тесно связанного с результативным признаком, т. е. такого факторного признака, которому соответствует максимальный по величине парный линейный коэффициент корреляции. Далее строится линейное уравнение регрессии, содержащее отобранную независимую переменную. Выбор следующих переменных осуществляется с помощью частных коэффициентов корреляции, в которых исключается влияние вошедших в модель факторов. Для каждой введенной переменной рассчитывается частный F-критерий, по величине которого судят о том, значим ли вклад этой переменной. Как только величина частного F-критерия, относящаяся к очередной переменной, оказывается незначимой, т. е. эффект от введения этой переменной становится малозаметным, процесс включения переменных заканчивается. Метод включения связан с меньшим объемом вычислений, чем предыдущие методы. Но при введении новой переменной нередко значимость включенных ранее переменных изменяется. Метод включения этого не учитывает, что является его недостатком. Модификацией метода включения, исправляющей этот недостаток, является шаговый регрессионный метод.
Шаговый регрессионный метод кроме процедуры метода включения содержит анализ переменных, включенных в уравнение на предыдущей стадии. Потребность в таком анализе возникает в связи с тем, что переменная, обоснованно введенная в уравнение на ранней стадии, может оказаться лишней из-за взаимосвязи ее с переменными, позднее включенными в уравнение. Анализ заключается в расчете на каждом этапе частных F-критериев для каждой переменной уравнения и сравнении их с величиной Fкр, точкой F-распределения, соответствующей заданному исследователем уровню значимости. Частный F-критерий показывает вклад переменной в вариацию результативного признака в предположении, что она вошла в модель последней, а сравнение его с Fкр позволяет судить о значимости рассматриваемой переменной с учетом влияния позднее включенных факторов. Незначимые переменные из уравнения исключаются.
Рассмотренные методы предполагают довольно большой объем вычислений и практически неосуществимы без ЭВМ. Для реализации ступенчатого регрессионного метода вполне достаточно малой вычислительной техники.
Ступенчатый регрессионный метод включает в себя такую последовательность действий. Сначала выбирается наиболее тесно связанная с результативным признаком переменная и составляется уравнение регрессии. Затем находят разности фактических и выравненных значений и эти разности (остатки) рассматриваются как значения результативной переменной. Для остатков подбирается одна из оставшихся независимых переменных и т. д. На каждой стадии проверяется значимость регрессии. Как только обнаружится незначимость, процесс прекращается и окончательное уравнение получается суммированием уравнений, полученных на каждой стадии за исключением последней.
Ступенчатый регрессионный метод менее точен, чем предыдущие, но не столь громоздок. Он оказывается полезным в случаях, когда необходимо внести содержательные правки в уравнение. Так, для изучения факторов, влияющих на цены угля в Санкт-Петербурге в конце XIX— начале XX в., было получено уравнение множественной регрессии. В него вошли следующие переменные: цены угля в Лондоне, добыча угля в России и экспорт из России. Здесь не обосновано появление в модели такого фактора, как добыча угля, поскольку Санкт-Петербург работал исключительно на импортном угле. Модели легко придать экономический смысл, если независимую переменную «добыча» заменить независимой переменной «импорт». Формально такая замена возможна, поскольку между импортом и добычей существует тесная связь. Пользуясь ступенчатым методом, исследователь может совершить эту замену, если предпочтет содержательно интерпретируемый фактор.
§ 4. Нелинейная регрессия и нелинейная корреляция
Построение уравнений нелинейной регрессии. До сих пор мы, в основном, изучали связи, предполагая их линейность. Но не всегда связь между признаками может быть достаточно хорошо представлена линейной функцией. Иногда для описания существующей связи более пригодными, а порой и единственно возможными являются более сложные нелинейные функции. Ограничимся рассмотрением наиболее простых из них.
Одним из простейших видов нелинейной зависимости является парабола, которая
в общем виде может быть представлена функцией (6.2):
Неизвестные параметры а0, а1, а2 находятся в результате решения следующей системы уравнений:
Дает ли преимущества описание связи с помощью параболы по сравнению с описанием, построенным по гипотезе линейности? Ответ на этот вопрос можно получить, рассчитав последовательный F-критерий, как это делалось в случае множественной регрессии (см. пример 16).
На практике для изучения связей используются полиномы более высоких порядков (3-го и 4-го порядков). Составление системы, ее решение, а также решение вопроса о полезности повышения порядка функции для этих случаев аналогичны описанным. При этом никаких принципиально новых моментов не возникает, но существенно увеличивается объем расчетов.
Кроме класса парабол для анализа нелинейных связей можно применять и другие виды функций. Для расчета неизвестных параметров этих функций рекомендуется использовать метод наименьших квадратов, как наиболее мощный и широко применяемый.
Однако метод наименьших квадратов не универсален, поскольку он может использоваться только при условии, что выбранные для выравнивания функции линейны по отношению к своим параметрам. Не все функции удовлетворяют этому условию, но большинство применяемых на практике с помощью специальных преобразований могут быть приведены к стандартной форме функции с линейными параметрами.
Рассмотрим некоторые простейшие способы приведения функций с нелинейными параметрами к виду, который позволяет применять к ним метод наименьших квадратов.
Функция 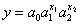
Прологарифмировав обе части приведенного равенства
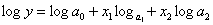
и переобозначив
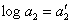
получим функцию, линейную относительно своих новых параметров:
Кроме логарифмирования для приведения функций к нужному виду используют обратные величины.
Например, функция
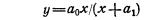
с помощью следующих переобозначений:

может быть приведена к виду
Подобные преобразования расширяют возможности использования метода наименьших квадратов, увеличивая число функций, к которым этот метод применим.
Измерение тесноты связи при криволинейной зависимости. Рассмотренные ранее линейные коэффициенты корреляции оценивают тесноту взаимосвязи при линейной связи между признаками. При наличии криволинейной связи указанные меры связи не всегда приемлемы. Разберем подобную ситуацию на примере.
Пример 17. В 1-м и 2-м столбцах табл. 5 приведены значения результативного признака у и факторного признака х (данные условные). Поставив вопрос о тесноте связи между ними, рассчитаем парный линейный коэффициент корреляции по формуле (6.3). Он оказался равным нулю, что свидетельствует об отсутствии линейной связи. Тем не менее связь между признаками существует, более того, она является функциональной и имеет вид
Для измерения тесноты связи при криволинейной зависимости используется индекс корреляции, вычисляемый по формуле
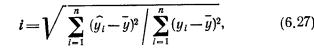
где уi—i-e значение результативного признака; ŷi—i-e выравненное значение этого признака; 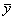
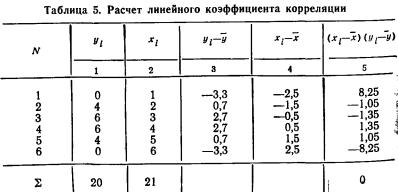
Таковы основные принципы и условия, методика и техника применения корреляционного и регрессионного анализа. Их подробное рассмотрение обусловлено тем, что они являются высокоэффективными и потому очень широко применяемыми методами анализа взаимосвязей в объективном мире природы и общества. Корреляционный и регрессионный анализ широко и успешно применяются и в исторических исследованиях (см. раздел III).
Содержание курса лекций «Статистика»
Причинность, регрессия, корреляция
Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей теории статистики. В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения ‑ это такая связь явлений и процессов, когда изменение одного из них ‑ причины ведет к изменению другого ‑ следствия.
Финансово-экономические процессы представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих процессов необходимо выявлять главные, основные причины, абстрагируясь от второстепенных.
В основе первого этапа статистического изучения связи лежит качественный анализ, связанный с анализом природы социального или экономического явления методами экономической теории, социологии, конкретной экономики.
Второй этап – построение модели связи, базируется на методах статистики: группировках, средних величинах, и так далее.
Третий, последний этап ‑ интерпретация результатов, вновь связан с качественными особенностями изучаемого явления. Статистика разработала множество методов изучения связей. Выбор метода изучения связи зависит от познавательной цели и задач исследования.
Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса.
Признаки, обуславливающие изменения других, связанных с ними признаков, называются факторными, или просто факторами.
Признаки, изменяющиеся под действием факторных признаков, называются результативными.
В статистике различают функциональную и стохастическую зависимости.
Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака.
Если причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, направлению и аналитическому выражению.
Таблица 11.1. ‑ Количественные критерии оценки тесноты связи
|
Величина показателя связи |
Характер связи |
|
До ±0,3 |
практически отсутствует |
|
±0.3 – ±0,5 |
слабая |
|
±0,5 – ±0,7 |
умеренная |
| ±0,7 -±1,0 |
сильная |
По направлению выделяют связь прямую и обратную.
Прямая ‑ это связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака.
Пример. Так, рост объемов производства способствует увеличению прибыли предприятия.
В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака, то есть обратная ‑ это связь, при которой с увеличением или с уменьшением значений одного признака происходит уменьшение или увеличение значений другого признака.
Пример. Так, снижение себестоимости единицы производимой продукции влечет за собой рост рентабельности.
По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные.
Если статистическая связь между явлениями может быть приблизительно выражена уравнением прямой линии, то ее называют линейной связью вида:
(11.1)
Если же связь может быть выражена уравнением какой-либо кривой, то такую связь называют нелинейной или криволинейной, например:
(11.2)
(11.3)
Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных; графический; аналитических группировок; корреляции, регрессии.
Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере.
Графически взаимосвязь двух признаков изображается с помощью поля корреляции. В системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат ‑ результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.
В статистике принято различать следующие виды зависимостей:
- Парная корреляция ‑ связь между двумя признаками (результативным и факторным, или двумя факторными).
- Частная корреляция ‑ зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков.
- Множественная корреляция ‑ зависимость результативного и двух или более факторных признаков, включенных в исследование.
Корреляционный анализ имеет своей задачей количественное определение тесноты и направления связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии. Знаки при коэффициентах корреляции характеризуют направление связи между признаками.
Регрессия тесно связана с корреляцией и позволяет исследовать аналитическое выражение взаимосвязи между признаками.
Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком), обусловлено влиянием одной или нескольких независимых величин (факторных признаков).
Одной из проблем построения уравнений регрессии является их размерность, то есть определение числа факторных признаков, включаемых в модель. Их число должно быть оптимальным. Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время, построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс.
При построении моделей регрессии должны соблюдаться требования:
- Совокупность исследуемых исходных данных должна быть однородной и математически описываться непрерывными функциями.
- Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.
- Все факторные признаки должны иметь количественное (числовое) выражение.
- Наличие достаточно большого объема исследуемой совокупности (в последующих примерах в целях упрощения изложения материала это условие нарушено, т.е. объем очень мал).
- Причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной форме зависимостью.
- Отсутствие количественных ограничений на параметры модели связи.
- Постоянство территориальной и временной структуры изучаемой совокупности.
Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные социально-экономические явления и процессы.
Парная регрессия на основе метода наименьших квадратов позволяет получить аналитическое выражение связи между двумя признаками: результативным и факторным.
Определить тип уравнения можно, исследуя зависимость графически, однако существуют более общие указания, позволяющие выявить уравнение связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи ‑ гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.
Оценка параметров уравнений регрессии ( и — в уравнении параболы второго порядка) осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и нахождении параметров модели , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
(11.4)
где п ‑ объем исследуемой совокупности (число единиц наблюдения).
В уравнениях регрессии параметр ао показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а1 показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения. xi – теоретические значения результативного признака; yi – наблюдаемые значения факторного признака.
Пример. Имеются данные по 10 однотипным предприятиям о выпуске продукции (х) в тыс.ед. и о расходе условного топлива (у) в тоннах (графы 1 и 2 табл. 17).
Требуется найти уравнение зависимости расхода топлива от выпуска продукции (или уравнение регрессии у по х) и измерить тесноту зависимости между ними. Для этого представим данные в табл. 11.2 (вместе с расчетными столбцами).
Таблица 11.2 – Расчет показателей для нахождения уравнения регрессии
| № п/п | Выпуск продукции, xi,тыс.ед. | Расход топлива, yi, тонн |
|
|
|
|
| 1 | 5 | 4 | 25 | 20 | 16 | 3,9 |
| 2 | 6 | 4 | 36 | 24 | 16 | 4,4 |
| 3 | 8 | 6 | 64 | 48 | 36 | 5,5 |
| 4 | 8 | 5 | 64 | 40 | 25 | 5,5 |
| 5 | 10 | 7 | 100 | 70 | 49 | 6,6 |
| 6 | 10 | 8 | 100 | 80 | 64 | 6,6 |
| 7 | 14 | 8 | 196 | 112 | 64 | 8,8 |
| 8 | 20 | 10 | 400 | 200 | 100 | 12,1 |
| 9 | 20 | 12 | 400 | 240 | 144 | 12,1 |
| 10 | 24 | 16 | 576 | 384 | 256 | 14,3 |
| ∑* | 125 | 80 | 1961 | 1218 | 770 | 80 |
Необходимые для решения суммы рассчитаны выше в таблице. Подставим их в уравнение и решим систему.
Из системы уравнений получим a1 = 0,547; а0 = 1,16.
Получив искомое уравнение регрессии можно утверждать, что с увеличение выпуска продукции на тыс. ед., расход топлива возрастет в среднем на 0,547 тонны.
*Если параметры уравнения найдены верно, то
(11.5)
Измерение тесноты (силы) и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака и одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков.
Линейный коэффициент корреляции (К. Пирсона) характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента.
Для измерения тесноты зависимости между у и х применяют линейный коэффициент корреляции, который может быть рассчитан по любой из нижеприведенных формул:
(11.6)
(11.7)
(11.8)
Таблица 11.3 – Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характеристика связи | Интерпретация связи |
| г = 0 | отсутствует | – |
| 0<г<1 | прямая | с увеличением х увеличивается у |
| -1<г<0 | обратная | с увеличением х уменьшается у и наоборот |
| г=1 | функциональная | каждому значению факторного признака строго соответствует одно значение результативного признака |
Пример вычисления коэффициента корреляции
Найдем коэффициент корреляции по данным табл. 11.2., используя формулы (11.6‑11.8):
Пример вычисления формула 11.6
Пример вычисления формула 11.7
Пример вычисления формула 11.8
Линейный коэффициент корреляции может принимать по модулю значения от 0 до 1 (знак + при прямой зависимости и знак – при обратной зависимости).
Найденный коэффициент корреляции означает, что характер связи между исследуемыми признаками прямой.
По степени тесноты связи между признаками (одним из критериев оценки служит коэффициент корреляции) различают связи:
Следовательно, 0,7≤0,96≤ 1 , значит, связь в данном примере сильная (с увеличением выпуска продукции увеличивается расход топлива).
Немного истории
Термин “корреляция” впервые применил французский палеонтолог Ж. Кювье, который вывел “закон корреляции частей и органов животных” (этот закон позволяет восстанавливать по найденным частям тела облик всего животного). В статистику указанный термин ввел в 1886 году английский биолог и статистик Френсис Гальтон (не просто связь – relation, а “как бы связь” – co-relation). Однако точную формулу для подсчёта коэффициента корреляции разработал его ученик – математик и биолог – Карл Пирсон (1857 – 1936).
Корреляционным называется исследование, проводимое для подтверждения или опровержения гипотезы о статистической связи между несколькими (двумя и более) переменными. В психологии переменными могут выступать психические свойства, процессы, состояния и др.
Содержание курса лекций «Статистика»
Контрольные задания.
По данным статистических сборников постройте таблицу: по 10 однотипным предприятиям с данными о численности персонала, выпуске продукции, расходах; данных о прожиточном минимуме и средней заработной плате и т.п.; найдите уравнение зависимости (или уравнение регрессии) и измерьте тесноту связи между показателями.