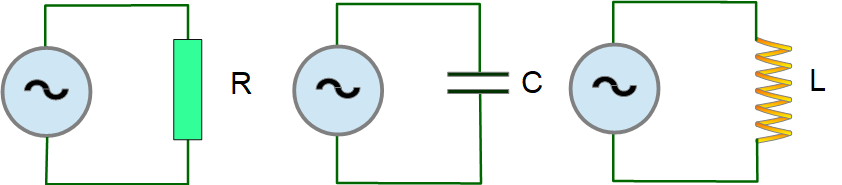
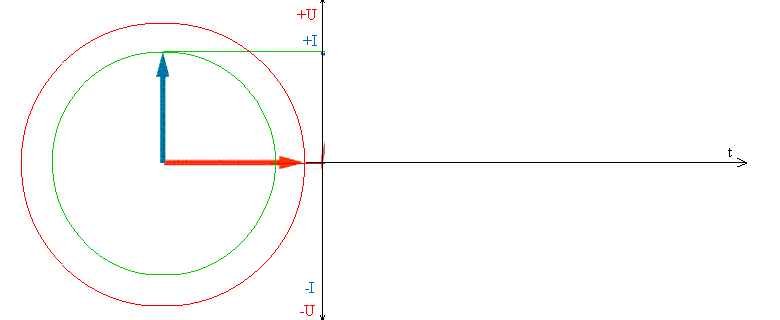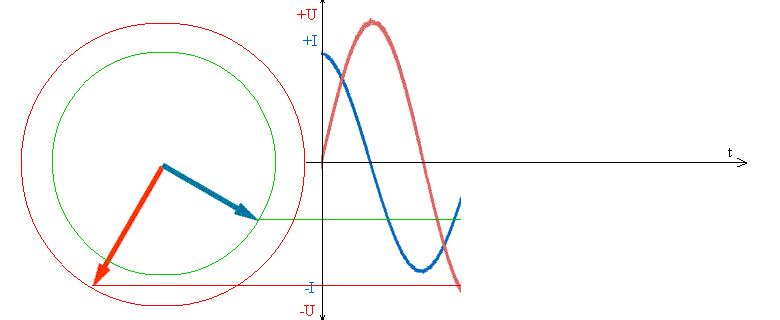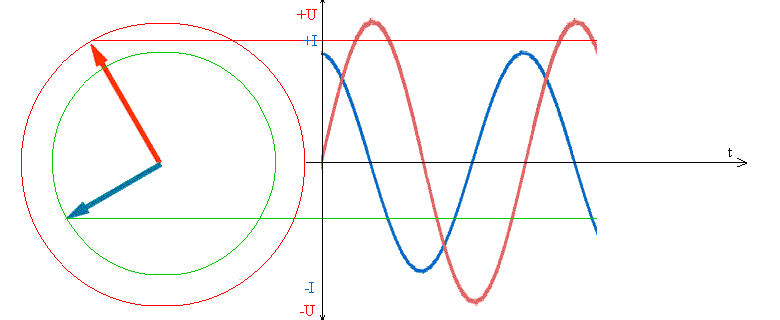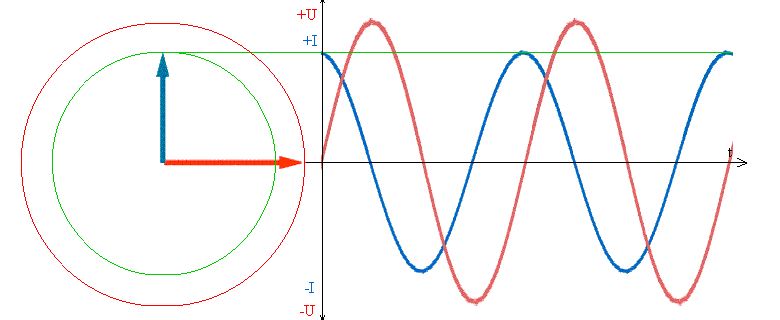
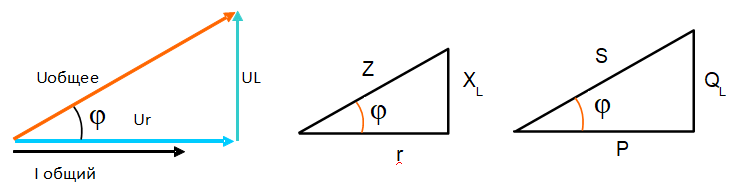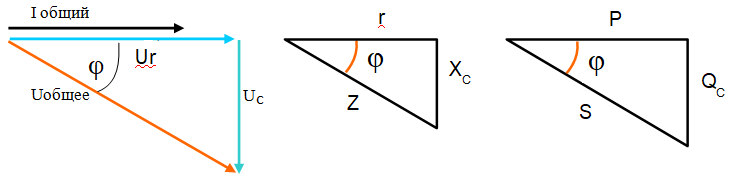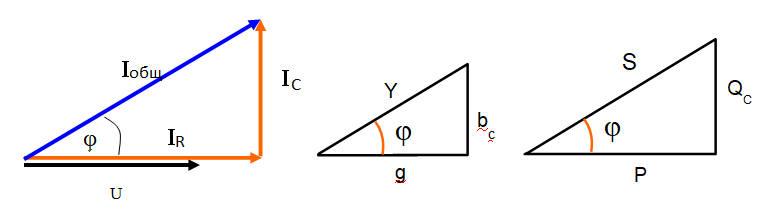Реактивное сопротивление XL и XC
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности
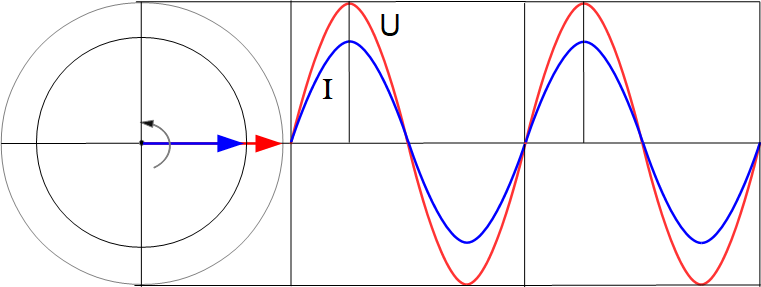
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток 
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока 
Для среднеквадратичных значений U и I в таком случае можно записать 
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
i = UampωCsin(ωt+π/2).
Отсюда выразим соотношение среднеквадратичных значений 
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора называют ёмкостным.
Предлагаем Вам рассмотреть непосредственно связанные с данным материалом статьи:
Что такое коэффициент мощности – Cos(φ)?
Реактивное сопротивление XL и XC
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток 
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока 
Для среднеквадратичных значений U и I в таком случае можно записать 
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
Отсюда выразим соотношение среднеквадратичных значений 
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора называют ёмкостным.
Предлагаем Вам рассмотреть непосредственно связанные с данным материалом статьи:
Что такое коэффициент мощности — Cos(φ)?
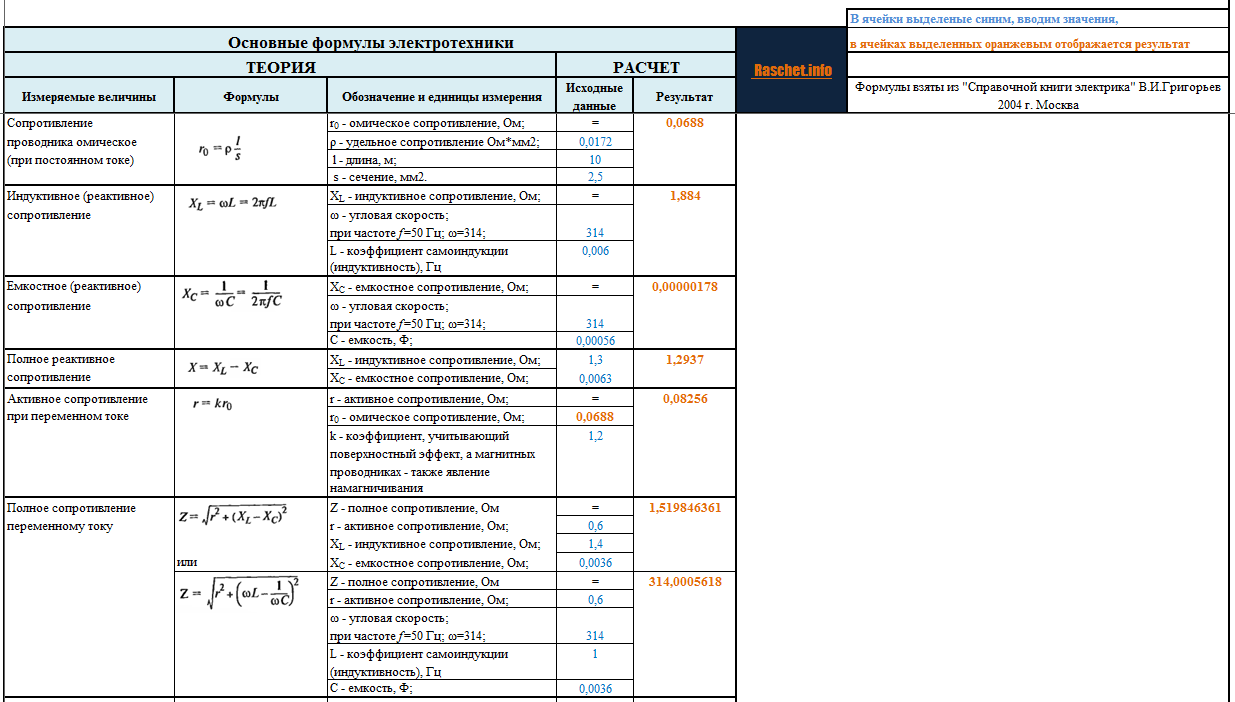
В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
Измеряемые величины
Формулы
Обозначение и единицы измерения
Сопротивление проводника омическое (при постоянном токе)



Активное сопротивление при переменном токе
r — активное сопротивление, Ом;
k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания
Зависимость омического сопротивления проводника от температуры




Индуктивное (реактивное) сопротивление



L — коэффициент самоиндукции (индуктивность), Гц;
Z — полное сопротивление, Ом
Емкостное (реактивное) сопротивление
Полное реактивное сопротивление
Полное сопротивление переменному току

Емкость пластинчатого конденсатора
S — площадь между двумя
n — число пластин;

b — толщина слоя диэлектрика, см
Общая емкость цепи:
а) при последовательном соединении емкостей
б) при параллельном соединении емкостей



Закон Ома; цепь переменного тока с реактивным сопротивлением

I — ток в цепи, А;
U — напряжение цепи, В;
1-й закон Кирхгофа (для узла)

Е — ЭДС, действующая в контуре, В;
r — сопротивление отдельных




2-й закон Кирхгофа (для замкнутого контура)
Распределение тока в двух параллельных ветвях цепи переменного тока
Закон электромагнитного индукции для синусоидального тока

w — число витков обмотки;
В — индукция магнитного поля в стали, Тс;
S — сечение магнитопровода, см2
Электродинамический эффект тока для двух параллельных проводников
F — сила, действующая на 1 (см) длины проводника, кГ;


а — расстояние между проводниками, си;

Подъемная сила электромагнита
Р — подъемная сила, кГ;
В3 — индукция в воздушном
зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей)
S — сечение стального сердечника, см2
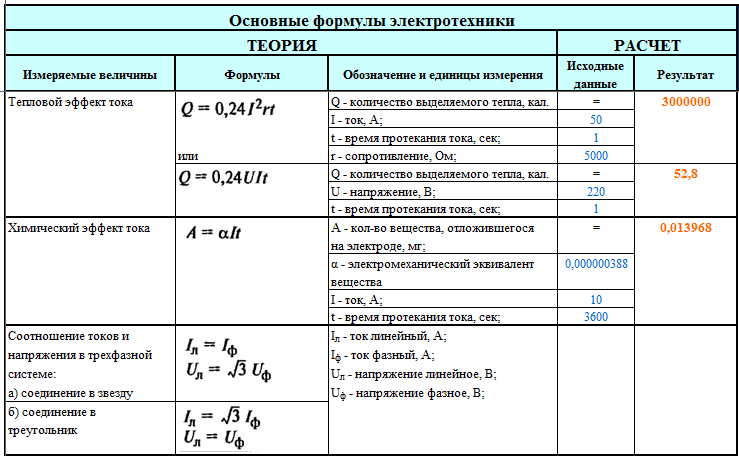
Тепловой эффект тока


t— время протекания тока, сек;
r — сопротивление, Ом;
А — количество вещества, от-
ложившегося на электроде, мг;
α — электрохимический эквивалент вещества
Химический эффект тока
Зависимости в цепи переменного тока при частоте 50 Гц:
а) период изменения тока
б) угловая скорость

Т — период изменения тока, сек;

Зависимости токов и напряжений в цепи переменного тока:
б) напряжение в цепи
I — полный ток в цепи, А;



U— напряжение в цепи, В;


Соотношения токов и напряжений в трехфазной системе:
а) соединение в звезду
б) соединение в треугольник




Р — активная мощность, Вт;
Q — реактивная мощность, нар;
S —полная мощность, B*А;
r — активное сопротивление,
z — полное сопротивление, Ом
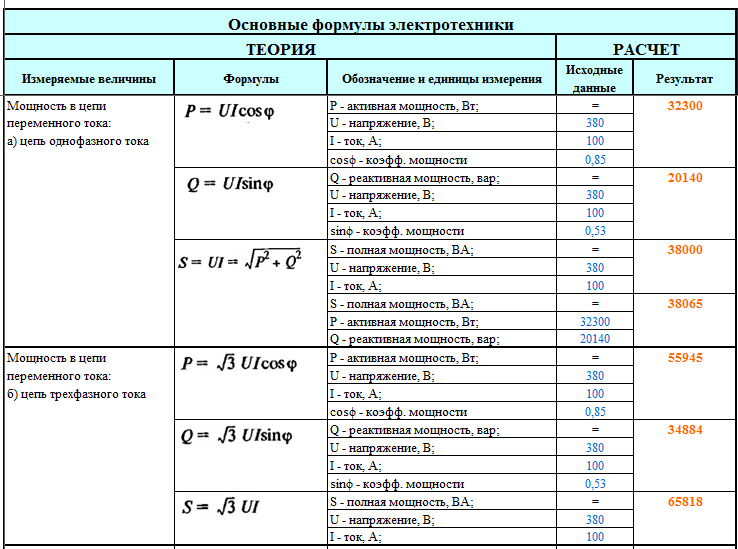
Мощность в цепи постоянного тока
Мощность в цепи переменного тока:
а) цепь однофазно тока
б) цепь трехфазного тока
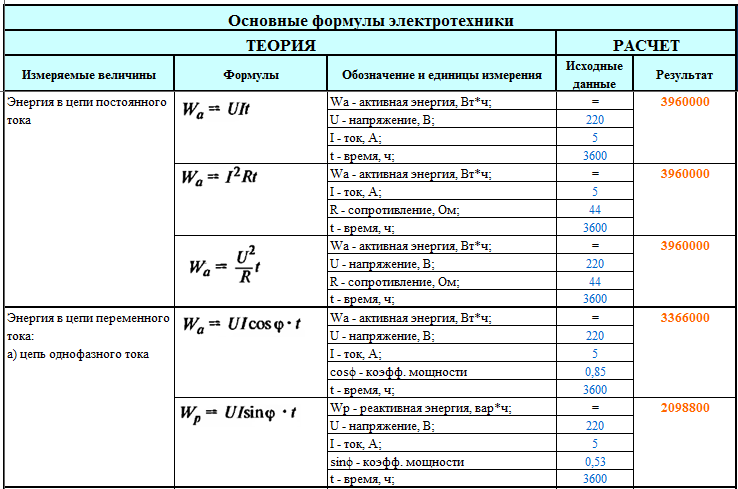
Энергия в цепи постоянного тока


В таблице представлены основные расчетные формулы по электротехнике для расчета тока, напряжения, сопротивления, мощности и других парметров электрических схем.
Измеряемые величины
Формулы
Обозначение и единицы измерения
Сопротивление проводника омическое (при постоянном токе)



Активное сопротивление при переменном токе
r — активное сопротивление, Ом;
k — коэффициент, учитывающий поверхностный эффект, а в магнитных проводниках — также явление намагничивания
Зависимость омического сопротивления проводника от температуры




Индуктивное (реактивное) сопротивление



L — коэффициент самоиндукции (индуктивность), Гц;
Z — полное сопротивление, Ом
Емкостное (реактивное) сопротивление
Полное реактивное сопротивление
Полное сопротивление переменному току

Емкость пластинчатого конденсатора
S — площадь между двумя
n — число пластин;

b — толщина слоя диэлектрика, см
Общая емкость цепи:
а) при последовательном соединении емкостей
б) при параллельном соединении емкостей



Закон Ома; цепь переменного тока с реактивным сопротивлением

I — ток в цепи, А;
U — напряжение цепи, В;
1-й закон Кирхгофа (для узла)

Е — ЭДС, действующая в контуре, В;
r — сопротивление отдельных




2-й закон Кирхгофа (для замкнутого контура)
Распределение тока в двух параллельных ветвях цепи переменного тока
Закон электромагнитного индукции для синусоидального тока

w — число витков обмотки;
В — индукция магнитного поля в стали, Тс;
S — сечение магнитопровода, см2
Электродинамический эффект тока для двух параллельных проводников
F — сила, действующая на 1 (см) длины проводника, кГ;


а — расстояние между проводниками, си;

Подъемная сила электромагнита
Р — подъемная сила, кГ;
В3 — индукция в воздушном
зазоре; В3 = 1000 Гс (электромагниты для подъема стружки и мелких деталей); В3 = 8000 — 10 000 Гс (электромагниты для подъема крупных деталей)
S — сечение стального сердечника, см2
Тепловой эффект тока


t— время протекания тока, сек;
r — сопротивление, Ом;
А — количество вещества, от-
ложившегося на электроде, мг;
α — электрохимический эквивалент вещества
Химический эффект тока
Зависимости в цепи переменного тока при частоте 50 Гц:
а) период изменения тока
б) угловая скорость

Т — период изменения тока, сек;

Зависимости токов и напряжений в цепи переменного тока:
б) напряжение в цепи
I — полный ток в цепи, А;



U— напряжение в цепи, В;


Соотношения токов и напряжений в трехфазной системе:
а) соединение в звезду
б) соединение в треугольник




Р — активная мощность, Вт;
Q — реактивная мощность, нар;
S —полная мощность, B*А;
r — активное сопротивление,
z — полное сопротивление, Ом
Мощность в цепи постоянного тока
Мощность в цепи переменного тока:
а) цепь однофазно тока
б) цепь трехфазного тока
Энергия в цепи постоянного тока


Данный калькулятор расчета основных измеряемых величин в электротехнике, выполненный в программе Microsoft Excel, позволяет оперативно рассчитать такие электрические величины как:
- сопротивление проводника при постоянном токе;
- активное сопротивление при переменном токе;
- индуктивное (реактивное) сопротивление;
- емкостное (реактивное) сопротивление;
- полное реактивное сопротивление;
- тепловой эффект тока;
- химический эффект тока;
- приводиться соотношение токов и напряжений в трехфазной системе в зависимости от соединения: в звезду или в треугольник;
- коэффициент мощности;
- мощность в цепи постоянного тока;
- мощность в цепи переменного тока: а) цепь однофазного тока; б) цепь трехфазного тока;
- энергия в цепи постоянного тока;
- энергия в цепи переменного тока: а) цепь однофазного тока; б) цепь трехфазного тока;
Данный калькулятор можно использовать и как справочник, возле каждого расчета измеряемой величины приведена формула, по которой выполняется расчет, а также расписано обозначение и единицы измерения.
На первом листе приводятся сами формулы и расчет. На втором листе приведены краткие справочные данные по электротехническим материалам из справочников.
Как найти xl в электротехнике
Удобные методы онлайн-расчета сопротивления емкости C и индуктивности L переменному току с частотой F.
[Xc — сопротивление конденсатора переменному току]
Формула для расчета: Xc = 1/(2*pi*F*C), где Xc — сопротивление конденсатора переменному току в Омах, F — частота в Герцах, C — емкость в Фарадах. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкФ, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Xl — сопротивление индуктивности переменному току]
Формула для расчета: Xl = 2*pi*F*L, где Xl — сопротивление индуктивности переменному току в Омах, F — частота в Герцах, L — индуктивность в Генри. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах — Гц, мкГн, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Общие замечания по использованию калькуляторов]
1. 1 микрофарад (мкф) = 1000000 пикофарад (пФ). 1 фарад (Ф) = 1000000 микрофарад (мкФ) = 10 12 пикофарад (пФ).
2. Десятичные значения с точкой нужно вводить с точкой, а не с запятой, иначе скрипт будет выдавать «infinity». Например, емкость 50 пФ следует ввести как 0.00005.
Загрузить PDF
Загрузить PDF
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Формулы
- Полное сопротивление Z = R или XLили XC (если присутствует что-то одно)
- Полное сопротивление (последовательное соединение) Z = √(R2 + X2) (если присутствуют R и один тип X)
- Полное сопротивление (последовательное соединение) Z = √(R2 + (|XL – XC|)2) (если присутствуют R, XL, XC)
- Полное сопротивление (любое соединение) = R + jX (j — мнимое число √(-1))
- Сопротивление R = I / ΔV
- Индуктивное сопротивление XL = 2πƒL = ωL
- Емкостное сопротивление XC = 1 / 2πƒL = 1 / ωL
-
1
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:[1]
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
-
2
Сопротивление — это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R.[2]
Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете измерить сопротивление при помощи мультиметра.- ΔV — это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I — сила тока, измеряемая в амперах (А).
- R — это сопротивление, измеряемое в омах (Ом).
-
3
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
Чем быстрее меняется направление тока, тем больше индуктивное сопротивление. - Емкостным сопротивлением XC обладают конденсаторы, которые накапливают электрический заряд. При изменении направления тока в цепи конденсатор неоднократно обнуляет и накапливает электрический заряд. Чем дольше конденсатор заряжается, тем больше емкостное сопротивление.[4]
Поэтому чем быстрее меняется направление тока, тем меньше емкостное сопротивление.
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
-
4
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: XL = 2πƒL, где L — индуктивность, измеряемая в генри (Гн).[5]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
Также вы можете измерить индуктивность. - Если вы знакомы с единичной окружностью, то представьте, что один цикл переменного тока равен одному полному вращению этой окружности (на 2π радиан). Если умножить это значение на ƒ, которая измеряется в герцах (единиц в секунду), вы получите результат, измеряемый в радианах в секунду. Это единица измерения угловой скорости, которая обозначается через ω. Вы можете переписать формулу для вычисления индуктивного сопротивления так: XL=ωL[7]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
-
5
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: XC = 1 / 2πƒC.[8]
С — это емкость конденсатора, измеряемая в фарадах (Ф).- Вы можете измерить электрическую емкость.
- Эту формулу можно переписать так: XC = 1 / ωL (объяснения см. выше).
Реклама
-
1
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.[9]
- Если резисторы соединены последовательно, то полное сопротивление R = R1 + R2 + R3…
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R1 + 1 / R2 + 1 / R3 …
-
2
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:[10]
- Последовательное соединение катушек: Xtotal = XL1 + XL2 + …
- Последовательное соединение конденсаторов: Ctotal = XC1 + XC2 + …
- Параллельное соединение катушек: Xtotal = 1 / (1/XL1 + 1/XL2 …)
- Параллельное соединение конденсаторов: Ctotal = 1 / (1/XC1 + 1/XC2 …)
-
3
Вычтите индуктивные и емкостные сопротивления, чтобы получить общее реактивное сопротивление. Так как при возрастании одного типа сопротивления другое уменьшается, то они, как правило, компенсируют друг друга. Чтобы найти общее реактивное сопротивление, вычтите меньшее сопротивление из большего.[11]
- Или воспользуйтесь формулой: Xtotal = |XC – XL|
-
4
Вычислите импеданс по активному и реактивному сопротивлениям в последовательной цепи. Нельзя просто сложить эти величины, так как они меняются с течением времени, но достигают максимальных значений в разное время.[12]
Поэтому воспользуйтесь формулой:Z = √(R2 + X2).[13]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
[15]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
-
5
Вычислите импеданс по активному и реактивному сопротивлениям в параллельной цепи. В этом случае используются комплексные числа (это единственный способ вычислить полное сопротивление в параллельной цепи, в которой есть как активное, так и реактивное сопротивление).
- Z = R + jX, где j — мнимая единица: √(-1). Используйте j вместо i, чтобы не перепутать мнимую единицу (j) с силой тока (I).
- Складывать эти числа нельзя. Например, полное сопротивление может быть представлено так: 60 Ом + j120 Ом.
- Если у вас есть две последовательные цепи, то вы можете отдельно сложить натуральные числа и отдельно — комплексные. Например, если Z1 = 60 Ом + j120 Ом, а к этой цепи последовательно подключен резистор с Z2 = 20Ω, то Ztotal = 80Ω + j120Ω.
Реклама
Советы
- Общее сопротивление (активное и реактивное сопротивления) также может быть выражено через мнимое число.
Реклама
Об этой статье
Эту страницу просматривали 168 436 раз.
Была ли эта статья полезной?
Список всех статей на технические темы
Простая электротехника все статьи
Простейшие цепи переменного тока
Сначала читаем статью “Переменный ток – краткие сведения”
Все электротехнические устройства состоят из сопротивлений индуктивностей и емкостей
Соотношение индуктивности емкости в цепи переменного тока принципиально определяют свойства цепи переменного тока.
Активное сопротивление R – это такой элемент электрической цепи, который оказывает сопротивление току с выделением тепла. Ведет себя одинаково в цепях постоянного и переменного тока, хотя величина сопротивления несколько отличается, это придется учитывать в точных расчетах.
Индуктивность L –это такой элемент электрической цепи, который состоит из витков провода и при протекании тока создает магнитное поле, это магнитное поле противодействует изменениям тока.
При протекании постоянного тока индуктивность ведет себя как проволока и не считается сопротивлением. Сопротивлением она является только для переменного тока, чем больше частота переменного тока, тем больше сопротивление индуктивности.
Емкость C – это такой элемент электрической цепи, в котором возникает электрическое поле. емкость проводит ток, только пока заряжается, или разряжается, поэтому в цепях постоянного тока, она тока не проводит, а в цепях переменного тока все время заряжается – разряжается и, значит, проводит ток. Сопротивление емкости переменному току тем меньше, чем выше частота переменного тока.
Емкость и индуктивность взаимно противоположные по свойствам элементы, значит, они могут снижать взаимное влияние в цепях переменного тока или совсем отключать друг друга. Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.
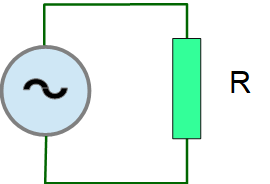
Активное сопротивление R в цепи переменного тока
Что нам интересно знать про простейшую электрическую цепь содержащую R ?
Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.
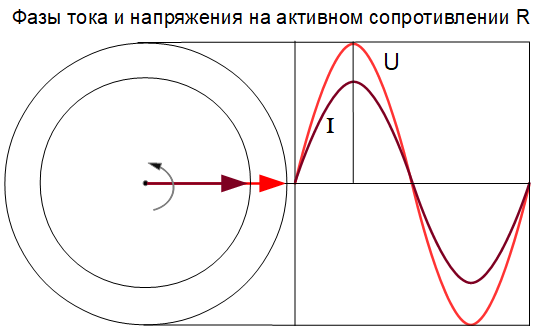
Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток
Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.
Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.
Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,
Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.
Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.
P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2
Средняя мощность за период равна постоянной составляющей мощности
Uа Iа/2
Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P
Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.
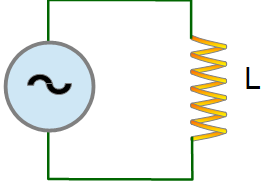
Индуктивное сопротивление в цепи переменного тока
XL = ωL
Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку
Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.
Что же происходит в цепи с индуктивностью при протекании переменного тока.
Оказывается, ток и напряжение действуют не одновременно,
то есть, сдвинуты по фазе
На активном сопротивлении R, появление напряжения, и сразу – в тот же момент, оно вызывает появление тока, и они действуют в одной фазе.
На индуктивности так не получается.
Если напряжение от источника начинает нарастать, то ток за ним не успевает.
Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.
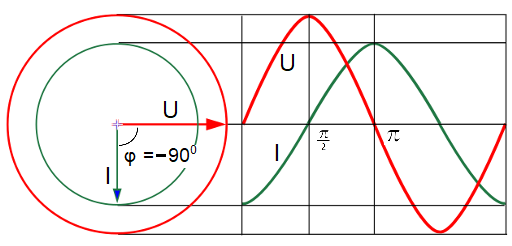
Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 900 то есть на π/2. Значит, фаза тока отрицательна и составляет – π/2
Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.
Более подробно об ЭДС самоиндукции смотри в статье Начальные представления об электромагнетизме
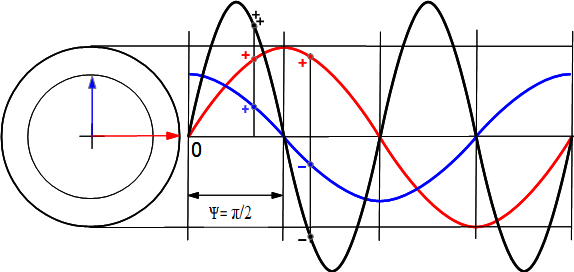
Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2
Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.
Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..
R – активное сопротивление – на нем выделяется тепло
X – реактивное сопротивление на нем не выделятся тепло
XL – сопротивление индуктивности
XL – сопротивление индуктивности L является реактивным, оно равно XL = ωL, то есть, оно прямо пропорционально частоте ω и индуктивности L, чем больше индуктивность, тем больше реактивное сопротивление и чем выше частота тем больше реактивное сопротивление.
Индуктивность тем сильнее ограничивает ток, чем выше частота тока.
Индуктивность пропускает переменный ток тем лучше, чем меньше индуктивность и чем меньше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток индуктивность пропускает без всякого сопротивления
Мощность на индуктивности
Мощность определяется как произведение тока на напряжение. Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.
Частота синусоиды мощности вдвое больше частоты тока и напряжения.
На индуктивности не получается выделение тепла, и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на индуктивности, называется реактивной и обозначается не Р, а другой буквой – QL
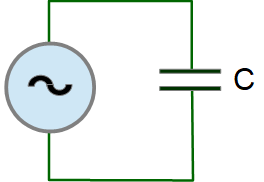
Емкость в цепи переменного тока
XC = 1/ ωc
При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.
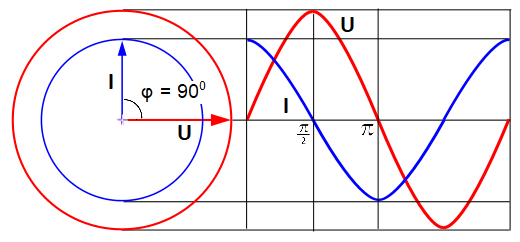
Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.
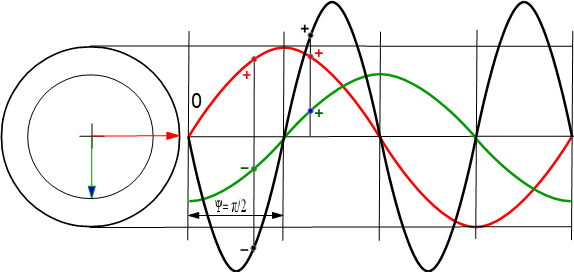
Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.
То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2
XC – сопротивление емкости
XC – сопротивление емкости является реактивным, оно равно XC = 1/ ωc, то есть оно обратно пропорционально частоте и емкости, чем больше емкость, тем меньше реактивное сопротивление и чем выше частота тем меньше меньше реактивное сопротивление.
Емкость пропускает переменный ток тем лучше, чем больше емкость и чем выше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток емкость вообще не пропускает.
Конденсатор часто ставят в участки цепей, в которых не должен проходить постоянный ток
Мощность в цепи с емкостью
Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.
Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник. Частота синусоиды мощности вдвое больше частоты тока и напряжения.
Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.
Реактивные сопротивления
Индуктивность и емкость проявляют себя в электрических цепях как сопротивления.
XC – реактивное сопротивление емкости
XL – реактивное сопротивление индуктивности
Формулы сопротивлений позволяют их использовать для расчета задач по закону Ома для участка цепи.
Формула XC = 1/ ωc показывает, что сопротивление емкости зависит от частоты ω. Это означает, что емкость по-разному пропускает ток низкой и высокой частоты.
Емкость пропускает переменный ток тем лучше, чем выше частота.
Емкость вообще не пропускает постоянный ток, и это ее важнейшее свойство. Одно из главных применений емкости (конденсатора) состоит в том, что его ставят в те ветви схем, где запрещено протекание постоянного тока.
Формула XL = ωL показывает, что сопротивление индуктивности зависит от частоты. Это означает, что индуктивность по-разному пропускает ток низкой и ток высокой частоты.
Индуктивность хуже пропускает переменный ток высокой частоты
Чем больше частота. Тем труднее проходит переменный ток. Катушка индуктивности используется для ограничения переменного тока.
Конденсатор и катушка являются противоположностями.
Конденсатор пропускает переменный ток и не пропускает постоянный
Катушка пропускает постоянный ток и не пропускает переменный
Реальные электрические цепи переменного тока
Такие цепи содержат сопротивление R, индуктивность L, и ёмкость C.
Реальное сопротивление цепи, содержащей одновременно R, L и C, зависит от величины каждого элемента цепи, и от частоты переменного тока, который протекает в этой цепи.
Расчет цепей переменного тока по аналогии с расчетом цепей постоянного тока невозможен, потому, что необходимо учитывать фазовый сдвиг между током и напряжением.
Можно упростить цепи, если какой-то элемент: R, L или C пренебрежительно мал.
Задачи на переменный ток решаются методом векторных диаграмм.
Ток и напряжение являются векторными величинами.Их изображают как вращающиеся радиус -векторы, в этом смысле они отличаются от векторов сил и скоростей в механике, но правила сложения и вычитания векторов аналогичны.
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
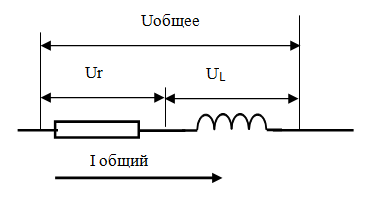
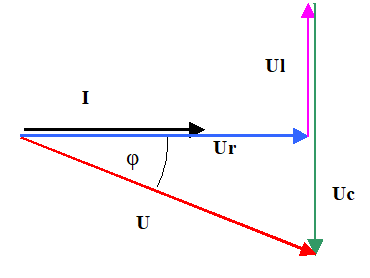
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
Выберем фазу общего тока равной 0, вектор тока откладывается как горизонтальный вектор слева на право. Далее строим векторную диаграмму напряжений. Сначала откладывается вектор напряжения на сопротивлении R. Этот вектор, пойдет горизонтально, так как его фаза совпадает с фазой тока. Затем строят вектор напряжения на индуктивности L. Его надо откладывать под углом 900 вверх, это потому, что напряжение на индуктивности впереди на 900.
Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.
Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора к концу второго.
Получился прямоугольный треугольник. Любую сторону этого треугольника можно найти по теореме Пифагора.
Острый угол этого треугольника и есть реальный сдвиг фаз в этой цепи между током и общим напряжением. Он обязательно меньше 90 градусов, потому что только на идеально индуктивности он составляет 90 градусов. Активное сопротивление обязательно уменьшает сдвиг фаз.
Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление, обозначается Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и XL
Z2, = Rа2 + X2L
В цепи L R, в отличие от цепи только с L, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.
Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и QL
S2 = Р2 + Q2L
Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников.
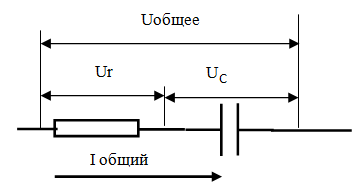
Последовательное соединение RC
Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие “добротность” конденсатора, которая проявляет активную составляющую его сопротивления
При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.
Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.
К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.
Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.
Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.
Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и XС
Z 2 = Rа2 + X2С
В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.
Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и QС
S2 = Р2 + Q2С
Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников
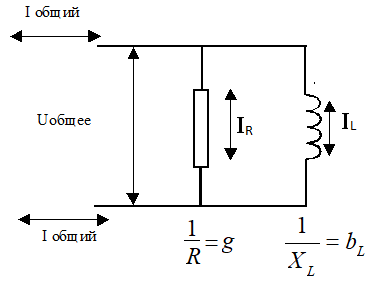
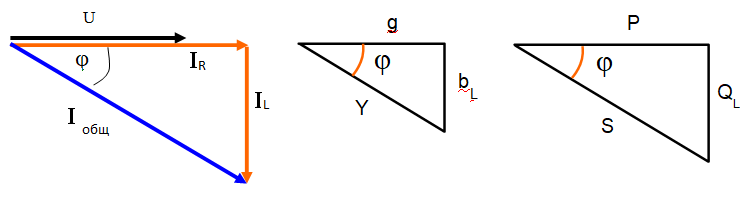
Параллельное соединение RL
При параллельном соединении RL одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через катушку отстает по фазе от напряжения. на 900. Общий ток отстает от напряжения меньше чем на 900.
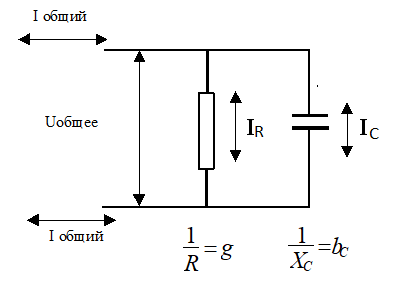
Для цепей с параллельным соединением элементов, гораздо удобнее использовать не сопротивления (активные и реактивные) а их обратные величины, которые называются проводимости. Вместо r используется g, вместо XL используется bL, вместо Xc используется bc
Параллельное соединение RC
При параллельном соединении RС одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через конденсатор опережает по фазе от напряжения. на 900. Общий ток опережает напряжение меньше чем на 900
Значение Cos φ
Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).
Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .
Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.
В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.
Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.
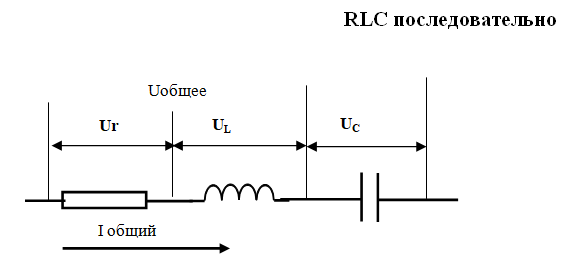
Цепи RLC
Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.
В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.
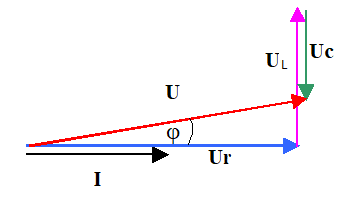
RLC последовательно
Как будет выглядеть векторная диаграмма в общем случае?
При последовательном соединении сопротивлений на каждом сопротивлении действует своя часть напряжения. На большем сопротивлении будет большая часть напряжения.
На первой векторной диаграмме видно, что напряжение на конденсаторе Uc больше, чем на катушке UL тогда суммарный вектор общего напряжения направлен вниз, и видно, xnj угол сдвига фаз отрицательный. На второй диаграмме видно, что напряжение на конденсаторе Uc, значительно меньше, чем UL , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.
В первом случае цепь имеет емкостный характер, во втором индуктивный.
На определенной частоте наступает равенство Uc = Ul, такое явление называется резонанс напряжений
Условие резонанса XL = XC
При резонансе напряжений Общее сопротивление цепи становится минимально, а ток становится максимальным, что может быть опасно для источника и требует надежной защиты.
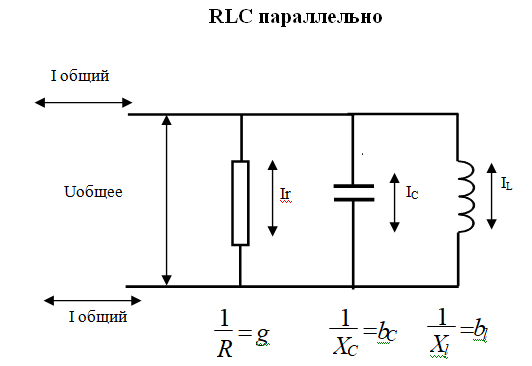
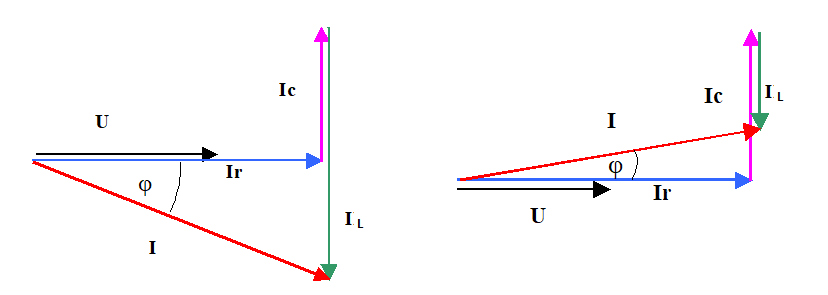
RLC параллельно
Векторные диаграммы токов при параллельном соединении
При параллельно соединении элементов RLC напряжение на всех элементах действует одно и то же, а токи разные, чем меньше сопротивление ветви, тем больше ток. В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.
В первом случае цепь имеет индуктивный характер, во втором емкостный
На определенной частоте наступает равенство токов Ic = IL такое явление называется резонанс токов.
При резонансе токов сопротивление цепи становится максимальным и ток уменьшается до величины, которая определяется сопротивлением R, которое остается в цепи.
Условия резонанса
Резонанс широко применяется в радиотехнических и различных электронных схемах.
XL = XC
Устройства для переменного тока и устройства для постоянного тока
Устройства. Которые включаются в электрические цепи
Лампочки
Нагреватели
Электромоторы
Электроинструмент
Бытовые приборы
Электроника
И т. п.
Лампочки и нагреватели работают одинаково в цепях переменного и постоянного тока. В некоторых случаях разница может быть заметной, так как активное сопротивление в цепи постоянного тока (омическое) может отличаться от сопротивления в цепи переменного тока.
Электромоторы и электроинструмент рассчитанный на переменный ток, при подключении в цепь постоянного тока скорее всего сгорят, так как, у них пропадает индуктивное сопротивление и ток сильно возрастает.
Если моторы, и инструмент рассчитанные на постоянный ток, включены на переменный ток, они сильно потеряют мощность, так как появляется индуктивное сопротивление и сильно ограничит потребляемый ток.
Добавил(а) microsin
Удобные методы онлайн-расчета сопротивления емкости C и индуктивности L переменному току с частотой F.
[Xc – сопротивление конденсатора переменному току]
Формула для расчета: Xc = 1/(2*pi*F*C), где Xc – сопротивление конденсатора переменному току в Омах, F – частота в Герцах, C – емкость в Фарадах. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах – Гц, мкФ, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Xl – сопротивление индуктивности переменному току]
Формула для расчета: Xl = 2*pi*F*L, где Xl – сопротивление индуктивности переменному току в Омах, F – частота в Герцах, L – индуктивность в Генри. В таблице ниже расчет ведется по той же формуле, но в более удобных единицах – Гц, мкГн, Ом. В качестве исходных параметров можно использовать числа с плавающей запятой (запятая указывается в виде точки).
[Общие замечания по использованию калькуляторов]
1. 1 микрофарад (мкф) = 1000000 пикофарад (пФ). 1 фарад (Ф) = 1000000 микрофарад (мкФ) = 1012 пикофарад (пФ).
2. Десятичные значения с точкой нужно вводить с точкой, а не с запятой, иначе скрипт будет выдавать “infinity”. Например, емкость 50 пФ следует ввести как 0.00005.
[Ссылки]
1. Микрофарад, Электрическая ёмкость site:convertworld.com. Очень удобный калькулятор для преобразования физических величин.
2. Расчёт резонансной частоты колебательного контура.
3. Расчет начальной магнитной проницаемости ферритовых колец по пробной обмотке.
4. Расчет дросселей на резисторах МЛТ.