Время на прочтение
6 мин
Количество просмотров 23K
Здравствуй, Хабр. И сразу к делу.
Задача:
Есть два целых числа: L и R. Нужно найти максимальное значение A xor B на промежутке [L; R], где L ≤ A ≤ B ≤ R.
Казалось бы ничего сложного. Сразу напрашивается решение простым перебором.
Развернуть
public int BruteForce(int one, int two)
{
int maxXor = 0;
while (one < two)
{
int oneTemp = one + 1;
while (oneTemp <= two)
{
int curXor = one ^ oneTemp;
if (maxXor < curXor) maxXor = curXor;
oneTemp++;
}
one++;
}
return maxXor;
}
Сложность этого решения O(n2).
А что, если в интервале будет 1000000 чисел. Возьмем L = 1, а R = 1000001. Сколько времени понадобится cреднестатистическому компьютеру для того, чтобы посчитать максимальное значение xor на этом интервале? Моему ноутбуку потребовалось 1699914 миллисекунд.
Существует решение, которое работает значительно быстрее, именно о нем и пойдет речь в этой статье.

Основная идея.
Чтобы результирующее число было наибольшим, необходимо в как можно старшем бите этого числа получить единицу от функции xor. И так далее, по направлении к самому младшему биту. Другими словами будем последовательно работать с каждым битом результирующего числа по направлению от старших битов к младшим. Для этого очень удобно использовать структуру данных, которая называется trie-дерево (мне нравится как эта структура данных описана в книге Р.Сейджвика «Алгоритмы на Java»).
Trie-деревья представляют собой структуры данных, которые состоят из узлов, содержащих ссылки — или нулевые, или ссылки на другие узлы. На каждый узел указывает только один другой узел (на корневой узел не указывает ни один узел). Каждый узел содержит R ссылок, где R — размер алфавита ( в нашем случае R = 2, так как алфавит это 0 и 1). Как правило, trie-деревья содержат значительное количество нулевых ссылок, поэтому на картинках они будут опущены. Каждая ссылка соответствует очередному биту числа. Каждое целое число кодируется как путь от корня к листу.
Пример пустого trie-дерева.

Так выглядит trie-дерево после добавления 0, 1, 2, 3, 4, 5, 6, 7.
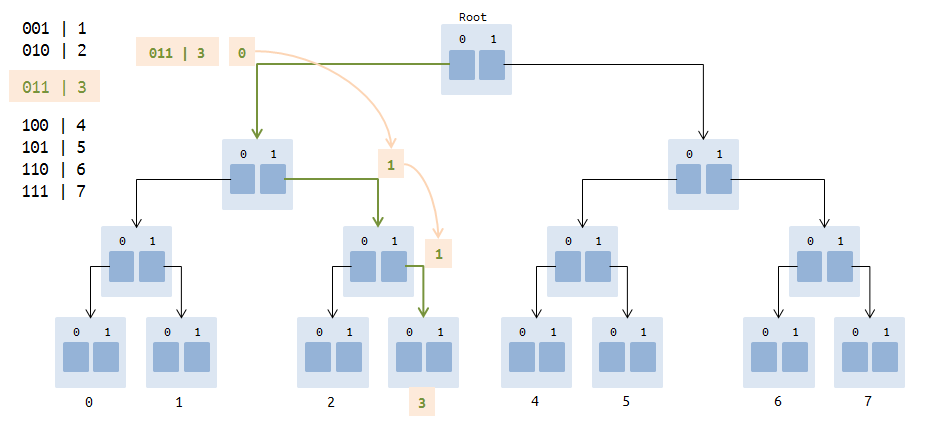
На рисунке выделен путь, состоящий из 3 ссылок — 0 ->1->1( 011 это двоичное представление числа 3).
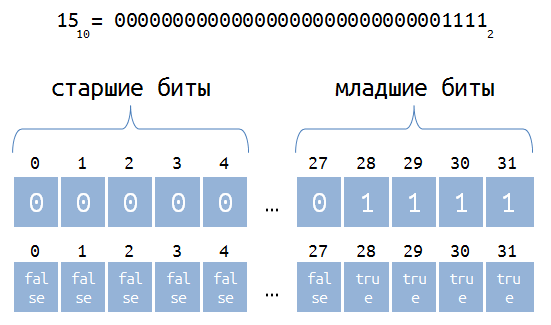
Сразу хочу пояснить, что мы будем работать только с 32-битными числами, причем старшие биты будут заполняться нулями при необходимости. Этим мы добиваемся, что числа будут храниться в массивах с одинаковой длиной. Двоичное представление целых чисел я решил хранить в массиве типа bool.
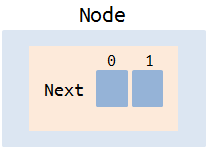
Каждый узел хранит массив ссылок на другие узлы дерева ( 2 ссылки, по одной для каждого возможного значения бита числа).
Вообще trie-дерево — это структура данных, построенная из символов строковых ключей, которая позволяет использовать символы искомого ключа для управления поиском. Строковые ключи могут быть разной длины, поэтому в каждом узле дерева дополнительно хранят значение, которое может быть нулевым или реальным значением, связанным с одним из строковых ключей. В нашем же случае, нам не обязательно хранить значение, так как ключами являются целые 32-битные числа, хранящиеся в двоичном виде в массивах одинаковой длины. Итак, trie-дерево:
using System;
namespace MaxXor
{
public class Trie
{
//for integer representation in binary system 2^32
public static readonly int MaxLengthOfBits = 32;
//size of alphabet
public static readonly int N = 2;
class Node
{
public Node[] next = new Node[Trie.N];
}
private Node _root;
}
}
Во-первых нам понадобятся функции перевода чисел из десятичной в двоичную и обратно. Тут все предельно понятно и просто. Если нужно освежить память, то можете подглядеть.
ConvertDecimalToBInary
private bool[] ConvertDecimalToBInary(int number)
{
int counter = Trie.MaxLengthOfBits;
bool[] result = new bool[counter];
while (number > 0)
{
result[--counter] = Convert.ToBoolean(number % 2);
number /= 2;
}
return result;
}
ConvertBinaryToDecimal
private int ConvertBinaryToDecimal(bool[] bits)
{
int result = 0;
int base_val = 1;
for (int i = bits.Length - 1; i >= 0; i--)
{
result += Convert.ToInt32(bits[i]) * base_val;
base_val *= 2;
}
return result;
}
Во-вторых нам понадобится функция добавления целого числа в trie-дерево. Здесь остановимся по-подробнее. Для вставки в trie-дерево сначала нужно выполнить поиск нужного узла. Поиск, начинается с корня, а затем следует по ссылке, связанной с нулевым(самым старшим) битом числа; от этого узла проходит по ссылке, связанной с первым битом числа; оттуда — по ссылке, связанной со вторым битом числа; и т.д., то есть нужно просто просматривать узлы по пути от корня до некоторого узла в trie-дереве. Биты числа используются для спуска по дереву до достижения последнего бита или нулевой ссылки. Если обнаружена нулевая ссылка до выборки последнего бита числа, т.е. в trie-дереве нет узла, соответствующего последнему биту числа, то необходимо создавать узлы для каждого из отсутствующих битов.
public void AddValue(bool[] binaryNumber)
{
_root = AddValue(_root, binaryNumber, 0);
}
private Node AddValue(Node node, bool[] val, int d)
{
if (node == null) node = new Node();
//if least sagnificient bit has been added
//need return
if (d == val.Length)
{
return node;
}
// get 0 or 1 index of next array(length 2)
int index = Convert.ToInt32(val[d]);
node.next[index] = AddValue(node.next[index], val, ++d);
return node;
}Теперь построим trie-дерево, добавив все числа из заданного промежутка.
Update: Как верно первым подметил freopen,
достаточно найти самый первый бит, который различается, с битами выше ничего сделать нельзя, биты ниже легко сделать единицами
Итак, найдем самый первый бит, который различается, для этого будем двигаться от корня по ссылкам, пока не встретим узел, у которого существуют обе ссылки. Затем все биты ниже сделаем единицами. В итоге получим результат.
public bool[] GetMaxXor()
{
bool[] result = new bool[Trie.MaxLengthOfBits];
Node cur = _root;
//find index the most significant bit, which is different
int index;
for (index = 0; index < Trie.MaxLengthOfBits; index++)
{
//are bits differ?
if (cur.next[0] != null && cur.next[1] != null)
{ //the most significant bit, which is different
result[index] = true;
break;
}
//descent down the tree
cur = cur.next[0] ?? cur.next[1];
}
//all the bits below do 1
while (index < Trie.MaxLengthOfBits)
{
result[index] = true;
index++;
}
return result;
}
Существенное упрощение кода, но сложность остается прежней! Архив с обновленным солюшеном проекта можно скачать здесь.
Старая версия
Переходим к самому главному. Для поиска максимального значения xor, будем двигаться по trie-дереву от корня по ссылкам, то есть будем работать с битами по направлению от старших к младшим. Причем мы можем находится как в одном узле, так и в разных. При каждом проходе будем стараться получить единицу, если это возможно, от xor-а очередных битов чисел, и так далее, пока не получим все 32 бита. Получившиеся 32 бита — это и есть максимальное значение xor на нашем промежутке.
public bool[] GetMaxXor()
{
bool[] result = new bool[Trie.MaxLengthOfBits];
Node oneNode = _root, twoNode = _root;
//for each bit from most significant bit to least significant bit
for (int i = 0; i < Trie.MaxLengthOfBits; i++)
{
//getting current bit
result[i] = GetBit(oneNode, twoNode);
//go to next nodes
UpdateNodes(ref oneNode, ref twoNode);
}
return result;
}
//we need update nodes after each iteration
//we can stay on single node or split on two nodes
private void UpdateNodes(ref Node one, ref Node two)
{
if (one.Equals(two))
{
if (one.next[1] != null && one.next[0] != null)
{
two = one.next[1];
one = one.next[0];
}
else
{
one = two = ((one.next[1] != null) ? one.next[1] : one.next[0]);
}
}
else
{
if (one.next[1] != null && two.next[0] != null)
{
one = one.next[1];
two = two.next[0];
}
else if (one.next[0] != null && one.next[1] == null)
{
one = one.next[0];
two = two.next[1];
}
else
{
one = one.next[1] ?? one.next[0];
two = two.next[1] ?? two.next[0];
}
}
}
//if it's possible, we will try to get one.
private bool GetBit(Node one, Node two)
{
if (one.Equals(two))
{
// 0 xor 1 == 1; 1 xor 0 == 1
if (one.next[0] != null && one.next[1] != null) return true;
// 0 xor 0 == 0; 1 xor 1 == 0
else return false;
}
else
{
if ((one.next[1] != null && two.next[0] != null) || // 1 xor 0 == 1
(one.next[0] != null && one.next[1] == null)) // 0 xor 1 == 1
{
return true;
}
else
{// 0 xor 0 == 0; 1 xor 1 == 0
return false;
}
}
}
Пример для 3-битных чисел
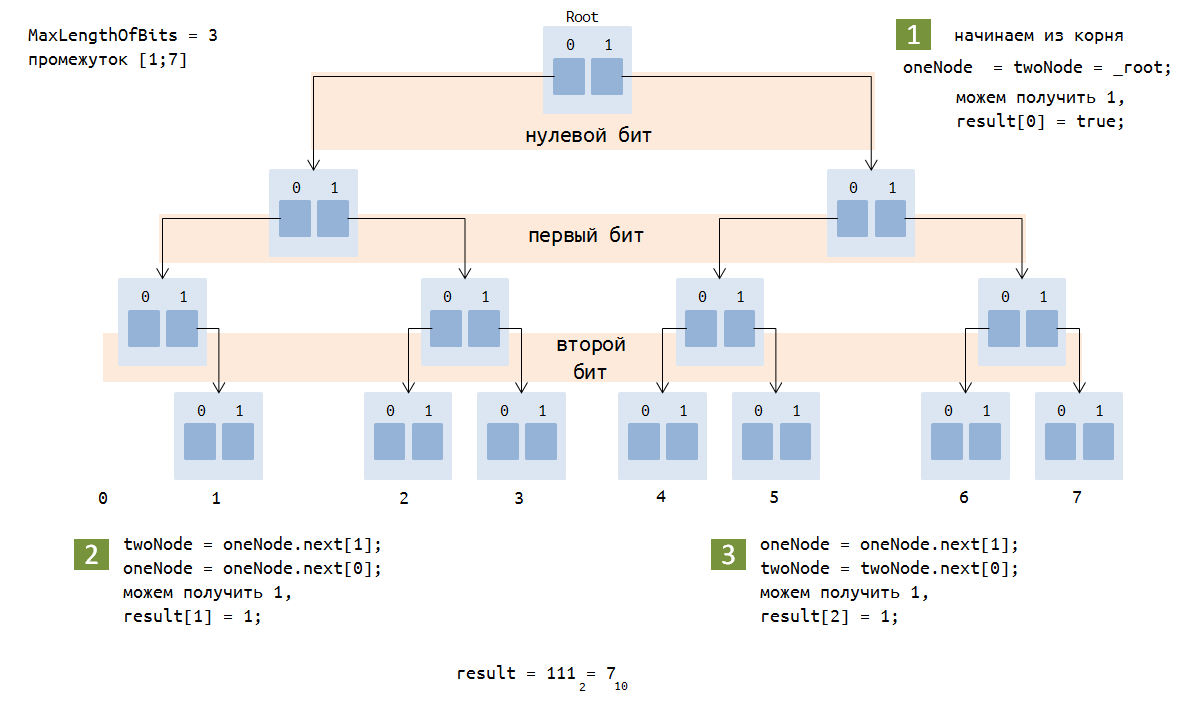
Архив с солюшеном проекта можно скачать здесь.
Теперь, можно сравнить время работы каждого из подходов для промежутков разной длины.
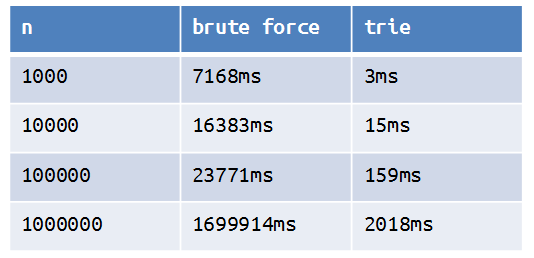
Как видно из таблицы вычисление максимального значения xor с помощью trie-дерева работает значительно быстрее. Оценка сложности алгоритма O(nlogn).
P.S. Для решения данной задачи, да и вообще для хранения целых чисел в двоичном виде можно слегка упростить наше trie-дерево. Так как алфавит состоит всего из 2 символов, можно избавиться от массива и хранить просто две ссылки, например Node left и Node right, которые являются представлением 0 и 1 соответственно.
Bit stands for binary digit. A bit is the basic unit of information and can only have one of two possible values that is 0 or 1.
In our world, we usually with numbers using the decimal base. In other words. we use the digit 0 to 9 However, there are other number representations that can be quite useful such as the binary number systems.

Introduction to Bitwise Algorithms – Data Structures and Algorithms Tutorial
Unlike humans, computers have no concepts of words and numbers. They receive data encoded at the lowest level as a series of zeros and ones (0 and 1). These are called bits, and they are the basis for all the commands they receive. We’ll begin by learning about bits and then explore a few algorithms for manipulating bits. We’ll then explore a few algorithms for manipulating bits. The tutorial is meant to be an introduction to bit algorithms for programmers.
Need of the Bitwise Algorithms :-
Bitwise algorithms are an important tool in computer science and programming because they allow for efficient manipulation and processing of binary data. Here are a few reasons why bitwise algorithms are necessary:
Space Efficiency: Bitwise algorithms can be used to represent data in a more compact form, saving space in memory and on disk.
Time Efficiency: Bitwise operations are often faster than their equivalent operations using other data types, such as integers. This can lead to significant performance gains in time-sensitive applications.
Masking and Bitwise Encoding: Bitwise algorithms can be used to mask bits of data, which is useful for data encryption and compression. Bitwise encoding is also used to encode and decode data in a compact form, which is useful for transmitting data over networks and storing data on disk.
Optimization: Bitwise algorithms can be used to optimize algorithms by allowing for efficient manipulations of data at the binary level.
Hardware Interaction: Bitwise algorithms are often used to interact directly with hardware components, such as memory, networks, and processors, as well as to manipulate binary data in machine-level programming languages, such as Assembly.
Overall, bitwise algorithms play a critical role in modern computing and are a valuable tool for efficient data manipulation and processing.
Advantages of Bitwise Algorithms:
Speed: Bitwise operations are fast and efficient as they are performed directly on the binary representation of data, without the need for conversion to other data types.
Space Efficiency: Bitwise algorithms can be used to represent data in a more compact form, saving space in memory and on disk.
Masking and Bitwise Encoding: Bitwise algorithms can be used to mask bits of data, which is useful for data encryption and compression. Bitwise encoding is also used to encode and decode data in a compact form, which is useful for transmitting data over networks and storing data on disk.
Optimization: Bitwise algorithms can be used to optimize algorithms by allowing for efficient manipulations of data at the binary level.
Hardware Interaction: Bitwise algorithms are often used to interact directly with hardware components, such as memory, networks, and processors, as well as to manipulate binary data in machine-level programming languages, such as Assembly.
Disadvantages of Bitwise Algorithms:
Complexity: Bitwise algorithms can be difficult to understand and implement, particularly for those who are not familiar with binary representations of data and bitwise operations.
Portability: Bitwise algorithms can be platform-specific and may not be portable across different systems, particularly when dealing with binary data at the machine level.
Maintenance: Bitwise algorithms can be difficult to maintain and debug, particularly when dealing with complex bitwise operations and manipulations.
Performance: While bitwise operations can be fast and efficient, they may not be the best choice for every situation. In some cases, other data types and algorithms may be more suitable for a particular task.
Basics of Bit manipulation (Bitwise Operators)
An algorithmic operation known as bit manipulation involves the manipulation of bits at the bit level (bitwise). Bit manipulation is all about these bitwise operations. They improve the efficiency of programs by being primitive, fast actions.
The computer uses this bit manipulation to perform operations like addition, subtraction, multiplication, and division are all done at the bit level. This operation is performed in the arithmetic logic unit (ALU) which is a part of a computer’s CPU. Inside the ALU, all such mathematical operations are performed.
There are different bitwise operations used in bit manipulation. These bit operations operate on the individual bits of the bit patterns. Bit operations are fast and can be used in optimizing time complexity. Some common bit operators are:
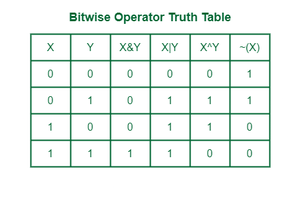
Bitwise Operator Truth Table
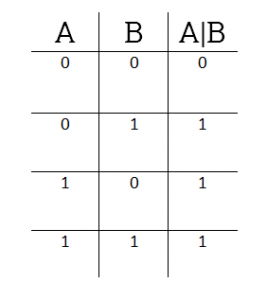
1. Bitwise AND Operator (&)
The bitwise AND operator is denoted using a single ampersand symbol, i.e. &. The & operator takes two equal-length bit patterns as parameters. The two-bit integers are compared. If the bits in the compared positions of the bit patterns are 1, then the resulting bit is 1. If not, it is 0.
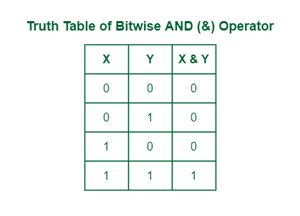
Truth table of AND operator
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y
Bitwise ANDof (7 & 4)
Implementation of AND operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 7, b = 4;
int result = a & b;
cout << result << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main (String[] args) {
int a = 7, b = 4;
int result = a & b;
System.out.println(result);
}
}
C#
using System;
public class GFG{
static public void Main (){
int a = 7, b = 4;
int result = a & b;
Console.WriteLine(result);
}
}
Python3
a = 7
b = 4
result = a & b
print(result)
Javascript
let a = 7, b = 4;
let result = a & b;
console.log(result);
Time Complexity: O(1)
Auxiliary Space: O(1)
2 Bitwise OR Operator (|)
The | Operator takes two equivalent length bit designs as boundaries; if the two bits in the looked-at position are 0, the next bit is zero. If not, it is 1.
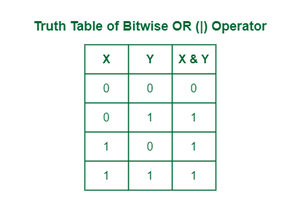
Truth table of OR operator
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise OR of both X, y
Bitwise OR of (7 | 4)
Explanation: On the basis of truth table of bitwise OR operator we can conclude that the result of
1 | 1 = 1
1 | 0 = 1
0 | 1 = 1
0 | 0 = 0We used the similar concept of bitwise operator that are show in the image.
Implementation of OR operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a = 12, b = 25;
int result = a | b;
cout << result;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a | b;
System.out.println(result);
}
}
Python3
a = 12
b = 25
result = a | b
print(result)
C#
using System;
public class GFG{
static public void Main (){
int a = 12, b = 25;
int result = a | b;
Console.WriteLine(result);
}
}
Javascript
let a = 12, b = 25;
let result = a | b;
document.write(result);
Time Complexity: O(1)
Auxiliary Space: O(1)
3. Bitwise XOR Operator (^)
The ^ operator (also known as the XOR operator) stands for Exclusive Or. Here, if bits in the compared position do not match their resulting bit is 1. i.e, The result of the bitwise XOR operator is 1 if the corresponding bits of two operands are opposite, otherwise 0.
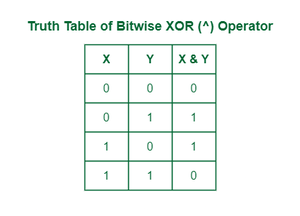
Truth Table of Bitwise Operator XOR
Example:
Take two bit values X and Y, where X = 7= (111)2 and Y = 4 = (100)2 . Take Bitwise and of both X & y
Bitwise OR of (7 ^ 4)
Explanation: On the basis of truth table of bitwise XOR operator we can conclude that the result of
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0We used the similar concept of bitwise operator that are show in the image.
Implementation of XOR operator:
C++
#include <iostream>
using namespace std;
int main()
{
int a = 12, b = 25;
cout << (a ^ b);
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 12, b = 25;
int result = a ^ b;
System.out.println(result);
}
}
Python3
a = 12
b = 25
result = a ^ b
print(result)
C#
using System;
public class GFG {
static public void Main()
{
int a = 12, b = 25;
int result = a ^ b;
Console.WriteLine(result);
}
}
Javascript
let a = 12;
let b = 25;
console.log((a ^ b));
Time Complexity: O(1)
Auxiliary Space: O(1)
4. Bitwise NOT Operator (!~)
All the above three bitwise operators are binary operators (i.e, requiring two operands in order to operate). Unlike other bitwise operators, this one requires only one operand to operate.
The bitwise Not Operator takes a single value and returns its one’s complement. The one’s complement of a binary number is obtained by toggling all bits in it, i.e, transforming the 0 bit to 1 and the 1 bit to 0.

Truth Table of Bitwise Operator NOT
Example:
Take two bit values X and Y, where X = 5= (101)2 . Take Bitwise NOT of X.
Explanation: On the basis of truth table of bitwise NOT operator we can conclude that the result of
~1 = 0
~0 = 1We used the similar concept of bitwise operator that are show in the image.
Implementation of NOT operator:
C++
#include <iostream>
using namespace std;
int main()
{
int a = 0;
cout << "Value of a without using NOT operator: " << a;
cout << "nInverting using NOT operator (with sign bit): " << (~a);
cout << "nInverting using NOT operator (without sign bit): " << (!a);
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int a = 0;
System.out.println(
"Value of a without using NOT operator: " + a);
System.out.println(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
System.out.println(
"Inverting using NOT operator (without sign bit): 1");
else
System.out.println(
"Inverting using NOT operator (without sign bit): 0");
}
}
Python3
a = 0
print("Value of a without using NOT operator: " , a)
print("Inverting using NOT operator (with sign bit): " , (~a))
print("Inverting using NOT operator (without sign bit): " , int(not(a)))
C#
using System;
public class GFG {
static public void Main()
{
int a = 0;
Console.WriteLine(
"Value of a without using NOT operator: " + a);
Console.WriteLine(
"Inverting using NOT operator (with sign bit): "
+ (~a));
if (a != 1)
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 1");
else
Console.WriteLine(
"Inverting using NOT operator (without sign bit): 0");
}
}
Javascript
let a =0;
document.write("Value of a without using NOT operator: " + a);
document.write( "Inverting using NOT operator (with sign bit): " + (~a));
if(!a)
document.write( "Inverting using NOT operator (without sign bit): 1" );
else
document.write( "Inverting using NOT operator (without sign bit): 0" );
Output
Value of a without using NOT operator: 0 Inverting using NOT operator (with sign bit): -1 Inverting using NOT operator (without sign bit): 1
Time Complexity: O(1)
Auxiliary Space: O(1)
5. Left-Shift (<<)
The left shift operator is denoted by the double left arrow key (<<). The general syntax for left shift is shift-expression << k. The left-shift operator causes the bits in shift expression to be shifted to the left by the number of positions specified by k. The bit positions that the shift operation has vacated are zero-filled.
Note: Every time we shift a number towards the left by 1 bit it multiply that number by 2.

Logical left Shift
Example:
Input: Left shift of 5 by 1.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 1)
Left shift of 5 by 1
Output: 10
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010102, Which is equivalent to 10Input: Left shift of 5 by 2.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 2)
Left shift of 5 by 2
Output: 20
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 101002, Which is equivalent to 20Input: Left shift of 5 by 3.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 3)
Left shift of 5 by 3
Output: 40
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010002, Which is equivalent to 40
Implementation of Left shift operator:
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 << 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 << 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num1 = 1024;
String bt1 = Integer.toBinaryString(num1);
bt1 = String.format("%32s", bt1).replace(' ', '0');
System.out.println(bt1);
int num2 = num1 << 1;
String bt2 = Integer.toBinaryString(num2);
bt2 = String.format("%32s", bt2).replace(' ', '0');
System.out.println(bt2);
int num3 = num1 << 2;
String bitset13 = Integer.toBinaryString(num3);
bitset13 = String.format("%16s", bitset13)
.replace(' ', '0');
System.out.println(bitset13);
}
}
Python3
num1 = 1024
bt1 = bin(num1)[2:].zfill(32)
print(bt1)
num2 = num1 << 1
bt2 = bin(num2)[2:].zfill(32)
print(bt2)
num3 = num1 << 2
bitset13 = bin(num3)[2:].zfill(16)
print(bitset13)
C#
using System;
class GFG {
public static void Main(string[] args)
{
int num1 = 1024;
string bt1 = Convert.ToString(num1, 2);
bt1 = bt1.PadLeft(32, '0');
Console.WriteLine(bt1);
int num2 = num1 << 1;
string bt2 = Convert.ToString(num2, 2);
bt2 = bt2.PadLeft(32, '0');
Console.WriteLine(bt2);
int num3 = num1 << 2;
string bitset13 = Convert.ToString(num3, 2);
bitset13 = bitset13.PadLeft(16, '0');
Console.WriteLine(bitset13);
}
}
Javascript
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 << 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 << 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
Output
00000000000000000000010000000000 00000000000000000000100000000000 0001000000000000
Time Complexity: O(1)
Auxiliary Space: O(1)
6. Right-Shift (>>)
The right shift operator is denoted by the double right arrow key (>>). The general syntax for the right shift is “shift-expression >> k”. The right-shift operator causes the bits in shift expression to be shifted to the right by the number of positions specified by k. For unsigned numbers, the bit positions that the shift operation has vacated are zero-filled. For signed numbers, the sign bit is used to fill the vacated bit positions. In other words, if the number is positive, 0 is used, and if the number is negative, 1 is used.
Note: Every time we shift a number towards the right by 1 bit it divides that number by 2.
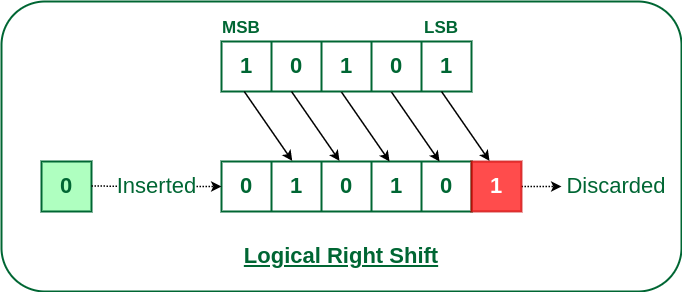
Logical Right Shift
Example:
Input: Left shift of 5 by 1.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 1)
Right shift of 5 by 1
Output: 10
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010102, Which is equivalent to 10Input: Left shift of 5 by 2.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 2)
Right shift of 5 by 2
Output: 20
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 101002, Which is equivalent to 20Input: Left shift of 5 by 3.
Binary representation of 5 = 00101 and Left shift of 001012 by 1 (i.e, 00101 << 3)
Right shift of 5 by 3
Output: 40
Explanation: All bit of 5 will be shifted by 1 to left side and this result in 010002, Which is equivalent to 40
Implementation of Right shift operator:
C++
#include <bitset>
#include <iostream>
using namespace std;
int main()
{
unsigned int num1 = 1024;
bitset<32> bt1(num1);
cout << bt1 << endl;
unsigned int num2 = num1 >> 1;
bitset<32> bt2(num2);
cout << bt2 << endl;
unsigned int num3 = num1 >> 2;
bitset<16> bitset13{ num3 };
cout << bitset13 << endl;
}
Javascript
let num1 = 1024;
let bt1 = num1.toString(2).padStart(32, '0');
console.log(bt1);
let num2 = num1 >> 1;
let bt2 = num2.toString(2).padStart(32, '0');
console.log(bt2);
let num3 = num1 >> 2;
let bitset13 = num3.toString(2).padStart(16, '0');
console.log(bitset13);
Output
00000000000000000000010000000000 00000000000000000000001000000000 0000000100000000
Time Complexity: O(1)
Auxiliary Space: O(1)
Application of BIT Operators
- Bit operations are used for the optimization of embedded systems.
- The Exclusive-or operator can be used to confirm the integrity of a file, making sure it has not been corrupted, especially after it has been in transit.
- Bitwise operations are used in Data encryption and compression.
- Bits are used in the area of networking, framing the packets of numerous bits which are sent to another system generally through any type of serial interface.
- Digital Image Processors use bitwise operations to enhance image pixels and to extract different sections of a microscopic image.
Important Practice Problems on Bitwise Algorithm:
1. How to Set a bit in the number?
If we want to set a bit at nth position in the number ‘num’, it can be done using the ‘OR’ operator( | ).
- First, we left shift 1 to n position via (1<<n)
- Then, use the “OR” operator to set the bit at that position. “OR” operator is used because it will set the bit even if the bit is unset previously in the binary representation of the number ‘num’.
Note: If the bit would be already set then it would remain unchanged.
Below is the implementation:
C++
#include <iostream>
using namespace std;
void set(int& num, int pos)
{
num |= (1 << pos);
}
int main()
{
int num = 4, pos = 1;
set(num, pos);
cout << (int)(num) << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 4, pos = 1;
num = set(num, pos);
System.out.println(num);
}
public static int set(int num, int pos)
{
num |= (1 << pos);
return num;
}
}
Python3
def set(num, pos):
num |= (1 << pos)
print(num)
num, pos = 4, 1
set(num, pos)
C#
using System;
public class GFG {
static public void Main()
{
int num = 4, pos = 1;
set(num, pos);
}
static public void set(int num, int pos)
{
num |= (1 << pos);
Console.WriteLine(num);
}
}
Javascript
<script>
function set(num,pos)
{
num |= (1 << pos);
console.log(parseInt(num));
}
let num = 4;
let pos = 1;
set(num, pos);
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
2. How to unset/clear a bit at n’th position in the number
Suppose we want to unset a bit at nth position in number ‘num’ then we have to do this with the help of “AND” (&) operator.
- First, we left shift ‘1’ to n position via (1<<n) then we use bitwise NOT operator ‘~’ to unset this shifted ‘1’.
- Now after clearing this left shifted ‘1’ i.e making it to ‘0’ we will ‘AND'(&) with the number ‘num’ that will unset bit at nth position.
Below is the implementation:
C++
#include <iostream>
using namespace std;
void unset(int& num, int pos)
{
num &= (~(1 << pos));
}
int main()
{
int num = 7;
int pos = 1;
unset(num, pos);
cout << num << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 7, pos = 1;
num = unset(num, pos);
System.out.println(num);
}
public static int unset(int num, int pos)
{
num = num & (~(1 << pos));
return num;
}
}
Python3
def unset(num, pos):
num &= (~(1 << pos))
print(num)
num, pos = 7, 1
unset(num, pos)
C#
using System;
public class GFG {
static public void Main()
{
int num = 7, pos = 1;
unset(num, pos);
}
static public void unset(int num, int pos)
{
num &= (~(1 << pos));
Console.WriteLine(num);
}
}
Javascript
function unset(num, pos)
{
return num &= (~(1 << pos));
}
let num = 7;
let pos = 1;
console.log(unset(num, pos));
Time Complexity: O(1)
Auxiliary Space: O(1)
3. Toggling a bit at nth position
Toggling means to turn bit ‘on'(1) if it was ‘off'(0) and to turn ‘off'(0) if it was ‘on'(1) previously. We will be using the ‘XOR’ operator here which is this ‘^’. The reason behind the ‘XOR’ operator is because of its properties.
- Properties of ‘XOR’ operator.
- 1^1 = 0
- 0^0 = 0
- 1^0 = 1
- 0^1 = 1
- If two bits are different then the ‘XOR’ operator returns a set bit(1) else it returns an unset bit(0).
Below is the implementation:
C++
#include <iostream>
using namespace std;
void toggle(int& num, int pos) { num ^= (1 << pos); }
int main()
{
int num = 4;
int pos = 1;
toggle(num, pos);
cout << num << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 4, pos = 1;
num = toggle(num, pos);
System.out.println(num);
}
public static int toggle(int num, int pos)
{
num ^= (1 << pos);
return num;
}
}
Python3
def toggle(num, pos):
num ^= (1 << pos)
print(num)
num, pos = 4, 1
toggle(num, pos)
C#
using System;
public class GFG {
static public void Main()
{
int num = 4, pos = 1;
toggle(num, pos);
}
static public void toggle(int num, int pos)
{
num ^= (1 << pos);
Console.WriteLine(num);
}
}
Javascript
function toggle(num, pos){
num ^= (1 << pos)
console.log(num)
}
let num = 4;
let pos = 1;
toggle(num, pos);
Time Complexity: O(1)
Auxiliary Space: O(1)
4. Checking if the bit at nth position is Set or Unset
We used the left shift (<<) operation on 1 to shift the bits to nth position and then use the & operation with number given number, and check if it is not-equals to 0.
Below is the implementation:
C++
#include <iostream>
using namespace std;
bool at_position(int num, int pos)
{
bool bit = num & (1 << pos);
return bit;
}
int main()
{
int num = 5;
int pos = 2;
bool bit = at_position(num, pos);
cout << bit << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 5;
int pos = 0;
int bit = at_position(num, pos);
System.out.println(bit);
}
public static int at_position(int num, int pos)
{
int bit = num & (1 << pos);
return bit;
}
}
Python3
def at_position(num, pos):
bit = num & (1 << pos)
return bit
num = 5
pos = 0
bit = at_position(num, pos)
print(bit)
C#
using System;
public class GFG {
public static bool at_position(int num, int pos)
{
int bit = num & (1 << pos);
if (bit == 0)
return false;
return true;
}
static public void Main()
{
int num = 5;
int pos = 2;
bool bit = at_position(num, pos);
Console.WriteLine(bit);
}
}
Javascript
<script>
function at_position(num,pos)
{
return num & (1<<pos);
}
let num = 5;
let pos = 0;
console.log(at_position(num, pos));
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
5. Multiply a number by 2 using the left shift operator
Below is the implementation:
C++
#include <iostream>
using namespace std;
int main()
{
int num = 12;
int ans = num << 1;
cout << ans << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 12;
int ans = num << 1;
System.out.println(ans);
}
}
C#
using System;
public class GFG {
static public void Main()
{
int num = 12;
Console.WriteLine(num << 1);
}
}
Python3
num = 12
ans = num << 1
print(ans)
Javascript
<script>
var num = 12;
var ans = num<<1;
document.write(ans);
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
6. Divide a number 2 using the right shift operator
Below is the implementation:
C++
#include <iostream>
using namespace std;
int main()
{
int num = 12;
int ans = num >> 1;
cout << ans << endl;
return 0;
}
Java
import java.io.*;
class GFG {
public static void main(String[] args)
{
int num = 12;
int ans = num >> 1;
System.out.println(ans);
}
}
C#
using System;
public class GFG {
static public void Main()
{
int num = 12;
Console.WriteLine(num >> 1);
}
}
Python3
num = 12
ans = num >> 1
print(ans)
Javascript
<script>
var num = 12;
var ans = num>>1;
document.write(ans);
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
7. Compute XOR from 1 to n (direct method)
The problem can be solved based on the following observations:
Say x = n % 4. The XOR value depends on the value if x.
If, x = 0, then the answer is n.
x = 1, then answer is 1.
x = 2, then answer is n+1.
x = 3, then answer is 0.
Below is the implementation of the above approach.
C++
int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
Java
import java.io.*;
class GFG {
public static int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
public static void main(String[] args) {}
}
Python
def set(num, pos):
num |= (1 << pos)
print(num)
num, pos = 4, 1
set(num, pos)
C#
using System;
public class GFG {
public static int computeXOR(int n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
public static void Main() {}
}
Javascript
<script>
function computeXOR(n)
{
if (n % 4 == 0)
return n;
if (n % 4 == 1)
return 1;
if (n % 4 == 2)
return n + 1;
else
return 0;
}
</script>
Time Complexity: O(1)
Auxiliary Space: O(1)
8. How to know if a number is a power of 2?
This can be solved based on the following fact:
If a number N is a power of 2, then the bitwise AND of N and N-1 will be 0. But this will not work if N is 0. So just check these two conditions, if any of these two conditions is true.
Below is the implementation of the above approach.
C++
bool isPowerOfTwo(int x)
{
return x && (!(x & (x - 1)));
}
Java
public static boolean isPowerOfTwo(int x)
{
return x != 0 && ((x & (x - 1)) == 0);
}
Python
def isPowerOfTwo(x):
return x and (not(x & (x - 1)))
C#
using System;
public class GFG {
static public bool isPowerOfTwo(int x)
{
return (x != 0) && ((x & (x - 1)) == 0);
}
static public void Main() {}
}
Javascript
function isPowerOfTwo(x)
{
return x && (!(x & (x - 1)));
}
Time Complexity: O(1)
Auxiliary Space: O(1)
9. Count Set bits in an integer
Counting set bits means, counting total number of 1’s in the binary representation of an integer. For this problem we go through all the bits of given number and check whether it is set or not by performing AND operation (with 1).
Below is the implementation:
C++
int countBits(int n)
{
int count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
Java
public static int countBits(int n)
{
int count = 0;
while (n > 0) {
count += n & 1;
n >>= 1;
}
return count;
}
Python3
def countBits(n):
count = 0
while n:
count += n & 1
n >>= 1
return count
C#
using System;
public class GFG {
public static int countBits(int n)
{
int count = 0;
while (n > 0)
{
count += n & 1;
n >>= 1;
}
return count;
}
static public void Main() {}
}
Javascript
function countBits(n)
{
let count = 0;
while (n) {
count += n & 1;
n >>= 1;
}
return count;
}
Time Complexity: O(log(n))
Auxiliary Space: O(1)
10. Position of rightmost set bit
The idea is to unset the rightmost bit of number n and XOR the result with n. Then the rightmost set bit in n will be the position of the only set bit in the result. Note that if n is odd, we can directly return 1 as the first bit is always set for odd numbers.
Example:
The number 20 in binary is 00010100, and the position of the rightmost set bit is 3.
00010100 & (n = 20)
00010011 (n-1 = 19)
——————-
00010000 ^ (XOR result number with n)
00010100
——————-
00000100 ——-> rightmost set bit will tell us the position
Below is the implementation:
C++
int positionOfRightmostSetBit(int n)
{
if (n & 1) {
return 1;
}
n = n ^ (n & (n - 1));
int pos = 0;
while (n) {
n = n >> 1;
pos++;
}
return pos;
}
Java
public static int positionOfRightmostSetBit(int n)
{
if ((n & 1) != 0) {
return 1;
}
n = n ^ (n & (n - 1));
int pos = 0;
while (n != 0) {
n = n >> 1;
pos++;
}
return pos;
}
Python
def positionOfRightmostSetBit(n):
if n & 1:
return 1
n = n ^ (n & (n - 1))
pos = 0
while n:
n = n >> 1
pos = pos + 1
return pos
C#
public static int positionOfRightmostSetBit(int n)
{
if ((n & 1) != 0) {
return 1;
}
n = n ^ (n & (n - 1));
int pos = 0;
while (n != 0) {
n = n >> 1;
pos++;
}
return pos;
}
Javascript
function positionOfRightmostSetBit( n)
{
if (n & 1) {
return 1;
}
n = n ^ (n & (n - 1));
let pos = 0;
while (n) {
n = n >> 1;
pos++;
}
return pos;
}
Time Complexity: O(log(n))
Auxiliary Space: O(1)
More Practice Problems on Bitwise Algorithms
Related article:
- Bits manipulation (Important tactics)
- Bitwise Hacks for Competitive Programming
- Bit Tricks for Competitive Programming
Комбинаторный оператор XOr—Справка | ArcGIS for Desktop
Доступно с лицензией Spatial Analyst.
- Краткая информация
- Рисунок
- Использование
- Синтаксис
- Пример кода
- Параметры среды
- Информация о лицензировании
Краткая информация
Выполняет Комбинаторную операцию исключающего Или (XOr) для значений ячеек двух входных растров.
Если одно входное значение истинно (не-нулевое), а другое – ложное (нулевое), выходное значение будет уникальным для каждой комбинации входных значений. Если оба входных значения истинные или оба входных значения ложные, выходное значение будет равно нулю.
Более подробно о работе инструментов группы Логические
Рисунок
OutRas = CombinatorialXOr(InRas1, InRas2)
Использование
-
Комбинаторные математические инструменты интерпретируют входные данные как логические значения, когда ненулевые значения рассматриваются как истинные, а нулевые значения – как ложные.
-
Для выполнения операции комбинаторного сравнения необходимо наличие двух входных файлов.
-
Порядок входных данных для этого инструмента имеет значение только для выходной таблицы атрибутов.
-
См. раздел Среда анализа и Spatial Analyst для получения дополнительной информации о среде геообработки данного инструмента.
Синтаксис
CombinatorialXOr (in_raster_or_constant1, in_raster_or_constant2)
| Параметр | Объяснение | Тип данных |
|
in_raster_or_constant1 |
Первый входной растр для выполнения комбинаторной операции. Должен быть положительным целым числом. В качестве входных данных для этого параметра может использоваться число, при условии, что для другого параметра задан растр. Чтобы можно было задать число для двух входных данных, необходимо сперва указать экстент и размер ячейки в параметрах среды. |
Raster Layer | Constant |
|
in_raster_or_constant2 |
Второй входной растр для выполнения этой комбинаторной операции. Должен быть положительным целым числом. В качестве входных данных для этого параметра может использоваться число, при условии, что для другого параметра задан растр. Чтобы можно было задать число для двух входных данных, необходимо сперва указать экстент и размер ячейки в параметрах среды. |
Raster Layer | Constant |
Возвращено значение
| Имя | Объяснение | Тип данных |
| out_raster |
Выходной растр. Выходные данные всегда будут целочисленными. |
Raster |
Пример кода
Комбинаторный оператор XOr. Пример 1 (окно Python)
В этом примере выполняется комбинаторная операция XOr для двух растров GRID, в результате чего получается растр IMG.
import arcpy
from arcpy import env
from arcpy.sa import *
env.workspace = "C:/sapyexamples/data"
outCXOr = CombinatorialXOr("degs", "cost")
outCXOr.save("C:/sapyexamples/output/outcxor.img")
Комбинаторный оператор XOr. Пример 2 (автономный скрипт)
В этом примере выполняется комбинаторная операция XOr для двух растров GRID.
# Name: CombinatorialXOr_Ex_02.py
# Description: Performs a Combinatorial Exclusive Or operation on
# the cell values of two input rasters
# Requirements: Spatial Analyst Extension
# Import system modules
import arcpy
from arcpy import env
from arcpy.sa import *
# Set environment settings
env.workspace = "C:/sapyexamples/data"
# Set local variables
inRaster1 = "degs"
inRaster2 = "cost"
# Check out the ArcGIS Spatial Analyst extension license
arcpy.CheckOutExtension("Spatial")
# Execute CombinatorialXOr
outCXOr = CombinatorialXOr(inRaster1, inRaster2)
# Save the output
outCXOr.save("C:/sapyexamples/output/outcxor")
Параметры среды
- Автоподтверждение (Auto Commit)
- Размер ячейки (Cell size)
- Сжатие (Compression)
- Текущая рабочая область (Current Workspace)
- Экстент (Extent)
- Географические преобразования (Geographic Transformations)
- Маска (Mask)
- Выходное ключевое слово CONFIG (Output CONFIG Keyword)
- Выходная система координат (Output Coordinate System)
- Статистика растра (Raster Statistics)
- Временная рабочая область (Scratch Workspace)
- Растр привязки (Snap Raster)
- Размер листа (Tile Size)
Связанные темы
Отзыв по этому разделу?
XOR • ZX Spectrum — играть онлайн
Издатель: Proxima Software 1992
АВТОР: GCC (Гениальное вычислительным Компания)
Poslední HRA, kterou muzete па kompletu ее жестяным najit, JE HRA XOR.
NAHRANI SPUSTENI
Prectete си totez у nejake predchozi hry – JE к uplne stejne – pouze jmeno programu JE Цинем.
OVLADANI
По spusteni hry си muzete vybrat ovladani – Кемпстон, klavesnici (QAOPM), Синклер Нево kurzorove klavesy. Тим, ге си zvolite ovladani себе HRA принять spusti. Objevi себе napisy HRA VAS буде mystifikovat тим, ге napise Stisknete mezernik, правда JE, ге muzete stisknout я strileni. Nasleduje Seznam logickych problemu (mistnosti), ktere musite vyresit – JE jich celkem 30 Маджи opravdu zajimava lakava jmena (Obvykle Добре vystihuji, о сотрудничестве се V датчанин urovni jedna).
HRA
V kazde mistnosti спариваться zdanlive jednoduchy ukol – sesbirat даный pocet smejicich себе Masek. Jste predstavovan! Тебе netradicne erbem – vlastne dvema Erby. Z jednoho па druhy себе muzete prepinat klavesou strileni (FIRE). Чтобы, ге товарищем Erby DVA, skryva netusene moznosti, па ktere jiste Сами prijdete.
На pergamenu vpravo naleznete nasledujici údaje: nazev hry, Активное Еврорадио (десять, себе kterym zrovna pohybujete), pocet Masek, ktere jste jiz vzali pocet Masek, ktere помощник celkem sebrat.
Nahore помощник pocet Таху, ktere jste уз ujeli. ГРУ muzete kdykoliv opusti stiskem klavesy пространстве.
Со VAM vlastne ве sbirani вади?
ZDI – samozrejme ZDI, kterymi nemuzete projizdet.
SLEPICE ZAVAZI – slepice LETA zpráva doleva pokud narazi сделать jadnoho г vasich Erbu, тaк JE к VAS konec. Podobne в Plati я про zavazi, чтобы vsak (Дикий gravitaci) пада долу. Pozor, я люблю Роздол, kdyz сделать VAS narazi Нево kdyz себе (tesne) от должного пе postavite – к себе VAM nestane NIC. Nesmite пак vsak треба ujet г стручка zavazi долу – zavazi totiz spadne zabije VAS, totez Плати analogicky я про slepici. Slepice я zavazi muzete posunovat (tlacit) от должного Себу ро rovnych plochach, о ktere себе opiraji.
CTVERCE – další zajimave objekty, ktere VAM budou ztezovat Zivot nazveme ctverce. Jsou зде DVA druhy: Prvni jsou oznaceny rovnobeznymi carami Шора долу muzete JE prorazit (Projet) ве smeru Право-levem (Я Лево-pravem). Ve smeru svislem себе овсем chovaji stejne яко Zed. Druhe jsou oznaceny rovnobeznymi carami zleva Doprava. Muzete JE prorazit ве svislem smeru. Stejne Яко па VAS, pusobi Tyto ctverce я па další objekty – slepice, zavazi, Bomby, rakety panacky.
Druhe jsou oznaceny rovnobeznymi carami zleva Doprava. Muzete JE prorazit ве svislem smeru. Stejne Яко па VAS, pusobi Tyto ctverce я па další objekty – slepice, zavazi, Bomby, rakety panacky.
PANACEK – Je jednim г nejneskodnejsich objektu – stoji па Miste dokud сделать Nej nevrazite, пак лети сделать nejblizsi zabrany.
Bomby RAKETY – jsou pravy Opak panacka – rozhodne nejsou “neskodne”. Бомба пада черствый долу, podobne яко zavazi, S тим rozdilem, ге ро dopadu vybuchuje. Vybuch znici vsechny objekty, ktere bezprostredne mistem souvisi сек, KDE себе бомба PRI Padu zastavila. Бомба vybuchne принять V pripade, ге сделать п narazi zavazi Нево slepice Нево vedle п dojde K vybuchu. Pokud делать Bomby narazi panacek, бомба nevybuchuje, panacek себе о п pouze zarazi. Kdyz бомба dopadne па ctverec, бутон хо prorazi NABO себе па нэм zastavi – взять nevybuchne. Pro Raketu Плати stejna pravidla яко про bombu, jediny Роздол JE ве smeru pohybu, Ракета себе pohybuje stejne яко slepice – zpráva doleva.
Dveře – jsou Величена dulezity Объект – musite себе к NIM dostat Потье, со sesbirate veskere Маски – Тим принять uspesne dohravate mistnost. Dveře lze, stejne яко vsechno ostatni, znicit bombou Нево raketou, dejte си прото pozor, абы себе VAM с omylem nepodarilo – jinak totiz koncite.
ZAVER
Hra XOR JE Prvni HRA ве strojovem Kodu од Фирмы в MarkWare, nemusi себе дза п stydet, Skoda жень, ге уз дзи nikdy neopravi.
Prijemnou zabavu PRI Грани!
Играйте в XOR онлайн. Игра жанра “головоломки”, изданная в Великобритании в 1987 году компанией Logotron Ltd, которую разработали Astral Software Ltd и Stuart Gregg.
XOR Calculator — Tool Slick
Спасибо, что попробовали наши инструменты. Если вам понравились наши инструменты, отметьте нашу страницу в Facebook и поделитесь ею с друзьями.
Вместо этого вам могут помочь следующие инструменты.
Некоторый текст в модальном режиме.
| CTRL + ALT + H | Открыть эту помощь |
CTRL + ALT + Shift + S. + S.0015 + S.0015 |
Configure Global Settings |
| Ctrl + Alt + Enter | Calculate ( Submit ) |
| Ctrl + Alt + Shift + F | Полноэкранный ввод |
| Ctrl + Alt + U | Текстовое поле Focus URL |
| Введите текст 90 URL0013 Load URL | |
| Ctrl + Alt + L | Load Input File |
| Ctrl + Alt + E | Load Example |
| Ctrl + ALT + I | Фокусный входной редактор |
| CTRL + ALT + S | Настройки фокуса |
Focus на входе.0003
Пример процесса при нагрузке
Свиток к результатам после представления
Предложить связанные инструменты
Binaryoctaldecimalhexasciiauto обнаружение входной базы
Auto DetectNew Linespacecommasemi Colon Delimiter
Auto Очистка 9000. 9000 2
9000 2
Расчеты.
..
Результат операции XOR в двоичном формате
- Восьмеричный результат:
-
..
The result of XOR operation in Octal
- Decimal Result:
-
..
The result of XOR operation in Decimal
- Hex Result:
-
..
The result of XOR operation in Hex
- Ascii Результат:
-
..
Результат операции XOR в Ascii
- База ввода:
-
..
Основание введенных чисел либо явно задано, либо определено автоматически 0160
Калькулятор обратного XOR
-
Предположим, у вас есть два исходных двоичных числа A и B
-
Вы применили XOR к A и B, чтобы получить C
-
Теперь вы хотите получить обратную операцию XOR и получить A
-
Для этого вам понадобятся B и C
-
Чтобы найти A, просто XOR B и C. Поскольку XOR является обратным, вы получите A
-
Аналогично, чтобы найти B , все, что вам нужно сделать, это XOR A и C
-
Пример: xoring 1011 и 1100 дает 0111. Применение XOR на 1011 и 0111 возвращает 1100
О расчете XOR
XOR – это цифровой логический приклад битовые входы к нему неравны, т. е. для ввода
е. для ввода 0 и 1 или 1 и 0 .
Вы также можете запомнить приведенный выше результат, используя одну из этих логик: –
- Возвращает истину, когда только один из входов равен 1
- Возвращает false, если оба входа одинаковы.
Это также называется EOR или EXOR (исключающее ИЛИ). Таким образом, он похож на вентиль ИЛИ, но отличается тем, что только один вход должен быть 1 для результата High, тогда как в ИЛИ любой из входов может быть истинным, чтобы он вернул 1.
В некотором смысле XOR представляет неравенство функция, != или не равно. Ознакомьтесь с приведенной ниже таблицей истинности для получения дополнительной информации о результатах.
Что можно делать с помощью этого инструмента?
Проще говоря, вы можете использовать его для вычисления XOR онлайн. Инструмент поддерживает ввод в распространенных числовых базах: двоичном, восьмеричном, десятичном, шестнадцатеричном и даже ASCII. Это означает, что вы также можете XOR шестнадцатеричных значений или строк XOR в ASCII. Это делается путем преобразования входных данных в их двоичные эквиваленты, а затем выполнения над ними операции XOR. Наконец, результаты возвращаются во всех приведенных выше числовых базах, так что вы можете выбрать те, которые хотите.
Это делается путем преобразования входных данных в их двоичные эквиваленты, а затем выполнения над ними операции XOR. Наконец, результаты возвращаются во всех приведенных выше числовых базах, так что вы можете выбрать те, которые хотите.
Промежуточный расчет
Промежуточные результаты отображаются в табличном формате, что может помочь вам диагностировать любые проблемы, с которыми вы столкнулись при выполнении операции XOR вручную. В этой таблице ваши входные данные показаны в исходном виде. Если входная база не является двоичной, то каждый перевод входных данных в двоичный также отображается в другом столбце.
Создано Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 27 сентября 2022 г.
Содержание:
- Что такое операция XOR?
- Схема XOR
- Таблица истинности исключающего ИЛИ
- Как вычислить XOR двух чисел?
- Как пользоваться калькулятором XOR?
- Применение логической операции XOR
- Часто задаваемые вопросы
Используйте калькулятор XOR для выполнения побитовой операции XOR над двумя числами . Вы можете вводить данные в двоичном, десятичном или восьмеричном представлении. Если вы хотите выполнять операции побитового И или побитового ИЛИ, вам может подойти наш побитовый калькулятор.
Вы можете вводить данные в двоичном, десятичном или восьмеричном представлении. Если вы хотите выполнять операции побитового И или побитового ИЛИ, вам может подойти наш побитовый калькулятор.
Продолжайте читать, чтобы узнать:
- Что такое операция XOR?
- Как вычислить XOR двух чисел?
- Каковы применения логической операции XOR?
Что такое операция XOR?
Исключающее ИЛИ или исключающее ИЛИ — это логическая операция , которая сравнивает входные значения (биты) и генерирует выходное значение (биты). Логика исключающего ИЛИ очень проста. Если входные значения совпадают, на выходе будет 0 9, Исключающее ИЛИ или Исключающее ИЛИ. Логическое выражение для операции XOR:
Для реализации двоичной операции XOR в электронных схемах мы используем вентили XOR. В следующем разделе мы увидим, что такое вентиль XOR.
Вентиль XOR
Вентиль XOR (или исключающее ИЛИ) представляет собой комбинацию вентилей ИЛИ, И и НЕ (см. рис. 1). Выход логического элемента XOR имеет высокий уровень (
рис. 1). Выход логического элемента XOR имеет высокий уровень ( 1 ), когда любой из входов имеет высокий уровень ( 1 ). Если на обоих входах высокий уровень ( 1 ) или на обоих входах низкий уровень ( 0 ), на выходе низкий уровень ( 0 ).
Рис. 1: Вентиль исключающее ИЛИ.
На рис. 2 показан логический символ вентиля XOR.
Рис. 2: Логический символ XOR Gate.
Чтобы узнать больше о других логических элементах, воспользуйтесь калькулятором логических элементов.
Таблица истинности исключающего ИЛИ
В следующей таблице показана таблица истинности двоичной операции XOR (исключающее ИЛИ) между двумя входами A и B (A XOR B).
|
А |
Б |
Выход (Y) |
|---|---|---|
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Из таблицы истинности видно, что операция XOR является бинарным сложением, если не учитывать переносы. Поэтому операция XOR также называется mod-2 add .
Поэтому операция XOR также называется mod-2 add .
В данной таблице истинности мы рассмотрели операцию XOR только для двух одиночных битов. Однако нам нужно выполнить побитовую операцию XOR при работе с битовыми векторами (например, байтом).
Как вычислить XOR двух чисел?
Чтобы понять логическую операцию побитового исключающего ИЛИ, давайте вычислим XOR двух чисел, 80 и 100 .
-
Во-первых, мы выразим оба числа в двоичном представлении:
- 8-битное двоичное представление
80:0101 0000. - 8-битное двоичное представление
100равно0110 0100.
Обязательно оба числа имеют одинаковую битовую длину .
- 8-битное двоичное представление
-
Теперь мы найдем XOR каждой пары соответствующих битов , от первого до последнего, используя правило:
- Если оба бита одинаковы, т.
 е.
е. 1(или0), выходной бит равен0. - Если оба бита различны, вывод равен
1.
- Если оба бита одинаковы, т.
-
Например, первая пара битов
0⊕0, выходной бит будет0. Точно так же мы можем определить выходной бит для всех пар.
|
XOR операция: |
|
|---|---|
|
0101 0000 |
|
|
0110 0100 |
|
|
= |
0011 0100 |
- Следовательно, результатом операции XOR для
80и100является0011 0100.
Если вас интересуют более сложные логические операции, такие как сдвиг битов, рекомендуем воспользоваться калькулятором сдвига битов.
Как пользоваться калькулятором XOR?
Теперь давайте посмотрим, как мы можем использовать калькулятор XOR для вычисления XOR двух чисел:
-
С помощью раскрывающегося меню выберите количество битов в двоичном представлении .
 Мы выберем 8 бит, так как это позволяет использовать десятичные числа от -128 до 127.
Мы выберем 8 бит, так как это позволяет использовать десятичные числа от -128 до 127. -
Выберите тип входных данных как десятичный. Побитовый калькулятор XOR позволяет вводить числа в двоичной, десятичной и восьмеричной системах.
-
Теперь введите числа
80и100в поля Номер 1 и Номер 2 соответственно. -
Калькулятор побитового XOR выдаст результат операции XOR в двоичной (
0011 0100), десятичной (52) и восьмеричной системах (64).
Применение логической операции XOR
Логическая операция XOR широко используется в цифровых электронных схемах и компьютерном программировании. Некоторые из распространенных применений логики XOR:
-
Криптография : Логика исключающего ИЛИ широко применяется в методах шифрования.
-
Обнаружение ошибки : Логика XOR дает результат
0, если четное количество входных битов равно1(четная четность), и дает результат1, если нечетное количество входных битов равно
1 Поэтому мы используем логику XOR для определения четности передаваемых данных. Этот метод помогает определить, были ли данные повреждены при отправке цифровой информации.
Поэтому мы используем логику XOR для определения четности передаваемых данных. Этот метод помогает определить, были ли данные повреждены при отправке цифровой информации.
-
Защита данных RAID : Располагая жесткие диски таким образом, что один из дисков содержит XOR всех остальных, системы RAID (избыточные массивы недорогих дисков) восстанавливают поврежденные диски.
-
Схема сумматора : логические элементы XOR широко используются в компьютерных схемах для выполнения основных арифметических операций, таких как сложение и вычитание.
Часто задаваемые вопросы
Что означает побитовое XOR?
В побитовой операции XOR над двумя двоичными числами мы сравниваем пару отдельных битов в соответствующих позициях. Выходной бит равен 1, если только один из входных битов равен 1. В противном случае он равен нулю.
Как найти XOR двух чисел?
Чтобы найти XOR двух чисел, следуйте этим инструкциям:
- Преобразуйте числа в двоичное представление .
Побитовые операции (англ. bitwise operations) — операции, производимые над цепочками битов. Выделяют два типа побитовых операций: логические операции и побитовые сдвиги.
Содержание
- 1 Принцип работы
- 1.1 Логические побитовые операции
- 1.1.1 Побитовое И
- 1.1.2 Побитовое ИЛИ
- 1.1.3 Побитовое НЕ
- 1.1.4 Побитовое исключающее ИЛИ
- 1.2 Побитовые сдвиги
- 1.1 Логические побитовые операции
- 2 Применение
- 2.1 Сложные операции
- 2.1.1 Определение знака числа
- 2.1.2 Вычисление модуля числа без использования условного оператора
- 2.1.3 Нахождение минимума и максимума из двух чисел без использования условного оператора
- 2.1.4 Проверка на то, является ли число степенью двойки
- 2.1.5 Нахождение младшего единичного бита
- 2.1.6 Нахождение старшего единичного бита
- 2.1.7 Циклический сдвиг
- 2.1.8 Подсчет количества единичных битов
- 2.1.9 Разворот битов
- 2.2 Применение для решения задач
- 2.2.1 Работа с битовыми масками
- 2.2.2 Алгоритм Флойда
- 2.2.3 Дерево Фенвика
- 2.1 Сложные операции
- 3 См. также
- 4 Примечания
- 5 Источники информации
Принцип работы
Логические побитовые операции
Битовые операторы И , ИЛИ , НЕ и исключающее ИЛИ используют те же таблицы истинности, что и их логические эквиваленты.
Побитовое И
Побитовое И используется для выключения битов. Любой бит, установленный в , вызывает установку соответствующего бита результата также в .
| & | |
|---|---|
| 11001010 11100010 |
|
| 11000010 |
Побитовое ИЛИ
Побитовое ИЛИ используется для включения битов. Любой бит, установленный в , вызывает установку соответствующего бита результата также в .
| | | |
|---|---|
| 11001010 11100010 |
|
| 11101010 |
Побитовое НЕ
Побитовое НЕ инвертирует состояние каждого бита исходной переменной.
| ~ | |
|---|---|
| 11001010 | |
| 00110101 |
Побитовое исключающее ИЛИ
Исключающее ИЛИ устанавливает значение бита результата в , если значения в соответствующих битах исходных переменных различны.
| ^ | |
|---|---|
| 11001010 11100010 |
|
| 00101000 |
Побитовые сдвиги
Операторы сдвига и сдвигают биты в переменной влево или вправо на указанное число. При этом на освободившиеся позиции устанавливаются нули (кроме сдвига вправо отрицательного числа, в этом случае на свободные позиции устанавливаются единицы, так как числа представляются в двоичном дополнительном коде и необходимо поддерживать знаковый бит).
Сдвиг влево может применяться для умножения числа на два, сдвиг вправо — для деления.
x = 7 // 00000111 (7) x = x >> 1 // 00000011 (3) x = x << 1 // 00000110 (6) x = x << 5 // 11000000 (-64) x = x >> 2 // 11110000 (-16)
В языке программирования Java существует также оператор беззнакового битового сдвига вправо . При использовании этого оператора на освободившиеся позиции всегда устанавливаются нули.
x = 7 // 00000111 (7) x = x << 5 // 11100000 (-32) x = x >>> 2 // 00111000 (56)
Применение
Сложные операции
Определение знака числа
Пусть дано число . Поскольку при сдвиге вправо на освобождающиеся позиции устанавливается бит знака, знак числа можно определить, выполнив сдвиг вправо на всю длину переменной:
int32 getSign(x: int32):
if x != 0:
mask = 1
else:
mask = 0
return mask | (x >> 31) // результатом будет -1, 0, или +1
// для отрицательного, равного нулю и положительного числа x соответственно
Используя побитовые операции можно также узнать, различны ли знаки двух переменных и . Если числа имеют различный знак, то результат операции XOR, произведенной над их знаковыми битами, будет единицей. Поэтому неравенство будет верно в том случае, если числа и разного знака.
Вычисление модуля числа без использования условного оператора
Пусть дано число . Если положительно, то , и . В случае, если отрицательно, . Тогда получается, что мы работаем с числом так, как будто оно представлено в
коде со сдвигом с тем отличием, что у нас знаковый бит принимает значение для отрицательных чисел, а — для положительных.
int32 abs1(x: int32):
mask = x >> 31
return (x + mask) XOR mask
int32 abs2(x: int32):
mask = x >> 31
return (x + mask) XOR mask
Нахождение минимума и максимума из двух чисел без использования условного оператора
Этот способ корректен только если можно утверждать, что величина лежит между граничными значениями типа int.
Пусть даны числа и разрядности . Тогда если , то , а если , то . Выражение принимает значение , если , и , если .
int32 min(x, y: int32):
return y + ((x - y) & ((x - y) >> 31))
int32 max(x, y: int32):
return x - ((x - y) & ((x - y) >> 31))
Проверка на то, является ли число степенью двойки
Пусть дано число . Тогда, если результатом выражения является единица, то число — степень двойки.
Правая часть выражения будет равна единице, только если число равно или является степенью двойки. Если число является степенью двойки, то в двоичной системе счисления оно представляется следующим образом: , где — показатель степени. Соответственно, выражение будет иметь вид , и равно .
Операция логического И в данном выражении отсекает тот случай, когда и не является степенью двойки, но при этом правая часть равна единице.
Нахождение младшего единичного бита
Пусть дано число и необходимо узнать его младший единичный бит.
Применим к числу побитовое отрицание, чтобы инвертировать значения всех его бит, а затем прибавим к полученному числу единицу. У результата первая часть (до младшего единичного бита) не совпадает с исходным числом , а вторая часть совпадает. Применив побитовое И к этим двум числам, получим степень двойки, соответствующую младшему единичному биту исходного числа .
К такому же результату можно прийти, если сначала отнять от числа единицу, чтобы обнулить его младший единичный бит, а все последующие разряды обратить в , затем инвертировать результат и применить побитовое И с исходным числом .
Нахождение старшего единичного бита
Пусть дано число и необходимо узнать его старший единичный бит.
Рассмотрим некоторое число, представим его как , где — любое значение бита. Тогда, если совершить битовый сдвиг этого числа вправо на и произвести побитовое ИЛИ результата сдвига и исходного числа, мы получим результат . Если мы повторим эту последовательность действий над полученным числом, но устроим сдвиг на , то получим . При каждой следующей операции будем увеличивать модуль сдвига до следующей степени двойки. После некоторого количества таких операций (зависит от разрядности числа) мы получим число вида . Тогда результатом выполнения действий будет число, состоящее только из старшего бита исходного числа.
int32 greatestBit(x: int32):
power = 1
for i = 1 :
x |= x >> power
power <<= 1
return x - (x >> 1)
Циклический сдвиг
Пусть дано число и надо совершить циклический сдвиг его битов на величину .
Желаемый результат можно получить, если объединить числа, полученные при выполнении обычного битового сдвига в желаемую сторону на и в противоположном направлении на разность между разрядностью числа и величиной сдвига. Таким образом, мы сможем поменять местами начальную и конечную части числа.
int32 rotateLeft(x, d: int32):
return (x << d) | (x >>> (32 - d))
int32 rotateRight(x, d: int32):
return (x >>> d) | (x << (32 - d))
Подсчет количества единичных битов
Для подсчета количества единичных битов в числе можно воспользоваться следующим алгоритмом:
// Для чисел других разрядностей необходимо использовать соответствующие константы.
int16 setBitsNumber(x: int16):
x = x - ((x >>> 1) & 0x5555)
x = (x & 0x3333) + ((x >>> 2) & 0x3333)
x = (x + (x >>> 4)) & 0x0F0F
return (x * 0x0101) >>> 8
Поскольку равно , результатом операции является число, в котором все нечетные биты соответствуют нечетным битам числа . Аналогично, результатом операции является число, в котором все нечетные биты соответствуют четным битам . Четные биты результата в обоих случаях равны нулю.
Мысленно разобьем двоичную запись нашего числа на группы по бита. Результатом операции будет такое число, что если разбить его двоичную запись на группы по два бита, значение каждой группы соответствует количеству единичных битов в соответствующей паре битов числа .
Аналогично, число равно и операция , примененная к результату, полученному на первом этапе, выполняет подсчет количества единичных битов в блоках по . В свою очередь, число равно и операция позволяет подсчитать число единичных бит в блоках по .
Теперь необходимо просуммировать числа, записанные в блоках по битов, чтобы получить искомую величину. Это можно сделать, домножив результат на . Ответ на задачу будет находиться в первых восьми битах произведения. Выполнив сдвиг вправо на (для шестнадцатибитных чисел), мы получим долгожданный ответ.
Подведем итог:
int16 setBitsNumber(x: int16):
x = (x & 0x5555) + ((x >>> 1) & 0x5555)
x = (x & 0x3333) + ((x >>> 2) & 0x3333)
x = (x & 0x0F0F) + ((x >>> 4) & 0x0F0F)
return (x * 0x0101) >>> 8
Заметим, что операция равносильна операции , в чем легко убедиться, рассмотрев все числа из двух бит.
В свою очередь, операцию можно заменить на . Эта замена не повлияет на результат, так как максимальное значение в любой группе из четырех битов данного числа равно четырем, то есть требует только трех битов для записи, и выполнение суммирования не повлечет за собой переполнения и выхода за пределы четверок.
Таким образом, мы получили код, приведенный в начале раздела.
Разворот битов
Чтобы получить биты числа , записанные в обратном порядке, применим следующий алгоритм.
// Для чисел других разрядностей нужны соответствующие константы. int16 reverseBits(x: int16): x = ((x & 0x5555) << 1) | ((x >>> 1) & 0x5555) // Четные и нечетные биты поменялись местами. x = ((x & 0x3333) << 2) | ((x >>> 2) & 0x3333) // Биты "перетасовываются" группами по два. x = ((x & 0x0F0F) << 4) | ((x >>> 4) & 0x0F0F) // Биты "перетасовываются" группами по четыре. x = ((x & 0x00FF) << 8) | ((x >>> 8) & 0x00FF) // Биты "перетасовываются" группами по восемь. return x
Более подробно про то, что за константы выбраны для данного алгоритма, можно прочитать в разделе подсчет количества единичных битов.
Применение для решения задач
Работа с битовыми масками
Для работы с подмножествами удобно использовать битовые маски. Применяя побитовые операции легко сделать следующее: найти дополнение , пересечение , объединение множеств, установить бит по номеру , снять бит по номеру .
Битовые маски используются, например, при решении некоторых задач[1] динамического программирования.
Алгоритм Флойда
Алгоритм Флойда–Уоршелла (англ. the Floyd–Warshall algorithm) — алгоритм для нахождения длин кратчайших путей между всеми парами вершин во взвешенном ориентированном графе. Работает корректно, если в графе нет циклов отрицательной величины, а если же такой цикл есть, позволяет найти хотя бы один такой цикл. Асимптотическая сложность алгоритма , также требует памяти.
Дерево Фенвика
Дерево Фенвика (англ. Binary indexed tree) — структура данных, которая может выполнять следующие операции:
- изменять значение любого элемента в массиве,
- выполнять некоторую ассоциативную, коммутативную, обратимую операцию на отрезке .
Данная структура требует памяти, а выполнение каждой операции происходит за .
Функция, позволяющая делать операции вставки и изменения элемента за , задается следующей формулой .
Пусть дан массив . Деревом Фенвика называется массив из элементов: , где и — функция, которую мы определили ранее.
См. также
- Определение булевой функции
- Сумматор
- Триггеры
Примечания
- ↑ Динамическое программирование по подмножествам (по маскам)
Источники информации
- Онлайн справочник программиста на С и С++
- Побитовые операторы
- Bit Twiddling Hacks by Sean Eron Anderson
- Habrahabr — Алгоритмы поиска старшего бита
- STP’s blog — Counting the number of set bits in an integer
В этой статье я расскажу вам о том, как работают битовые операции. С первого взгляда они могут показаться вам чем-то сложным и бесполезным, но на самом деле это совсем не так. В этом я и попытаюсь вас убедить.
Введение
Побитовые операторы проводят операции непосредственно на битах числа, поэтому числа в примерах будут в двоичной системе счисления.
Я расскажу о следующих побитовых операторах:
- | (Побитовое ИЛИ (OR)),
- & (Побитовое И (AND)),
- ^ (Исключающее ИЛИ (XOR)),
- ~ (Побитовое отрицание (NOT)),
- << (Побитовый сдвиг влево),
- >> (Побитовый сдвиг вправо).
Битовые операции изучаются в дискретной математике, а также лежат в основе цифровой техники, так как на них основана логика работы логических вентилей — базовых элементов цифровых схем. В дискретной математике, как и в цифровой технике, для описания их работы используются таблицы истинности. Таблицы истинности, как мне кажется, значительно облегчают понимание битовых операций, поэтому я приведу их в этой статье. Их, тем не менее, почти не используют в объяснениях побитовых операторов высокоуровневых языков программирования.
О битовых операторах вам также необходимо знать:
- Некоторые побитовые операторы похожи на операторы, с которыми вы наверняка знакомы (&&, ||). Это потому, что они на самом деле в чем-то похожи. Тем не менее, путать их ни в коем случае нельзя.
- Большинство битовых операций являются операциями составного присваивания.
Побитовое ИЛИ (OR)
Побитовое ИЛИ действует эквивалентно логическому ИЛИ, но примененному к каждой паре битов двоичного числа. Двоичный разряд результата равен 0 только тогда, когда оба соответствующих бита в равны 0. Во всех других случаях двоичный результат равен 1. То есть, если у нас есть следующая таблица истинности:
38 | 53 будет таким:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A | B | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
В итоге мы получаем 1101112 , или 5510 .
Побитовое И (AND)
Побитовое И — это что-то вроде операции, противоположной побитовому ИЛИ. Двоичный разряд результата равен 1 только тогда, когда оба соответствующих бита операндов равны 1. Другими словами, можно сказать, двоичные разряды получившегося числа — это результат умножения соответствующих битов операнда: 1х1 = 1, 1х0 = 0. Побитовому И соответствует следующая таблица истинности:
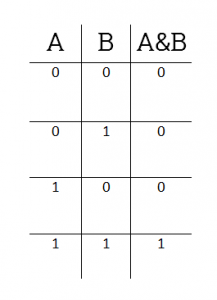
Пример работы побитового И на выражении 38 & 53:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A & B | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
Как результат, получаем 1001002 , или 3610 .
С помощью побитового оператора И можно проверить, является ли число четным или нечетным. Для целых чисел, если младший бит равен 1, то число нечетное (основываясь на преобразовании двоичных чисел в десятичные). Зачем это нужно, если можно просто использовать %2? На моем компьютере, например, &1 выполняется на 66% быстрее. Довольно неплохое повышение производительности, скажу я вам.
Исключающее ИЛИ (XOR)
Разница между исключающим ИЛИ и побитовым ИЛИ в том, что для получения 1 только один бит в паре может быть 1:
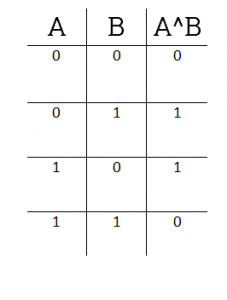
Например, выражение 138^43 будет равно…
| A | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|
| B | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| A ^ B | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
… 101000012 , или 16010
С помощью ^ можно поменять значения двух переменных (имеющих одинаковый тип данных) без использования временной переменной.
Также с помощью исключающего ИЛИ можно зашифровать текст. Для этого нужно лишь итерировать через все символы, и ^ их с символом-ключом. Для более сложного шифра можно использовать строку символов:
String msg = "This is a message";
char[] message = msg.toCharArray();
String key = ".*)";
String encryptedString = new String();
for(int i = 0; i< message.length; i++){
encryptedString += message[i]^key.toCharArray()[i%key.length()];
}
Исключающее ИЛИ не самый надежный способ шифровки, но его можно сделать частью шифровального алгоритма.
Побитовое отрицание (NOT)
Побитовое отрицание инвертирует все биты операнда. То есть, то что было 1 станет 0, и наоборот.

Вот, например, операция ~52:
| A | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
| ~A | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Результатом будет 20310
При использовании побитового отрицания знак результата всегда будет противоположен знаку исходного числа (при работе со знаковыми числами). Почему так происходит, узнаете прямо сейчас.
Дополнительный код
Здесь мне стоит рассказать вам немного о способе представления отрицательных целых чисел в ЭВМ, а именно о дополнительном коде (two’s complement). Не вдаваясь в подробности, он нужен для облегчения арифметики двоичных чисел.
Главное, что вам нужно знать о числах, записанных в дополнительном коде — это то, что старший разряд является знаковым. Если он равен 0, то число положительное и совпадает с представлением этого числа в прямом коде, а если 1 — то оно отрицательное. То есть, 10111101 — отрицательное число, а 01000011 — положительное.
Чтобы преобразовать отрицательное число в дополнительный код, нужно инвертировать все биты числа (то есть, по сути, использовать побитовое отрицание) и добавить к результату 1.
Например, если мы имеем 109:
| A | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| ~A | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ~A+1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Представленным выше методом мы получаем -109 в дополнительном коде.
Только что было представлено очень упрощенное объяснение дополнительного кода, и я настоятельно советую вам детальнее изучить эту тему.
Побитовый сдвиг влево
Побитовые сдвиги немного отличаются от рассмотренных ранее битовых операций. Побитовый сдвиг влево сдвигает биты своего операнда на N количество битов влево, начиная с младшего бита. Пустые места после сдвига заполняются нулями. Происходит это так:
| A | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
| A<<2 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Интересной особенностью сдвига влево на N позиций является то, что это эквивалентно умножению числа на 2N. Таким образом, 43<<4 == 43*Math.pow(2,4). Использование сдвига влево вместо Math.pow обеспечит неплохой прирост производительности.
Побитовый сдвиг вправо
Как вы могли догадаться, >> сдвигает биты операнда на обозначенное количество битов вправо.
Если операнд положительный, то пустые места заполняются нулями. Если же изначально мы работаем с отрицательным числом, то все пустые места слева заполняются единицами. Это делается для сохранения знака в соответствии с дополнительным кодом, объясненным ранее.
Так как побитовый сдвиг вправо — это операция, противоположная побитовому сдвигу влево, несложно догадаться, что сдвиг числа вправо на N количество позиций также делит это число на 2N. Опять же, это выполняется намного быстрее обычного деления.
Вывод
Итак, теперь вы знаете больше о битовых операциях и не боитесь их. Могу предположить, что вы не будете использовать >>1 при каждом делении на 2. Тем не менее, битовые операции неплохо иметь в своем арсенале, и теперь вы сможете воспользоваться ими в случае надобности или же ответить на каверзный вопрос на собеседовании.
Источники: «Understanding Bitwise Operators»,
«How to program with Bitwise Operators: The House with 8 Doors»,
«Understand how bitwise operators work».











