Как найти y больше 0 по графику

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Остановимся подробнее на свойствах функций.

Нули функции

Определение

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.
Внимание!

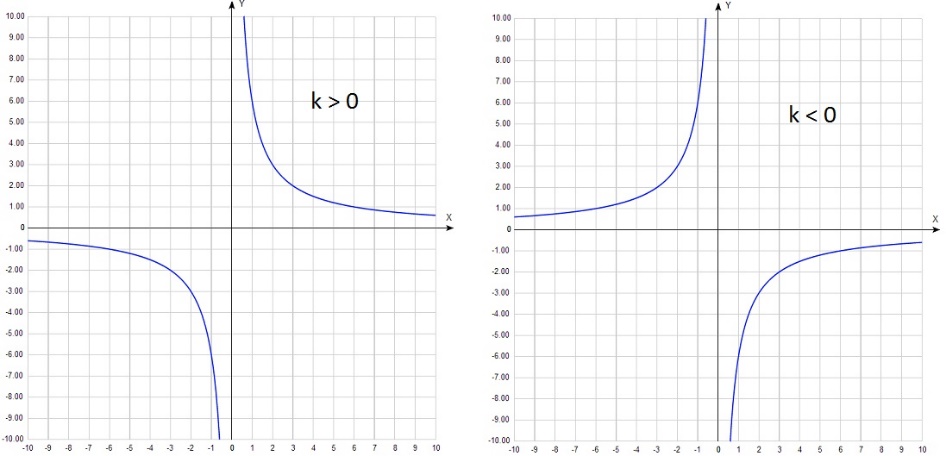
Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

График функции у=k/x выглядит следующим образом:

По данному рисунку видно, что нулей функции не существует.
Как найти нули функции?

1. Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
2. Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции.

Пример №1. Найти нули функции (если они существуют):

а) у= –11х +22

б) у= (х + 76)(х – 95)

в) у= – 46/х

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11

Получим х=2.

Таким образом, мы нашли нуль функции: х=2

б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95. Значит, нули функции это числа (-76) и 95.

в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Определение

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.

На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.

Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Определение

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Даниил Романович | Просмотров: 15.9k

На прошлых уроках мы рассмотрели линейную функцию и научились строить ее график на координатной плоскости. На этом уроке мы углубимся в теорию и разберем, почему график выглядит именно так.

Вспомним, что линейная функция имеет вид $y = kx+b$, где $x$ – переменная, а $k$ и $b$ – некоторые числа, называемые коэффициентами.

Например,

• $y = textcolor{blue}{5}x + color{green}{10}$ – линейная функция
• $color{blue} k = 5$
• $color{green} b = 10$.

График линейной функции – прямая линия, а ее положение на плоскости зависит от того, какие у функции $k$ и $b$.

Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$

При $k > 0$ угол между графиком и осью $Ox$ меньше $90 degree$ (острый)

При $k < 0$ угол между графиком и осью $Ox$ больше $90 degree$ (тупой)

Коэффициент b

Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат. 

Другими словами, коэффициент $b$ показывает, насколько график выше или ниже оси $Oy$.

• Если $b > 0$, график сдвинут вверх,
• если $b < 0$, то график сдвинут вниз.

На нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).

Частные случаи. b = 0

Если коэффициент $b = 0$, функция приобретает вид $y = kx + 0$, что можно сократить до $y = kx$.

Подставим в формулу $x = 0$, получим: $$y = k times 0$$

Значит, график будет проходить через начало координат $O(0;0)$.

Для построения графика функции вида $y = kx$ достаточно найти одну точку, вторая – начало координат.

k = 0

Если коэффициент $k = 0$, угол наклона также будет равен $0$.

Функция при этом принимает вид $y = 0 times x + b$, то есть $y = b$.

Куда делась переменная $x$? Она нам больше не нужна, так как какой бы $x$ мы не подставили, значение $y$ не изменится.

Таблица

Исследование графика функции

На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

• область определения функции;
• область значений функции;
• нули функции;
• промежутки возрастания и убывания;
• точки максимума и минимума;
• наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.

Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).

На нашем рисунке область определения функции  — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок  — от самого нижнего до самого верхнего значения .

Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .

Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .

Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества  можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.

Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.

Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Для убывающей функции большему значению  соответствует меньшее значение . График идет вправо и вниз.

На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке  — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке  — точка минимума.

Точка  — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и  на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это  и .

А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен . Он достигается в точке .

Можно сказать, что экстремумы функции равны  и .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке равно  и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.

Вы открыли страницу вопроса Как определить по графику где у = 0, где у = больше 0, и где у = меньше нуля?. Он относится к категории
Алгебра. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Алгебра,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.