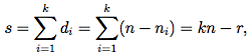Как найти ядро функции

Примеры экзаменационных задач.

1. Пусть X,
   Y – два множества,
   состоящие из n и m
   элементов соответственно. Какова
   мощность множества всех тотальных
   функций, определенных на X,
   со значением в Y?

Решение.

Чтобы задать любую тотальную функцию
нужно выполнить n
действий: указать образ каждого элемента
множества X, но каждое
действие можно выполнить m
способами  число
функций равно mⁿ.

1. Доказать,
   что
   ,
   f : XY,
   A, B
   
   X.

Доказательство.

Пусть

или

или
.

Пусть

или

.

1. Доказать,
   что
   ,
   y = f(x),
   A, B
    Y,
   
   – не обязательно функция.

Доказательство.

1. Пусть
   
   и
   
   и
   .

2. Пусть
   
   и
   
   и
   .

3. 

Лекция 9. Композиция функций.

Т.к. всякая функция – это бинарное
отношение, то мы можем строить композицию
функций, как композицию бинарных
отношений. Если

f: X
Z , то z
= f(x).
Если g: Z
Y, то y
= g(z),
тогда fg:
X
Y .

Композиция функций fg
= {(x, y)|
xX,
yY,
(zZ):
(x, z)
f и

(z, y)
g} = {(x,
y)| (z):
z = f(x)
и y = g(z)}
= {(x, y)|
y = g(f(x))}.

Композиция функций – это не просто
бинарное отношение, это снова функция.
Действительно, если элемент х задан,
то z = f(x)
определяется однозначно, тогда y
= g(z)
тоже определяется однозначно.

Пример.

F(x)
= 2x + 1, g(x)
=

f
g(x)
= g(f(x))
=,

gf(x)
= f(g(x))
= 2+1,.

Из примера видно, что композиция
некоммутативна:

f
g(x)
≠ gf(x),
зато ассоциативна: (f

g)h
= f
(gh).

Предполагается, что области определения
и значений функций f,
g, h
согласованы так, что композицию можно
определить:

(f
g)h(x)
= h(f
g(x))
= h(g(f(x)))

f(gh)(x)=
(gh)(f(x))
= h(g(f(x)))

Закон ассоциативности справедлив для
любого числа функций, и та единственная
функция, которая получается в результате
композиции функций f₁,
f₂,
f₃,
… , f_n
в указанном порядке, так и обозначается:

f₁

f₂

f₃


…
f_n.

Пример.

F₁
= x²,
f₂
= sin(x),
f₃
= x³
– 1

f₁

f₂

f₃
= (sin(x²))³
– 1,

f₁

f₃

f₂
= sin(x⁶
– 1),

f₂

f₁

f₃
= sin⁶(x)
– 1,

f₂

f₃

f₁
= (sin³(x)–1)²,

f₃

f₁

f₂
= sin(x³
– 1)²,

f₃

f₂

f₁
= sin²(x³
– 1).

Пусть теперь функции f
и g взаимнооднозначны.
Если z = f(x),
то

–
взаимнооднозначная функция. Если y
= g(z),
то z = g^–1(y)
– взаимнооднозначная функция. Выясним,
какими свойствами обладает композиция
взаимнооднозначных функций.

Теорема.

Композиция взаимнооднозначных функций
– взаимнооднозначная функция, при этом
(fg)^–1
= g ^–1f
^–1.

Доказательство.

1. Пусть.
   Тогда g(f(x₁))
   = g(f(x₂))
   = y. В силу взаимной
   однозначности функции g:
   f(x₁)
   = f(x₂).
   В силу взаимной однозначности функции
   f: x₁
   = x₂.

2. Пусть
   .

Пусть g ^–1f
^–1(y)
=
,
тогда

Отсюда

в силу условия взаимной однозначности
функций

и
.

Таким образом, функции

и

отображают элемент y
в один и тот же элемент, т.е. представляют
собой одну и ту же функцию.

Ядро функции).

Определяется обычным образом: Ker
f = ff
^–1
 XX
(f: XY,
f ^–1:
YX).

Найдем сначала ядро взаимнооднозначной
функции f:

f
f
^–1(x)
= f ^–1(f(x))
= f ^–1(y)
= x, f
^–1f(y)
= f(f
^–1(y))
= f(x)
= y. Таким образом
ядро взаимнооднозначной функции –
тождественное отображение области
определения функции на нее же.

f
f
^–1
= Ix, f
^–1f
= Iy.

В общем случае f ^–1
уже не функция, а просто бинарное
отношение, и тогда справедлива следующая
теорема.

Теорема.

Ядро функции является отношением
эквивалентности на области определения
функции.

Чтобы доказать эту теорему выясним
какие упорядоченные пары принадлежат
ядру функции f.

Пусть

и
и

.
Если пара (x₁,
x₂) принадлежит
ядру, то у этой пары один и тот же образ.
Пусть f(x₁)
= f(x₂)
= y 
(x₁, y)f
и (x₂,
y)f
(x₁,
y)f
и (y, x₂)f
^–1
 (x₁,
x₂)
f
f
^–1.

Таким образом: (x₁,
x₂)
f
f
^–1
 f(x₁)
= f(x₂).

Доказательство.

1. Рефлексивность:
   f(x)
   = f(x)
    (x,
   x)Ker
   f;

2. Симметричность:
   Если f(x₁)
   = f(x₂),
   то f(x₂)
   = f(x₁).
   Значит, ((x₁,
   x₂)Ker
   f 
   (x₂,
   x₁)
   Ker f);

3. Транзитивность:
   Если f(x₁)
   = f(x₂),
   f(x₂)
   = f(x₃),
   то f(x₁)
   = f(x₃);
   (x₁,
   x₂)Ker
   f и
   (x₂,
   x₃)
   Ker f 
   (x₁,
   x₃)Ker
   f.

Теорема доказана.

Всякое
отношение эквивалентности определяет
разбиение множества, на котором оно
задано, на непересекающиеся непустые
классы эквивалентности. В случае ядра
функции, класс
эквивалентности состоит из всех элементов
области определения имеющих один и тот
же образ.

Пример1.

Y = x²

(1, 1)Ker
y, (1,
–1)Ker
y, (8,
–8)Ker
y, (0,
0)Ker
y, (8,
2)Ker
y.

Класс эквивалентности – это множество
элементов [x] = {a|
a²
= x²}

Например, [2]_Ker
y = {2;
–2}, [0]_{Ker y}
= {0}.

Фактормножество области определения
X функции f
по ядру ker f
обозначим через
.
Область значений функции f
обозначим через

(от англ. Image 
образ). Из сказанного следует, что
соответствие



по правилу

это тотальная биекция.

Пример2 (теорема о гомоморфизме).

Определение. Группой

называется произвольное множество, на
элементах которого определена функция
,
которая называется «групповой
операцией» или «умножением»,
обозначается

и обладает следующими свойствами.

1. Ассоциативность.
   .

2. Существование единицы.
   .
   Элемент
   
   называется единицей группы
   .

3. Существование обратного элемента.

.
Элемент

называется обратным элементу
.

Пусть

две группы. Тотальная функция

называется гомоморфизмом (от
гр. morphē 
форма и гр. homos 
равный, одинаковый; в сложных словах
означает сходство, единство), если она
сохраняет групповую операцию:
.
Множество

Утверждение 1. Область значений
гомоморфизма

множество

 это
группа, подгруппа
,
с той же самой групповой операцией.

Доказательство.

Пусть

.
Множество

замкнуто относительно групповой
операции, заданной в группе
,
поэтому доказывать ассоциативность
операции не нужно.

Покажем, что
,
где

единица группы
,
 это единица множества
.
Действительно,

и
.

Покажем, что

это элемент, обратный элементу
.
В самом деле:

и

=
.
Утверждение доказано.

Ядро гомомормизма
,
как ядро всякой функции, определяет
разбиение группы
,
области определения функции
,
на непустые непересекающиеся классы
эквивалентности. Каждый класс
эквивалентности состоит из тех и только
тех аргументов, которые имеют один и
тот же образ.

Утверждение 2. Множество классов
эквивалентности (фактормножество
)
это  группа, если
положить, что

для всяких
.

Доказательство. Пусть

и
.
Тогда

,
поэтому групповая операция определена
корректно.

Докажем ассоциативность групповой
операции:

,
так как умножение в группе

ассоциативно.

Докажем, что класс

 единица множества
.

.

Докажем, что класс

обратен классу
.

.

Утверждение доказано

Ранее было показано, что всякое
соответствие вида

по правилу

является тотальной биекцией. Покажем,
что если

 гомоморфизм, то
соответствие

 тоже гомоморфизм.

,
что и требовалось.

Гомоморфизм, который одновременно есть
биекция, называется изоморфизмом
(от гр. isos 
равный, одинаковый, подобный). Группы,
между которыми установлено изоморфное
соответствие, называются изоморфными.
Таким образом, нами доказана следующая
теорема об изоморфизме.
Факторгруппа

по ядру произвольного гомоморфизма

изоморфна группе образов этого
гомоморфизма.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Минимальная ДНФ — наименьшее число литералов (вхождений переменных). Кратчайшая ДНФ — наименьшее число элементарных конъюнкций. Геометрия булева куба. Импликанты и простые импликанты. Сокращенная ДНФ. Избыточные импликанты и тупиковые ДНФ. Методы построения сокращенной ДНФ. Алгоритм Квайна — Мак-Клоски. Склейка. Таблицы Квайна и простые импликанты. Ядровые импликанты. Тупиковые ДНФ и функция Патрика. Выбор кратчайших и минимальных ДНФ.

Каждая функция может быть представлена дизъюнктивной нормальной формой различными способами. например, изменить ДНФ можно, если в одно из ее слагаемых ввести фиктивную переменную с помощью сомножителя x + x. Возникает задача из всех ДНФ найти наиболее простую в том или ином смысле.

Возможны по крайней мере два подхода к оценке сложности ДНФ: по количеству элементарных конъюнкций в ней (это количество называют длиной ДНФ) и по общему количеству литералов, т.е. по сумме длин элементарных конъюнкций, входящих в ДНФ (эту сумму называют сложностью ДНФ). ДНФ называют минимальной, если она имеет наименьшую сложность, и кратчайшей, если она имеет наименьшую длину.

В приведенной терминологии задача состоит в выборе среди всех ДНФ, представляющих данную функцию, наименьших и кратчайших. Решение такой задачи сводится к отбору некоторого ограниченного круга ДНФ, ”подозрительных на минимум“, и последующему перебору отобранных ДНФ. Здесь возможны различные приемы. Чтобы описать и объяснить эти приемы, перейдем к геометрической интерпретации области определения булевой функции — булева куба.

Отдельные элементы, составляющие булев куб Bⁿ, т.е. булевы векторы принято называть вершинами куба. Множество булевых векторов, у которых компоненты заданного набора, например с номерами i₁, …, i_k, имеют определенные значения образуют подалгебру булевой алгебры, называемую гранью булева куба. Грань представляет собой булев куб, но меньшей размерности, равной n − k, где n — размерность булева куба, k — количество фиксированных номеров. Грань размерности 1 называется ребром булева куба. Кортеж номеров фиксированных компонент, определяющий грань куба называют направлением грани. Грани, имеющие одинаковое направление, не пересекаются. Они называются параллельными. Среди паралельных граней выделим соседние, у которых совпадают значения всех фиксированных компонент, кроме одной.

Грани булева куба удобно обозначать, как слово из трех символов 0, 1 и ∗, где 0 и 1 обозначают фиксированные значения компонент, а ∗ указывает меняющиеся компоненты. Например, слово 00 ∗ 1, обозначает ребро четырехмерного булева куба, определяемое условиями x₁ = 0, x₄ = 0, x₄ = 0. Третья компонента, отмеченная звездочкой, варьируется. При таком способе записи размерность грани совпадает с количеством звездочек, грани параллельны, если у них совпадает положение звездочек (например 10 ∗ 0 и 01 ∗ 1). Грани соседние, если их записи раз- личаются только в одной позиции, в которой для одной грани указано значение 0, а для другой 1 (например 01∗0∗1 и 11∗0∗1).

Будем говорить, что булева функция f, определенная на Bn, подчиняется булевой функции g, определенной на том же кубе (или f меньше g), если f(x)≤g(x) для любого x ∈ Bⁿ. В этом случае будем писать f ≤g. Множество вершин куба, в которых функция f принимает значение 1, будем называть уровнем единицы функции, сами эти вершины называют конституентами единицы. Если f ≤ g, то уровень единицы функции f является подмножеством уровня единицы функции g.

Элементарная конъюнкция принимает значение 1 в том и только в том случае, когда каждый литерал в ней принимает значение 1. Часть переменных может не входить в конъюнкцию, т.е. эти переменные будут фиктивными. Варьируя значения фиктивных переменных, получим грань n-мерного булева куба. Таким образом, уровень единицы любой элементарной конъюнк- ции есть некоторая грань булева куба.

Любую ДНФ данной функции f можно интерпретировать как набор граней булева куба, объединение которых совпадает с уровнем единицы функции f. При этом каждая элементар- ная конъюнкция рассматриваемой ДНФ будет подчинена функции f. Любую элементарную конъюнкцию, подчиненную функции f, будем называть импликантой.

Замечание. Далее будем предполагать, что исследуемая функция от n аргументов не меняется, так что можно заранее каждый аргумент функции связать с некоторой переменной, а точнее, с i-м аргументом связывается переменная x_i. Это позволяет не различать булевы функции и формулы, составленные из переменных x₁, . . . , x_n. Именно в этом контексте элементарная конъюнкция трактуется как функция от n аргументов.

Чтобы получить кратчайшую ДНФ заданной функции, надо выбрать минимальное количество импликант (граней булева куба, содержащихся в уровне единицы функции), в совокупности накрывающих уровень 1. Для минимальной ДНФ минимума достигает сумма длин импликант, а для этого надо стремиться увеличить сумму размерностей граней куба, соответствующих элементарным конъюнкциям ДНФ. В самом деле, пусть d_i и n_i, i = 1, k, — длины конъюнкций, составляющих ДНФ, и размерности соответствующих граней булева куба; s — сложность ДНФ; r — сумма размерностей граней, соответствующих конъюнкциям ДНФ. Тогда и мы видим, что увеличение суммы размерностей граней ведет к уменьшению сложности ДНФ.

При небольших размерностях булева куба (до 4) его геометрию можно представить на плоскости с помощью так называемых карт Карно. Представим куб Bn как декартово произведение двух кубов Bk × Bl, где k, l ≤2. Такое произведение можно изобразить таблицей, в которой каждая строка соответствует вершине куба Bk , а каждый столбец — вершине куба Bl . Существенным моментом является такой порядок строк и соответственно столбцов, при котором соседним строкам и столбцам отвечают соседние вершины соответствующего булева куба. А именно, при k, l = 1, берем естественный порядок 0, 1. при k, l = 2 используем порядок 00, 01, 11, 10 (табл. 1.5).

В такой таблице соседние клетки соответствуют соседним вершинам четырехмерного булева куба. Если представить, что эта ”шахматная доска“ склеена по горизонтали и вертикали, т.е. соседними, например, являются (00, 11) и (10, 11), а также (01, 00) и (01, 10), то соседние на доске будет в точности соответствовать соседним на кубе.

На карте Карно ребро — это пара соседних (в том числе и ”через край“) клеток. Легко изобразить на карте Карно и двумерные грани, состоящие из 4-х вершин. это либо квадрат из двух примыкающих пар клеток, либо одна строка, либо один столбец. Трехмерная грань — это две соседние строки или два соседних столбца.

К сожалению, при увеличении размерности такая простая интерпретация исчезает. Например, для пятимерного куба (табл. 1.6), соседние клетки (включая ”соседство через край“) будут соответствовать со- седним вершинам. Но, кроме того, и другие пары клеток, например (01, 001) и (01, 101), не будучи со- седними в таблице, соответствуют соседним верши- нам. Причина в том, что на карте Карно у каждой клетки четыре соседних, в то время как в n-мерном кубе каждая вершина имеет n соседних вершин, которые получаются, если в булевом векторе изменить одну компоненту из n возможных.

Рассмотрим два приема, с помощью которых из имеющейся ДНФ можно получить более простую ДНФ (и в смысле длины, и в смысле сложности).

Склейка. Дизъюнктивная нормальная форма данной функции может содержать пару импликант, соответствующих соседним граням булева куба. Но две соседние грани булева куба вместе составляют грань большей размерности. Например, две двумерные грани 01∗∗10 и 01∗∗11 пятимерного куба в совокупности составляют трехмерную грань 01∗∗1∗. Замена в ДНФ двух таких импликант одной более короткой приводит к 0*0* уменьшению и длины, и сложности ДНФ. Такую замену называют склейкой.

Импликанты, соответствующие соседним граням, имеют один и тот же набор переменных, причем они различаются только по одной переменной: в одной импликанте стоит сама переменная, а в другой — ее отрицание. Например, грани 01∗∗10 и 01∗∗11 соответствуют элементарным конъюнкциям x1 x2 x4 x5 и x1 x2 x4 x5 . Изменение ДНФ выполняется в данном случае в соответствии с тождеством x1 x2 x4 x5 + x1 x2 x4x5 = x1 x2 x4 Примеры возможных склеек показаны с помощью карты Карно на рис. 1.3.

Отталкиваясь от совершенной ДНФ, мы можем сперва склеивать различные пары соседних нульмерных граней (вершин) в ребра, затем в соседние ребра в двумерные грани и т.д. Процесс подобной склейки приведет к выявлению граней максимальной размерности, содержащихся в уровне единицы функции. Этим граням соответствуют максимальные импликанты функции (максимальные относительно введенного порядка ≤ на импликантах функции). Такие импликанты называются простыми импликантами. ДНФ данной функции, в которую входят все простые импликанты, называют сокращенной ДНФ.

Отметим, что если исходная ДНФ не является совершенной, то склейка может и не привести к сокращенной ДНФ. Так, если на рис. 1.3 выбрать грани ∗0∗0, 01∗1, 0001, 0100, получим покрытие уровня единицы функции. В соответствующей ДНФ x₂x₄+x₁x₂x₄+x₁x₂x₃x₄+x₁x₂x₃x₄ нельзя склеить какие-либо грани, но эта ДНФ не является сокращенной, так как два последних слагаемых не являются простыми импликантами.

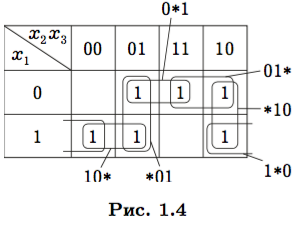Избыточные импликанты. В сокращенной ДНФ одна из импликант может накрываться остальными. Такую импликанту можно удалить из формулы, уменьшая и длину, и сложность ДНФ. Рассмотрим, например, функцию, представленную картой Карно на рис. 1.4. У этой функции максимальными являются шесть импликант 1∗0, 10∗, ∗01, 0∗1, 01∗,01* ∗10. Их сумма даст сокращенную ДНФ. Но из рисунка видно, что, например, импликанта 10∗ накрывается двумя импликантами 1∗0 и ∗01. Значит, эту импликанту можно из ДНФ удалить.

Импликанта в ДНФ, подчиненная сумме остальных импликант этой ДНФ, называется избыточной. Если из сокращенной ДНФ удалить избыточные импликанты, то получим тупиковую ДНФ. По определению, тупиковая ДНФ — это ДНФ, состоящая из простых импликант, ни одна из которых в этой ДНФ не является избыточной. Например, на рис. 1.4 тупиковую ДНФ образуют импли-

канты 1∗0, ∗01, 01∗.

Основной целью каждого метода минимизации ДНФ является выявление всех тупиковых ДНФ. Именно среди них находится минимальная и кратчайшая формы.

Построение сокращенной ДНФ. Один из методов построения сокращенной ДНФ — это метод Квайна — МакКлоски. Его суть в следующем. В качестве исходной выбирается совершенная ДНФ. На первом этапе проводится склейка импликант совершенной ДНФ в ребра, которые добавляются в ДНФ. После того как проведены все склейки вершин, из ДНФ удаляются все избыточные вершины, т.е. те, которые подчиняются добавленным ребрам. На втором этапе проводится склейка всех ребер в четырехмерные грани, которые добавляются к ДНФ. После проведения всех склеек между ребрами удаляются ребра, подчиненные двумерным граням. На третьем этапе выполняется склейка двумерных граней и удаление избыточных двумерных гра- ней. Процесс останавливается, когда между гранями соответствующей размерности не удается провести ни одной склейки. Результатом этих преобразований и будет сокращенная ДНФ.

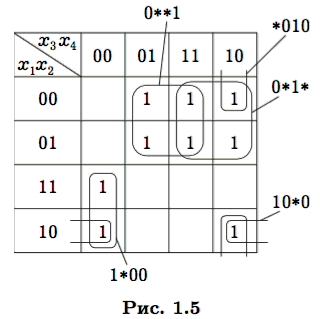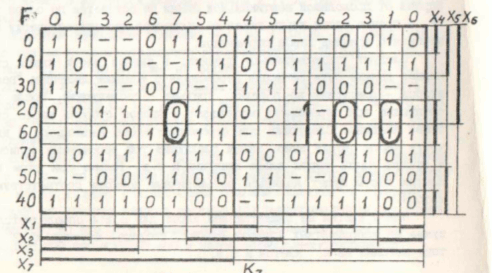
Пример 1.6. Рассмотрим функцию, заданную картой Карно на рис. 1.5. Первый этап склейки по методу Квайна приведет к ребрам 1∗00, 10∗0, ∗010, а также четырем ребрам двумерной грани 0∗∗1 и четырем ребрам двумерной грани 0∗1∗. Все исходные импликанты будут удалены как избыточные. На втором этапе мы получим две двумерные грани 0∗∗1 и 0∗1∗. При этом будут удалены 6 ребер, входящих в эти грани. Поскольку склеить две эти грани нельзя, процесс вы- явления простых импликант на этом завершится. Сокращен- ная ДНФ будет содержать пять импликант, соответствующих граням 0∗∗1, 0∗1∗, 1∗00, 10∗0, ∗010. #

Другой метод построения сокращенной ДНФ — метод Блейка, в котором в качестве исходной можно взять любую ДНФ. В этом методе на первом этапе многократно выполняется операция обобщенного склеивания, при которой сумма xK₁ +xK₂ заменяется суммой xK₁ +xK₂ +K₁K₁. Такая операция выполняется до тех пор, пока удается получать новые импликанты вида K₁K₂. После завершения первого этапа выполняется операция поглощения согласно формуле K₁K₂ + K₂ = K₂.

Выявление всех тупиковых ДНФ. Создать список всех тупиковых ДНФ можно, используя следующий прием. Обозначим все простые импликанты символами K₁, K₂, . . . , K_m. Перенумеруем все вершины уровня единицы функции. Пусть первая вершина накрывается склейками K_i1 , K_i2 , . . . , K_ip . Тогда элементарная дизъюнкция K_i1 + K_i2 + . . . + K_ip задает условие, что первая вершина уровня единицы функции накрывается одной из простых импликант. Составив конъюнкцию из указанных элементарных дизъюнкций по всем вершинам уровня единицы функции, мы получим КНФ, представляющее собой логическое условие того, что весь уровень единицы функции накрыт простыми импликантами. Эта КНФ называют функцией Патрика. Преобразуем КНФ в ДНФ, пользуясь свойствами булевых операций (дистрибутив- ностью, коммутативностью, идемпотентностью). В ДНФ каждая элементарная конъюнкция будет описывать набор простых импликант, целиком покрывающих уровень единицы функ- ции, т.е. набор, описывающий конкретную тупиковую ДНФ рассматриваемой функции. Можно показать, что таким образом можно выявить все тупиковые ДНФ.

Среди простых импликант рассматриваемой функции есть те, которые входят в любую тупиковую ДНФ. К таким относится любая импликанта, для которой среди накрываемых вершин есть хотя бы одна, не накрываемая никакой другой импликантой. Например, на рис. 1.5 вершина 1100 накрывается единственной простой импликантой 1∗00. Эта импликанта должна входить в любую тупиковую ДНФ. Импликанты, удовлетворяющие описанному условию, называются ядровыми импликантами. Совокупность ядровых импликант — ядро — постоянная часть всех тупиковых ДНФ. Например, на рис. 1.5 ядро составляют импликанты 0∗∗1, 0∗1∗, 1∗00, а импликанты ∗010 и 10∗0 неядровые. При выявлении тупиковых ДНФ ядровые импликанты и накрываемые ими вершины из функции Патрика можно исключить.

Пример 1.7. У функции, представленной на рис. 1.5 диаграммой Карно, имеется пять простых импликант. Введем обозначения:

K₁ = 0∗∗1, K₂ = 0∗1∗, K₃ = 1∗00, K₄ = 10∗0, K₅ = ∗010.

Тогда функция Патрика для 9 вершин уровня 1 при их нумерации по строкам будет иметь следующий вид:

P = K₁(K₁ + K₂)(K₂ + K₅)K₁(K₁ + K₂)K₂K₃(K₃ + K₄)(K₄ + K₅).

Упростив согласно идемпотентности операций и тождествам поглощения (x(x + y) = x), получим

P = K₁K₂K₃(K₄ + K₅).

Используя дистрибутивность и идемпотентность, приходим к ДНФ:

P = K₁K₂K₃(K₄ + K₅) = K₁K₂K₃K₄ + K₁K₂K₃K₅.

Таким образом, рассматриваемая функция имеет две сокращенные ДНФ, описываемые двумя списками склеек K₁, K₂, K₃, K₄ и K₁, K₂, K₃, K₅. В результате получим

D₁ = x ₁x₄ + x₁x₃ + x₁x ₃x ₄ + x₁x₂x₄, D₂ = x₁ x₄ + x₁x₃ + x₁x3x₄ + x₂x₃x₄.

Видно, что у обоих сокращенных ДНФ есть общая часть — первые три конъюнкции. Это ядро, входящее в каждую сокращенную ДНФ. Его можно исключить из рассмотрения, рассматривая условия накрытия только для тех вершин, которые не накрываются склейками ядра. В данном случае это единственная вершина 1010. При этом функция Патрика будет иметь вид Pˆ = K₄ + K₅. Добавив к каждому слагаемому элементарную конъюнкцию K₁K₂K₃, описывающую ядро, получим полную функцию Патрика. #

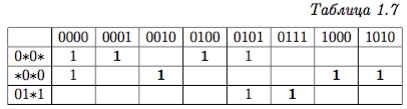
Ядро данной функции можно получить с помощью таблицы Квайна, в которой каждая строка соответствует одной простой импликанте, а каждый столбец — одной вершине уровня единицы функции. В каждой клетке указывается 1, если импликанта накрывает вершину, и пробел в противном случае Например, составим таблицу Квайна функции, представленной картой Карно на рис. 1.3 (табл. 1.7). Чтобы определить ядро функции, необходимо выявить столбцы, в которых находится только одна единица, и пометить соответствующие строки. Импликанты, соответствующие помеченным строкам, образуют ядро. Например, в табл. 1.7 по одной единице содержится в столбцах, отвечающих вершинам 0001, 0010, 0100, 0111, 1000, 1010 (эти единицы выделены полужирным шрифтом). Поскольку в каждой строке содержится хотя бы одна выделенная единица, все простые импликанты ядровые, т.е. рассматриваемая функция имеет единственную тупиковую ДНФ.

Минимальная ДНФ — наименьшее число литералов (вхождений переменных). Кратчайшая ДНФ — наименьшее число элементарных конъюнкций. Геометрия булева куба. Импликанты и простые импликанты. Сокращенная ДНФ. Избыточные импликанты и тупиковые ДНФ. Методы построения сокращенной ДНФ. Алгоритм Квайна — Мак-Клоски. Склейка. Таблицы Квайна и простые импликанты. Ядровые импликанты. Тупиковые ДНФ и функция Патрика. Выбор кратчайших и минимальных ДНФ.

Каждая функция может быть представлена дизъюнктивной нормальной формой различными способами. например, изменить ДНФ можно, если в одно из ее слагаемых ввести фиктивную переменную с помощью сомножителя x + x. Возникает задача из всех ДНФ найти наиболее простую в том или ином смысле.

Возможны по крайней мере два подхода к оценке сложности ДНФ: по количеству элементарных конъюнкций в ней (это количество называют длиной ДНФ) и по общему количеству литералов, т.е. по сумме длин элементарных конъюнкций, входящих в ДНФ (эту сумму называют сложностью ДНФ). ДНФ называют минимальной, если она имеет наименьшую сложность, и кратчайшей, если она имеет наименьшую длину.

В приведенной терминологии задача состоит в выборе среди всех ДНФ, представляющих данную функцию, наименьших и кратчайших. Решение такой задачи сводится к отбору некоторого ограниченного круга ДНФ, ”подозрительных на минимум“, и последующему перебору отобранных ДНФ. Здесь возможны различные приемы. Чтобы описать и объяснить эти приемы, перейдем к геометрической интерпретации области определения булевой функции — булева куба.

Отдельные элементы, составляющие булев куб Bⁿ, т.е. булевы векторы принято называть вершинами куба. Множество булевых векторов, у которых компоненты заданного набора, например с номерами i₁, …, i_k, имеют определенные значения образуют подалгебру булевой алгебры, называемую гранью булева куба. Грань представляет собой булев куб, но меньшей размерности, равной n − k, где n — размерность булева куба, k — количество фиксированных номеров. Грань размерности 1 называется ребром булева куба. Кортеж номеров фиксированных компонент, определяющий грань куба называют направлением грани. Грани, имеющие одинаковое направление, не пересекаются. Они называются параллельными. Среди паралельных граней выделим соседние, у которых совпадают значения всех фиксированных компонент, кроме одной.

Грани булева куба удобно обозначать, как слово из трех символов 0, 1 и ∗, где 0 и 1 обозначают фиксированные значения компонент, а ∗ указывает меняющиеся компоненты. Например, слово 00 ∗ 1, обозначает ребро четырехмерного булева куба, определяемое условиями x₁ = 0, x₄ = 0, x₄ = 0. Третья компонента, отмеченная звездочкой, варьируется. При таком способе записи размерность грани совпадает с количеством звездочек, грани параллельны, если у них совпадает положение звездочек (например 10 ∗ 0 и 01 ∗ 1). Грани соседние, если их записи раз- личаются только в одной позиции, в которой для одной грани указано значение 0, а для другой 1 (например 01∗0∗1 и 11∗0∗1).

Будем говорить, что булева функция f, определенная на Bn, подчиняется булевой функции g, определенной на том же кубе (или f меньше g), если f(x)≤g(x) для любого x ∈ Bⁿ. В этом случае будем писать f ≤g. Множество вершин куба, в которых функция f принимает значение 1, будем называть уровнем единицы функции, сами эти вершины называют конституентами единицы. Если f ≤ g, то уровень единицы функции f является подмножеством уровня единицы функции g.

Элементарная конъюнкция принимает значение 1 в том и только в том случае, когда каждый литерал в ней принимает значение 1. Часть переменных может не входить в конъюнкцию, т.е. эти переменные будут фиктивными. Варьируя значения фиктивных переменных, получим грань n-мерного булева куба. Таким образом, уровень единицы любой элементарной конъюнк- ции есть некоторая грань булева куба.

Любую ДНФ данной функции f можно интерпретировать как набор граней булева куба, объединение которых совпадает с уровнем единицы функции f. При этом каждая элементар- ная конъюнкция рассматриваемой ДНФ будет подчинена функции f. Любую элементарную конъюнкцию, подчиненную функции f, будем называть импликантой.

Замечание. Далее будем предполагать, что исследуемая функция от n аргументов не меняется, так что можно заранее каждый аргумент функции связать с некоторой переменной, а точнее, с i-м аргументом связывается переменная x_i. Это позволяет не различать булевы функции и формулы, составленные из переменных x₁, . . . , x_n. Именно в этом контексте элементарная конъюнкция трактуется как функция от n аргументов.

Чтобы получить кратчайшую ДНФ заданной функции, надо выбрать минимальное количество импликант (граней булева куба, содержащихся в уровне единицы функции), в совокупности накрывающих уровень 1. Для минимальной ДНФ минимума достигает сумма длин импликант, а для этого надо стремиться увеличить сумму размерностей граней куба, соответствующих элементарным конъюнкциям ДНФ. В самом деле, пусть d_i и n_i, i = 1, k, — длины конъюнкций, составляющих ДНФ, и размерности соответствующих граней булева куба; s — сложность ДНФ; r — сумма размерностей граней, соответствующих конъюнкциям ДНФ. Тогда и мы видим, что увеличение суммы размерностей граней ведет к уменьшению сложности ДНФ.

При небольших размерностях булева куба (до 4) его геометрию можно представить на плоскости с помощью так называемых карт Карно. Представим куб Bn как декартово произведение двух кубов Bk × Bl, где k, l ≤2. Такое произведение можно изобразить таблицей, в которой каждая строка соответствует вершине куба Bk , а каждый столбец — вершине куба Bl . Существенным моментом является такой порядок строк и соответственно столбцов, при котором соседним строкам и столбцам отвечают соседние вершины соответствующего булева куба. А именно, при k, l = 1, берем естественный порядок 0, 1. при k, l = 2 используем порядок 00, 01, 11, 10 (табл. 1.5).

В такой таблице соседние клетки соответствуют соседним вершинам четырехмерного булева куба. Если представить, что эта ”шахматная доска“ склеена по горизонтали и вертикали, т.е. соседними, например, являются (00, 11) и (10, 11), а также (01, 00) и (01, 10), то соседние на доске будет в точности соответствовать соседним на кубе.

На карте Карно ребро — это пара соседних (в том числе и ”через край“) клеток. Легко изобразить на карте Карно и двумерные грани, состоящие из 4-х вершин. это либо квадрат из двух примыкающих пар клеток, либо одна строка, либо один столбец. Трехмерная грань — это две соседние строки или два соседних столбца.

К сожалению, при увеличении размерности такая простая интерпретация исчезает. Например, для пятимерного куба (табл. 1.6), соседние клетки (включая ”соседство через край“) будут соответствовать со- седним вершинам. Но, кроме того, и другие пары клеток, например (01, 001) и (01, 101), не будучи со- седними в таблице, соответствуют соседним верши- нам. Причина в том, что на карте Карно у каждой клетки четыре соседних, в то время как в n-мерном кубе каждая вершина имеет n соседних вершин, которые получаются, если в булевом векторе изменить одну компоненту из n возможных.

Рассмотрим два приема, с помощью которых из имеющейся ДНФ можно получить более простую ДНФ (и в смысле длины, и в смысле сложности).

Склейка. Дизъюнктивная нормальная форма данной функции может содержать пару импликант, соответствующих соседним граням булева куба. Но две соседние грани булева куба вместе составляют грань большей размерности. Например, две двумерные грани 01∗∗10 и 01∗∗11 пятимерного куба в совокупности составляют трехмерную грань 01∗∗1∗. Замена в ДНФ двух таких импликант одной более короткой приводит к 0*0* уменьшению и длины, и сложности ДНФ. Такую замену называют склейкой.

Импликанты, соответствующие соседним граням, имеют один и тот же набор переменных, причем они различаются только по одной переменной: в одной импликанте стоит сама переменная, а в другой — ее отрицание. Например, грани 01∗∗10 и 01∗∗11 соответствуют элементарным конъюнкциям x1 x2 x4 x5 и x1 x2 x4 x5 . Изменение ДНФ выполняется в данном случае в соответствии с тождеством x1 x2 x4 x5 + x1 x2 x4x5 = x1 x2 x4 Примеры возможных склеек показаны с помощью карты Карно на рис. 1.3.

Отталкиваясь от совершенной ДНФ, мы можем сперва склеивать различные пары соседних нульмерных граней (вершин) в ребра, затем в соседние ребра в двумерные грани и т.д. Процесс подобной склейки приведет к выявлению граней максимальной размерности, содержащихся в уровне единицы функции. Этим граням соответствуют максимальные импликанты функции (максимальные относительно введенного порядка ≤ на импликантах функции). Такие импликанты называются простыми импликантами. ДНФ данной функции, в которую входят все простые импликанты, называют сокращенной ДНФ.

Отметим, что если исходная ДНФ не является совершенной, то склейка может и не привести к сокращенной ДНФ. Так, если на рис. 1.3 выбрать грани ∗0∗0, 01∗1, 0001, 0100, получим покрытие уровня единицы функции. В соответствующей ДНФ x₂x₄+x₁x₂x₄+x₁x₂x₃x₄+x₁x₂x₃x₄ нельзя склеить какие-либо грани, но эта ДНФ не является сокращенной, так как два последних слагаемых не являются простыми импликантами.

Избыточные импликанты. В сокращенной ДНФ одна из импликант может накрываться остальными. Такую импликанту можно удалить из формулы, уменьшая и длину, и сложность ДНФ. Рассмотрим, например, функцию, представленную картой Карно на рис. 1.4. У этой функции максимальными являются шесть импликант 1∗0, 10∗, ∗01, 0∗1, 01∗,01* ∗10. Их сумма даст сокращенную ДНФ. Но из рисунка видно, что, например, импликанта 10∗ накрывается двумя импликантами 1∗0 и ∗01. Значит, эту импликанту можно из ДНФ удалить.

Импликанта в ДНФ, подчиненная сумме остальных импликант этой ДНФ, называется избыточной. Если из сокращенной ДНФ удалить избыточные импликанты, то получим тупиковую ДНФ. По определению, тупиковая ДНФ — это ДНФ, состоящая из простых импликант, ни одна из которых в этой ДНФ не является избыточной. Например, на рис. 1.4 тупиковую ДНФ образуют импли-

канты 1∗0, ∗01, 01∗.

Основной целью каждого метода минимизации ДНФ является выявление всех тупиковых ДНФ. Именно среди них находится минимальная и кратчайшая формы.

Построение сокращенной ДНФ. Один из методов построения сокращенной ДНФ — это метод Квайна — МакКлоски. Его суть в следующем. В качестве исходной выбирается совершенная ДНФ. На первом этапе проводится склейка импликант совершенной ДНФ в ребра, которые добавляются в ДНФ. После того как проведены все склейки вершин, из ДНФ удаляются все избыточные вершины, т.е. те, которые подчиняются добавленным ребрам. На втором этапе проводится склейка всех ребер в четырехмерные грани, которые добавляются к ДНФ. После проведения всех склеек между ребрами удаляются ребра, подчиненные двумерным граням. На третьем этапе выполняется склейка двумерных граней и удаление избыточных двумерных гра- ней. Процесс останавливается, когда между гранями соответствующей размерности не удается провести ни одной склейки. Результатом этих преобразований и будет сокращенная ДНФ.

Пример 1.6. Рассмотрим функцию, заданную картой Карно на рис. 1.5. Первый этап склейки по методу Квайна приведет к ребрам 1∗00, 10∗0, ∗010, а также четырем ребрам двумерной грани 0∗∗1 и четырем ребрам двумерной грани 0∗1∗. Все исходные импликанты будут удалены как избыточные. На втором этапе мы получим две двумерные грани 0∗∗1 и 0∗1∗. При этом будут удалены 6 ребер, входящих в эти грани. Поскольку склеить две эти грани нельзя, процесс вы- явления простых импликант на этом завершится. Сокращен- ная ДНФ будет содержать пять импликант, соответствующих граням 0∗∗1, 0∗1∗, 1∗00, 10∗0, ∗010. #

Другой метод построения сокращенной ДНФ — метод Блейка, в котором в качестве исходной можно взять любую ДНФ. В этом методе на первом этапе многократно выполняется операция обобщенного склеивания, при которой сумма xK₁ +xK₂ заменяется суммой xK₁ +xK₂ +K₁K₁. Такая операция выполняется до тех пор, пока удается получать новые импликанты вида K₁K₂. После завершения первого этапа выполняется операция поглощения согласно формуле K₁K₂ + K₂ = K₂.

Выявление всех тупиковых ДНФ. Создать список всех тупиковых ДНФ можно, используя следующий прием. Обозначим все простые импликанты символами K₁, K₂, . . . , K_m. Перенумеруем все вершины уровня единицы функции. Пусть первая вершина накрывается склейками K_i1 , K_i2 , . . . , K_ip . Тогда элементарная дизъюнкция K_i1 + K_i2 + . . . + K_ip задает условие, что первая вершина уровня единицы функции накрывается одной из простых импликант. Составив конъюнкцию из указанных элементарных дизъюнкций по всем вершинам уровня единицы функции, мы получим КНФ, представляющее собой логическое условие того, что весь уровень единицы функции накрыт простыми импликантами. Эта КНФ называют функцией Патрика. Преобразуем КНФ в ДНФ, пользуясь свойствами булевых операций (дистрибутив- ностью, коммутативностью, идемпотентностью). В ДНФ каждая элементарная конъюнкция будет описывать набор простых импликант, целиком покрывающих уровень единицы функ- ции, т.е. набор, описывающий конкретную тупиковую ДНФ рассматриваемой функции. Можно показать, что таким образом можно выявить все тупиковые ДНФ.

Среди простых импликант рассматриваемой функции есть те, которые входят в любую тупиковую ДНФ. К таким относится любая импликанта, для которой среди накрываемых вершин есть хотя бы одна, не накрываемая никакой другой импликантой. Например, на рис. 1.5 вершина 1100 накрывается единственной простой импликантой 1∗00. Эта импликанта должна входить в любую тупиковую ДНФ. Импликанты, удовлетворяющие описанному условию, называются ядровыми импликантами. Совокупность ядровых импликант — ядро — постоянная часть всех тупиковых ДНФ. Например, на рис. 1.5 ядро составляют импликанты 0∗∗1, 0∗1∗, 1∗00, а импликанты ∗010 и 10∗0 неядровые. При выявлении тупиковых ДНФ ядровые импликанты и накрываемые ими вершины из функции Патрика можно исключить.

Пример 1.7. У функции, представленной на рис. 1.5 диаграммой Карно, имеется пять простых импликант. Введем обозначения:

K₁ = 0∗∗1, K₂ = 0∗1∗, K₃ = 1∗00, K₄ = 10∗0, K₅ = ∗010.

Тогда функция Патрика для 9 вершин уровня 1 при их нумерации по строкам будет иметь следующий вид:

P = K₁(K₁ + K₂)(K₂ + K₅)K₁(K₁ + K₂)K₂K₃(K₃ + K₄)(K₄ + K₅).

Упростив согласно идемпотентности операций и тождествам поглощения (x(x + y) = x), получим

P = K₁K₂K₃(K₄ + K₅).

Используя дистрибутивность и идемпотентность, приходим к ДНФ:

P = K₁K₂K₃(K₄ + K₅) = K₁K₂K₃K₄ + K₁K₂K₃K₅.

Таким образом, рассматриваемая функция имеет две сокращенные ДНФ, описываемые двумя списками склеек K₁, K₂, K₃, K₄ и K₁, K₂, K₃, K₅. В результате получим

D₁ = x ₁x₄ + x₁x₃ + x₁x ₃x ₄ + x₁x₂x₄, D₂ = x₁ x₄ + x₁x₃ + x₁x3x₄ + x₂x₃x₄.

Видно, что у обоих сокращенных ДНФ есть общая часть — первые три конъюнкции. Это ядро, входящее в каждую сокращенную ДНФ. Его можно исключить из рассмотрения, рассматривая условия накрытия только для тех вершин, которые не накрываются склейками ядра. В данном случае это единственная вершина 1010. При этом функция Патрика будет иметь вид Pˆ = K₄ + K₅. Добавив к каждому слагаемому элементарную конъюнкцию K₁K₂K₃, описывающую ядро, получим полную функцию Патрика. #

Ядро данной функции можно получить с помощью таблицы Квайна, в которой каждая строка соответствует одной простой импликанте, а каждый столбец — одной вершине уровня единицы функции. В каждой клетке указывается 1, если импликанта накрывает вершину, и пробел в противном случае Например, составим таблицу Квайна функции, представленной картой Карно на рис. 1.3 (табл. 1.7). Чтобы определить ядро функции, необходимо выявить столбцы, в которых находится только одна единица, и пометить соответствующие строки. Импликанты, соответствующие помеченным строкам, образуют ядро. Например, в табл. 1.7 по одной единице содержится в столбцах, отвечающих вершинам 0001, 0010, 0100, 0111, 1000, 1010 (эти единицы выделены полужирным шрифтом). Поскольку в каждой строке содер

Еще раз о минимизации булевых функций

В предыдущей статье я рассказал, как симметричные карты позволяют достаточно просто и быстро минимизировать булевые функции, но не осветил два момента: получение разных вариантов минимального решения и автоматизацию самого алгоритма минимизации. Расскажу здесь об этом более подробно.

Напомню, что задача минимизации — для каждой единицы найти наибольшее покрытие. Если такое покрытие найдено и оно единственное, то оно записывается в так называемое ядро функции, а все единицы, им покрываемые выбывают из дальнейшего рассмотрения. Однако, если максимальное покрытие не единственное, возникают варианты решения, которые возможно использовать, например, для учета каких-либо дополнительных требований. Кроме того, как я покажу далее, отбрасывание вариантов приводит к тому, что полученное решение может оказаться не минимальным.

Итак, в примере из предыдущей статьи, можно найти ядро функции для следующей симметричной карты:

Оно равно:

!X1*X5 V X2*X3*X4 V X1*!X2*!X5

Можно найти, что единица в строке с индексом 0 и столбце с индексом 4 может быть покрыта двумя способами:

!X1*X3*!X4 (1)
X3*!X4*!X5 (2)

Аналогично, единица в строке с индексом 10 и столбце с индексом 4 может быть покрыта четыремя способами:

!X1*X3*!X4 (1)
X3*!X4*!X5 (2)
!X1*X2*X3 (3)
X2*X3*!X5 (4)

Заметим, что при покрытии разных единиц встречаются одинаковые импликанты, обозначенные здесь одинаковыми цифрами.

Далее, единица в строке с индексом 30 и столбце с индексом 4 может быть покрыта тремя способами:

X3*!X4*!X5 (2)
X1*X3*!X5 (5)
X2*X3*!X5 (4)

И единица в строке с индексом 20 и столбце с индексом 1 может быть покрыта двумя способами:

X1*!X2*!X3*!X4 (6)
!X2*!X3*!X4*X5 (7)

Поскольку в окончательном решении должны быть покрыты все единицы, запишем следующее выражение в виде произведения вариантов для каждой единицы:

(1 V 2)(1 V 2 V 3 V 4)(2 V 5 V 4)(6 V 7)

Раскроем первые две скобки:

(1*1 V 1*2 V 1*3 V 1*4 V 2*1 V 2*2 V 2*3 V 2*4)(2 V 5 V 4)(6 V 7)

Поскольку импликанта, будучи умноженная сама на себя дает ту же импликанту, первую скобку можно переписать в следующем виде:

(1 V 1*2 V 1*3 V 1*4 V 2*1 V 2 V 2*3 V 2*4)(2 V 5 V 4)(6 V 7)

Далее, поскольку вариант с одной импликантой дает лучшее решение, чем с двумя, можно переписать решение в виде:

(1 V 2)(2 V 5 V 4)(6 V 7)

Раскрывая скобки далее и используя подобные сокращения, получаем окончательное решение, которое уже нельзя сократить:

2(6 V 7)

Первый множитель 2 — единственная импликанта в группе и должна быть довавлена в ядро функции (так называемое расширенное ядро функции):

X3*!X4*!X5

А скобка дает два варианта:

X1*!X2*!X3*!X4

и

!X2*!X3*!X4*X5

Можно выбрать любой из них.

Естественно, возникает вопрос про автоматизацию данного алгоритма. Для этого мной была написана программа apssymmap, которую можно найти на моем сайте:

http://andyplekhanov.narod.ru/soft/soft.htm

Представляет интерес сравнить результаты применения данного метода с другими известными методами. Сравним результаты работы программы apssymmap с известной программой espresso на примере, представленном ниже:

Результат работы программы espresso:

espresso -Dexact -oeqntott test.txt

Результат работы программа apssymmap:

Видно, что программа apssymmap выдает 8 различных вариантов вместо одного у espresso. Однако, более интересным фактом является то, что результат espresso не является оптимальным. Если отбросить все общие части в этих решениях, можно увидеть, что у espresso останется две импликанты:

!X7*!X5*!X4*X2*X1
и
X7*!X6*X5*X4*X3*X1

содержащие соответственно 5 и 6 переменных, а в решении apssymmap будут импликанты

!X5*X3*X2*X1
и
X7*!X6*X3*X2*X1

содержащие 4 и 5 переменных, то есть на две меньше. В качестве вывода можно сделать заключение, что симметричные карты являются не только более удобным методом при ручной минимизации булевых функций, но и превосходят другие методы при решении этой задачи на компьютере.

To find the kernel, you need to find some way to neatly specify which elements get sent to the same place. Obviously if $x=y$, $f(x)=f(y)$, so that’s not interesting. So we look for cases where $xneq y$ and yet $f(x)=f(y)$. Here’s a proof by cases.

Suppose two elements $x, y$ are distinct and share the same $f$-image. Then suppose they’re both odd, so $$f(x)=3x+1=3y+1=f(y)$$
Clearly this implies $x=y$, so this isn’t the interesting case we’re looking for.

Now suppose both are even, so $$f(x)=frac{x}{2}=frac{y}{2}=f(y)$$ Oh dear, $x=y$ again. Not interesting. So whenever $x, y$ have the same parity, they could only have the same $f$-image if they were equal in the first place.

So the interesting case for your relation must occur when $x$ is even and $y$ is odd (or vice versa). Then $$f(x)=frac{x}{2}=3y+1=f(y)$$
Now we can solve for $x$ in terms of $y$ i.e. $x=6y+2$. So your relation can be defined by this equation; $$xrho y quadtext{iff}quad x=6y+2 quadtext{(or}quad y=6x+2)$$

Now if you think about that, you’ll realise that means every odd number gets paired with exactly even number, and they both get mapped to an even number. So to the image of $f$ can only contain even numbers. Now can you find a way to prove that every even number is reached by the function $f$? If you manage that, then you have shown $f(mathbb{Z}setminus{0})=2mathbb{Z}$. Et voila.

Интервал ранга R содержит 2^N–R векторов.

N – количество рассматриваемых векторов.

Интервал – носитель элементарной конъюнкции.

Теорема

Носитель дизъюнкции двух функций равен объединению носителей этих функций.

Доказательство.

_{f V g}  f() V g() = 1  f() = 1 ИЛИ g() = 1  _f ИЛИ  _g

ч.т.д.

Носитель ДНФ является объединением интервалов.

Допустимым интервалом для данной функции называется интервал, который целиком содержится в носителе этой функции.

N_f = I₁ V I₂ V … V I_k

Интервал для данной функции является максимальным, если он не содержится целиком ни в каком другом допустимом интервале.

Элементарная конъюнкция, носителем которой является допустимый интервал, называется импликантой.

ЭК, N – максимальный интервал – простая импликанта.

Представление носителя в виде объединения максимальных интервалов будем называть покрытием носителя максимальными интервалами.

Дизъюнкция всех возможных простых импликант называется сокращенной ДНФ функции.

Покрытие носителя интервалами будем называть неприводимым, если ни один нельзя отбросить из правой части равенства, не нарушив это равенство.

ДНФ, которая соответствует неприводимому покрытию, называется тупиковой ДНФ.

Утверждение.

Минимальная ДНФ содержится среди тупиковых ДНФ.

Определение

Максимальный интервал называется ядровым, если он содержит хотя бы одну вершину из носителя функции, которая не принадлежит больше никакому другому максимальному интервалу.

Элементарная конъюнкция, соответствующая ядровому интервалу – ядровая импликанта.

Объединение всех ядровых интервалов – ядро функции.

Дизъюнкция всех ядровых импликант – ядровая ДНФ.

Ядро функции обязательно входит в любое неприводимое покрытие.

Алгоритм получения минимальной ДНФ.

1. Выделяем носитель функции.

2. Выделяем все возможные интервалы.

3. Выписываем все простые импликанты.

4. Выделяем ядровый интервал.

5. Используя ядро функции и комбинацию неядровых интервалов, получаем все неприводимые покрытия, для каждого из которых выписываем тупиковую ДНФ.

6. С реди тупиковых ДНФ выбираем минимальную.

X1	X2	X3	F
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Выделение всех возможных интервалов.

1. Для булева куба размерности 3 интервалом ранга 1 могут быть 4 вершины, лежащие в одной грани.

2. Ранга 2 – любые 2 вершины, соединенные ребром.

3. Ранга 3 – любая отдельная вершина.

1. Нет _

2. I₁ = { 001 011} <-> П₁ = x₁x₃ – ядровый

I₂ = { 011 111} <-> П₂ = x₂x₃

Если координата вектора меняет значения, то переменная не входит

I₃ = { 111 110} <-> П₃ = x₁x₂

_

I₄ = { 110 100} <-> П₄ = x₁x₃

D_сокр. = П₁ V П₂ V П₃ V П₄

N_f = I₁ U I₄ U I₂ (U – объединение)

Получили неприводимое покрытие, добавив к ядру недостающие интервалы так, чтобы все единичные вершины были задействованы.

D₁= П₁ V П₄ V П₂

N_f = I₁ U I₄ U I₃

D₂= П₁ V П₄ V П₃

Сосчитаем ранги тупиковых ДНФ

R₁ = 6

R₂ = 6

D_min = D₁ = D₂

Метод карт Карно для нахождения минимальной ДНФ

n = 4

Карта Карно – плоскостная интерпретация 4-мерного булева куба.

	00	01	11	10
00		0001
01	0100	0101	0111	0110
11		1101
10

Считаем, что левый край склеен с правым, а верхний – с нижним.

Если таблицу Карно свернуть таким образом, то получится тор (torus – геометрическая фигура, напоминающая бублик).

Правила поиска интервалов.

1. Интервалом ранга 1 могут быть 2 соседних строки (2 соседних столбца)

2. Интервалом ранга 2 может быть вся строка, весь столбец или квадрат 2х2.

3. Интервалом ранга 3 – любые 2 соседние по горизонтали и вертикали клетки.

4. Одна отдельно взятая вершина будет интервалом ранга 4.

Алгоритм – тот же самый.

Лекция 6

Метод Квайна – Мак-Клоски для нахождения минимальной ДНФ

Этот метод удобен для нахождения минимальной ДНФ функции от любого числа переменных.

Определение. Элементарная конъюнкция K₁ покрывает ЭК K₂, если каждая переменная, входящая в K₁, входит и в K₂.

__ __ __

X₁X₃ – покрытие X₁X₂X₃X₄

N_k1  N_k2

K₂ = K₁K

K – конъюнкция из других переменных.

__ _ _ __ _ _

X₁X₃ V X₁X₂X₃X₄ = X₁X₃ (1 V X₂X₄) = X₁X₃ – поглощение

Склеивание двух ЭК

_

Kx V Kx = K

Идея метода Квайна (алгоритм)

1. Выписываются все элементарные конъюнкции из СДНФ функции.

2. Проводятся все возможные склеивания между этими ЭК. Полученные новые ЭК сохраняются вместе со старыми.

3. Между ними снова проводим все возможные склеивания до тех пор, пока это возможно. В результате среди ЭК появятся все простые импликанты функции.

4. Проводим поглощение между всеми получившимися ЭК, то есть оставляем только те ЭК, которые не покрываются никакими другими.

5. В результате получаются только простые импликанты. Их дизъюнкция является сокращенной ДНФ. Дальше все идет в соответствии с тривиальным алгоритмом минимизации.

Формализация Мак-Клоски.

Каждой ЭК ставим в соответствие булев вектор. (x с отрицанием – 0, без отрицания – 1).

1. Выписываем все ЭК из СДНФ функции в формализованном виде в столбец, располагая их в порядке возрастания числа единиц в векторах и разбивая на классы по числу единиц.

2. Между ЭК проводим все возможные склеивания. Результат записываем в новый столбец справа, а ЭК, участвовавшие в склеивании, помечаем звездочкой. Склеивать можно только ЭК из соседних классов.

3. Для полученного столбца еще раз применяем шаг 2.

4. Все ЭК, которые остались непомеченными звездочкой, являются простыми импликантами.

5. Строим таблицу Квайна по следующему правилу:

А) Каждой строке ставим в соответствие простую импликанту П_i.

Б) Каждому столбцу – ЭК из СДНФ K_j.

1. Если П_i.покрывает K_j , то в соответствующей клетке ставим знак +.

2. Ищем ядровые импликанты (столбец, содержащий только 1 знак +). Та строка и есть ядровая (строка, в какой этот крестик содержится).

3. Строим сокращенную таблицу (Вычеркиваем ядровые строки, а затем – столбцы, где есть вычеркнутые крестики).

4. Ядро дополняем до тупиковой ДНФ (Ищем минимальную комбинацию строк так, чтобы в каждый столбец входил хотя бы один крестик). Дизъюнкция этих строк даст тупиковые ДНФ.

5. Среди всех тупиковых ДНФ выбираем минимальную.

Лекция 7

Функционально полные системы функций

Определение. Система функций {f₁…f_n} называется полной, если любую булеву функцию можно представить в виде суперпозиции функций из этой системы (т.е. можно представить формулой, куда входят только функции из этой системы).

F_

{V, &, NOT или отрицание – –}

Теорема 1.

Если система полна, и любая ее функция представима в виде суперпозиции функций из системы то и система также полна.

Доказательство

_{ф₁…ф_k}

_iЕ_условие.

fF = F₂ – ч.т.д.

Мы заменили все функции суперпозицией из 



Теорема 2.

Если система функций полна, то будет полной и система, состоящая из двойственных функций.

Доказательство следует из принципа двойственности.

Основные типы функционально полных систем.

{&, V, NOT}

{&, NOT}

____

_ _

X V Y = (XY)

{/} – полна.

___

X/Y = (XY)

X/X = NOT(XX) = NOT(X)

 = {}

Система Жегалкина {+,&,1}.

NOT (X) = x+1

X V Y = xy+x+y

Многочлены Жегалкина.

Одночленом будем называть любое выражение вида

А * X₁X₂X₃…X_n

A = {0 или 1} x₁x₃ – одночлен.

Многочленом Жегалкина называется сумма по модулю 2 различных одночленов.

А1X1+А2X2+А3X3+A4X1X2 + A5X1X3+A6X2X3+A7X1X2X3 – общий вид многочлена Жегалкина для трех переменных. Чтобы выписать общий вид многочлена Жегалкина для нужного числа переменных нужно перебрать все возможные конъюнкции переменных и сложить их по модулю 2 друг с другом, а также с переменными, входящими в функцию. Перед каждой конъюнкцией нужно расставить буквенные коэффициенты.

Теорема

Любая булева функция, тождественно не равная нулю, представима и притом единственным образом в виде многочлена Жегалкина.

Доказательство на лекции 8.

Поиск многочлена Жегалкина (МЖ) для любой выбранной булевой функции производится методом неопределенных коэффициентов. Для этого нужно выписать общий вид МЖ для нужного числа переменных, затем, подставив искомые значения переменных в МЖ, приравнять его к функции на нужном векторе. Таким образом получается система уравнений с неизвестными числами А. Решив ее, мы получим искомый МЖ.

Лекция 8

Продолжение темы «Многочлены Жегалкина»

Теорема.

Любая булева функция представима в виде многочлена Жегалкина (МЖ).

Доказательство

1. Существование

F = ДНФ = F{&,V, NOT}

X V Y = XY+X+Y

NOT(X) = X+1

Из этого следует, что функция представима в виде МЖ.

1. Единственность

Сосчитаем МЖ

ЭК без отрицания 2ⁿ – 1 + 1

Всего разных многочленов Жегалкина 2^N – 1, где N = 2ⁿ

Это число совпадает с числом разных булевых функций, отличных от нуля.

Отсюда следует, что любой булевой функции соответствует единственный многочлен Жегалкина. Теорема доказана полностью.

Классы функций. Замкнутые и незамкнутые классы. Получение констант и элементарных булевых функций из заданной системы функций

Определение. Функция называется линейной, если ее многочлен Жегалкина не содержит ни одной конъюнкции переменных.

Замкнутые классы функций.

Определение.

Пусть дан класс функций B (т.е. конечное или бесконечное множество функций),объединенных по общему признаку. Замыканием этого класса (обозначение – [B]) будем называть множество всех суперпозиций функций из класса B.