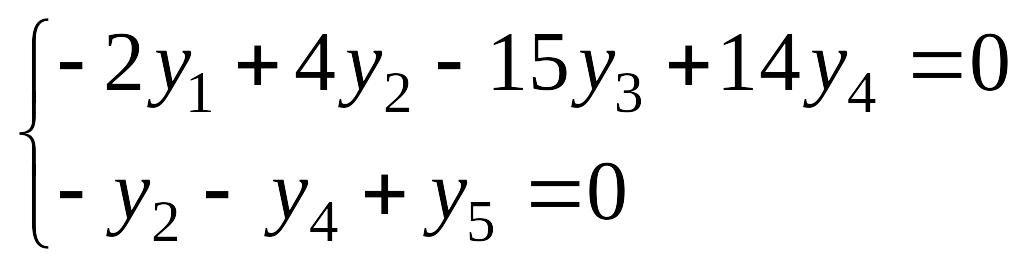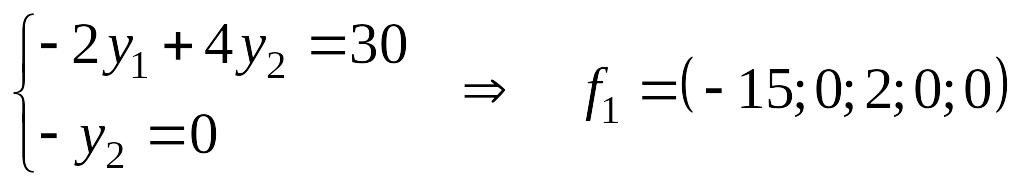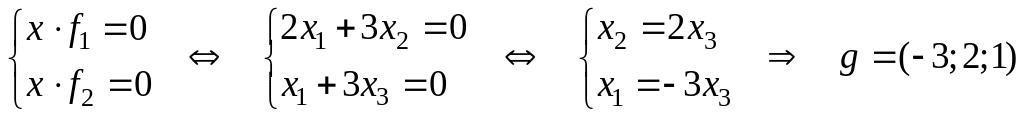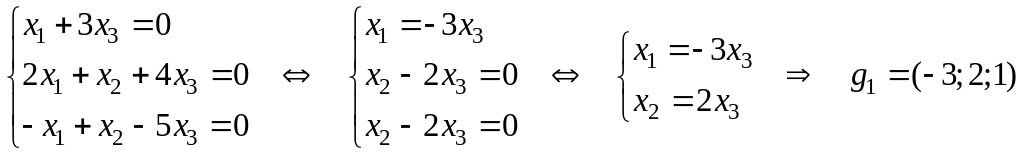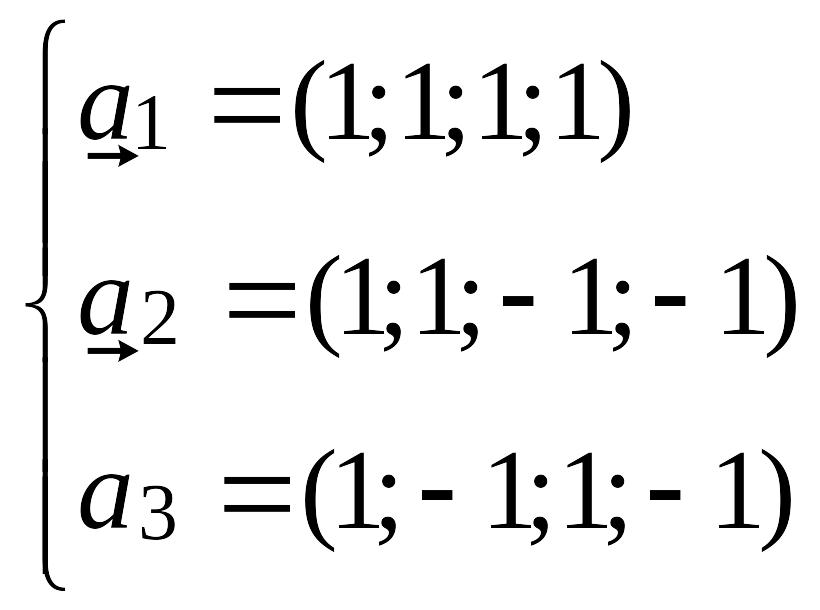Как найти ядро линейного оператора онлайн

Решение.

Множество  всех векторов  называется образом оператора A.

То есть  в том и только том случае, когда найдется вектор  $xin R^3$ такой, что $y=Ax$ или, в координатной записи,

Найдем ядро оператора.

Определение. Ядром (или нуль-пространством) линейного оператора  называется множество всех элементов из V , которые отображаются линейным оператором A в нулевой вектор. Ядро оператора A обозначается ker A. 

 В соответствии с определением ядра

 

Итак, ядром оператора A является точка  

Найдем собственные вектора заданного линейного оператора.

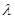
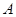
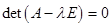
Число  есть собственное число оператора  в том и только том случае, когда . Запишем характеристическое уравнение:

Решая его, имеем 

 Таким образом, получаем собственные числа оператора:

Для каждого из полученных собственных значений найдем собственные векторы.

Их можно найти их системы .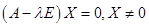

А) 

 

Решим однородную систему уравнений.

 

Матрица коэффициентов  имеет ранг 1. Выберем в качестве базисного минора  Тогда, полагая , имеем

Таким образом, общее решение системы

.

Из общего решения находим фундаментальную систему решений:

.

С использованием фундаментальной системы решений, общее решение может быть записано в виде .

Б) 

 

Решим однородную систему уравнений.

 

Матрица коэффициентов   имеет ранг 1. Выберем в качестве базисного минора  Тогда, полагая  имеем 

Таким образом, общее решение системы .

Из общего решения находим фундаментальную систему решений: .

С использованием фундаментальной системы решений, общее решение может быть записано в виде .

Ответ:

 

Собственные числа оператора:  

Собственные векторы: ;  .

Задача №1. В арифметическом пространстве [math]mathbb{R}^4[/math] линейный оператор [math]displaystyle varphi[/math] задан матрицей

[math]A= left(!!begin{array}{rrrr} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{array}!!right)[/math]

Найти базисы ядра и образа, ранг и дефект линейного оператора. Найти операторы, индуцированныe в ядре и образе.

Решение.
1) По определению ядро линейного оператора [math]displaystyle varphi[/math] ([math]displaystyle ker varphi[/math]) есть множество всех векторов [math]displaystyle x[/math], которые [math]displaystyle varphi[/math] переводит в нулевой вектор. Это означает, что [math]displaystyle ker varphi[/math] состоит из векторов, координаты которыx [math]displaystyle x_1, x_2, x_3, x_4[/math] (в некотором базисе [math]displaystyle { e_1, e_2, e_3, e_4 }[/math]) удовлетворяет условию:

[math]begin{pmatrix} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{pmatrix}!!! begin{pmatrix} x_1\ x_2 \ x_3 \ x_4 end{pmatrix}!=! begin{pmatrix} 0\ 0 \ 0 \ 0 end{pmatrix}[/math]. То есть, [math]kervarphi[/math] cooтветствует пространству [math]L[/math] решений системы [math]begin{cases}x_1-2x_2+x_3+3x_4=0,\ -2x_1+5x_2+6x_3-12x_4=0,\ 5x_1+9x_2+13x_3+9x_4=0,\ -x_1+3x_2+7x_3-9x_4=0.end{cases}[/math]

Общим решением системы является семейство векторов [math]left(-frac{15}{4}C , 0, frac{3}{4}C, C right)[/math]. Полагая [math]C=4[/math], находим базис [math]ker varphi[/math]: [math](-15,,0,,3,,4)[/math].

2) Дефектом линейного оператора называется размерность его ядра ([math]dim ker varphi[/math]). Здесь [math]dim ker varphi=1[/math], т.к. в ядре существует лишь один линейно независимый вектор.

Верны ли мои рассуждения?

3) Не знаю, как найти образ линейного отображения [math]varphi[/math] ([math]im varphi[/math]). Подскажите идею.

4) Рангом линейного отображения [math]varphi[/math] называется размерность его образа ([math]dim im varphi[/math]). Здесь всё ясно.

5) Что такое операторы, индуцированные в ядре и образе?

Задача №2. Найти матрицу, область значений и ядро оператора [math]A[/math] проектирования на плоскость [math]x-z=0[/math]. Если [math]x={x_1, x_2, x_3 }[/math], то [math]Ax={x_1-x_2-x_3, -2x_1+3x_2, x_2- x_3 }[/math].

1) Cовершенно не знаю, как найти матрицу. И что означает проектирование на плоскость?

2) Если найду матрицу, то можно найти ядро.

3) Область значений – это синоним образа или что-то другое?

И ещё один вопрос общего характера. Существует ли какое-то обозначение для базиса линейного пространства (как, например, для ядра или размерности)?

Решение. Очевидно,
что данное линейное преобразование
действует

,
т.к. умножение матриц

определено, когда количество столбцов
1-й матрицы равно количеству строк
второго вектора (в нашем случае 4), а
полученная матрица имеет размерность

(т.к. в матрице A
5 строк).

Совокупность N
векторов x
таких, что Ax=0,
называется ядром
преобразования A.

Совокупность M
векторов вида Ax,
когда x
пробегает все R
(в нашем случае

)
называется образом
пространства
R
при преобразовании A
(другими
словами образ – множество векторов y,
для которых уравнение Ax=y
имеет хотя бы одно решение).

1) Находим ядро.
Пусть

– вектор столбец. Решаем систему уравнений

.

Решаем систему
методом Гаусса

.

Переменные

– базисные, а

– небазисная.

Находим все
фундаментальные решения. В нашем случае
оно одно: положив

,
получаем

– который и будет образовывать базис
ядра (т.к. все вектора вида

отображаются в 0). Размерность базиса
равна 1.

2) Находим образ.
Пусть

– вектор столбец. Решаем систему уравнений
Ax=y.

Для того, чтобы
вектор

принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.

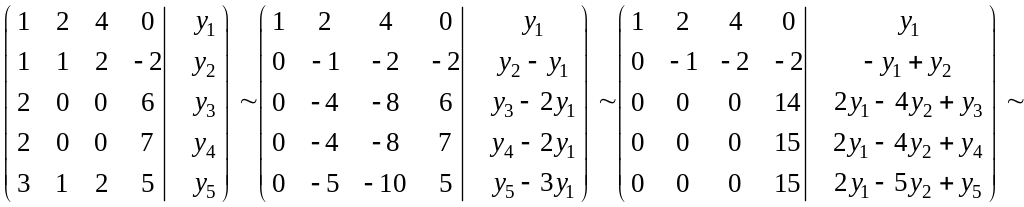
Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

.

Находим фундаментальные
решения (базис образа). Т.к. определитель
из коэффициентов при

:

,
то

– базисные, а

– небазисные.

1-е фундаментальное
решение. Положим

,
находим решение системы

– первое базисное
решение.

2-е фундаментальное
решение. Положим

,
находим решение системы

– второе базисное
решение.

3-е фундаментальное
решение. Положим

,
находим решение системы

– второе базисное
решение.

Итак, размерность
образа равна 3, базис – вектора

.

(Видно, что
размерность образа + размерность ядра
= размерности пространства R⁴).

7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .

Решение.

– ядро,

– образ. Преобразование

.

1) Находим ядро.
Решаем систему уравнений

Следовательно,
одно базисное решение

– базис ядра. Размерность

.

2) Находим образ.

Пусть

– вектор столбец. Решаем систему уравнений
Ax=y.

Для того, чтобы
вектор

принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

Отсюда,

–
базисная, а

не базисные переменные.

1-е фундаментальное
решение:

.

2-е фундаментальное
решение:

.

Следовательно,

– базис образа. Размерность

.

3) Находим
ортогональное дополнение

.
Т.к. любой вектор

,
перпендикулярен любому вектору из

,
то заключаем, что скалярное произведение

– фундаментальное
решение системы или базис

.

4) Найдем базис
линейной оболочки векторов

,

.
Т.к.

,
то заключаем, что

,

– базис в

,
и следовательно, размерность

.

5) Находим пространство
решений системы уравнений

.

– фундаментальное
решение системы или базис M.

6) Находим
ортогональное дополнение

.
Т.к. любой вектор

,
перпендикулярен любому вектору из

,
то заключаем, что скалярное произведение

.

Отсюда,

–
базисная, а

не базисные переменные.

1-е фундаментальное
решение:

.

2-е фундаментальное
решение:

.

Следовательно,

– базис

.
Размерность

.

7) Найдем базис
линейной оболочки векторов

,

,

,

.

Очевидно, что

,
а

,

– базис в

,
и следовательно, размерность

.

8. Пусть U
– подпространство
линейного пространства R⁴,
являющееся линейной оболочкой. векторов

,
V
– подпространство
линейного пространства R⁴
являющееся
линейной оболочкой векторов

.
Найдите: базис U
+ V
и
базис

.

Решение.

1) Находим базис в
U.

rang=3
, сл-но,

– базис U.

1) Находим базис в
V.

rang=3
, сл-но,

– базис V.

3) Находим базис в
U
+ V.

Находим линейно
независимые вектора в объединении

.

,
а вектора

– базис U
+ V
, а размерность
dim(U
+ V)=4.

4) Найдем общие
вектора в U
и
V
.

Нам известно, что
в конечномерном пространстве
подпространства могут быть заданы
системами линейных уравнений. Тогда их
пересечение задаётся системой уравнений,
полученной объединением систем, задающих
подпространства.

Система уравнений
задающая U:

Для того, чтобы
вектор

принадлежал линейной оболочке U,
необходимо и достаточно, чтобы ранг
матрицы А и ранг расширенной матрицы
(A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к. rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы

– искомая система
линейных уравнений.

Система уравнений
задающая V:

Для того, чтобы
вектор

принадлежал линейной оболочке U,
необходимо и достаточно, чтобы ранг
матрицы А и ранг расширенной матрицы
(A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

Т.к.
rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы

– искомая система
линейных уравнений.

Решаем общую
систему:

.

Отсюда фундаментальные
решения (которые получаются при

и при

),
а следовательно базис

есть:

.

9. Подпространство
L₁
в R⁴
порождено векторами (1;-4;6;7) и (0;1;-3;1), а
подпространство L₂
– векторами
(0;1;-4;5) и (1;-4;7;-11). Постройте базисы следующих
подпространств: пересечения

и ортогонального дополнения к сумме

.

Решение.

1) Находим базис в
L₁.
Т.к. матрица, составленная из координат
векторов

,
имеет ранг=2 (т.к. в ней есть определитель
второго порядка

),
то заключаем, что вектора

=(1;-4;6;7)
и

=(0;1;-3;1)
линейно независимые и образуют базис
в L₁.

2) Аналогично,
заключаем, что вектора

=(0;1;-4;5)
и

=(1;-4;7;-11)
линейно независимые и образуют базис
в L₂.

3) Находим базис
L₁+
L₂.

Рассматриваем
объединенную систему векторов

=(1;-4;6;7),

=(0;1;-3;1),

=(0;1;-4;5),

=(1;-4;7;-11)

и находим среди
них линейно независимые. Находим ранг
матрицы, столбцами которой являются
координаты

:

.

Ранг = 4, следовательно,
все вектора

– линейно независимые и образуют базис
в L₁+
L₂.

4)
Находим базис ортогонального дополнения

.

Каждый вектор из

ортогонален любому вектору из L₁+
L₂.
Следовательно, скалярные произведения

на вектора базиса из L₁+
L₂
равны 0. Получаем однородную систему

.

Т.к. определитель
системы не равен 0 (показано выше, что
ранг=4), то система имеет единственное
тривиальное решение

.

Следовательно,

состоит
только из одного вектора

.

(Это и так было
видно, т.к. линейная оболочка

,
ибо 4 линейно независимых вектора

образуют базис в

,
а

).

5) Находим систему
уравнений описывающую L₁.

Для того, чтобы
вектор

принадлежал линейной оболочке

,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов

,
и ранг расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

– искомая система
линейных уравнений.

Находим систему
уравнений описывающую L₂.

Для того, чтобы
вектор

принадлежал линейной оболочке

,
необходимо и достаточно, чтобы ранг
матрицы А – составленной из координат
векторов

,
и ранг расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:

.

Т.к. rang(A)
= 2, то для того чтобы rang(A|y)
=2, необходимо и достаточно, чтобы

– искомая система
линейных уравнений.

Решаем общую
систему:

Т.к. определитель
матрицы коэффициентов

,
то система имеет единственное решение

.
Следовательно,

состоит из
одного вектора (0;0;0;0).

(Это и так было
видно, т.к. вектора

– линейно независимые,
линейные оболочки

и

не имеют общих (кроме нулевого) векторов,
т.к. линейная комбинация векторов

не может дать вектора

,
а следовательно и их линейные комбинации).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #