Как найти ядро оператора на плоскости - Сайт, где вы сможете решить свои вопросы

Задача №1. В арифметическом пространстве [math]mathbb{R}^4[/math] линейный оператор [math]displaystyle varphi[/math] задан матрицей

[math]A= left(!!begin{array}{rrrr} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{array}!!right)[/math]

Найти базисы ядра и образа, ранг и дефект линейного оператора. Найти операторы, индуцированныe в ядре и образе.

Решение.
1) По определению ядро линейного оператора [math]displaystyle varphi[/math] ([math]displaystyle ker varphi[/math]) есть множество всех векторов [math]displaystyle x[/math], которые [math]displaystyle varphi[/math] переводит в нулевой вектор. Это означает, что [math]displaystyle ker varphi[/math] состоит из векторов, координаты которыx [math]displaystyle x_1, x_2, x_3, x_4[/math] (в некотором базисе [math]displaystyle { e_1, e_2, e_3, e_4 }[/math]) удовлетворяет условию:

[math]begin{pmatrix} 1 & -2 & 1 & 3\ -2 & 5 & 6 & -12 \ 5 & 9 & 13 & 9 \ -1 & 3 & 7 & -9 end{pmatrix}!!! begin{pmatrix} x_1\ x_2 \ x_3 \ x_4 end{pmatrix}!=! begin{pmatrix} 0\ 0 \ 0 \ 0 end{pmatrix}[/math]. То есть, [math]kervarphi[/math] cooтветствует пространству [math]L[/math] решений системы [math]begin{cases}x_1-2x_2+x_3+3x_4=0,\ -2x_1+5x_2+6x_3-12x_4=0,\ 5x_1+9x_2+13x_3+9x_4=0,\ -x_1+3x_2+7x_3-9x_4=0.end{cases}[/math]

Общим решением системы является семейство векторов [math]left(-frac{15}{4}C , 0, frac{3}{4}C, C right)[/math]. Полагая [math]C=4[/math], находим базис [math]ker varphi[/math]: [math](-15,,0,,3,,4)[/math].

2) Дефектом линейного оператора называется размерность его ядра ([math]dim ker varphi[/math]). Здесь [math]dim ker varphi=1[/math], т.к. в ядре существует лишь один линейно независимый вектор.

Верны ли мои рассуждения?

3) Не знаю, как найти образ линейного отображения [math]varphi[/math] ([math]im varphi[/math]). Подскажите идею.

4) Рангом линейного отображения [math]varphi[/math] называется размерность его образа ([math]dim im varphi[/math]). Здесь всё ясно.

5) Что такое операторы, индуцированные в ядре и образе?

Задача №2. Найти матрицу, область значений и ядро оператора [math]A[/math] проектирования на плоскость [math]x-z=0[/math]. Если [math]x={x_1, x_2, x_3 }[/math], то [math]Ax={x_1-x_2-x_3, -2x_1+3x_2, x_2- x_3 }[/math].

1) Cовершенно не знаю, как найти матрицу. И что означает проектирование на плоскость?

2) Если найду матрицу, то можно найти ядро.

3) Область значений – это синоним образа или что-то другое?

И ещё один вопрос общего характера. Существует ли какое-то обозначение для базиса линейного пространства (как, например, для ядра или размерности)?

Источник

Рассмотрим
сначала
случай линейного оператора

,
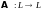
действующего из пространства

в себя.
Итак,
пусть в линейном пространстве

заданы два базиса:

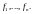
Разложим “новые” базисные вектора в
линейные комбинации “старых” базисных
векторов:

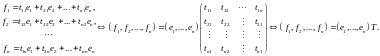
Стоящая
здесь матрица

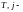
м
столбцом которой является координатный
столбец

го
базисного вектора

в “старом” базисе

называется матрицей перехода от
“старого”базиса к “новому“.
Если теперь

координаты вектора

в “старом” базисе

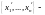
координаты того же вектора

в “новом” базисе

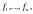
то имеет место равенство

Так
как разложение по базису

единственно, то отсюда следует, что

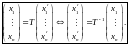
Получен
следующий результат.

Теорема
1. Координаты

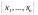
вектора

в базисе

и координаты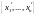

того же вектора в базисе

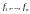
связаны соотношениями (2), где

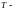
матрица перехода от “старого”базиса

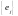
к “новому“

.

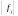
Посмотрим
теперь, как связаны между собой матрицы

одного и того же оператора

в различных базисах

пространства

Матрицы

определяются равенствами

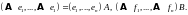
Пусть

Это равенство в базисе

равносильно
матричному равенству

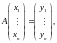
а
в базисе

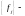
матричному равенству

(
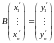
здесь приняты те же обозначения, что и
в (1)). Используя теорему (1), будем иметь

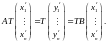
так
как столбец

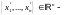
произвольный,
то отсюда получаем равенство

Доказан
следующий результат.

Теорема
2. Если

матрица оператора

в базисе

матрица того же оператора в базисе

то

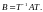
Замечание
1. Две
произвольные матрицы

связанные соотношением

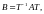
где

некоторая невырожденная матрица

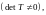
называются
подобными матрицами. Таким
образом, две матрицы одного и того же
оператора в различных базисах подобны.

Пример
1. Матрица

оператора

в базисе

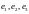
имеет
вид

Найти
матрицу

этого оператора в базисе

Вычислить
координаты вектора

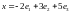
в базисе

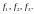
Решение.
Матрица

перехода от старого базиса к новому и
обратная к ней матрица имеют вид

поэтому
по теореме 2 матрица

оператора

и новом базисе будет такой:

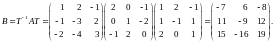
Далее,
вектор

имеет следующий координатный столбец
в базисе

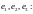
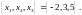
По теореме 1 координатный столбец этого
вектора в базисе

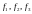
будет иметь вид

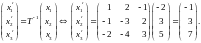
_{Пусть

теперь оператор}

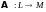
действует из линейного пространства

в другое линейное пространство

и пусть в пространстве

выбраны два базиса:

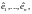
а в пространстве

– базисы

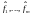
. Тогда можно составить две матрицы

линейного оператора

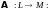
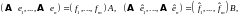
и
две матрицы

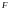
перехода от “старых” базисов к “новым”:

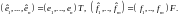
Нетрудно
показать, что в этом случае имеет место
равенство

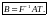
2. Ядро и образ линейного оператора

Пусть
дан линейный оператор

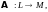
действующий
из линейного пространства

в
линейное пространство

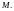
Следующие
понятия бывают полезными при решении
линейных уравнений.

Определение
1.
Ядром
оператора

называется множество

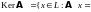
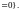
Образом
оператора

называется множество

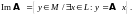
Нетрудно
доказать следующее утверждение.

Теорема
3. Ядро
и образ линейного оператора являются
линейными подпространствами пространств

соответственно, причем имеет место
равенство

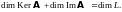
Для
вычисления ядра оператора

надо записать уравнение

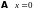
в матричной форме (выбрав базисы в
пространствах

)
и решить соответствующую алгебраическую
систему уравнений. Поясним теперь, как
можно вычислить образ оператора

Пусть

матрица оператора

в каком-нибудь базисе

.
Обозначим через

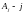
-й
столбец матрицы

Принадлежность вектора

образу

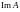
означает, что существуют числа

такие, что вектор столбец

представляется в виде

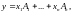
т.е.

является элементом пространства линейных
комбинаций столбцов

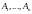
матрицы

Выбрав в этом пространстве базис

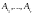
(например,
максимальную совокупность линейно
независимых столбцов матрицы

),
вычислим сначала образ оператора-матрицы

а затем построим образ оператора

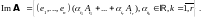
Пример
2. Найти
матрицу, ядро и образ оператора
проектирования

на плоскость

(
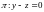
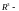
трехмерное
пространство геометрических векторов).

Решение.
Выберем
в пространстве

какой-нибудь базис (например, стандартный
базис

).
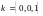
В этом базисе матрица

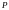
оператора проектирования

находится из равенства

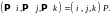
Найдем образы базисных векторов. Так
как плоскость

проходит через ось

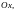
то

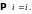
Д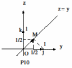
алее
(см. Р10)

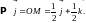
И аналогично

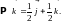
Таким
образом,

Значит,
матрица

оператора

имеет вид

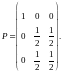
Ядро
оператора-матрицы

вычисляем из уравнения

Таким образом,

(
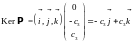
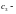
произвольная
постоянная).

Образ
оператора-матрицы

натянут на все линейно независимые
столбцы матрицы

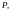
т.е.

поэтому

(
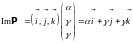
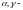
произвольные
постоянные).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Оператор Проектирования. Пусть требуется найти матрицу линейного оператора, осуществляющего проектирование трехмерного пространства на координатную ось Е1 в базисе Е1, Е2, Е3. Матрица линейного оператора – это матрица, в столбцах которой должны стоять образы базисных векторов Е1 = (1,0,0), Е2 = (0,1,0), Е3 = (0,0,1). Эти образы, очевидно, есть: Ае1 = (1,0,0)

Ае2 = (0,0,0)

Ае3 = (0,0,0)

Следовательно, в базисе Е1, Е2, Е3 матрица искомого линейного оператора будет иметь вид:

Найдем ядро этого оператора. Согласно определению ядро – это множество векторов Х, для которых АХ = 0. Или

Т. е. ядро оператора составляет множество векторов, лежащих в плоскости Е1, Е2. Размерность ядра равна n – rangA = 2.

Множество образов этого оператора – это, очевидно, множество векторов, коллинеарных Е1. Размерность пространства образов равна рангу линейного оператора и равна 1, что меньше размерности пространства прообразов. Т. е. оператор А – вырожденный. Матрица А тоже вырождена.

Еще пример: найти матрицу линейного оператора, осуществляющего в пространстве V3 (базис I, J, K) линейное преобразование – симметрию относительно начала координат.

Имеем: Ai = – i

Aj = – j

Ak = – k

Т. е. искомая матрица

Рассмотрим линейное преобразование – Симметрию относительно плоскости Y = X.

Ai = j (0,1,0)

Aj = I (1,0,0)

Ak = K (0,0,1)

Матрица оператора будет:

Ai Aj Ak

Еще пример – уже знакомая матрица, связывающая координаты вектора при повороте осей координат. Назовем оператор, осуществляющий поворот осей координат, – оператор поворота. Допустим, осуществляется поворот на угол j:

Ai ’ = cosjI + sinjJ

Aj ’ = – sinjI + cosjJ

Матрица оператора поворота:

Ai ‘ Aj ‘

Вспомним формулы преобразования координат точки при смене базиса – замена координат на плоскости при смене базиса:

Эти формулы можно рассматривать двояко. Ранее мы рассматривали эти формулы так, что точка стоит на месте, поворачивается координатная система. Но можно рассматривать и так, что координатная система остается прежней, а перемещается точка из положения М* в положение М. Координаты точки М и М* определены в той же координатной системе.

Все сказанное позволяет подойти к следующей задаче, которую приходится решать программистам, занимающимся графикой на ЭВМ. Пусть необходимо на экране ЭВМ осуществить поворот некоторой плоской фигуры (например треугольника) относительно точки О’ с координатами (a, b) на некоторый угол j. Поворот координат описывается формулами:

Параллельный перенос обеспечивает соотношения:

Для того, чтобы решить такую задачу, обычно применяют искусственный прием: вводят так зазываемые “однородные” координаты точки на плоскости XOY: (x, y, 1). Тогда матрица, осуществляющая параллельный перенос, может быть записана:

Действительно:

А матрица поворота:

Рассматриваемая задача может быть решена в три шага:

1й шаг: параллельный перенос на вектор А(-а, – b) для совмещения центра поворота с началом координат:

2й шаг: поворот на угол j:

3й шаг: параллельный перенос на вектор А(а, b) для возвращения центра поворота в прежнее положение:

Искомое линейное преобразование в матричном виде будет выглядеть:

(**)

Где

По формуле (**) можно пересчитать координаты любой точки плоской фигуры, а затем построить ее на экране, осуществив тем самым ее поворот.

< Предыдущая		Следующая >

Источник

Ядро и образ линейного оператора

Пусть линейный оператор , действует из пространства в себя и пусть в линейном пространстве выбраны два базиса: и Разложим “новые” базисные вектора в линейные комбинации “старых” базисных векторов :

Стоящая здесь матрица м столбцом которой является координатный столбец го базисного вектора в “старом” базисе называется матрицей перехода от “старого”базиса к “новому“. Если теперь координаты вектора в “старом” базисе а координаты того же вектора в “новом” базисе то имеет место равенство

Так как разложение по базису единственно, то отсюда следует, что

Получен следующий результат.

Теорема 1.Координаты вектора в базисе и координаты того же вектора в базисе связаны соотношениями (2), где матрица перехода от “старого”базиса к “новому“ .

Посмотрим теперь, как связаны между собой матрицы и одного и того же оператора в различных базисах и пространства Матрицы и определяются равенствами Пусть Это равенство в базисе равносильно матричному равенству

а в базисе матричному равенству ( здесь приняты те же обозначения, что и в (1)). Используя теорему (1), будем иметь

так как столбец произвольный, то отсюда получаем равенство

Доказан следующий результат.

Теорема 2.Если матрица оператора в базисе а матрица того же оператора в базисе то

Замечание 1.Две произвольные матрицы и связанные соотношением где некоторая невырожденная матрица называются подобными матрицами. Таким образом, две матрицы одного и того же оператора в различных базисах подобны.

Пример 1.Матрица оператора в базисе имеет вид

Найти матрицу этого оператора в базисе Вычислить координаты вектора в базисе

Решение. Матрица перехода от старого базиса к новому и обратная к ней матрица имеют вид

поэтому по теореме 2 матрица оператора и новом базисе будет такой:

Далее, вектор имеет следующий координатный столбец в базисе По теореме 1 координатный столбец этого вектора в базисе будет иметь вид

Замечание 2. Можно обобщить этот результат на операторы, действующие из одного линейного пространства в другое. Пусть оператор действует из линейного пространства в другое линейное пространство и пусть в пространстве выбраны два базиса: и а в пространстве – два базиса и Тогда можно составить две матрицы и линейного оператора

и две матрицы и перехода от “старых” базисов к “новым”:

Нетрудно показать, что в этом случае имеет место равенство

Пусть дан линейный оператор действующий из линейного пространства в линейное пространство Следующие понятия бывают полезными при решении линейных уравнений.

Определение 1. Ядром оператора называется множество

Образом оператора называется множество

Нетрудно доказать следующее утверждение.

Теорема 3.Ядро и образ линейного оператора являются линейными подпространствами пространств и соответственно, причем имеет место равенство

Для вычисления ядра оператора надо записать уравнение в матричной форме (выбрав базисы в пространствах и соответственно) и решить соответствующую алгебраическую систему уравнений. Поясним теперь, как можно вычислить образ оператора .

Пусть матрица оператора в в базисах и Обозначим через -й столбец матрицы Принадлежность вектора образу означает, что существуют числа такие, что вектор столбец представляется в виде т.е. является элементом пространства линейных комбинаций столбцов матрицы Выбрав в этом пространстве базис (например, максимальную совокупность линейно независимых столбцов матрицы ), вычислим сначала образ оператора-матрицы : а затем построим образ оператора :

Приведем пример вычисления ядра и образа оператора, действующего из пространства в себя. В этом случае базисы и совпадают.

Пример 2.Найти матрицу, ядро и образ оператора проектирования на плоскость ( трехмерное пространство геометрических векторов).

Решение.Выберем в пространстве какой-нибудь базис (например, стандартный базис ). В этом базисе матрица оператора проектирования находится из равенства Найдем образы базисных векторов. Так как плоскость проходит через ось то

Далее (см. Р10) И аналогично

Значит, матрица оператора имеет вид

Ядро оператора-матрицы вычисляем из уравнения

Образ оператора-матрицы натянут на все линейно независимые столбцы матрицы т.е.

Ядро оператора

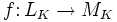
удовлетворяющее условию линейности

f(αx + βy) = αf(x) + βf(y) .

для всех 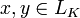и .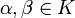

Содержание

Важные частные случаи

Связанные понятия

Примеры

Примеры линейных однородных операторов:

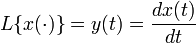оператор дифференцирования: $L<x(cdot)>=y(t)=frac<dx(t)> <dt>» width=»» height=»» />;</li> <li>оператор интегрирования: <img decoding=$ ;
оператор умножения на определённую функцию ;
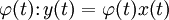оператор интегрирования с заданным «весом» ;
;

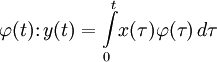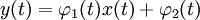где 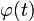, , 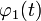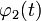— вполне определённые функции, а x(t) — преобразуемая оператором функция.

См. также

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Ядро оператора» в других словарях:

Ядро (значения) — Ядро нечто центральное и самое важное, часто круглое. Это слово имеет различные значения в разных областях: Содержание 1 Ядерная физика 2 Биология 3 Науки о Земле 4 Спорт … Википедия

Ядро — Содержание 1 Ядерная физика 2 Биология 3 Науки о Земле … Википедия

ЯДРО — линейного оператора линейное подпространство области определения линейного оператора, состоящее из всех векторов, к рые отображаются этим оператором в нуль. Я. линейного непрерывного оператора, определенного на нек ром топологическом векторном… … Математическая энциклопедия

Ядро интегрального уравнения — Ядром интегрального оператора называется функция двух аргументов , определяющая некий интегральный оператор равенством где пространство с мерой , а принадлежит некоторому … Википедия

Ядро (матем.) — Интегральное уравнение функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро дифференциальном уравнении.… … Википедия

ЯДРО — интегрального оператора функция двух аргументов К( х, у), определяющая интегральный оператор . равенством где хпробегает пространство . с мерой а принадлежит нек рому пространству функций, определенных на X. Г. Л. Литвинов … Математическая энциклопедия

ВЫРОЖДЕННОЕ ЯДРО — ядро линейного интегрального Фредгольма оператора, имеющее вид где Ри Q точки евклидовых пространств. А. Б. Бакушинский … Математическая энциклопедия

ИТЕРИРОВАННОЕ ЯДРО — функция ( х, s) К п( х, s), к рая образуется из данного ядра Кинтегрального оператора по рекуррентным соотношениям: К п наз. n й итерацией, или n м итерированным ядром, ядра K. И. я. иногда наз. повторным ядром. Если ядро Кнепрерывно или… … Математическая энциклопедия

ДЕФИНИТНОЕ ЯДРО — определенное ядро, ядро К( Р, Q )линейного интегрального Фредголъма оператора, удовлетворяющее соотношению где Р, Q точки евклидова пространства, j произвольная суммируемая с квадратом функция, j комплексно сопряженная функция. В зависимости от… … Математическая энциклопедия

ВОЛЬТЕРРА ЯДРО — функция (матрица функция) К(s, t).двух действительных переменных s, t такая, что или при или при Если такая функция является ядром линейного интегрального оператора, действующего в пространстве и сама квадратично суммируема в треугольнике, в к… … Математическая энциклопедия

Как найти базис ядра

Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!

Дано четырехмерное пространство (как я понимаю, в нём находится базис, состоящий из четырех векторов). Нужно найти матрицу оператора в четырехмерном пространстве (получается, самим придумать и составить; как я понимаю, она будет состоять из 4 строк и 4 столбцов?), причём размерность ядра Ker равно размерности образа Im и равно 2. Далее необходимо найти исходя из составленной матрицы базис ядра и образа.

Прошу помочь разобраться в этом задании. С этими линейными операторами, ядрами, образами прям совсем туго((

задан 10 Янв 20:35

Достаточно взять любую матрицу 4×4 ранга 2. Для этого пишем первые две строки наугад, чтобы они не были пропорциональными. Скажем, 1 0 -2 3 и 0 1 4 -1. В качестве третьей строки берём любые, которые выражаются через первые две. Можно брать значения a+b, 2a-b, 3a+2b и т.п.

Базис ядра — это базис в пространстве решений однородной системы. Решаем её методом Гаусса, находя два базисных вектора. В качестве базиса образа можно взять любые два столбца, которые не пропорциональны.

Все эти абстрактные понятия на самом деле легко освоить на конкретных примерах.

@falcao вы сделали вывод о том, что ранг матрицы будет равен 2 исходя из размерности образа? Всегда такое правило действует?

@Yu_Ko: здесь оба числа равны 2, поэтому разницы нет. А общее правило такое: если матрица имеет размер nxn и ранг r, то образ имеет размерность r, а размерность ядра равна n-r. Это более или менее очевидно — особенно для образа. Ведь он состоит из столбцов матрицы и всех их линейных комбинаций. А линейно независимых столбцов, дающих базис образа, будет в точности r. Сумма же размерностей образа и ядра равна размерности всего пространства, то есть n.

@falcao как же вы выручаете! Спасибо огромное! Благодаря вам всё прояснилось, чего не добьёшься от нынешних преподавателей в вузе(

@Yu_Ko: форму для того и существует, чтобы смысл разных понятий прояснять. Преподаватели так поступают не от хорошей жизни. Дело в том, что когда в короткий по времени курс надо уложить много разных методов решения задач (включая дифференциальные уравнения, или ряды Фурье), то там поневоле приходится ограничиваться изложением типовых “рецептов”. Типа, капусты вот столько, а морковки в 3 раза меньше Тут как бы уже не до кулинарных “изысков”

Построение базисов в ядре и образе линейного оператора.

Речь пойдёт о построении базисов в ядре и образе линейного оператора.

Будут рассмотрены два примера: первый пример с пояснениями; вто-

рой как образец оформления. Значок будет указывать на утверждения, требующие доказательств. Рекомендуется рассматривать эти утверждения как хорошие теоретические задачи для самостоятельного решения. Полный список теоретических задач приведён в конце.

Пусть L векторное пространство, A линейный оператор в L. Ядро (=нуль-пространство) линейного оператора полный прооб-

раз множества <0>, т. е. множество всех векторов, которые переводятся линейным оператором в 0:

Образ (=множество значений) линейного оператора множество всех векторов, у которых есть прообразы относительно A:

Ядро и образ линейного оператора являются подпространствами . Например, если L координатная плоскость (двумерное векторное

пространство с базисом e 1 , e 2 ) и оператор A проектирует радиус-векторы на ось абсцисс (=на линейную оболочку вектора e 1 ) параллельно оси ординат (=параллельно линейной оболочке вектора e 2 ), то ker A ось ординат (линейная оболочка вектора e 2 ), im A ось абсцисс (линейная оболочка вектора e 1 ):

ker A = `(e 2 ), im A = `(e 1 ).

Рассмотрим на примере, как находить базисы ядра и образа линейного оператора, заданного матрицей в некотором базисе.

Пример 1. Дана матрица линейного оператора A в базисе e = (e 1 , e 2 , e 3 , e 4 ):

Источник

Ядро линейного отображения — это такое линейное подпространство области определения отображения, каждый элемент которого отображается в нулевой вектор ^[1]^[2]. А именно: если задано линейное отображение между двумя векторными пространствами V и W, то ядро отображения L — это векторное пространство всех элементов пространства V, таких что , где обозначает нулевой вектор из W^[3], или более формально:

{displaystyle ker(L)=left{mathbf {v} in Vmid L(mathbf {v} )=mathbf {0} right}.}

Свойства[править | править код]

Ядро и образ отображения

Ядро отображения L — это линейное подпространство области определения V^[4].
В линейном отображении два элемента V имеют один и тот же образ в W тогда и только тогда, когда их разность лежит в ядре отображения L:

${displaystyle L(mathbf {v} _{1})=L(mathbf {v} _{2})iff L(mathbf {v} _{1}-mathbf {v} _{2})=mathbf {0} .}$

Из этого следует, что образ L изоморфен факторпространству пространства V по ядру:

{displaystyle operatorname {im} (L)cong V/ker(L).}

В случае, когда V конечномерно, из этого следует теорема о ранге и дефекте^[en]:

{displaystyle dim(ker L)+dim(operatorname {im} L)=dim(V),}

где под рангом мы понимаем размерность образа отображения L, а под дефектом — размерность ядра отображения L^[5].

Если V является предгильбертовым пространством, факторпространство можно отождествить с ортогональным дополнением к V пространства . Это является обобщением линейных операторов пространства строк или кообраза матрицы.

Приложение к модулям[править | править код]

Понятие ядра также имеет смысл для гомоморфизмов модулей, которые являются обобщениями векторных пространств, где скаляры — элементы кольца, а не поля. Область определения отображения — это модуль с ядром, образующий подмодуль. Здесь концепции ранга и размерности ядра не обязательны.

В функциональном анализе[править | править код]

Если и являются топологическими векторными пространствами, а конечномерно, то линейный оператор непрерывен тогда и только тогда, когда ядро отображения является замкнутым подпространством пространства .

Представление в виде матричного умножения[править | править код]

Рассмотрим линейное отображение, представленное матрицей размера с коэффициентами из поля (обычно из или ), то есть оперирующие с вектор-столбцами с элементами из поля .
Ядро этого линейного отображения — это множество решений уравнения , где понимается как нулевой вектор. Размерность ядра матрицы называется дефектом матрицы . В виде операций на множествах,

${displaystyle operatorname {N} (A)=operatorname {Null} (A)=operatorname {ker} (A)=left{mathbf {x} in K^{n}|Amathbf {x} =mathbf {0} right}.}$

Матричное уравнение эквивалентно однородной системе линейных уравнений:

${displaystyle Amathbf {x} =mathbf {0} ;;Leftrightarrow ;;left{{begin{alignedat}{7}a_{11}x_{1}&&;+;&&a_{12}x_{2}&&;+;cdots ;+;&&a_{1n}x_{n}&&;=;&&&0\a_{21}x_{1}&&;+;&&a_{22}x_{2}&&;+;cdots ;+;&&a_{2n}x_{n}&&;=;&&&0\vdots ;;;&&&&vdots ;;;&&&&vdots ;;;&&&&&;vdots \a_{m1}x_{1}&&;+;&&a_{m2}x_{2}&&;+;cdots ;+;&&a_{mn}x_{n}&&;=;&&&0{text{.}}\end{alignedat}}right.}$

Тогда ядро матрицы — это то же самое, что и решение набора приведённых выше однородных уравнений.

Свойства подпространства[править | править код]

Ядро матрицы над полем является линейным подпространством K^n . То есть ядро матрицы , множество , имеет следующие три свойства:

всегда содержит нулевой вектор, поскольку .
Если и , то . Это следует из свойства дистрибутивности матричного умножения.
Если , а является скаляром , то , поскольку .

Пространство строк матрицы[править | править код]

Произведение может быть записано в терминах скалярного произведения векторов следующим образом:

${displaystyle Amathbf {x} ={begin{bmatrix}mathbf {a} _{1}cdot mathbf {x} \mathbf {a} _{2}cdot mathbf {x} \vdots \mathbf {a} _{m}cdot mathbf {x} end{bmatrix}}.}$

Здесь ${displaystyle mathbf {a} _{1},dots ,mathbf {a} _{m}}$ означают строки матрицы . Отсюда следует, что принадлежит ядру матрицы тогда и только тогда, когда вектор ортогонален (перпендикулярен) каждой из вектор-строк матрицы (поскольку ортогональность определяется как равенство нулю скалярного произведения).

Пространство строк, или кообраз матрицы , — это линейная оболочка вектор-строк матрицы . По указанным выше причинам ядро матрицы является ортогональным дополнением пространству строк. То есть вектор лежит в ядре матрицы тогда и только тогда, когда он перпендикулярен любому вектору из пространства строк матрицы .

Размерность пространства строк матрицы называется рангом матрицы , а размерность ядра матрицы называется дефектом матрицы . Эти величины связаны теоремой о ранге и дефекте^[en]

{displaystyle operatorname {rank} (A)+operatorname {nullity} (A)=n.}

^[5]

Левое нуль-пространство (коядро)[править | править код]

Левое нуль-пространство или коядро матрицы состоит из всех векторов , таких что ${displaystyle mathbf {x} ^{T}A=mathbf {0} ^{T}}$ , где обозначает транспонирование матрицы. Левое нуль-пространство матрицы — это то же самое, что и ядро матрицы $A^{T}$ . Левое нуль-пространство матрицы является ортогональным дополнением пространству столбцов матрицы и двойственно коядру связанного линейного преобразования. Ядро, пространство строк, пространство столбцов
и левое нуль-пространство матрицы являются четырьмя фундаментальными подпространствами, ассоциированными с матрицей .

Неоднородные системы линейных уравнений[править | править код]

Ядро играет также большую роль при решении неоднородных систем линейных уравнений:

${displaystyle Amathbf {x} =mathbf {b} ;;Leftrightarrow ;;left{{begin{alignedat}{7}a_{11}x_{1}&&;+;&&a_{12}x_{2}&&;+;cdots ;+;&&a_{1n}x_{n}&&;=;&&&b_{1}\a_{21}x_{1}&&;+;&&a_{22}x_{2}&&;+;cdots ;+;&&a_{2n}x_{n}&&;=;&&&b_{2}\vdots ;;;&&&&vdots ;;;&&&&vdots ;;;&&&&&;vdots \a_{m1}x_{1}&&;+;&&a_{m2}x_{2}&&;+;cdots ;+;&&a_{mn}x_{n}&&;=;&&&b_{m}.\end{alignedat}}right.}$

Пусть векторы и являются решениями уравнения выше, тогда

{displaystyle A(mathbf {u} -mathbf {v} )=Amathbf {u} -Amathbf {v} =mathbf {b} -mathbf {b} =mathbf {0} .}

Таким образом, разность любых двух решений системы лежит в ядре матрицы .

Отсюда следует, что любое решение уравнения может быть выражено как сумма фиксированного решения и какого-либо элемента ядра. То есть множеством решений уравнения является

{displaystyle left{mathbf {v} +mathbf {x} mid Amathbf {v} =mathbf {b} land mathbf {x} in operatorname {Null} (A)right}.}

Геометрически это означает, что множество решений уравнения образовано параллельным переносом ядра матрицы на вектор . См. также Альтернатива Фредгольма.

Иллюстрация[править | править код]

Ниже приведена простая иллюстрация вычисления ядра матрицы (см. Вычисление методом Гаусса ниже для метода, более подходящего для более сложных вычислений). Иллюстрация затрагивает также пространства строк и их связь с ядром.

Рассмотрим матрицу

${displaystyle A={begin{bmatrix}2&3&5\-4&2&3end{bmatrix}}.}$

Ядро этой матрицы состоит из всех векторов ${displaystyle (x,y,z)in mathbb {R} ^{3}}$ , для которых

${displaystyle {begin{bmatrix}2&3&5\-4&2&3end{bmatrix}}{begin{bmatrix}x\y\zend{bmatrix}}={begin{bmatrix}0\0end{bmatrix}},}$

что можно выразить в виде однородной системы линейных уравнений относительно , и :

${displaystyle {begin{aligned}2x+3y+5z&=0,\-4x+2y+3z&=0.end{aligned}}}$

Те же самые равенства можно выписать в матричном виде:

${displaystyle left[{begin{array}{ccc|c}2&3&5&0\-4&2&3&0end{array}}right].}$

С помощью метода Гаусса матрица может быть сведена к:

${displaystyle left[{begin{array}{ccc|c}1&0&1/16&0\0&1&13/8&0end{array}}right].}$

Преобразование матрицы в уравнения даёт:

${displaystyle {begin{aligned}x&=-{frac {1}{16}}z\y&=-{frac {13}{8}}z.end{aligned}}}$

Элементы ядра можно выразить в параметрическом виде следующим образом:

${displaystyle {begin{bmatrix}x\y\zend{bmatrix}}=c{begin{bmatrix}-1/16\-13/8\1end{bmatrix}}quad ({text{где}}quad cin mathbb {R} )}$

Поскольку является свободной переменной^[en], пробегающей по всем вещественным числам, это выражение можно эквивалентно переписать в виде:

${displaystyle {begin{bmatrix}x\y\zend{bmatrix}}=c{begin{bmatrix}-1\-26\16end{bmatrix}}.}$

Ядро матрицы — это в точности множество решений этих уравнений (в этом случае прямая через начало координат в $mathbb {R} ^{3}$ ). Здесь вектор (−1,−26,16)^T образует базис ядра матрицы . Дефект матрицы равен 1.

Следующие скалярные произведения равны нулю:

${displaystyle {begin{bmatrix}2&3&5end{bmatrix}}{begin{bmatrix}-1\-26\16end{bmatrix}}=0quad {text{ и }}quad {begin{bmatrix}-4&2&3end{bmatrix}}{begin{bmatrix}-1\-26\16end{bmatrix}}=0mathrm {,} }$

что показывает, что вектора ядра матрицы ортогональны каждой вектор-строке матрицы .

Линейная оболочка этих двух (линейно независимых) вектор-строк — это плоскость, ортогональная вектору ${displaystyle (-1,-26,16)^{T}}$ .

Поскольку ранг матрицы равен 2, размерность ядра матрицы равна 1, а размерность матрицы равна 3, мы имеем иллюстрацию теоремы о ранге и дефекте.

Примеры[править | править код]

${displaystyle L(x_{1},x_{2},x_{3})=(2x_{1}+3x_{2}+5x_{3},;-4x_{1}+2x_{2}+3x_{3})}$

то ядром оператора L является множество решений системы

${displaystyle {begin{alignedat}{7}2x_{1}&;+;&3x_{2}&;+;&5x_{3}&;=;&0\-4x_{1}&;+;&2x_{2}&;+;&3x_{3}&;=;&0end{alignedat}}}$

Тогда ядро of L состоит из всех функций

, для которых

${displaystyle D(f)={frac {df}{dx}}{text{.}}}$

Тогда ядро of D состоит из всех функций в ${displaystyle C^{infty }(mathbb {R} )}$

, производная которых равна нулю, то есть из всех постоянных функций.

${displaystyle s(x_{1},x_{2},x_{3},x_{4},ldots )=(x_{2},x_{3},x_{4},ldots ){text{.}}}$

Тогда ядром оператора s будет одномерное подпространство, состоящее из всех векторов ${displaystyle (x_{1},0,0,dots )}$

Вычисления по методу Гаусса[править | править код]

Базис ядра матрицы можно вычислить с помощью метода Гаусса.

Для этой цели, если дана матрица , мы строим сначала расширенную^[en] по строкам матрицу ${displaystyle left[{begin{array}{c}A\hline Eend{array}}right],}$ , где — это единичная матрица.

Если вычислим ступенчатый по столбцам вид матрицы методом Гаусса (или любым другим подходящим методом), мы получим матрицу ${displaystyle left[{begin{array}{c}B\hline Cend{array}}right].}$ Базис ядра матрицы состоит из ненулевых столбцов матрицы , таких что соответствующие столбцы матрицы a нулевые.

Фактически вычисление может быть остановлено, как только матрица принимает ступенчатый по столбцам вид — остальное вычисление состоит из изменения базиса векторного пространства, образованного столбцами, верхняя часть которых равна нулю.

Например, представим, что

${displaystyle A=left[{begin{array}{cccccc}1&0&-3&0&2&-8\0&1&5&0&-1&4\0&0&0&1&7&-9\0&0&0&0&0&0end{array}},right].}$

Тогда

${displaystyle left[{begin{array}{c}A\hline Eend{array}}right]=left[{begin{array}{cccccc}1&0&-3&0&2&-8\0&1&5&0&-1&4\0&0&0&1&7&-9\0&0&0&0&0&0\hline 1&0&0&0&0&0\0&1&0&0&0&0\0&0&1&0&0&0\0&0&0&1&0&0\0&0&0&0&1&0\0&0&0&0&0&1end{array}}right].}$

Если привести верхнюю часть с помощью операций над столбцами к ступенчатому виду, получим

${displaystyle left[{begin{array}{c}B\hline Cend{array}}right]=left[{begin{array}{cccccc}1&0&0&0&0&0\0&1&0&0&0&0\0&0&1&0&0&0\0&0&0&0&0&0\hline 1&0&0&3&-2&8\0&1&0&-5&1&-4\0&0&0&1&0&0\0&0&1&0&-7&9\0&0&0&0&1&0\0&0&0&0&0&1end{array}}right].}$

Последние три столбца матрицы нулевые. Поэтому три последних вектора матрицы ,

${displaystyle left[!!{begin{array}{r}3\-5\1\0\0\0end{array}}right],;left[!!{begin{array}{r}-2\1\0\-7\1\0end{array}}right],;left[!!{begin{array}{r}8\-4\0\9\0\1end{array}}right]}$

являются базисом ядра матрицы .

Доказательство, что метод вычисляет ядро: поскольку операции над столбцами соответствуют умножению справа на обратимую матрицу, из факта, что ${displaystyle left[{begin{array}{c}A\hline Eend{array}}right]}$ сводится к ${displaystyle left[{begin{array}{c}B\hline Cend{array}}right]}$ вытекает, что существует обратимая матрица , такая что ${displaystyle left[{begin{array}{c}A\hline Eend{array}}right]P=left[{begin{array}{c}B\hline Cend{array}}right],}$ где имеет ступенчатый вид. Тогда и Вектор-столбец принадлежит ядру матрицы (то есть ) тогда и только тогда, когда где ${displaystyle w=P^{-1}v=C^{-1}v.}$ Так как имеет ступенчатый вид, тогда и только тогда, когда ненулевые элементы соответствуют нулевым столбцам матрицы После умножения на можно сделать вывод, что это случается тогда и только тогда, когда является линейной комбинацией соответствующих столбцов матрицы

Численные вычисления[править | править код]

Задача вычисления ядра на компьютере зависит от природы коэффициентов.

Точные коэффициенты[править | править код]

Если коэффициенты матрицы заданы как точные числа, ступенчатый вид матрицы может быть вычислен алгоритмом Барейса, который более эффективен, чем метод Гаусса. Ещё более эффективно использование сравнения по модулю и китайской теоремы об остатках, которые сводят задачу к нескольким аналогичным задачам над конечными полями (что сокращает издержки, порождённые нелинейной вычислительной сложностью целочисленного умножения).

Для коэффициентов из конечного поля метод Гаусса работает хорошо, но для больших матриц, которые случаются в криптографии и при вычислении базиса Грёбнера, известны более эффективные алгоритмы, которые имеют почти ту же вычислительную сложность, но работают быстрее и более подходят для современных компьютерных устройств.

Вычисления с плавающей точкой[править | править код]

Для матриц, элементами которых служат числа с плавающей запятой, задача вычисления ядра имеет смысл только для матриц, число строк которых равно её рангу — ввиду ошибок округления^[en] матрицы с плавающими значениями почти всегда имеют полный ранг, даже когда они являются аппроксимацией матрицы много меньшего ранга. Даже для матрицы полного ранга можно вычислить её ядро только тогда, когда она хорошо обусловлена, то есть имеет низкое число обусловленности^[6].

И для хорошо обусловленной матрицы полного ранга метод Гаусса не ведёт себя корректно: ошибки округления слишком велики для получения значимого результата. Так как вычисление ядра матрицы является специальным случаем решения однородной системы линейных уравнений, ядро может быть вычислено любым алгоритмом, предназначенным для решения однородных систем. Передовым программным обеспечением для этих целей является библиотека Lapack.

См. также[править | править код]

Ядро (алгебра)
Нуль функции
Пространство столбцов
Пространство функций^[en]
Альтернатива Фредгольма

Примечания[править | править код]

↑ The Definitive Glossary of Higher Mathematical Jargon — Null. Math Vault (1 августа 2019). Дата обращения: 9 декабря 2019.
↑ Weisstein, Eric W. Kernel. mathworld.wolfram.com. Дата обращения: 9 декабря 2019.
↑ Kernel (Nullspace) | Brilliant Math & Science Wiki. brilliant.org. Дата обращения: 9 декабря 2019.
↑ Линейная алгебра в том виде, как обсуждается в этой статье, является хорошо проработанной математической дисциплиной, для которой можно найти много книг. Почти весь материал статьи можно найти в лекциях Лея (Lay, 2005), Мейера (Meyer, 2001) и Стренга.
↑ ¹ ² Weisstein, Eric W. Rank-Nullity Theorem. mathworld.wolfram.com. Дата обращения: 9 декабря 2019.
↑ Archived copy. Дата обращения: 14 апреля 2015. Архивировано 29 августа 2017 года.

Литература[править | править код]

Sheldon Jay Axler. Linear Algebra Done Right. — 2nd. — Springer-Verlag, 1997. — ISBN 0-387-98259-0.
Гилберт Стренг. Линейная алгебра и её применение. — Москва: «Мир», 1980.
David C. Lay. Linear Algebra and Its Applications. — 3rd. — Addison Wesley, 2005. — ISBN 978-0-321-28713-7.
Carl D. Meyer. Matrix Analysis and Applied Linear Algebra. — Society for Industrial and Applied Mathematics (SIAM), 2001. — ISBN 978-0-89871-454-8.
David Poole. Linear Algebra: A Modern Introduction. — 2nd. — Brooks/Cole, 2006. — ISBN 0-534-99845-3.
Howard Anton. Elementary Linear Algebra (Applications Version). — 9th. — Wiley International, 2005.
Steven J. Leon. Linear Algebra With Applications. — 7th. — Pearson Prentice Hall, 2006.
Serge Lang. Linear Algebra. — Springer, 1987. — ISBN 9780387964126.
Lloyd N. Trefethen, David III Bau. Numerical Linear Algebra. — SIAM, 1997. — ISBN 978-0-89871-361-9.

Ссылки[править | править код]

Hazewinkel, Michiel, ed. (2001), Kernel of a matrix, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Khan Academy, Introduction to the Null Space of a Matrix

Источник

2. Ядро и образ линейного оператора

Ядро и образ линейного оператора

Ядро оператора

Содержание

Важные частные случаи

Связанные понятия

Примеры

См. также

Полезное

Смотреть что такое «Ядро оператора» в других словарях:

Как найти базис ядра

Свойства[править | править код]

Приложение к модулям[править | править код]

В функциональном анализе[править | править код]

Представление в виде матричного умножения[править | править код]

Свойства подпространства[править | править код]

Пространство строк матрицы[править | править код]

Левое нуль-пространство (коядро)[править | править код]

Неоднородные системы линейных уравнений[править | править код]

Иллюстрация[править | править код]

Примеры[править | править код]

Вычисления по методу Гаусса[править | править код]

Численные вычисления[править | править код]

Точные коэффициенты[править | править код]

Вычисления с плавающей точкой[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как отключить найти телефон на samsung galaxy

Как найти машины сказки

Как найти похожую картинку или фотографию

Добавить комментарий Отменить ответ