From Wikipedia, the free encyclopedia
In astronomy, surface brightness (SB) quantifies the apparent brightness or flux density per unit angular area of a spatially extended object such as a galaxy or nebula, or of the night sky background. An object’s surface brightness depends on its surface luminosity density, i.e., its luminosity emitted per unit surface area. In visible and infrared astronomy, surface brightness is often quoted on a magnitude scale, in magnitudes per square arcsecond (MPSAS) in a particular filter band or photometric system.
Measurement of the surface brightnesses of celestial objects is called surface photometry.
General description[edit]
The total magnitude is a measure of the brightness of an extended object such as a nebula, cluster, galaxy or comet. It can be obtained by summing up the luminosity over the area of the object. Alternatively, a photometer can be used by applying apertures or slits of different sizes of diameter.[1] The background light is then subtracted from the measurement to obtain the total brightness.[2] The resulting magnitude value is the same as a point-like source that is emitting the same amount of energy.[3] The total magnitude of a comet is the combined magnitude of the coma and nucleus.
The apparent magnitude of an astronomical object is generally given as an integrated value—if a galaxy is quoted as having a magnitude of 12.5, it means we see the same total amount of light from the galaxy as we would from a star with magnitude 12.5. However, a star is so small it is effectively a point source in most observations (the largest angular diameter, that of R Doradus, is 0.057 ± 0.005 arcsec), whereas a galaxy may extend over several arcseconds or arcminutes. Therefore, the galaxy will be harder to see than the star against the airglow background light. Apparent magnitude is a good indication of visibility if the object is point-like or small, whereas surface brightness is a better indicator if the object is large. What counts as small or large depends on the specific viewing conditions and follows from Ricco’s law.[4] In general, in order to adequately assess an object’s visibility one needs to know both parameters.
This is the reason the extreme naked eye limit for viewing a star is apparent magnitude 8,[5] but only apparent magnitude 6.9 for galaxies.[6]
| Object | apmag |
|---|---|
| Andromeda Galaxy (M31) | 3.4 |
| Orion Nebula (M42) | 4 |
| Triangulum Galaxy (M33) | 5.7 |
| Bode’s Galaxy (M81) | 6.9 |
Calculating surface brightness[edit]
Surface brightnesses are usually quoted in magnitudes per square arcsecond. Because the magnitude is logarithmic, calculating surface brightness cannot be done by simple division of magnitude by area. Instead, for a source with a total or integrated magnitude m extending over a visual area of A square arcseconds, the surface brightness S is given by
For astronomical objects, surface brightness is analogous to photometric luminance and is therefore constant with distance: as an object becomes fainter with distance, it also becomes correspondingly smaller in visual area. In geometrical terms, for a nearby object emitting a given amount of light, radiative flux decreases with the square of the distance to the object, but the physical area corresponding to a given solid angle or visual area (e.g. 1 square arcsecond) decreases by the same proportion, resulting in the same surface brightness.[7] For extended objects such as nebulae or galaxies, this allows the estimation of spatial distance from surface brightness by means of the distance modulus or luminosity distance.[clarification needed]
Relationship to physical units[edit]
The surface brightness in magnitude units is related to the surface brightness in physical units of solar luminosity per square parsec by[citation needed]
where 

Surface brightness can also be expressed in candela per square metre using the formula [value in cd/m2] = 10.8×104 × 10(-0.4*[value in mag/arcsec2]).
There is an online calculator available here http://unihedron.com/projects/darksky/magconv.php?ACTION=SOLVE&txtMAGSQA=21.83
Examples[edit]
A truly dark sky has a surface brightness of 2×10−4 cd m−2 or 21.8 mag arcsec−2.[9][clarification needed]
The peak surface brightness of the central region of the Orion Nebula is about 17 Mag/arcsec2 (about 14 millinits) and the outer bluish glow has a peak surface brightness of 21.3 Mag/arcsec2 (about 0.27 millinits).[10]
See also[edit]
- Araucaria Project
- Low-surface-brightness galaxy
- Limiting magnitude
- Sigma-D relation
References[edit]
- ^ Daintith, John; Gould, William (2006). The Facts on File dictionary of astronomy. Facts on File science library (5th ed.). Infobase Publishing. p. 489. ISBN 0-8160-5998-5.
- ^ Palei, A. B. (August 1968). “Integrating Photometers”. Soviet Astronomy. 12: 164. Bibcode:1968SvA….12..164P.
- ^ Sherrod, P. Clay; Koed, Thomas L. (2003). A Complete Manual of Amateur Astronomy: Tools and Techniques for Astronomical Observations. Astronomy Series. Courier Dover Publications. p. 266. ISBN 0-486-42820-6.
- ^ Crumey, Andrew (2014). “Human contrast threshold and astronomical visibility”. Monthly Notices of the Royal Astronomical Society. 442 (3): 2600–2619. arXiv:1405.4209. Bibcode:2014MNRAS.442.2600C. doi:10.1093/mnras/stu992.
- ^ John E. Bortle (February 2001). “The Bortle Dark-Sky Scale”. Sky & Telescope. Archived from the original on 23 March 2009. Retrieved 2009-11-18.
- ^ “Messier 81”. SEDS (Students for the Exploration and Development of Space). 2007-09-02. Archived from the original on 2017-07-14. Retrieved 2009-11-28.
- ^ Sparke & Gallagher (2000, § 5.1.2)
- ^ Absolute magnitudes of the Sun in different color-bands can be obtained from Binney & Merrifield (1998) or Absolute Magnitude of the Sun in Several Bands Archived 2007-07-18 at the Wayback Machine
- ^ Based on the equivalence 21.83 mag arcsec−2 = 2×10−4 cd m−2, from description of a “truly dark sky”, Section 1.3 of Crumey, A. (2014). Human contrast threshold and astronomical visibility. MNRAS 442, 2600–2619.
- ^ Clark, Roger (2004-03-28). “Surface Brightness of Deep Sky Objects”. Retrieved 2013-06-29.. The conversion to nits is based on 0 magnitude being 2.08 microlux.
General references[edit]
- Binney, James; Merrifield, Michael (1998). Galactic Astronomy. Princeton University Press. ISBN 978-0-691-02565-0.
- Sparke, L.; Gallagher, J. (2000). Galaxies in the Universe: An Introduction (1st ed.). Cambridge University Press. ISBN 0-521-59241-0.
2017-11-29 23:05
Экраны кинотеатров и аудитория, окрашенные потолки, стены, декорации и т. д. представляют собой диффузно отражающие поверхности.
Такого рода поверхности при освещении играют роль протяженных источников с большими поверхностями и обычно с умеренной яркостью. В этом смысле они удачно дополняют мало протяженные самосветящиеся источники (лампы накаливания, газосветные лампы, свечи и т. п.), которые обычно обладают небольшими поверхностями и большими яркостями.
Яркость такой освещенной поверхности будет, очевидно, пропорциональна ее освещенности. Действительно, чем больше освещенность, т. е. чем больший световой поток падает на единицу поверхности, тем больше будет и поток, отраженный этой поверхностью, а следовательно, и яркость освещенной поверхности.
Яркость освещенной поверхности будет, кроме того, тем больше, чем больше ее альбедо, т.е. чем большая часть падающего на поверхность потока рассеивается ею. Таким образом, яркость освещенной поверхности
![]()
должна быть пропорциональна произведению освещенности
![]()
на альбедо
![]()
, т. е.
![]()
. В зависимости от диаграммы рассеяния яркость по разным направлениям может быть различна, и вычисление ее представляет очень сложную задачу. Задача эта упрощается, если поверхность рассеивает свет равномерно по всем направлениям. В таком случае и яркость по всем направлениям будет одинаковой и равной
![]()
. (77.1)
Если освещенность
![]()
выражается в люксах, то яркость получится в канделах на квадратный метр.
Найдем, например, яркость киноэкрана, если его коэффициент отражения
![]()
, а освещенность равна
![]()
. Пользуясь формулой (77.1), имеем
![]()
.
Приведем значения яркости освещенных поверхностей (табл. 3) с которыми часто приходится встречаться в жизни.
Таблица 3. Яркость некоторых освещенных поверхностей
![]()
| Яркость экрана в кинотеатре | от5 до 10 |
|
» листа белой бумаги при освещенности, достаточной для письма |
от 10 до 15 |
| » снега под прямыми лучами Солнца | 3000 |
| » поверхности Луны | 2500 |
Яркость
источников. До
сих пор мы рассматривали только точечные
источники света. В действительности
источники обычно являются протяженными,
т. е. рассматривая их с заданного
расстояния, мы различаем их форму и
размеры. Для характеристики протяженных
источников, даре в том простейшем
случае, когда они представляют собой
равномерно светящиеся шарики, недостаточно
одной только величины— силы света.
Действительно, представим себе два
светящихся шарика, испускающих свет
равномерно во все стороны и имеющих
одинаковую силу света, но разный диаметр.
Освещенность, создаваемая каждым из
этих шариков на одинаковом расстоянии
от их центра, будет одинакова. Однако
по своему виду эти шарики будут
представлять сильно различающиеся
источники света: маленький шарик
оказывается более ярким, чем большой.
Это происходит вследствие того, что при
одинаковой силе света излучающая
поверхность одного шарика больше, чем
второго, и, следовательно, сила света,
испускаемого с единицы площади источника,
в том и другом случаях различна. Отметим,
что когда мы рассматриваем какой-либо
источник света, для нас имеет значение
не площадь самой излучающей поверхности,
а размеры видимой поверхности, т. е.
проекции излучающей поверхности на
плоскость, перпендикулярную к направлению
наблюдения (рис. 159).
Итак,
мы приходим к выводу, что для характеристики
‘свойств протяженного источника света
нужно знать силу
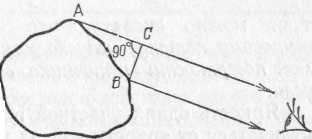
Рис.
159. Соотношение между действительной
излучающей поверхностью (АВ) и
поверхностью, видимой по данному
направлению (ВС)
*)
Приставка тера образована от греческого
слова «терас» — чудовище.
света,
рассчитанную на единицу площади видимой
поверхности источника. Эта
световая величина называется яркостью
источника;
мы будем ее обозначать буквой L.
Если
источник имеет силу света I
и площадь видимой светящейся поверхности
его есть ,
то
яркость этого источника равна
![]()
(73.1)
Пользуясь
формулой (70.1), имеем также
![]()
(73.2)
т.
е. можно сказать, что яркость
источника равна световому потоку,
испускаемому с единицы площади видимой
поверхности источника внутри единичного
телесного угла.
Яркость
одних участков поверхности источника
может отличаться от яркости других
участков. Например, различные участки
пламени свечи, лампы и т, п. имеют сильно
различающиеся яркости. Кроме того,
яркость зависит от направления, в котором
происходит излучение источника.
Это связано с тем, что сила света
многих источников зависит от направления.
Например, электрическая дуга по
некоторым направлениям совсем не
посылает света (рис. 160).
Итак,
яркость может служить для характеристики
излучения какого-либо участка
поверхности источника в заданном
направлении. Вместе с тем яркость имеет
большое значение в силу того, что, как
мы увидим ниже, это — та световая
величина, на которую непосредственно
реагирует глаз.
Единицей
яркости является кандела
на квадратный метр. Такой
яркостью обладает светящаяся площадка,
дающая с каждого квадратного метра силу
света, равную 1 кд в направлении,
перпендикулярном к площадке.
Характеристики
яркости различных светящихся тел
приведены в табл. 2.
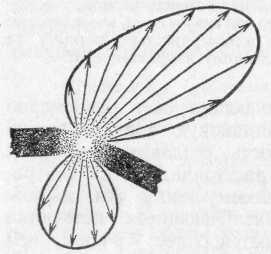
Рис.
160. Яркость электрической дуги,
пропорциональная длине стрелок на
рисунке, зависит от направления излучения
Таблица
2. Яркость
некоторых источников света (в кд/м2)

Источники
света с большой яркостью (свыше 1 ,6•105
кд/м2)
вызывают болезненное ощущение в глазу.
Для того чтобы глаз не подвергался
действию яркого света источников,
применяют различные приспособления.
Так, например, рассматривание раскаленной
спирали лампы накаливания вредно и
даже болезненно для глаза. Если же колба
лампочки сделана из матового или
молочного стекла или прикрыта арматурой
в виде матового шара, то излучаемый
ею световой поток исходит с большей
поверхности. Благодаря этому яркость
падает, тогда как световой поток
практически не изменяется и,
следовательно, освещенность, создаваемая
лампой, также остается неизменной.
Яркость
освещенных поверхностей. Экраны
кинотеатров и аудиторий, окрашенные
потолки, стены, декорации и т. д.
представляют собой диффузно отражающие
поверхности.
Такого
рода поверхности при освещении играют
роль протяженных источников с большими
поверхностями и обычно с умеренной
яркостью. В этом смысле они удачно
дополняют мало протяженные самосветящиеся
источники (лампы накаливания, газосветные
лампы, свечи и т. п.), которые обычно
обладают небольшими поверхностями и
большими яркостями.
Яркость
такой освещенной поверхности будет,
очевидно, пропорциональна
ее освещенности. Действительно,
чем больше освещенность, т. е. чем бо’льший
световой поток падает на единицу
поверхности, тем больше будет и поток,
отраженный этой поверхностью, а
следовательно, и яркость освещенной
поверхности.
Яркость
освещенной поверхности будет, кроме
того, тем больше, чем больше ее альбедо,
т. е. чем большая часть падающего на
поверхность потока рассеивается ею.
Таким образом, яркость освещенной
поверхности L
должна
быть пропорциональна произведению
освещенности Е
на
альбедо ,
т. е. L~•E.
В
зависимости от диаграммы рассеяния
яркость по разным направлениям может
быть различна, и вычисление ее представляет
очень сложную задачу. Задача эта
упрощается, если поверхность рассеивает
свет равномерно по всем направлениям.
В таком случае и яркость по всем
направлениям будет одинаковой и равной
![]()
(77.1)
Если
освещенность Е
выражается
в люксах, то яркость получится в канделах
на квадратный метр.
Найдем,
например, яркость киноэкрана, если его
коэффициент отражения =0,75,
а освещенность равна 50 лк. Пользуясь
формулой (77.1), имеем
![]()
Приведем
значения яркости освещенных поверхностей
(табл. 3), с которыми часто приходится
встречаться в жизни
Таблица
3. Яркость
некоторых освещенных поверхностей (в
кд/м2)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Как создать качественное освещение
Здравствуйте!
В прошлый раз мы разобрались с тем, как можно управлять светом: направлять его в нужные стороны и ограничить там, где он будет лишним. Однако для создания качественного освещения одного умения управлять светом недостаточно. Нужно также разбираться в показателях качества.
Показатели качества — это световые величины. Без их учета невозможно:
- выбрать подходящее световое оборудование;
- придумать, где его установить;
- проверить, соответствует ли система освещения предъявляемым требованиям.
В сегодняшнем уроке мы познакомимся с основными световыми величинами. Узнаем, как они связаны друг с другом и чем их измеряют.
Что такое световые величины и какими они бывают
Световые величины — это величины, которые описывают свойства света с учетом его способности вызывать у человека зрительные ощущения. К ним относятся:
- световой поток и световая отдача;
- сила света;
- освещенность;
- яркость.
Световой поток и световая отдача

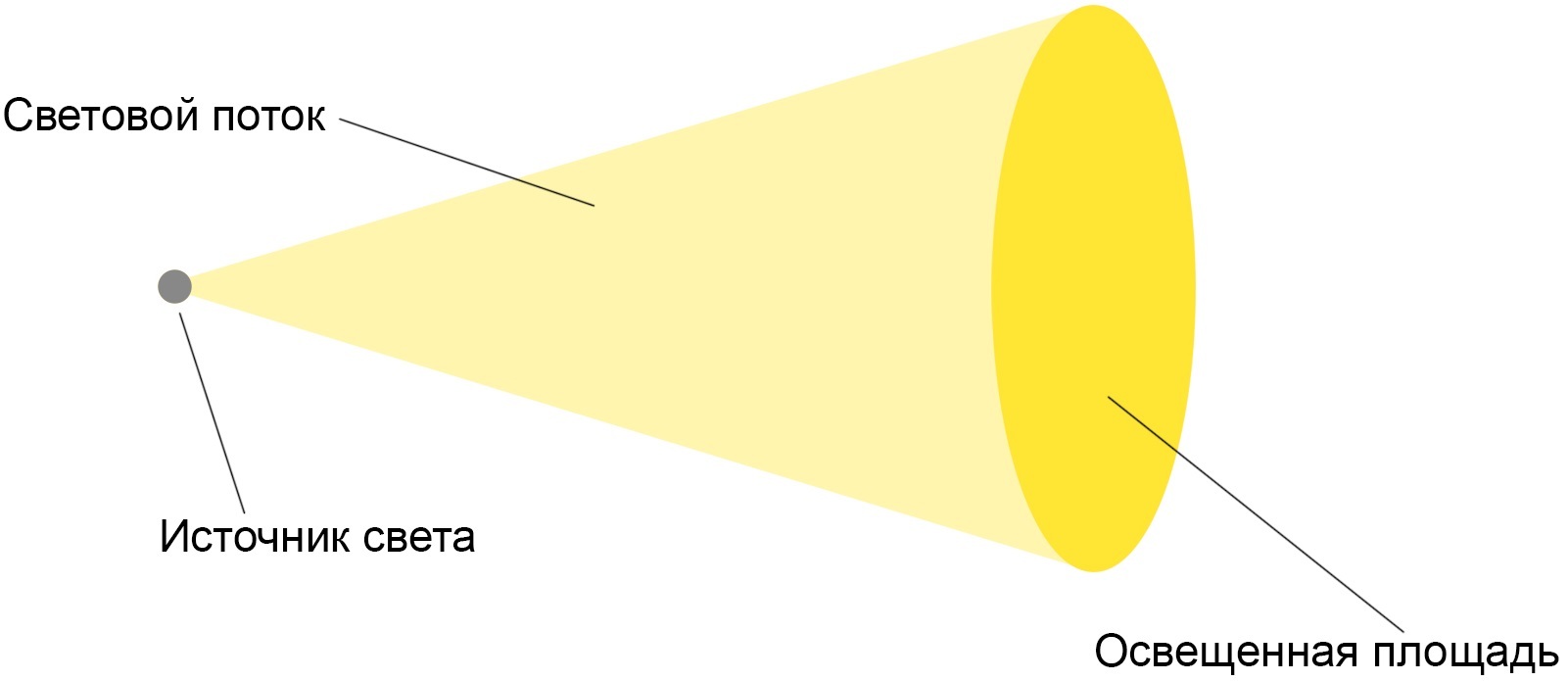
Световой поток показывает, сколько света излучает светильник за единицу времени. Измеряется в люменах (лм), обозначается буквой Φ. С помощью светового потока вычисляют световую отдачу источника света.
Световая отдача — это отношение светового потока источника к электроэнергии, которую он потребляет.
Формула вычисления светоотдачи
H = Ф / P
Допустим, лампа накаливания потребляет 20 Вт электроэнергии, чтобы создать световой поток 250 лм. Тогда ее светоотдача вычисляется так: 250 лм / 20 Вт = 12.5 лм/Вт.
Чем выше светоотдача, тем меньше энергии потребляет источник света и тем меньше вы платите за электричество. Например, если заменить лампу накаливания со светоотдачей 7-22 лм/Вт на люминесцентную со светоотдачей 50-90 лм/Вт, то расход электроэнергии уменьшится в 5-6 раз, а уровень освещенности не изменится.
Среднее значение световой отдачи разных ламп:
- лампа накаливания — 10 лм/Вт;
- флуоресцентная лампа — 100 лм/Вт;
- натриевая лампа низкого давления — 175 лм/Вт;
- светодиод — 104 лм/Вт.
Сила света показывает, сколько света излучает светильник в определенном направлении за единицу времени. Измеряется в канделах (кд), обозначается буквой I.
Для лучшего понимания представьте кран, из которого течет вода. Если она еле течет, говорят, напор слабый, и наоборот. То же самое и со светом.
Сила света вычисляется так: берут световой поток, идущий в каком-либо направлении, и делят его на телесный угол (ω):
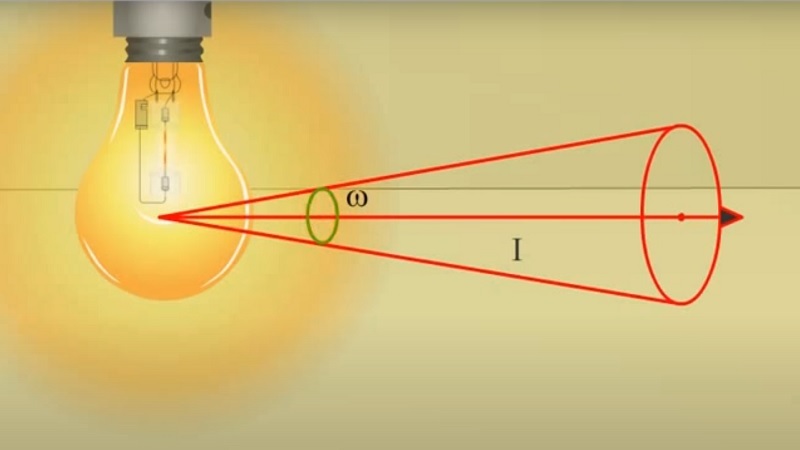
Что такое телесный угол
Телесный угол — часть пространства, которая объединяет все световые лучи, выходящие из заданной точки и пересекающих некоторую поверхность.
Формула вычисления силы света
I = Ф / ω
Освещенность показывает, сколько света падает на определенную площадь за единицу времени. Измеряется в люксах (лк) или люменах на квадратный метр (лм/м2). Обозначается буквой E.
Для лучшего понимания представьте кран, из которого течет свет, и стакан, куда этот свет попадает. Освещенность — это сколько света попадает в стакан за определенное время. Чтобы совсем не оставалось вопросов по поводу значения освещенности, сравните картинки ниже.

Освещенность, создаваемая ясным небом в полдень летнего дня

Освещенность в пасмурный день

Освещенность офисного кабинета, создаваемая искусственным светом и естественным, проникающим из окон

Освещенность, создаваемая луной на ясном небе
Освещенность вычисляется так: берут световой поток и делят его на площадь участка, который он освещает.
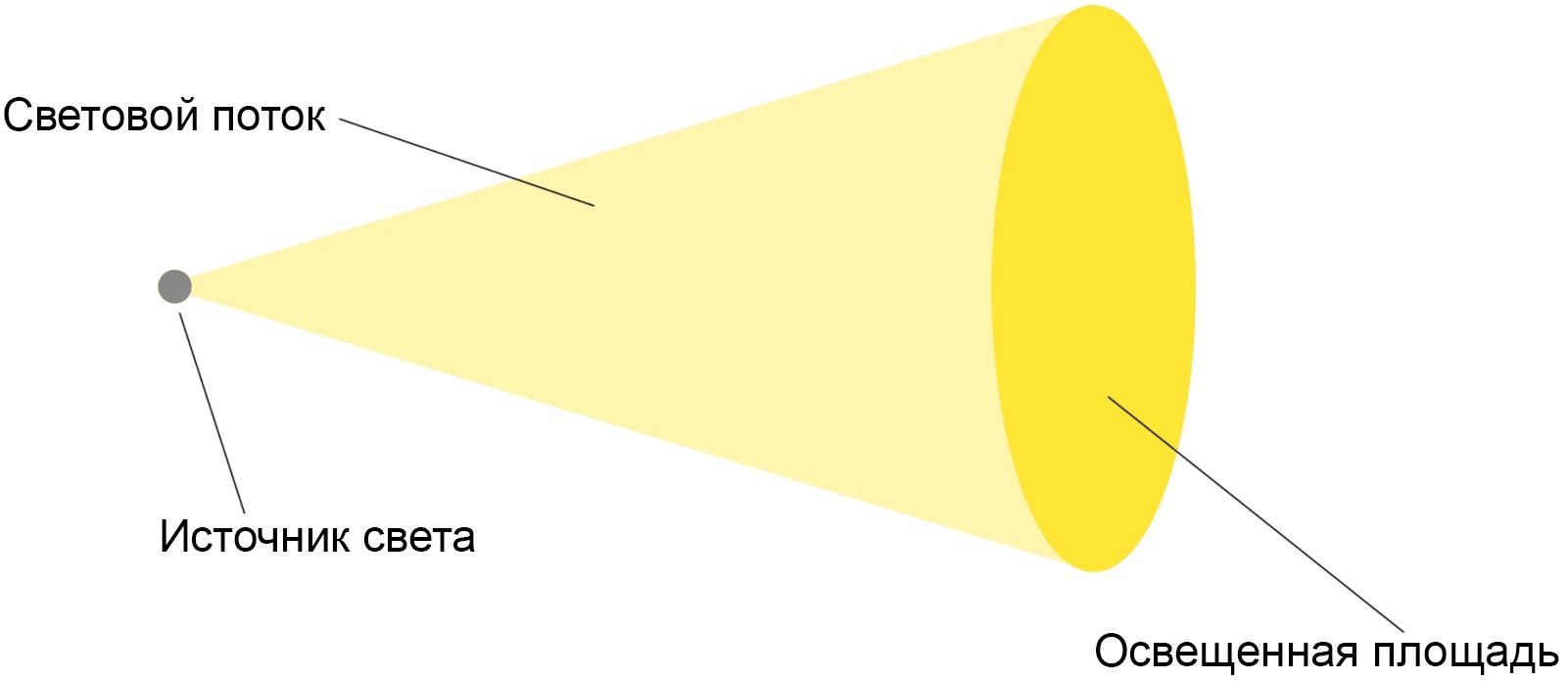
Интересный факт, о котором мало кто знает
При разработке освещения для объектов также берется во внимание естественное освещение. Это освещение прямыми солнечными лучами или рассеянным светом небосвода.
Значение освещенности, создаваемой естественным светом, зависит от природных условий, степени облачности и времени года и суток.
Естественная освещенность:
- в ясный день — 100 000 лк;
- в пасмурный день — 5 000 лк;
- в ясную ночь при полной луне — 0.25 лк.
Яркость — отношение силы света, излучаемого поверхностью, к площади её проекции на плоскость, перпендикулярную оси наблюдения. Измеряется в канделах на квадратный метр (кд/м2), обозначается буквой L.
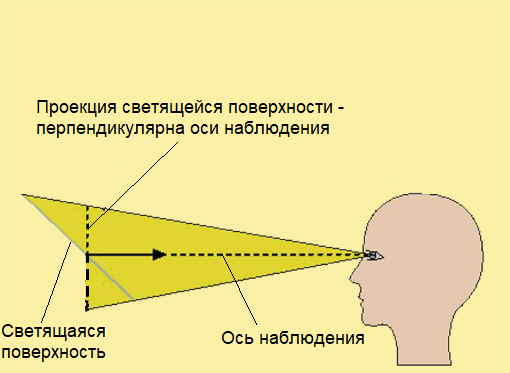
Чтобы было понятнее, продолжим аналогию с напором воды. Если подать одинаковый напор воды на кухонный кран и пожарный шланг, то будет казаться, что из крана вода течет сильно, а из шланга — еле-еле.
То же самое и с яркостью. Если у двух светильников одинаковая сила света, ярче будет казаться тот, что меньше.

Оба шара светят с одинаковой силой и создают одинаковую освещенность. Однако шар, который больше, кажется тусклее, потому что светящаяся поверхность у него больше.
Яркости разных участков одного светильника отличаются. Например, люминесцентная лампа тусклее по краям, а пламя свечи ярче в ореоле вокруг фитиля.

Кроме этого, то, насколько ярким будет казаться источник света, зависит от того, с какой стороны на него смотреть. Например, если посмотреть на сварочную дугу перпендикулярно направлению разряда, ее яркость доставит дискомфорт и частично ослепит. А если посмотреть сбоку — яркость будет терпимой.
Из этого следует, что яркость нам нужна для того, чтобы проектировать комфортное освещение, которое не слепит глаза.
Яркость применяется не только к светильникам
Яркость имеют не только светильники и лампы, но и поверхности, которые отражают свет: дорога, стены, потолки, пол, стол и другие освещенные предметы. Их называют вторичными источниками света.
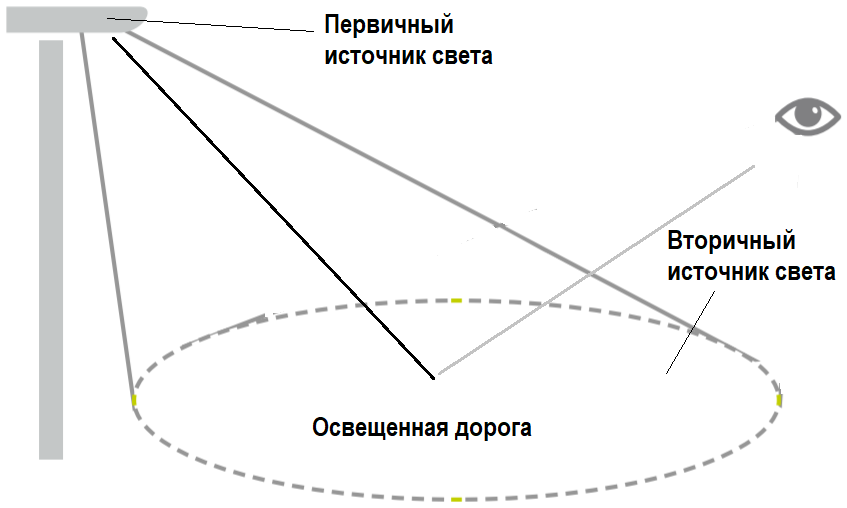
Мы видим предметы благодаря свету, который они отразили в наши глаза. Если бы они не отражали свет, то мы бы их не видели. Вспомните смешные случаи с идеально чистой стеклянной дверью: человек ее не замечал и врезался в нее. А не замечал он ее потому, что она не отражала свет, а пропускала его через себя.

Яркость некоторых первичных и вторичных источников света
- солнце — 1 650 000 000 кд/м2;
- нить лампы накаливания — 7 000 000 кд/м2;
- ясное небо — 20 000 кд/м2;
- люминесцентная лампа — 5000-15000 кд/м2;
- письменный стол — 100 кд/м2;
- дорожное покрытие — 0.5-2 кд/м2.
Человеческий глаз воспринимает яркость только видимой области источника света. Видимая область — это проекция источника света на плоскость. Форма этой проекции зависит от того, с какой стороны мы смотрим на предмет:
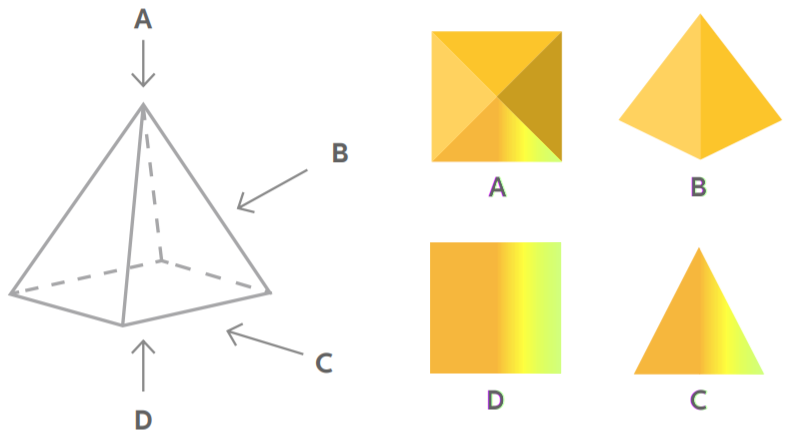
Представьте, что на картинке выше изображена светящаяся призма. В этом случае вы воспринимаете яркость только тех частей призмы, которые видите. А что это за части и как они выглядят, зависит от того, с какой стороны вы смотрите на призму. То же самое и со светящимся цилиндром:
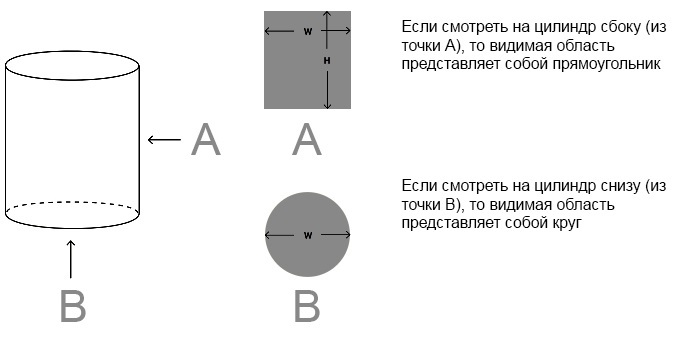
При выборе светильника важно учитывать не только яркость, указанную в характеристиках, но и субъективную яркость — яркость, которую воспринимает человек. Она зависит от многих обстоятельств, в том числе и от обстановки.
Для примера возьмем серый квадрат, поместим его в темный и светлый фон, а потом посмотрим на него. В результате окажется, что на темном фоне он кажется ярче, чем на светлом:
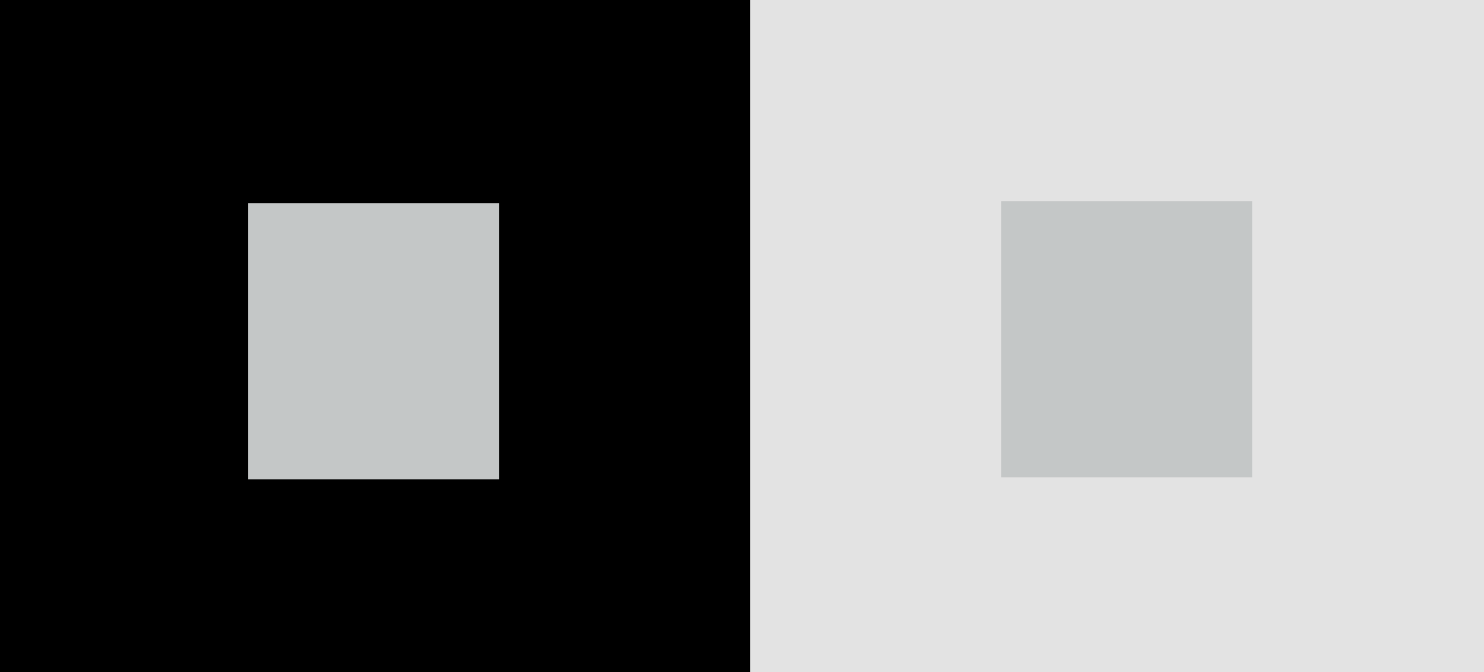
Яркость одного и того же источника света может казаться разной. И зависит это от фона
Как световые величины связаны друг с другом
Световые величины не живут отдельно друг от друга. Они взаимосвязаны. И это хорошо: если знаешь одну величину, то запросто найдешь остальные. Эта связь описывается формулами. Ниже рассмотрим основные.
Связь между освещенностью и световым потоком
Пример:
Φ = 10 000 лм
S = 12 м2
E = 10000 / 12 =833 лк
Связь между освещенностью и силой света
Эта связь зависит от того, под каким углом к поверхности падает свет.
Когда свет падает на некоторую точку под прямым углом к поверхности, на которой лежит эта точка, освещенность точки рассчитывается по закону обратных квадратов.
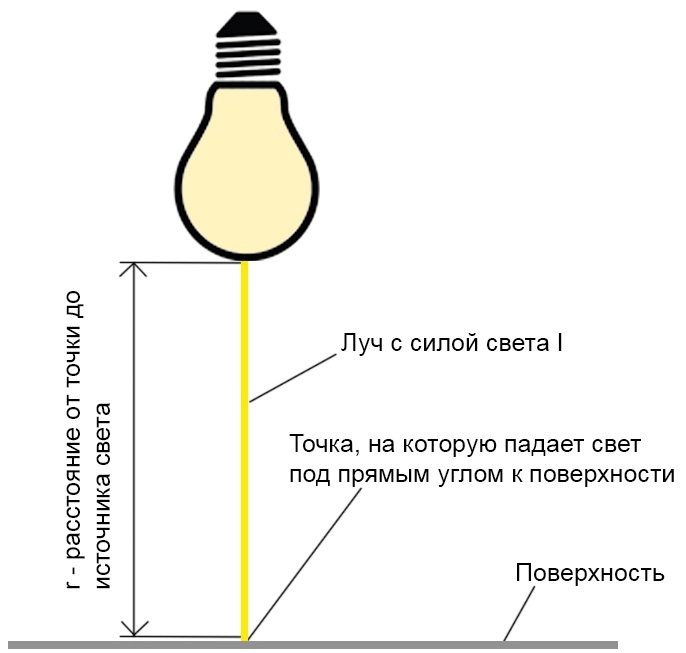
Пример:
I = 100 кд
r = 0.5 м
E = 100 / (0.5)2 = 400 лк
Интересный факт, о котором мало кто знает
Закон обратных квадратов действует только в случаях, когда рассматриваются точечные источники света. Он подразумевает, что чем дальше источник света от освещаемой поверхности, тем меньше освещенность этой поверхности.
При этом освещенность уменьшается нелинейно расстоянию. Например, если увеличить расстояние между источником и освещаемой поверхностью в два раза, освещенность поверхности уменьшится не в 2 раза, а квадратично расстоянию — то есть в 4 раза.
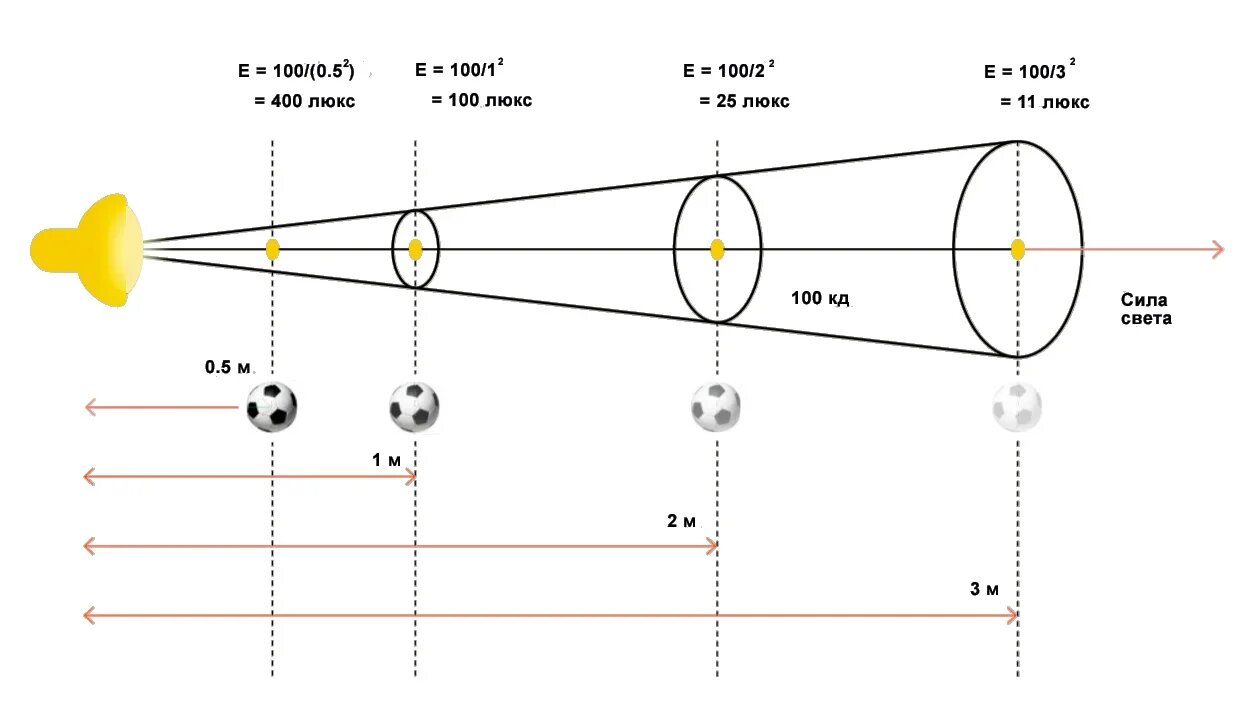
Освещенность падает квадратично расстоянию от источника света. Об этом необходимо помнить при проектировании освещения
Когда свет падает на некоторую точку не под прямым углом к поверхности, освещенность точки рассчитывается по закону косинусов.
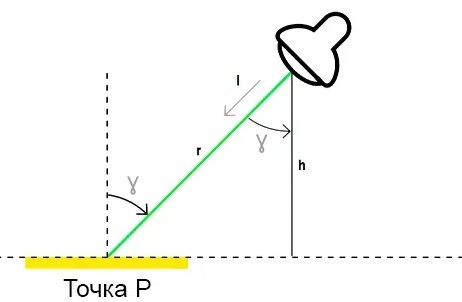
Пример:
I = 1200 кд
r = 3 м
Угол падения γ — 60о
E = (1200 / 32) х cos γ = 67 лк
Связь между горизонтальной освещенностью и силой света
Горизонтальную освещенность некоторой точки обычно рассчитывают для рабочих поверхностей: столешницы рабочего стола, спортивной площадки и т.д.
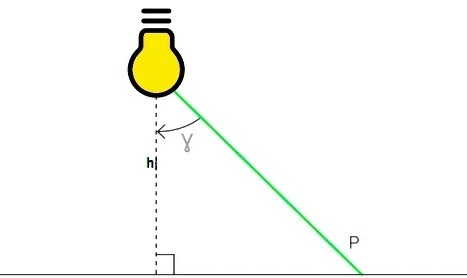
Связь между вертикальной освещенностью и силой света
Световые приборы должны обеспечивать подходящую освещенность не только на горизонтальных поверхностях, но и на вертикальных.
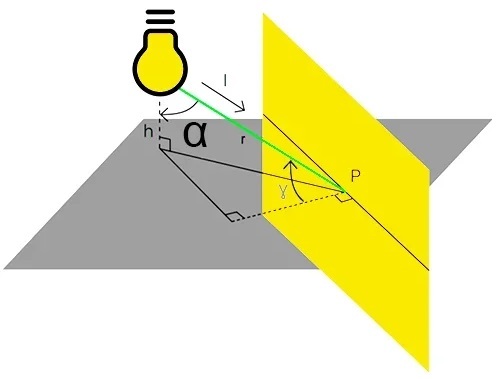
Связь между освещенностью и яркостью
Чтобы рассчитать яркость поверхности, которая отражает свет, освещенность этой поверхности умножают на ее коэффициент отражения (ρ) и делят полученный результат на число «пи».
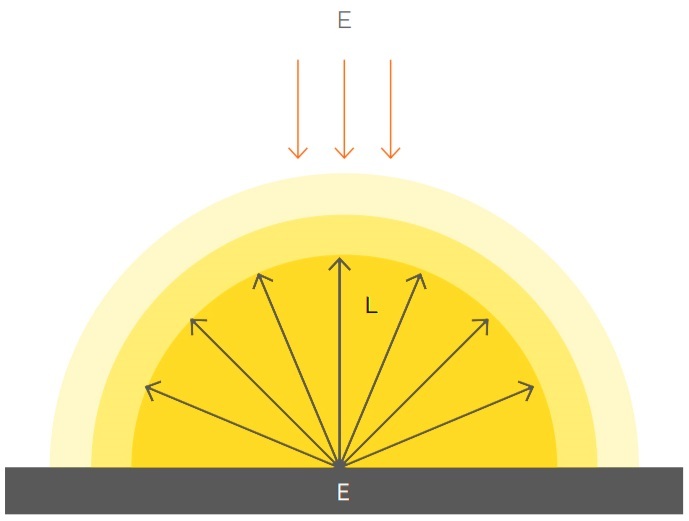
Пример:
Освещенность листа бумаги — 500 лк
Коэффициент отражения бумаги — 0.7
L = 500 x 0.7 / π = 111 кд/м2
Эта формула применима только к поверхностям, которые создают диффузное отражение.
Как вы помните из прошлого урока, диффузное отражение — это когда лучи света после отражения расходятся в разные стороны, а не в одну. Такое отражение создается на шероховатых поверхностях: бумаге, дорожном покрытии и т.д.
Связь между световым потоком и силой света
Если светильник распределяет свет равномерно по всем направлениям, то сила света находится так: световой поток умножают на коэффициент пропускания материала, через который проходит свет, и полученный результат делят на 4π.
Пример:
Световой поток лампы накаливания — 1000 лм
Коэффициент пропускания опалового стекла (τ) — 0.9
I = 1000 x 0,9 / 4 π = 72 кд
Представленные формулы необязательно запоминать
Все эти формулы мы показали вам для того, чтобы вы понимали физическую взаимосвязь между световыми величинами.
Зубрить их не надо, потому что все расчеты при проектировании освещения ведутся в специализированных программах, куда уже заложены все эти формулы.
Одна из самых распространенных программ — DIALux.
Когда требуется определить качество освещения, пользуются измерительными приборами. Для каждой световой величины свой прибор. Давайте разберемся, что это за приборы.
Все измерительные приборы устроены одинаково. Их главная деталь — фотоэлемент. Когда на фотоэлемент попадает свет, он создает небольшой электрический ток или меняет его величину. Нынешние фотоэлементы изготавливают из полупроводниковых материалов.
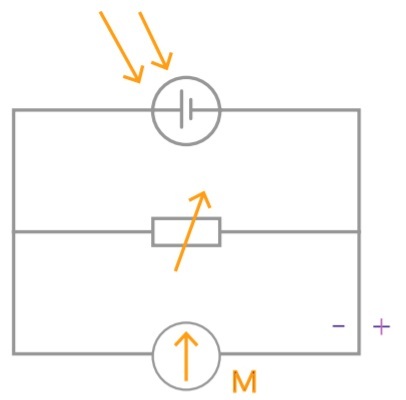
Обычно приборы измеряют освещенность — количество света, попадающего на фотоэлемент. Чтобы узнать другие световые величины, например, световой поток, силу и яркость света, пользуются формулами, о которых мы говорили выше.
Чувствительность фотоэлементов не такая, как у наших глаз. Чтобы к ней приблизиться, фотоэлементы дополняют светофильтрами. Чем больше светофильтров, тем точнее измерения и выше цена прибора.
Люксметр — для измерения освещенности и яркости
Обычно этот прибор используют для измерения уровня освещенности определенных мест, например, офисных кабинетов.

Гониофотометры — для измерения силы света
Эти приборы используют производители светового оборудования. Их устанавливают в специальных лабораториях. С их помощью измеряют силу света или светораспределение определенной группы светильников с нескольких сторон. В них светильники или система зеркал (или и то и другое вместе) вращаются вокруг фотоэлемента. Если интересно, посмотрите видео, как работает этот прибор.

Фотометрический шар Ульбрихта — для измерения светового потока
Прибор работает так: лампу подвешивают в центре пустой сферы и включают, а установленный в специальном отверстии сферы фотоэлемент измеряет освещенность. Затем программа рассчитывает значение светового потока. Стены сферы матово-белые, чтобы идеально рассеивать свет.

Приборы для измерения яркости
Такие приборы состоят из фотоэлемента и оптической системы. Оптическая система проецирует изображение измеряемой поверхности источника света на фотоэлемент. В результате последний получает некоторую освещенность, на ее основе прибор рассчитывает и выдает значение яркости. Часто эти функции совмещают в люксметре.

Спектрометр — самый продвинутый измерительный прибор. Чтобы определить необходимые световые величины существующего или проектируемого освещения, вам не придется везти каждый светильник в лабораторию. Всю необходимую информацию вам предоставит портативный спектрометр.
Характеристики, которые способен определить спектрометр:
- спектральный состав излучения;
- уровень мерцания (видимого и невидимого);
- силу света, яркость и освещенность;
- длину волны и частоту.
Плюс к этому, он может определять качество цвета (о качестве цвета мы подробно расскажем в 6-м уроке).

Итак, сегодня мы узнали, что освещение должно соответствовать определенным показателям качества. Этими показателями являются световые величины.
Теперь, когда вы стали разбираться в световых величинах, вы сможете подобрать подходящее световое оборудование и проверить, соответствует ли ваша система освещения заданным требованиям.
Кем задаются требования к освещению
Показатели качественного освещения устанавливаются государственными и международными стандартами и диктуются назначением и устройством объекта. Это говорит о том, что к освещению учебных классов, коридоров, погрузочных площадок и даже футбольных полей предъявляются разные требования.
Перечень СНиПов, которыми нужно руководствоваться при проектировании
Чтобы закрепить эти знания, кратко повторим все, что мы изучили в этом уроке.
1. Световые величины характеризуют свет с учетом его способности вызывать у человека зрительные ощущения.
2. К световым величинам относятся:
- световой поток показывает, сколько света излучает источник;
- световая отдача — сколько электроэнергии понадобится источнику, чтобы давать нужное количество света;
- сила света — сколько света излучает источник в одном направлении;
- освещенность — сколько света падает на поверхность;
- яркость — сила света, поделенная на площадь проекции светящегося участка.
3. Яркость бывает не только расчетной, но и субъективной — такой, какой ее воспринимает наблюдатель. Субъективная яркость зависит от многого, в том числе и от обстановки. Один и тот же источник света может восприниматься как очень яркий и недостаточно яркий в разных помещениях.
4. Световые величины взаимосвязаны. Эта взаимосвязь описывается математическими формулами. Однако их запоминать не нужно, потому что есть специальные программы, куда все эти формулы уже загружены.
5. Для измерения световых величин используют специальные приборы. Все они устроены примерно одинаково. Их основа — фотоэлемент, который определяет освещенность. И уже из освещенности рассчитываются другие величины.
На сегодня все. В следующем уроке поговорим о том, как работает зрение и как оно воспринимает свет.
Это пригодится вам для того, чтобы разрабатывать системы освещения, которые не только обеспечивают хорошую видимость, но и не утомляют зрение, не вредят здоровью, поддерживают работоспособность и помогают расслабиться в зависимости от назначения объекта.
Всегда ваша,
команда Азбуки Света
|
Отписаться от бесплатного курса по основам света можно здесь |
2018-07-01 ![]()
Определить светимость поверхности, яркость которой зависит от направления по закону $L = L_{0} cos theta$, где $theta$ — угол между направлением излучения и нормалью к поверхности.
Решение:
Яркость $L$ – это энергия света, излучаемая на единицу площади излучающей поверхности в заданном направлении на единицу телесного угла, деленная на $cos theta$. Светимость $M$ – это просто энергия, излучаемая на единицу площади.
Таким образом $M = int L cos theta d Omega$
где интегрирование должно быть произведено в переднем полушарии излучающей поверхности (при условии, что свет излучается только в одном направлении, указывающем внешнее направление поверхности). Но
$L = L_{0} cos theta$
Таким образом $M = int L_{0} cos^{2} theta d Omega = 2 pi int_{0}^{ pi /2} L_{0} cos^{2} theta sin theta d theta = frac{2}{3} pi L_{0}$


