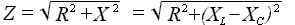-
не работает пишет удалите неиспользованные компоненты хотя все соединено
-
-
Не работает ошибка! Значения элемента
-
-
Почему пишет,что в схеме отсутствует эдс хотя я его поставит
-
-
Ошибка! В ветви отсуствует сопротивление: R
-
В ветви должно быть хотя бы одно сопротивления
-
-
спасибо вам , помогли. все работает если правильно заполнить и нарисовать.
Основные законы электротехники для начинающих
Содержание
- 1 Великий Ом
- 2 Вычисление полного сопротивления цепи (Z)
- 3 Определение полной мощности (S) в электротехнике
- 4 Закон Джоуля-Ленца
- 5 Первый закон Кирхгофа
- 6 Второй закон Кирхгофа
- 7 Видео по теме
Сегодня сложно представить мир без электричества, а также приборов, машин и устройств, работающих на нем. Электротехника окружает нас в быту и на улицах. Без нее до сих пор бы на производствах преобладал ручной труд. Чтобы развивать эту отрасль, следует знать основные законы электротехники.
Великий Ом
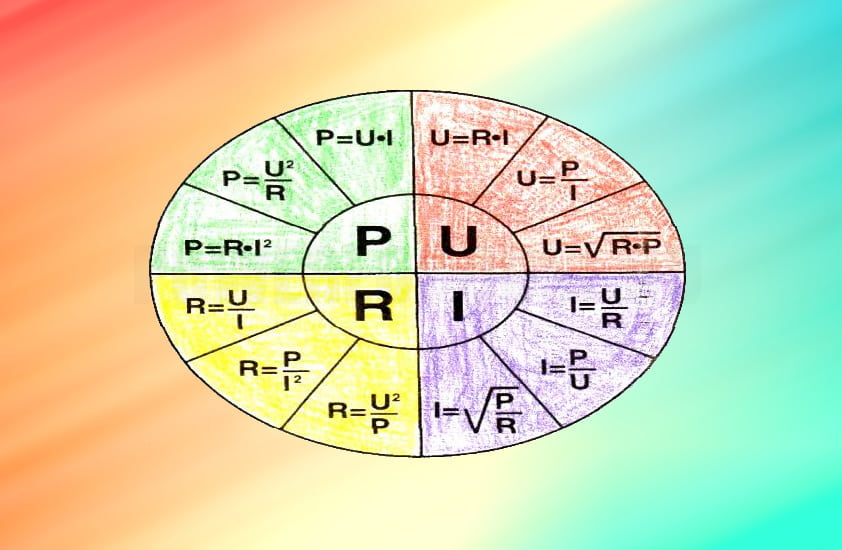
Его закон признан самым главным в физике электроцепей, ведь без него невозможно рассчитать в них ни силу тока, ни степень падения напряжения, ни уровень сопротивления. Открытый немецким ученым Омом закон определяет соотношение в электрической цепи ее составляющих. Формулировка представлена ниже на картинке.
То есть, в электроцепи при высоком показателе напряжения показатели тока будут также высокие. С другой стороны, при высоком показателе сопротивления в ней меньше сила тока. Если сравнивать с потоком жидкости в трубе, то закон будет выглядеть так: при высоком давлении (в случае с током — напряжении) и малом сопротивлении стенок напор будет сильным, и наоборот.
Математически закон выглядит так: сопротивление (R) в цепи или на ее участке = 1 Ом, если по ней проходит ток с силой 1 Ампер при напряжении равном 1 Вольту. Величина тока (в А) определится, если напряжение (В) поделить на сопротивление (Ом).
Формула также может быть представлена в виде треугольника: если закрыть параметр, который требуется определить, оставшиеся два станут решением для его вычисления.
Использовать треугольник в качестве решения задач можно только в том случае, если параметры даются в вольтах (U), в омах (R) и в амперах (I).
Ниже приведен пример, как действует этот закон электротехники. В нем источником напряжения является аккумулятор. Через него пропущено два провода, которые подсоединены к резистору с разных сторон. Формула на рисунке отображает, как рассчитать R (сопротивление в омах), разделив U (напряжение в вольтах) на I (ток в амперах).
Под основной формулой в круге изображены ее варианты. Чтобы работать с ними, нужно закрыть любой параметр, проводя вычисления с оставшимися. Сделать это легко: если составляющие формулы расположены рядом, например, R и I, то их показатели нужно умножить, а если друг под другом, то производится деление.
Например, нужно найти величину R, используя показатели амперметра (I=2.6 А) и вольтметра (U=12 В). Сопротивление будет равно: R = 12:2.6 = 4.6 Ом.
Это основные формулы электротехники, благодаря им находим не только сопротивление в электрической цепи, но и напряжение, и силу тока (однофазного переменного с емкостным или индуктивным сопротивлением). Для начинающего электрика азами профессии является именно закон Ома.
Вычисление полного сопротивления цепи (Z)
Чтобы узнать показатель Z, нужно воспользоваться представленной ниже формулой:
Активное сопротивление — это какой-либо вид энергии, полученный путем перехода в нее электрической энергии в цепи или ее части. Например, она может превратиться в механическую, которая используется в электродвигателях, химическую или тепловую (электролиз и диэлектрики соответственно). Обозначается буквой R.
Емкостное сопротивление — это параметр, который обозначает уровень сопротивления электрической емкости цепи или ее части переменному току. То есть показатели тока или напряжения меняются из-за коэффициента самоиндукции или емкостного элемента. Обозначается Xc.
Индуктивное сопротивление — это степень сопротивления проводника, входящего в электрическую цепь переменного тока. То есть, индуктивность (обозначается L) в электроцепи создает состояние, когда электроток запаздывает по сравнению с электронапряжением. Обозначается XL.
Чтобы вычислить общее (полное) сопротивление Z в электрической цепи, необходимо знать параметры всех видов сопротивления. Все величины используются в ТОЭ для упрощения решения задач и проведения расчетов согласно формулам.
Определение полной мощности (S) в электротехнике
Мощность — важный показатель в электротехнике. Чтобы определить полную S, нужно использовать приведенную ниже формулу:
В данной формуле представлены:
- Активная мощность, то есть потребляемая, является частью полной. Обозначается P и выражается в Вт.
- Реактивная мощность — величина, которая обозначает колебания энергии в работающих электрических устройствах. Обозначается буквой Q, измеряется в ВАр (вольт/ампер реактивный).
- Полная мощность. Обозначается S и измеряется в ВА (вольт/ампер).
Чтобы определить уровень активной и реактивной мощностей, нужно воспользоваться приведенными ниже формулами:
В которых:
- U — напряжение;
- I — сила тока;
- cosΦ — коэффициент мощности.
Ниже представлены формулы для вычисления активной мощности для различных электрических цепей:
Чтобы определить S, нужно произвести расчеты активной и реактивной мощностей, после чего воспользоваться формулой:
Закон Джоуля-Ленца
Он применяется для определения теплового действия тока: Q = I2Rt. Благодаря этой формуле можно вычислить Q (теплоту в джоулях) при прохождении постоянного тока через проводник. При этом Q будет пропорционально силе тока в квадрате (I2 в амперах), сопротивлению проводника (R в омах) и времени прохождения тока (t в секундах).
Без определения уровня теплоты, выделяемого электротоком при прохождении через проводник, невозможно создание электрических нагревательных приборов и печей.
Первый закон Кирхгофа
Законы Кирхгофа универсальны для всех электротехнических задач, так как связаны с соотношением токов и напряжений в разветвленных цепях. Они подходят как для постоянных и переменных электротоков и электронапряжений, так и для линейных и нелинейных электрических цепей.
Первый закон представлен ниже:
Краткий вариант этого закона гласит: если по электроцепи проходит только постоянный электроток, то в ней нет ни единой точки, в которой бы мог накапливаться электрозаряд, в противном случае он не был бы постоянным. То есть, первый закон Кирхгофа дает определение непрерывности потока электрического тока. При этом входящие в узлы и исходящие из них электротоки имеют разные заряды: одни — положительные, а другие — отрицательные. В виде формулы этот закон выглядит так:
Ниже приведен пример использования первого закона:
Второй закон Кирхгофа
Это правило относится к замкнутым контурам. Закон гласит:
То есть суммы параметров электротоков и внешних/внутренних сопротивлений на всех участках контура будут равны сумме параметров сторонних электродвижущих сил (ЭДС), входящих в этот контур. Формула выглядит так:
При этом:
- Im и Rm — параметры падения напряжения;
- N — количество участков контура.
Ниже приведен пример применения законов:
Таково общее представление об основных законах электротехники.
Видео по теме
Закон Ома — калькулятор, формулы, методика расчета
Закон Ома — эмпирический физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.
В данном обзоре приведены программы и калькуляторы закона Ома. Также дополнительно приведены основные формулы и методики расчетов.
Закон Ома — калькулятор онлайн
Онлайн калькулятор закона Ома позволяет быстро просчитать основные переменные для участка цепи. Для этого вам необходимо ввести любые два известных значения и нажать «рассчитать».
| U Напряжение (В): | |
| P Мощность (Вт): | |
| R Сопротивление (Ом): | |
| I Сила тока (А): | |
Закон Ома для постоянного тока — расчет, формулы
Закон Ома для постоянного тока определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи.
Закон Ома для полной цепи:
I = ε / (R + r), где:
- ε — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Из закона Ома для полной цепи вытекают следующие следствия:
- При r < R сила тока в цепи обратно пропорциональна ее сопротивлению, а сам источник в ряде случаев может быть назван источником напряжения.
- При r > R сила тока не зависит от свойств внешней цепи (величины нагрузки), и источник может быть назван источником тока.
Часто выражение I = U / R тоже называют законом Ома. При этом формулировка следующая — сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, где:
- I — сила тока, измеряемая в Амперах (A).
- U — напряжение, измеряемое в Вольтах (V).
- R — сопротивление, измеряемое в Омах (Ом, Ω).
Помимо закона Ома, важнейшим является понятие электрической мощности. Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U):
P = I × U, где:
- P — электрическая мощность, измеряемая в Ваттах (W).
- I — сила тока, измеряемая в Амперах (A).
- U — напряжение, измеряемое в Вольтах (V).
Комбинируя две формулы можно получить зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
Множительные приставки в системе СИ примирительные к закону Ома:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А; 1 миллиампер (1 mA) = 0,001 A; 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V; 1 милливольт (1 mV) = 0,001 V; 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Ом): 1 мегаом (1 MОм) = 1000000 Ом; 1 килоом (1 kОм) = 1000 Ом.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W; 1 киловатт (1 kW) = 1000 W; 1 милливатт (1 mW) = 0,001 W.
Закон Ома для цепи переменного тока
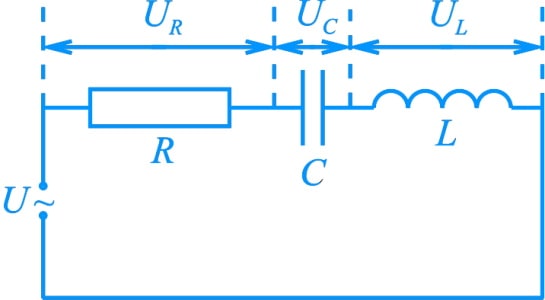
В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.
Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).
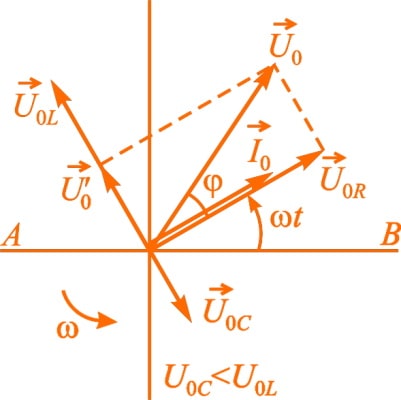
Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.
Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.
Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.
В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U’0 = [U¯0R + U¯0C]. Пусть ωL > 1 / ωC, тогда: U’0 = I0 × (ωL — 1 / ωC).
Теперь сложим векторы U¯0R и U’¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L — U0C)² = I0² × R² + I0² × (ωL — 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):
I0 = U0 / √(R² + (ωL — 1 / ωC)²) = U0 / Z, где:
- Z — полное сопротивление (импеданс) цепи.
- R — его активное сопротивление.
- ωL — 1 / ωC — реактивное сопротивление цепи переменного тока.
- ω = 2 × π × γ — циклическая, угловая частота. γ — частота переменного тока.
Импеданс при параллельном подключении Z = 1 / √(1 / R² + 1 / (1 / ωL — ωC)²).
Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL — 1 / ωC) / R.
Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.
Тогда:
- UR = I0 × R × sin × (ωt + φ).
- UL = I0 × ωL × sin × (ωt + φ + π / 2).
- UC = (I0 / ωС) × sin × (ωt + φ — π / 2).
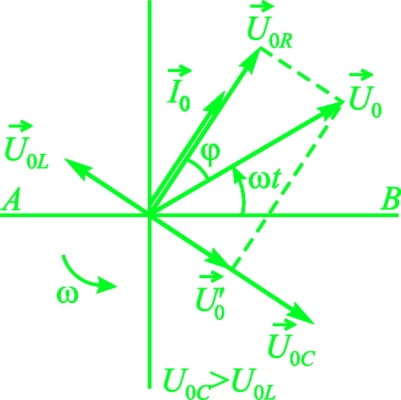
Если 1 / ωС > ωL, то:
- U’0 = I0 × (1 / ωС — ωL).
- tgφ = (1 / ωC — ωL) / R, причем ток опережает напряжение по фазе на угол φ.
Таблица удельных сопротивлений проводников
Электрическое сопротивление (ρ) 1 метра провода, сечением 1 мм², при температуре 20 С°:
| Материал проводника | Удельное сопротивление ρ, Ом |
| Серебро | 0.015 |
| Медь | 0.0175 |
| Золото | 0.023 |
| Латунь | 0,025. 0,108 |
| Хром | 0,027 |
| Алюминий | 0.028 |
| Натрий | 0.047 |
| Иридий | 0.0474 |
| Вольфрам | 0.05 |
| Цинк | 0.054 |
| Молибден | 0.059 |
| Никель | 0.087 |
| Бронза | 0,095. 0,1 |
| Железо | 0.1 |
| Сталь | 0,103. 0,137 |
| Олово | 0.12 |
| Свинец | 0.22 |
| Никелин (сплав меди, никеля и цинка) | 0.42 |
| Манганин (сплав меди, никеля и марганца) | 0,43. 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,44-0,52 |
| Копель (медно-никелевый сплав с 43% никеля и 0,5% марганца) | 0.5 |
| Титан | 0.6 |
| Ртуть | 0.94 |
| Хромель (хром 8,7 — 10 %; никель 89 — 91 %; кремний, медь, марганец, кобальт — примеси) | 1.01 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05. 1,4 |
| Фехраль | 1,15. 1,35 |
| Висмут | 1.2 |
| Хромаль (Сплав 4,5 — 6% алюминия, 17 — 30% хрома, железа) | 1,3. 1,5 |
Сопротивление проводника определяется по формуле r = (ρ × l) / S, где:
- r — сопротивление проводника, Ом.
- ρ — удельное сопротивление проводника, Ом.
- l — длина проводника, м.
- S — сечение проводника, мм².
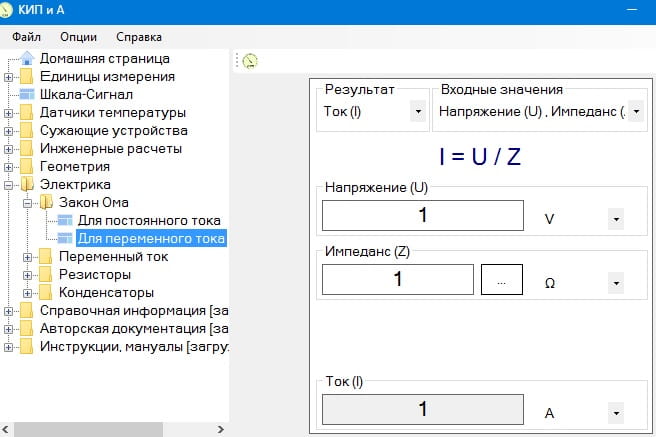
Закон Ома — скачать программу
Расчеты с использованием закона Ома также можно проводить в офлайн режиме. Для этого необходимо воспользоваться бесплатной программой «КИП и А». В пункте Электрика находится калькулятор, производящий расчеты по закону Ома для цепей постоянного и переменного тока:
Электри́ческая цепь (гальвани́ческая цепь) — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.
Закон Ома в комплексной форме
Известно , что напряжение {U} на сопротивлении{Z} связано с током {I}, протекающим через это сопротивление, согласно закону Ома:
{U} = {Z} {I}.
Кроме того, известны соотношения, определяющие активное сопротивление резистора, индуктивное сопротивление катушки и ёмкостное сопротивление конденсатора:
{Z}_{R} = R,
{Z}_{L} = jX_{L},
{Z}_{L} = -jX_{C},
где X_{L} = omega L, X_{C} = frac{1}{omega C}, R – сопротивление резистора, L – индуктивность катушки, C – ёмкость конденсатора, omega = 2 pi f – циклическая частота, f – частота сети, j – мнимая единица.
Пример схемы и расчёт:
Исходные данные и схема:
- E1:
- Номер элемента: 1
- Амплитудное значение: 100 В
- Начальная фаза: 0
- R1:
- Номер элемента: 1
- Сопротивление, Ом: 1
Электрический импеданс
Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.
Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.
Последовательное соединение
При последовательном соединении, согласно Закону Ома для переменного тока,
во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.
Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL – UC .
Пропорционально напряжению, получим общее реактивное сопротивление X = XL – XC .
Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.
U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах,
определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.
XL = ωL = 2πfL – реактивное сопротивление индуктивности.
XC = 1/(ωC) = 1/(2πfC) – реактивное сопротивление ёмкости.
Угол сдвига фаз φ и его дополнение до 90° δ
определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:
Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
где действительной его частью является активное сопротивление, а мнимой – реактивное.
Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
Z = R + jX
Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом – угол φ.
В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
Z = |Z|ejargZ = Zejφ
Отсюда активная составляющая импеданса R = Zcosφ
Реактивная составляющая X = Zsinφ.
Параллельное соединение
Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений
будем исходить из суммы обратных им величин – проводимостей y = 1/Z, G = 1/R, b = 1/X.
y = 1/Z = √(G2 + b2)
Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:
Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
Y = G – jb
Либо в показательной форме:
Y = |Y|e -jφ = ye -jφ
Здесь:
Y – комплексная проводимость.
G – активная проводимость.
b – реактивная проводимость.
y – общая проводимость цепи, равная модулю комплексной проводимости.
e – константа, основание натурального логарифма.
j – мнимая единица.
φ – угол сдвига фаз.
Онлайн-калькулятор расчёта импеданса и угла сдвига фаз
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
|
Последовательное соединение |
Параллельное соединение |
Похожие страницы с расчётами:
Реактивное сопротивление. Расчёт.
Частота резонанса колебательного контура LC. Расчёт.
Реактивная мощность и компенсация. Расчёт.