Как найти задачи на вероятность огэ

Задания на вероятность в ОГЭ

Опубликовано 28.05.2021

Чтобы понять – что такое вероятность и записать основные формулы, которые нам понадобятся, советуем прочить статью про вероятность. Мы же с вами рассмотрим решение некоторых задач. В ОГЭ по математике они идут под номером 10 в каждом варианте.

Задача 1

На экзамене 40 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.

Источник: тексты задач взяты из сборника заданий по математике ОГЭ 2021 под ред Ященко.

Решение.

Используем формулу нахождения вероятностей:

,

где – число случаев, вероятность выпадения которых надо определить;

– общее число случаев.

В нашей задаче – это число выученных билетов, вероятность попадания которых на экзамене и нужно было определить.

.

Тогда .

Ответ: 0,7

Задача 2

В среднем из 150 садовых насосов, поступивших в продажу, 6 подтекает. Найдите вероятность того, что случайно выбранный для контроля насос подтекает.

Решение. Используем ту же формулу, что и в задаче 1. В нашей задаче , .

Тогда .

Ответ: 0,04.

Задача 3

Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 71 спортсмен, среди которых 22 спортсмена из России, в том числе Т. Найдите вероятность того, что в первом туре Т. будет играть с каким-либо спортсменом из России.

Решение:

Для нашего спортсмена благоприятных исходов будет 21: 22-1=21, так как спортсмен Т. не может играть сам с собою. А вот с любым другим участником из России он сыграть может. Тогда число всех событий 71-1=70, потому что спортсменов без Т. всего 70.

Подставляем полученные значения в формулу нахождения вероятности и получаем:

.

Ответ: 0,3.

Решим аналогичную задачу.

Задача 4

Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 51 спортсмен, среди которых 14 спортсменов из России, в том числе Д. Найдите вероятность того, что в первом туре Д. будет играть с каким-либо спортсменом не из России.

Решение:

Формула для определения вероятностей та же. Определим числитель и знаменатель в ней. Так как Д. – из России должен играть со спортсменом не из России – то спортсменов не из России 51-14=37. Всего спортсменов, с которыми может играть Д. 50, так как Д. не может играть с собой: 51-1=50.

Тогда получим:

Ответ: 0,74.

Задача 5

На экзамене 60 билетов, Николай не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.

Решение:

Выученных билетов 60-9=51. Находим вероятность того, что Николаю попадется выученный билет.

Ответ: 0,85.

Таким образом, основная сложность в таких задачах – это определение числа благоприятных исходов. В дальнейшем мы просто делим число благоприятных исходов на число всех исходов и находим десятичную дробь, которая и будет являться вероятностью благоприятного события.

( 4 оценки, среднее 5 из 5 )

Задача №10. Первый пример решения

Чтобы определить вероятность события, необходимо подсчитать число благоприятных событий для заданного события, определить общее число исходов и поделить первое число на второе. Вероятность лежит в пределах от нуля до единицы. Чтобы выразить вероятность события в процентах, необходимо умножить ее на 100%. Иногда требуется определить вероятность противоположного события, она равна: единица минус вероятность события.

Рассмотрим характерные задачи.

Решение:

1. Подсчитаем число благоприятных исходов. У нас 6 неисправных фонариков, тогда исправных фонариков будет 80 – 6 = 74 штуки.

2. Подсчитаем общее число исходов. Это общее число фонариков, т.е. 80.

3. Вероятность того, что выбранный наудачу в магазине фонарик окажется исправен равна 74/80=37/40=0,925.

Ответ: 0,925.

---

Задача №10. Второй пример решения

Решение:

1. Общее число исходов (сколько всего ручек) равно 132.

2. Подсчитаем число благоприятных исходов, это количество зеленых или черных ручек. Зеленых ручек 39. Количество черных найдем из уравнения 132 – 34- 39 – 5 – 2*х =0, 54 = 2*х, х=27. Таким образом, число благоприятных исходов 39 +27=66.

3. Вероятность того, что случайно выбранная в этом магазине ручка будет зеленой или черной равна 66 / 132 = 1 /2 = 0,5.

Ответ: 0,5.

---

Задача №10. Третий пример решения

Решение:

1. Подсчитаем количество девочек. Их двое: Оля и Рита. Таким образом, число благоприятных исходов 2.

2. Подсчитаем общее количество исходов. Это общее число ребят, их пятеро.

3. Вероятность того, что начинать игру должна будет девочка, равна: 2/5=0,4.

Ответ: 0,4.

---

Задача №10. Четвертый пример решения

Решение:

В данной задаче рассматриваются противоположные события. А – событие, которое состоит в том, что ручка не пишет (вероятность равна 0,02); В – событие, которое состоит в том, что ручка пишет. Тогда вероятность события В равна 1-0,02=0,98.

Ответ: 0,98.

---

Задача №10. Пятый пример решения

Решение:

1. Подсчитаем число благоприятных исходов. У нас имеется две девочки: пусть это будут Оля и Лена. Они могут сесть рядом в порядке “Оля-Лена” или “Лена-Оля”. Таким образом, у нас число благоприятных исходов 2.

2. Общее число исходов определим следующим образом. Пусть первой садится девочка (кстати, вероятность этого события 2/11). Тогда остается 10 свободных стульев для дальнейшего рассаживания.

3. Вероятность того, что две девочки окажутся на соседних местах, равна 2/10=0,2.

Ответ: 0,2.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Джамиля Агишева

Задание 10 ОГЭ по математике – это задача по теории вероятностей.

Теория вероятностей рассматривает случайные действия, явления, процессы, исход которых заранее неизвестен. Например, высаживая семена огурцов, мы проводим эксперимент. В результате из десяти семечек может взойти от 0 до 10 ростков, т.е. случайное количество.

Событие – результат некоторого действия. Случайное событие – событие, которое может произойти или не произойти в данном эксперименте. Например, проигрыш или выигрыш нашей любимой футбольной команды заранее предсказать невозможно – это стечение обстоятельств, а сам исход игры мы узнаем по её окончании.

События принято обозначать заглавными латинскими буквами: A, B, C  и т.д.

Пример: A – взошло ровно 9 ростков из десяти посаженных семян огурцов. Оно может произойти или не произойти.

Вероятность события P(A) – это отношение числа  исходов, благоприятствующих событию , к числу всех исходов , возможных в данном эксперименте. Итак,

Имейте в виду, что числитель такой дроби не может быть больше знаменателя, а значит, вероятность всегда меньше либо равна 1.

Приступим к решению задач.

Пример 1. Бабушка испекла одинаковые на вид пирожки: 7 с мясом, 8 с капустой и 5 с яблоками. Внучка Даша наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с мясом.

Выбор пирожка – несомненно, испытание для Даши. А вдруг попадётся нелюбимый, с капустой?

Решение. Событие A – достался пирожок с мясом. Найдём m и n.

m – число исходов, благоприятствующих событию A.

n – число всех исходов, возможных в данном эксперименте.

Давайте перефразируем на языке пирожков: m – количество пирожков с мясом, т.е. m=7, n  – количество всех испечённых пирожков, т.е.

Осталось найти вероятность. Вспомним формулу и вычислим. Итак,

Замечание: не забудьте ответ представить в виде десятичной дроби!

Ответ: 0,35.

Давайте рассмотрим задачу посложнее.

Пример 2. В коробке хранятся жетоны с номерами от 5 до 54 включительно. Какова вероятность того, что на извлечённом наугад из коробки жетоне написано двузначное число?

Решение. Событие A – извлечённый наугад жетон содержит двузначное число. Найдём m и n.

m – число жетонов с двузначным номером,  n – число всех жетонов.

Сначала определимся с n. Типичная ошибка считать так: . На самом деле когда-то были жетоны от 1 до 54. Но номера 1, 2, 3 и 4 со временем потерялись, т.е. пропало четыре штуки. Тогда,  .

Сколько жетонов с двузначными номерами? Всего 50, номера 5, 6, 7, 8, 9 (их пять штук) – однозначные. Тогда, .

Итак,

Ответ: 0,9.

Пример 3. В лыжных гонках участвуют 10 спортсменов из России, 8 спортсменов из Швеции и 7 спортсменов из Норвегии. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что спортсмен из Швеции будет стартовать последним.

Решение. Событие A – спортсмен из Швеции будет стартовать последним.

– число спортсменов из Швеции,  – число всех спортсменов.

Т.к. старт определяется жребием, то не важно, под каким стартовым номером будет выступать тот или иной лыжник, под вторым или последним.

Итак,

Ответ: 0,32.

Пример 4. Оля наугад выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.

Решение. Событие A – выбранное число делится на 51. Найдём m и n.

m – количество трёхзначных чисел, кратных 51, n – число всех трёхзначных чисел.

Последнее трёхзначное число 999. Найдём все числа, кратные 51 среди чисел от 1 до 999 (их даже можно попробовать пересчитать непосредственно: 51, 102, 153, …, 969). Разделим 999 на 51. Получим  , т.е. ровно 19 чисел, кратных 51. Но среди этого количества окажется двузначное число 51, которое не учитывается в задаче, значит, .

Теперь определим n. Чисел от 1 до 999 ровно 999, исключим из них однозначные и двузначные числа от 1 до 99. Таким образом,  .

Итак,

Ответ: 0,02.

Пример 5. Фабрика выпускает сумки. В среднем на 200 качественных сумок приходится двадцать сумок с дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Обратите внимание на условие задачи. Здесь не говорится, что из 200 сумок двадцать – с дефектами. В тексте чётко обозначено, что качественных – 200 штук, а некачественных – 20 штук.

Решение. Событие A – купленная сумка окажется качественной. Найдём m и n.

Всё просто, , .

Итак,

Что-то пошло не так? Полученный результат невозможно будет записать в бланк ответов, т.к. ответом может быть либо целое число, либо конечная десятичная дробь. Ещё раз внимательно перечитываем задачу, а точнее, вопрос задачи. Там сказано: результат округлите до сотых. Помним, калькулятор использовать нельзя. Честно делим в столбик. Т.к. округлить нужно до сотых, то мы найдём три цифры после запятой и только потом запишем результат.

Ответ: 0,91.

Больше задач по теории вероятностей: https://ege-study.ru/teoriya-veroyatnostej/ и  https://ege-study.ru/teoriya-veroyatnostej-na-ege-po-matematike/

Задачи на вероятность

Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Но как решать задачи на вероятность. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.

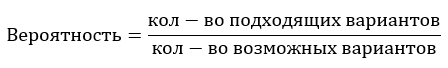
Вероятность может быть выражена как в процентах, так и в обычных числах. Принято считать, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда вероятность подходящих событий + вероятность неподходящих событий = 1. В задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.

Вероятность нескольких событий

Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки: 1. Если нужно первое И второе событие, то умножаем. 2. Если нужно первое ИЛИ второе событие, то складываем.

Теория вероятностей

Классическое определение вероятности
Вероятностью события A называется отношение числа благоприятных для A исходов к числу всех равновозможных исходов: Р (А) =   
где n — общее число равновозможных исходов, m — число исходов, благоприятствующих событию A.
Противоположные события
Событие, противоположное событию A, обозначают Ā. При проведении испытания всегда происходит ровно одно из двух противоположных событий и  
   Объединение несовместных событий
Два события A и B называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событий  A и B:               P(A U B) =P(A) + P(B)                          

Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Событие C называют пересечением событий A и B                     (пишут C = A∩B), если событие C означает, что произошли оба события A и B.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей  событий A и B:
 P(A∩B) = P(A) • P(B)

Формула сложения вероятностей совместных событий:

                           P(A U B) =P(A) + P(B)  – P(A∩B)

Задачи и решения задач на вероятность

Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5. Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12. Вероятность тогда:  Ответ: 0,8.

Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек? Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников. Вероятность что первый дежурный мальчик: Вероятность что второй дежурный мальчик:

Раз оба должны быть мальчики, вероятности перемножим: Ответ: 0,2.

Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест. Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1. Ответ: 0,1.

Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам. Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6. Ответ: 0,6.

Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам. Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8. Ответ: 0,8.

Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996. Ответ: 0,996.

Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе? Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005). Ответ: 0,005

Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии. Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18). Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36. Ответ: 0,36.

Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275. Ответ: 0,275.

Задача 10.Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов. Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России? Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52. Ответ: 0,52.

Задача 11. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25. Ответ: 0,25.

Задача 12.  В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин? Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4. Ответ: 0,4.

Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта. Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2. Ответ: 0,2.

Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три? Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3. Ответ: 0,3.

Задача 15. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру. Решение:  Нас устроит следующий вариант: «Стартер» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125. Ответ: 0,125.

Задача 16. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4. Решение:  Задачу выполняют несколько вариантов:

игра №1	игра №2	Вероятность данного варианта
3	1	0,4 · 0,2 = 0,08
1	3	0,2 · 0,4 = 0,08
3	3	0,4 · 0,4 = 0,16

Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32. Ответ: 0,32.

Задача 17. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе. Решение: Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1. Ответ: 0,1.

Задача 18. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане. Решение: Способ №1 Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1. Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.

Способ №2 Задачу выполняют в несколько вариантов: Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):

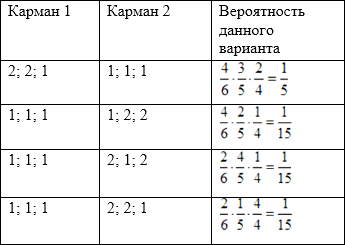
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:  Ответ: 0,4.

Задача 19. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах. Решение: Способ №1 Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6. Способ №2 Задачу выполняют несколько вариантов: Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):

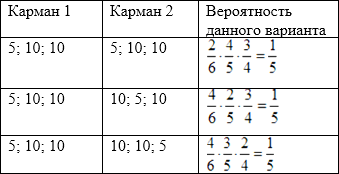
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов:  Ответ: 0,6.

Задача 20. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза. Решение:  Нас устраивают три варианта: Орёл ― решка ― орёл; Орёл ― орёл ― решка; Решка ― орёл ― орёл; Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8) Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375. Ответ: 0,375.

Задача 21. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. Решение: В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17. Ответ: 0,17.

Задача 22. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными. Решение: Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604. Ответ: 0,9604. 0,17.

Задача 23. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых. Решение: Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада): … США, КАН, КИТ … … США, КИТ, КАН … … КИТ, США, КАН … … КАН, США, КИТ … … КАН, КИТ, США … … КИТ, КАН, США … США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна: ≈ 0,33. Ответ: 0,33.

Задача 24. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная батарейка будет забракована. Решение:  Существуют 2 варианта, которые нам подходят: Вариант А: батарейка забракована, она неисправна; Вариант Б: батарейка забракована, она исправна. Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194; Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049; Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684. Ответ: 0,0684.

Задача 25. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. Решение:  Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018. Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02. Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038. Ответ: 0,038.

Задача 26. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных. Решение:  Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).

Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х / 0,92х ≈ 0,978. Ответ: 0,978.

Задача 27. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099. Ответ: 0,0099

Задача 28. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм. Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039. Ответ: 0,039.

Задача 29. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач. Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1. Ответ: 0,1.

Задача 30. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20. Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22. Ответ: 0,22.