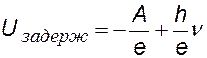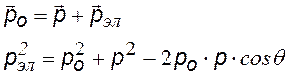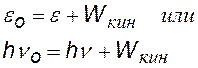Что такое задерживающая разность потенциалов
Содержание
- 1 Фотоэффект
- 2 Задерживающая разность потенциалов — определение и используемые формулы
- 3 Пример задачи
- 4 Заключение
- 5 Видео по теме
Внешние воздействия на проводник вызывают возникновение в нем различных реакций, которые оказывают влияние на его проводимость, а также способствуют появлению совершенного иного вида энергии. Статья расскажет о том, что такое задерживающая разность потенциалов, приведет пример возникновения этого эффекта и используемые формулы для его расчетов.
Фотоэффект
Фотоэффект называется способность металла испускать часть своих электронов под воздействием света. Если проводник или металл находятся в состоянии покоя, то в их структуре происходит свободное перемещение электронов. Причем эти частицы все время пытаются сместиться к поверхности тела и покинуть его пределы. Препятствием для свободного покидания электронами данного тела служат положительно заряженные ионы. Ведь именно этими положительными зарядами и удерживаются электроны. Открыл фотоэффект в 1887 г. немецкий ученый Генрих Р. Герц. Кроме того над изучением фотоэффекта довольно долго работали такие ученые — А.Г. Столетов и Ф. Леонард.
Задерживающая разность потенциалов — определение и используемые формулы
Величину фототока насыщения Iнас определяет количество электронов, которые испускаются катодом под воздействием света за единицу времени.
В таком случае количество фотоэлектронов n, которые покидают катод в течение 1 секунды, получится вычислить с помощью такого выражения:
В данном выражении е является абсолютной величиной заряда электрона.
Фотоэлектроны, которые испускают катод, будут иметь разные начальные скорости. При этом кинетические энергии их будут также различными. Когда U равняется 0, определенная часть фотоэлектронов с достаточной кинетической энергией, чтобы достигнуть анода будут преодолевать поле, создаваемое облаком фотоэлектронов на поверхности катода. За счет этого будет создаваться небольшой по величине фототок. Если напряжение будет уменьшаться от ноля до –U0, фототок плавно уменьшается, а для случая U = –U0 он прекращается. В данном случае напряжение U0 и будет задерживающим напряжением.
Задерживающая разность потенциалов или задерживающее напряжение — это величина отрицательного напряжения U0, при котором фототок будет иметь силу I равную 0. За счет работы сил тормозящего электрополя, происходит уменьшение кинетической энергии фотоэлектронов. Чтобы удержать все электроны, имеющих наибольшую кинетическую энергию, электрическое поле должно будет совершать работу e×U0. В данном случае будет верным следующее выражение:
Экспериментальным путем на данный момент определены 3 закона внешнего фотоэффекта:
- Если спектральный состав света, попадающего на катод неизменный, то в данном случае световой поток будет пропорционален фототоку насыщения Iнас~Ф.
- Величина максимальной кинетической энергии фотоэлектронов для этого вещества будет иметь прямую зависимость от частоты падающего света, а от интенсивности эта энергия зависеть не будет.
- У всех веществ имеется красная граница внешнего фотоэффекта, то есть наименьшая частота света νкр (наибольшая длина волны λкр). Только при таком условии фотоэффект будет еще возможен.
Альбертом Эйнштейном в 1905 г. было доказано, что задерживающая разность потенциалов прямопропорциональна величине частоты падающего на поверхность металла света. Нобелевской премией за объяснение фотоэффекта ученый был награжден в 1921 г.
Он вывел свою формулу для фотоэффекта, которую можно увидеть ниже
Пример задачи
Приведем только для ознакомительных целей решение следующей задачи. Необходимо найти задерживающую разность потенциалов U, если освещаемый металл катода это литий. При этом А=2.3 эВ, а длина световой волны λ равняется 200 нм.
Решение данной задачи можно увидеть на рисунке, который приведен ниже.
Таким образом согласно приведенного выше решения получается, что задерживающая разность потенциалов лития при таких условиях будет составлять 3.92 вольт. При увеличении этого значения, фотоэлектрон сможет покинуть поверхность металла.
Заключение
Фотоэффект и задерживающая разность потенциалов нашли очень широкое применение в различных сферах. Их в наше время используют во многих областях науки и техники. В астрономии, ядерной физике, фототелеграфии и телевидении устройства на основе фотоэффекта (ФЭУ) используются, чтобы измерить малые световые потоки или сделать спектральный анализ какого-то вещества. А в медицине на данном эффекте работают различные электронно-оптические преобразователи (ЭОП), которые используются, например, для усиления яркости рентгеновского изображения. За счет этого снимки становятся более яркими и четкими, а сама доза облучения человека при этом довольно сильно уменьшается.
Видео по теме
Условие задачи:
Найти задерживающий потенциал для фотоэлектронов при действии на калий излучения с длиной волны 0,33 мкм, если красная граница фотоэффекта для него 0,62 мкм.
Задача №11.2.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(lambda = 0,33) мкм, (lambda_{max} = 0,62) мкм, (U_з-?)
Решение задачи:
Согласно уравнению Эйнштейна для фотоэффекта энергия поглощенного кванта (hnu) идет на совершение работы выхода (A_{вых}) и на сообщение кинетической энергии вылетевшему электрону (frac{{{m_e}{upsilon ^2}}}{2}). Поэтому:
[hnu = {A_{вых}} + frac{{{m_e}{upsilon ^2}}}{2};;;;(1)]
В этой формуле (h) – это постоянная Планка, равная 6,62·10-34 Дж·с, (m_e) – масса электрона, равная 9,1·10-31 кг.
Если изменить полярность источника напряжения в установке для исследования фотоэффекта, то электрическое поле между катодом и анодом будет тормозить фотоэлектроны. При задерживающем напряжении (U_з) фототок становится равным нулю. При этом по закону сохранения энергии справедливо равенство:
[frac{{{m_e}{upsilon ^2}}}{2} = e{U_з};;;;(2)]
Принимая во внимание равенство (2), уравнение (1) примет вид:
[hnu = {A_{вых}} + e{U_з};;;;(3)]
Работа выхода (A_{вых}) – это минимальная работа, которую надо совершить, чтобы удалить электрон из металла.
Минимальная частота света ({nu _{min }}), при которой ещё возможен фотоэффект, соответствует максимальной длине волны (lambda_{max}). Эту длину волны (lambda_{max}) называют красной границей фотоэффекта. При этом верно записать:
[h{nu _{min }} = {A_{вых}};;;;(4)]
Частоту колебаний можно выразить через скорость света (c), которая равна 3·108 м/с, и длину волны, имеем:
[left{ begin{gathered}
nu = frac{c}{lambda } hfill \
{nu _{min }} = frac{c}{{{lambda _{max }}}} hfill \
end{gathered} right.]
Подставим соответствующие выражения в формулы (3) и (4), получим следующую систему уравнений:
[left{ begin{gathered}
frac{{hc}}{lambda } = {A_{вых}} + e{U_з} hfill \
frac{{hc}}{{{lambda _{max }}}} = {A_{вых}} hfill \
end{gathered} right.]
Тогда имеем:
[frac{{hc}}{lambda } – frac{{hc}}{{{lambda _{max }}}} = e{U_з}]
Приведем в левой части уравнения под общий знаменатель:
[frac{{hcleft( {{lambda _{max }} – lambda } right)}}{{lambda {lambda _{max }}}} = e{U_з}]
Откуда задерживающий потенциал для фотоэлектронов (U_з) равен:
[{U_з} = frac{{hcleft( {{lambda _{max }} – lambda } right)}}{{elambda {lambda _{max }}}}]
Задача решена в общем виде, теперь посчитаем численный ответ:
[{U_з} = frac{{6,62 cdot {{10}^{ – 34}} cdot 3 cdot {{10}^8} cdot left( {0,62 cdot {{10}^{ – 6}} – 0,33 cdot {{10}^{ – 6}}} right)}}{{1,6 cdot {{10}^{ – 19}} cdot 0,33 cdot {{10}^{ – 6}} cdot 0,62 cdot {{10}^{ – 6}}}} = 1,76;В]
Ответ: 1,76 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
11.2.22 Излучение какой частоты падает на поверхность фотокатода из цезия, если для прекращения
11.2.24 При удвоении частоты падающего на металл света задерживающее напряжение для фотоэлектронов
11.2.25 До какого максимального потенциала зарядится уединенный медный шарик, если его облучать
Ученик
(105),
на голосовании
2 недели назад
Дополнен 1 месяц назад
1.Что такое дифракция и чем она отличается от интерференции.
2.В чем сущность дифракиции Френеля? Фраунгофера?
3.В чем сущность принципа Гюйгенса – Френеля?
4.Как определяется условия максимумов и минимумов при дифракции на одиночной щели.
5.В чем сущность метода зон Френеля?
6.Как применить метод векторного сложения ам
расчета дифракции?
7.Как применить Фурье-преобразование для расчета
отдельной щели?
8. Как применить Фурье-преобразование для расчета
дифракционной решетки?
9.Определите положение максимумов и минимумов при дифракции на решетке.
10.Что характеризует дисперсия и разрешающая способность решетки?
Голосование за лучший ответ
АI
Мыслитель
(5680)
1 месяц назад
Фотоэффект – это явление взаимодействия света или любого другого электромагнитного излучения с веществом, при котором энергия фотонов передается электронам вещества1.
Законы Столетова для фотоэффекта: а) число вылетевших электронов пропорционально интенсивности падающего света; б) скорость вылетевших электронов не зависит от интенсивности падающего света, а определяется только его частотой; в) существует минимальная частота падающего света, ниже которой фотоэффект не наблюдается2.
Уравнение Эйнштейна: E = hν – A, где E – кинетическая энергия вылетевшего электрона, h – постоянная Планка, ν – частота падающего света, A – работа выхода электрона из вещества. Смысл уравнения в том, что энергия фотона расходуется на преодоление работы выхода и на придание кинетической энергии электрону2.
Законы фотоэффекта объясняются на основании квантовых представлений о свете так: свет состоит из дискретных порций энергии – фотонов, каждый из которых может столкнуться с одним электроном и передать ему всю свою энергию. Чем больше интенсивность света, тем больше фотонов падает на единицу площади в единицу времени и тем больше электронов вылетает. Чем больше частота света, тем больше энергия каждого фотона и тем больше скорость вылетевшего электрона. Если частота света меньше минимальной, то энергии фотона не хватает для преодоления работы выхода и фотоэффект не происходит2.
Красная граница фотоэффекта – это минимальная частота падающего света, при которой наблюдается фотоэффект. Она зависит от материала вещества и равна отношению работы выхода к постоянной Планка2.
Задерживающая разность потенциалов – это такая разность потенциалов между анодом и катодом в цепи фотоэлемента, при которой ток в цепи обращается в нуль. Задерживающий потенциал равен максимальной кинетической энергии вылетевших электронов, деленной на заряд электрона2.
6.3.1.
На поверхность лития падает монохроматический
свет (
= 3100 Å). Чтобы прекратить эмиссию
электронов, нужно приложить задерживающую
разность потенциалов не менее 1,7 В.
Определите работу выхода (в эВ).
Ответ:
2,3 эВ.
6.3.2.
На платиновую пластинку падают
ультрафиолетовые лучи. Для прекращения
фотоэффекта нужно приложить задерживающую
разность потенциалов не менее 3,7 В. Если
платиновую пластинку заменить пластинкой
из другого металла, то задерживающую
разность потенциалов придется увеличить
до 6 В. Определите работу выхода электрона
с поверхности этой пластинки (в эВ);
работа выхода электрона для платины
6,3 эВ.
Ответ:
4 эВ.
6.3.3.
Определите
максимальную скорость электронов,
вылетающих из металла под действием
гамма-излучения с длиной волны 3 Å.
Работой выхода пренебречь.
Ответ:
Электрон релятивистский; v
= 0,83 с; v
= 2,49108
м/c.
6.3.4.
Определите
максимальную скорость электронов,
вылетающих из металла при облучении
гамма-квантами с энергией 1,53 МэВ; работой
выхода пренебречь.
Ответ:
2,91108
м/c.
6.3.5.
Максимальная скорость фотоэлектронов,
вылетающих из металла при облучении
гамма-квантами, равна 2, 9108
м/c.
Определите энергию гамма-квантов (в
МэВ). (Работой выхода можно пренебречь).
Ответ:
1,5 МэВ.
6.3.6.
Определите максимальную скорость
электронов (vmax),
вылетающих из цинка под действием
гамма-излучения с длиной волны 0,1 Å. Как
изменится vmax,
если гамма-лучи заменить ультрафиолетовыми
лучами? Работа выхода для цинка равна
4,0 эВ.
Ответ:
1,8108
м/с; vmax
– уменьшится.
6.3.7.
Плоский алюминиевый электрод освещается
ультрафиолетовым светом с длиной волны
83 нм. На какое минимальное расстояние
от поверхности электрода может удалиться
фотоэлектрон, если вне электрода имеется
задерживающее электрическое поле
напряженностью 750 В/м? Красная граница
фотоэффекта для алюминия кр
= 332 нм. Результат представьте в сантиметрах.
Ответ:
1,47 см.
6.3.8.
При освещении
фотокатода светом с длиной волны 1
= 400 нм, а затем с 2
= 500 нм обнаружено, что задерживающее
напряжение, прекращающее фотоэффект,
изменилось в 2 раза. Определите работу
выхода электрона из материала фотокатода.
Результат представьте в электрон-вольтах.
Ответ:
1,86 эВ.
6.3.9.
До какого
максимального потенциала зарядится
удаленный от других тел медный шарик
при облучении его электромагнитным
излучением с длиной волны 140 нм? (Для
меди Авых
= 4,47 эВ).
Ответ:
4,4 В.
6.3.10.
Найдите
постоянную Планка, если фотоэлектроны,
вырываемые с поверхности некоторого
металла электромагнитным излучением
с частотой 1
= 1,21015
Гц, задерживаются потенциалом 3,1 В, а
вырываемые электромагнитным излучением
с длиной волны 2
= 125 нм – потенциалом 8,1 В.
Ответ:
6,610–34
Джс.
6.3.11.
Шар радиусом
1 см, несущий заряд 1,1110–10
Кл, облучается светом с длиной волны
331 нм. Определите, на какое расстояние
удалится электрон, если работа выхода
электрона с поверхности металла, из
которого изготовлен шар, равна 210–19
Дж.
Ответ:
0,255 мм.
6.3.12.
Изолированная
металлическая пластинка облучается
монохроматическим светом с длиной волны
450 нм. До какого потенциала зарядится
пластинка при длительном освещении,
если работа выхода электрона с ее
поверхности равна 2 эВ?
Ответ:
0,76 В.
6.3.13.
На поверхность
лития падает монохроматический свет с
длиной волны 310 нм. Чтобы прекратить
эмиссию электронов, нужно приложить
задерживающую разность потенциалов не
менее 1,7 В. Определите работу выхода для
лития (в эВ).
Ответ:
2,3 эВ.
6.3.14.
Определите
максимальную скорость фотоэлектронов,
вылетающих из металла под действием
гамма-излучения с длиной волны 0,3 нм.
(Работой выхода пренебрегаем).
Ответ:
6.3.15.
Определите максимальную скорость
фотоэлектронов, вылетающих из металла
под действием гамма квантов с энергией
= 1,53 МэВ. (Работой выхода пренебрегаем).
Ответ:
291 Мм/c.
6.3.16.
Максимальная
скорость фотоэлектронов, вылетающих
из металла при облучении его гамма
фотонами, равна 291 Мм/c.
Определите энергию -фотона
(в МэВ). (Работой выхода пренебречь).
Ответ:
1,53 МэВ.
6.3.17.
Поверхностный
скачок потенциала у магния 3,69 В, а у
цезия 1,93 В. Они освещаются лучами с
длиной волны 590 нм. Возникает ли при этом
фотоэффект у каждого из металлов?
Ответ:
Возникает у цезия, а у магния – нет, т.к.
кр(Cs)
= 643 нм, кр(Mg)
= 337 нм.
6.3.18.
Поверхностный скачок потенциала для
алюминия 4,25 В. Определите длину волны
красной границы фотоэффекта у алюминия.
Ответ:
291 нм.
6.3.19.
Кванты света с энергией
= 4,93 эВ вырывают фотоэлектроны из металла
с работой выхода, равной 4,5 эВ. Определите
максимальный импульс, передаваемый
поверхности металла при вылете каждого
электрона.
Ответ:
3,4510–25
гм/с.
6.3.20.
Определите
частоту света, вырывающего с поверхности
металла электроны, полностью задерживаемые
потенциалом 3 В. Фотоэффект у этого
металла начинается при частоте падающего
света 61014
с–1.
Ответ:
13,21014
Гц.
6.3.21.
Определите
величину задерживающего потенциала
для фотоэлектронов, испускаемых при
освещении калия светом, длина волны
которого равна 3300 Å. Работа выхода
электрона для калия равна 2,2 эВ.
Ответ:
1,75 В.
6.3.22.
При фотоэффекте
с платиновой поверхности величина
задерживающего потенциала оказалась
равной 0,8 В. Определите: 1) длину волны
применяемого излучения; 2) максимальную
длину волны, при которой еще возможен
фотоэффект. Работа выхода электронов
для платины 6,3 эВ.
Ответ:
= 204 нм; кр
= 234 нм.
6.3.23.
Определите постоянную Планка, если
известно, что фотоэлектроны, вырываемые
с поверхности некоторого металла светом
с частотой 2,21015с–1,
полностью задерживаются разностью
потенциалов 6,6 В, а вырываемые светом с
частотой 4,61015с–1
– разностью потенциалов 16,5 В.
Ответ:
h
= 6,610–34
Джс.
6.3.24.
Вакуумный фотоэлемент состоит из
вольфрамового катода и анода. Контактная
разность потенциалов между электродами,
численно равная U0
= 0,6 В, ускоряет вылетающие электроны.
Фотоэлемент освещается светом, длина
волны которого
= 2,310–7
м. Какую задерживающую разность
потенциалов надо приложить между
электродами, чтобы фототок упал до нуля?
Ответ:
1,5 В.
6.3.25.
Между
электродами фотоэлемента предыдущей
задачи приложена задерживающая разность
потенциалов 1 В. При каком предельном
значении длины волны падающего на катод
света начинается фотоэффект?
Ответ:
254 нм.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кинетическая энергия, скорость и импульс в формуле Эйнштейна являются максимальными, т. е. электрон имеет их сразу же после отрыва от атома. «Пробираясь к выходу» из вещества за счет взаимодействия с другими частицами, он может потерять энергию, поэтому вылетевшие электроны имеют различные скорости (вплоть до 0).
Uзадерж
задерживающее напряжение (потенциал) [viii]– это обратное напряжение, которое нужно приложить между катодом и анодом фотоэлемента, чтобы прекратился фототок (см. рис. ниже)
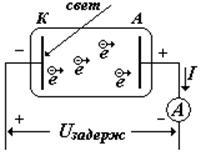
На рисунке показана схема, используемая для изучения фотоэффекта. Внутри стеклянного баллона, из которого откачен воздух, имеются два электрода: катод (К) и анод (А). Такое устройство называется вакуумным фотоэлементом. При освещении катода светом, из него будут вылетать электроны, образуя электронное облако. Часть электронов по инерции достигнут анода. Если катод и анод замкнуть вне баллона и подсоединить микроамперметр, то прибор покажет ток.
Этот очень небольшой ток называется инерционным (Iин).
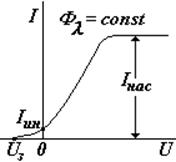
Ф остается постоянным. Максимальный ток называется током насыщения (Iнас). Существование тока насыщения объясняется следующим образом. Один фотон выбивает только один электрон, но не каждый фотон выбивает по электрону. Отношение числа выбитых электронов Nэл к числу падающих фотонов Nфот в единицу времени называется квантовым выходом. Квантовый выход a зависит от природы вещества и частоты фотонов.
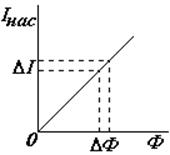
2) Световая характеристика.
Световой характеристикой фотоэлемента называется зависимость фототока насыщения от падающего светового потока ( см. рис.). Квантовый подход приводит к прямой пропорциональности тока насыщения световому потоку
Iнасыщ ~ Ф. Действительно:
|
|
ток насыщения, е – заряд электрона, t— время. |
|
|
|
световой поток |
|
|
|
квантовый выход |
|
|
|
чувствительность фотоэлемента |
Iнасыщ = g Ф |
Отсюда для n = const следует, что сила тока насыщения прямо пропорциональна световому потоку.[ix] Коэффициент пропорциональности g называется чувствительностью фотоэлемента – она показывает, на сколько изменяется сила тока насыщения при изменении светового потока на единицу
3) Задерживающий потенциал.
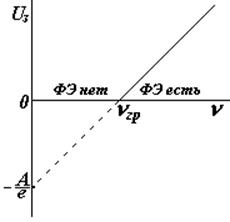
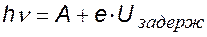
На рисунке показан график зависимости задерживающего потенциала от частоты падающего света. По графику можно найти работу выхода А, красную границу nгр , а по наклону прямой можно определить величину постоянной Планка h.
Фотоэлементы широко используются в физике и технике. Вакуумные фотоэлементы довольно громоздки и дают небольшие токи, но вследствие своей безинерционности и линейной световой характеристики они незаменимы в тех случаях, когда необходимо превратить световые сигналы в электрические без каких-либо искажений. Существование тока насыщения в фотоэлементах позволят использовать их в стабилизаторах (напряжение изменяется, а ток остается постоянным). Фотоэлементы очень часто применяют в турникетах, для подсчета движущихся изделий на конвейерах и т. п.
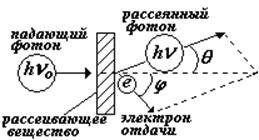
ЭФФЕКТ КОМПТОНА
Эффектом Комптона называется рассеяние веществом электромагнитного излучения, при котором частота рассеянного излучения уменьшается по сравнению с первоначальной, и одновременно наблюдается вылет быстрых электронов (электроны отдачи). Изменение частоты оказывается различной в зависимости от угла наблюдения. Американский ученый Комптон, открывший это явление (1923 г) разработал теорию явления. Он предложил рассматривать наблюдаемое взаимодействие света с веществом как упругое столкновение
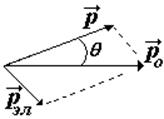
частиц — фотона и электрона. Используя законы сохранения импульса и энергии, Комптон получил формулу для изменения длины волны в зависимости от угла рассеяния..
Мы не будем приводить полный вывод формулы для изменения длины волны, а запишем только законы сохранения и окончательную формулу. Так как эффект Комптона наблюдается только для фотонов с большой энергией (рентгеновские и гамма-лучи), то при вычислениях необходимо использовать формулы СТО, и вывод становится громоздким. [x]
|
|
закон сохранения импульса в векторном и скалярном виде (теорема косинусов).
q — угол рассеяния |
|
|
|
|
|
закон сохранения энергии
(электрон релятивистский). |
Подставив в эти законы выражения для указанных величин, приведенные ниже, после преобразований получим:








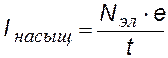
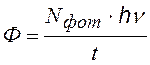
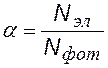
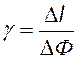 А/Вт
А/Вт