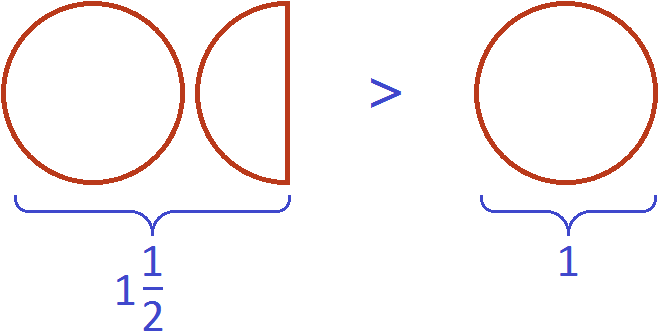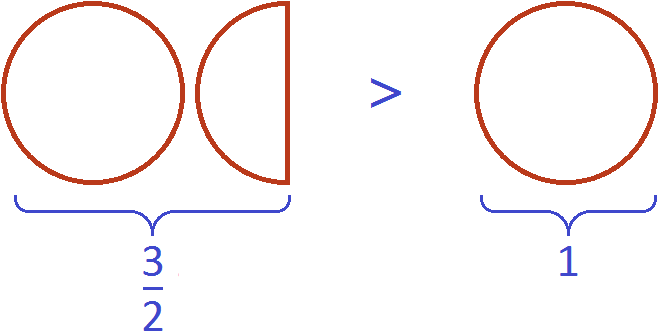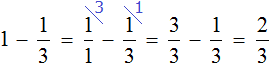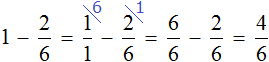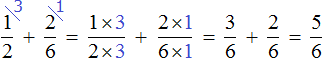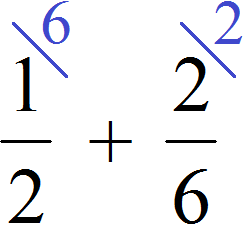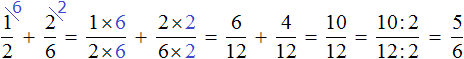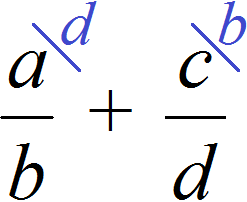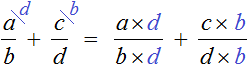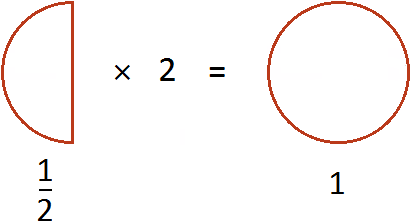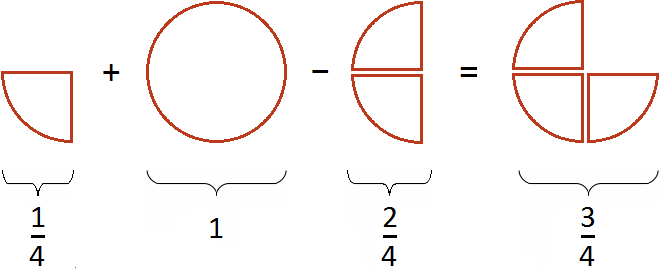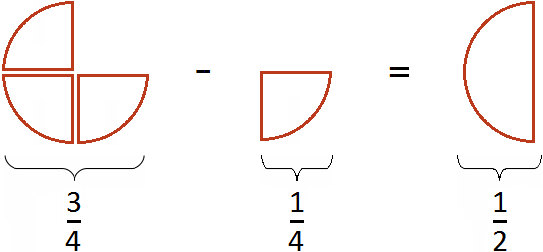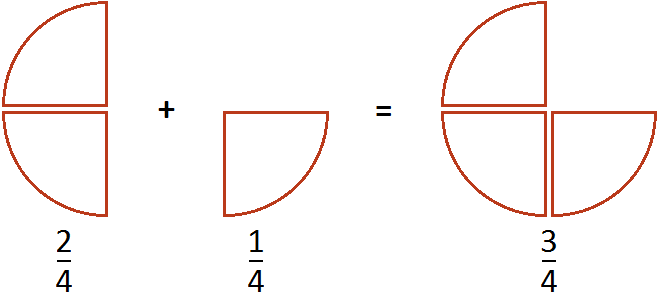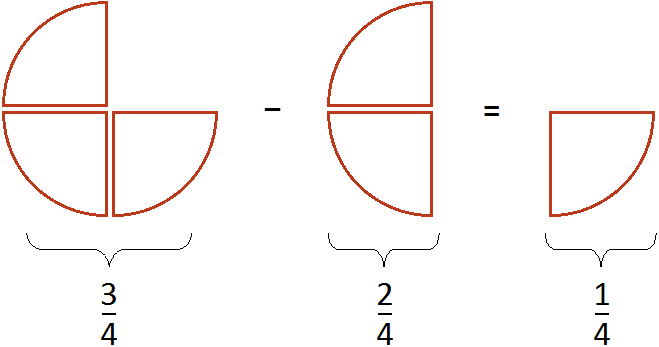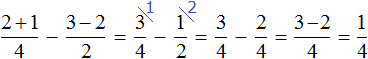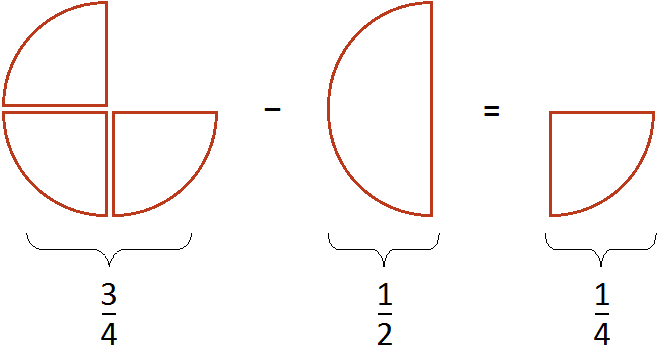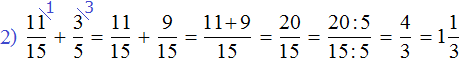|
Нужно привести эти дроби к общему знаменателю. 1/5 = 3/15; 1/3 = 5/15 Между ними лежит число 4/15. Если нужно больше чисел в промежутке, то увеличиваем знаменатель. 1/5 = 3/15 = 6/30; 1/3 = 5/15 = 10/30 Между ними будут числа 7/30, 8/30 = 4/15 и 9/30 = 3/10 автор вопроса выбрал этот ответ лучшим
Андрей А-ч 5 лет назад Для того чтобы найти другие дроби между двумя какими то известными дробями математически, можно например сотавить уравнение в котором неизвестной будет общий знаменатель при известной разнице в числителях. Знаете ответ? |
ОБЪЯСНИТЕ ПОЖАЛУЙСТА!!! У МЕНЯ ЗАДАНИЕ ПО МАТЕМАТИКЕ НАЙТИ ЗАКЛЮЧЁННОЕ ЧИСЛО
ян безумов
Ученик
(231),
закрыт
2 года назад
У МЕНЯ ЗАДАНИЕ ПО МАТЕМАТИКЕ НАЙТИ ЗАКЛЮЧЁННОЕ ЧИСЛО МЕЖДУ ЧИСЛАМИ ( В ДАННОМ СЛУЧАИ ДРОБИ) 1/7 И 1/8. ПОМОГИТЕ ПЖ
Михаил
Оракул
(53584)
2 года назад
а если я скажу, что между ними заключено бесконечное количество чисел (в данном случае, дробных), ты поверишь?
LukОракул (96144)
2 года назад
1/87654321 неверно
Михаил
Оракул
(53584)
Luk, угу, “мисклик” сделал (
1/78654321 разумеется
Какая десятичная дробь между 1 и 2? – Обзоры Вики
1.5 находится точно между 1 и 2, но есть много других чисел, таких как 1.157, 1.781, 1.3312.
Итак, какая дробь находится между 1 и 2? Между любыми двумя целыми числами стоит дробь. Между 0 и 1 12, между 1 и 2 112=3/2, и так далее. На самом деле между любыми двумя целыми числами бесконечно много дробей.
Сколько действительных чисел находится между 1 и 2? Первоначальный ответ: Сколько действительных чисел находится между 1 и 2? Есть бесконечные действительные числа между 1 и 2. Между 1 и 1.1 лежат бесконечные действительные числа.
Дополнительно Что такое 1 как число? 1 (число)
| ← 0 1 2 → | |
|---|---|
| Кардинальный | one |
| порядковый | 1-й (первый) |
| Система счисления | унарный |
| факторизация | 1 |
Как найти середину между двумя числами? Середина между двумя числами — это число, находящееся ровно посередине двух чисел. Вычисление средней точки — это то же самое, что вычисление среднего значения двух чисел. Следовательно, вы можете вычислить среднюю точку между любыми двумя числами. сложив их вместе и разделив на два.
Какая дробь стоит перед 1 2?
Таблица преобразования десятичных и дробных чисел
| Доля | Эквивалентные дроби | |
|---|---|---|
| 1/2 | 2/4 | 4/8 |
| 1/3 | 2/6 | 4/12 |
| 2/3 | 4/6 | 8/12 |
| 1/4 | 2/8 | 4/16 |
Что находится между 1 2 и 3/4 на числовой прямой? Итак, средняя дробь между 1/2 и 3/4 равна 5/8.
Что находится между половиной и 3 4? Числитель и знаменатель требуемого числа должны быть между заданным числом, т. е. числитель может быть равен 3, а знаменатель может быть равен 5. Следовательно, рациональное число между 1/2 и 3/4 равно 3/5.
Какое из следующих рациональных чисел находится между 1 и 2?
Следовательно, четыре рациональных числа между 1 и 2 — это 9/8, 5 / 4, 3 / 2 и 7 / 4.
Также Какие два рациональных числа между 1 и 2? Следовательно, 4 / 3 и 5 / 3 два рациональных числа между 1 и 2.
Сколько иррациональных чисел находится между 1 и 2?
Это может быть любое число между двумя с любым количеством цифр. Следовательно, у нас есть бесконечное количество иррациональных чисел между двумя числами.
Что такое два как число? 2 (два) — число, цифра и цифра. Это натуральное число после 1 и до 3 . Это наименьшее и единственное четное простое число.
…
| ← 1 2 3 → | |
|---|---|
| -1 0 1 2 3 4 5 6 7 8 9 → Список чисел — Целые числа ← 0 10 20 30 40 50 60 70 80 90 → | |
| Кардинальный | два |
| порядковый | 2-й (второй/второй) |
| Система счисления | двоичный |
Какой тип числа 1 2?
Рациональное число (В).
Это все дроби, в которых верхние и нижние числа являются целыми числами; например, 1/2, 3/4, 7/2, ⁻4/3, 4/1 [Примечание: знаменатель не может быть равен 0, но числитель может быть]. Вещественные числа (R) (также называемые измерительными числами или числами измерений).
Кто изобрел ноль в мире?
Первый современный эквивалент цифры ноль происходит от индуистский астроном и математик Брахмагупта в 628 году. Его символом для изображения числа была точка под числом.
Как найти половину расстояния между двумя точками? Определите половину расстояния
- Разделите полное расстояние на два.
- Измерьте это расстояние от одной из двух исходных точек и отметьте на карте.
- Проверьте свою работу, проделав то же самое с другой отправной точки.
Как найти режим? Мода набора данных — это число, которое чаще всего встречается в наборе. Чтобы легко найти режим, расположите числа по порядку от наименьшего к наибольшему и посчитайте, сколько раз встречается каждое число.
Число, которое встречается чаще всего, — это режим!
Как найти середину между двумя дробями?
Что такое 1/2 в целом числе? Следовательно, 1/2 как целое число будет 0 или 1.
1 2 — натуральное число?
Множеством натуральных чисел в математике называется множество {1, 2, 3, …}. Итак, -1 — отрицательное число, поэтому это не натуральное число. 0 тоже не натуральное число. 1/2, будучи дробное число, тоже не натуральное число.
Что находится между третью и половиной? Если умножить числитель и знаменатель обеих дробей на 2, то получим 6/12 и 4/12, здесь мы можем вставить одну дробь т.е. 5/12. Между ними можно вставить три дроби 11/24, 10/24 или 5/12, 9/24 или 3/8. …
Что находится между половиной и четвертью?
Нарежьте пиццу, и мы получим дроби:
| 1 / 2 | 1 / 4 | 3 / 8 |
| (Одна половина) | (Одна четверть) | (три восьмых) |
Что такое 0.
75, переведенное в дробь? Значение 0.75 как дробь равно 3/4.
Между какими целыми числами заключено число?
Задача #1 (номер задачи на fipi.ru — 8F6802). Между какими целыми числами заключено число 130/11?
- 10 и 11
- 11 и 12
- 12 и 13
- 13 и 14
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 11 и 12.
Ответ: 2 — 11 и 12.
Задача #2 (номер задачи на fipi.ru — 344704). Между какими целыми числами заключено число 140/17?
- 5 и 6
- 6 и 7
- 7 и 8
- 8 и 9
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 4 — 8 и 9.
Задача #3 (номер задачи на fipi.ru — B64AD1). Между какими целыми числами заключено число 172/15?
- 9 и 10
- 10 и 11
- 11 и 12
- 12 и 13
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 11 и 12.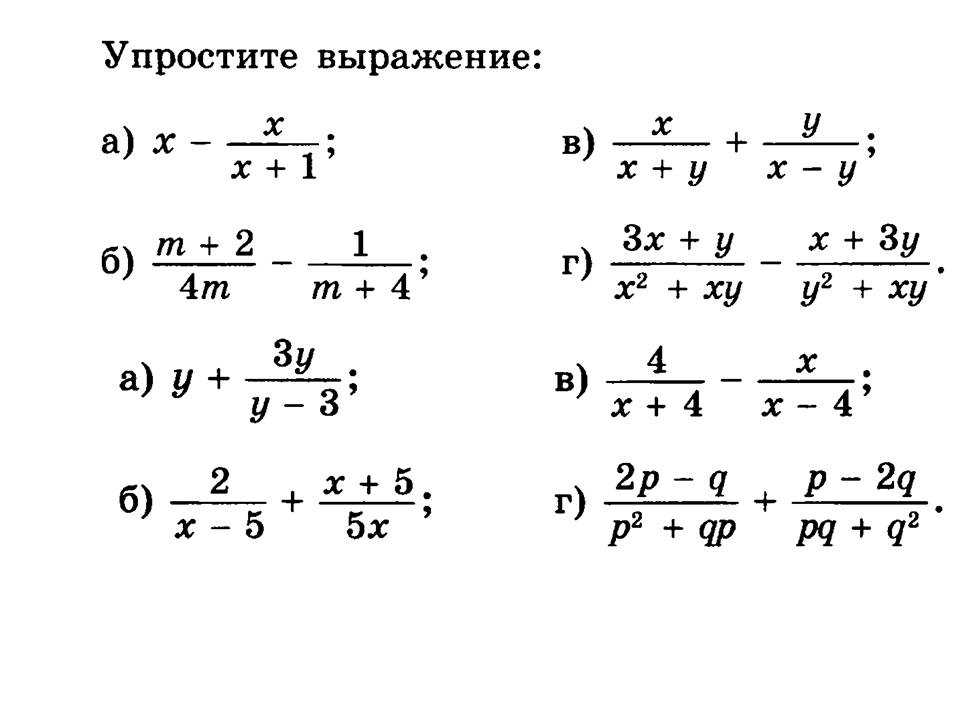
Ответ: 3 — 11 и 12.
Задача #4 (номер задачи на fipi.ru — F2CF43). Между какими целыми числами заключено число 110/13?
- 8 и 9
- 9 и 10
- 10 и 11
- 11 и 12
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 1 — 8 и 9.
Задача #5 (номер задачи на fipi.ru — F4AE19). Между какими целыми числами заключено число 230/19?
- 11 и 12
- 12 и 13
- 13 и 14
- 14 и 15
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 12 и 13.
Ответ: 2 — 12 и 13.
Задача #6 (номер задачи на fipi.ru — 4DD651). Между какими целыми числами заключено число 160/11?
- 12 и 13
- 13 и 14
- 14 и 15
- 15 и 16
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 14 и 15.
Ответ: 3 — 14 и 15.
Задача #7 (номер задачи на fipi.ru — 9179F3). Между какими целыми числами заключено число 131/12?
- 10 и 11
- 11 и 12
- 12 и 13
- 13 и 14
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 10 и 11.
Ответ: 1 — 10 и 11.
Задача #8 (номер задачи на fipi.ru — 648BA1). Между какими целыми числами заключено число 124/15?
- 8 и 9
- 9 и 10
- 10 и 11
- 11 и 12
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 1 — 8 и 9.
Задача #9 (номер задачи на fipi.ru — 2FC0DC). Между какими целыми числами заключено число 190/17?
- 10 и 11
- 11 и 12
- 12 и 13
- 13 и 14
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 11 и 12.
Ответ: 2 — 11 и 12.
Задача #10 (номер задачи на fipi.ru — 37B64D). Между какими целыми числами заключено число 170/19?
- 8 и 9
- 9 и 10
- 10 и 11
- 11 и 12
Решение:
Выделим целую часть в дроби:
Очевидно, что из предложенных вариантов число заключено между 8 и 9.
Ответ: 1 — 8 и 9.
Творческий проект для классов К-8
Планы уроков
- Задача «3N+1»
- Задача с Всероссийской олимпиады по математике
- Доказательство теоремы Пифагора с использованием подобных треугольников
- Головоломка с 1089
- Дополнительная плата
- Прибавление в детском саду и первом классе
- Арифметический вундеркинд из 1899 года
- Старый купец и четверо его детей
- Древний узел
- Анимации на TI
- Районы и границы
- Площадь и периметр
- Средний балл за тест
- Мяч в коробке
- Банан
- Бочки, бочонки и другие изогнутые емкости
- Большие числа АКА Зерна риса на шахматной доске
- Блочные дома
- Сборка собачьей будки в масштабе
- Создание каркасной коробки в соответствии со спецификациями
- Свечи
- Корзины для конфет
- Емкость
- Наутилус с камерой
- Проверка, является ли число простым
- Коробка с китайским календарем
- Аккорды по кругу
- Круг, квадрат и треугольник
- Часы и время
- Монеты
- Раскрашивание линий в шестиугольнике
- Разноцветные треугольники
- Конгруэнтные треугольники
- Счет
- Счетная доска для юных учащихся
- Счет до 100
- Биговка бумаги по изгибам
- Кубики
- Куб со срезанным краем
- Кулинарные полоски
- Вырезание прямоугольника
- Вырезание треугольника
- Разрезание треугольника на две части равной площади и равного периметра
- Вырезание равностороннего треугольника
- Резка многогранников
- Вывод формулы площади треугольника
- Диагональ квадрата
- Разделение квадрата
- Дивизион с остатком на ТИ-108: Два экземпляра
- Собаки, кошки и мыши
- Точка за точкой
- Удвоение и деление пополам
- Рисование прямоугольника
- Рисование простой фигуры по словесным инструкциям
- Рисование треугольников
- Легкие квадраты
- Яичная дилемма (Часть 1)
- Возведение в степень
- Факторинг
- Необычные конверты
- Нахождение дроби между двумя дробями
- Пятиконечная трехмерная звезда
- Подбрасывание монет
- Сложенный бумажный цветок с шестью лепестками
- Четыре жука
- Четыре карты
- Четыре кубика
- От одного миллиарда до нуля
- От одного до одного триллиона
- Игра кругов и звезд
- Игра десятков
- Гигантская энчилада
- Шапка для Хэллоуина
- Орел или решка?
- Шестиугольная головоломка
- Как калькулятор вычисляет квадратный корень числа?
- Сколько пентамино?
- Как измерить угол без транспортира
- Как преобразовать прямоугольник в другой прямоугольник
- Гиперболы и эллипсы
- Вписанный треугольник
- Интерес
- Юлекурв АКА Валентинка Корзина
- Воздушные змеи
- Дырявая крыша
- Ушастые твари
- Волшебные бобы
- Волшебный складной кубик
- Волшебный квадрат
- Создание животных путем вырезания многоугольников
- Изготовление блоков из четырех кубиков
- Изготовление коробок
- Изготовление эвольвенты
- Лабиринт
- Мини-слот-машина
- Луны
- Больше задач с точностью до точки
- Больше старых словесных задач
- Умножения «Сделано по Адаму Райсу»
- Натан подбрасывает монету 20 раз
- Числовая игра с кубиками
- Одна треть
- Парадокс средних
- Разделение квадрата
- Пазлы Пентагона
- Алгебра телефонных номеров
- Копилка
- Игра с формами
- Powerball 55
- Красивая подарочная коробка
- Тыквы
- Пазл с камешками
- Пирамида на четверти
- Пирамида кубов
- Пирамида из мрамора
- Четырехугольники
- Правильные многоугольники с равными площадями
- Связанные проблемы
- Прямоугольный треугольник
- Последовательности составных чисел: конкурс
- Формы чисел
- Формы чисел с использованием треугольников
- Шесть пирамид
- Шестнадцать квадратных дюймов
- Печать Соломона
- Сортировочная игра
- Спираль (марки К-4)
- Спираль (5-8 классы)
- Спираль Феодора на калькуляторе ТИ-83/84
- Квадратные и кубические единицы
- Квадрат в треугольнике
- Соломенные многогранники
- Алгоритм вычитания
- Вычитание со счетчиками
- Сумма двух квадратов
- Выживший на шестиугольном острове
- Татами
- Чайные коробки
- Преобразование температуры
- Мозаика круга
- Задача о лестнице и ящике
- Контейнеры для сыра «Смеющаяся корова»
- Практическая ценность доказательств
- Три четверти
- Круглая головоломка из трех частей
- Бросание одного кубика
- От треугольника к квадрату: Шарнирное рассечение
- Превращение прямоугольника в квадрат путем рассечения
- Двенадцать простых фигур
- Двадцать четыре кубика
- Две старые проблемы
- Два брата пастуха
- Понимание длинного деления
- Необычные контейнеры
- Что дальше?
- Что это за прямоугольник?
- Инь Ян
Дробь между двумя дробями: определения и примеры
- Автор
Рачана - Последнее изменение 19-10-2022
Фракция между двумя фракциями: Фракция — это небольшая часть большего целого или набора.
Когда объект или целое делится на равные части, каждая часть представляет собой часть данного объекта или целого. В числовом выражении дробь состоит из двух частей: числителя и знаменателя.
Числитель показывает, сколько у нас есть выделенных или заштрихованных частей, тогда как знаменатель показывает, сколько всего частей объекта или целого у нас есть. Мы можем найти дроби между любыми двумя дробями. В этой статье обсуждается, как найти дробь между двумя заданными дробями. Прочитайте полную статью, чтобы получить полную информацию.
Определение дроби
Дроби представлены в виде числовых значений в математике и могут быть определены как части целого. Дробь — это часть или часть целого, которая может быть любым числом, заданным значением или элементом.
Таким образом,
({text{Дробь}} = frac{{{text{Число}},{text{из}},{text{выбрано}},{text {или}} , { text {заштриховано}} , { text {части}} , { text {из}} , { text {an}} , { text {объект}} , { text {или}} , { text {a}} , { text {целое}}}} {{{ text {Всего}} , { text {число}} , { текст {из}} , { текст {равно}} , { текст {частей}} , { текст {из}} , { текст {an}} , { текст {объект}} ,{text{или}},{text{a}},{text{целое}}}} = frac{{{text{Числитель}}}}{{{text{Знаменатель }}}})
Учитывать дробь (frac{5}{{12}}) Эта дробь читается как «пять двенадцатых», что означает, что (5) частей из (12) равны разделить на целое.
В дроби (frac{7}{{12}},7) известен как числитель, а (12) известен как знаменатель.
Ниже приведены еще несколько примеров:
| Дробь | Значение дроби | Числитель | 0355 Знаменатель |
| (frac{5}{{11}}) или Пять одиннадцатых | Пять равных частей из (11) равных частей, на которые делится целое. | (5) | (11) |
| (frac{3}{{8}}) или Три восьмых | Три равные части из (8) равных частей в котором целое разделено. | (3) | (8) |
| (frac{1}{{3}}) или Одна треть | Одна часть из (3) равных частей в что целое разделено. |
(1) | (3) |
Примеры дробей
Дробь — это число, представляющее часть целого. Один объект или группа объектов могут составлять целое. Возьмите прямоугольный лист и сложите его пополам. Сложите его по горизонтали и вертикали, чтобы разделить на четыре равные части. Как показано на рисунке ниже, один из четырех компонентов должен быть затенен. Заштрихованная область составляет четверть всей композиции. Число одна четвертая записывается как (frac{1}{{4}},), что не что иное, как дробь.
Если три части затемнены, как на рисунке ниже, заштрихованная часть представляет собой три четверти от общего числа. Три четверти записываются как (frac{3}{{4}}) и читаются как «три на четыре» или «три на четыре». Таким образом, три части из (4) равных частей равны (frac{3}{{4}}.)
Аналогично, (frac{3}{{7}}) получается, когда делим целое на (7) равных частей и берем три части (см.
рис. ниже).
Для (frac{1}{{8}},) делим целое на восемь равных частей и берем одну его часть (см. рис. ниже).
Дробь между двумя дробями
Дробь состоит из двух элементов. Число в верхней части строки или дроби называется числителем. Он определяет, сколько берется равных частей всей коллекции или целого. Знаменатель – это число под чертой. Он отображает общее количество равных частей, на которые делится целое, или общее количество равных частей в коллекции.
Калькулятор нахождения дроби между двумя дробями не сложный процесс. Просто сделайте сумму числителей в качестве нового числителя и сумму знаменателей в качестве нового знаменателя, чтобы получить дробь между двумя заданными дробями.
Ниже приведены примеры того, как вставить дробь между двумя дробями:
Если (frac{p}{q}) и (frac{r}{s}) две заданные дроби и ( гидроразрыв {р} {q}
Где (p,q,r) и (s) — натуральные числа.
Пример. Вставьте дробь между двумя дробями (frac{5}{7}) и (frac{3}{5},), учитывая (frac{5}{7})
Решение.
Требуемая дробь между (frac{5}{7}) и (frac{2}{5}) равна (frac{{(5 + 2)}}{{(7 + 5)}} = frac{7}{{12}})
Следовательно, (frac{5}{7}
Решаемые примеры – дробь между двумя заданными дробями
Q.1. Вставьте дробь между двумя дробями (frac{1}{3}) и (frac{2}{5},) учитывая (frac{1 }{3} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Здесь сумма числителей(=1+ 2=3) и
сумма знаменателей(=3+5=8)
Итак, новая дробь образовалась между двумя дробями (frac{1}{3}) и (frac{2}{5} ) равно (frac{3}{8}.)
Q.2. Найдите дробь между двумя дробями (frac{2}{7}) и (frac{4}{5},) при заданном (frac{2 }{7} < frac{4}{5}.)
Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{2}{7}) и (frac{4}{5}) равна (frac{{(2 + 4)}}{{( 7 + 5)}} = frac{6}{{12}} = frac{1}{2}.)
Q.3. Найдите дробь между двумя дробями (frac{4}{7}) и (frac{1}{3},) при заданном (frac{4 {7} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{4}{7}) и (frac{1}{3}) равна (frac{{(4 + 1)}}{{( 7 + 3)}} = frac{5}{{10}} = frac{1}{2}.)
Q.4. Вставьте дробь между двумя дробями (frac{5}{6}) и (frac{7}{11},) учитывая (frac{5 {6} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Требуемая дробь между двумя дробями (frac{5}{6}) и (frac{7}{11}) равна (frac{{(5 + 7)}}{{( 6 + 11)}} = frac{{12}}{{17}}.)
Q.5. Вставьте дробь между двумя дробями (frac{5}{7}) и (frac{8}{11},) учитывая (frac{5 {7} Ответ: Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Здесь сумма числителей(=5+8=13) и
сумма знаменателей(=7+11=18)
Итак, между двумя дробями образовалась новая дробь (frac {5}{7}) и (frac{8}{11}) равно (frac{13}{18}.)
Резюме
В этой статье мы узнали об определении дроби, примеры дробей, калькулятор нахождения дроби между двумя дробями, решенные примеры дроби между двумя заданными дробями и часто задаваемые вопросы о дроби между двумя заданными дробями. Вы также можете найти «Как найти дробь между двумя дробями» в приложении и на веб-сайте Embibe.
В результате изучения этой статьи мы поняли, как вставить дробь между двумя заданными дробями. Чтобы вставить дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Узнайте о различных типах фракций
Часто задаваемые вопросы (FAQ)
Q.1. Как найти дробь между двумя дробями?
Ответ. Нахождение дроби между двумя дробями — несложный процесс. Просто сделайте сумму числителей новым числителем и знаменателей новым знаменателем, чтобы получить дробь между двумя дробями.
Ниже приведены примеры того, как вставить дробь между двумя предоставленными дробями:
Если (frac{p}{q}) и (frac{r}{s}) две заданные дроби и (frac{p} {q} < frac{r}{s}), затем (frac{p}{q} < frac{{p + r}}{{q + s}} < frac{r}{s}. )
Q.2. Всегда ли между любыми двумя дробями есть дробь?
Ответ: Между любыми двумя целыми числами есть дробь.
Существует (frac{1}{2}) между (0) и (1,frac{3}{2}) между (1) и (2,) и т.д. на. Между любыми двумя целыми числами может быть бесконечное количество дробей.
Существуют также (frac{1}{3},frac{1}{4},frac{1}{5},) и любые другие числа, которые могут быть выражены как (frac{1 {n},), где (n) — целое число, от (0) до бесконечности, а значение дроби лежит между (0) и (1.). дроби, такие как (frac{2}{3},frac{3}{4},frac{4}{5},) и так далее. (frac{m}{n}) — дробь между (0) и (1), если m и n оба являются положительными целыми числами и (m) меньше, чем (n. ) Точно так же существует бесконечное число дробей между любыми двумя целыми числами.
Q.3. Какая дробь находится между 1/3 и 2/3?
Ответ: Чтобы найти дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Даны две дроби: (frac{1}{3}) и (frac{2}{3},frac{1}{3} < frac{2}{3})
Здесь сумма числителей(=1+2=3) и
сумма знаменателей(=3+3=6)
Итак, между двумя дробями образовалась новая дробь (frac{ 1}{3}) и (frac{2}{3}) равно (frac{3}{6} = frac{1}{2}.
)
Q.4. Какая дробь находится между 1 и 2?
Ответ: Чтобы найти дробь между двумя дробями, сделайте сумму числителей новым числителем, а сумму знаменателей новым знаменателем.
Даны две дроби: (frac{1}{1}) и (frac{2}{1},1 Здесь сумма числителей(=1+2=3) и
сумма знаменателей(=1+1=2)
Итак, новая дробь, образованная между двумя дробями (1) и (2), равна (frac{3}{2}. )
Q.5. Что такое дробь?
Ответ: В математике дроби представлены числовыми значениями и могут быть определены как части целого. Дробь — это часть или часть целого, которая может быть любым числом, заданным значением или элементом.
Рассмотрим дробь (frac{3}{5}.) Эта дробь читается как «три пятых», что означает, что (3) частей из (5) равных частей, в которых целое поделен. В дроби (frac{3}{5},3) называется числителем, а (5) называется знаменателем.
Q.6. Чему равно в дробях?
Ответ: Равные дроби — это дроби с одинаковым значением, но разными числителями и знаменателями. (frac{6}{9}) и (frac{10}{15},), например, являются эквивалентными дробями, поскольку они обе равны (frac{2}{3}. )
Q.7. Как определить, равны ли дроби?
Ответ: Когда различные дроби упрощаются и сводятся к одной дроби, они являются эквивалентными дробями. Кроме того, существует несколько альтернативных подходов к определению сопоставимости поставляемых фракций. Вот несколько примеров:
1. Сделать числители и знаменатели одинаковыми.
2. Нахождение десятичной версии обеих дробей является первым шагом.
3. Метод перекрестного умножения.
4. Наглядным способом.
Теперь у вас есть вся необходимая информация о дроби между двумя дробями, и мы надеемся, что эта подробная статья будет вам полезна.
В этом уроке мы коснёмся тех моментов, о которых не упоминали при изучении дробей, посчитав что на первых порах они создают трудности для обучения.
Правильные и неправильные дроби
В самом начале своего пути при изучении дробей мы узнали, что правильная дробь — это та дробь, у которой числитель меньше знаменателя.
В школьной литературе можно встретить другое определение правильной дроби. Выглядит оно следующим образом:
Правильная дробь всегда меньше единицы.
Как понять данное определение? Дробь сама по себе указывает на то, что какой-либо объект разделен на несколько частей. И это всегда один единственный объект. Под единицей именно это и подразумевается.
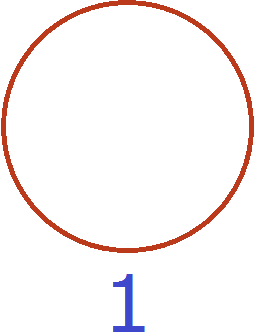
Например, пусть у нас имеется одна пицца:
В данном случае она и является единицей.
Если мы отрежем от этой пиццы половину, то есть 
(одну вторую пиццы), то наш кусок будет меньше, чем вся целая пицца:
В этом и заключается суть фразы «правильная дробь всегда меньше единицы».
Наша половинка пиццы является дробью и она меньше одной целой пиццы, то есть меньше единицы:
Это выражение можно доказать. Если мы вычислим дробь , то получим десятичную дробь 0,5. А это рациональное число меньше единицы:
На координатной прямой можно увидеть, как располагаются эти числа:
Видно, что рациональное число 0,5 располагается левее, чем 1. А мы помним, что чем левее число располагается на координатной прямой, тем оно меньше.
С неправильными дробями всё было наоборот. Неправильной дробью мы назвали ту дробь, у которой числитель больше знаменателя.
Но в школьной литературе можно встретить другое определение неправильной дроби. Выглядит оно следующим образом:
Неправильная дробь всегда больше единицы или равна ей.
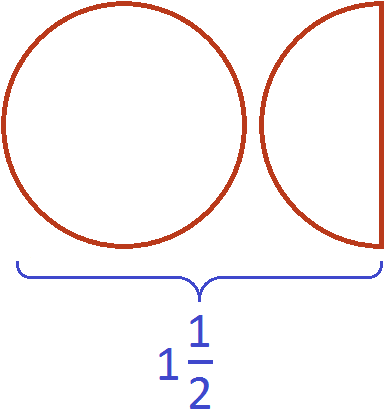
Например, рассмотрим неправильную дробь 
. Выделим в этой дроби целую часть, получим 
. Изобразим эту смешанную дробь в виде одной целой пиццы и ещё половинки пиццы:
Вместе одна целая пицца и ещё половина пиццы больше, чем просто одна целая пицца
В этом и заключается суть фразы «неправильная дробь всегда больше единицы».
Одна целая пицца и ещё половина пиццы описывается смешанной дробью и эта смешанная дробь больше единицы:
Переведём смешанную дробь обратно в неправильную дробь, чтобы не противоречить правилу. Ведь речь в данном случае идёт о неправильных дробях:
что схематически будет выглядеть так:
Выражение можно доказать. Если мы вычислим дробь , то получим десятичную дробь 1,5. А это рациональное число больше единицы:
На координатной прямой можно увидеть, как располагаются эти числа:
Видно, что рациональное число 1,5 располагается правее, чем 1. А мы помним, что чем правее число располагается на координатной прямой, тем оно больше.
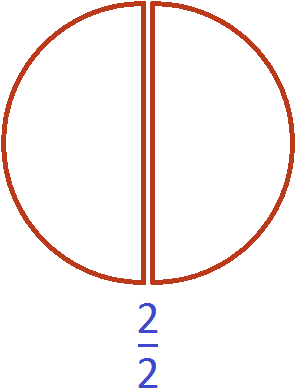
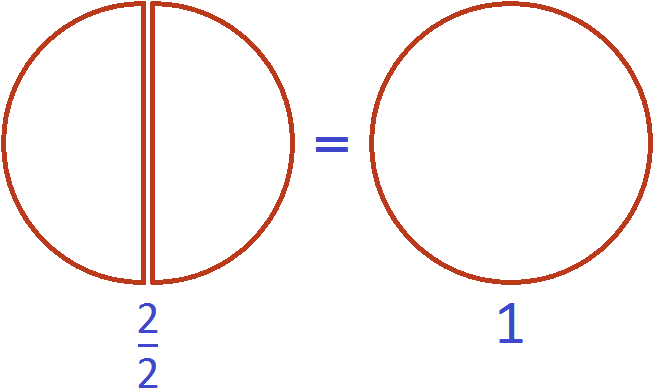
Неправильной также называется дробь равная единице. Речь в данном случае идет о тех дробях, у которых числитель и знаменатель равны.
Рассмотрим дробь 
. Изобразим её в виде двух одинаковых кусочков пиццы:
Фактически речь идёт не о дроби, а об одной целой пицце:
В этом и заключается суть фразы «неправильная дробь может равняться единице».
Любое целое число отличное от нуля (не равное нулю) можно представить в виде неправильной дроби со знаменателем 1. Например, числа 3, 5, 9, 12 можно представить в виде неправильных дробей со знаменателем 1
Представление объекта в виде единицы позволяет проще решать задачи. Рассмотрим примеры.
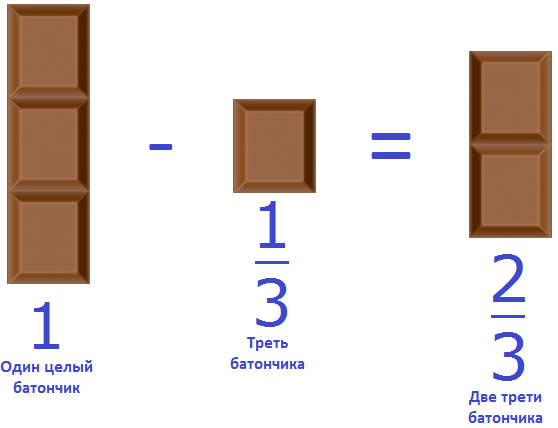
Пример 1. Куплен один шоколадный батончик. От него отрезали треть. Сколько батончика осталось?
Осталось две трети батончика. Сам батончик можно описать цифрой 1, далее из этой единицы вычесть треть:
Не приводя на бумаге никаких вычислений, можно ответить на вопрос подобной задачи. Сказано «отрезали треть» — значит сразу нужно обратить внимание на то, что знаменатель равен 3.
Если отрезали одну часть из трёх, то сколько частей должно остаться? Верно, две части. Поэтому и ответ «две части из трёх» или «две трети».
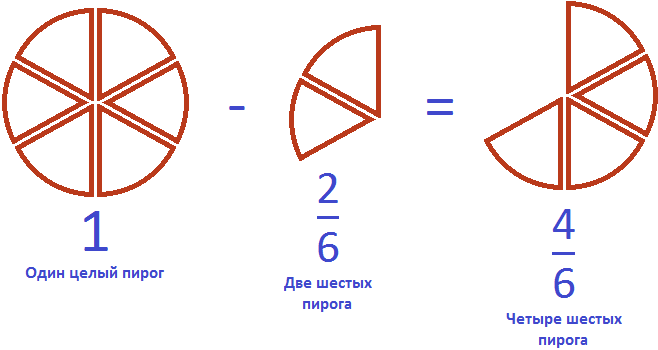
Пример 2. Куплен один пирог. От него отрезали две шестых. Сколько пирога осталось?
Осталось четыре шестых пирога. Сам пирог можно описать цифрой 1, далее из этой единицы вычесть две шестых:
Приведение дробей к общему знаменателю
Чтобы привести дроби к общему знаменателю, мы находили НОК (наименьшее общее кратное) знаменателей этих дробей. Затем делили найденный НОК на знаменатель первой дроби и получали дополнительный множитель для первой дроби.
То же самое мы делали и для второй дроби — делили НОК на знаменатель второй дроби и получали дополнительный множитель для второй дроби.
Затем дроби умножались на свои дополнительные множители. В результате они обращались в дроби, у которых одинаковые знаменатели. К примеру, выражение 
вычисляется следующим образом:
Но есть и другой способ приведения дробей к общему знаменателю. Этим способом часто пользуются школьники и ленивые студенты. Суть этого способа заключается в том, что роль дополнительных множителей берут на себя знаменатели обеих дробей, причем происходит это «крест-накрест» — знаменатель первой дроби становится дополнительным множителем второй дроби, а знаменатель второй дроби становится дополнительным множителем первой дроби.
Вычислим предыдущее выражение этим способом. Знаменатель первой дроби 2 становится дополнительным множителем второй дроби, а знаменатель второй дроби 6 становится дополнительным множителем первой дроби:
Далее числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель и вычисляем:
Преимущество данного способа в том, что не нужно находить НОК знаменателей обеих дробей. В процессе вычисления всё выравнивается само. Единственный недостаток заключается в том, что выражение становится более длинным и корявым.
Сравните выражения, которые мы вычислили сначала первым способом, а затем вторым:
Выражение, вычисленное первым способом, намного аккуратнее и короче, нежели второе.
Вторым способом мы будем пользоваться при изучении алгебры. В алгебре работать с буквенными выражениями приходиться чаще, чем с числовыми.
К примеру, если перед нами будет стоять задача привести буквенное выражение 
к общему знаменателю, то у нас не будет другого выхода, кроме как воспользоваться методом «крест-накрест», то есть использовать второй способ, который мы сейчас рассмотрели:
Нахождение дроби от числа
Чтобы найти дробь от числа, мы делим это число на знаменатель искомой дроби и полученный результат умножаем на числитель искомой дроби.
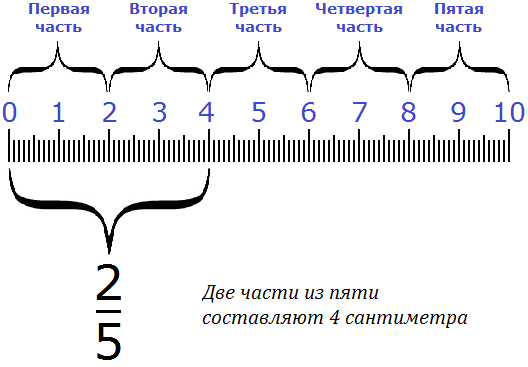
Например, чтобы найти 
от 10 сантиметров, нужно 10 разделить на 5, и полученный результат умножить на 2
10 : 5 = 2
2 × 2 = 4
Получили ответ 4. Значит от десяти сантиметров составляют 4 сантиметра. Схематически это выглядит примерно так:
Но есть и второй вариант решения. Для нахождения от десяти сантиметров, достаточно умножить 10 на . Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
Поэтому можно взять на заметку следующее правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число умножить на искомую дробь.
Пример 2. Найти 
от двух часов.
Два часа это 120 минут. Чтобы найти от 120 минут, нужно 120 умножить на дробь
Значит от двух часов составляют 80 минут.
Нахождение числа по дроби
Чтобы найти всё число по его дроби, мы делили это число на числитель имеющейся дроби и полученный результат умножали на знаменатель имеющейся дроби.
Например, зная что рулетки составляет 12 см, мы можем найти длину всей рулетки. Для этого 12 нужно разделить на 2, и полученный результат умножить на 3
12 : 2 = 6
6 × 3 = 18
Получили 18. Значит длина всей рулетки равна 18 см.
Но есть и второй вариант решения. Для нахождения длины всей рулетки, достаточно 12 разделить на дробь . Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
Поэтому можно взять на заметку следующее правило нахождения числа по дроби:
Чтобы найти число по дроби, нужно это число разделить на данную дробь.
Пример 2. всего пути составляет 6 км. Найти длину всего пути.
Чтобы найти длину всего пути, достаточно 6 разделить на дробь
Получили ответ 15. Значит длина всего пути составляет 15 километров.
Десятичная точка в дробях
Запятую в десятичной дроби, которая отделяет целую часть от дробной, по-другому называют десятичной точкой.
Дело в том, что в некоторых источниках целая часть от дробной отделяется именно точкой, а не запятой. Например:
2.5 (две целых пять десятых)
15.65 (пятнадцать целых шестьдесят пять сотых)
Точка часто используется для записи десятичных дробей на компьютере — в программировании и при работе в математических пакетах. В остальных случаях: на письме и при подготовке документов, в десятичных дробях чаще используется запятая, а не точка.
Мы используем в десятичных дробях запятую, а не точку, поэтому разумнее называть эту запятую десятичной запятой.
Но десятичную запятую большинство людей тоже называют десятичной точкой. Что в принципе не является ошибкой, потому как речь всё равно идёт о разделителе, котором отделяет целую часть от дробной.
Давайте и мы будем называть свою запятую в десятичных дробях десятичной точкой. Это словосочетание проговаривается легче и приятнее на слух.
Десятичная точка используется для увеличения или уменьшения дроби в 10, 100, 1000 и более раз. При увеличении десятичной дроби, десятичная точка передвигается вправо, а при уменьшении — влево. Чтобы быстро запомнить это, можно воспользоваться фразами «чем правее, тем больше» и «чем левее, тем меньше».
Пример 1. Увеличить десятичную дробь 6,3 в десять раз.
Чтобы увеличить десятичную дробь 6,3 в десять раз, достаточно передвинуть десятичную точку вправо на одну цифру, получим 63.
Пример 2. Уменьшить десятичную дробь 6,3 в десять раз.
Для уменьшения дроби 6,3 в десять раз достаточно передвинуть десятичную точку влево на одну цифру, получим 0,63
На вопрос «как узнать на сколько цифр передвигать десятичную точку?», нужно смотреть во сколько увеличивается (или уменьшается) десятичная дробь. Если дробь нужно увеличить (или уменьшить) в десять раз, то десятичная точка сдвигается на одну цифру.
Если дробь нужно увеличить (или уменьшить) в сто раз, то десятичная точка сдвигается на две цифры.
Если дробь нужно увеличить (или уменьшить) в тысячу раз, то десятичная точка сдвигается на три цифры. В общем, всё зависит от количества нулей во множителе.
Например, увеличить дробь в десять раз означает умножить её на 10. Мы помним, что для того чтобы умножить десятичную дробь на 10, нужно в этой дроби передвинуть запятую вправо на одну цифру (поскольку в числе 10 один ноль). Теперь можно не заучивать подобные правила. Такое умножение можно легко выполнить, передвинув десятичную точку.
Пример 3. Увеличить десятичную дробь 6,3 в тысячу раз.
Чтобы увеличить десятичную дробь 6,3 в тысячу раз, достаточно передвинуть десятичную точку вправо на три цифры, получим 6300. Если после запятой не хватает цифр, то вместо недостающих цифр записывают нули, что мы и сделали.
Пример 4. Уменьшить десятичную дробь 12,5 в сто раз.
Для уменьшения дроби 12,5 в сто раз, достаточно передвинуть десятичную точку влево на две цифры, получим 0,125
Десятичную точку можно использовать не только в десятичных дробях. Её можно использовать для увеличения (уменьшения) и других чисел в 10, 100 или в 1000 раз.
Возьмём к примеру целое число 325 и поставим в конце точку, получим 325 с точкой. Воспользуемся в этот раз точкой, так как её легче изобразить на рисунке:
Попробуем уменьшить это число в десять раз. Для этого достаточно будет передвинуть точку влево на одну цифру, получим 32.5
Попробуем увеличить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры вправо, получим 123000.
Попробуем уменьшить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,123
Попробуем уменьшить число 65 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,065
Попробуем увеличить число 65 в сто раз. Для этого достаточно передвинуть десятичную точку на две цифры вправо, получим 6500.
Составные выражения
Встречаются задачи, в которых требуется вычислить выражение составленное из нескольких дробей. Например,
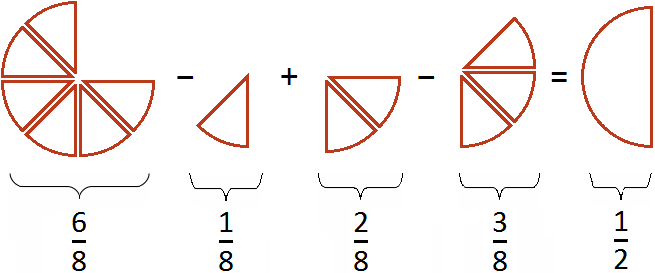
Такое выражение вычисляется согласно порядку действий. В данном случае вычисление будет выполнено последовательно слева направо:
Если из 
пиццы вычесть 
пиццы, затем прибавить 
пиццы, затем вычесть 
пиццы, то останется пиццы
Если вам тяжело понять данный пример, попробуйте самостоятельно решить его на бумаге, делая соответствующие рисунки к каждой дроби.
Пример 2. Найти значение выражения 
В данном примере сначала необходимо выполнить умножение затем сложение и вычитание
Если пиццы увеличить в два раза, то получится одна целая пицца
Затем если к 
пиццы прибавить эту целую пиццу, а затем из полученного результата вычесть 
пиццы, то получится 
пиццы
Пример 3. Найти значение выражения 
Сначала желательно вычислить выражения, находящиеся в числителях обеих дробей, а именно выражения 2−1 и 1+1,
Дальнейшее вычисление не составляет особого труда плюс равно
Конечно, можно было записать в одном числителе выражения, находящиеся в числителях обеих дробях. От этого ответ не изменился бы:
Но в некоторых случаях возможны подвохи, особенно если из одной дроби вычитается другая. Следующий пример демонстрирует это.
Пример 4. Найти значение выражения 
Вычислим выражения, находящиеся в числителях обеих дробей, а именно выражения 2+1 и 2−1
Ну и нетрудно догадаться, что 
равно или (при условии, что дробь будет сокращена на 2)
Все логично. Если из пиццы вычесть пиццы, то получится пиццы.
Теперь попробуем решить данный пример, записав в одном числителе оба выражения, находящиеся в числителях обеих дробей:
Получается совсем другой ответ. Этот ответ не является правильным. Давайте посмотрим, что представляет собой выражение 
.
Для начала запишем его следующим образом:
Теперь попробуем проследить весь процесс вычисления этого выражения. Предположим, что имелось пиццы
К ней добавили еще пиццы
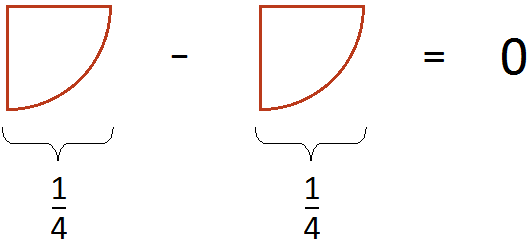
Затем из получившейся пиццы вычитается
Затем из получавшейся пиццы вычитают еще пиццы
Получился 0, то есть пицца исчезла. Но мы знаем, что должно было остаться пиццы. Поэтому при вычислении дробных выражений следует быть внимательным, особенно при вычитании выражений, содержащих в числителе другие выражения.
Если хочется сэкономить время и записать в числителе оба выражения, находящиеся в числителях обеих дробей, то второй числитель нужно взять в скобки. Это спасёт от ошибки:
Пример 5. Найти выражения 
Вычислим выражения, находящиеся в числителях обеих дробей:
Приведем полученные дроби к общему знаменателю и как обычно вычислим полученное выражение:
Если из вычесть пиццы, то получится пиццы
Пример 6. Найти значение выражения 
В первую очередь необходимо выполнить умножение:
Далее выполняется сложение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Дробь – это значение в двух частях; каждая часть, числитель или знаменатель, является целым числом. Числитель – это верхнее число дроби, а знаменатель – ее нижнее число. Дробная математика младшего порядка, такая как сложение и вычитание, требует, чтобы знаменатели участвующих дробей имели одинаковое значение. Находя дробь, которая находится между двумя другими, вы игнорируете нормальную дробную математику в пользу более простого метода.
-
Запишите начальные дроби
-
Добавьте Числители Вместе
-
Добавьте знаменатели вместе
-
Написать новую фракцию
-
Упростить дробь
-
Чтобы проверить свой ответ, напишите дроби с общими знаменателями и сравните числители. Дробные примеры 1/2, 2/3 и 3/4 с общими знаменателями становятся 6/12, 8/12 и 9/12. Числитель 8 находится между 6 и 9, поэтому созданная вами дробь – 8/12 или 2/3 в упрощенном виде – находится между двумя дробями, с которых вы начали.
Получить две фракции для примера. Для этого примера пусть дроби будут 1/2 и 3/4.
Суммируйте числители дробей. В этом примере 1 + 3 = 4.
Суммируйте знаменатели дроби. В этом примере 2 + 4 = 6.
Запишите новую дробь с суммой числителей в качестве нового числителя и суммой знаменателей в качестве нового знаменателя. В этом примере новая фракция 4/6.
Упростите дробь, исключив наибольший общий множитель, разделяемый числителем и знаменателем. Для этого перечислите факторы каждого числа и выведите наибольшее общее число.
В этом случае коэффициенты 4 равны 1, 2 и 4, а коэффициенты 6 равны 1, 2, 3 и 6. Оба числа имеют коэффициенты 1 и 2, причем 2 является наибольшим фактором.
Исключение 2 из числителя и знаменателя приводит к (4 ÷ 2) / (6 ÷ 2), который становится 2/3.
