ГЛАВА1
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И
ПРОСТЕЙШИХ СИСТЕМ
1.1. Теоретический материал
Физическая величина – это количественная характеристика свойства материальных объектов или явлений (процессов). Каждая физическая величина устанавливается однозначным способом ее измерения – экспериментального определения или расчета. Определение физической величины указывает принципиальный способ ее измерения.
Физическое понятие (модель объекта или явления) – это абстракция (филос.), которая отражает только основные, наиболее существенные, свойства материальных объектов или явлений (процессов).
Критерий правильности выбора модели. Если в данной задаче физическая величина, описывающая неосновное свойство, от которого мы абстрагируемся, много меньше другой, характерной для этой задачи, величины той же размерности, то модель выбрана верно.
Заметим, что один и тот же материальный объект или одно и то же явление в различных условиях могут быть рассмотрены в рамках различных моделей, если они удовлетворяют критериям правильности выбора этих моделей.
Тело отсчета – тело, относительно которого рассматривается движение других тел.
Часы – неподвижный относительно тела отсчета прибор для измерения времени, принцип действия которого основан на сравнении длительности исследуемого временного интервала с длительностью выбранного за эталон периодического процесса.
Система отсчета – совокупность системы координат[1], связанной с телом отсчета, и набора синхронизированных часов, размещенных в разных точках координатной системы.
Условие синхронизации часов A и B, расположенных в разных точках системы отсчета (в предположении об изотропности пространства):
![]() (1.1)
(1.1)
Здесь – момент времени излучения из точки A светового сигнала (кванта света) по часам в точке A, – момент времени регистрации этого сигнала в точке B по часам в точке B, – момент времени регистрации в точке A отраженного в точке B сигнала по часам в точке A.
Материальная точка – физическое понятие (модель, абстракция), представляющее тело, размерами (и формой) которого можно пренебречь в условиях данной задачи.
Положение материальной точки относительно данной системы отсчета (в данной системе отсчета) S задается ее координатами или радиус-вектором .
Радиус-вектор материальной точки относительно данной системы отсчета – вектор, начало которого находится в начале координат этой системы, а конец – в месте расположения материальной точки (см. рис. 1.1а):
, (1.2)
где , и – орты декартовой системы координат: , , ; x, y, z – координаты материальной точки.
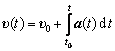 |
Закон движения материальной точки относительно данной системы отсчета – зависимость радиус-вектора или координат материальной точки от времени:
(1.3)
Траектория движения материальной точки – линия, описываемая в пространстве концом радиус-вектора материальной точки.
Уравнение траектории задается совокупностью двух уравнений
(1.4)
которые можно получить, исключая время из закона движения в координатной форме (1.3). Заметим, что сам закон движения в координатной форме представляет собой уравнение траектории, заданное в параметрическом виде.
Перемещение материальной точки – изменение радиус-вектора материальной точки за время Dt с момента времени t (рис. 1а):
. (1.5)
Скорость материальной точки относительно данной системы отсчета – физическая величина, равная производной радиус-вектора материальной точки по времени (производная берется при постоянных ортах системы координат, поскольку они жестко связаны с телом отсчета):
, (1.6)
где , , – проекции скорости на соответствующие оси системы координат. Скорость можно представить в виде суммы составляющих скорости вдоль осей системы координат:
. (1.7)
При этом модуль скорости равен
. (1.8)
В соответствии с определением скорость всегда направлена по касательной к траектории (см. рис. 1.1б).
Зная закон изменения скорости материальной точки , и радиус-вектор в начальный момент времени t0, можно найти закон движения:
. (1.9)
Путь s(t), пройденный материальной точкой вдоль траектории (длина траектории) за время t, равен
, (1.10)
при этом модуль скорости в любой момент времени равен
. (1.11)
Ускорение материальной точки относительно данной системы отсчета – физическая величина, равная производной скорости материальной точки по времени (при постоянных ортах системы координат):
, (1.12)
где ax, ay, az – проекции ускорения на соответствующие оси системы координат. Ускорение можно представить в виде суммы составляющих ускорения вдоль осей системы координат:
. (1.13)
При этом модуль ускорения равен
. (1.14)
Зная закон изменения ускорения материальной точки , а также скорость и радиус-вектор в начальный момент времени t0, можно найти закон изменения скорости и закон движения:
, (1.15)
. (1.16)
Начальные условия для материальной точки – значения радиус-вектора и скорости в начальный момент времени t0 относительно заданной системы отсчета:
(1.17)
Тангенциальное ускорение – составляющая ускорения вдоль направления скорости (см. рис. 1.2):
, , , (1.18)
, (1.19)
где – проекция ускорения на направление скорости .
Движение материальной точки при – ускоренное, при – замедленное, при – равномерное, а при – равнопеременное.
Нормальное ускорение – составляющая ускорения , перпендикулярная направлению скорости (рис. 1.2):
, , , (1.20)
где – проекция ускорения на направление , перпендикулярное скорости и направленное к центру кривизны траектории.
Нормальное ускорение всегда направлено к центру кривизны траектории – центру окружности максимального радиуса (радиуса кривизны траектории), касательной к траектории в данной точке, при этом
, (1.21)
где – радиус кривизны траектории в данной точке, а – угол между скоростями в моменты времени t и t + dt.
Ускорение можно представить в виде суммы нормального и тангенциального ускорений:
. (1.22)
При этом модуль ускорения равен
. (1.23)
В соответствии с (1.21) и (1.22) ускорение всегда отклонено от направления скорости в сторону центра кривизны траектории в данной точке, то есть внутрь траектории (см. рис. 1.2).
В частном случае движения материальной точки по окружности, т.е. движения в плоскости по траектории с постоянным радиусом кривизны – (рис. 1.3), можно ввести угловую скорость и угловое ускорение :
(1.24)
При этом:
(1.25)
Механическая система – совокупность материальных тел.
Система материальных точек – совокупность тел, каждое из которых можно считать материальной точкой. Далее будем считать, что всякую рассматриваемую нами механическую систему можно рассматривать как систему материальных точек.
Абсолютно твердое тело – тело (система материальных точек), расстояния между двумя любыми материальными точками которого не меняются в условиях данной задачи.
Поступательное движение абсолютно твердого тела – движение, при котором прямая, соединяющая любые две материальные точки тела, перемещается параллельно самой себе.
Принцип суперпозиции движений – в случае поступательного движения системы отсчета S¢ относительно системы S (рис. 1.4) радиус-вектор (скорость, ускорение) произвольной материальной точки относительно системы S равен сумме радиус-векторов (скоростей, ускорений) начала отсчета O’ системы S’ и той же материальной точки относительно системы S’:
(1.26)
Здесь и – переносные скорость и ускорение соответственно.
Уравнения кинематической связи – уравнения, связывающие кинематические характеристики различных тел системы:
(1.27)
Существуют два способа нахождения уравнений кинематической связи.
Способ 1. Принцип независимых перемещений. Перемещение какого-либо тела в системе связанных тел складывается из так называемых «независимых» перемещений, каждое из которых обусловлено (вызвано) перемещением соответствующего другого тела системы при покоящихся остальных телах:
. (1.28)
Способ 2. Записать величины постоянных кинематических характеристик элементов связей (нитей, штанг, блоков, поверхностей и т.д.) через координаты тел системы, используя свойства этих элементов (нерастяжимость, неподвижность, недеформированность), и продифференцировать эти величины по времени.
1.2. Основные типы задач и методы их решения
1.2.1. Классификация задач кинематики
Основной задачей кинематики является определение кинематических характеристик тел, движущихся относительно данной системы отсчета.
Большинство задач кинематики можно условно отнести к следующим типам задач или их комбинациям:
1) кинематика материальной точки,
2) принцип суперпозиции движений,
3) уравнения кинематической связи,
4) кинематика простейших механических систем.
Как правило, один из типов задач имеет основное, другие – подчиненное по отношению к условию задачи значение.
1.2.2. Общая схема решения задач кинематики
I. Определиться с моделями материальных объектов и явлений.
1. Нарисовать чертеж, на котором изобразить рассматриваемые тела.
2. Выбрать систему отсчета и изобразить на чертеже ее систему координат (из соображений удобства).
3. Изобразить и обозначить кинематические характеристики тел.
4. Выбрать модели тел и их движения (если это не сделано в условии задачи).
II. Записать полную систему уравнений для искомых величин.
1. Записать в проекциях на оси координат:
а) законы движения,
б) законы изменения скорости,
в) законы изменения ускорения.
2. Записать начальные условия.
3. Записать уравнения кинематических связей.
4. Использовать результаты ранее решенных задач и особые условия задачи (например, заданные соотношения между характеристиками системы).
III. Получить искомый результат в аналитическом и численном видах.
1. Решить систему полученных уравнений.
2. Провести анализ решения (проверить размерность и лишние корни, рассмотреть характерные случаи, установить область применимости).
3. Получить численный результат.
Примечания.
В случае решения задач на кинематику материальной точки в пп. I.3 – II.2 речь идет о кинематических характеристиках материальной точки, а п. II.3 надо опустить.
В случае решения задач на кинематику простейших механических систем в пп. I.3 – II.2 речь идет о кинематических характеристиках тел рассматриваемой системы.
Пункты II.1 – II.3 (в том числе II.2.a – II.2.в) можно выполнять в той или иной последовательности в зависимости от типа задачи.
1.3. Примеры решения задач
Задача 1.1
(Кинематика материальной точки)
Скорость материальной точки зависит от ее положения в декартовой системе координат следующим образом: , где c и b – положительные постоянные величины. В начальный момент времени радиус-вектор материальной точки равен нулю: . Определить:
а) законы движения , изменения скорости и ускорения , тангенциальную и нормальную проекции ускорения;
б) уравнение траектории y(x) материальной точки;
в) радиус кривизны траектории ;
г) угол между скоростью и ускорением .
Решение
Следуем общей схеме решения задач кинематики материальной точки и простейших систем.
I. По условию задачи движение происходит в плоскости XY, образованной координатными осями, направления которых заданы ортами и .
II. Запишем начальные условия и закон изменения скорости тела в проекциях на оси выбранной системы координат:
(1.29)
(1.30)
III. Записанные дифференциальные уравнения относительно координат материальной точки (1.29) с учетом начальных условий (1.29) позволяют найти закон движения материальной точки в проекциях на оси координат и зависимость от времени радиус-вектора :
(1.31)
. (1.32)
Используя найденную зависимость x(t) (1.31), определим закон изменения скорости и закон изменения ускорения :
, (1.33)
. (1.34)
Уравнение траектории находится из закона движения материальной точки путем исключения из (1.31) времени t:
. (1.35)
Остальные искомые величины определяются в соответствии с формулами, приведенными в п. 1 данной Главы.
Модуль скорости (1.7) равен:
. (1.36)
Проекции ускорения и (1.19, 1.23) получим в виде:
(1.37)
Радиус кривизны траектории (1.21) равен:
. (1.38)
Угол между скоростью и ускорением определяется соотношением:
. (1.39)
Заметим, что материальная точка движется по параболической траектории (1.35) с постоянным ускорением, направленным вдоль оси Y (1.34). На рис. 1.5 схематично изображена траектория движения материальной точки и изображены векторы ускорения и начальной скорости.
Нетрудно видеть, что при решения соответствуют начальным условиям задачи. При этом тангенциальное ускорение в указанный момент времени равно нулю, радиус кривизны траектории в данный момент времени , а угол между скоростью и ускорением .
При значения координат точки и модуль скорости, как и следовало ожидать, неограниченно возрастают, нормальное ускорение и угол между скоростью и ускорением стремятся к нулю, а радиус кривизны траектории – к бесконечности.
Задача 1.2
(Кинематика материальной точки)
Находящееся на высоте H над Землей тело бросили горизонтально с начальной скоростью . Найти закон движения тела, уравнение траектории, законы изменения скорости и ускорения, а также нормальную и тангенциальную проекции ускорения и радиус кривизны траектории в произвольный момент времени.
Решение
I. Нарисуем чертеж и изобразим на нем заданную в условии задачи скорость тела в начальный момент времени (t = 0) и предполагаемую траекторию движения тела (рис. 1.6).
Выберем систему отсчета, связанную с Землей. Ось X декартовой системы координат направим горизонтально вдоль поверхности Земли по направлению начальной скорости , а ось Y – вертикально вверх на положение тела в начальный момент времени. Будем считать, что тело является материальной точкой, а движение тела у поверхности Земли происходит с постоянным ускорением свободного падения .
II. В соответствии с выбранной системой отсчета и выбранными моделями тела и его движения запишем начальные условия и закон изменения ускорения тела в проекциях на оси координат:
(1.40)
(1.41)
III. Записанные дифференциальные уравнения относительно проекций скорости материальной точки с учетом начальных значений позволяют найти закон изменения скорости тела и закон его движения в проекциях на оси координат:
(1.42)
(1.43)
Уравнение траектории находится из закона движения тела в координатной форме (1.43) путем исключения времени t:
. (1.44)
Остальные искомые величины определяются в соответствии с формулами, приведенными в п. 1 данной Главы.
Модуль скорости (1.8) равен:
. (1.45)
Модуль ускорения (1.14) имеет вид:
. (1.46)
Проекции ускорения на направление скорости и перпендикулярное ему направление (1.19, 1.23) равны:
, . (1.47)
Радиус кривизны (1.21) определяется соотношением:
. (1.48)
Заметим, что в данной задаче все формулы для нахождения искомых величин справедливы с начального момента времени t0 = 0 до момента падения тела на Землю t0 £ t£ tпад. Этот момент времени легко найти из закона движения (1.43), приняв координату y равной нулю:
. (1.49)
Задача 1.3
(Кинематика материальной точки и принцип
суперпозиции движений)
Лодка пересекает реку с постоянной относительно воды скоростью , перпендикулярной направлению течения реки. Модуль скорости течения реки, ширина которой d, нарастает от берегов к середине реки по параболическому закону, изменяясь от 0 до um. Найти уравнение траектории лодки, время ее движения , а также снос лодки l вниз по течению от места ее отплытия до места причаливания на противоположном берегу реки.
Решение
I. Выберем декартову систему координат, жестко связанную с берегом реки, и с началом в месте отплытия лодки. Оси системы координат и скорость течения реки изображены на рис. 1.7.
При решении задачи лодку будем считать материальной точкой, а берега реки параллельными.
II. Запишем начальные условия для лодки в соответствии с условиями задачи:
(1.50)
где , – проекции скорости лодки на оси выбранной системы координат.
В соответствии с принципом суперпозиции движений (1.26) в любой момент времени или в проекциях на оси координат:
(1.51)
По условию задачи модуль скорости течения реки, ширина которой d, нарастает от берегов к середине реки по параболическому закону, поэтому можно записать:
, (1.52)
где и – постоянные величины. Для определения величины используем условие задачи:
. (1.53)
Используя начальные условия и соотношение (1.53), получим величину a:
. (1.54)
III. Система уравнений (1.51) с учетом (1.52) – (1.54) преобразуется к виду:
(1.55)
Интегрируя уравнения (1.55) с учетом начальных условий для координат лодки (1.50), находим закон движения:
, (1.56)
. (1.57)
Уравнение траектории получаем, исключая время t из закона движения в координатной форме (1.56) и (1.57):
. (1.58)
Поскольку в момент причаливания , время движения лодки равно:
. (1.59)
Следовательно, для искомого сноса лодки l получим (см. 1.58):
. (1.60)
Задача 1.4
(Принцип суперпозиции движений)
Определить форму траектории капель дождя на боковом стекле трамвая, движущегося горизонтально со скоростью , во время его торможения с ускорением . Капли дождя падают на землю вертикально вниз, и скорость их относительно земли постоянна и равна .
Решение
I. Нарисуем чертеж и изобразим на нем заданные в условии задачи кинематические характеристики капли дождя и трамвая в момент начала торможения трамвая (рис. 1.8).
Выберем систему координат XY, связанную с Землей, так, чтобы ось X была направлена горизонтально вдоль ускорения трамвая, а ось Y – вертикально вниз. Выберем также вторую систему координат X¢Y¢, связанную со стеклом трамвая, так, чтобы ее оси X¢ и Y¢ были сонаправлены с осями X и Y. Время в обеих системах отсчитываем от момента начала торможения трамвая.
Будем считать, что капля дождя является материальной точкой, положение которой в момент начала торможения трамвая совпадает с началом координат системы X¢Y¢.
II. Используя принцип суперпозиции движений (1.26), запишем скорость и ускорение капли дождя относительно стекла трамвая (системы координат X¢Y¢):
, (1.61)
. (1.62)
В соответствии с выбранной системой отсчета запишем начальные условия для капли дождя:
, (1.63)
, (1.64)
III. Записанные дифференциальные уравнения (1.61) и (1.62) с учетом начальных условий (1.63) и (1.64) позволяют найти закон движения капли в проекциях на оси координат:
(1.65)
Уравнение траектории находится из закона движения капли путем исключения из (1.65) времени t:
. (1.66)
Как видим, траектория в системе координат X¢Y¢, связанной со стеклом трамвая, является параболой (см. рис. 1.9) с вершиной в точке с координатами:
, . (1.67)
Задача 1.5
(Уравнения кинематической связи)
Концы твердого стержня MN могут свободно скользить по сторонам прямого угла MON (см. рис. 1.10). Найти уравнение траектории точки P стержня, которая делит его на части длиной а и b.
Решение
I. Выберем и изобразим декартову систему координат, оси которой совпадают со сторонами угла MON (см. рис. 1.10).
В соответствии с условием задачи будем считать стержень абсолютно твердым. Следовательно, его положение в любой момент времени t однозначно задается углом j(t) между осью OX и стержнем MN.
II. Запишем закон движения точки P стержня в координатной форме (см. рис. 1.10):
(1.68)
Искомое уравнение траектории точки P можно получить, исключив время из закона движения (1.68).
III. Преобразуя уравнения (1.68), получаем:
. (1.69)
Следовательно, искомое уравнение траектории принимает вид:
. (1.70)
Уравнение (1.70) является уравнением эллипса с полуосями, совпадающими по направлению с осями выбранной системы координат и равными a и b. В случае, когда a = b, эллипс вырождается в окружность.
Задача 1.6
(Уравнения кинематической связи)
На клине с углом при основании a, расположенном на горизонтальной поверхности, находится система двух тел 1 и 2 (см. рис. 1.11), связанных нерастяжимой нитью, перевешенной через маленький блок, ось которого закреплена в верхней точке клина. Записать уравнение кинематической связи для ускорений клина и двух тел, если тело 2 не отрывается от вертикальной поверхности клина в процессе движения.
Решение
I. Выберем систему отсчета, связанную с горизонтальной поверхностью. Ось X декартовой системы координат направим горизонтально, а ось Y вертикально вверх (см. рис. 1.11).
Будем считать тела 1 и 2 материальными точками, связанными нерастяжимой нитью, а клин – абсолютно твердым телом, которое может двигаться поступательно вдоль оси X. Обозначим координаты первого и второго тел в системе координат XY – (x1, y1) и (x2, y2), соответственно. Линейные размеры блока по условию задачи малы по сравнению с длиной нити, поэтому не будем учитывать их при записи уравнений кинематической связи для координат тел системы.
II. Выразим длину нити l через вертикальные координаты различных точек рассматриваемой системы тел:
, (1.71)
где – координата блока, не изменяющаяся в процессе движения.
Если длину наклонного участка нити выразить через горизонтальные координаты тел системы, то выражение для длины нити принимает вид:
. (1.72)
III. Дифференцируя (1.71) и (1.72) дважды по времени и учитывая, что и , получаем искомые уравнения кинематической связи для ускорений тел рассматриваемой системы:
(1.73)
Задача 1.7
(Уравнения кинематической связи)
Система тел состоит из двух блоков и двух подвешенных к ним тел (см. рис. 1.12). Один из блоков составлен из двух коаксиальных цилиндров с неподвижной относительно потолка осью, имеющих различные радиусы r и R. Первое тело подвешено на нити, намотанной на цилиндр радиуса r, второй – на нити, прикрепленной к оси другого блока. Найти ускорение второго тела, если известно, что ускорение первого тела равно a1. Нити считать нерастяжимыми.
Решение
I. Выберем систему отсчета, жестко связанную с потолком. Направление осей декартовой системы координат, связанной с телом отсчета, показано на рис. 1.12.
Считаем тела 1 и 2 материальными точками, нити – нерастяжимыми. Проскальзывания нитей относительно блоков нет.
II. Пусть за малый интервал времени Dt изменение координаты первого тела равно Dx1 (для определенности будем считать, что оно опускается). Поскольку нить нерастяжима, то угол поворота Dj цилиндра радиусом r связан с величиной Dx1 следующим соотношением:
. (1.74)
При этом второй цилиндр радиусом R повернется на тот же угол Dj, а длина нити, на которой лежит блок с подвешенным к нему телом 2, изменится на величину:
. (1.75)
Изменение координаты центра второго блока, а значит и второго тела, равно:
. (1.76)
III. Решая систему уравнений (1.74) – (1.76), получим уравнение, связывающее изменения координат двух тел:
. (1.77)
Поделив левую и правую части (1.77) на малый интервал времени, получим уравнение кинематической связи для скоростей тел:
. (1.78)
Дифференцируя полученное соотношение по времени, получаем искомую связь между ускорениями тел:
. (1.79)
Задача 1.8
(Кинематика простейших механических систем)
На вал радиуса R, закрепленный на оси, намотана веревка, на конце которой висит груз, опускающийся вниз (см. рис. 1.13). Закон движения груза: x = x0 + bt2, где x0 и b – постоянные положительные величины. Определить угловые скорость w и ускорение b произвольной точки обода вала, модуль ускорения a, его нормальную an и тангенциальную at проекции. Записать закон движения этой точки.
Решение
I. Нарисуем чертеж и изобразим на нем направление скорости движения груза. В соответствии с условием задачи направим ось X декартовой системы координат вертикально вниз (рис. 1.13). Для определения ускорения и закона движения произвольной точки A на ободе вала выберем полярную систему координат с полярной осью Y, в которой угол j однозначно определяет положение рассматриваемой точки A. Поскольку в условии задачи не оговаривается иное, веревку считаем нерастяжимой и что проскальзывания веревки относительно вала нет.
II. Запишем заданный в задаче закон движения груза в декартовой системе координат:
. (1.80)
Поскольку веревка нерастяжима, уравнение кинематической связи имеет вид:
. (1.81)
Для решения задачи записанные уравнения необходимо дополнить определениями (1.24) и выражениями (1.25) для интересующих нас величин, приведенными в п. 1.1.
III. Найдем законы изменения скорости груза и его ускорения в проекциях на оси декартовой системы координат, используя определения (1.6) и (1.12):
, ; (1.82)
, . (1.83)
Точки обода вала совершают неравномерное движение по окружности, причем модуль их скорости (поскольку нить нерастяжима и не проскальзывает по поверхности обода) в каждый момент времени равен модулю скорости груза, поэтому, используя (1.22) для угловой скорости w и углового ускорения b, получаем:
, (1.84)
. (1.85)
Поскольку проекция ускорения груза на ось X равна тангенциальной проекции ускорения точек обода, то:
. (1.86)
Нормальную проекцию ускорения определим, используя (1.22):
. (1.87)
Модуль полного ускорения произвольной точки A на ободе колеса найдем из соотношения (1.20):
. (1.88)
Закон движения произвольной точки A на ободе вала запишем в полярной системе координат:
, (1.89)
где j0 – начальное значение угловой координаты точки A в выбранной полярной системе координат.
Задача 1.9
(На кинематику материальной точки)
Закон движения движущейся в плоскости материальной точки, заданный в полярной системе координат, имеет следующий вид: r = r(t), φ = φ(t). Определить законы изменения проекций скорости и ускорения материальной точки на направления, задаваемые ортами декартовой и полярной систем координат, жестко связанных с телом отсчета. Начало декартовой системы координат совпадает с полюсом полярной системы, а ось X декартовой системы направлена вдоль полярной оси (см. рис. 1.14).
Решение
I. Выберем ось Y декартовой системы координат так, чтобы плоскость XY совпадала с плоскостью, в которой движется материальная точка M (рис. 1.14). Для решения задачи используем две системы координат – декартову систему координат XOY c ортами и , и полярную, орты которой и изображены на рис. 1.14. Заметим, что при движении материальной точки происходит изменение ориентации ортов полярной системы и , в то время как орты декартовой системы координат и не изменяют своего направления.
II, III. Закон движения материальной точки, заданный в полярной системе, запишем в декартовой системе координат XOY:
(1.90)
Дифференцируя закон движения (1.90) по времени, получаем искомые законы изменения проекций скорости материальной точки и ее ускорения в декартовой системе координат:
(1.91)
(1.92)
В формулах (1.92), (1.92) и далее для краткости опустим запись зависимости кинематических величин от времени.
Проекции скорости и ускорения материальной точки в полярной системе координат находим двумя способами.
1 способ. Скорость и ускорение материальной точки в полярной системе координат записываются в виде:
, (1.93)
. (1.94)
Следовательно, проекции скорости и ускорения материальной точки на направления, задаваемые ортами рассматриваемых систем координат, связаны соотношениями:
(1.95)
(1.96)
Сравнивая соотношения (1.90) и (1.95), а также (1.91) и (1.96), получим искомые проекции скорости и ускорения материальной точки в полярной системе координат:
(1.97)
(1.98)
2 способ. Запишем радиус-вектор материальной точки в полярной системе координат:
. (1.99)
Поскольку при движении материальной точки происходит изменение ориентации ортов полярной системы и , найдем скорость их изменения (см. рис. 1.15):
(1.100)
Теперь для нахождения скорости и ускорения точки в той же системе координат необходимо продифференцировать радиус-вектор (1.99) по времени с учетом (1.100):
, (1.101)
. (1.102)
В соответствии с (1.101) и (1.102) искомые проекции скорости и ускорения материальной точки в полярной системе координат равны:
(1.103)
(1.104)
Как видим, оба способа решения дают одинаковый результат.
Задача 1.10
(На кинематику материальной точки)
Движение материальной точки в полярной системе координат задается взаимосвязью полярных координат , при этом полярный угол возрастает линейно во времени . Определить зависимость модуля скорости и модуля ускорения материальной точки от времени.
Решение
I. Решаем задачу в заданной полярной системе координат. Заметим, что материальная точка M движется по замкнутой траектории, периодически, с периодом , возвращаясь в ту же точку пространства (см. рис. 1.16).
II. Определим закон изменения проекций скорости и ускорения материальной точки в полярной системе координат, воспользовавшись формулами (1.103) и (1.104), полученными в предыдущей задаче:
(1.105)
(1.106)
Тогда искомые модули скорости и ускорения материальной точки равны:
, (1.107)
(1.108)
Заметим, что материальная точка в моменты времени (где = 0, 1, 2, …) находится в начале (полюсе) полярной системы координат, имеет нулевую скорость, а ускорение, по модулю равное , направлено противоположно полярной оси.
Задача 1.11
(На кинематику материальной точки)
Планета движется вокруг Солнца в соответствии с законами Кеплера по эллиптической траектории . Параметр эллипса , эксцентриситет и секторную скорость считать заданными. Определить проекции ускорения планеты в зависимости от координат и полярной системы.
Решение
I. При решении задачи будем считать планету и Солнце материальными точками. Согласно первому закону Кеплера все планеты движутся по эллиптическим орбитам, причем Солнце находится в одном из фокусов эллипса O (см. рис. 1.17).
В соответствии с условием задачи введем полярную систему координат в плоскости движения планеты, полюс которой совпадает с Солнцем, а полярная ось совпадает с одной из осей эллипса.
Согласно второму закону Кеплера секторная скорость планеты, равная скорости изменения площади, описываемой радиус-вектором материальной точки, представляющим планету, постоянна при движении планеты вокруг Солнца.
II. Для нахождения проекций ускорения планеты в полярной системе координат воспользуемся формулами (1.104):
(1.109)
Поскольку в уравнения (1.109) входят производные полярных координат по времени, дополним эту систему уравнением траектории планеты и выражением для ее секторной скорости :
, (1.110)
. (1.111)
III. В соответствии с условием задачи секторная скорость постоянна при движении планеты по эллиптической траектории, поэтому ее производная по времени равна нулю:
. (1.112)
Сравнивая (1.112) с выражением (1.109) для проекции ускорения , видим, что . Следовательно, ускорение в любой момент времени имеет только проекцию , которая в соответствии с (1.109) является функцией производных полярных координат по времени.
Продифференцируем обе части уравнения траектории (1.110) по времени:
. (1.113)
Используя уравнение траектории (1.110) и выражение для секторной скорости (1.111), преобразуем (1.113) к виду:
. (1.114)
Продифференцируем теперь обе части уравнения (1.114) по времени
. (1.115)
Опять воспользуемся уравнением траектории (1.110) и выражением для секторной скорости (1.111) для исключения и из (1.115):
. (1.116)
В результате находим:
. (1.117)
Для нахождения искомой проекции ускорения планеты , как функции только координат полярной системы, подставим (1.116) и (см. (1.111)) в выражение (1.109):
. (1.118)
Таким образом, ускорение планеты, движущейся по эллиптической траектории, направлено к Солнцу, не зависит от полярного угла и обратно пропорционально квадрату расстояния до Солнца:
(1.119)
Задача 1.12
(На кинематику материальной точки)
Небольшое тело движется по гладкой внутренней поверхности полого вертикального цилиндра радиуса R. В начальный момент времени скорость тела направлена перпендикулярно оси цилиндра и равна . Определить законы изменения скорости и ускорения материальной точки в цилиндрической системе координат, а также угол между скоростью и ускорением.
Решение
I. Будем считать тело материальной точкой, которая движется по цилиндрической поверхности с постоянной вертикальной составляющей ускорения, равной ускорению свободного падения . Для решения задачи выберем цилиндрическую систему координат, ось Z которой совпадает с осью цилиндра, как показано на рис. 1.18. На том же рисунке изображены орты er, ej и ez цилиндрической системы. Ось, от которой отсчитывается угол системы координат, направим на положение тела в начальный момент времени.
II. В соответствии с условиями задачи и выбранной системой координат запишем начальные значения проекций скорости для рассматриваемого тела:
, , . (1.120)
Воспользуемся формулами (1.103) и (1.104) для проекций скорости и ускорения тела на направления, задаваемые ортами цилиндрической системы:
, , , (1.121)
, , . (1.122)
Кроме того, в соответствии с условиями задачи, запишем:
, , . (1.123)
III. Используя (1.121) – (1.123), получим законы изменения проекций скорости и ускорения:
, , ; (1.124)
, , . (1.125)
Таким образом, искомый закон изменения скорости и ускорения в цилиндрической системе координат имеет следующий вид:
, (1.126)
. (1.127)
Определим также искомый угол a между скоростью и ускорением тела:
. (1.128)
1.4. Задачи для самостоятельного решения
Задача 1
Из пушки, находящейся на самолете, летящем горизонтально со скоростью , выпущен снаряд в направлении движения самолета. Скорость снаряда относительно самолета равна . Пренебрегая сопротивлением воздуха, найти:
1) уравнение траектории снаряда относительно Земли ;
2) уравнение траектории снаряда относительно самолета ;
3) уравнение траектории самолета относительно снаряда .
Ответ: 1) , 2) ,
3) , . Оси X, X‘ и X” декартовой системы координат направлены горизонтально вдоль скорости самолета, а оси Y, Y‘ и Y” – вертикально вверх, при этом начало координат системы XY совпадает с положением самолета в момент выстрела пушки.
Задача 2
Лодка пересекает реку шириной d с постоянной относительно воды скоростью , перпендикулярной скорости течения реки, модуль которой нарастает от берегов к середине реки по линейному закону, меняясь от 0 до u. Найти траекторию лодки, а также снос лодки l вниз по течению от места ее отплытия до места причаливания на противоположном берегу реки.
Ответ: , при y < d/2; , при y > d/2; . Ось X декартовой системы координат XY направлена вдоль берега реки, а ось Y – поперек реки. Начало системы координат, жестко связанной с берегом реки, совпадает с местом отплытия лодки.
Задача 3
По движущемуся вниз эскалатору спускается пассажир со скоростью относительно эскалатора. Скорость эскалатора равна u. Спускаясь по неподвижному эскалатору пассажир проходит N ступеней. Сколько ступеней N‘ пройдет пассажир, спускаясь по движущемуся эскалатору?
Ответ: .
Задача 4
Два трактора, движущиеся со скоростями и , буксируют с помощью тросов автомобиль (см. рис.).
Определить модуль и направление скорости автомобиля в тот момент, когда тросы параллельны векторам и , а угол между ними равен a.
Ответ: ,
, где – угол между векторами и .
Задача 5
Тело А подвешено на нитях, перекинутых через блоки В и С малого диаметра так, что АВ = ВС (см. рис.).
Концы нитей тянут с одинаковыми скоростями . Расстояние между блоками В и С равно L. Найти модуль скорости тела А в тот момент, когда оно находится на расстоянии H от прямой ВС.
Ответ: .
Задача 6
Лодку подтягивают к пристани высотой Н с помощью веревки, наматываемой на вал лебедки. Радиус вала равен R << H. Вал вращается с постоянной угловой скоростью w. Определить зависимость модулей скорости и ускорения лодки от длины веревки L > Н. Движение лодки считается поступательным.
Ответ: , .
Задача 7.
Найти уравнение кинематической связи для ускорений тел, подвешенных на нерастяжимых нитях (см. рис.).
Ответ: , где , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 8
Определить закон изменения модуля скорости материальной точки, движущейся в плоскости, если ее движение описывается в полярной системе координат следующим законом: , , где и – положительные постоянные величины.
Ответ: , при .
Задача 9
Четыре тела подвешены на нерастяжимых нитях (см. рис.). Найти ускорение тела 4, если известны ускорения остальных трех тел.
Ответ: , где , , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 10
Найти уравнение кинематической связи для ускорений тел, подвешенных на нерастяжимых нитях так, как показано на рисунке.
Ответ: ,
где , , , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 11
Два тела подвешены на нерастяжимых нитях, как показано на рисунке. Определить ускорение тела 2, если известно ускорение тела 1.
Ответ: , где и – проекции ускорений тел на вертикальную ось декартовой системы координат.
[1] Далее в тексте, если это не оговаривается особо, используется декартова система координат.
![]()
Физический смысл производной. В состав ЕГЭ по математике входит группа задач для решения которых необходимо знание и понимание физического смысла производной. В частности, есть задачи, где дан закон движения определённой точки (объекта), выраженный уравнением и требуется найти его скорость в определённый момент времени движения, либо время, через которое объект приобретёт определённую заданную скорость. Задачи очень простые, решаются они в одно действие. Итак:
Пусть задан закон движения материальной точки x (t) вдоль координатной оси, где x координата движущейся точки, t – время.
Скорость в определённый момент времени – это производная координаты по времени. В этом и состоит механический смысл производной.
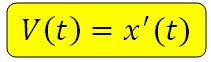
Аналогично, ускорение – это производная скорости по времени:
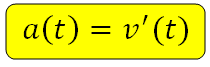
Таким образом, физический смысл производной это скорость. Это может быть скорость движения, скорость изменения какого-либо процесса (например роста бактерий), скорость совершения работы (и так далее, прикладных задач множество).
Кроме того, необходимо знать таблицу производных (знать её нужно также, как таблицу умножения) и правила дифференцирования. Если конкретно, то для решения оговоренных задач необходимо знание первых шести производных (см. таблицу):

Рассмотрим задачи:

Материальная точка движется прямолинейно по закону
x (t) = t2 – 7t – 20
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 5 c.
Физический смысл производной это скорость (скорость движения, скорость изменения процесса, скорость работы и т.д.)
Найдем закон изменения скорости: v (t) = x′(t) = 2t – 7 м/с.
При t = 5 имеем:
![]()
Ответ: 3
Решить самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = 6t2 – 48t + 17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 c.
Посмотреть решение
Материальная точка движется прямолинейно по закону x (t) = 0,5t3 – 3t2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = –t4 + 6t3 + 5t + 23
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
Посмотреть решение

Материальная точка движется прямолинейно по закону
x (t) = (1/6) t2 + 5t + 28
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 6 м/с?
Найдем закон изменения скорости:
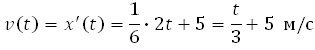
Для того, чтобы найти, в какой момент времени t скорость была равна 3 м/с, необходимо решить уравнение:
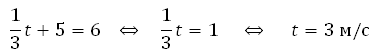
Ответ: 3
Решите самостоятельно:
Материальная точка движется прямолинейно по закону x (t) = t2 – 13t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Посмотреть решение
Материальная точка движется прямолинейно по закону
x (t) = (1/3) t3 – 3t2 – 5t + 3
где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Посмотреть решение
Отмечу, что ориентироваться только на такой тип задач на ЕГЭ не стоит. Могут совершенно неожиданно ввести задачи обратные представленным. Когда дан закон изменения скорости и будет стоять вопрос о нахождении закона движения.
Подсказка: в этом случае необходимо найти интеграл от функции скорости (это так же задачи в одно действие). Если потребуется найти пройденное расстояние за определённый момент времени, то необходимо подставить время в полученное уравнение и вычислить расстояние. Впрочем, мы такие задачи тоже будем разбирать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
15 мая 2014
Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:
[v={S}’={x}’left( t right)]
Точно так же мы можем посчитать и ускорение:
[a={v}’={{S}’}’={{x}’}’left( t right)]
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.
Давайте посмотрим, как это работает при решении реальных задач.
Пример № 1
Материальная точка движется по закону:
[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.
Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.
[v={S}’={x}’left( 2 right)]
Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.
Давайте решать. В первую очередь, посчитаем производную:
[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
Нам требуется найти производную в точке 2. Давайте подставим:
[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]
[=-16+32-12+5=9]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.
Пример № 2
Материальная точка движется по закону:
[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?
Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.
В первую очередь, вновь ищем производную:
[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]
[{x}’left( t right)={{t}^{2}}-8t+19]
От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:
[{{t}^{2}}-8t+19=3]
[{{t}^{2}}-8t+16=0]
[{{left( t-4 right)}^{2}}=0]
[t-4=0]
[t=4]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Смотрите также:
- Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!

- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром

- Схема Бернулли. Примеры решения задач

- Комбинаторика в задаче B6: средний тест

- Как решать задачи про летающие камни?

- B4: счетчики на электричество

изучает
механическое движение, то есть перемещение
одних тел относительно других.
Глава 1. Кинематика
раздел
механики, в котором изучается движение
тел без выяснения причин этого движения.
1.1. Закон движения материальной точки
Материальная
точка
– тело,
размером которого можно пренебречь в
данной задаче (размеры тел намного
меньше расстояний между ними; тела
движутся поступательно).
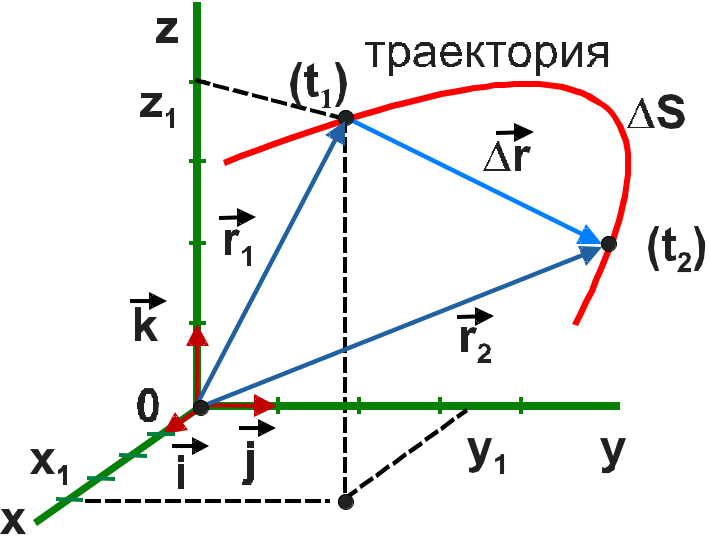
Рис.
1.1.1
Система
отсчета
выбирается
для описания движения тел. Система
отсчета включает тело отсчета (относительно
которого рассматривается движение),
связанную с ним систему координат и
способ отсчета времени (часы) (рис.
1.1.1).
Положение
материальной точки в пространстве
задается
радиусом–вектором
![]()
,
или его
проекциями на оси
![]()
(координатами
).
Связь
этих величин определяет формула
![]()
,
где
![]()
– единичные векторы (орты) осей
(рис.
1.1.1),
причем,
![]()
(теорема Пифагора).
![]()
или
![]()
.
Закон
движения
представляет зависимость
радиуса-вектора
![]()
( или координат
![]()
)
от времени
t
и
позволяет определить положение движущейся
материальной точки в любой момент:
Эти соотношения
связаны принципом
суперпозиции движений:
любое сложное движение в пространстве
можно представить суммой трех независимых
прямолинейных движений вдоль осей
![]()
![]()
Траектория
– линия,
по которой
движется тело (рис.
1.1.1).
Путь
![]()
(м) – расстояние,
пройденное
телом по траектории за время
![]()
.
Перемещение
![]()
(м) –
вектор, соединяющий
начальную и конечную точки пути:
![]()
.
1.2. Скорость определяет быстроту движения.
Математика.
Средней
скоростью
изменения
функции
![]()
называется отношение приращения функции
![]()
к приращению аргумента
![]()
:
![]()
.
Мгновенной,
истинной скоростью
изменения
![]()
называется предел, к которому стремиться
средняя скорость при
![]()
:
![]()
.
Таким образом,
Чтобы определить скорость изменения функции, надо взять производную этой функции по времени.
Скорости
движения
определяют
быстроту движения.
При
движении материальной точки
![]()
становятся функциями от времени
![]()
,
поэтому, вводится три типа скоростей:
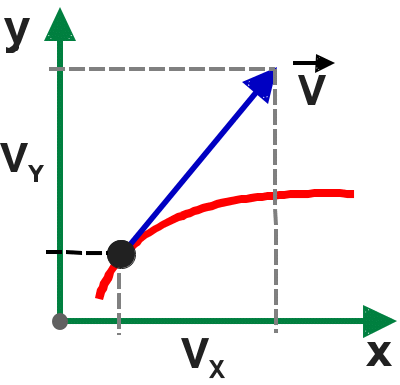
Рис.
1.2.1
Мгновенная
скорость
![]()
(м/с)
– первая
производная радиуса-вектора по времени:
![]()
.
Вектор мгновенной
скорости направлен по касательной к
траектории (рис. 1.2.1)
Координатные
скорости
–
проекции
вектора скорости
на оси координат (рис.
1.2.1)
– равны первой производной соответствующей
координаты по времени:
![]()
.
Скалярная,
путевая скорость
![]()
(м/с)
– первая
производная пути
![]()
по времени:
![]()
.
Связи
между скоростями.
Дифференцируя
принцип суперпозиции, получаем:
![]()
![]()
.
Так как
![]()
,
то
![]()
.
Из теоремы Пифагора
—
![]()
.
1.3. Ускорение
определяет
быстроту изменения скорости (скорость
изменения скорости).
Аналогично
скорости, можно ввести три типа ускорений.
Ускорение
![]()
(м/с2)
– первая
производная скорости
или вторая производная радиуса-вектора
по времени
![]()
:
![]()
.
Координатные
ускорения
– проекции
вектора ускорения
![]()
на оси координат:
![]()
.
Связи
между ускорениями.
Дифференцируя
принцип суперпозиции два раза, получаем:
![]()
![]()
.
Из теоремы Пифагора:
![]()
.
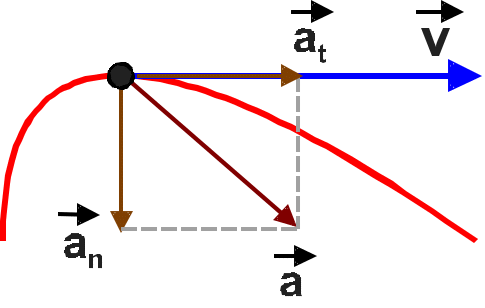
Рис.
1.3.1
Тангенциальная
и нормальная составляющие ускорения.
В общем случае
ускорение
направлено под любым углом к скорости
.
Поэтому, его удобно представлять
векторной суммой двух ускорений
(рис.1.3.1):
![]()
.
![]()
– тангенциальное
ускорение –
направлено вдоль (против) направления
скорости и определяет
изменение скорости движения
материальной точки по
величине:
![]()
.
![]()
– нормальное
ускорение –
направлено перпендикулярно скорости.
Определяет изменение
скорости материальной точки по
направлению:
![]()
,
где
![]()
– радиус кривизны траектории.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предмет – “Элементы высшей математики”.
Условие задачи:
13.Найти закон изменения скорости материальной точки, если a(t) = t5 + 3t – 1.
И варианты ответов:
———————————————————————————————————
Исходя из чего не трудно догадаться, что студенты учебного заведения НТиВТ (Новосибирск), явно обладают способностями ясновидения и чем является a(t) указывать не обязательно. Что забыл здесь данный студент (я), пока неизвестно  .
.
Вероятно a(t) – есть координата.
Так как ускорение это производная скорости по времени, или a(t)’ = 5t4 + 3, а похожего ответа не имеется.
Стало быть находить закон изменения скорости, v(t) будем по формуле:
Кликните здесь для просмотра всего текста
v0 в условии задачи не задано, значит считаем его равным налю.
t и t0 так же не задано, да и в ответах имеется “+ C”, значит и наш интеграл неопределённый.
И пусть мне кто скажет, что верный ответ не A., сразу в дыню 
