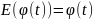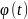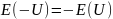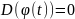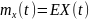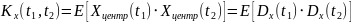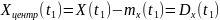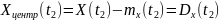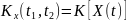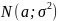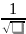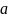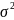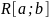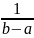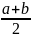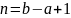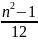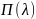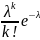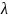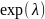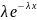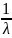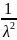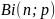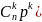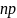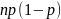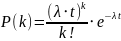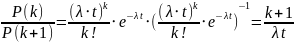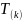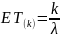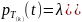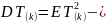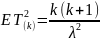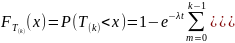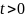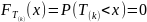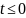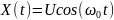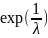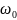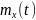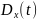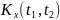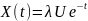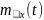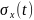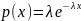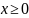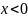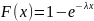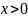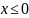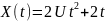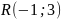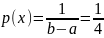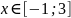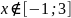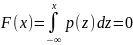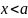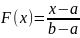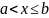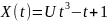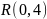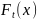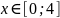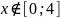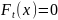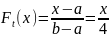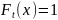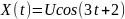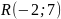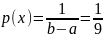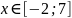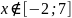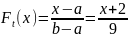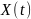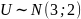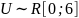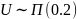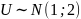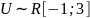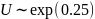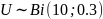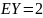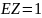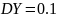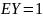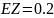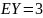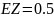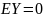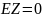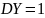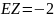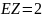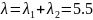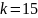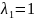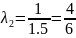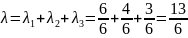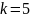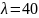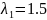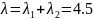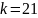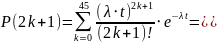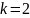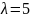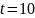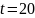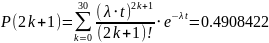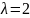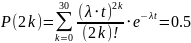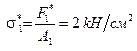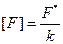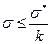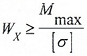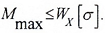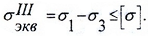Как найти закон распределения сечения

Свойства (для
работы №1)

1. 
   ;
   

   – неслучайная величина

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. Используемые распределения: нормальное,
   равномерное дискретное, пуассоновское,
   экспоненциальное, биномиальное

   Название	Обозначение	Плотность	Мат. ожидание	Дисперсия
   Нормальное
   Равномерное дискретное
   Пуассоновское
   Экспоненциальное
   Биномиальное

10. Для равномерного распределения:

    

Свойства (для
работы №2)

1. Для пуассоновского потока
   

2. Для пуассоновского потока наиболее
   вероятное k находится с помощью отношения
   
   ;
   отношение сравнивается с 1

3. Интенсивность потока Эрланга k-го
   порядка совпадает с математическим
   ожиданием
   
   :
   

4. Плотность распределения:
   

5. 

6. 

7. Функция распределения потока Эрланга
   k-го порядка:

   
   ;
   при
   

   
   ;
   при
   

№ 1.11

Рассматривается случайная функция

,
где U – случайная величина, распределённая
по экспоненциальному закону

,

– константа. Найти математическое
ожидание

,
дисперсию

и корреляционную функцию

.

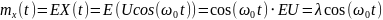
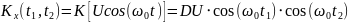
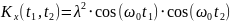
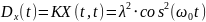
№ 1.12

Рассматривается случайная функция

,
где U – случайная величина, распределённая
по экспоненциальному закону

.
Найти плотность распределения сечения,
математическое ожидание

,
дисперсию

,

и корреляционную функцию

.

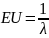
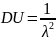
при

;
при

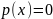
при

;
при

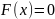
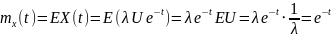
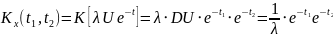
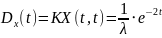
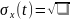
№ 1.13

Рассматривается случайная функция

,
где U – случайная величина, распределённая
по равномерному закону

.
Найти плотность распределения сечения,
математическое ожидание

,
дисперсию

,

и корреляционную функцию

.

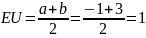
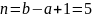
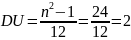
при

;
при

при

;

при

;
иначе 1

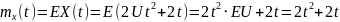
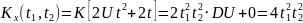
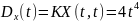
№ 1.14

Рассматривается случайная функция

,
где U – случайная величина, распределённая
по закону

.
Найти закон распределения сечения этой
случайной функции

,
её математическое ожидание

,
дисперсию

,

и корреляционную функцию

.

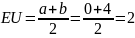
при

;
при

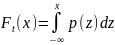
при

при

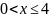
при

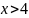
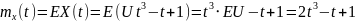
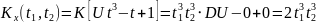
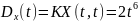
№ 1.15

Рассматривается случайная функция

,
где U – случайная величина, распределённая
по равномерному закону

.
Найти плотность распределения сечения,
математическое ожидание

,
дисперсию

,

и корреляционную функцию

.

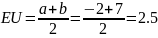
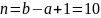
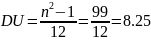
при

;
при

при

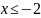
при

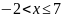
при

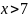
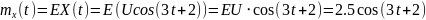
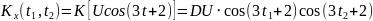
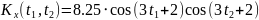
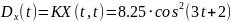
№ 1.17 (задание)

Найти математическое ожидание

,
корреляционную функцию

,
дисперсию

случайного процесса

.
U, V – некоррелированные случайные величины
для следующих случаев.

№ 1.17a

,

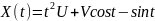
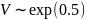
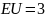
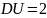
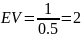
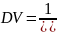
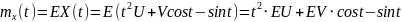
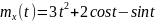
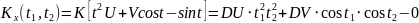
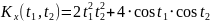
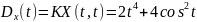
№ 1.17b

,

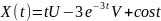
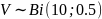
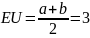
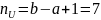
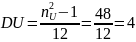
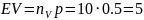
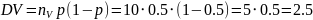
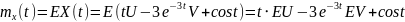
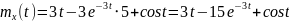
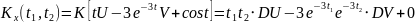
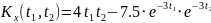
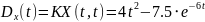
№ 1.17c

,

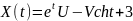
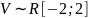
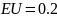
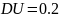
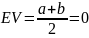
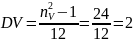
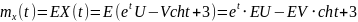
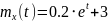
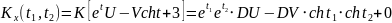
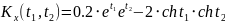
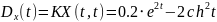
№ 1.17d

,

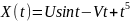
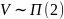
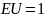
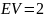
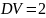
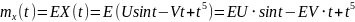
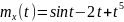
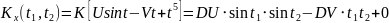
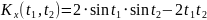
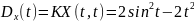
№ 1.17e

,

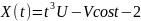
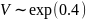
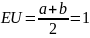
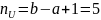
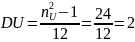
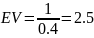
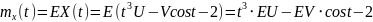
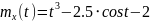
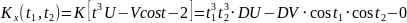
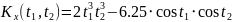
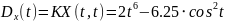
№ 1.17f

,

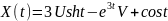
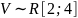
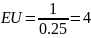
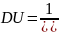
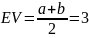
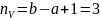
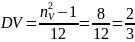
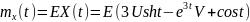
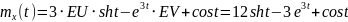
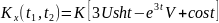
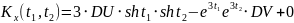
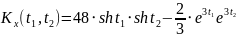
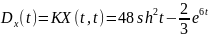
№ 1.17g

,

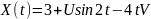
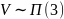
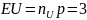
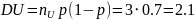
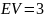
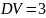
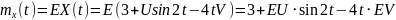
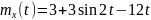
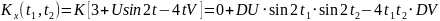
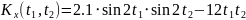
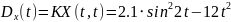
№ 1.18 (задание)

Найти математическое ожидание,
корреляционную функцию и дисперсию
случайного процесса

,
зависящего от Y и Z, где Y и Z – случайные
величины, характеризуемые следующими
числовыми характеристиками.

№ 1.18a

,

,

,

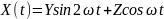
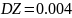
Корреляция между Y и Z равна 0

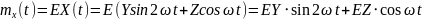
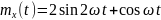
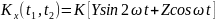
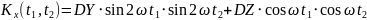
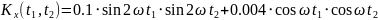
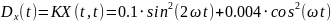
№ 1.18b

,

,

,

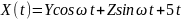
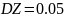
Корреляция между Y и Z равна 0

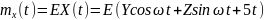
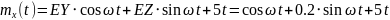
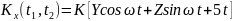
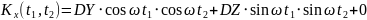
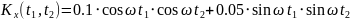
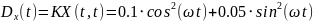
№ 1.18c

,

,

,

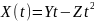
Корреляция между Y и Z равна 0

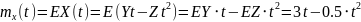
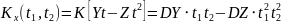
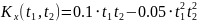
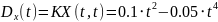
№ 1.18d

,

,

,

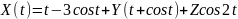
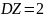
Корреляция между Y и Z равна 0

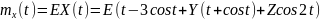
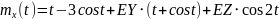
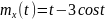
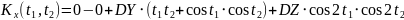
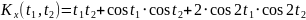
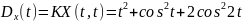
№ 1.18e

,

,

,

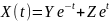
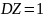
Корреляция между Y и Z равна 0

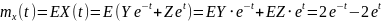
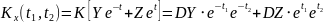
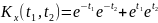
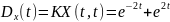
№ 1.18f

,

,

,

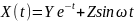
Корреляция между Y и Z равна 0

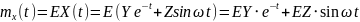
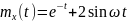
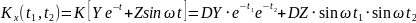
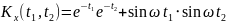
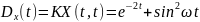
№ 3.44

В аэропорт прибывает 2 простейших потока
самолётов с интенсивностями в среднем
3 и 2.5 самолёта в час. Найти вероятность
того, что за полчаса прибудет не более
4-х самолётов объединённого потока.
Найти наиболее вероятное число прибывающих
самолётов объединённого потока за 3
часа.

;

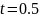
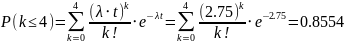
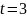
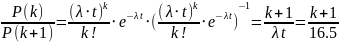
Наиболее вероятное

и

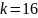
№ 3.45

Устройство состоит из 3 узлов, причём 1
узел в среднем отказывает 1 раз в месяц,
2 узел – 1 раз в полтора месяца, а 3 узел –
1 раз в 2 месяца. Потоки отказов узлов
простейшие. Найти вероятности того, что
за 1 месяц устройство: а) откажет ровно
1 раз; б) откажет хотя бы 2 раза. Найти
наиболее вероятное число отказов за 3
месяца.

;

;

;

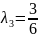
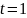
а)

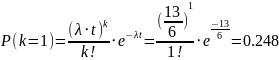
б)

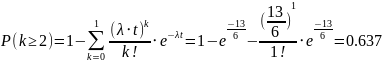
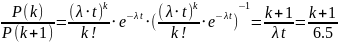
Наиболее вероятное

и

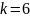
№ 3.49

Поток автомобилей, движущихся по шоссе
в одном направлении, является потоком
Эрланга 5-го порядка с параметром

авт/мин. Найти интенсивность данного
потока, плотность распределения,
математическое ожидание и дисперсию
участка времени между автомобилями в
потоке.

Интенсивность потока Эрланга k-го порядка
совпадает с математическим ожиданием

:

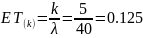
Плотность распределения:

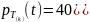
Функция распределения потока Эрланга
k-го порядка:

;
при

;
при

№ 3.50

По шоссе в одном направлении движется
два простейших потока автомобилей с
интенсивностями

(авт/мин) и

(авт/мин). Найти наиболее вероятное число
автомобилей объединённого потока за 5
минут, а также вероятность этого числа.
Найти вероятность того, что за 6 минут
проедет нечётное число автомобилей
объединённого потока.

;

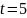
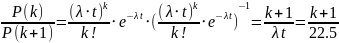
Наиболее вероятное

и

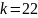
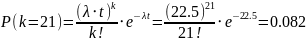
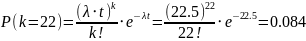
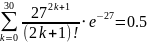
№ 3.52

Система представляет собой простейший
пуассоновский поток отказов радиотехнической
системы с интенсивностью 0.1 отказа в
минуту. Найти вероятность того, что: а)
за 1 час работы наступит более одного
отказа; б) за 2 часа работы не будет ни
одного отказа; в) за полчаса будет чётное
число отказов. Найти наиболее вероятное
число отказов.

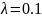
а)

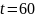
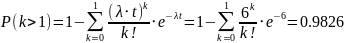
б)

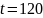
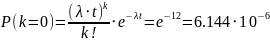
в)

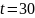
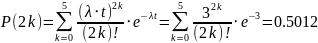
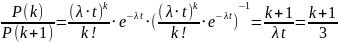
Наиболее вероятное

и

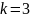
№ 3.58

Поток автомобилей, движущихся по шоссе
в одном направлении, является простейшим
потоком с интенсивностью

авт/мин. Инспектор выходит на шоссе,
чтобы остановить первый попавшийся
автомобиль. Найти плотность распределения
того интервала T* между автомобилями,
на который попадает инспектор, его
математическое ожидание и дисперсию.

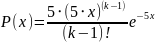
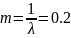
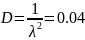
№ 3.64

В аэропорт прибывает простейший поток
самолётов, в среднем 2 самолёта за 5
минут. Найти вероятность того, что а) за
10 минут прибудет не менее 3 самолётов;
б) за 20 минут прибудет не более 5 самолётов;
в) за 5 минут прибудет нечётное число
самолётов.

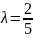
а)

;

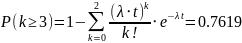
б)

;

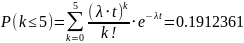
в)

;

(больше 30, уже нет различий)

№ 3.66

На АТС поступает простейший поток
вызовов с интенсивностью 2 вызова в
минуту. Найти вероятность того, что за
3 минуты а) не придёт ни одного вызова;
б) придёт хотя бы 1 вызов; в) придёт чётное
число вызовов.

;

;

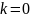
а)

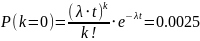
б)

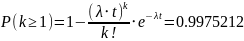
в)

(больше 30, уже нет различий)

№ 3.73

По шоссе в одном направлении движутся
2 простейших потока автомобилей с
интенсивностями 2,5 и 3,5 машины в минуту
соответственно. Найти вероятность того,
что за время

минут: а) не проедет ни одного автомобиля;
б) проедет ровно 6 автомобилей; в) проедет
менее 4 автомобилей; г) проедет чётное
число автомобилей.

Соседние файлы в папке Экзамен 2021

• #
• #
• #
• #
• #
• #

Сопротивление материалов

Метод сечений. Напряжения



Сущность метода сечений

Для расчетов элементов конструкции на прочность необходимо знать внутренние силы упругости, возникающие в результате приложения внешних сил в разных точках и частях конструкции.

Но как заглянуть внутрь материального тела, чтобы выяснить, какие же силы возникают между его частицами или отдельными частями, при приложении нагрузок? Представление о внутренних усилиях, возникающих в теле или элементе конструкции можно получить лишь с помощью воображения и аксиом статики, поясняющих условия равновесного состояния материальных тел.
Способы определения этих внутренних сил с помощью науки сопротивление материалов включают такой прием, как метод сечений.

Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается и взамен ее к сечению оставшейся части прикладываются внутренние силы, действовавшие на нее до разреза со стороны отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием приложенных к сечению внешних и внутренних сил (третий закон Ньютона – действие равно противодействию).
При применении этого метода выгоднее отбрасывать ту часть элемента конструкции (тела), для которой проще составить уравнение равновесия. Таким образом, появляется возможность определить внутренние силовые факторы в сечении, благодаря которым оставшаяся часть тела находится в равновесии (прием, часто применяемый в Статике).

Применяя к оставленной части тела условия равновесия, невозможно найти закон распределения внутренних сил по сечению, но можно определить статические эквиваленты этих сил (равнодействующие силовые факторы).
Так как основным расчетным объектом в сопротивлении материалов является брус, рассмотрим, какие статические эквиваленты внутренних сил проявляются в поперечном сечении бруса.

Рассечем брус (рис. 1) поперечным сечением а-а и рассмотрим равновесие его левой части.

Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а-а, будут главный вектор F_гл, приложенный в центре тяжести сечения, и главный момент М_гл = М_и, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.

Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси и лежащую в плоскости сечения. Эти составляющие главного вектора и главный момент называют внутренними силовыми факторами, действующими в сечении бруса. Составляющую N называют продольной силой, составляющую Q – поперечной силой, пару сил с моментом М_и – изгибающим моментом.

Для определения указанных трех внутренних силовых факторов применим известные из Статики уравнения равновесия оставленной части бруса:

Σ Z = 0;     Σ Y = 0;     Σ M = 0;    (ось z всегда направляем по оси бруса).

Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 2), для определения которых применяют известные из Статики шесть уравнений равновесия оставленной части бруса:

Σ X = 0;     Σ Y = 0;     Σ Z = 0;
Σ M_x = 0;     Σ M_y = 0;     Σ M_z = 0.

Эти силовые факторы в общем случае носят следующие названия: N – продольная сила, Q_x, Q_y – поперечные силы, М_кр – крутящий момент, М_их и М_иу – изгибающие моменты.

При разных деформациях в поперечном сечении бруса возникают различные силовые факторы.
Рассмотрим частные случаи:

1. В сечении возникает только продольная сила N. Это деформация растяжения (если N направлена от сечения) или сжатия (если N направлена к сечению).

2. В сечении возникает только поперечная сила Q. Это деформация сдвига.

3. В сечении возникает только крутящий момент М_кр. Это деформация кручения.

4. В сечении возникает только изгибающий момент М_и. Это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент М_и и поперечная сила Q, то изгиб называют поперечным.

5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий момент и продольная сила), то имеет место сочетание основных деформаций (сложное сопротивление).

***



Напряжение

Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение (обозначается р).
Напряжение характеризует интенсивность внутренних сил, действующих в сечении, и определяется, как отношение величины внутренней силы к площади сечения.
Напряжение является величиной векторной.

Вектор напряжения можно разложить на две составляющие (рис. 3) – одну вдоль оси сечения, вторую – в плоскости сечения (перпендикулярно оси). Эти составляющие носят название нормальное напряжение (обозначается σ) и касательное напряжение (обозначается τ).

Поскольку нормальные и касательные напряжения расположены под прямым углом друг к другу, модуль полного напряжения p можно определить по теореме Пифагора:

р² = σ² + τ²

Единица измерения напряжения – паскаль (Па).
1 Па = Н / м². Поскольку эта единица очень мала, в расчетах часто применяют более крупную кратную единицу – мегапаскаль (МПа), который равен миллиону паскалей (10⁶ Па).

Объяснить сущность напряжения можно на таком простом примере.
В соответствии с гипотезой об отсутствии первоначальных внутренних усилий, считается, что когда к телу не приложены внешние нагрузки его частицы не взаимодействуют друг с другом, т. е. абсолютно равнодушны к “соседкам” справа, слева и т. п. Но стоит приложить к телу внешнюю нагрузку, его частицы начинают лихорадочно цепляться друг за друга, пытаясь удержаться в “кучке”. Если нагрузка растягивает тело, его частицы держатся друг за дружку, не давая разорвать тело, если нагрузка сжимающая – частицы тела стараются удержать “соседок” на прежнем расстоянии.
Совокупность всех этих усилий внутренних частиц, противостоящих внешним раздражителям-нагрузкам, и является напряжением.
Задачи сопромата чаще всего сводятся к тому, чтобы определить предельные величины нагрузок, способных разорвать связи между частицами, из которых состоит тело или, по известным предельным напряжениям определить, какие нагрузки способно выдержать тело не разрушаясь, не деформируясь и т. д.

Нетрудно заметить, что напряжение измеряется в тех же единицах, что и давление, поэтому можно провести некоторую аналогию между этими физическими понятиями. Принципиальная разница заключается в том, что давление – внешний силовой фактор (т. е. воздействующий на тело или его части извне), а напряжение – внутренний силовой фактор, характеризующий степень взаимодействия (взаимосвязи) частиц тела между собой.

***

Правила построения эпюр



Правильные ответы на вопросы Теста № 7

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	3	2	3	2	2	3	1	2	1	2

Закон равномерного распределения нормального напряжения при растяжении (сжатии)

При условии, что внешние силы действуют по центрам сечений (рис.2.4.1) считается, что напряжение σраспределено по сечению равномерно, то есть , причем, независимо от формы сечения.

И наоборот, если сила действует внецентренно, то напряжения распределены не равномерно (рис.2.4.2).

Следствие из закона равномерного распределения нормального напряжения.

Если σ = const, то

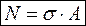
Следовательно σ = N / A

Предел прочности

Пусть стержень с площадью сечения А₁ =1см 2 разрушается при (под разрушением будем понимать разделение тела на части). Поскольку то

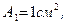
Для любых других стержней теперь можно найти силу, при которой происходит разрушение. Например, при А=2см 2 разрушающая сила F* = 4kH при А=0.3см 2 разрушающая сила F* = 0.6 kH и т.д.

И наоборот, пусть известна сила разрушающая сила F*₂ = 30 kH, при которой происходит разрушение стержня сечением 15 см 2 . Тогда можно найти напряжение, при котором происходит разрушение:

= 30 kH/15 см 2 = 2 kH/см 2

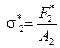
Определение: Напряжение σ * , больше которого не может выдержать материал (другими словами, σ * , при котором происходит разрушение образца), называется пределом прочности. Для него используют и другие обозначения, например, для бетона R, для стали σ_в и т.д.

Условие прочности

Согласно условиям заказчика, рабочая нагрузка F не должна превышать некоторую допустимую величину [F] (квадратные скобки означают фразу «допустимое значение величины»). Т.е. должно выполнятся условие

(2.7.1)

Оно называется условием прочности.

Обычно допустимое значение нагрузки получают, уменьшая нагрузку, при которой происходит разрушение, в k раз:

Константа k называется коэффициентом запаса (в строительстве нередко принимают k =1,5)

Чаще же условие прочности записывают в виде ограничения на рабочиенапряжения σ, которые возникнут в конструкции при приложении проектной нагрузки F:

При использовании введенного обозначения (квадратных скобок), условие прочности примет вид

Величина [σ] называется допустимым напряжением. Если пределы прочности на растяжение и сжатие у материала разные (как например, для чугуна, бетона, камня, дерева), то [σ] снабжается соответствующим индексом. Тогда в сечениях, испытывающих растяжение условие прочности записывают в виде

Там, где имеет место сжатие, условие прочности записывается в виде

Здесь учтено, что в области сжатия напряжения принимают отрицательный знак согласно принятому выше соглашению.

Дата добавления: 2015-11-28 ; просмотров: 1339 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Большая Энциклопедия Нефти и Газа

Закон — распределение — нормальное напряжение

Закон распределения нормальных напряжений в поперечном сечении бруса изображается обычно графиком, показывающим изменение их по высоте или ширине поперечного сечения. [1]

Закон распределения нормальных напряжений по сечению растягиваемого или сжимаемого бруса устанавливается на основе принятой в сопротивлении материалов гипотезы плоских сечений — г и п о т е з ы Я — Б е р — / у / / / / / / / / / / / / / У / / / / / / / / / / / /, н у л л и. Согласно указанной гипотезе поперечные сечения бру — Q) са, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и после деформации. [2]

Закон распределения нормальных напряжений в поперечном сечении бруса изображается облч-но графиком, показывающим изменение их по зы-соте или ширине поперечного сечения. [3]

Изучение закона распределения нормальных напряжений Производится в сечении на расстоянии а от опоры. [4]

Эта формула дает закон распределения нормальных напряжений под штампом. [5]

Таким образом, закон распределения нормальных напряжений по высоте сечений найден. Он изображен на эпюре ( рис. 156), из которой видно, что напряжения достигают максимальной величины в точках, наиболее удаленных от нейтральной линии. Этот закон является общим для балки с поперечным сечением любого профиля. [6]

Эта зависимость определяет закон распределения нормальных напряжений по сечению балки; величина их в какой-либо точке сечения прямо пропорциональна расстоянию этой точки от нейтральной оси, другими словами, величина напряжений меняется по высоте сечения по линейному закону. [7]

Эта зависимость определяет закон распределения нормальных напряжений по сечению балки: величина их в какой-либо точке сечения прямо пропорциональна расстоянию этой точки от нейтральной оси; другими словами, величина напряжений изменяется по высоте сечения по линейному закону. [8]

Поэтому для выяснения закона распределения нормальных напряжений в поперечных сечениях бруса необходимо провести эксперимент. [9]

Поэтому для выяснения закона распределения нормальных напряжений в поперечных сечениях бруса необходимо провести эксперимент. [10]

После того как установлен закон распределения нормальных напряжений в поперечном сечении балки при чистом изгибе, можно перейти к определению напряжений в зависимости от величины изгибающего момента в этом сечении. [11]

После того как установлен закон распределения нормальных напряжений в поперечном сечении балки при чистом изгибе, можно перейти к определению напряжений в зависимости от изгибающего момента в этом сечении. [12]

После того как установлен закон распределения нормальных напряжений в поперечном сечении балки при чистом изгибе, можно перейти к определению напряжений в зависимости от величины изгибающего момента в этом сечении. [13]

После TOFO как установлен закон распределения нормальных напряжений в поперечном сечении балки при чистом изгибе, можно перейти к определению напряжений в зависимости от величины изгибающего момента в этом сечении. [14]

После того как установлен закон распределения нормальных напряжений в поперечном сечении балки при чистом изгибе, можно перейти к определению напряжений в зависимости от величины изгибающего момента в этом сечении. [15]

Источник

iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x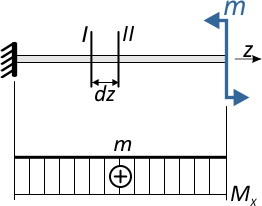

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.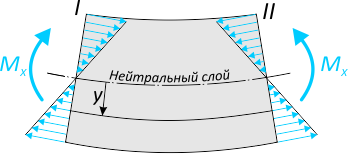

Закон распределения нормальных напряжений по высоте сечения выражается формулой: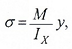

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: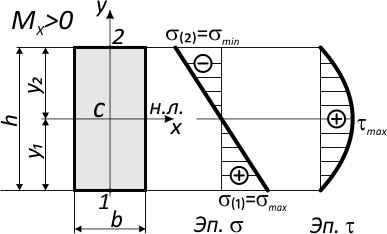

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.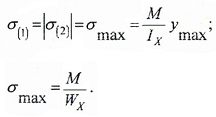

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: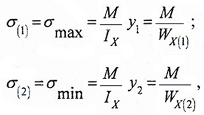

где: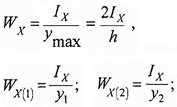

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.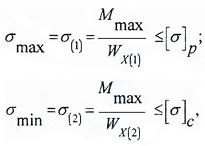

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского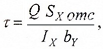

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max: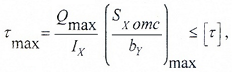

где [ τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: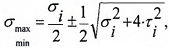

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник