Содержание:
- Случайные векторы
- Свойства функции распределения случайного вектора
- Двумерные дискретные случайные векторы
- Двумерные абсолютно непрерывные случайные векторы
- Сходимость случайных величин
Случайные векторы
Рассматриваем случайное явление и вероятностное пространство, которое отвечает этому случайному явлению. Пусть  – случайные величины, связанные с этим случайным явлением. Совместное распределение этих случайных величин будем называть случайным вектором и обозначать
– случайные величины, связанные с этим случайным явлением. Совместное распределение этих случайных величин будем называть случайным вектором и обозначать 
Определение. Функцией распределения случайного вектора  называется функция n переменных
называется функция n переменных 

Свойства функции распределения случайного вектора
1. Функция распределения непрерывна слева и монотонно неубывающая по всем аргументам.
2. 
3. 
4. 
5. Функция распределения компоненты  является границей функции распределения случайного вектора для всех
является границей функции распределения случайного вектора для всех 
Определение. Случайный вектор  называется дискретным, если он приобретает конечное или счетное количество значений.
называется дискретным, если он приобретает конечное или счетное количество значений.
Очевидно, что каждая компонента этого случайного вектора является дискретной случайной величиной.
Дискретный случайный вектор определяется значениями, которые он приобретает, и вероятностями, с которыми приобретаются эти значения.
Далее будем считать, что компонента ξ1 приобретает значения  компонента ξ1 –
компонента ξ1 –  компонента ξn –
компонента ξn –  а
а

Определение. Случайный вектор  называется абсолютно непрерывным, если существует n-мерная действительная функция
называется абсолютно непрерывным, если существует n-мерная действительная функция  которую мы будем называть плотностью абсолютно непрерывного случайного вектора
которую мы будем называть плотностью абсолютно непрерывного случайного вектора  такая, для которой выполняется равенство
такая, для которой выполняется равенство

Определение. Компоненты случайного вектора  называются независимыми, если
называются независимыми, если  выполняется равенство
выполняется равенство


Если случайный вектор является дискретным, то условие независимости конкретизируется так:


Для абсолютно непрерывного случайного вектора условие независимости является таким:

Пусть  – некоторая функция. Математическое ожидание случайной величины
– некоторая функция. Математическое ожидание случайной величины  равно
равно


Если случайный вектор является дискретным и

если вектор ξ – абсолютно непрерывный.
Определение. Ковариантной матрицей случайного вектора  называют числовую матрицу К размера
называют числовую матрицу К размера  вида
вида

где

и если  то величина
то величина  называется ковариацией.
называется ковариацией.
Понятно, что на диагоналях стоят дисперсии соответствующих компонент.
Легко видеть, что

Доказательство.




Коэффициентом корреляции компонент  является число
является число

корреляционной матрицей является матрица

Детальнее свойства случайных векторов рассмотрим для двумерного случая.
Двумерные дискретные случайные векторы
Рассматриваем двумерный случайный вектор  Предположим, что компонента ξ приобретает значения
Предположим, что компонента ξ приобретает значения  компонента η приобретает значения
компонента η приобретает значения  и
и  Распределение двумерного дискретного вектора удобно представлять в виде таблицы:
Распределение двумерного дискретного вектора удобно представлять в виде таблицы:

Очевидно, что 
где 
Пример. Дано распределение двумерного случайного вектора 

Найти 
Решение. Поскольку

то




Пример. Дано распределение двумерного случайного вектора 

Найти 
Решение. Очевидно, что



Распределение компонент находится так:

Далее определяем 

Пример. Дано распределение двумерного случайного вектора 

Найти распределение компонент.
Решение. 






Для контроля целесообразно сделать проверку. Известно, что  Убедимся, что это действительно так.
Убедимся, что это действительно так.

Следовательно, распределение компоненты ξ является таким:

Переходим к компоненте η:








Проверка: 
Следовательно, распределение компоненты η является таким:

Заметим, что распределение компонент можно находить значительно проще.
Запишем еще раз распределение вектора, добавив одну строку снизу и один столбец справа. Далее находим суммы элементов по строкам и записываем эти суммы в последний столбец, а также находим суммы элементов по столбцах и значения найденных сумм записываем в нижнюю строку. Полученные суммы являются значениями вероятностей. Например, сумма верхней строки является вероятностью  сумма второй строки является вероятностью
сумма второй строки является вероятностью  соответственно сумма третьей строки –
соответственно сумма третьей строки –  Для того, чтобы найти
Для того, чтобы найти  нужно найти сумму элементов второго столбца и т. д.
нужно найти сумму элементов второго столбца и т. д.

Определение. Условным распределением компоненты ξ при условии, что  называют совокупность значений
называют совокупность значений

Аналогично, условным распределением компоненты η при условии, что  называют совокупность значений
называют совокупность значений

Условным математическим ожиданием компоненты ξ при условии, что  называют число
называют число

Аналогично, условным математическим ожиданием компоненты η при условии, что  называют число
называют число

Пример. Дано распределение дискретного случайного вектора 

Найти условное распределение компоненты ξ при условии, что  условное распределение компоненты η при условии, что
условное распределение компоненты η при условии, что  условное математическое ожидание компоненты ξ при условии, что
условное математическое ожидание компоненты ξ при условии, что  условное математическое ожидание компоненты η при условии, что
условное математическое ожидание компоненты η при условии, что 
Решение. 
Значение вероятности  находим как сумму элементов второго справа столбца.
находим как сумму элементов второго справа столбца.

Далее



Следовательно, условное распределение компоненты ξ при условии, что  будет таким:
будет таким:

Сразу находим условное математическое ожидание компоненты ξ при условии, что 


Переходим к нахождения условного распределения компоненты η при условии, что 



Запишем это условное распределение в виде таблицы

Далее найдем условное математическое ожидание.


Условие независимости для двумерного дискретного случайного вектора является такой:

для произвольных 
Пример. Дано распределение двумерного случайного вектора 

Проверить, являются ли независимыми компоненты этого вектора.
Решение. 



Очевидно, условие  не выполняется. ■
не выполняется. ■
Функция распределения для двумерного случайного вектора  находится так. По определению имеем
находится так. По определению имеем

Очевидно, что функция распределения является кусочно-постоянной на отрезках  Поэтому ее можно представить в виде таблицы, которая содержит на одну строку больше чем таблица распределения этого случайного вектора и на один столбец больше чем таблица распределения этого случайного вектора.
Поэтому ее можно представить в виде таблицы, которая содержит на одну строку больше чем таблица распределения этого случайного вектора и на один столбец больше чем таблица распределения этого случайного вектора.
Поскольку случайный вектор  не содержит значений меньших, чем
не содержит значений меньших, чем  и
и  , то элементы в крайнем левом столбце и верхней строке будут нулевыми. Далее алгоритм заполнения таблицы будет таким: в
, то элементы в крайнем левом столбце и верхней строке будут нулевыми. Далее алгоритм заполнения таблицы будет таким: в  строке и
строке и  столбце будет записана сумма вероятностей, которые отвечают
столбце будет записана сумма вероятностей, которые отвечают 
Пример. Дано распределение двумерного случайного вектора  .
.

Найти функцию распределения.
Решение. Поскольку наименьшим значением среди  является 2, а среди
является 2, а среди  является — 1, то вероятность того, что случайный вектор будет приобретать меньшие значения, равно 0. Поэтому слева и сверху мы проставляем нули.
является — 1, то вероятность того, что случайный вектор будет приобретать меньшие значения, равно 0. Поэтому слева и сверху мы проставляем нули.
Осталось заполнить 4 строки и 3 столбца. Обозначим значения незаполненных клеточек через  Очевидно, что
Очевидно, что


Пусть  – некоторая кусочно-непрерывная функция. Математическое ожидание случайной функции
– некоторая кусочно-непрерывная функция. Математическое ожидание случайной функции  находится так:
находится так:

В частности ковариация находится по формуле

де



Коэффициент корреляции

Пример. Найти ковариацию и коэффициент корреляции случайного вектора 

Решение. Сначала найдем распределение компонент.


Далее находим 







И, наконец, находим


Переходим к коэффициенту корреляции.






Запишем ковариационную и корреляционную матрицы

Заметим, что если компоненты случайного вектора является независимыми, то ковариация, а следовательно, и коэффициент корреляции равняются нулю. Наоборот не всегда правильно.
Пример случайного вектора, у которого ковариация равна нулю и коэффициенты зависимы.

Сначала покажем, что ковариация равно нулю.





Далее проверяем компоненты на независимость


Следовательно,  а поэтому компоненты являются зависимыми. ■
а поэтому компоненты являются зависимыми. ■
Заметим, что если ковариация является ненулевой, то компоненты зависимы.
Двумерные абсолютно непрерывные случайные векторы
Рассматриваем двумерный абсолютно непрерывный вектор  с плотностью
с плотностью  Плотность компонент
Плотность компонент  находят так:
находят так:

Пример. Плотность двумерного случайного вектора  равна
равна

где область D ограничена линиями 

 Найти плотность компонент.
Найти плотность компонент.
Решение. Сначала изобразим область D.







Вероятность попадания в область  находится из формулы
находится из формулы

Очевидно, что 
Пример. Дана плотность абсолютно непрерывного случайного вектора 

Найти 



 если область D ограничена линиями
если область D ограничена линиями 


Решение. Сначала найдем неизвестную константу  Для этого графически изобразим область D
Для этого графически изобразим область D









Сначала найдем  Снова графически изобразим область
Снова графически изобразим область






Далее находим вероятность  Изобразим графически область
Изобразим графически область







Переходим к нахождению вероятности  Как и в предыдущих случаях сначала изображаем графически область интегрирования
Как и в предыдущих случаях сначала изображаем графически область интегрирования






И, наконец находим вероятность  Изображаем графически область интегрирования
Изображаем графически область интегрирования

Как видно из рисунка, сначала нужно найти точку пересечения прямых 










Условие независимости компонент проверяется так:

Пример. Дана плотность случайного вектора 

где область D ограничена линиями 


 Найти
Найти  и проверить, являются ли компоненты независимыми.
и проверить, являются ли компоненты независимыми.
Решение. Прежде всего изобразим область D.







Следовательно,

Проверяем независимость компонент. Для этого находим их плотности



Следовательно,

Переходим к нахождению плотности η




Находим произведение  в области D и проверяем, равно ли оно
в области D и проверяем, равно ли оно 


В области D имеем 
Следовательно, условие независимости не выполняется. ■
Пример. Известно, что компоненты случайного вектора  является независимыми. Их плотности равняются:
является независимыми. Их плотности равняются:


Найти совместную плотность случайного вектора  .
.
Решение. Из условия независимости 
Поэтому

где область D ограничена линиями 



Функция распределения находится по определению

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти  функцию распределения, если область D ограничена линиями
функцию распределения, если область D ограничена линиями 



Решение. Прежде всего находим неизвестную константу.





По определению имеем

Аналитический вид функции распределения зависит от того, где находится точка 
В частности:
1. Пусть  или
или 


Тогда, как видно из рисунка

2. 

Тогда





3. Далее рассмотрим точки  для которых выполняются условия
для которых выполняются условия 


Очевидно аналитический вид функции распределения в этом случае будет таким:


4. Далее рассматриваем множество точек  для которых выполняются условия
для которых выполняются условия 




5. Наконец, если 
 тогда
тогда



Условная плотность  находится по формуле
находится по формуле

соответственно, условная плотность 

Пример. Дана плотность абсолютно непрерывного случайного вектора 

Найти неизвестную константу  условные плотности
условные плотности 
 если область D ограничена линиями
если область D ограничена линиями 


Решение. Сначала изображаем область D и находим неизвестную постоянную.









Далее находим распределение составляющих











Следовательно, условия плотности будут такими:


Математическое ожидание от функции компонент вектора  равно
равно

Пример. Дана плотность абсолютно непрерывного случайного вектора

Найти ковариацию, коэффициент корреляции, ковариационную матрицу, корреляционную матрицу, если область D ограничена линиями 



Решение. Сначала находим неизвестную константу 






Переходим к ковариации













Следовательно,


Далее находим дисперсии











Ковариационная матрица является такой:

Корреляционная матрица имеет вид

Сходимость случайных величин
Определение. Рассматриваем последовательность случайных величин  Эта последовательность совпадает со случайной величиной ξ, если
Эта последовательность совпадает со случайной величиной ξ, если 

или

и это обозначают 
Определение. Последовательность случайных величин  сходится к случайной величине ξ в среднеквадратичном, если
сходится к случайной величине ξ в среднеквадратичном, если 
 и
и

Это обозначают 
Теорема. Если  и
и  – непрерывная функция, то
– непрерывная функция, то 
Закон больших чисел
Рассматриваем последовательность случайных величин  Для нее выполняется закон больших чисел (ЗБЧ) или эта последовательность удовлетворяет закон больших чисел, если
Для нее выполняется закон больших чисел (ЗБЧ) или эта последовательность удовлетворяет закон больших чисел, если

Сходимость по вероятности всегда проверять нет смысла, потому что есть теоремы, которые являются достаточными условиями для выполнения закона больших чисел.
Теорема Чебышева. Пусть дана последовательность независимых случайных величин  для которых существуют
для которых существуют  Если существует константа С такая, что
Если существует константа С такая, что 
 то для этой последовательности выполняется закон больших чисел.
то для этой последовательности выполняется закон больших чисел.
Теорема Хинчина. Пусть дана последовательность независимых одинаково распределенных случайных величин  для которых существует математическое ожидание
для которых существует математическое ожидание  тогда для этой последовательности выполняется закон больших чисел.
тогда для этой последовательности выполняется закон больших чисел.
Теорема Маркова. Пусть дана последовательность произвольных случайных величин  для которых существуют
для которых существуют  и выполняется равенство
и выполняется равенство

Тогда для этой последовательности выполняется закон больших чисел.
Теорема Бернулли. В схеме независимых испытаний  Тут μ – относительная частота появления события, р – вероятность появления события в одном испытании.
Тут μ – относительная частота появления события, р – вероятность появления события в одном испытании.
Пример. Дана последовательность независимых случайных величин 

Проверить, выполняется ли для этой последовательности закон больших чисел.
Решение. Для проверки используем теорему Чебышева. Независимость дана в условии.



Очевидно, что

Поэтому для данной последовательности выполняются условия теоремы Чебышева, а следовательно, выполняется закон больших чисел. ■
Пример. Дана последовательность независимых случайных величин, которые имеют распределение Коши. Проверить, выполняется ли для этой последовательности закон больших чисел  .
.
Решение. Поскольку для распределения Коши не существует математического ожидания, то речь не идет о выполнении закона больших чисел. ■
Лекции:
- Биномиальный закон
- Равномерный закон
- Закон Пуассона
- Показательный закон
- Нормальный закон
- Теория вероятности: формулы, примеры
- Схема Бернулли теория вероятности
- Формула Пуассона теория вероятности
- Формула лапласа
- Статистическая вероятность
системы случайных
величин
2.10.1 Случайные векторы
Упорядоченную
пару (X,Y)
назовем двумерной
случайной величиной
или случайным
вектором,
если для любых XR,
YR
неравенство X<x,
Y<y
является событием. Т.о., определена
вероятность P(X<x,Y<y),
которая называется функцией
распределения
двумерной случайной величины. Тогда X
и Y
называют компонентами
двумерной случайной величины или
координатами
случайного
вектора.
Рассмотрим примеры.
1)
Железнодорожный билет можно охарактеризовать
системой пяти случайных величин, где
X1
– стоимость,
X2
– номер поезда, X3
– номер вагона, X4
номер места, X5
– номер паспорта его владельца.
2)
Академическую успеваемость студентов
вашей группы можно охарактеризовать
n-мерной
случайной величиной – оценками за
прошедшие семестры, где n
число оцененных предметов за время
учебы.
Т.о.,
функцией распределения
двумерной случайной величины (X,Y)
называется функция F(x,y),
определяющая для каждой пары (X,Y)
вероятность одновременного выполнения
двух неравенств X<x
и Y<y,
т.е.
F(x,
y)=P(X<x,Y<y).
Двумерную
дискретную СВ
можно задать аналитически с помощью
формулы закона её распределения F(x,y),
с помощью таблиц или графически.
При
табличном
способе задания двумерной дискретной
случайной величины перечисляются все
возможные значения каждой из переменных
и соответствующие им вероятности
случайных величин, расположенных на
пересечении i-ой
строки (для случайной величины X)
и j-го
столбца (для случайной величины Y):
|
Х1 |
Х2 |
… |
X |
|
|
Y1 |
P11 |
p12 |
… |
P1n |
|
Y2 |
P21 |
P22 |
… |
P2n |
|
… |
… |
… |
… |
… |
|
Ym |
Pn1 |
Pn2 |
… |
Pmn |
С
геометрической точки зрения функция
распределения F(x,y)
двумерной случайной величины есть
вероятность того, что случайная точка
(X,Y)
попадет в бесконечный прямоугольник с
вершиной в точке (x,y),
расположенный левее и ниже этой точки,
т.е. в ту часть плоскости, все точки
которой удовлетворяют неравенствам
X<x
и
Y<y
(рис.20).

Рис.20
Аналогично,
с геометрической точки зрения, функция
распределения первой компоненты X
случайного вектора –
![]() ,
,
есть вероятность попадания случайной
точки в полуплоскость, ограниченную
справа абсциссойx
(рис. 21а).
Функция
распределения случайной величины Y
–
![]()
– вероятность попадания в полуплоскость,
ограниченную сверху ординатой y
(рис. 21б)

а) б)
Рис.21
Функция
распределения двумерной случайной
величины имеет свойства,
аналогичные функции распределения
одномерной случайной величины:
1) Функция
распределения удовлетворяет двойному
неравенству
0F(x,
y)1.
2)
F(x,
y)
– неубывающая функция по каждому из
своих аргументов, т.е. справедливы
неравенства F(x2,
y)
≥ F(x1,
y)
для x2>x1,
и F(x,
y2)
≥ F(x,
y1)
для y2>y1.
3)
Справедливы предельные
соотношения:
F(x,
∞)=0,
F(∞,
y)=0,
F(∞,
∞)=0,
F(∞,
∞)=1.
4)
F(x,
∞)=FX(x),
F(+∞,
y)
= FY(y).
5) Вероятность
попадания случайной точки в прямоугольник
x1X<
x2,
y1Y<y2
равна
P(aX<b,
cY<d)=F(b,
d)F(a,
d)F(b,
c)F(a,
c). (2.50)
Закон
распределения системы непрерывных
случайных величин (X,Y)
зададим через функцию плотности
вероятности.
Если
существует такая функция f(x,y),
что при xR,
yR
имеет место равенство
![]() , (2.51)
, (2.51)
то
эта функция называется плотностью
распределения случайного вектора (X,Y),
а сам вектор
(X,Y)
называется непрерывной
двумерной случайной величиной.
Свойства
плотности
распределения вероятности
двумерной случайной величины также
аналогичны одномерной:
-
f(x,
y)≥0
; -
 ;
; -
 ; (2.52)
; (2.52) -
 и
и
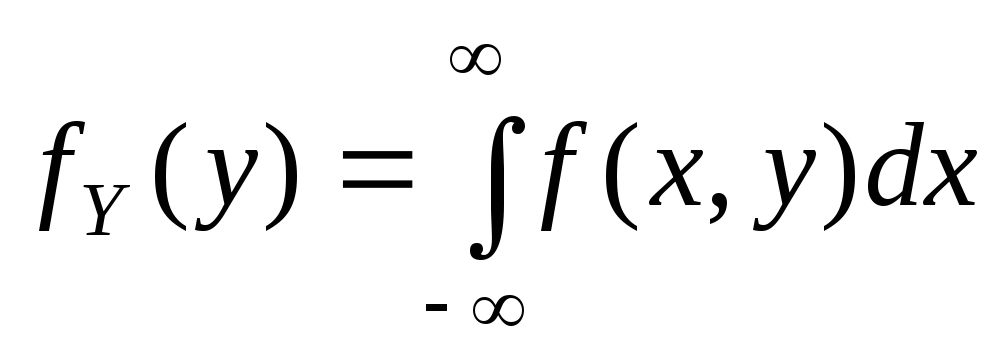 – плотности распределения отдельных
– плотности распределения отдельных
компонент двумерной случайной величины.
С
геометрической точки зрения плотность
вероятности
f(x,y)
двумерной непрерывной случайной величины
имеет вид некоторой поверхности,
называемой поверхностью
распределения.
Эта поверхность аналогична кривой
распределения одномерной случайной
величины (рис.22):




y
x
z
Рис.22
Объем
тела, ограниченного поверхностью f(x,y)
и плоскостью xOy,
равен единице.
Вероятность
попадания двумерной непрерывной
случайной точки (X,Y)
в произвольную область D
равна двойному интегралу по области D
от функции f(x,
y):
![]() . (2.53)
. (2.53)
В
частности, если область D
есть прямоугольник R,
ограниченный абсциссами a
и b
и ординатами c
и d
(рис.23), то
формула примет вид:

y
0
x
Рис.23
![]() . (2.54)
. (2.54)
Закон
распределения дискретного случайного
вектора (X,Y)
есть конечное
или счетное множество всех возможных
значений случайного вектора (X,Y)=(xi,
yj)
с указанием соответствующих вероятностей:
![]() ,
,
где
i=1,
2, …, n;
j=1,
2, …, m;
а n
и m
– число возможных значений случайных
величин соответственно X
и Y.
Сумма вероятностей pij
по всем
значениям i
и j
равна единице:
![]() .
.
Зная
закон распределения двумерной случайной
величины (X,Y),
можно найти закон распределения отдельных
ее компонент X
и Y.
Для этого, имея табличное задание закона
распределения двумерной случайной
величины, находят суммы вероятностей
«по строкам» – для переменной Y,
и «по столбцам» – для переменной X.
При подсчете вероятностей законов
распределения отдельных переменных
необходимо помнить об этапе контрольной
проверки, т.е. о нормировке:
![]()
Распределение
вероятностей координат вектора можно
найти, просуммировав вероятности {pij}
по соответствующему индексу:
![]()
![]()
Задача
17. Составить
законы распределения переменных X
и Y,
зная двумерный закон их распределения.
-
X
Y
2
3
5
8
0.12
0.24
0.16
10
0.23
0.18
0.07
Решение.
Найдем суммы вероятностей «по строкам»
– для переменной Y,
и «по столбцам» – для переменной X
и составим для них новую таблицу:
-
X
Y
2
3
5
Р(yj)
8
0.12
0.24
0.16
0.52
10
0.23
0.18
0.07
0.48
P(хi)
0.35
0.42
0.23

Тогда
законы распределения по отдельным
переменным X
и Y
примут вид:
|
X |
2 |
3 |
5 |
Y |
8 |
10 |
|
|
P(хi) |
0.35 |
0.42 |
0.23 |
Р(yj) |
0.52 |
0.48 |
Осуществляя
контроль, убеждаемся, что
![]()
Итак,
по закону распределения двумерной
случайной величины можно установить
законы распределения одномерных
случайных величин. Однако на практике
чаще более важной является обратная
задача: по распределениям вероятностей
отдельных переменных построить закон
распределения их композиций с помощью
выполнения математических операций
над случайными величинами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
–
определить одномерные законы распределения случайных величин X и Y;
– найти
условные плотности распределения вероятностей величин;
–
вычислить математические ожидания mx и my;
–
вычислить дисперсии σx и σy;
–
вычислить ковариацию μxy;
–
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |
Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) – двумерный случайный вектор или система двух СВ.
Изучать систему – значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Законы распределения СВДТ и СВНТ
Таблица распределения – закон распределения СВДТ:
Рассмотрим двумерный случайный вектор (X, У), где X и У – дискретные случайные величины с возможными значениями 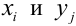

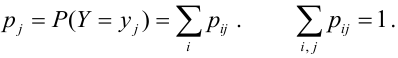
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х – число четных цифр в выборке, Y – число нечетных. Описать закон распределения.
Решение.
X (четные) – 2, 4, 6, 8; Y ( нечетные) – 1, 3, 9. Следовательно, возможные значения X 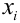 :
: 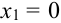 (нет четных цифр),
(нет четных цифр), 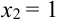 (одна цифра четная),
(одна цифра четная), 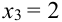 (обе цифры четные); возможные значения Y
(обе цифры четные); возможные значения Y 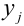 :
: 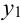
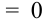 (нет нечетных цифр),
(нет нечетных цифр), 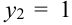 (одна цифра нечетная),
(одна цифра нечетная), 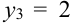 (обе цифры нечетные). Найдем вероятности.
(обе цифры нечетные). Найдем вероятности.
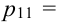 (0 четных, 0 нечетных) = 0, не выбираем ни одной цифры, а по условию выбираем две цифры. Аналогично,
(0 четных, 0 нечетных) = 0, не выбираем ни одной цифры, а по условию выбираем две цифры. Аналогично, 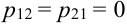 (выбираем всего одну цифру либо нечетную, либо четную),
(выбираем всего одну цифру либо нечетную, либо четную), 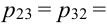
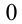 (выбираем три цифры вместо двух по условию),
(выбираем три цифры вместо двух по условию), 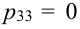 (выбираем четыре цифры вместо двух по условию).
(выбираем четыре цифры вместо двух по условию).
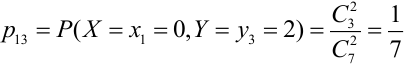 — (обе цифры нечетные),
— (обе цифры нечетные),
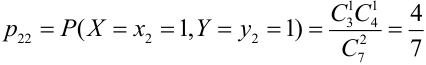 — (одна четная, одна нечетная),
— (одна четная, одна нечетная),
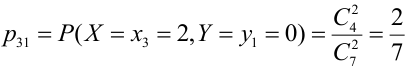 — (обе цифры четные).
— (обе цифры четные).
Таблица распределения имеет вид:

Проверка: 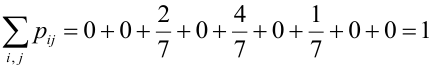
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
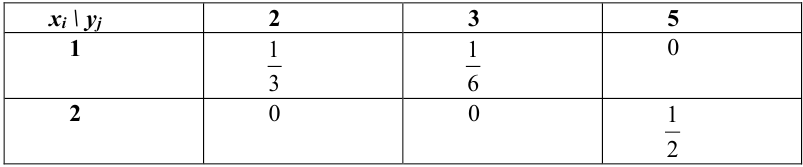
Решение.
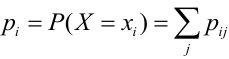 , (складываем по строкам), следовательно,
, (складываем по строкам), следовательно,
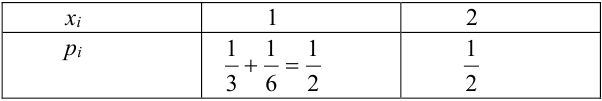
Проверка: 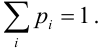
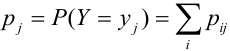 , (складываем по столбцам), следовательно,
, (складываем по столбцам), следовательно,

Проверка: 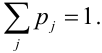
Функция распределения – закон распределения СВДТ и СВНТ
Функция распределения – универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X < х, Y < у, т.е. 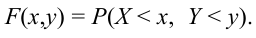
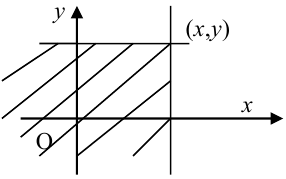
Геометрически F(x,y) представляет вероятность попадания случайной точки (X,Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (х,у).
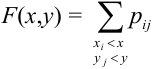 – для СВДТ
– для СВДТ
Свойства F(x;y).
1. Условие согласованности:
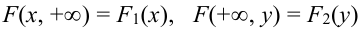
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.
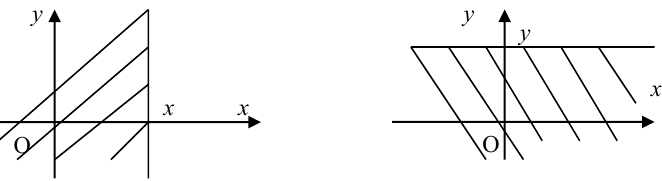
2. 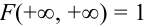
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3. 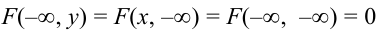
Пояснение. Отодвигая ту или иную границу квадранта в (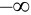 ), убеждаемся, что вероятность случайной точки попасть в квадрант равна нулю.
), убеждаемся, что вероятность случайной точки попасть в квадрант равна нулю.
4. F(x, у) – неубывающая функция по каждому аргументу.
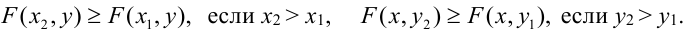
5. Вероятность попадания случайной точки (X, У) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
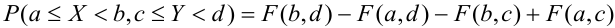
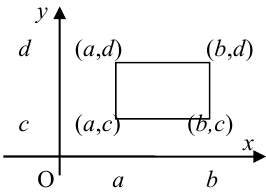
Определение 62. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по х, у функция 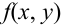 , называемая плотностью распределения СВНТ.
, называемая плотностью распределения СВНТ.
Пример №1
Найти функцию распределения, если случайный вектор задан таблицей распределения:
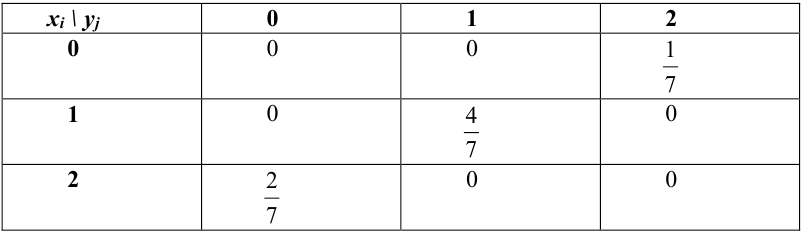
Решение.
Случайный вектор дискретного типа, следовательно, 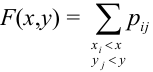
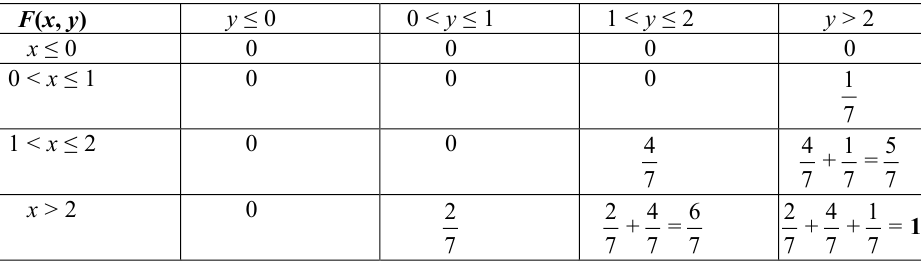
Плотность распределения (Для СВНТ)
Определение 63. (первое определение) Плотностью распределения системы двух непрерывных случайных величин называется предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади прямоугольника, когда оба его размера стремятся к нулю:
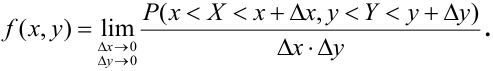
Распишем интервальную вероятность с помощью функции распределения:
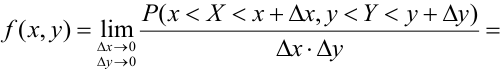
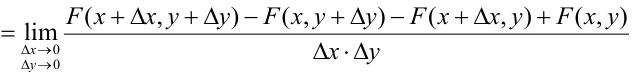
Правая часть равенства – определение смешанной производной функции двух переменных F(x, у), отсюда следует
Определение 64. (второе определение) Плотностью распределения системы двух непрерывных случайных величин называется смешанная частная производная от функции распределения системы:
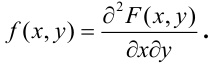
Отсюда, 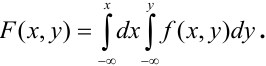
Геометрически 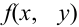 можно изобразить некоторой поверхностью, которую называют поверхностью распределения.
можно изобразить некоторой поверхностью, которую называют поверхностью распределения.
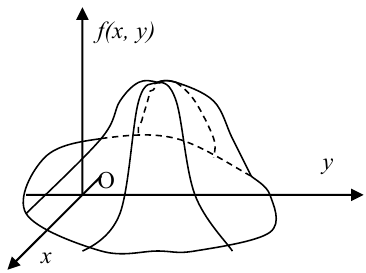
Вероятность попадания случайной точки в некоторую область D плоскости (Oxy) находится по формуле:
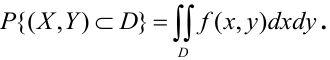
Геометрически вероятность попадания случайной точки в область D плоскости (Oxy) изображается объемом цилиндрического тела, ограниченного поверхностью распределения и опирающегося на эту область.
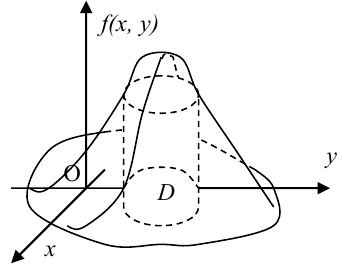
Свойства плотности
1. 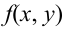 – неотрицательная функция, т.е.
– неотрицательная функция, т.е. 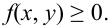
2. Условие нормировки: 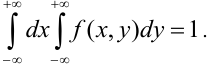
Пример №2
Дана плотность распределения непрерывного вектора 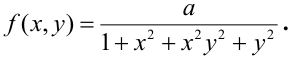
Найти: 1) коэффициент а, 2) функцию распределения F(x, у), 3) вероятность попадания случайной точки в прямоугольник с вершинами в точках O(0,0), A(0,1), 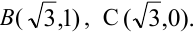
Решение.
1) Для вычисления коэффициента а применим условие нормировки:
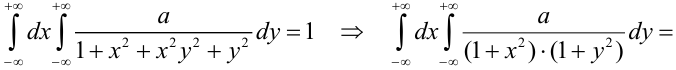
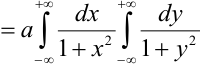
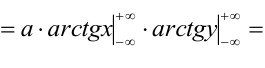
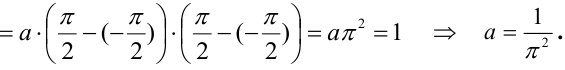
2) По определению 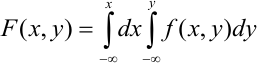
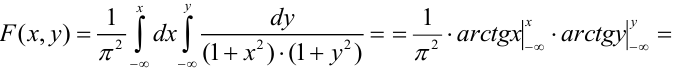
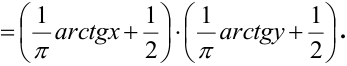
3) Вероятность попадания в прямоугольник.
1 способ:
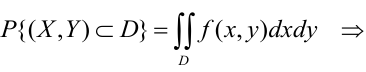
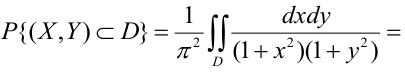
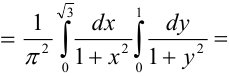
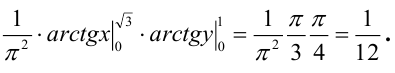
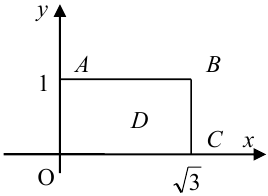
2 способ (по 5 свойству):
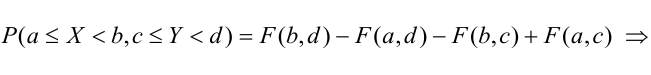
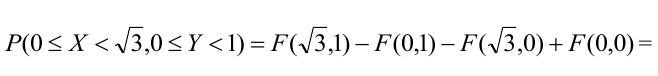
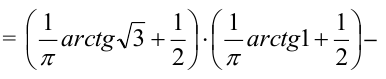
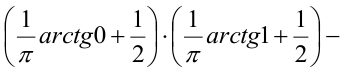
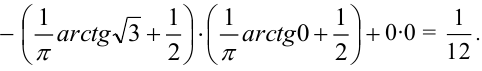
Пример №3
Дана плотность распределения непрерывного вектора 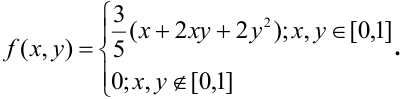 Найти вероятность того, что случайная точка принадлежит треугольнику с вершинами в точках O(0,0), A(1,2), B(0,1).
Найти вероятность того, что случайная точка принадлежит треугольнику с вершинами в точках O(0,0), A(1,2), B(0,1).
Решение.
Плотность распределения задана в квадрате. Область пересечения квадрата с заданным треугольником заштрихованный треугольник, ограниченный снизу прямой 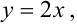 сверху – прямой
сверху – прямой 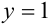 , причем,
, причем, 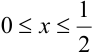 , следовательно,
, следовательно, 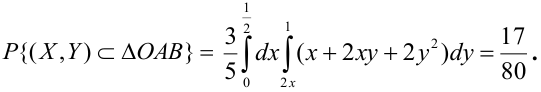
Плотности распределения отдельных величин, входящих в систему
Пусть известна плотность распределения 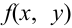 случайного вектора. Согласно свойству 1 (условие согласованности) для функции распределения
случайного вектора. Согласно свойству 1 (условие согласованности) для функции распределения 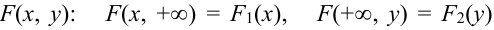 , можем записать, что,
, можем записать, что,
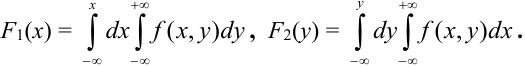
Отсюда, дифференцированием первого равенства по х, а второго по у, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:
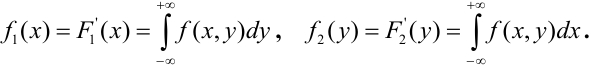
Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.
Определение 65. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.
Теорема. Для того, чтобы дискретные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
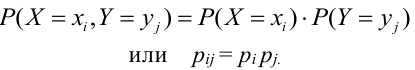
Для того, чтобы непрерывные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
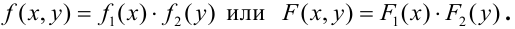
Пример №4
Дана плотность распределения непрерывного вектора: 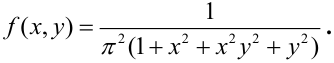
Зависимы или независимы случайные величины, входящие в систему?
Решение.
Представим плотность в виде произведения:
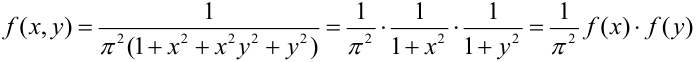 , следовательно, по теореме, X и Y – независимые величины.
, следовательно, по теореме, X и Y – независимые величины.
Пример №5
Дано распределение дискретных независимых случайных величин Х и Y:
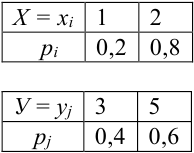
Записать закон распределения случайного вектора (Х + Y).
Решение.
Найдем возможные значения случайного вектора (Х+ Y): 1 + 3 = 4, 2 + 3 =5, 1+5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
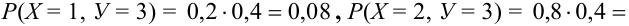
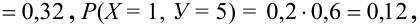
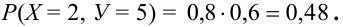
Следовательно, ряд распределения случайного вектора (Х + Y) имеет вид:

Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 66. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
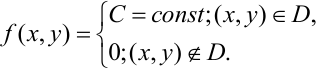
В силу свойства 2 плотности имеем, что 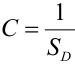 , где
, где 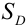 – площадь области D. Тогда вероятность попадания случайной точки в некоторую область
– площадь области D. Тогда вероятность попадания случайной точки в некоторую область 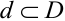 плоскости (Охy) находится по формуле:
плоскости (Охy) находится по формуле:
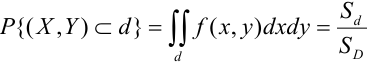
Определение 67. Пусть Х и Y независимые величины, распределенные по нормальному закону, их плотности распределения имеет вид:
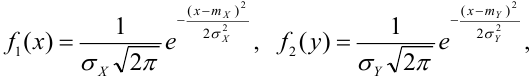
Следовательно, плотность распределения системы (Х,Y) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
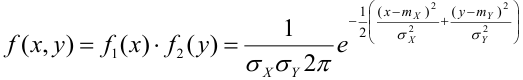
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 68. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (х,у) – множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у называется совокупность возможных значений 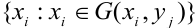 и соответствующих этим значениям условных вероятностей
и соответствующих этим значениям условных вероятностей 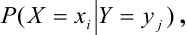 определяемых равенством:
определяемых равенством:
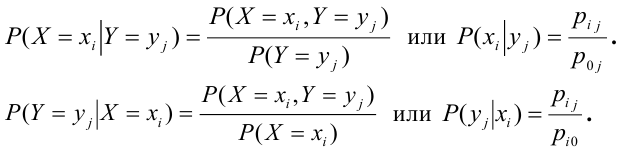
Рассмотрим CBHT.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у :
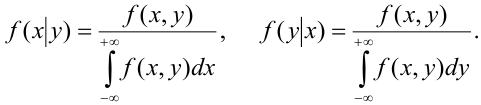
Теорема (умножения законов распределения): 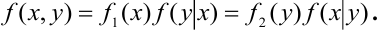
Условие нормировки: 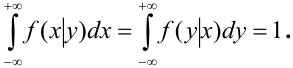
Условие независимости Х от Y: 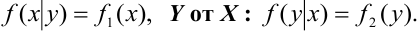
Числовые характеристики системы
Определение 69. Начальным моментом 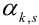 порядка
порядка 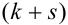 случайного вектора (X,Y) называется математическое ожидание произведения
случайного вектора (X,Y) называется математическое ожидание произведения 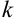 -ой степени Х на s-ую степень Y:
-ой степени Х на s-ую степень Y:
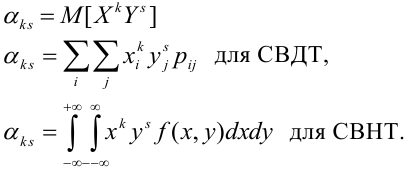
Математическое ожидание дискретных случайных величин Х и Y, входящих в систему:
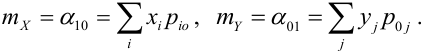
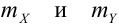 определяют координаты точки, называемой центром рассеивания системы на плоскости.
определяют координаты точки, называемой центром рассеивания системы на плоскости.
Определение 70. Центральным моментом 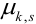 порядка
порядка 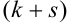 случайного вектора (Х,Y) называется математическое ожидание произведения
случайного вектора (Х,Y) называется математическое ожидание произведения 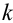 -ой и s-ой степеней соответствующих центрированных величин:
-ой и s-ой степеней соответствующих центрированных величин:
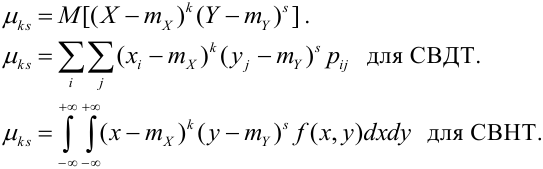
Дисперсия случайных величин X и Y, входящих в систему – характеристика рассеивания случайной точки в направлении осей (ох) и (оу):

Дисперсия дискретных случайных величин Х и Y, входящих в систему:
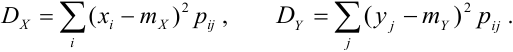
Дисперсия непрерывных случайных величин Х и Y, входящих в систему:
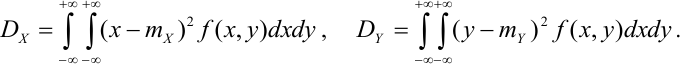
Замечание. Для краткого описания условных законов распределения используются различные характеристики, наиболее важной из которых является математическое ожидание:
Определение 71. Условным математическим ожиданием дискретной случайной величины X при условии, что Y принимает одно из своих возможных значений 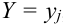 , называется сумма произведений возможных значений Х на их условные вероятности:
, называется сумма произведений возможных значений Х на их условные вероятности:
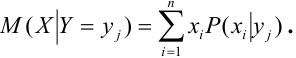
Для непрерывной случайной величины X: 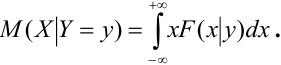
Аналогично, вводится понятие условного мат. ожидания для СВ Y.
Пример №6
По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна р. Рассмотрим две случайные величины: X – число попаданий в цель, Y – число промахов. Составить таблицу распределения, записать функцию распределения системы F(x,y) и найти числовые характеристики 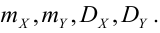
Решение.

Случайный вектор дискретного типа, следовательно, 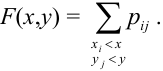


Пояснение: 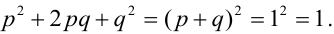
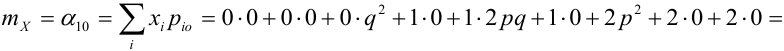
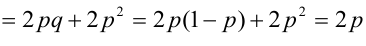
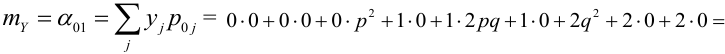
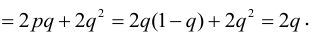
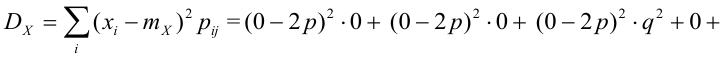
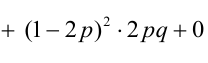
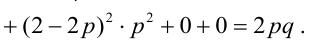
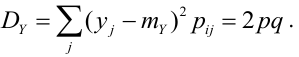
Ковариация, корреляция и линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент 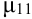 называется корреляционным или моментом связи или ковариацией:
называется корреляционным или моментом связи или ковариацией:
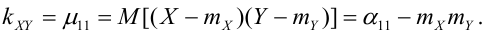
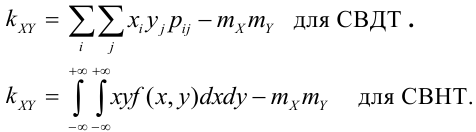
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
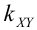 , помимо рассеивания, характеризует взаимное влияние случайных величин X и Y, входящих в систему. Для оценки степени влияния используется не сам момент, а безразмерное соотношение, которое называется нормированной ковариацией или коэффициентом корреляции:
, помимо рассеивания, характеризует взаимное влияние случайных величин X и Y, входящих в систему. Для оценки степени влияния используется не сам момент, а безразмерное соотношение, которое называется нормированной ковариацией или коэффициентом корреляции:
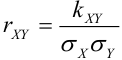 – коэффициент корреляции двух случайных компонент X и Y случайного вектора.
– коэффициент корреляции двух случайных компонент X и Y случайного вектора.
(Иногда его обозначают как 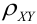 ).
).
Средние квадратические отклонения случайных величин X и Y равны 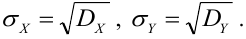
Определение 17. X и Y называются некоррелированными случайными величинами, если их коэффициент корреляции 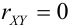 , и коррелированными, если отличен от нуля.
, и коррелированными, если отличен от нуля.
Свойства коэффициента корреляции
Свойства коэффициента корреляции 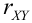 :
:
1. Если X и Y – независимые СВ, то 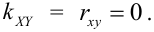 (X и Y некоррелированные случайные величины). Обратное утверждение неверно, так как X и Y могут быть зависимыми, но при этом
(X и Y некоррелированные случайные величины). Обратное утверждение неверно, так как X и Y могут быть зависимыми, но при этом 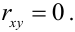
2. 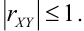
3. В случае 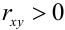 говорят о положительной корреляции X и Y , что означает: при возрастании одной из них другая тоже имеет тенденцию в среднем возрастать. Например, вес и рост человека.
говорят о положительной корреляции X и Y , что означает: при возрастании одной из них другая тоже имеет тенденцию в среднем возрастать. Например, вес и рост человека.
4. В случае 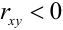 говорят об отрицательной корреляции X и Y , что означает: при возрастании одной из них другая имеет тенденцию в среднем убывать. Например, время, потраченное на подготовку прибора к работе и количество неисправностей, обнаруженных при его работе.
говорят об отрицательной корреляции X и Y , что означает: при возрастании одной из них другая имеет тенденцию в среднем убывать. Например, время, потраченное на подготовку прибора к работе и количество неисправностей, обнаруженных при его работе.
Взаимная связь двух случайных величин, помимо 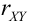 , может быть описана с помощью линий регрессии. Действительно, хотя при каждом значении Х = х величина У остается случайной величиной, допускающей рассеивание своих значений, однако зависимость Y от X сказывается часто в изменении средних размеров Y при переходе от одного значения х к другому. С изменением х будет изменяться и
, может быть описана с помощью линий регрессии. Действительно, хотя при каждом значении Х = х величина У остается случайной величиной, допускающей рассеивание своих значений, однако зависимость Y от X сказывается часто в изменении средних размеров Y при переходе от одного значения х к другому. С изменением х будет изменяться и 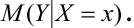 Это означает, что можно рассматривать функцию
Это означает, что можно рассматривать функцию 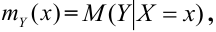 областью определения которой является множество возможных значений случайной величины X. Эта функция носит название регрессии Y и X.
областью определения которой является множество возможных значений случайной величины X. Эта функция носит название регрессии Y и X.
Аналогично, зависимость Х от Y описывает функция 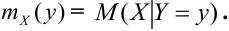
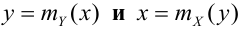 – уравнения регрессии
– уравнения регрессии
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
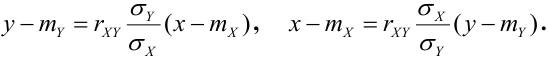
Связь коэффициента корреляции и линий регрессии
1) Если 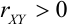 , то линии регрессии наклонены вправо.
, то линии регрессии наклонены вправо.
2) Если 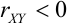 , то линии регрессии наклонены влево.
, то линии регрессии наклонены влево.
3) Если 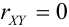 , то линии регрессии проходят параллельно осям координат.
, то линии регрессии проходят параллельно осям координат.
4) Если, 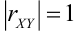 , то линии регрессии сливаются в одну линию, а случайные величины X и Y связаны между собой линейной функциональной зависимостью
, то линии регрессии сливаются в одну линию, а случайные величины X и Y связаны между собой линейной функциональной зависимостью 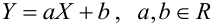 , причем знак коэффициента корреляции (
, причем знак коэффициента корреляции (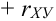 ) или (
) или (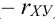 ) берется в зависимости от знака (+ или -) коэффициента а, который называется коэффициентом регрессии.
) берется в зависимости от знака (+ или -) коэффициента а, который называется коэффициентом регрессии.
Часто пишут уравнение в виде: 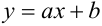 и называют его уравнением парной регрессии, где коэффициент регрессии
и называют его уравнением парной регрессии, где коэффициент регрессии 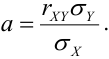
Определение 73. Ковариационной матрицей случайного вектора называется симметрическая действительная матрица, элемент которой представляет собой ковариации соответствующих пар компонент: 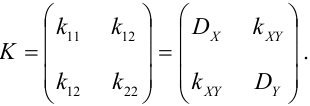
Определение 74. Корреляционной матрицей случайного вектора называется нормированная ковариационная матрица 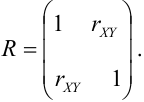
Пример №7
Дано уравнение парной регрессии 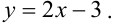 Выберите правильный коэффициент корреляции:
Выберите правильный коэффициент корреляции: 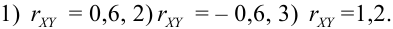
Решение.
Из рассмотрения исключаем 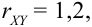 так как по 2 свойству
так как по 2 свойству 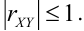 Коэффициент регрессии а = 2, т.е. со знаком «+», следовательно,
Коэффициент регрессии а = 2, т.е. со знаком «+», следовательно, 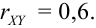
Замечание. Можно было знак 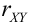 определить с помощью следующего рассуждения: возьмем два возрастающие значения х:
определить с помощью следующего рассуждения: возьмем два возрастающие значения х: 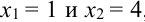 , тогда
, тогда 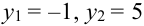 , т.е. с возрастанием х возрастает у, отсюда,
, т.е. с возрастанием х возрастает у, отсюда, 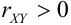 , следовательно,
, следовательно, 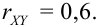
Пример №8
Дано уравнение парной регрессии  Найти
Найти 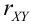 .
.
Решение.
Из формулы 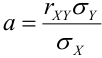 выразим
выразим 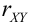 . Получим
. Получим 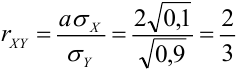 .
.
Свойства математического ожидания и дисперсии
1. X, Y как зависимые, так и независимые случайные величины, тогда 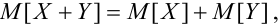
2. 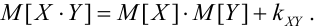
Если X, Y – некоррелированные, то 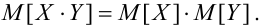
Если X, Y- независимые, то 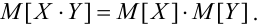
3. 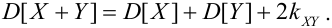
Если X, Y- некоррелированные, то 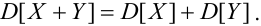
4. Если X, Y-независимые, то 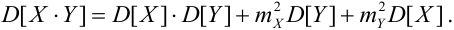
Пример №9
Даны законы распределения случайных величин X, Y:
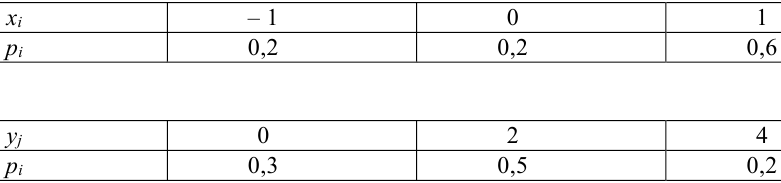
Найти 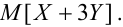
Решение.
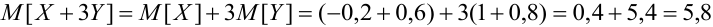 .
.
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок
- Алгебра событий – определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
Двумерная дискретная случайная величина
Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).
В случае двух величин (скажем, $X$ и $Y$) мы имеем дело с так называемой двумерной дискретной случайной величиной $(X,Y)$ (или системой случайных одномерных величин). Кратко выпишем основы теории.
Лучшее спасибо – порекомендовать эту страницу
Система двух случайных величин: теория
Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):
$$
P(X=x_i, Y=y_k)=p_{ik}, i=1,2,…,m; k=1,2,…,n; quad sum_{i,k}p_{ik}=1.
$$
По нему можно найти одномерные законы распределения (составляющих):
$$
p_i=P(X=x_i)=sum_{k}p_{ik}, i=1,2,…,m; \ p_k=P(Y=y_k)=sum_{i} p_{ik}, k=1,2,…,n.
$$
Интегральная функция распределения задается формулой $F(x,y)=P(Xlt x, Ylt y)$. Даже для самого простого закона распределения 2 на 2 функция занимает 5 строк, поэтому ее редко выписывают в явном виде.
Если для любой пары возможных значений $(X=x_i, Y=y_k)$ выполняется равенство
$$P(X=x_i, Y=y_k)=P(X=x_i)cdot P(Y=y_k),$$
то случайные величины $X, Y$ называются независимыми.
Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):
$$
P(X=x_i| Y=y_k)=frac{P(X=x_i, Y=y_k)}{P(Y=y_k)},\
P(Y=y_k| X=x_i)=frac{P(X=x_i, Y=y_k)}{P(X=x_i)}.
$$
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
$$
cov (X,Y)=M(XY)-M(X)M(Y), quad r_{XY} = frac{cov(X,Y)}{sqrt{D(X)D(Y)}}.
$$
Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 1. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта В – 20%. Годная продукция составляет 75%. Пусть X – индикатор дефекта А, a Y – индикатор дефекта В. Составить матрицу распределения двумерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и У и исследовать их зависимость.
Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.
Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.
Задача 4. $X, Y$ – индикаторы событий $A, B$, означающий положительные ответы соответственно на вопросы $alpha, beta$ социологической анкеты. По данным социологического опроса двумерная случайная величина $(X,Y)$ имеет следующую таблицу распределения.
Положительному ответу присвоен ранг 1, отрицательному – 0.
Найти коэффициент корреляции $rho_{XY}$.
Задача 5. Составить закон распределения X – сумм очков и Y – числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам (туз=11, дама=3, король=4)
Найти законы распределения величин Х и Y. Зависимы ли эти величины? Написать функцию распределения для (Х, Y). Построить ковариационный граф. Посчитать ковариацию (X,Y). Написать ковариационную матрицу. Посчитать корреляцию (X,Y) и написать корреляционную матрицу.
Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].
Задача 7. В урне лежат 100 шаров, из них 25 белых. Из урны последовательно вынимают два шара. Пусть $X_i$ – число белых шаров, появившихся при $i$-м вынимании. Найти коэффициент корреляции между величинами $X_1$ и $X_2$.
Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
YX 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.
Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02
Задача 10. Система (x, y) задана следующей двумерной таблицей распределения вероятностей. Определить:
А) безусловные законы распределения составляющих;
Б) условный закон распределения y при x=1;
В) условное математическое ожидание x при y=2.
Г) вероятность того, что случайная величина (x,y) будет принадлежать области $|x|+|y|le 3$.
-3 0 2
-1 0 0,1 0,15
1 0,05 0,3 0,05
2 0,15 0,05 0,15
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
