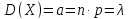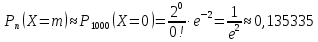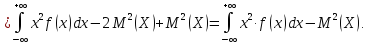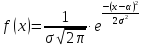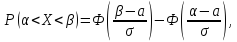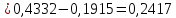Как найти закон распределения случайной величины пуассона

Как найти закон распределения случайной величины пуассона

Закон распределения Пуассона

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ

Краткая теория

Дискретная случайная величина
 имеет закон распределения Пуассона с
параметром

,
если она принимает значения 0,1,2,…,k,… (бесконечное, но счетное множество значений) с вероятностями

Ряд распределения закона Пуассона имеет вид:

Математическое ожидание и дисперсия случайной величины,
распределенной по закону Пуассона, совпадают и равны параметру этого закона,
т.е.

По закону Пуассона распределены, например, число рождений тройни,
число сбоев на автоматической линии, число отказов сложной системы в нормальном
режиме, число требований на обслуживания, поступивших в единицу времени в
системах массового обслуживания и тому подобное.

Если СВ представляет собой сумму двух независимых СВ,
распределенных каждая по закону Пуассона, то она также распределена по закону
Пуассона.

Распределение Пуассона также называют законом «редких» событий, так как оно всегда проявляется там, где производится большое
число испытаний, в каждом из которых с малой вероятностью происходит «редкое» событие.

Смежные темы решебника:

  • Биномиальный закон распределения дискретной случайной величины
  • Геометрический закон распределения дискретной случайной величины
  • Гипергеометрический закон распределения дискретной случайной величины
  • Простейший поток событий

Примеры решения задач

Пример 1

На
предприятии 1000 единиц оборудования определенного вида. Вероятность отказа
единицы оборудования в течение часа составляет 0,001. Составить закон
распределения числа отказов оборудования в течение часа. Найти числовые
характеристики.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Случайная
величина

 – число отказов оборудования, может принимать
значения

Воспользуемся
законом Пуассона:

где

Найдем
эти вероятности:

Найдем
вероятность того, что откажет более 5 единиц оборудования:

Искомый
закон распределения числа отказов оборудования в течение часа:

Проверка гипотезы о распределении выборки по закону Пуассона.

Математическое
ожидание и дисперсия случайной величины, распределенной по закону Пуассона
равна параметру

 этого распределения:

Среднее
квадратическое отклонение:

Пример 2

Станок-автомат штампует детали. Вероятность того, что изготовленная
деталь окажется бракованной, равна 0,001 Найти вероятность того, что среди 350
деталей   окажется ровно 3 бракованных.
Определить закон распределения СВ X и её числовые характеристики.

Решение

Вероятность
события, состоящее в том, что деталь окажется бракованной мало, а число

 велико. Поэтому воспользуемся распределением
Пуассона:

Искомая
вероятность:

Закон
распределения СВ

:

Математическое
ожидание:

Дисперсия:

Среднее
квадратическое отклонение:

Пример 3

Найти среднее число бракованных изделий в партии изделий, если
вероятность того, что в этой партии содержится хотя бы одно бракованное
изделие, равна 0,92. Предполагается, что число бракованных изделий в
рассматриваемой партии распределено по закону Пуассона.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Распределение
Пуассона:

Среднее
число бракованных изделий:

Пусть
событие

 –в партии содержится хотя бы одно бракованное
изделие

Тогда
противоположное событие

 – в партии нет ни одного бракованного изделия

Решая
уравнение, получаем:

Ответ:

Пример 4

Случайная величина ξ распределена по закону
Пуассона с параметром λ=0,2. Найти:

а)

;

б)

;

в)

Решение

Закон Пуассона:

Для закона Пуассона математическое ожидание:

Дисперсия:

а)

б)

в)

Ответ: а)

;  б)

; в)

.

Пример 5

Случайные величины

 распределены по закону Пуассона с одинаковым
математическим ожиданием, равным 6. Найдите математическое ожидание

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Поскольку случайные величины распределены по закону Пуассона и известны
их математические ожидания, соответствующие дисперсии равны:

Искомая величина:

Ответ: 504

Задачи контрольных и самостоятельных работ

Задача 1

Для пуассоновой случайной величины X
имеем

Найдите M(X)

Задача 2

Случайные величины X,Y распределены
по закону Пуассона. Найдите

, если M(X)=40 и M(Y)=70, а коэффициент корреляции X и
Y равен 0,8.

Задача 3

В
некоторой системе 810 приборов. Вероятность отказа каждого прибора в течение
заданного промежутка времени 0.001. Найти вероятность отказа не менее 3
приборов за данный промежуток времени. Найти характеристики данного
распределения случайной величины.

Задача 4

В партии
из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50
изделий, взятых наудачу из этой партии, ровно три окажутся дефектными.

Задача 5

Радиостанция
ведет передачу информации в течение 10 мкс. Работа ее происходит при наличии
хаотической импульсной помехи, среднее число импульсов которой в секунду
составляет

. Для срыва передачи
достаточно попадания одного импульса помехи в период работы станции. Считая,
что число импульсов помехи, попадающих в данный интервал времени, распределено
по закону Пуассона, найти вероятность срыва передачи информации.

Задача 6

Среди
семян пшеницы 0,6% семян сорняков. Какова вероятность при случайном отборе 1000
семян обнаружить не менее трех семян сорняков?

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 7

На
телефонную станцию поступает в среднем 5 заявок на переговоры в минуту. Поток заявок
описывается распределением Пуассона. Рассчитать вероятность того, что за минуту
на станцию придут ровно две заявки.

Задача 8

Вероятность попадания в
цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель ровно
100 раз, если было произведено 2000 выстрелов.

Задача 9

Вероятность
изготовления нестандартной детали p=0.003. Найти
вероятность того, что среди 1000 деталей окажется 4 нестандартных.

Задача 10

Вероятность
сбоя в работе банкомата при каждом запросе равна 0,0016. Банкомат обслуживает
2000 клиентов в неделю. Определить вероятность того, что при этом число сбоев
не превзойдет 3.

Задача 11

Прядильщица
обслуживает 800 веретен. Вероятность обрыва нити на одном веретене в течение
одной минуты 0,003. Найти вероятность того, что в течение одной минуты обрыв
произойдет на трех веретенах.

Задача 12

Телефонный кабель состоит из 400 жил. С какой вероятностью этим
кабелем можно подключить к телефонной сети не менее 395 абонентов, если для
подключения каждого из них нужна одна жила, а вероятность того, что она
повреждена – 0,0125.

Задача 13

Вероятность «сбоя» в работе телефонной станции при каждом вызове
равна 0.05. Поступило 100 вызовов. Определить вероятность того, что произойдет
не более 3 сбоев.

Задача 14

На базе получено 10000 электроламп. Вероятность того, что в пути
лампа разобьется, равна 0,0003. Найдите вероятность того, что среди полученных
ламп будет пять ламп разбито.

Задача 15

Завод отправил в торговую сеть 500 изделий. Вероятность повреждения
в пути равна 0.002. Найти вероятность того, что при транспортировке будет
повреждено ровно три изделия.

  • Краткая теория
  • Примеры решения задач
  • Задачи контрольных и самостоятельных работ
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 июля 2022 года; проверки требует 1 правка.

Распределение Пуассона
Функция вероятностиФункция вероятности
Функция распределенияФункция распределения
Обозначение {mathrm {P}}(lambda )
Параметры lambda in (0,infty )
Носитель kin {0,1,2,ldots }
Функция вероятности {displaystyle {frac {e^{-lambda }lambda ^{k}}{k!}}}
Функция распределения {displaystyle {frac {Gamma (k+1,lambda )}{k!}}}
Математическое ожидание lambda
Медиана approx lfloor lambda +1/3-0.02/lambda rfloor
Мода lfloor lambda rfloor
Дисперсия lambda
Коэффициент эксцесса {displaystyle lambda ^{-1}}
Дифференциальная энтропия lambda [1!-!ln(lambda )]!+!e^{{-lambda }}sum _{{k=0}}^{infty }{frac {lambda ^{k}ln(k!)}{k!}}
Производящая функция моментов {displaystyle exp(lambda (e^{t}-1))}
Характеристическая функция {displaystyle exp(lambda (e^{it}-1))}

Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.

Распределение Пуассона играет ключевую роль в теории массового обслуживания.

Определение[править | править код]

Выберем фиксированное число lambda >0 и определим дискретное распределение, задаваемое следующей функцией вероятности:

p(k)equiv mathbb {P} (Y=k)={frac {lambda ^{k}}{k!}},e^{-lambda },

где

Тот факт, что случайная величина Y имеет распределение Пуассона с математическим ожиданием lambda , записывается: Ysim ~{mathrm {P}}(lambda ).

Моменты[править | править код]

Производящая функция моментов распределения Пуассона имеет вид:

E_{Y}(t)=e^{{lambda left(e^{t}-1right)}},

откуда

{mathbb {M}}[Y]=lambda ,
{mathbb {D}}[Y]=lambda .

Для факториальных моментов распределения справедлива общая формула:

{displaystyle mathbb {M} Y^{[k]}=sum _{i=0}^{k}lambda ^{i}left{{begin{matrix}k\iend{matrix}}right}},

где {displaystyle k=1,2,...} Фигурные же скобки обозначают Числа Стирлинга второго рода.

А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.

Свойства распределения Пуассона[править | править код]

  • Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть Y_{i}sim {mathrm {P}}(lambda _{i}),;i=1,ldots ,n. Тогда
Y=sum limits _{{i=1}}^{n}Y_{i}sim {mathrm {P}}left(sum limits _{{i=1}}^{n}lambda _{i}right).
Y_{1}mid Y=ysim {mathrm {Bin}}left(y,{frac {lambda _{1}}{lambda _{1}+lambda _{2}}}right).
p(k)approxfrac{1}{sqrt{2pilambda}}expleft(-frac{(k-lambda)^2}{2lambda}right)

Асимптотическое стремление к распределению[править | править код]

Довольно часто в теории вероятностей рассматривают не само распределение Пуассона, а последовательность распределений, асимптотически равных ему. Более формально, рассматривают последовательность случайных величин xi _{1},xi _{2},dots , принимающих целочисленные значения, такую что для всякого k выполнено P{xi _{n}=k}sim {frac {lambda ^{k}e^{{-lambda }}}{k!}} при nto infty .

Простейшим примером является случай, когда xi _{n} имеет биномиальное распределение с вероятностью успеха {frac {lambda }{n}} в каждом из n испытаний.

Обратная связь с факториальными моментами[править | править код]

Рассмотрим последовательность случайных величин {displaystyle xi _{1},xi _{2},dots ,} принимающих целые неотрицательные значения. Если mu _{r}({xi _{n}})sim lambda ^{r} при nto infty и любом фиксированном r (где mu _{r}({xi _{n}}) — r-й факториальный момент), то для всякого k при nto infty выполнено P{xi _{n}=k}sim {frac {lambda ^{k}e^{{-lambda }}}{k!}}.

Доказательство

Лемма

Для начала докажем общую формулу вычисления вероятности появления конкретного значения случайной величины через факториальные моменты. Пусть для некоторого xi известны все mu _{r}(xi ) и mu _{r}(xi )to 0 при rto infty . Тогда

{displaystyle sum limits _{r=k}^{infty }{(-1)^{r-k}{frac {mu _{r}(xi )}{k!(r-k)!}}}=sum limits _{r=k}^{infty }{sum limits _{s=r}^{infty }{(-1)^{r-k}{frac {s!}{k!(r-k)!(s-r)!}}P{xi =s}}}.}

Изменяя порядок суммирования, это выражение можно преобразовать в

{displaystyle sum limits _{s=k}^{infty }{P{xi =s}sum limits _{r=k}^{s}{frac {(-1)^{r-k}s!}{k!(r-k)!(s-r)!}}}=sum limits _{s=k}^{infty }{P{xi =s}{frac {s!}{k!}}sum _{t=0}^{s-k}{frac {(-1)^{t}}{t!((s-k)-t)!}}}.}

Далее, из известной формулы sum limits _{{k=0}}^{{n}}{(-1)^{k}C_{n}^{k}}=0 получаем, что {frac {s!}{k!}}sum _{{t=0}}^{{s-k}}{{frac {(-1)^{t}}{t!((s-k)-t)!}}}=0 при s>k и то же выражение вырождается в 1 при s=k.

Тем самым доказано, что {displaystyle P{xi =k}=sum limits _{r=k}^{infty }{(-1)^{r-k}{frac {mu _{r}(xi )}{k!(r-k)!}}}.}

Доказательство теоремы

Согласно лемме и условиям теоремы, P{xi _{n}=k}sim sum limits _{{r=k}}^{{infty }}{(-1)^{{r-k}}{frac {lambda ^{r}}{k!(r-k)!}}}=sum limits _{{r=0}}^{{infty }}{(-1)^{r}{frac {lambda ^{{r+k}}}{k!r!}}}={frac {lambda ^{k}}{k!}}sum limits _{{r=0}}^{{infty }}{{frac {(-lambda )^{r}}{r!}}}={frac {lambda ^{k}e^{{-lambda }}}{k!}} при nto infty .

Q.E.D.

Как пример нетривиального следствия этой теоремы можно привести, например, асимптотическое стремление к {mathrm {P}}(lambda ) распределения количества изолированных рёбер (двухвершинных компонент связности) в случайном n-вершинном графе, где каждое из рёбер включается в граф с вероятностью p_{n}sim {frac {2lambda }{n^{2}}}.[1]

История[править | править код]

Работа Симеона Дени Пуассона «Исследования о вероятности приговоров в уголовных и гражданских делах»[2], в которой было введено данное распределение, была опубликована в 1837 году[3]. Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи, импульсы счётчика радиоактивного излучения, количество забиваемых футбольной командой голов и др.[4]

См. также[править | править код]

  • Биномиальное распределение
  • Обобщенное распределение Пуассона на локально компактной абелевой группе

Примечания[править | править код]

  1. ↑ Видеолекция Школы Анализа Данных. Дата обращения: 7 декабря 2014. Архивировано 8 апреля 2014 года.
  2. ↑ Пуассон, 1837.
  3. ↑ Чукова Ю. П.  Распределение Пуассона // «Квант» : науч.-поп. физ.-мат. журн. — М.: «Наука», 1988. — № 8. — С. 15‒18. — ISSN 0130-2221.
  4. ↑ Винс, 2012, с. 370.

Литература[править | править код]

  • Вентцель Е. С., Овчаров Л. А. Теория вероятностей и её инженерные приложения. 2-е изд. — М.: Высшая школа, 2000. — 480 с. — ISBN 978-5-406-00565-1. — С. 135.
  • Винс, Ральф. Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров = The mathematics of money management risk analysis techniques for traders. — М.: Альпина Паблишер, 2012. — 400 с. — ISBN 978-5-9614-1894-1.
  • Пуассон С. Д. Исследования о вероятности приговоров в уголовных и гражданских делах = Poisson S.-D. Recherches sur la probabilité des jugements en matière criminelle et en matière civile. — Berlin: NG Verlag (Viatcheslav Demidov Inhaber), 2013. — 330 p. — ISBN 978-3-942944-29-8. [Poisson.pdf]. Архивировано 1 ноября 2014 года.
  • Guerriero V. Power Law Distribution: Method of Multi-scale Inferential Statistics. — Journal of Modern Mathematics Frontier, 2012, 1. — P. 21—28. Архивная копия от 21 февраля 2018 на Wayback Machine

Ссылки[править | править код]

  • Распределение Пуассона — онлайн-калькулятор
Источник

Дискретная
случайная величина распределена по
закону Пуассона, если она принимает
значения 0,1,2…m…n…,
бесконечное, но счетное число раз, с
вероятностями, определяемыми по формуле
Пуассона:

где,p.

Закон
распределения примет вид:

0

1

2

…

m

…

…

…

,

и
т.д.

Теорема.
Математическое
ожидание и дисперсия случайной величины,
распределенной по закону Пуассона,
равны параметру Пуассона.

Пример
1.

Станок
изготавливает за смену 100000 деталей.
Вероятность изготовления бракованной
детали p
= 0,0001.

Найти
вероятность того, что за смену будет
изготовлено 5 бракованных деталей.

Решение:

Обозначим
n
= 100 000,
k
= 5, p
= 0,0001. События, состоящие в том, что
отдельная деталь бракована, независимы,
число испытаний n
велико, а вероятность p
мала, поэтому воспользуемся распределением
Пуассона:

где

Пример
2.

Устройство
состоит из 1000 элементов. Вероятность
отказа любого элемента в течение времени
t
равна 0,002.

Найти
математическое ожидание,
дисперсию,
среднее квадратическое отклонениеи
моду.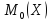

Решение:

X
‒ случайная величина ‒ число отказавших
за время t
элементов.

,
.
Следовательно, случайная величина
распределена по закону Пуассона.

элемента

Составим
закон распределения Пуассона:

0

1

2

3

…

m

…

0,135335

0,270671

0,270671

0,180447

…

…

и
т.д.

9. Непрерывная случайная величина. Функция распределения. Плотность вероятности. Вероятность попадания в заданный интервал.

Непрерывной
случайной величиной
называют случайную величину, значения
которой сплошь заполняют некоторый
интервал.

Например,
рост человека ‒ непрерывная случайная
величина.

Функцией
распределения случайной величины
называют вероятность того, что случайная
величина Х
принимает значения, меньшие х.

F
(x)
= P
(
X

Геометрически,
формула F(x)
= P
(Xозначает,
что все значения Х
будут находиться, левее х.
Функция F(x)
называется интегральной функцией.

Плотностью
вероятности непрерывной
случайной величины f
(x)
называется производная от функции
распределения этой случайной величины:

Следовательно,
F(x)
первообразная для f
(x).

Теорема.
Вероятность попадания непрерывной
случайной величины X
в интервал от a
до b
находится по формуле:

Доказательство.

Следствие.
Если все возможные значения случайной
величины

10. Математическое ожидание и дисперсия непрерывной случайной величины

1.
Математическое ожидание:

2.
Дисперсия:

Преобразуем
эту формулу:

‒
формула
дисперсии для непрерывных случайных
величин.

Тогда
среднее квадратическое отклонение:

11. Основные законы распределения непрерывных случайных величин.

1.Нормальный закон распределения.

Из
всех законов распределения для непрерывных
случайных величин на практике чаще
всего встречается нормальный
закон
распределения. Этот закон распределения
является предельным, то есть все остальные
распределения стремятся к нормальному.

Теорема
1. Непрерывная
случайная величина распределена по
нормальному
закону с
параметрами а
и
,если
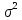
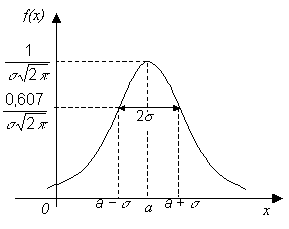
плотность вероятности имеет вид:

Математическое
ожидание случайной величины, распределённой
по нормальному закону распределения,
равно а,
то естьдисперсия.

Теорема
2. Вероятность
попадания непрерывной случайной
величины, распределенной по нормальному
закону распределения в интервал от α
до β,
находится по формуле:

Пример.

Полагая,
что рост мужчин определенной возрастной
группы есть нормально распределенная
случайная величина  X, c параметрами а =
173 и
=
36.

Найти:
а)
выражение плотности вероятностей и
функции распределения случайной
величины X;

б)
долю костюмов 4-го роста (176 – 182 см) в
общем объеме производства.

Решение:

Плотность
вероятности нормально распределенной
случайной величины:

Доля
костюмов 4-го роста (176 – 182 см.) в общем
объеме производства определяется по
формуле как вероятность

0,2417100%24,2%
‒ доля костюмов 4-го роста в общем объеме
производства.

Итак,
функция плотности вероятностей
нормального закона распределения имеет
вид:

Тогда
функция распределения:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Закон распределения Пуассона

На этой странице мы собрали примеры решения учебных задач, где используется распределение Пуассона.

Краткая теория

Рассмотрим некоторый поток событий, в котором события наступают независимо друг от друга и с некоторой фиксированной средней интенсивностью $lambda$ (событий в единицу времени). Тогда случайная величина $X$, равная числу событий $k$, произошедших за фиксированное время, имеет распределение Пуассона. Вероятности вычисляются по следующей формуле:

$$
P(X=k)=frac{lambda^k}{k!}cdot e^{-lambda}, k=0,1,2,…
$$

Для пуассоновской случайной величины математическое ожидание и дисперсия совпадают с интенсивностью потока событий:

$$M(X)=lambda, quad D(X)=lambda.$$

Распределение Пуассона играет важную роль в теории массового обслуживания. При увеличении $lambda$ данное распределение стремится к нормальному распределению $N(lambda, sqrt{lambda})$. В свою очередь, оно само является “приближенной” моделью биномиального распределения при больших $n$ и крайне малых $p$ (см. теорию про формулу Пуассона).

Лучшее спасибо – порекомендовать эту страницу

Примеры решенных задач

Задача 1. Среднее число самолетов, взлетающих с полевого аэродрома за одни сутки, равно 10. Найти вероятность того, что за 6 часов взлетят:
А) три самолета,
Б) не менее двух самолетов.

Задача 2. На автовокзале время прибытия автобусов различных рейсов объявляет дежурный. Появление информации о различных рейсах происходит случайной и независимо друг от друга. В среднем на автовокзал прибывает 5 рейсов каждые полчаса.
А) Составьте ряд распределения числа сообщений о прибытии автобусов в течение получаса.
Б) Найдите числовые характеристики этого распределения.
В) Запишите функцию распределения вероятностей и постройте ее график.
Г) Чему равна вероятность того, что в течение получаса прибудут не менее трех автобусов?
Д) Чему равна вероятность того, что в течение четверти часа не прибудет ни один автобус?

Задача 3. АТС получает в среднем за час 480 вызовов. Определить вероятность того, что за данную минуту она получит: ровно 3 вызова; от 2 до 5 вызовов.

Задача 4. Случайная величина $X$ распределена по закону Пуассона с параметром $lambda=0,8$. Необходимо:
А) выписать формулу для вычисления вероятности $P(X=m)$;
Б) найти вероятность $P(1 le X lt 3)$;
В) найти математическое ожидание $M(2X+5)$ и дисперсию $D(5-2X)$.

Задача 5. Среднее число ошибочных соединений, приходящееся на одного телефонного абонента в единицу времени, равно 8. Какова вероятность того, что для данного абонента число ошибочных соединений будет больше 4?

Задача 6. В среднем в магазин заходят 3 человека в минуту. Найти вероятность того, что за 2 минуты в магазин зайдет не более 1 человека.

Задача 7. Автомобиль проходит технический осмотр и обслуживание. Число неисправностей, обнаруженных во время техосмотра, распределяется по закону Пуассона с параметром 0,63. Если неисправностей не обнаружено, техническое обслуживание автомобиля продолжается в среднем 2 ч. Если обнаружены одна или две неисправности, то на устранение каждой из них тратится в среднем еще полчаса. Если обнаружено больше двух неисправностей, то автомобиль становится на профилактический ремонт, где он находится в среднем 4 ч.
Определите закон распределения среднего времени $T$ обслуживания и ремонта автомобиля и его математическое ожидание $M(T)$.

Задача 8. В тексте учебника по психологии содержатся опечатки: в среднем, одна на
десять страниц. Пусть Х – число опечаток на одной странице. Определить закон распределения для Х. Найти вероятность, что на странице есть хотя бы одна опечатка.

Мы отлично умеем решать задачи по теории вероятностей

Решебник по терверу

Если решения нужны срочно и почти даром? Ищите в решебнике по теории вероятностей:

Источник

Определение распределения Пуассона

Распределение Пуассона относится к процессу определения вероятности повторения событий в течение определенного периода времени. Переменные для этого распределения вероятностей должны быть счетными, случайными и независимыми.

Этот статистический инструмент используется для понимания будущих возможностей и тенденций. Он используется бизнес-организациями, финансовыми аналитиками. Финансовые аналитики. Финансовый аналитик анализирует проект или компанию с основной целью консультировать руководство / клиентов по поводу жизнеспособных инвестиционных решений. Они проводят тщательный финансовый анализ и делают подходящие объективные прогнозы, чтобы прийти к своим выводам. Читать далее, исследователи рынка, астрономы, ученые, физиологи, спортивные власти и правительственные учреждения. Впервые он был введен Симеоном Дени Пуассоном в 1830 году. Используя этот метод, французский математик рассчитал вероятность успеха в азартных играх.

Оглавление

  • Определение распределения Пуассона
    • Как работает распределение Пуассона?
    • Формула распределения Пуассона
    • Расчет с графиком
    • Примеры распределения Пуассона в Excel
      • Пример №1
      • Пример #2
    • Приложения распределения Пуассона
    • Часто задаваемые вопросы (FAQ)
    • Рекомендуемые статьи
  • Распределение Пуассона — это однопараметрический вероятностный инструмент, используемый для определения шансов на успех, т. е. для определения того, сколько раз событие происходит в течение определенного периода времени.
  • Формула распределения Пуассона: P(x;µ)=(e^(-µ) µ^x)/x!.
  • Распределение считается моделью Пуассона, когда количество вхождений является счетным (в целых числах), случайным и независимым. Другими словами, оно должно быть независимым от других событий и их возникновения.
  • Кроме того, среднее значение X ∼P(µ) = µ; Дисперсия X ∼P(µ) = µ; и стандартное отклонение X ∼P(µ) = +√µ.

Как работает распределение Пуассона?

Распределение Пуассона есть не что иное, как прогноз события, происходящего в определенный период. Устанавливается возможность возникновения события заданное количество раз для заданного периода времени. Например, шансы получить определенное количество ударов сердца в течение минуты — это распределение вероятностей. Рассмотрим другой пример, предположим, что больница хочет реструктурировать персонал своего отделения неотложной помощи. Скажем, больница ежедневно принимает три неотложных случая. Администрация использует распределение Пуассона, чтобы определить возможность приема пяти экстренных случаев в день для найма резервного персонала.

Этот статистический инструмент является однопараметрическим. В результате знание средней переменной возникновения события можно использовать для определения других возможностей. Распределение ПуассонаРаспределение ПуассонаРаспределение Пуассона относится к процессу определения вероятности повторения событий в течение определенного периода времени. X ∼ P(μ). Более того, мы также можем найти его среднее значение, дисперсию и стандартное отклонение, используя следующие уравнения:

  • Среднее значение X ∼P(µ) = µ
  • Дисперсия X ∼P(µ) = µ
  • Стандартное отклонениеСтандартное отклонениеСтандартное отклонение (SD) — это популярный статистический инструмент, обозначаемый греческой буквой «σ», для измерения вариации или дисперсии набора значений данных относительно их среднего (среднего) значения, таким образом интерпретируя надежность данных.Подробнее о X ∼P(μ) = +√μ

Результаты двух распределений Пуассона можно суммировать, чтобы получить вероятность более широкой случайной величины. То есть X1∼P(µ1) и X2∼P(µ2) могут предоставить значение третьей переменной Y. Здесь Y = X1+X2∼P (µ1+ µ2). Например, предположим, что хоккейная команда выигрывает в среднем два матча на каждые пять сыгранных игр. Какова вероятность выиграть одно соревнование в этом году? Команда может выиграть 0 или 1 матч. Таким образом, чтобы вычислить желаемые результаты, сложите обе вероятности. То есть сложите вероятность выигрыша нулевого матча и вероятность выигрыша одного матча.

В 1830 году Симеон Дени Пуассон представил модель распределения Пуассона. Он был французским математиком, который вычислил шансы на успех в азартных играх, используя этот метод. Однако это был непопулярный инструмент среди игроков. Тем не менее, концепция приобрела значение в области статистики после Второй мировой войны. Британский статистик Р. Д. Кларк использовал этот инструмент, чтобы помочь британскому правительству получить представление о немецких бомбардировках Лондона. Кларк проанализировал, что немцы сбросили бомбы случайным образом. Кларк пришел к выводу, что в атаках не указан регион или город.

Формула распределения Пуассона

Это распределение вероятности определяет вероятность повторения события в течение заданного интервала времени. Формула выглядит следующим образом:

Формула распределения яда

Формула распределения яда 1

Здесь P(x; µ) — вероятность того, что событие произойдет определенное число раз за определенный период;

e обозначает число Эйлера, основное значение которого равно 2,72;

µ — среднее количество вхождений за определенный период; и

Икс! является факториалом числа событий, для которых определяется вероятность.

Расчет с графиком

Рассмотрим следующее числовое значение, чтобы лучше понять вычисления, используемые в этом математическом инструменте.

Компания-производитель часов хочет сократить количество бракованных изделий. Было отобрано в среднем 100 партий, и было обнаружено, что 7 часов из каждой партии были бракованными. Какова вероятность того, что 10 часов будут бракованными в одной партии?

Решение:

Данный:

Среднее количество бракованных часов в партии (µ) = 7

Ожидаемое количество бракованных часов в конкретной партии (x) = 10

Р (х; мк) = [e^(-μ) μ^x]/Икс!

Р (10;7) = [e^ (-7) 7^10]/10!

Р (10;7) = 0,07098 или 7,098%

Таким образом, вероятность того, что в данной партии будет 10 бракованных часов, составляет 7,098%.

График распределения Пуассона

На том же примере изобразим на графике вероятность наличия 0,1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 бракованных часов.

График распределения яда

Примеры распределения Пуассона в Excel

Рассмотрим этот простой пример Excel, чтобы лучше понять, как применяется формула распределения Пуассона.

Пример №1

Среднее количество событий в заданном временном интервале равно 10. Какова вероятность того, что это событие произойдет 15 раз?

В этом примере u = среднее количество появлений события = 10

И х = 15

Пример распределения яда 1

Следовательно, расчет распределения Пуассона можно выполнить следующим образом:

Пример распределения яда 1-1

P (15;10) = e^(-10)*10^15/15!

Пример распределения яда 1-2

Р (15; 10) = 0,0347 = 3,47%

Следовательно, вероятность того, что это событие произойдет 15 раз, составляет 3,47%.

Пример #2

Другое использование формулы Пуассона в страховой отрасли. Компания, занимающаяся страховым бизнесом, определяет размер страховой премии на основе количества исков и суммы требований в год. Так, для оценки суммы своей премии страховая компания будет определять среднее количество заявленной суммы в год. Затем, основываясь на этом среднем, он также определит минимальное и максимальное количество исков, которые можно обоснованно подать в год. Основываясь на максимальном количестве суммы претензии, а также стоимости и прибыли от премии, страховая компания определит, какая сумма премии будет хорошей для безубыточности.

Скажем, среднее количество претензий, обрабатываемых страховой компанией в день, равно 5. Она выяснит, какова вероятность 10 претензий в день.

Пример распределения яда 2

Следовательно, расчет можно провести следующим образом:

Пример распределения яда 2-1

Р(10;5) = е^(-5). 5^10/10!

Пример распределения яда 2-2

Р(10;5) = 1,81%

Следовательно, вероятность того, что компания будет иметь 10 претензий в день, очень мала. На основании этих данных компания может принять решение о размере премии.

Приложения распределения Пуассона

Распределение Пуассона полезно для прогнозирования, отслеживания и повышения эффективности компании. Он часто применяется для оценки эффективности бизнеса и направления организационных усилий для достижения операционной эффективности. Например, руководство может определить пиковые часы продаж и эффективности обслуживания клиентов, чтобы спланировать потребности в рабочей силе. Таким образом, можно комфортно переносить периоды спешки и суеты.

Этот статистический инструмент очень эффективен для проверки осуществимости и жизнеспособности страхового покрытия. Он включает в себя анализ различных факторов, таких как вероятность несчастных случаев, стоимость страхового покрытия, количество раз, когда может быть предъявлен иск, является ли компания чрезмерно застрахованной или недостаточно застрахованной. Кроме того, используя этот метод, менеджеры по производству контролируют потери, отслеживая количество бракованных изделий в каждом цикле производства.

Это одинаково важный инструмент в области финансов для фондовых аналитиков и рыночных прогнозов. Это помогает определить уровень риска, связанный с инвестициями в ценные бумаги. Это достигается путем установления возможности падения рынка в определенный период. Этот метод даже облегчает анализ поведения инвесторов и частоты инвестиций.

Часто задаваемые вопросы (FAQ)

Что такое распределение Пуассона в статистике?

Распределение Пуассона — это не что иное, как предсказание события, происходящего в течение заданного периода времени. Устанавливается возможность возникновения события заданное количество раз для заданного периода времени.

Какими свойствами обладает распределение Пуассона?

Модель называется распределением Пуассона, если она обладает следующими свойствами:

• Возможность успеха в конкретный период времени не зависит от его более раннего наступления.
• Переменные или количество вхождений должны быть целыми числами, т. е. быть исчисляемыми.
• Шансы на успешный исход более одного раза за данный период ничтожны.
• Следует указать значение µ, т. е. среднее количество событий за определенный период.

В чем разница между процессом Пуассона и распределением Пуассона?

Процесс Пуассона — это непрерывное возникновение независимых событий, подобных безостановочному сердцебиению человека. В то время как распределение Пуассона — это средство нахождения возможности повторения события несколько раз за определенный период, т. е. количества повторений события в процессе Пуассона. Например, шансы получить определенное количество ударов сердца в течение минуты — это распределение вероятностей.

Рекомендуемые статьи

Это было руководство к тому, что такое распределение Пуассона и его определение. Здесь мы дополнительно обсудим его формулу, расчет, примеры и загружаемые шаблоны Excel. Вы можете узнать больше о финансовом моделировании из следующих статей –

  • Распределение Пуассона в Excel
  • Формула распределения T
  • Формула биномиального распределения
  • Формула распределения выборки
  • годовых против годовых
Источник

Добавить комментарий