Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
В чем смысл игры?
Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.
Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей:
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.
Задания для 1 класса
Задание 1
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.
Задание 3
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
- 2, 4, 6,…
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Задания для 2 класса
Задание 1
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
- 95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
- 2, 3, 5, 8, …, …, …, …
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Задания для 3 класса
Задание 1
Рассмотрите картинку и найдите закономерность в задаче.
Решение: В таблице мы увидим такую закономерность:
8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.
Задание 2
В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат и т. д.
Задание 3
Найди закономерность и продолжи ряды:
- 12, 23, 34, 45, 56…
- 13, 24, 35, 46…
Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу. 12=10+2, 23=20+3, 34=30+5 и т. д.
Задание 4
Продолжи ряд, сохраняя закономерность.
- 12, 36, 13, 39, 14, 42, 15,…
Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
- 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем — ромба, в четвертом – параллелограмма и трапеции.


Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Игры на поиск закономерностей интересны в любом возрасте. Дети 7-8 лет уже знакомы с закономерностями в природе. Первоклашки умеют складывать и вычитать в пределах 20, делают вычисления в уме, поэтому задания для этого возраста будут содержать сюжетные картинки, комбинации чисел, геометрических фигур и символов.
Как установить закономерность
Установить закономерность – значит найти правило, по которому составлена последовательность элементов, продолжить или восстановить пропущенные элементы.
Закономерность событий
Для развития логики и речи предложите ребенку игру на установление закономерности в последовательности событий. Задания помогают раскрыть причинно–следственные связи и воссоздать временную последовательность: раньше — позже. Ребенок научится понимать взаимосвязь событий и выстраивать логическую цепочку действий или превращений.
Числовые закономерности
Закономерность, в которой числа увеличиваются называется возрастающая, а закономерность, где числа уменьшаются — убывающая.
Числа в циклической закономерности повторяются снова и снова, как лампочки на гирлянде.
Пример: 1 2 2 1 2 2 ? 2 2 1 2 2.
Прежде, чем приступать к заданиям — разберите с ребенком несколько примеров, которые доступно объясняют как устанавливать числовые закономерности.
Пример 1. Продолжи закономерность чисел 1,3,5,7, ? Сначала найдем разность соседних чисел — из большего числа вычтем меньшее (предыдущее): 7-5=2 5-3=2 3-1=2
Вывод: числа закономерно увеличиваются на одно и тоже значение, каждое последующее число на 2 больше, чем предыдущее, значит неизвестное число будет на 2 больше, чем 7. 7+2=9 Ответ: 1,3,5,7,9.
В числовой закономерности должно быть не меньше трех чисел. Иногда одно число может быть суммой или произведением других двух чисел.
Пример 2. Продолжи ряд чисел 2,3,5,8, ?
Сначала найдем разность соседних чисел.
3-2=1 5-3=2 8-5=3
Какую закономерность можно отметить?
Вывод: разность соседних чисел увеличивается на 1, значит, чтобы узнать искомое число нужно предыдущее увеличить на 4(8+4=12). Ответ: 12.
Чтобы установить числовую закономерность найди разницу между соседними числами, определи правило составления последовательности и примени его к пропущенному числу.
Закономерности с фигурами и символами
Закономерности с фигурами и символами развивают внимание, зрительную память, учат сравнивать и анализировать.
Детям 7-8 лет будет посильно и интересно выполнять задания, в которых «спрятано» несколько закономерностей одновременно.
Рассмотри закономерность с фигурами, проследи, что изменяется и подбери недостающий элемент. Не знаешь как справится с заданием? Познакомься со способом решения таких заданий на странице Закономерности для детей 6-7 лет .
После определения последовательности картинок попросите ребенка составить рассказ о происходящих событиях.
Играй и учись!
Установи порядок событий и составь рассказ о том, что изображено на картинках в логичной последовательности.
Проанализируй закономерности и найди числа, которых не хватает.
Продолжи ряд, выбери подходящую фигуру.
Какой фигуры не хватает?
Содержание
- Закономерности 7-8 лет
- Как установить закономерность
- Закономерность событий
- Числовые закономерности
- Закономерности с фигурами и символами
- Играй и учись!
- Закономерность что это простыми словами для детей
- Как понять найти закономерность
- Выбирайте игру для старта
- Что такое закономерность в математике?
- Последовательность букв
- Закономерности 5-6 лет
- Подготовка к игре
- Закономерность это в математике
- Выбирайте игру для старта
- Что такое закономерность в математике?
Закономерности 7-8 лет
Учимся узнавать закономерности расположения чисел и фигур, определять логическую последовательность действий и состояний в природе.
Игры на поиск закономерностей интересны в любом возрасте. Дети 7-8 лет уже знакомы с закономерностями в природе. Первоклашки умеют складывать и вычитать в пределах 20, делают вычисления в уме, поэтому задания для этого возраста будут содержать сюжетные картинки, комбинации чисел, геометрических фигур и символов.
Как установить закономерность
Установить закономерность – значит найти правило, по которому составлена последовательность элементов, продолжить или восстановить пропущенные элементы.
Закономерность событий
Для развития логики и речи предложите ребенку игру на установление закономерности в последовательности событий. Задания помогают раскрыть причинно–следственные связи и воссоздать временную последовательность: раньше — позже. Ребенок научится понимать взаимосвязь событий и выстраивать логическую цепочку действий или превращений.
Числовые закономерности
Закономерность, в которой числа увеличиваются называется возрастающая, а закономерность, где числа уменьшаются — убывающая.
Числа в циклической закономерности повторяются снова и снова, как лампочки на гирлянде.
Пример: 1 2 2 1 2 2 ? 2 2 1 2 2.
Прежде, чем приступать к заданиям — разберите с ребенком несколько примеров, которые доступно объясняют как устанавливать числовые закономерности.
Пример 1. Продолжи закономерность чисел 1,3,5,7, ? Сначала найдем разность соседних чисел — из большего числа вычтем меньшее (предыдущее): 7-5=2 5-3=2 3-1=2
Вывод: числа закономерно увеличиваются на одно и тоже значение, каждое последующее число на 2 больше, чем предыдущее, значит неизвестное число будет на 2 больше, чем 7. 7+2=9 Ответ: 1,3,5,7,9.
В числовой закономерности должно быть не меньше трех чисел. Иногда одно число может быть суммой или произведением других двух чисел.
Пример 2. Продолжи ряд чисел 2,3,5,8, ?
Сначала найдем разность соседних чисел.
3-2=1 5-3=2 8-5=3
Какую закономерность можно отметить?
Вывод: разность соседних чисел увеличивается на 1, значит, чтобы узнать искомое число нужно предыдущее увеличить на 4(8+4=12). Ответ: 12.
Чтобы установить числовую закономерность найди разницу между соседними числами, определи правило составления последовательности и примени его к пропущенному числу.
Закономерности с фигурами и символами
Закономерности с фигурами и символами развивают внимание, зрительную память, учат сравнивать и анализировать.
Детям 7-8 лет будет посильно и интересно выполнять задания, в которых «спрятано» несколько закономерностей одновременно.
После определения последовательности картинок попросите ребенка составить рассказ о происходящих событиях.
Играй и учись!
Установи порядок событий и составь рассказ о том, что изображено на картинках в логичной последовательности.
Проанализируй закономерности и найди числа, которых не хватает.


Продолжи ряд, выбери подходящую фигуру.

Источник
Закономерность что это простыми словами для детей
Как объяснить ребенку понятие закономерность? понятие ребенок закономерность
а как объяснить решее задачи, заданной на лето/1 класс/ продолжить ряд чисел не нарушая закономерноси: 5,2005,3005.
Еще, 50 лет назад, когда моя дочь пошла в 1-й класс, подобные задачки тоже ей задавали. Я, возмущаясь, говорил: один дурак может задать столько вопросов, что сто умных на них не ответят. И это продолжается. к сожалению.
Закономерности бывают разные. Если ваш ребенок школьник, могу предположить, что нужна математическая закономерность. Тут задачи на закономерности решаются логически. Самый простой пример. 1,2,3,4,5,6. Продолжить по закономерности ряд чисел. Логично же что дальше будет 7,8,9 и так далее..
формула событий. развитие событий на основе анализа предыдущих событий и свойств природы. Законов Вселенной… Гроза. Гром. Молния. Идёт дождь. Снегопад…. Отсутствие денег в бюджете при неразумном расходовании.. покупка игрушки любимой при правильном поведении.
На примере существования/наступления дня и ночи или времени года. Также постараться объяснить как и почему это происходит и желательно при этом использовать какие нибудь наглядные пособия. Это будет убедительным примером объективной закономерности.
Людмила, начните объяснять прямо сейчас. Спросите, что сейчас-день, ночь, потом, что будет? И так далее, лучше про дни рождения,праздники. Вот тут то и вставьте-это закономерность, дальше-сложнее. Удачи вам.
Всё вокруг нас подчиняется порядку. После лета осень, после осени зима. Не будет порядка, будет ералаш. Закономерность, это подчинение общим законам.
Можете ему показать на примере:-Налейте в чашку с водой немного масла и покажите ему что оно плавает на поверхности. Это закономерность.
НАШКОДИЛ ПРОВЕРИТЬ РЕМЕШКОМ ОТ КУДА НОГИ РАСТУТ ХОРОШО СЕБЯ ВЕЛ ПОЛУЧИ МОРОЖЕНОЕ ЭТО С МАЛОЛЕТСТВА А ДАЛЬШЕ ПРОЦЕСС САМ ПОЙДЕТ
после детского сада ребёнок идёт в школу это есть закономерность, закончив школу идет в армию или снова учится
Терпеливо объяснить,привести примеры,продемонстрировать. Взрослым это тоже полезно,кто не усвоил в детстве.
пусть сам на себе это прочувствует, всунув два пальца в розетку над которой написано НЕ ВЛАЗЬ,! УБЬЕТ!
Источник
Как понять найти закономерность
Тема: Закономерности в числах и фигурах
Всё в нашей жизни подчиняется каким-то правилам. Есть правила и в математике. Например, посмотрите на такой ряд чисел: 1, 2, 3. Числа стоят по порядку. Или такой ряд: 1, 3, 5: числа стоят через 1 число. 10, 20, 30: каждое следующее число больше предыдущего на 10. То есть при составлении какого-то последовательного ряда соблюдается какое-то правило. Это правило называется закономерность.
Закономерность – это правило, по которому что-то повторяется время от времени.
Повторяться могут изображения, буквы, числа и любые другие символы. Но обязательно в ряду должно быть не менее трёх чисел.
Например, 2, 3. Есть ли в этом ряду закономерность? Этого мы утверждать не можем. А если ряд 3, 6, 9, то какое число мы можем поставить дальше? Конечно. 12. Мы должны поставить это число по правилу данной закономерности (каждое число в ряду больше другого на 3).
В закономерности всегда не менее 3-х элементов!
На первых двух мы обычно предполагаем закономерность, а на третьем проверяем. Два элемента могут находиться рядом абсолютно случайно. А три – это уже правило.
Как находить закономерности?
1. Внимательно смотрим на ряд чисел, фигур или других картинок.
2. Если в этом ряду есть закономерность, то думаем, какая.
3. Проверяем, соблюдается ли это правило во всей последовательности чисел.
4. Вставляем числа (или фигуры), которые должны эту закономерность продолжить.

Как решать задания на закономерности, вы подробно можете посмотреть на сайте заочных школ на Методической страничке в пособии «Закономерности в цифрах и фигурах. Аналогичная закономерность». Скачайте и просмотрите. Там есть примеры аналогичных заданий.
Будьте очень внимательны при решении этих последовательностей!
КОНТРОЛЬНАЯ РАБОТА № 3 по предмету «Математическая мозаика» для 1 класса
Фамилия _______________________________ Имя __________________
Школа _______________ Класс ______________
Задание 1. Назовите следующее число в ряду:
Задание 2. Помогите коту Мурзику выбрать из предлагаемых вариантов геометрическую фигуру, которую нужно поместить в пустую клетку.
Задание 3. Машенька – ужасная модница. У нее два ящика с красивыми косынками. В первом ящике: красная косынка, синяя косынка в белый горошек, желтая косынка в мухоморчик, красная косынка в рыбку, зеленая косынка с птичкой, зеленая косынка в мороженку. Во втором ящике: синяя косынка в белочку, красная косынка в горошек, зеленая косынка в мухоморчик. Сколько различных по цвету косынок у Машеньки? Ответ: ________
Задание 4. Определи, какую картинку надо вставить в пустую клетку.

Задание 5. Найдите числа, которых не хватает каждой змейке. Впишите цифры в ответе.

Жёлтая змейка (верхняя) – ____
Зелёная змейка (средняя) – ______
Малиновая змейка (нижняя) – _____
Задание 6. Какая фигура лишняя?
3 4 5 Ответ: _______
Задание 7. Какой пример соответствует картинке?

Задачи на поиск закономерностей развивают логическое мышление ребёнка, учат сравнивать, рассуждать, классифицировать и делать выводы.
Выбирайте игру для старта
На платформе LogicLike.com дети с удовольствием развивают логику и способности к математике (смотреть отзывы). У нас 3500 занимательных заданий с ответами и пояснениями!
Что такое закономерность в математике?
Математическая закономерность – это определенное правило, по которому в числовом, фигурном или другом ряду элементов происходит повторение или изменение самих элементов или их свойств в соответствии с заданным правилом.
Из учебных материалов с картинками и видео, подготовленных опытными педагогами, ваш ребёнок узнает:
Очень часто в головоломках на закономерность встречаются буквы и цифры. Иногда могут встречаться и геометрические фигуры, и различные картинки, но это очень редко. Именно исходя из представленных букв и цифр, необходимо найти закономерность и додумать, какое же число или буква будет идти следующим. Очень часто в таких головоломках на закономерность буквы означают какие либо количественные признаки, а цифры – наоборот, зачастую обозначают буквы, или даже целые слова.
Последовательность букв
Автор получил 7 рублей за добавление этой Головоломки на сайт
Хочу так же
Источник
Закономерности 5-6 лет
Нахождение закономерностей – один из способов развития логического мышления. Игры на поиск логических закономерностей научат ребенка анализировать, сравнивать, обобщать и делать выводы. Такие задания тренируют ум, развивают смекалку и находчивость.
Логическая закономерность – это правило, по которому происходит повторение или изменение свойств предметов, чисел или других элементов в соответствии с заданным правилом.
Подготовка к игре
Прежде, чем приступать к игровым заданиям, наглядно объясните ребенку, что такое закономерность. Для этого возьмите три- четыре предмета и составьте ряд, в котором будет прослеживаться закономерность. Попросите ребенка рассмотреть предметы и выдвинуть гипотезу: по какой закономерности составлен ряд. После этого ребенок сам сможет правильно продолжить ряд предметов.
Закономерность наглядно показывают с помощью предметов, чисел, фигур или других элементов.
Расскажите ребенку, что признак может закономерно добавляться или уменьшаться. Предложите малышу внимательно посмотреть на божьих коровок и сказать, что изменяется. Верно, количество точек увеличивается на одну. Уточните, какой рисунок спрятался под вопросом. Малыш наверняка догадался – это божья коровка с 4-мя точками.
Решая логическую задачу, ребенок научится устанавливать разнообразные связи, выявлять причину по следствию и комбинировать исходные элементы.
Играя в игру «Найди закономерность» ребенок научится устанавливать логические связи, выявлять причину по следствию и комбинировать исходные элементы. Рассматривайте картинки и находите логические закономерности вместе с ребенком.




Если ваш ребенок смог самостоятельно выполнить последнее задание — смело переходите на страницу для детей 6-7 лет со следующим уровнем сложности игры!
Источник
Закономерность это в математике
Задачи на поиск закономерностей развивают логическое мышление ребёнка, учат сравнивать, рассуждать, классифицировать и делать выводы.
Выбирайте игру для старта
На платформе LogicLike.com дети с удовольствием развивают логику и способности к математике (смотреть отзывы). У нас 3500 занимательных заданий с ответами и пояснениями!
Что такое закономерность в математике?
Математическая закономерность – это определенное правило, по которому в числовом, фигурном или другом ряду элементов происходит повторение или изменение самих элементов или их свойств в соответствии с заданным правилом.
Из учебных материалов с картинками и видео, подготовленных опытными педагогами, ваш ребёнок узнает:
Тема: Закономерности в числах и фигурах
Всё в нашей жизни подчиняется каким-то правилам. Есть правила и в математике. Например, посмотрите на такой ряд чисел: 1, 2, 3. Числа стоят по порядку. Или такой ряд: 1, 3, 5: числа стоят через 1 число. 10, 20, 30: каждое следующее число больше предыдущего на 10. То есть при составлении какого-то последовательного ряда соблюдается какое-то правило. Это правило называется закономерность.
Закономерность – это правило, по которому что-то повторяется время от времени.
Повторяться могут изображения, буквы, числа и любые другие символы. Но обязательно в ряду должно быть не менее трёх чисел.
Например, 2, 3. Есть ли в этом ряду закономерность? Этого мы утверждать не можем. А если ряд 3, 6, 9, то какое число мы можем поставить дальше? Конечно. 12. Мы должны поставить это число по правилу данной закономерности (каждое число в ряду больше другого на 3).
В закономерности всегда не менее 3-х элементов!
На первых двух мы обычно предполагаем закономерность, а на третьем проверяем. Два элемента могут находиться рядом абсолютно случайно. А три – это уже правило.
Как находить закономерности?
1. Внимательно смотрим на ряд чисел, фигур или других картинок.
2. Если в этом ряду есть закономерность, то думаем, какая.
3. Проверяем, соблюдается ли это правило во всей последовательности чисел.
4. Вставляем числа (или фигуры), которые должны эту закономерность продолжить.

Как решать задания на закономерности, вы подробно можете посмотреть на сайте заочных школ на Методической страничке в пособии «Закономерности в цифрах и фигурах. Аналогичная закономерность». Скачайте и просмотрите. Там есть примеры аналогичных заданий.
Будьте очень внимательны при решении этих последовательностей!
КОНТРОЛЬНАЯ РАБОТА № 3 по предмету «Математическая мозаика» для 1 класса
Фамилия _______________________________ Имя __________________
Школа _______________ Класс ______________
Задание 1. Назовите следующее число в ряду:
Задание 2. Помогите коту Мурзику выбрать из предлагаемых вариантов геометрическую фигуру, которую нужно поместить в пустую клетку.
Задание 3. Машенька – ужасная модница. У нее два ящика с красивыми косынками. В первом ящике: красная косынка, синяя косынка в белый горошек, желтая косынка в мухоморчик, красная косынка в рыбку, зеленая косынка с птичкой, зеленая косынка в мороженку. Во втором ящике: синяя косынка в белочку, красная косынка в горошек, зеленая косынка в мухоморчик. Сколько различных по цвету косынок у Машеньки? Ответ: ________
Задание 4. Определи, какую картинку надо вставить в пустую клетку.

Задание 5. Найдите числа, которых не хватает каждой змейке. Впишите цифры в ответе.

Жёлтая змейка (верхняя) – ____
Зелёная змейка (средняя) – ______
Малиновая змейка (нижняя) – _____
Задание 6. Какая фигура лишняя?
3 4 5 Ответ: _______
Задание 7. Какой пример соответствует картинке?

Недавно, решая какую-то математическую задачу, ко мне в голову вдруг вклинилась мысль о том, что надо найти какую-нибудь закономерность в каких-то числах. С чего бы вдруг это – я не знаю.
Закономерность долго не заставила себя ждать. Я вывел интересную на мой взгляд, но при этом абсолютно бесполезную закономерность(хотя может, когда-нибудь её и доведут до чего-нибудь полезного).
Вся суть в квадратах чисел. Между квадратами соседних чисел существует определённый порядок, закономерность. Например:
0) 0^2 = 0
1) 1^2 = 1
2) 2^2 = 4
3) 3^2 = 9
4) 4^2 = 16
5) 5^2 = 25
.
Каждое следующее число(результат) увеличивается на определённое значение, а именно: 1,3,5,7,9,11 и т.д.
Так, к примеру, разница между 5^2 и 6^2 составляет 11, между 6^2 и 7^2 – 13.
Скорее всего кто-то когда-то уже и до меня додумался до этого, но я нигде не встречал)) Может у кого-то из этого и получится что-то полезное сделать)
Источник
Найди закономерность и продолжи ряд
Задачи на поиск закономерностей развивают логическое мышление ребёнка, учат сравнивать,
рассуждать, классифицировать и делать выводы. 3500+ задач с ответами и пояснениями.
Рекомендуем наш курс развития для детей 5-12 лет!
Выберите возраст ребёнка, чтобы начать занятия

На платформе LogicLike.com дети с удовольствием развивают логику
и способности к математике. У нас 3500 занимательных заданий
с ответами и пояснениями!
Что такое закономерность в математике?
Математическая закономерность – это определенное правило, по которому в числовом, фигурном
или другом ряду элементов происходит повторение или изменение самих элементов или их свойств в
соответствии с заданным правилом.
Из учебных материалов с картинками и видео,
подготовленных опытными педагогами, ваш ребёнок узнает:
- что собой представляют закономерности, каких видов они
бывают (циклические, возрастающие и убывающие); - с чего начать решение задачи и как понять, в каких
направлениях думать; - как строятся умозаключения о том, какое число, буква или
фигура должны продолжить предложенный ряд.
Рекомендуем взрослым и детям сначала решить несколько заданий вместе. Продолжить
занятия ребёнок может самостоятельно.
В курсе развития мышления LogicLike
есть всё, что вы искали!
Пройдите 3 главы-разминки и откройте доступ к закономерностям и другим
занимательным заданиям на логику.
Задачи типа «Найди закономерность»
Для ознакомления с темой предлагаем несколько примеров заданий по математике на поиск
закономерностей разного уровня сложности.
Задачи для 1 класса
Найди закономерность и продолжи числовой ряд:
Картинки расставили в определённом порядке (в виде закономерности). Подумай,
какой элемент будет следующим.
Догадайся, как нужно раскрасить последние 3 карандаша, чтобы сохранить
закономерность в этом ряду:
Примеры заданий для 2-3 классов
Фигуры разложили в виде закономерности (в определённом порядке). Продолжи
закономерность: выбери подходящий набор фигур.
Какую закономерность можно заметить? Продолжи ряд чисел:
Помоги Алисе найти числовую закономерность и запиши следующие два числа,
которые ее продолжат:

Задача повышенной сложности (математика 4 класс)
Ученики посадили дерево. Его высота составляла 72 см.
Через год дерево выросло до 80 см, через 2 года – до 86 см, через 3 года –
до 90 см.

Какой высоты (в см) будет деревце через 9 лет, если закономерность его роста
не изменится?
Как научить детей находить закономерности?
Объясните понятие закономерности и покажите на конкретных примерах несколько типов
последовательностей. Поясните, как вы рассуждаете, чтобы найти закономерность между числами,
буквами, картинками, любыми элементами ряда.
В видеоуроке по теме «Закономерности» мы на примерах разбираем: что такое возрастающая и
убывающая закономерности, как правильно
решать задачи на поиск закономерностей.
Действуем по такой схеме:
- Внимательно смотрим на ряд чисел, фигур, животных, предметов.
- Пробуем догадаться, на чем основана закономерность – по какому правилу расположены элементы.
- Пробуем определить тип закономерности.
- Проверяем наши предположения одно за другим, чтобы увидеть какое правило соблюдается.
-
Убедившись, что «задуманное» правило соблюдается, мы сможем точно назвать следующие элементы
ряда.
Найди закономерность и продолжи ряд — математические закономерности
Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
В чем смысл игры?
Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.
Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей:
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.
Задания для 1 класса
Задание 1
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.
Задание 3
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Задания для 2 класса
Задание 1
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
- 95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
- 2, 3, 5, 8, …, …, …, …
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Задания для 3 класса
Задание 1
Рассмотрите картинку и найдите закономерность в задаче.
Решение: В таблице мы увидим такую закономерность:
8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.
Задание 2
В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат и т. д.
Задание 3
Найди закономерность и продолжи ряды:
- 12, 23, 34, 45, 56…
- 13, 24, 35, 46…
Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу.
Задание 4
Продолжи ряд, сохраняя закономерность.
- 12, 36, 13, 39, 14, 42, 15,…
Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
- 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Логическая игра «Найди закономерность. Логическая игра «Найди закономерность Продолжи ряд нарисовав следующие фигуры
Задания, направленные на поиск математических закономерностей, улучшают способность рассуждать и логически мыслить, помогают научиться сравнивать, обобщать и делать выводы. Эта игра активизирует умственную деятельность ребенка и окажет существенное влияние на формирование образного мышления, развитие сообразительности и смекалки.
Распечатайте предложенные на сайте карточки и дайте их ребенку для работы.
Математическая закономерность представляет собой правило, согласно которому в цепочке (ряду) происходит повторение, замещение или изменение свойств определенных элементов в соответствии с установленным правилом.
Перед тем, как малыш преступит к заданию, объясните ему на нескольких примерах, что такое закономерность, как ее можно установить между различными звеньями ряда (числами, буквами, геометрическими фигурами). При решении первых заданий помогите ему подсказками и дополнительными вопросами, которые помогут в рассуждении о том, какое число или фигура должна продолжить цепь. Пусть внимательно рассмотрит рисунок и попробует самостоятельно определить, в чем основа его закономерности и каким должен быть следующий элемент ряда. В завершении пусть нарисует свой правильный ответ – фигуру или предмет, продолжающий ряд.
Найди закономерность и продолжи ряд
Это учебная статья по математике, перед началом занятий мы рекомендуем ознакомиться с
вводной частью
В этом занятии речь пойдет о задачах, в которых нужно найти какую-то закономерность, продолжить последовательность или, используя найденную закономерность, ответить на вопрос задачи.
Такие задачи развивают логику, внимание и фантазию.
Первая задача на отыскание закономерности на картинке. Решая задачи с рисунками, стоит посмотреть, чем отличаются соседние, какие картинки есть в каждом ряду, столбце, какой порядок рисунков.
Задача 1.
Найдите закономерность и раскрасьте последний квадрат.
Решение.
Можно заметить, что раскрашенных квадратов всего три различных вида: 1) левая половина чёрная, правая – белая; 2) левая половина белая, правая – крест; 3) левая половина – крест, правая – чёрная. Причём в первом и во втором ряду все квадраты разные. Поэтому и в третьем ряду квадраты тоже должны быть все разные. Второй и третий виды там есть, значит, не хватает первого.
В следующих задачах нужно продолжить последовательность. Обычно, если требуется продолжить числовую последовательность, то стоит посмотреть на разность соседних чисел, на их сумму или заметить ещё какое-то свойство.
Задача 2.
Продолжите числовой ряд: 1, 2, 4, 7, 11, …
Решение.
Посмотрим на разность соседних чисел. Разность первого и второго равна 1. Второго и третьего – 2. Третьего и четвёртого – 3 . Четвёртого и пятого – 4. Наверно, разница пятого и шестого 5.
А значит, шестое число равно 11 + 5 = 16.
Ответ:
Задача 3.
Продолжите числовой ряд: 1, 2, 4, 8, …
Решение.
Можно заметить, что 1 + 1 = 2, 2+ 2 = 4, 4 + 4 = 8. Значит, каждое число в два раза больше предыдущего – сумма предыдущего с самим собой. А тогда следующее число равно 8 + 8 = 16.
Ответ:
Более сложным является поиск закономерностей в нечисловых последовательностях. Например, в занятии «Зазеркалье» была следующая задача:
Задача 4.
Установите закономерность и нарисуйте на месте многоточия очередную фигуру.
Решение.
Поскольку эта задача была в теме «Зазеркалье», то логично предположить, что её решение, так или иначе, связано с зеркалом. Действительно, эти рисунки получены с помощью отражения в зеркале.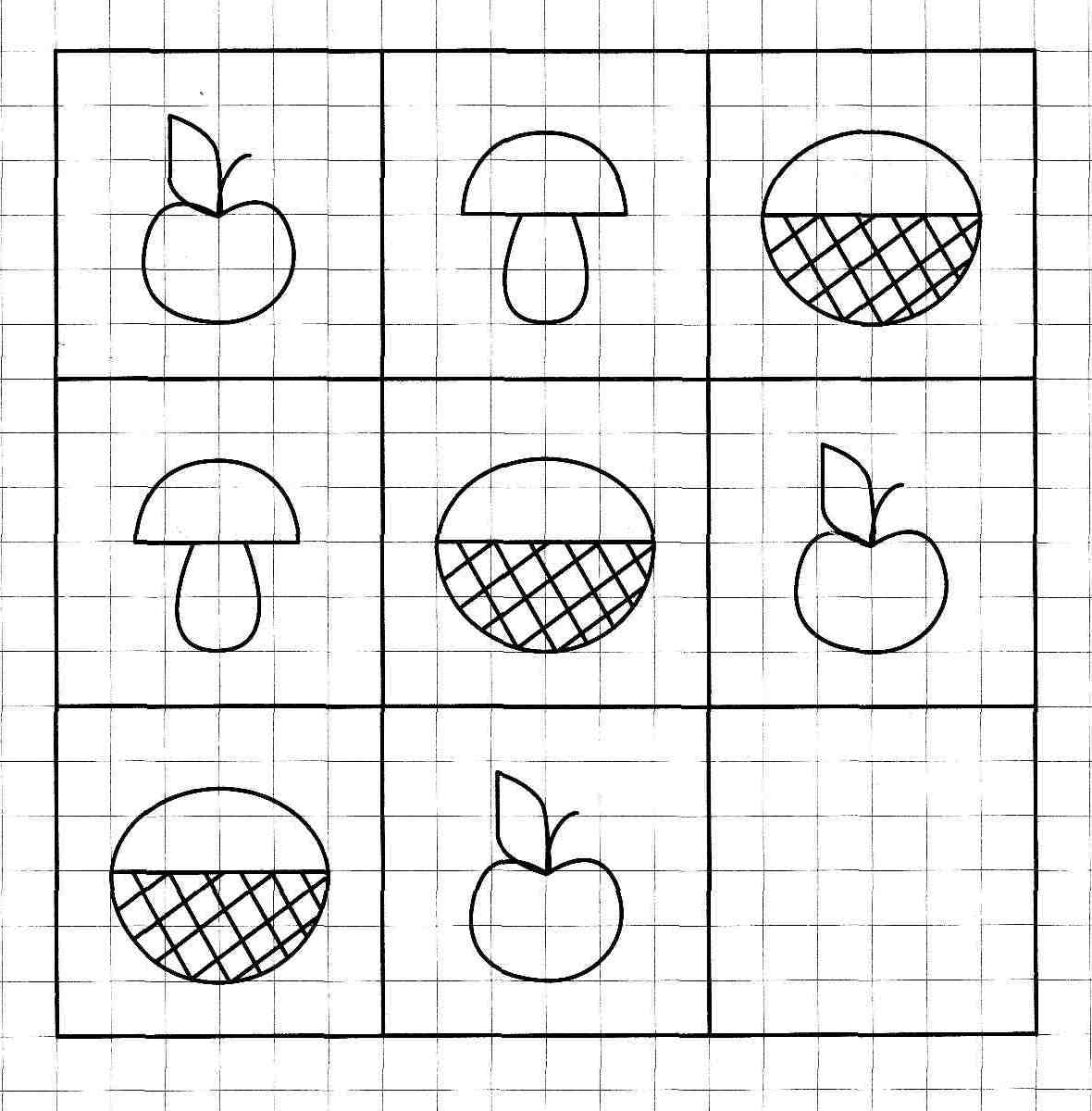
Итак, если мы сотрём все зеркальные отражения фигур, то получим такую картинку:
В ней мы узнаем цифры в той их записи, которую используют на почтовых конвертах. Если посмотреть на конверт, то можно увидеть, как на нём записывается цифра 7. А теперь нарисуем её зеркальное отражение. Получим нужную нам следующую фигуру. Вы можете продолжить это упражнение с оставшимися цифрами.
Ответ:
Последовательность представляет собой цифры, записанные, как принято на почтовых конвертах, но вместе со своими отражениями. Очередная фигура:
До сих пор мы говорили о поиске закономерностей, если у нас имеется одна последовательность. Бывают случаи, когда вместо одной последовательности предлагаются 2-3 примера, показывающие, как по первым двум элементам определить третий. В частности, такие задания популярны при выполнении тестов, определяющих уровень IQ.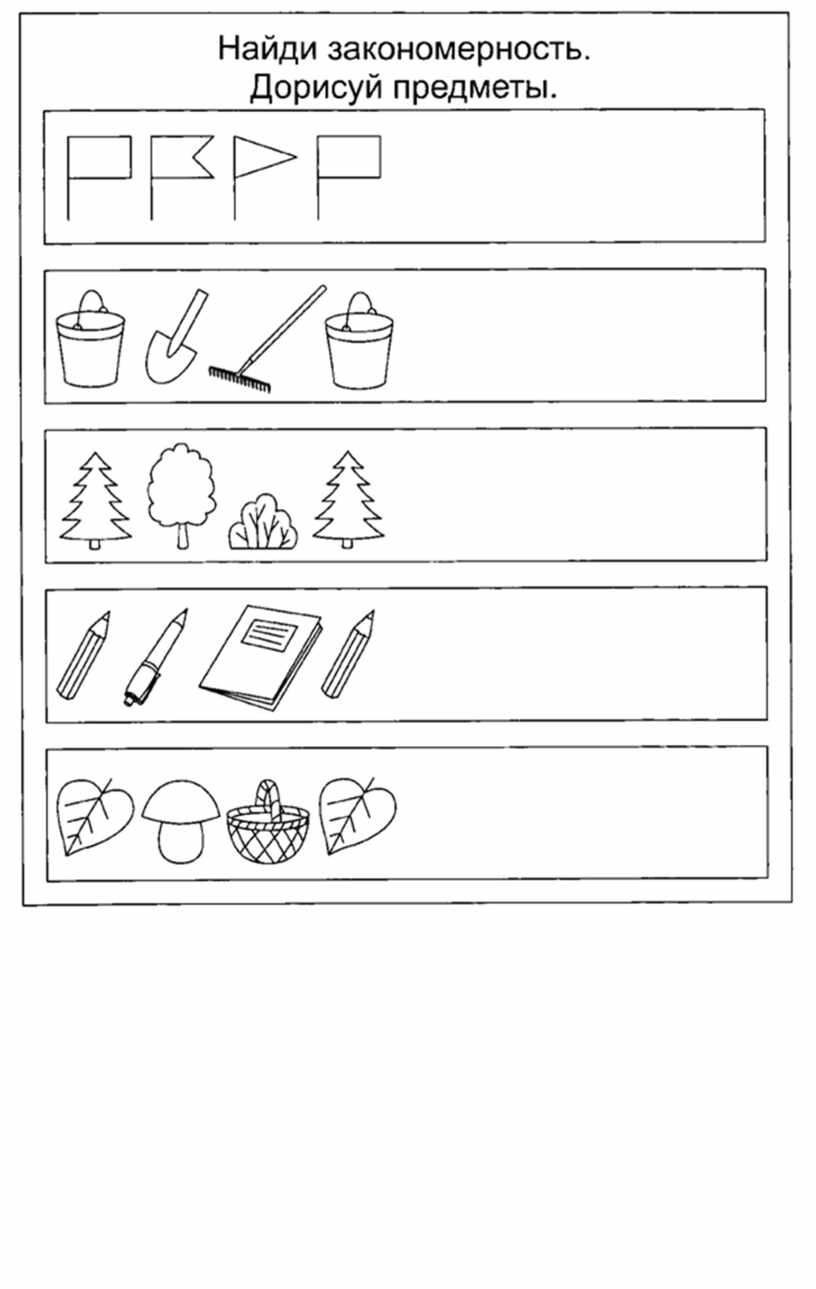
Найдите закономерность и нарисуйте третью фигурку в нижнем ряду.
Решение.
Можно заметить, что третья фигурка в каждой строчке получается путем «слияния» двух первых. Поэтому для получения нужной картинки нужно совместить две первых картинки третьей строчки.
Ответ:
Ещё один вид заданий на нахождение закономерности представляет собой чаще всего числовые примеры, заключённые в какие-либо геометрические фигуры. Разберем на примере задачи.
Задача 6.
Какое число должно стоять в третьем круге вместо вопросительного знака?
Решение.
Рассмотрим внимательно, как расположены числа в кругах. Самые большие числа стоят внизу. Стоит проверить, может быть, это сумма двух других чисел? Проверяем: 5 + 1 = 6 – верно, 3 + 4 = 7 – верно. Наша гипотеза подтвердилась. Поэтому, так как 2 + 2 = 4, вместо знака вопроса должно стоять число 4.
Ответ: должно стоять число 4.
Желаем успехов!
Испытайте свои знания!
Для самых умных и талантливых учеников мы проводим на сайте дистанционную интернет-олимпиаду.
Сразу же после прохождения олимпиады показываются результаты и полный разбор задач для работы над ошибками. В зависимости от успехов олимпиадника выдаются электронные дипломы
и похвальные грамоты
.
Каждый участник получает электронный сертификат
участника.
1. Игра на внимание “Посчитай – не ошибись” (3 мин)
Правила игры: ученики поочерёдно, цепочкой называют числа по порядку: 1, 2, 3, 4 и т. д. Если число делится на 3 или содержит в себе цифру 3, оно не произносится, а ученик говорит “Бом”.
Игра проводится на выбывание: ученик, допустивший ошибку, садится, а следующий ученик начинает считать с самого начала.
2. Проверка домашнего задания (5 мин)
Учитель зачитывает варианты алгоритмов, а дети всем классом их пробуют выполнять (по ходу отмечаются неточности в составлении алгоритма).
3. Упражнение на поиск закономерности числового ряда (6–7 мин)
Числовые ряды с закономерностями – это такие ряды, в которых числа связаны между собой по определённому правилу.

На доске заранее написаны 4–5 числовых рядов. Учитель предлагает детям найти закономерность их построения и продолжить числовой ряд: назвать два следующих числа.
По ходу выполнения задания учитель записывает на доске правильные ответы и в скобках указывает, выполнением каких действий образован ряд (возможно несколько вариантов объяснения).
Примеры числовых рядов:
После окончания работы – обсуждение: на какие группы по способу решения можно разделить данные числовые ряды?
Например:
– каждое последующее число получается при выполнении какого-то одного постоянного арифметического действия. Например: +8,2 и т. п.;
– каждое последующее число получается при выполнении нескольких постоянных арифметических действий. Например: +4–3;:52 и т. п.;
– каждое последующее число получается при выполнении действий с числами, находящимися в определённой последовательности. Например: +1,+2,+3; – 7, – 5, – 3 и т. п.
Затем предлагается составить алгоритм, как решать числовые ряды.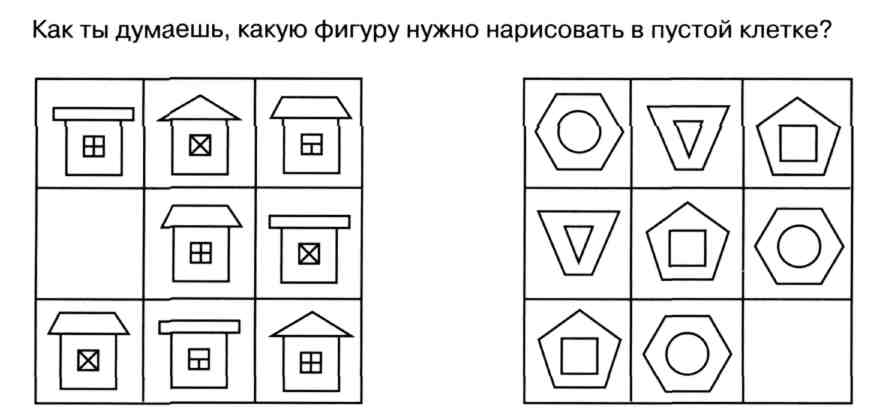
Шаг 1: зафиксировать разницу между двумя рядом стоящими числами.
Шаг 2: определить правило построения ряда.
Шаг 3: проверить это правило на другой паре чисел.
Шаг 4: используя это правило, определить следующее число в ряду.
4. Упражнение “Проверь себя” (5 мин)
На доске рисунки с числами, необходимо вместо вопроса поставить нужное число. Примеры рисунков:
1. “Паровоз”:
2. “Домик”:
3. “Ступеньки”:
После окончания работы – анализ правильности выполнения задания (в “домике” сумма чисел в окнах равна сумме чисел в крыше и в двери; в “паровозе” произведение чисел в колёсах равно числу в трубе; в “ступеньках” верхний кубик – утроенная сумма нижних) и составление краткого алгоритма решения подобных заданий.
5. Работа в группах “Продолжи ряд” (6–7 мин)
Каждая группа получает 3–4 рисунка на нахождение закономерности в рядах с фигурами. Необходимо продолжить закономерность.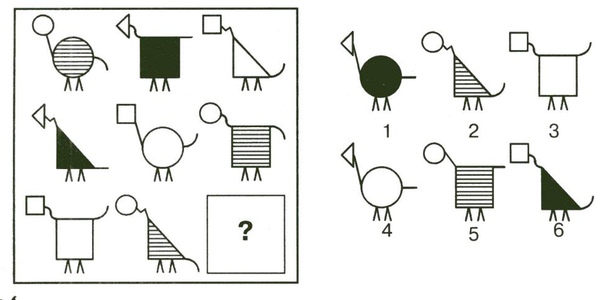
Для проверки учитель открывает на доске ответы всех заданий.
6. Упражнение на нахождение закономерности в серии фигур (10 мин)
На доске серия рисунков. Необходимо выбрать недостающую фигуру из четырёх пронумерованных и объяснить свой выбор.
В конце работы – анализ: как нужно было выполнить задание.
Например:
Шаг 1. Определить, из каких частей состоит рисунок: голова, уши, усы, туловище, хвост.
Шаг 2. Определить по каждой строчке, какие части изменяются, какие – нет: уши у всех кошек одинаковые, все остальные части изменяются.
Шаг 3. Установить по каждой строчке, какими вариантами выражена каждая из изменяющихся частей: туловище: круг, квадрат, треугольник; голова: круг, квадрат, треугольник; хвост: вправо, влево, прямо; усы: одна пара, две пары, три пары.
Шаг 4. Определить, каких вариантов не хватает в 3-й строчке: круглой головы, пары усов, квадратного туловища, хвоста в правую сторону.
Шаг 5. Выбрать рисунок, подходящий под это описание: номер 3.
7. Домашнее задание (3–4 мин)
Нарисовать подобные рисунки, в которых нужно вставить недостающую фигуру.
Желательно обсудить темы рисунков: человечки, геометрические фигуры, животные, домики, машины и т. д. – т. е. любые объекты, представляющие собой совокупность отдельных частей; какими вариантами может быть представлена каждая часть: может изменяться размер, форма, цвет, количество частей, направление линий и др.
Проверка выполнения этого домашнего задания проводится на уроке математики.
8. Задание на смекалку (3–4 мин)
Одно яйцо варится 5 мин. Сколько варятся 3 яйца? (5 мин)
Петух на одной ноге весит 4 кг. Сколько весит петух на двух ногах? (4 кг)
Карета, запряжённая шестёркой лошадей, проехала 3 км. Сколько км пробежала каждая лошадь? (3 км)
Мальчик идёт до школы 10 мин. Сколько времени он потратит, если будет идти вместе с сестрой? (Неизвестно: время может остаться прежним, может уменьшиться (если сестра будет торопить мальчика) или увеличиться (если они будут увлечённо беседовать по дороге).
Закономерности для 4 класса | Научим решать за 5 минут
Решайте закономерности 4 класс у нас! На странице размещены задания “найти закономерность 4 класс”. Так же задачи на закономерности “продолжи ряд” и различные виды. Удачи!
Начнем сейчас! Мы будем решать:
- Задачи на поиск закономерностей
- Составлять закономерности
- Продолжать ряд
- Продолжать циклические закономерности
Найди закономерность 4 класс
Найди закономерность:
1, 5, 10, 16, 23, 31, 40, 50, 61.
2, 3, 5, 8, 13, 21, 34, 55.
100, 90, 80, 70, 60, 50, 40, 30.
60, 62, 64, 66, 68, 70.
2, 4, 12, 48.
Составляем закономерности чисел
Составь закономерность из 7 чисел но с циклом -1, уменьшающимся на 2 каждый раз.
Составь закономерность из 5 чисел чтобы с циклом *2, увеличивающимся на 1 каждый раз.
Придумай закономерность с циклом x, чтобы последнее число было 5x.
Попробуй сделать закономерность с циклом Фиббоначчи – число = сумма 2 предыдущих.
Пример: 2, 3, 5, 8, 13. 2+3=5, 3+5=8, 8+5=13.
Составь эту закономерность из 8 чисел.
Придумай закономерность, чтобы были 2 в 1. Смешанную, чтобы через клетку. Цикл первой – +4, второй – /2.
Продолжи закономерность 4 класс
3, 7, 12, 18, 25, 33, 42, 52, 63, …?
10, 20, 30, 40, 50, 60, 70, …, …?
100, 4, 95, 8, 90, 16, …, …, …?
4, 7, 11, 18, 29, 47, …?
1923453525, 39, 12, …?
1, 3, 7, 13, 21, 31, …, …?
Циклические числовые закономерности
Доделай, чтобы максимальное число не было больше 50.
1, 12, 22, 31, ?
Доделай до 1 (потому что закономерность убывающая).
256, 128, 64, ?
Придумай до 3 в степени 6, но вычисли.
3 в степени 2, 3 в степени 3, 3 в степени 4, ?
Задачи на закономерность
В миске лежит много конфет.
В строительстве офиса участвовали 4 рабочих. Первый работник построил 7 этажей. Второй – 14. Работник №3 сделал 28 этажей. Сколько этажей в офисе?
На верхней полке было 200 мандаринов. Семья ела их 4 дня.
Папа – 4, 8, 16
Мама – 3, 6, 9
Ярослав – 5, 9, 13
Сколько мандаринов осталось на полке?
Как решать закономерности и их разновидности? Ответ ниже:
https://matsharik.ru/istoria-zadach/vidy-zakonomernostej
Логическая игра «Найди закономерность. Логическая игра «Найди закономерность Шетсь шсеть сетьш штсеь естьш стешь
1. Игра на внимание “Посчитай – не ошибись” (3 мин)
Правила игры: ученики поочерёдно, цепочкой называют числа по порядку: 1, 2, 3, 4 и т. д. Если число делится на 3 или содержит в себе цифру 3, оно не произносится, а ученик говорит “Бом”.
Игра проводится на выбывание: ученик, допустивший ошибку, садится, а следующий ученик начинает считать с самого начала.
2. Проверка домашнего задания (5 мин)
Учитель зачитывает варианты алгоритмов, а дети всем классом их пробуют выполнять (по ходу отмечаются неточности в составлении алгоритма).
3. Упражнение на поиск закономерности числового ряда (6–7 мин)
Числовые ряды с закономерностями – это такие ряды, в которых числа связаны между собой по определённому правилу.
На доске заранее написаны 4–5 числовых рядов. Учитель предлагает детям найти закономерность их построения и продолжить числовой ряд: назвать два следующих числа.
По ходу выполнения задания учитель записывает на доске правильные ответы и в скобках указывает, выполнением каких действий образован ряд (возможно несколько вариантов объяснения).
Примеры числовых рядов:
После окончания работы – обсуждение: на какие группы по способу решения можно разделить данные числовые ряды?
Например:
– каждое последующее число получается при выполнении какого-то одного постоянного арифметического действия.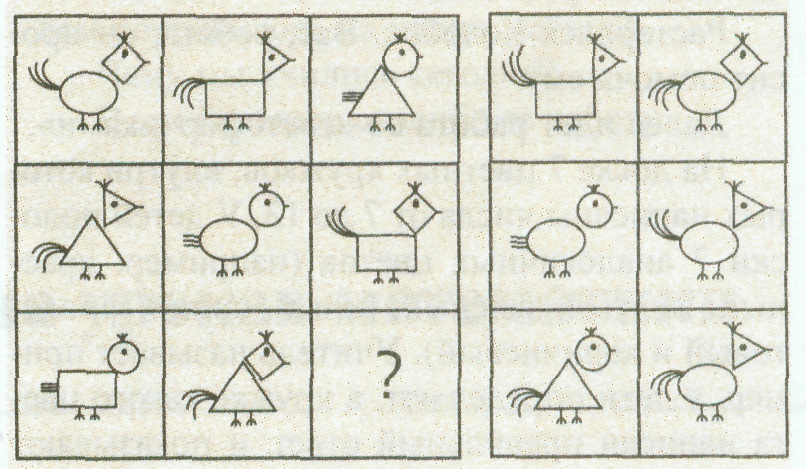
– каждое последующее число получается при выполнении нескольких постоянных арифметических действий. Например: +4–3;:52 и т. п.;
– каждое последующее число получается при выполнении действий с числами, находящимися в определённой последовательности. Например: +1,+2,+3; – 7, – 5, – 3 и т. п.
Затем предлагается составить алгоритм, как решать числовые ряды. Например (если действие постоянное):
Шаг 1: зафиксировать разницу между двумя рядом стоящими числами.
Шаг 2: определить правило построения ряда.
Шаг 3: проверить это правило на другой паре чисел.
Шаг 4: используя это правило, определить следующее число в ряду.
4. Упражнение “Проверь себя” (5 мин)
На доске рисунки с числами, необходимо вместо вопроса поставить нужное число. Примеры рисунков:
1. “Паровоз”:
2. “Домик”:
3. “Ступеньки”:
После окончания работы – анализ правильности выполнения задания (в “домике” сумма чисел в окнах равна сумме чисел в крыше и в двери; в “паровозе” произведение чисел в колёсах равно числу в трубе; в “ступеньках” верхний кубик – утроенная сумма нижних) и составление краткого алгоритма решения подобных заданий.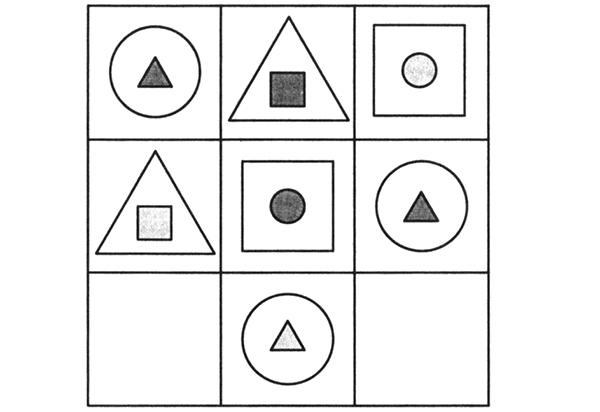
5. Работа в группах “Продолжи ряд” (6–7 мин)
Каждая группа получает 3–4 рисунка на нахождение закономерности в рядах с фигурами. Необходимо продолжить закономерность. Возможен вариант, когда у всех групп могут быть одинаковые рисунки. Примеры рисунков:
Для проверки учитель открывает на доске ответы всех заданий.
6. Упражнение на нахождение закономерности в серии фигур (10 мин)
На доске серия рисунков. Необходимо выбрать недостающую фигуру из четырёх пронумерованных и объяснить свой выбор.
В конце работы – анализ: как нужно было выполнить задание.
Например:
Шаг 1. Определить, из каких частей состоит рисунок: голова, уши, усы, туловище, хвост.
Шаг 2. Определить по каждой строчке, какие части изменяются, какие – нет: уши у всех кошек одинаковые, все остальные части изменяются.
Шаг 3. Установить по каждой строчке, какими вариантами выражена каждая из изменяющихся частей: туловище: круг, квадрат, треугольник; голова: круг, квадрат, треугольник; хвост: вправо, влево, прямо; усы: одна пара, две пары, три пары.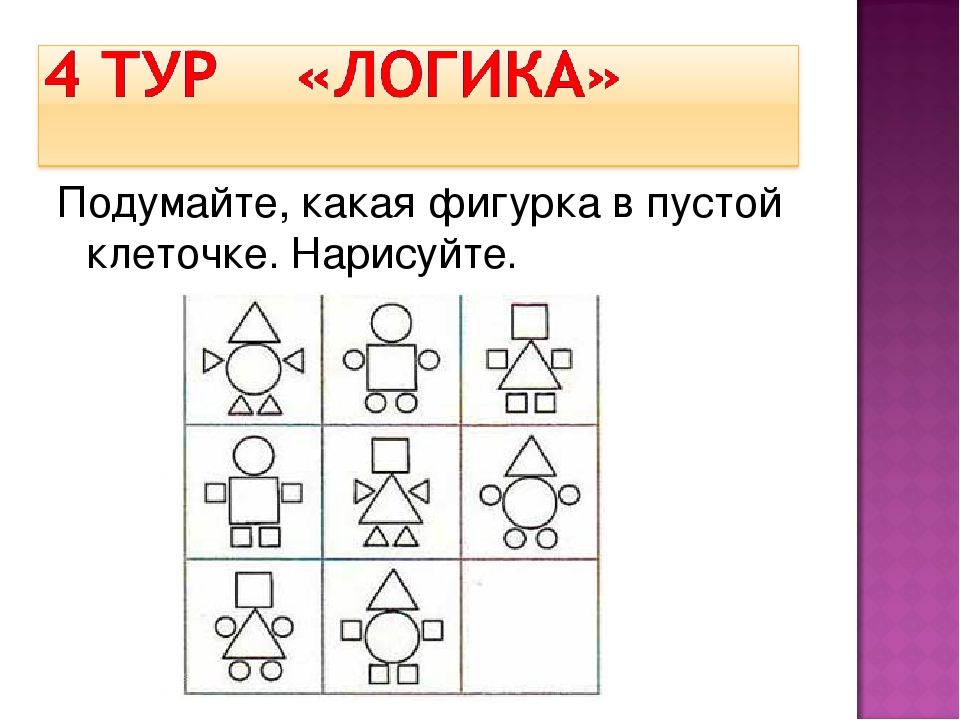
Шаг 4. Определить, каких вариантов не хватает в 3-й строчке: круглой головы, пары усов, квадратного туловища, хвоста в правую сторону.
Шаг 5. Выбрать рисунок, подходящий под это описание: номер 3.
7. Домашнее задание (3–4 мин)
Нарисовать подобные рисунки, в которых нужно вставить недостающую фигуру.
Желательно обсудить темы рисунков: человечки, геометрические фигуры, животные, домики, машины и т. д. – т. е. любые объекты, представляющие собой совокупность отдельных частей; какими вариантами может быть представлена каждая часть: может изменяться размер, форма, цвет, количество частей, направление линий и др.
Проверка выполнения этого домашнего задания проводится на уроке математики.
8. Задание на смекалку (3–4 мин)
Одно яйцо варится 5 мин. Сколько варятся 3 яйца? (5 мин)
Петух на одной ноге весит 4 кг. Сколько весит петух на двух ногах? (4 кг)
Карета, запряжённая шестёркой лошадей, проехала 3 км. Сколько км пробежала каждая лошадь? (3 км)
Мальчик идёт до школы 10 мин.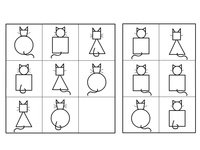
Задания, направленные на поиск математических закономерностей, улучшают способность рассуждать и логически мыслить, помогают научиться сравнивать, обобщать и делать выводы. Эта игра активизирует умственную деятельность ребенка и окажет существенное влияние на формирование образного мышления, развитие сообразительности и смекалки.
Распечатайте предложенные на сайте карточки и дайте их ребенку для работы.
Математическая закономерность представляет собой правило, согласно которому в цепочке (ряду) происходит повторение, замещение или изменение свойств определенных элементов в соответствии с установленным правилом.
Перед тем, как малыш преступит к заданию, объясните ему на нескольких примерах, что такое закономерность, как ее можно установить между различными звеньями ряда (числами, буквами, геометрическими фигурами).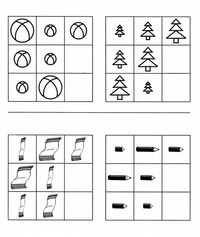
Найди закономерность и продолжи ряд
Реши примеры с помощью сказочного числового ряда.
В примерах пропущены знаки + и – . Впиши их, используя числовой ряд.
Логические квадраты
Подбери рифму
В конце каждого стихотворения подбери
подходящее по смыслу и рифме слово
(жираф, щенок, зайчишку, крошки).
а) Уронила белка шишку
Шишка стукнула _______________________
б)Прыгал птенчик по дорожке
И клевал большие ______________________
в)На дверях висел замок,
Взаперти сидел ________________________
г)Вяжет мама длинный шарф,
Потому что сын ________________________
Замени одним словом
1) родник и то, чем открывают дверь __________________
2) прическу у девочки и инструмент для срезания травы_________
3) ветку винограда и инструмент, которым рисуют ______________
4) овощ, от которого плачут, и оружие для стрельбы стрелами (жгучий овощ и стрелковое оружие) __________________________
5) часть ружья и часть дерева ________________________________
6) то, на чем рисуют, и зелень на ветках _____________________
7) подъемный механизм для стройки и механизм, который нужно открыть, чтобы полилась вода ____________________________
Убери из слова один слог так, чтобы осталось другое слово.
Смородина,
смо
/ро/ди/на = родина
Волки Ласточка Забор Лесник Бабочка Машина Баранка
Стрекоза Кисточка Листок Колбаса Присоска Каток Листок
Каравай Картина Паркет Стрижка Рукава
Добавь одну букву к каждому слову и напиши полученные слова
Сказочные цифры
Катя решила примеры и стёрла в сказочном числовом ряду некоторые цифры. Впиши в числовой ряд цифры из примеров.
Z
+ 1 =
L
Z
– 1 =
T
Z
+ 2 =
V
Z
– 2 =
J
В каждой паре чисел обведи кругом то число, которое больше, и запиши, на сколько оно больше: на 2 или 1. Узнать это можно с помощью сказочного числового ряда.
Реши примеры.
Задача
У кошки Машки три котёнка: белый, рыжий и разноцветный. Серёжа назвал их Рыжик, Снежок и Букет, но так, что цвет и имя не совпадают. Как зовут котят, если самый светлый из них Букет?
|
Сказочные цифры Разгадай сказочные цифры V + V + 1 = 5 4) Z + Z + 1= 7 6 – L – L = L 5) 7 – 1 – J = J 7 – 3 – Y = Y 6) Y + Y + 2 = 10 Выбери для пары чисел одну подходящую сказочную запись (соедини стрелкой). Разминка для ума Найди общий признак для всех слов: Арбуз, мяч, колесо, кольцо Крокодил, трава, лягушка, зелёнка, огурец Ёжик, кактус, иголка, шип Какое слово из перечисленных не происходит от слова Подчеркни его. Допиши словечко МАС….. (например, мас ____________________________________________________________________ |
К словам в левом столбике подберите близкие по значению из правого, соедини их стрелочками. Логическая задача Три подружки – Вера, Оля и Таня – пошли в лес по ягоды. Для сбора ягод у них были корзина, лукошко и ведёрко. Известно, что Оля была не с корзиной и не с лукошком. ёмкости |
Подружки |
|
|
Вера |
Оля |
Таня |
|
|
корзина |
|||
|
лукошко |
|||
|
ведёрко |
Помоги художнику дорисовать картину
Сказочные цифры
В схеме записан состав сказочного числа. Найди в схеме ответы к примерам. Берегись «ловушек».
Реши пример сначала в обычном виде, а потом в сказочном.
10 + 7 =
10 + K =
6 + 10 =
L
+ 10 =
13 – 3 =
1
Z
–
Z
=
14 – 10 =
1
V
– 10 =
Продолжи ряды, нарисовав следующие фигуры
Дорисуй недостающую фигуру
Собери из букв как можно больше названий животных,буквы в словах не должны повторяться.
И В Р Е О Ы Н Л С К Ь Т А
_____________________________________________________________________
_____________________________________________________________________
Помоги художнику дорисовать картину
Перестановки
В слове КРЯ переставили буквы и получилось ЯРК. Такая же перестановка была в слове ПЛИ. Подчеркни, что получилось
ИПЛ ИЛП ПИЛ ЛИП ЛПИ ПЛИ
В слове МОРЕ переставили буквы, и получилось ОМРЕ. Что получится, если так же переставят буквы в слове ГРУЗ?
РУЗГ РЗГУ ГУРЗ РГУЗ ЗУРГ ЗГУР
В слове БАТОН переставили буквы, и получилось БОТАН. Что получится при перестановке букв в слове ШЕСТЬ?
ШЕТСЬ ШСЕТЬ СЕТЬШ ШТСЕЬ ЕСТЬШ СТЕШЬ
Найди слово
На доске цветными мелками написаны слова
МОРЕ МАЧТА КАНАВА
У синего и белого слов одинаковая первая буква. У белого и красного одинаковая вторая буква. Подчеркни каждое слово его цветом.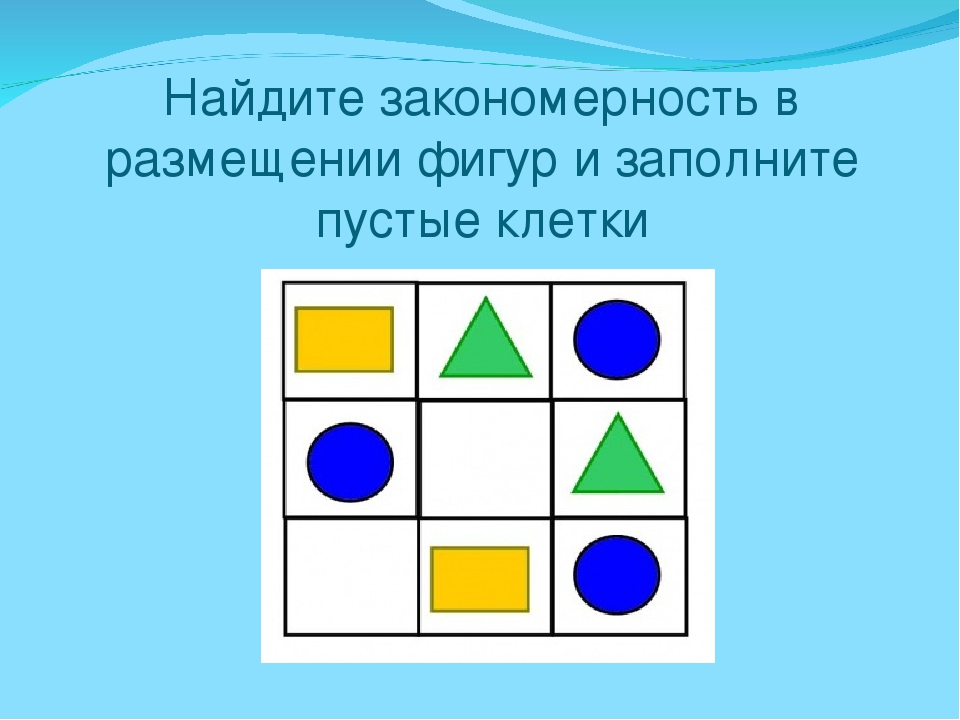
Продолжи ряд на две фигуры сохраняя закономерность. Логическая игра «Найди закономерность. Шетсь шсеть сетьш штсеь естьш стешь
1. Игра на внимание “Посчитай – не ошибись” (3 мин)
Правила игры: ученики поочерёдно, цепочкой называют числа по порядку: 1, 2, 3, 4 и т. д. Если число делится на 3 или содержит в себе цифру 3, оно не произносится, а ученик говорит “Бом”.
Игра проводится на выбывание: ученик, допустивший ошибку, садится, а следующий ученик начинает считать с самого начала.
2. Проверка домашнего задания (5 мин)
Учитель зачитывает варианты алгоритмов, а дети всем классом их пробуют выполнять (по ходу отмечаются неточности в составлении алгоритма).
3. Упражнение на поиск закономерности числового ряда (6–7 мин)
Числовые ряды с закономерностями – это такие ряды, в которых числа связаны между собой по определённому правилу.
На доске заранее написаны 4–5 числовых рядов. Учитель предлагает детям найти закономерность их построения и продолжить числовой ряд: назвать два следующих числа.
По ходу выполнения задания учитель записывает на доске правильные ответы и в скобках указывает, выполнением каких действий образован ряд (возможно несколько вариантов объяснения).
Примеры числовых рядов:
После окончания работы – обсуждение: на какие группы по способу решения можно разделить данные числовые ряды?
Например:
– каждое последующее число получается при выполнении какого-то одного постоянного арифметического действия. Например: +8,2 и т. п.;
– каждое последующее число получается при выполнении нескольких постоянных арифметических действий. Например: +4–3;:52 и т. п.;
– каждое последующее число получается при выполнении действий с числами, находящимися в определённой последовательности. Например: +1,+2,+3; – 7, – 5, – 3 и т. п.
Затем предлагается составить алгоритм, как решать числовые ряды. Например (если действие постоянное):
Шаг 1: зафиксировать разницу между двумя рядом стоящими числами.
Шаг 2: определить правило построения ряда.
Шаг 3: проверить это правило на другой паре чисел.
Шаг 4: используя это правило, определить следующее число в ряду.
4. Упражнение “Проверь себя” (5 мин)
На доске рисунки с числами, необходимо вместо вопроса поставить нужное число. Примеры рисунков:
1. “Паровоз”:
2. “Домик”:
3. “Ступеньки”:
После окончания работы – анализ правильности выполнения задания (в “домике” сумма чисел в окнах равна сумме чисел в крыше и в двери; в “паровозе” произведение чисел в колёсах равно числу в трубе; в “ступеньках” верхний кубик – утроенная сумма нижних) и составление краткого алгоритма решения подобных заданий.
5. Работа в группах “Продолжи ряд” (6–7 мин)
Каждая группа получает 3–4 рисунка на нахождение закономерности в рядах с фигурами. Необходимо продолжить закономерность. Возможен вариант, когда у всех групп могут быть одинаковые рисунки. Примеры рисунков:
Для проверки учитель открывает на доске ответы всех заданий.
6. Упражнение на нахождение закономерности в серии фигур (10 мин)
На доске серия рисунков. Необходимо выбрать недостающую фигуру из четырёх пронумерованных и объяснить свой выбор.
В конце работы – анализ: как нужно было выполнить задание.
Например:
Шаг 1. Определить, из каких частей состоит рисунок: голова, уши, усы, туловище, хвост.
Шаг 2. Определить по каждой строчке, какие части изменяются, какие – нет: уши у всех кошек одинаковые, все остальные части изменяются.
Шаг 3. Установить по каждой строчке, какими вариантами выражена каждая из изменяющихся частей: туловище: круг, квадрат, треугольник; голова: круг, квадрат, треугольник; хвост: вправо, влево, прямо; усы: одна пара, две пары, три пары.
Шаг 4. Определить, каких вариантов не хватает в 3-й строчке: круглой головы, пары усов, квадратного туловища, хвоста в правую сторону.
Шаг 5. Выбрать рисунок, подходящий под это описание: номер 3.
7. Домашнее задание (3–4 мин)
Нарисовать подобные рисунки, в которых нужно вставить недостающую фигуру.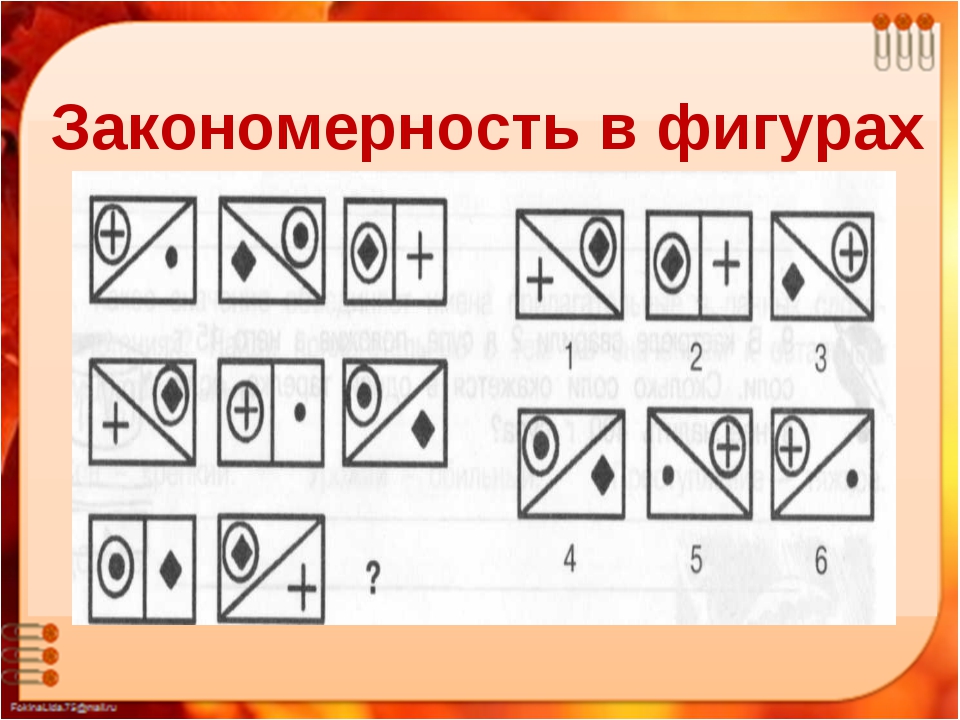
Желательно обсудить темы рисунков: человечки, геометрические фигуры, животные, домики, машины и т. д. – т. е. любые объекты, представляющие собой совокупность отдельных частей; какими вариантами может быть представлена каждая часть: может изменяться размер, форма, цвет, количество частей, направление линий и др.
Проверка выполнения этого домашнего задания проводится на уроке математики.
8. Задание на смекалку (3–4 мин)
Одно яйцо варится 5 мин. Сколько варятся 3 яйца? (5 мин)
Петух на одной ноге весит 4 кг. Сколько весит петух на двух ногах? (4 кг)
Карета, запряжённая шестёркой лошадей, проехала 3 км. Сколько км пробежала каждая лошадь? (3 км)
Мальчик идёт до школы 10 мин. Сколько времени он потратит, если будет идти вместе с сестрой? (Неизвестно: время может остаться прежним, может уменьшиться (если сестра будет торопить мальчика) или увеличиться (если они будут увлечённо беседовать по дороге).)
Это учебная статья по математике, перед началом занятий мы рекомендуем ознакомиться с
вводной частью
В этом занятии речь пойдет о задачах, в которых нужно найти какую-то закономерность, продолжить последовательность или, используя найденную закономерность, ответить на вопрос задачи.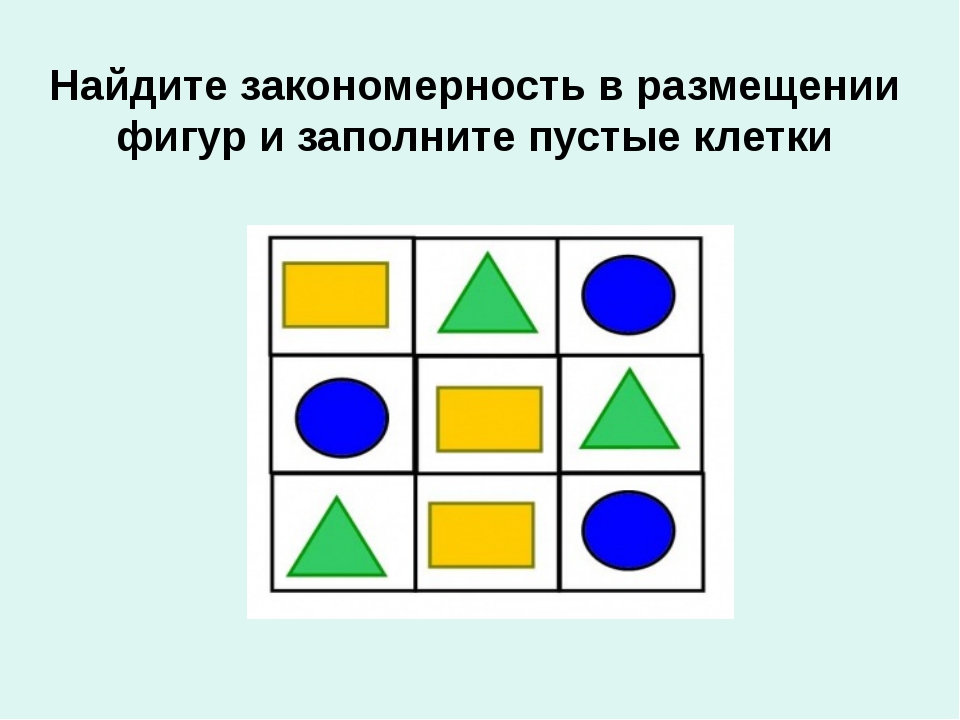
Первая задача на отыскание закономерности на картинке. Решая задачи с рисунками, стоит посмотреть, чем отличаются соседние, какие картинки есть в каждом ряду, столбце, какой порядок рисунков.
Задача 1.
Найдите закономерность и раскрасьте последний квадрат.
Решение.
Можно заметить, что раскрашенных квадратов всего три различных вида: 1) левая половина чёрная, правая – белая; 2) левая половина белая, правая – крест; 3) левая половина – крест, правая – чёрная. Причём в первом и во втором ряду все квадраты разные. Поэтому и в третьем ряду квадраты тоже должны быть все разные. Второй и третий виды там есть, значит, не хватает первого.
В следующих задачах нужно продолжить последовательность. Обычно, если требуется продолжить числовую последовательность, то стоит посмотреть на разность соседних чисел, на их сумму или заметить ещё какое-то свойство.
Задача 2.
Продолжите числовой ряд: 1, 2, 4, 7, 11, …
Решение.
Посмотрим на разность соседних чисел. Разность первого и второго равна 1. Второго и третьего – 2. Третьего и четвёртого – 3 . Четвёртого и пятого – 4. Наверно, разница пятого и шестого 5.
А значит, шестое число равно 11 + 5 = 16.
Ответ:
Задача 3.
Продолжите числовой ряд: 1, 2, 4, 8, …
Решение.
Можно заметить, что 1 + 1 = 2, 2+ 2 = 4, 4 + 4 = 8. Значит, каждое число в два раза больше предыдущего – сумма предыдущего с самим собой. А тогда следующее число равно 8 + 8 = 16.
Ответ:
Более сложным является поиск закономерностей в нечисловых последовательностях. Например, в занятии «Зазеркалье» была следующая задача:
Задача 4.
Установите закономерность и нарисуйте на месте многоточия очередную фигуру.
Решение.
Поскольку эта задача была в теме «Зазеркалье», то логично предположить, что её решение, так или иначе, связано с зеркалом. Действительно, эти рисунки получены с помощью отражения в зеркале.
Итак, если мы сотрём все зеркальные отражения фигур, то получим такую картинку:
В ней мы узнаем цифры в той их записи, которую используют на почтовых конвертах. Если посмотреть на конверт, то можно увидеть, как на нём записывается цифра 7. А теперь нарисуем её зеркальное отражение. Получим нужную нам следующую фигуру. Вы можете продолжить это упражнение с оставшимися цифрами.
Ответ:
Последовательность представляет собой цифры, записанные, как принято на почтовых конвертах, но вместе со своими отражениями. Очередная фигура:
До сих пор мы говорили о поиске закономерностей, если у нас имеется одна последовательность. Бывают случаи, когда вместо одной последовательности предлагаются 2-3 примера, показывающие, как по первым двум элементам определить третий. В частности, такие задания популярны при выполнении тестов, определяющих уровень IQ.
Найдите закономерность и нарисуйте третью фигурку в нижнем ряду.
Решение.
Можно заметить, что третья фигурка в каждой строчке получается путем «слияния» двух первых. Поэтому для получения нужной картинки нужно совместить две первых картинки третьей строчки.
Ответ:
Ещё один вид заданий на нахождение закономерности представляет собой чаще всего числовые примеры, заключённые в какие-либо геометрические фигуры. Разберем на примере задачи.
Задача 6.
Какое число должно стоять в третьем круге вместо вопросительного знака?
Решение.
Рассмотрим внимательно, как расположены числа в кругах. Самые большие числа стоят внизу. Стоит проверить, может быть, это сумма двух других чисел? Проверяем: 5 + 1 = 6 – верно, 3 + 4 = 7 – верно. Наша гипотеза подтвердилась. Поэтому, так как 2 + 2 = 4, вместо знака вопроса должно стоять число 4.
Ответ: должно стоять число 4.
Желаем успехов!
Испытайте свои знания!
Для самых умных и талантливых учеников мы проводим на сайте дистанционную интернет-олимпиаду.
Сразу же после прохождения олимпиады показываются результаты и полный разбор задач для работы над ошибками. В зависимости от успехов олимпиадника выдаются электронные дипломы
и похвальные грамоты
.
Каждый участник получает электронный сертификат
участника.
Реши примеры с помощью сказочного числового ряда.
В примерах пропущены знаки + и – . Впиши их, используя числовой ряд.
Логические квадраты
Подбери рифму
В конце каждого стихотворения подбери
подходящее по смыслу и рифме слово
(жираф, щенок, зайчишку, крошки).
а) Уронила белка шишку
Шишка стукнула _______________________
б)Прыгал птенчик по дорожке
И клевал большие ______________________
в)На дверях висел замок,
Взаперти сидел ________________________
г)Вяжет мама длинный шарф,
Потому что сын ________________________
Замени одним словом
1) родник и то, чем открывают дверь __________________
2) прическу у девочки и инструмент для срезания травы_________
3) ветку винограда и инструмент, которым рисуют ______________
4) овощ, от которого плачут, и оружие для стрельбы стрелами (жгучий овощ и стрелковое оружие) __________________________
5) часть ружья и часть дерева ________________________________
6) то, на чем рисуют, и зелень на ветках _____________________
7) подъемный механизм для стройки и механизм, который нужно открыть, чтобы полилась вода ____________________________
Убери из слова один слог так, чтобы осталось другое слово.
Смородина,
смо
/ро/ди/на = родина
Волки Ласточка Забор Лесник Бабочка Машина Баранка
Стрекоза Кисточка Листок Колбаса Присоска Каток Листок
Каравай Картина Паркет Стрижка Рукава
Добавь одну букву к каждому слову и напиши полученные слова
Сказочные цифры
Катя решила примеры и стёрла в сказочном числовом ряду некоторые цифры. Впиши в числовой ряд цифры из примеров.
Z
+ 1 =
L
Z
– 1 =
T
Z
+ 2 =
V
Z
– 2 =
J
В каждой паре чисел обведи кругом то число, которое больше, и запиши, на сколько оно больше: на 2 или 1. Узнать это можно с помощью сказочного числового ряда.
Реши примеры.
Задача
У кошки Машки три котёнка: белый, рыжий и разноцветный. Серёжа назвал их Рыжик, Снежок и Букет, но так, что цвет и имя не совпадают. Как зовут котят, если самый светлый из них Букет?
|
Сказочные цифры Разгадай сказочные цифры V + V + 1 = 5 4) Z + Z + 1= 7 6 – L – L = L 5) 7 – 1 – J = J 7 – 3 – Y = Y 6) Y + Y + 2 = 10 Выбери для пары чисел одну подходящую сказочную запись (соедини стрелкой). Разминка для ума Найди общий признак для всех слов: Арбуз, мяч, колесо, кольцо Крокодил, трава, лягушка, зелёнка, огурец Ёжик, кактус, иголка, шип Какое слово из перечисленных не происходит от слова Подчеркни его. Допиши словечко МАС….. (например, мас ____________________________________________________________________ |
К словам в левом столбике подберите близкие по значению из правого, соедини их стрелочками. Логическая задача Три подружки – Вера, Оля и Таня – пошли в лес по ягоды. Для сбора ягод у них были корзина, лукошко и ведёрко. Известно, что Оля была не с корзиной и не с лукошком. ёмкости |
Подружки |
|
|
Вера |
Оля |
Таня |
|
|
корзина |
|||
|
лукошко |
|||
|
ведёрко |
Помоги художнику дорисовать картину
Сказочные цифры
В схеме записан состав сказочного числа. Найди в схеме ответы к примерам. Берегись «ловушек».
Реши пример сначала в обычном виде, а потом в сказочном.
10 + 7 =
10 + K =
6 + 10 =
L
+ 10 =
13 – 3 =
1
Z
–
Z
=
14 – 10 =
1
V
– 10 =
Продолжи ряды, нарисовав следующие фигуры
Дорисуй недостающую фигуру
Собери из букв как можно больше названий животных,буквы в словах не должны повторяться.
И В Р Е О Ы Н Л С К Ь Т А
_____________________________________________________________________
_____________________________________________________________________
Помоги художнику дорисовать картину
Перестановки
В слове КРЯ переставили буквы и получилось ЯРК. Такая же перестановка была в слове ПЛИ. Подчеркни, что получилось
ИПЛ ИЛП ПИЛ ЛИП ЛПИ ПЛИ
В слове МОРЕ переставили буквы, и получилось ОМРЕ. Что получится, если так же переставят буквы в слове ГРУЗ?
РУЗГ РЗГУ ГУРЗ РГУЗ ЗУРГ ЗГУР
В слове БАТОН переставили буквы, и получилось БОТАН. Что получится при перестановке букв в слове ШЕСТЬ?
ШЕТСЬ ШСЕТЬ СЕТЬШ ШТСЕЬ ЕСТЬШ СТЕШЬ
Найди слово
На доске цветными мелками написаны слова
МОРЕ МАЧТА КАНАВА
У синего и белого слов одинаковая первая буква. У белого и красного одинаковая вторая буква. Подчеркни каждое слово его цветом.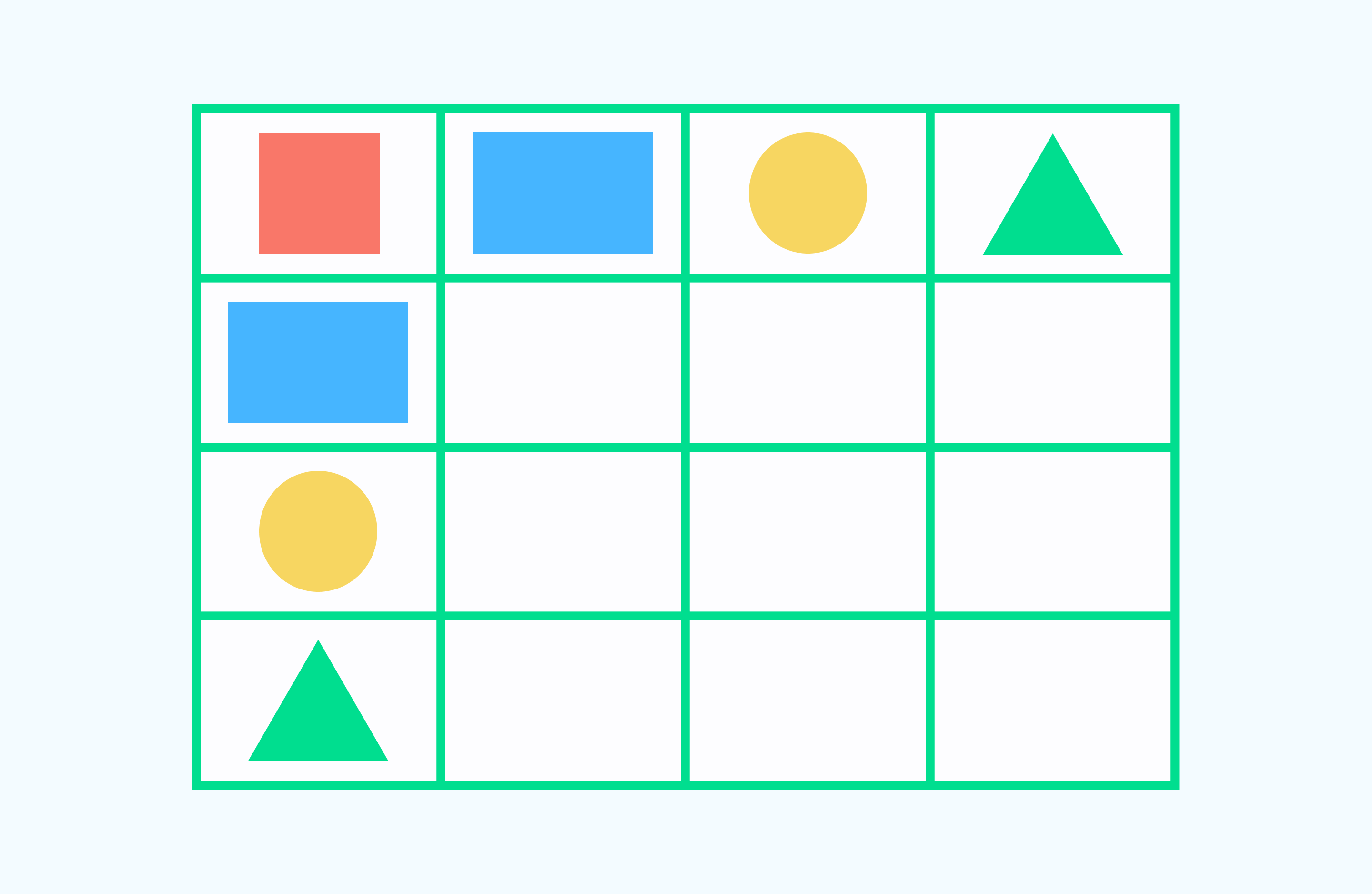
Детский сад №103 г. Липецк
Добро пожаловать!
Коллектив
муниципального бюджетного дошкольного образовательного учреждения № 103 г. Липецка рад приветствовать Вас на нашем сайте!
Детский сад – это милые, добрые, умные, весёлые, замечательные дети. Всё что мы делаем в нашем детском саду – мы делаем ради них, ради того, чтобы они росли и развивались.
Детский сад – это сотрудники. Самые трудолюбивые, творческие, всё умеющие, болеющие за всё душой, любящие детей люди.
Детский сад – это семья. И как в любой дружной семье у нас есть свои традиции. Детский сад – это уникальная система, которая обеспечивает оздоровление, образование, воспитание, питание, уход и присмотр. Ни одна система не выполняет столько функций одновременно.
Что такое День Победы? Что такое День Победы?
Это утренний парад: Это песни за столом,
Едут танки и ракеты, Это речи и беседы,
Марширует строй солдат.
Что такое День Победы? Это фрукты и конфеты,
Это праздничный салют: Это запахи весны…
Фейерверк взлетает в небо, Что такое День Победы –
Рассыпаясь там и тут. Это значит – нет войны.
задания из IQ теста
Связь чисел в IQ задачах может подчиняться сразу нескольким закономерностям. В этом случае приходится решать не одну, а больше задач. Рассмотрим задания из IQ теста.
Чтобы решить iq задачи такого типа, нужно попробовать сначала найти связь между последовательно стоящими числами, потом попытаться найти закономерности при чередовании через одно или через два числа.
Заменить вопросы числами:
1) 2; 5; 5; 7; 8; 9; 11; ?; ?
Показать решение
(Ответ: 11; 14. Здесь надо отдельно найти закономерность чисел, стоящим на нечетных местах, отдельно — на нечетных. В первом случае последовательно прибавляем 3; во втором — 2).
2) 1; 1; 5; 2; 25; 4; 125; 8; ?; ?
Показать решение
(Ответ: 625; 16. Связь чисел такова: числа на нечетных местах последовательно умножаем на 5, на четных — на 2).
3) 3; 5; 10; 12; 31; 19; 94; ?; ?
Показать решение
(Ответ: 26; 283. На нечетных местах: умножаем предыдущее число на 3 и прибавляем 1; на четных местах числа последовательно увеличиваем на 7).
Найти закономерность чисел:
216; 72; 144; 48; 96; ?; ?
Показать решение
(Ответ: 32; 64.
Найти пропущенные числа:
1) 4; 250; ?; 50; 16; ?; 32; 2; 64
Показать решение
(Ответ: 8 и 10. Числа, стоящие на нечетных местах, умножаем на 2; на четных — делим на 5).
2) 32; 16; 48; 24; 72; ?; ?; 54; 162
Показать решение
(Ответ: 36 и 108. Число делим на 2, результат умножаем на 3, затем действия повторяем).
3) 3; 81; ?; 27; 48; ?; 192; 3
Показать решение
(Ответ: 12 и 9. На нечетных местах — последовательное умножение на 4; на четных — деление на 3).
Найти пропущенные цифры:
1; 9; 2; ?; ?; 7
Показать решение
(Ответ: 8; 3. На нечетных местах стоят цифры в порядке возрастания, на четных — по убыванию).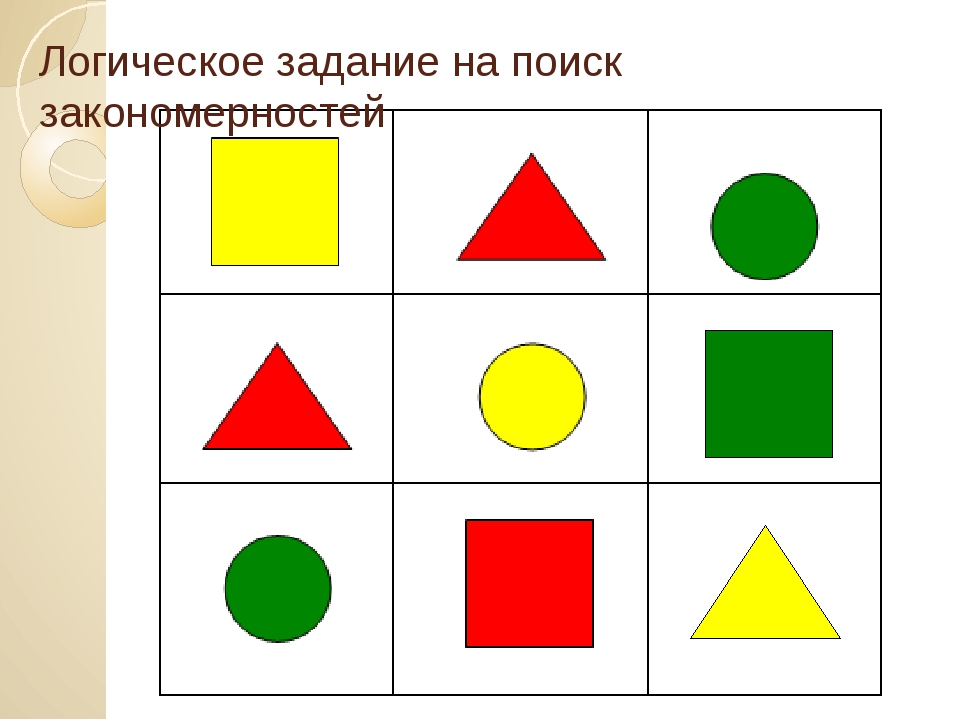
Теперь придумайте свои собственные iq задачи на связь чисел. Предложите ребенку найти пропущенные числа в готовых примерах. Если надо, поработайте вместе с ним, подводя к получению правильных выводов. Следующий этап — попросите ребенка придумать похожие iq задачи для вас. Ответьте на них. Можно привлечь к решениям других членов семьи, друзей ребенка.
Распознавание визуальных паттернов | Блестящая вики по математике и науке
При поиске визуальных паттернов рекомендуется выдвигать гипотезу на основе одного или двух терминов, а затем проверять ее на дополнительном элементе, чтобы увидеть, соответствует ли ожидаемый паттерн всей последовательности.
Умение распознавать визуальные образы позволит вам решать такие задачи:
Что должно быть в правом нижнем углу?
Этот вопрос взят из олимпиады моей страны.
Что будет дальше?
изображениеЕсли мы проследим за синим квадратом, мы увидим, что он идет сверху вниз ко второму, а затем к третьему, так что он, скорее всего, будет в четвертом (внизу). Обратите внимание, что есть 222 варианта с синим квадратом внизу.
Если мы посмотрим на любой другой квадрат, скажем на желтый квадрат, мы увидим, что он аналогичным образом движется вниз, а после четвертого – наверх.{ text {nd}} 2-й квадрат должен быть желтым, первый квадрат – зеленым, а третий квадрат – красным.
Таким образом, ответ – B. □ _ square □
Что будет дальше?
изображениеМы видим, что количество кругов увеличивается, при этом они имеют одинаковую высоту. Подсчитав количество кругов, мы видим, что там 1,1,1, затем 2,2,2, а затем 4.4.4. Эта последовательность удваивается, поэтому в следующей должно быть 888 кругов.Тщательно посчитав, мы получим, что ответ – D. □ _ square □
Что будет дальше?
ParallelAngleBisectorГлядя на первые три фигуры, мы понимаем, что порядок их расположения таков, что количество сторон в каждом многоугольнике увеличивается на единицу слева направо. У первого 333 стороны, у второго 4,4,4, у третьего 5.5.5. Таким образом, у четвертого должно быть 666 сторон, а это значит, что а) а) а) является ответом.
Также цвета первых трех многоугольников – красный, оранжевый и желтый, соответственно, что является первыми тремя цветами радуги. Таким образом, следующий цвет должен быть зеленым, что опять же является ответом a) .a) .a). □ _ квадрат □
Что будет дальше?
Обозначим вершины (углы) пятиугольника следующим образом:
Затем красная диагональная стрелка соединяет 1 → 4,1 rightarrow 4,1 → 4, затем 2 → 5,2 rightarrow 5,2 → 5, а затем 3 → 1.3 rightarrow 1.3 → 1. Другими словами, он соединяет первую вершину с вершиной, которая находится на расстоянии 3 по часовой стрелке. Таким образом, мы ожидаем, что следующая стрелка соединит 4 → 24 rightarrow 24 → 2, поэтому ответ будет B. □ _ square □
Архивы распознавания образов – SharpBrains
Нейропластичность определяется как «способность мозга перестраиваться через опыт».
Обычно мы резюмируем множество исследований мозга, поощряя читателей SharpBrains искать новизны, разнообразия и проблем , как руководящие принципы для «упражнений для мозга», которые помогут построить новые связи в мозгу, заставят человека быть внимательным и платить внимание, улучшают такие способности, как распознавание образов, и в целом способствуют здоровью мозга на протяжении всей жизни.
Подруга только что прислала обновленную информацию о своем удивительном опыте в Намибии (на фото справа показан вход в Университет Намибии), который показывает, как путешествия и участие в значимых проектах могут обеспечить превосходную умственную стимуляцию или «упражнения для мозга». Это актуально для всех возрастов, и мы рады видеть такие организации, как Civic Ventures и Elderhostel, которые предлагают возможности для бэби-бумеров и пожилых людей, которые хотят поддерживать активный ум.
Попытайтесь представить в своем уме, когда вы читаете это, все ее различные области мозга, которые получают необходимую стимуляцию благодаря ее опыту в Намибии.
ОБНОВЛЕНИЕ: мой друг просто написал, чтобы расширить точку зрения «будь внимателен», сказав, что «это определенно требует целенаправленной обработки информации, которую вы потребляете, чтобы сделать ее полезным упражнением для мозга. Например, я всегда стараюсь вести дневник или писать содержательные электронные письма о своем опыте, чтобы попытаться лучше понять его.Отличный момент.
С ее разрешения, вот вам:
———————————-
Дорогие друзья,
Я только что возвращаюсь из Намибии и с нетерпением жду всех наших возможностей окажем там влияние, когда мы вернемся с нашими учениками следующей весной.
Намибия сильно отличается от того, что я ожидал. Это была последняя страна в Африке, получившая независимость от колониализма всего 20 лет назад. Таким образом, она намного более развита, чем любая африканская страна, в которой я побывал, с относительно хорошей инфраструктурой и без существующей задолженности.Тем не менее, наследие апартеида все еще ощущается в сегодняшнем обществе, и люди совершенно очевидно постоянно имеют дело с проблемами расы и идентичности. Одним из самых интересных событий, которые я испытал, было посещение «браай» (намибийская версия барбекю, которая в основном состоит из [Подробнее…] о путешествиях и взаимодействии как полезном упражнении для мозга
Числовые шаблоны
Эта страница содержит ссылки на бесплатные рабочие листы по математике для задач с числовыми шаблонами.Нажмите одну из кнопок ниже, чтобы увидеть все рабочие листы в каждом наборе. Вы также можете использовать меню «Рабочие листы» сбоку на этой странице, чтобы найти рабочие листы по другим математическим темам.
Рабочие листы с числовым образцом
Рабочие листы с числовым образцом на этой странице – отличная практика для тестов по математике, с которыми ваши ученики будут сталкиваться в классе или на экзаменах штата. В то время как числовые шаблоны часто рассматриваются во многих учебных программах по математике лишь кратко, практика с числовыми шаблонами – отличный способ повысить не только результаты тестов, но и беглость числовых навыков.
Что такое числовые шаблоны?
Шаблоны чисел – очень распространенный тип задач, когда студенту дается последовательность чисел и просят определить, как этот список создается и какие будут следующие значения. Это обычные функции стандартизированных тестов, и вы также найдете их как часть стандарта Common Core (в частности, 4.0A.C.5) в Соединенных Штатах. Простые числовые шаблоны обычно вводятся в 4-м классе, а их концепции закрепляются в 5-м и 6-м классах, но более сложные геометрические числовые шаблоны с более сложными правилами (например, последовательность Фибоначчи) являются распространенными вопросами теста на протяжении всех классов средней школы.
Обучение студентов распознаванию и пониманию числовых образов выходит за рамки фундаментальных арифметических навыков и также обучает логике и навыкам распознавания образов. В типичной задаче о числовом шаблоне ученику дается последовательность чисел, а затем он должен описать правило или шаблон, генерирующий числа. Часто проблема требует, чтобы учащийся указал следующие числа в шаблоне, но некоторые варианты задачи также будут запрашивать предыдущие числа. Требование от ученика проработать шаблон вперед и назад – один из способов обеспечить полное понимание.
Базовые шаблоны чисел
Самые основные типы шаблонов чисел включают в себя базовые правила сложения и вычитания, и они используют знакомство учащихся с шаблонами подсчета пропусков для быстрого создания соответствующего правила. Многие из этих числовых шаблонов будут начинаться с числа, расположенного выше в последовательности (например, если шаблон – «добавить 3», обеспечивая последовательность «12, 15, 18 …»).
Варианты с обратным отсчетом паттернов (например, паттерн «минус 3» с последовательностью «21, 18, 15… “) вводят шаблоны чисел вычитания.
Шаблоны чисел также являются отличным способом постепенного повышения уверенности в распознавании последовательностей в незнакомом контексте. Например, шаблон подсчета по тройкам, описанный выше, может начинаться с числа, которое обычно не входит в знакомый шаблон. (например, «5, 8, 11 …»), который дает возможность изучающему математику заново открыть для себя знакомый числовой шаблон.
Числовые шаблоны с обычными приращениями
Многие из рабочих листов числовых шаблонов на этом page имеют дело с приращениями, которые часто встречаются в реальных последовательностях чисел, и способность быстро определять эти закономерности является полезным навыком.Здесь вы найдете образцы пятерок, образцы десятков, образцы пятнадцати и образцы 25 для практики. Это также отличная практика, когда учащиеся овладевают базовыми шаблонами сложения чисел или шаблонов чисел вычитания, когда они ищут что-то немного более сложное.
Шаблоны чисел умножения и не только
На этой странице также есть набор рабочих листов, в которых есть правила шаблонов, использующие операции умножения и деления. Хотя этот тип числового шаблона менее распространен в 4 или 5-м классе, когда умножение только вводится, вы довольно часто встретите шаблоны умножения чисел на вступительных экзаменах в колледж, поэтому важно знакомство с этими шаблонами.
Шаблоны чисел умножения служат мостом к шаблонам геометрических чисел, таким как последовательность Фибоначчи. Это шаблоны, в которых следующая последовательность значений зависит от предыдущих чисел. Паттерн Фибоначчи включает в себя суммирование двух предыдущих цифр в последовательности, поэтому правило, по сути, «сложите два предыдущих числа». Канонический паттерн Фибоначчи – «0, 1, 1, 2, 3, 5, 8 …» и аналогичный, но вы часто будете видеть проблемы с числовым паттерном, которые начинаются с другой базы и используют то же правило.
Другие шаблоны чисел
Другие типы шаблонов чисел, которые могут встречаться, представляют собой просто списки общих чисел, например, шансы или равны, простые числа, составные числа, времена. Усиление концепции шаблонов, встречающихся практически в любом приложении, позволит учащимся определить их, когда они появляются как в математических тестах, так и в реальной жизни.
Упражнения в конце главы | Числовые узоры
(4 ;; ; 13 ;; ; 22 ;; ; 31 ;; ; ldots )
Нам сначала нужно найти (d ):
begin {align *}
d & = T_ {2} – T_ {1} \
& = 13-4 \
& = 9
end {выровнять *}
Далее отметим, что для каждого следующего члена мы добавляем (d ) к последнему члену.Мы можем выразить это как:
begin {align *}
Т_ {1} & = а = 4 \
T_ {2} & = a + d = 4 + 9 \
& = 4 + 9 (1) \
Т_ {3} & = Т_ {2} + d = 4 + 9 + 9 \
& = 4 + 9 (2) \
T_ {n} & = T_ {n-1} + d = 4 + 9 (n-1) \
& = 9n – 5
end {выровнять *}
Общая формула (T_n = 9n – 5 ).
(T_ {6} ) составляет:
begin {align *}
Т_ {6} & = 9 (6) – 5 \
& = 49
end {выровнять *}
(T_ {6} = text {49} )
(5 ;; ; 2 ;; ; -1 ;; ; -4 ;; ; ldots )
Нам сначала нужно найти (d ):
begin {align *}
d & = T_ {2} – T_ {1} \
& = 2 – 5 \
& = -3
end {выровнять *}
Далее отметим, что для каждого следующего члена мы добавляем (d ) к последнему члену.Мы можем выразить это как:
begin {align *}
Т_ {1} & = а = 5 \
T_ {2} & = a + d = 5 + (-3) \
& = 5 + (-3) (1) \
T_ {3} & = T_ {2} + d = 5 + (-3) + (-3) \
& = 5 + (-3) (2) \
T_ {n} & = T_ {n-1} + d = 5 + (-3) (n-1) \
& = 7 – 3n
end {выровнять *}
Общая формула (T_n = 7 – 3n ).
(T_ {6} ) составляет:
begin {align *}
Т_ {6} & = 7 – 3 (6) \
& = -11
end {выровнять *}
(T_ {6} = – text {11} )
( text {7,4} ;; ; text {9,7} ;; ; text {12} ;; ; text {14,3} ;; ; ldots )
Нам сначала нужно найти (d ):
begin {align *}
d & = T_ {2} – T_ {1} \
& = text {9,7} – text {7,4} \
& = текст {2,3}
end {выровнять *}
Далее отметим, что для каждого следующего члена мы добавляем (d ) к последнему члену.Мы можем выразить это как:
begin {align *}
T_ {1} & = a = text {7,4} \
T_ {2} & = a + d = text {7,4} + text {2,3} \
& = text {7,4} + text {2,3} (1) \
T_ {3} & = T_ {2} + d = text {7,4} + text {2,3} + text {2,3} \
& = text {7,4} + text {2,3} (2) \
T_ {n} & = T_ {n-1} + d = text {7,4} + text {2,3} (n-1) \
& = text {7,4} + text {2,3} n – text {2,3} = text {2,3} n + text {5,1}
end {выровнять *}
Общая формула (T_n = text {2,3} n + text {5,1} ).
(T_ {6} ) составляет:
begin {align *}
T_ {6} & = text {2,3} (6) + text {5,1} \
& = текст {18,9}
end {выровнять *}
(T_ {6} = text {18,9} )
Модели роста – математика для 3-го класса
Узнайте о моделях роста
Вы помните, что такое шаблон ? 🤔
Верно! 😎
Шаблон – это расположение или последовательность, которая следует определенному порядку.
На последнем уроке вы узнали о повторяющихся узорах _ – шаблонах, которые повторяются.
Но есть и другие типы узоров.
В этом уроке давайте рассмотрим другую категорию моделей – модели роста ! 🤗
Каковы модели роста?
Посмотрите на эти шаблоны. 🤓
2, 4, 6, 8, 10, 12
Можете сказать, что у них общего? 🤔
Правильно!
👉 Термины в обоих этих шаблонах: , каким-то образом увеличивающиеся на .
Шаблоны
, которые увеличиваются (или растут) в соответствии с определенным правилом, называются шаблонами увеличения , шаблонами роста или .
Части модели роста
Схема роста состоит из 2 важных частей – условий и правила.
__
1. Условия
Каждый шаг схемы роста – это член .
Например, в приведенных выше примерах 👆 количество или группа объектов, которые мы получаем на каждом шаге, является членом шаблона.
2. Правило
Фиксированный порядок увеличения шаблона роста называется правилом .
Например, в приведенных выше примерах 👆 правила: +3 и добавить 1 синий треугольник, затем добавить 1 зеленый квадрат.
Поиск правила модели роста
😃 Чтобы работать с растущим шаблоном, нам нужно найти его правило .
Например,
👉 Посмотрите на этот узор.
Как вы найдете правило этого шаблона? 🤔
Вы поняли! 😎
✅ Чтобы найти правило паттерна, наблюдайте, как паттерн увеличивается при переходе от одной последовательности к другой.
Попробуем! 🤗
Давайте посмотрим, как этот паттерн растет.
Итак, как вы думаете, в чем состоит правило этого шаблона?
Очень хорошо! 👍
Правило этого шаблона:
Отлично сделано! 😎
Нахождение неизвестных условий модели роста
Иногда нам может понадобиться найти неизвестных термина в растущей структуре.
Давайте узнаем, как это сделать, на нескольких примерах!
👉 Посмотрите на этот узор.
Можете ли вы найти следующие три члена этого шаблона?
Как вы это сделаете? 🤔
Правильно! 👌
✅ Чтобы найти неизвестные термины схемы роста, сначала найдите ее правило, а затем используйте его для поиска неизвестных терминов.
Давай попробуем! 🤗
✅ Сначала давайте найдем правило этого паттерна.
Вы видите, как растет узор? 🤓
Очень хорошо!
Итак, можете ли вы сказать, что такое правило в этом шаблоне ?
✅ Теперь давайте воспользуемся этим правилом, чтобы найти следующие 3 члена.
Отличная работа! 😎
Рассмотрим еще один пример.
👉 Найдите восьмой член этой последовательности.
Вперед! Вы знаете шаги! 🤗
✅ Сначала давайте найдем правило узора.
Вы видите, как растет узор? 🤓
Очень хорошо! 👌
Итак, правило выкройки:
Добавить 5
✅ Теперь давайте воспользуемся этим правилом, чтобы найти восьмой член паттерна.
Отлично! 👏
Смотри и учись
Вы отлично поработали на уроке! 🤗 А теперь попробуйте несколько практических вопросов.
Практические вопросы последовательностей
1. Определите следующий номер в последовательности.
5, 13, 21, 29, __
- 37
- 38
- 39
- 42
- 43
2. Напишите последовательность из пяти последовательных четных чисел, которые в сумме дают 60.
- 6, 8, 10, 12, 14
- 8, 10, 12, 14, 16
- 9, 10, 11, 12, 13
- 10, 11, 12, 13, 14
- 10, 12, 14, 16, 18
3. Определите следующий номер в последовательности.
4.Первые два числа в последовательности Фибоначчи – это 0 и 1. После этого каждое число является суммой двух предыдущих. Запишите первые шесть чисел в последовательности Фибоначчи.
- 0, 1, 1, 2, 2, 4
- 0, 1, 1, 2, 3, 4
- 0, 1, 1, 2, 3, 5
- 0, 1, 2, 3 , 5, 8
- 0, 1, 2, 3, 6, 9
5. Запишите первые шесть чисел в последовательности, в которой каждое число в три раза больше предыдущего числа, а первое число равно 2.
- 2, 4, 8, 16, 32, 64
- 2, 4, 12, 32, 96, 288
- 2, 6, 12, 24, 72, 216
- 2, 6, 12, 36, 108 , 324
- 2, 6, 18, 54, 162, 486
6.Напишите последовательность из пяти последовательных четных чисел, которые добавляют к 0.
- -4, -2, 0, 2, 4
- -3, -1, 1, 3, 5
- -2, 0, 2, 4, 6
- -2, -1, 0, 1, 2
- 0, 2, 4, 6, 8
7. Найдите 23-й член в приведенной ниже последовательности.
9, 15, 21, 27, 33,…
- 135
- 136
- 138
- 141
- 142
8. Запишите следующие четыре числа в последовательности ниже.
32, 48, 72, 108,…
9.Определите следующий номер в последовательности.
0, 1, 3, 6, 10, __
- 13
- 14
- 15
- 16
- 17
10. Найдите 31-й член в приведенной ниже последовательности.
69, 60, 51, 42, 33,…
- -279
- -201
- -189
- -188
- -31
Ключ ответа
1. A. Проверьте последовательность найти выкройку. Шаблон таков, что каждое число на восемь больше, чем последнее.Добавьте, чтобы найти следующий номер.
29 + 8 = 37
2. B. Последовательность из пяти последовательных четных чисел – это последовательность четных чисел, так что разница между одним числом и следующим всегда равна 2. Вот несколько примеров:
0, 2, 4, 6, 8
12, 14, 16, 18, 20
100, 102, 104, 106, 108
Один из способов найти правильную последовательность – это составить и решить уравнение. Если x представляет собой первый член, последующие члены будут x + 2, x + 4, x + 6 и x + 8.Сумма всех членов равна 60, поэтому
x + ( x + 2) + ( x + 4) + ( x + 6) + ( x + 8) = 60
5 x + 20 = 60
5 x = 40
x = 8
Следовательно, последовательность 8, 10, 12, 14, 16.
3. B. Изучите последовательность, чтобы найти узор. Шаблон состоит в том, что каждое число составляет половину предыдущего числа. Умножьте на, чтобы найти следующее число.
4. C. Как указано в задаче, первые два числа равны 0 и 1. Сложите их, чтобы найти третье число в последовательности Фибоначчи.
0 + 1 = 1
Продолжайте этот процесс добавления последовательных членов в последовательность, чтобы найти следующие три числа в последовательности.
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
Следовательно, первые шесть чисел в последовательности Фибоначчи равны 0, 1, 1, 2, 3, 5.
5. E. Как указано в задаче, первое число равно 2. Чтобы найти второе число, умножьте 2 на 3.
2 x 3 = 6
Продолжайте этот процесс умножения на 3, чтобы найти следующие четыре числа в последовательности.
6 x 3 = 18
18 x 3 = 54
54 x 3 = 162
162 x 3 = 486
Следовательно, первые шесть чисел в последовательности – 2, 6, 18, 54, 162, 486
6. A. Последовательность из пяти последовательных четных чисел – это последовательность четных чисел, такая, что разница между одним числом и следующим всегда равна 2.Вот несколько примеров:
0, 2, 4, 6, 8
12, 14, 16, 18, 20
100, 102, 104, 106, 108
Если все числа в последовательности положительные , то сумма последовательности также будет положительной. Следовательно, чтобы сумма была равна нулю, половина чисел должна быть отрицательной. В частности, каждому положительному числу в последовательности соответствует отрицательное число. Таким образом, последовательность должна быть -4, -2, 0, 2, 4.
7. D. Изучите последовательность, чтобы найти шаблон.Шаблон таков, что каждое число на шесть больше предыдущего. Таким образом, самый простой способ вычислить 23-й член – это выписать первые 23 члена в последовательности, но это было бы очень утомительно. Намного более простой способ – найти формулу f ( n ) для n -го числа в последовательности, а затем подставить 23 для n .
Поскольку каждое число на шесть больше предыдущего, формула будет выглядеть примерно так: f ( n ) = 6 n .Однако обратите внимание, что эта формула отличается на 3 для каждого числа в данной последовательности. Исправьте это, просто добавив 3 в формулу. Результат: f ( n ) = 6 n + 3, что работает для любого значения n . Замените 23 на n в этой формуле и произведите расчет.
f (23) = 6 (23) + 3
= 138 + 3
= 141
8. C. Изучите последовательность, чтобы найти закономерность. Шаблон состоит в том, что каждое число умножается на предыдущее.Умножьте 108 на, чтобы найти следующее число в последовательности.
Продолжайте умножение, чтобы найти следующие три числа в последовательности.
Следовательно, следующие четыре числа – 162, 243,,.
9. C. Изучите последовательность, чтобы найти узор. Вычислите разницу между последовательными числами.
(2-е число) – (1-е число) = 1-0 = 1
(3-е число) – (2-е число) = 3-1 = 2
(4-е число) – (3-е число) = 6-3 = 3
(5-е число) – (4-е число) = 10-6 = 4
Следовательно, следующее число будет на 5 больше, чем последнее.
10 + 5 = 15
10. B. Изучите последовательность, чтобы найти образец. Шаблон таков, что каждое число на девять меньше предыдущего. Таким образом, самый простой способ вычислить 31-й член – это выписать первые 31 член в последовательности, но это было бы очень утомительно. Намного более простой способ – найти формулу f ( n ) для n -го числа в последовательности, а затем подставить 31 для n .
Поскольку каждое число на девять меньше последнего, формула будет выглядеть примерно так: f ( n ) = – 9 n .Однако обратите внимание, что эта формула отличается на 78 для каждого числа в данной последовательности. Исправьте это, просто добавив 78 в формулу. Результат: f ( n ) = -9 n + 78, что работает для любого значения n . Чтобы ответить на вопрос, замените 31 вместо n в этой формуле и произведите вычисление.
Рабочие листы с выкройками
Повторяющийся и растущий узор
Повторяющийся узор: определение следующего изображения
Обведите следующий рисунок в каждом шаблоне.Эти рабочие листы в формате pdf больше всего подходят для детей дошкольного и детского сада.
Лист 1 | Лист 2 | Лист 3
Повторяющийся узор: действие “вырезать-вставить”
Вырежьте графику внизу каждого рабочего листа для печати. Вставьте следующий рисунок в каждый рисунок изображения.
Лист 1 | Лист 2 | Лист 3
Схема выращивания: Тип 1
В каждом вопросе есть возрастающие последовательности. Завершите рисунок, который будет следующим в последовательности.В некоторых вопросах есть частично нарисованные картинки, чтобы вам было легче рисовать.
Лист 1 | Лист 2 | Лист 3
Схема выращивания: Тип 2
Дети 3-х и 4-х классов должны нарисовать рисунок, который будет следующим в каждом шаблоне.
Лист 1 | Лист 2 | Лист 3
Повторение и рост: смешанный образец
Этот раздел содержит повторяющийся и растущий узор на каждом рабочем листе для печати.
Лист 1 | Лист 2 | Лист 3
Размер выкройки
Каждый узор содержит картинки разных размеров.Выберите размер, который будет следующим в последовательности.
Лист 1 | Лист 2 | Лист 3
Образец формы
На каждом уровне есть три рабочих листа в формате pdf. Ожидается, что дети 2-го и 3-го классов будут определять и расширять рисунок формы.
Легко:
Лист 1 | Лист 2 | Лист 3 |
Средне:
Лист 1 | Лист 2 | Лист 3 |
Сложность:
Лист 1 | Лист 2 | Лист 3 |
Правила написания
Напишите правило, за которым следует каждый рисунок изображения.
Лист 1 | Лист 2 | Лист 3
Цветовой узор
Определение цветового образца
Определите цветовой узор. Дополните картину правильным цветом. У каждого уровня своя тема.
Easy (самолет):
Лист 1 | Лист 2 | Лист 3 |
Умеренный (поезд):
Лист 1 | Лист 2 | Лист 3 |
Сложный (цепочка):
Лист 1 | Лист 2 | Лист 3 |
Вызов (змея):
Лист 1 | Лист 2 | Лист 3 |
Отображение узора: раскраски изображений
Дети 1-го класса могут использовать свои любимые цвета, чтобы раскрасить картинки, чтобы показать узор.
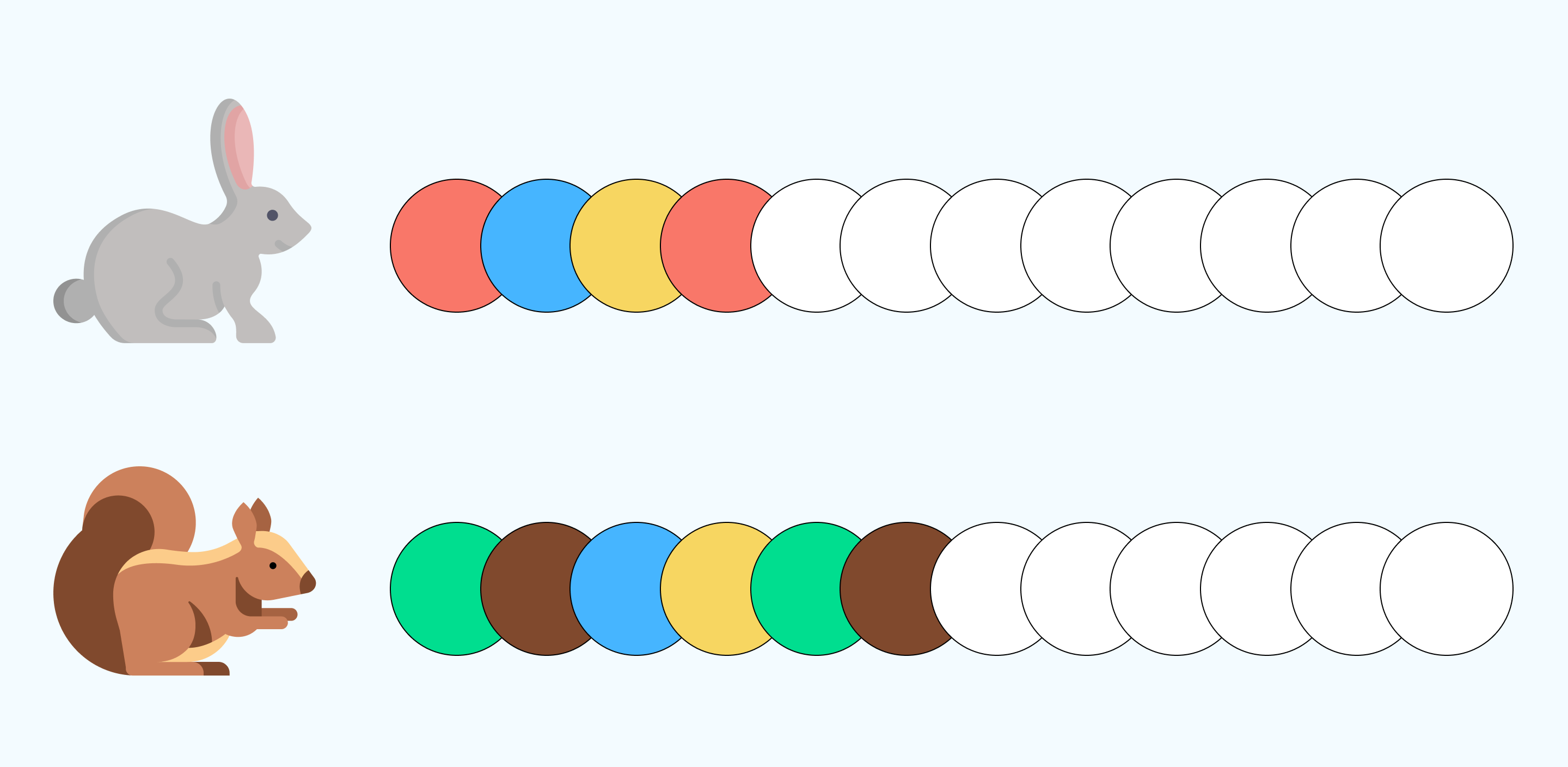

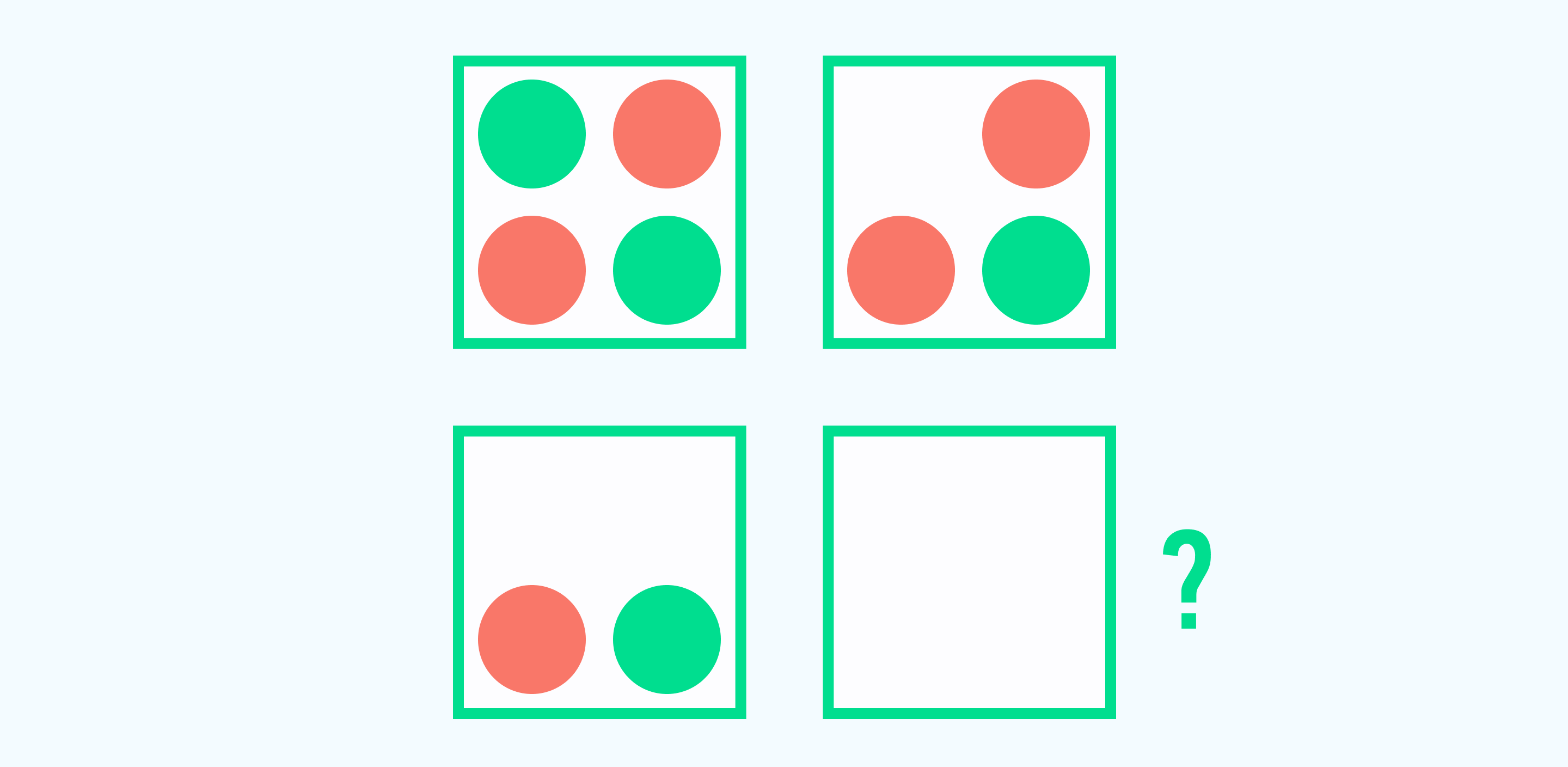
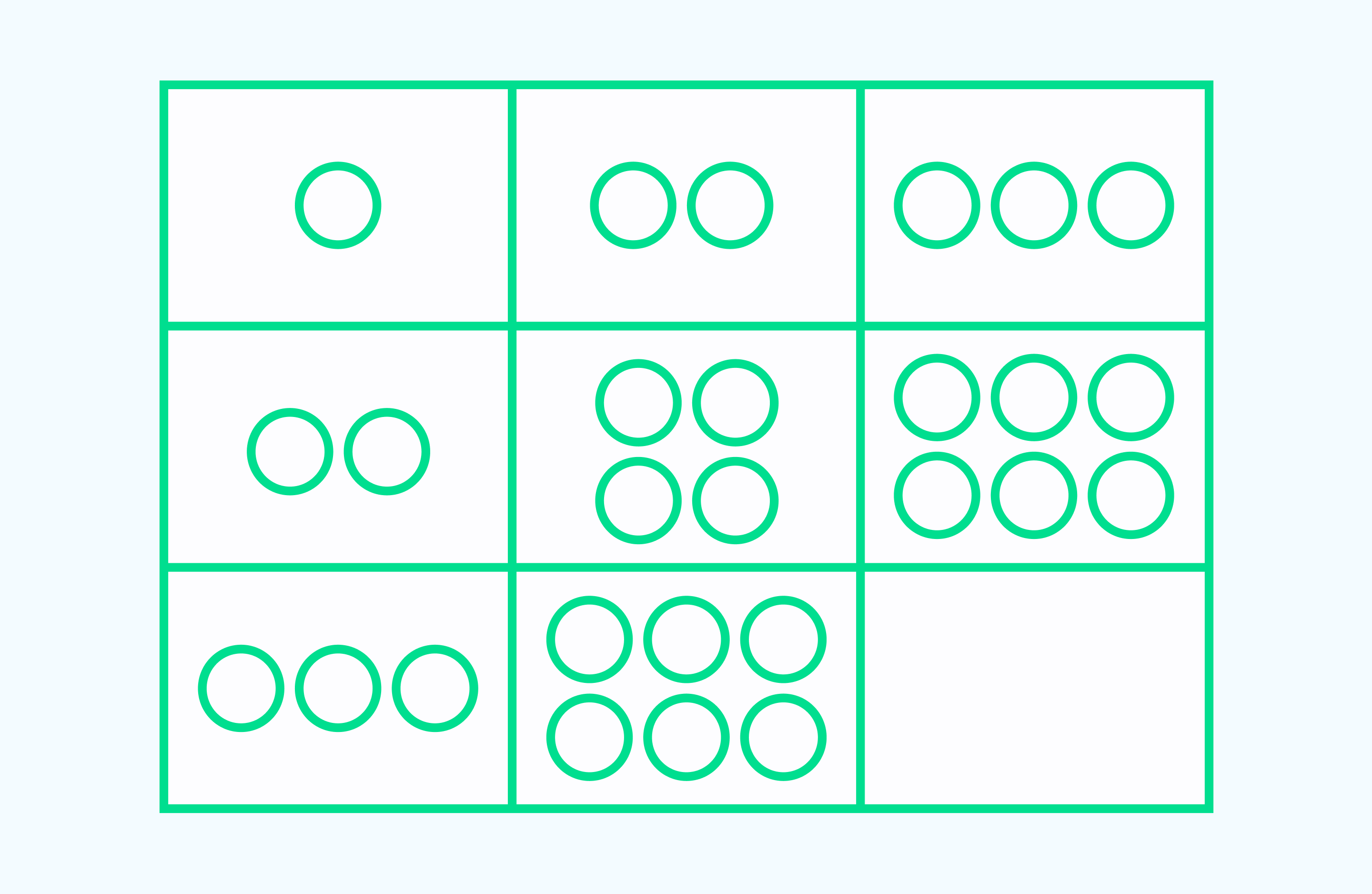
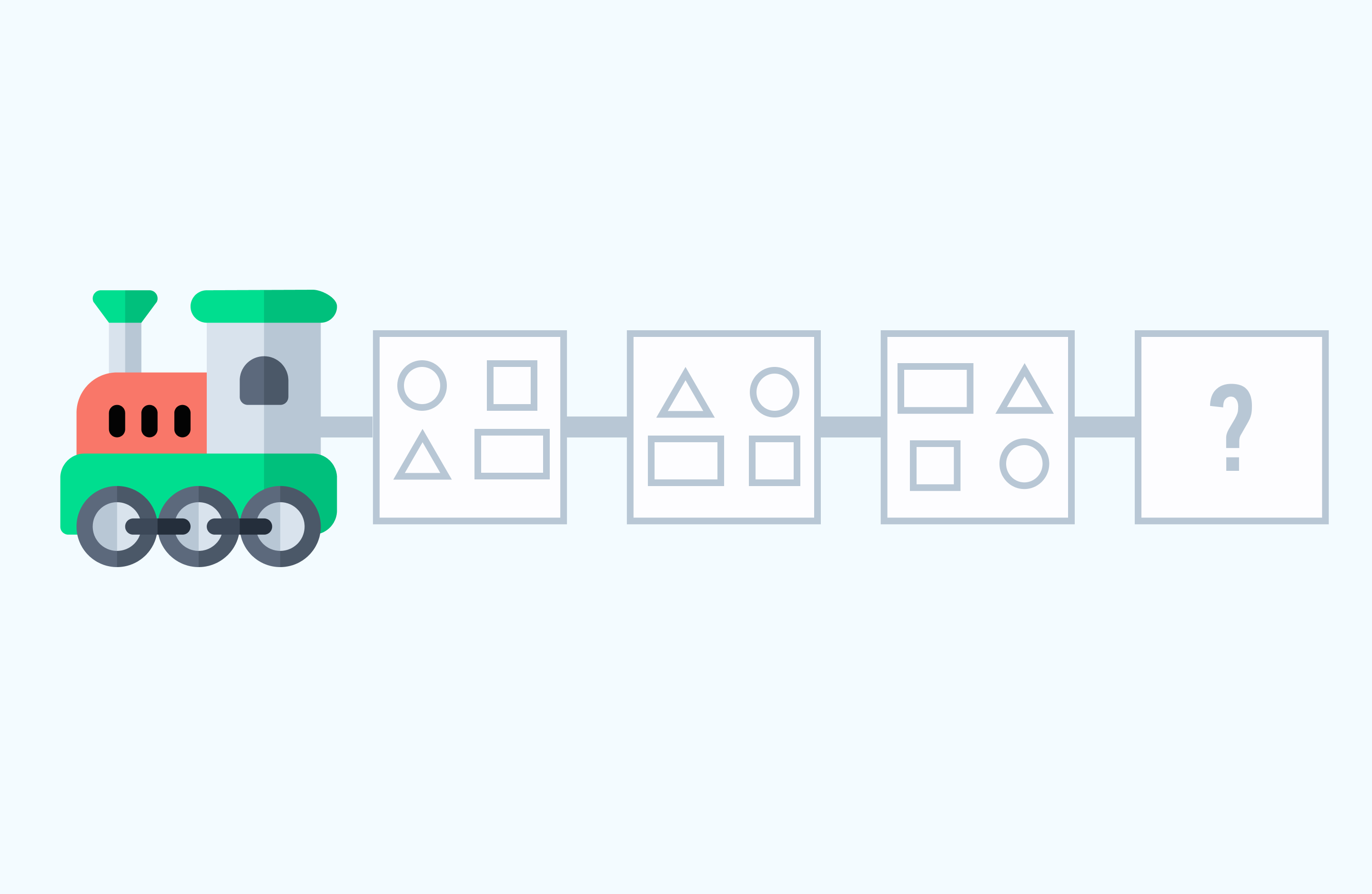
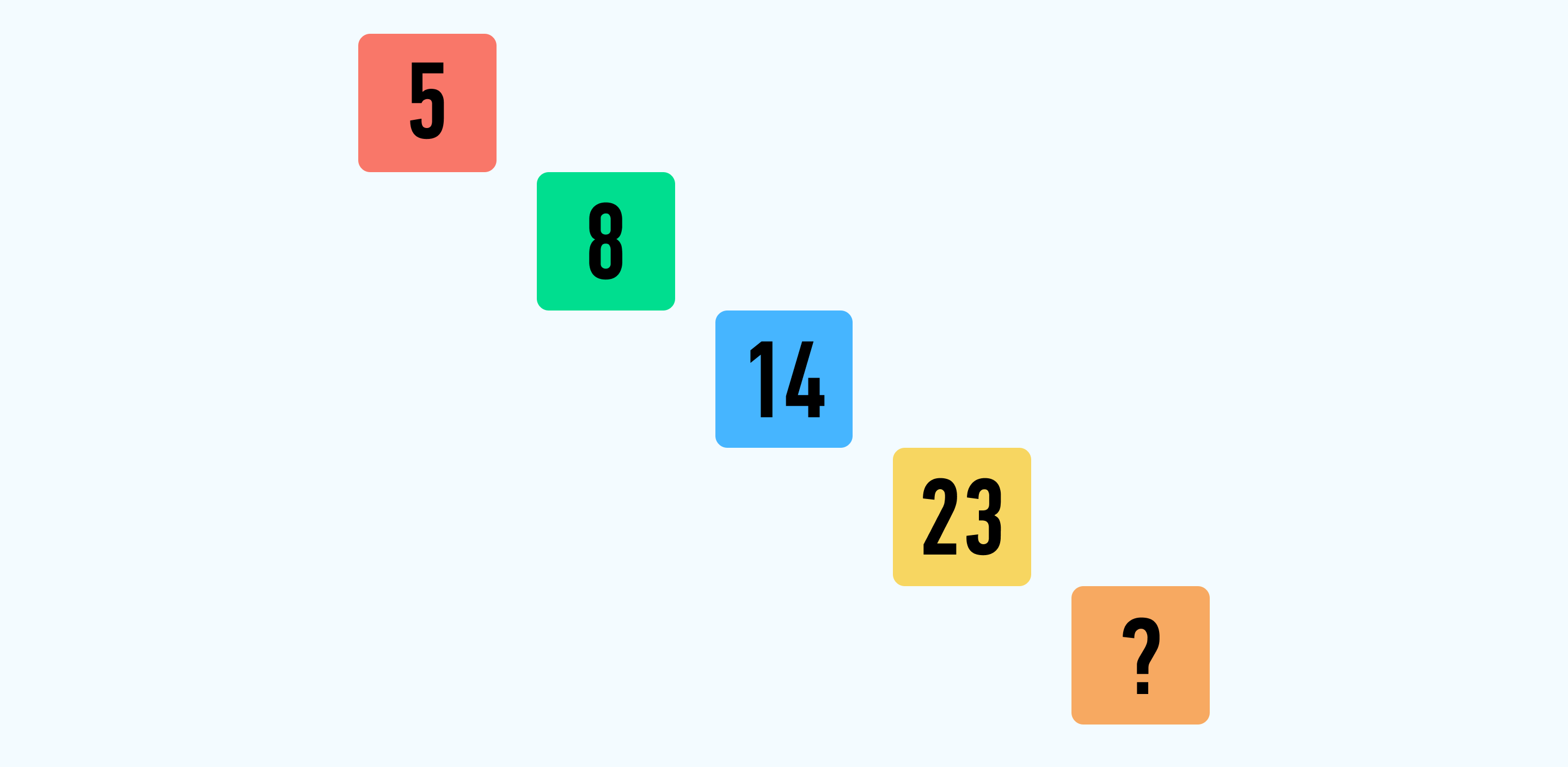
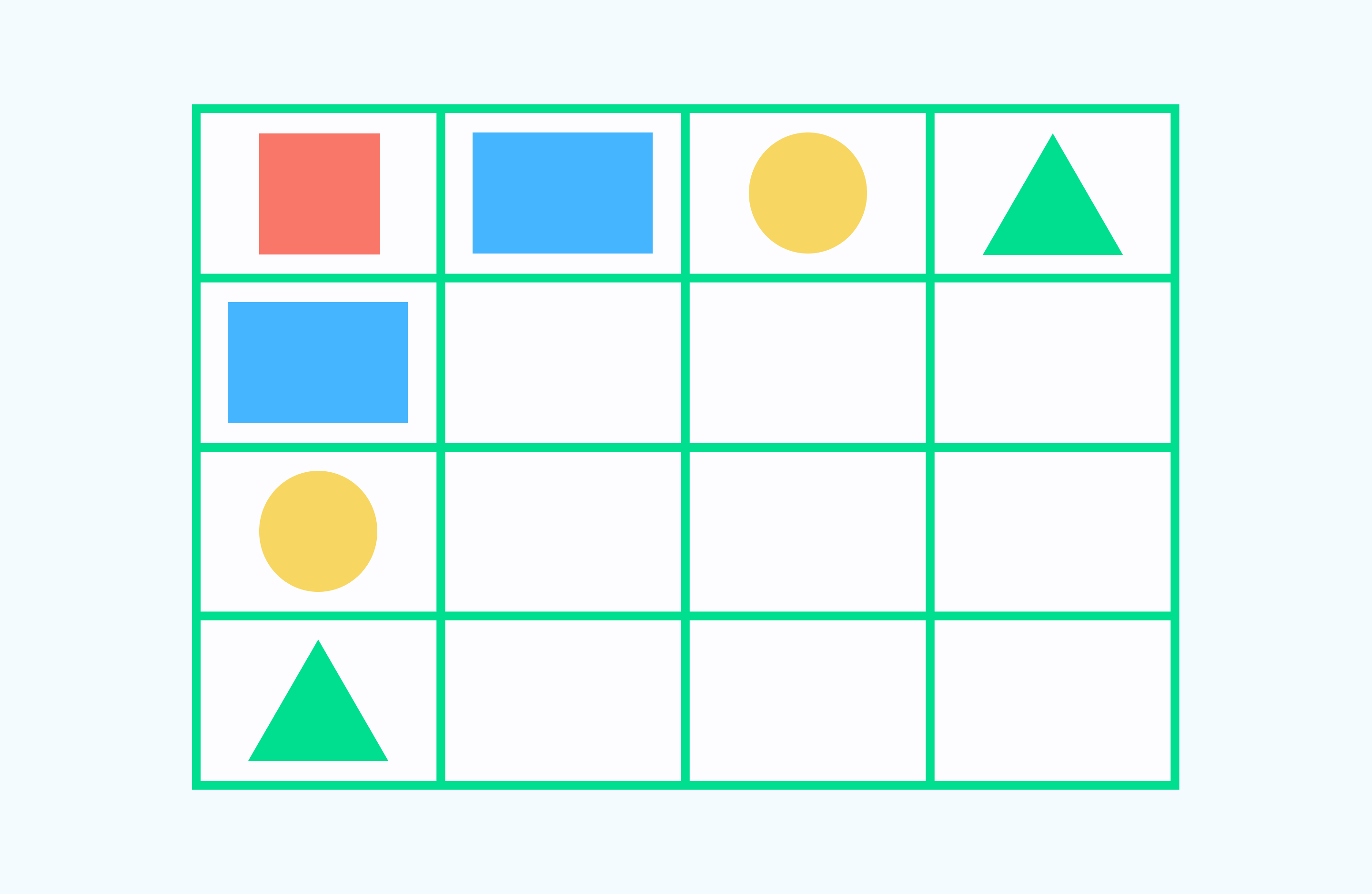

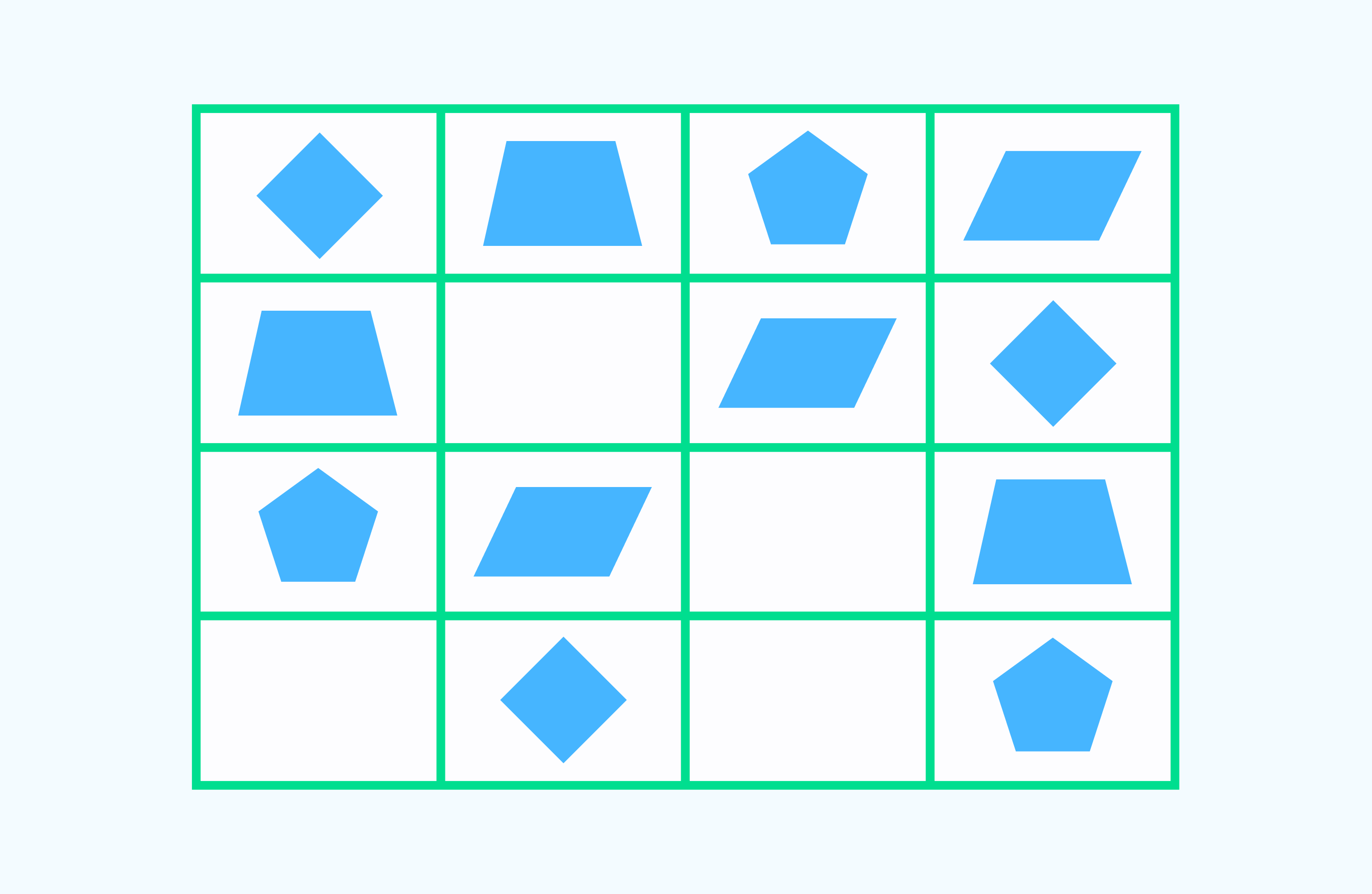






















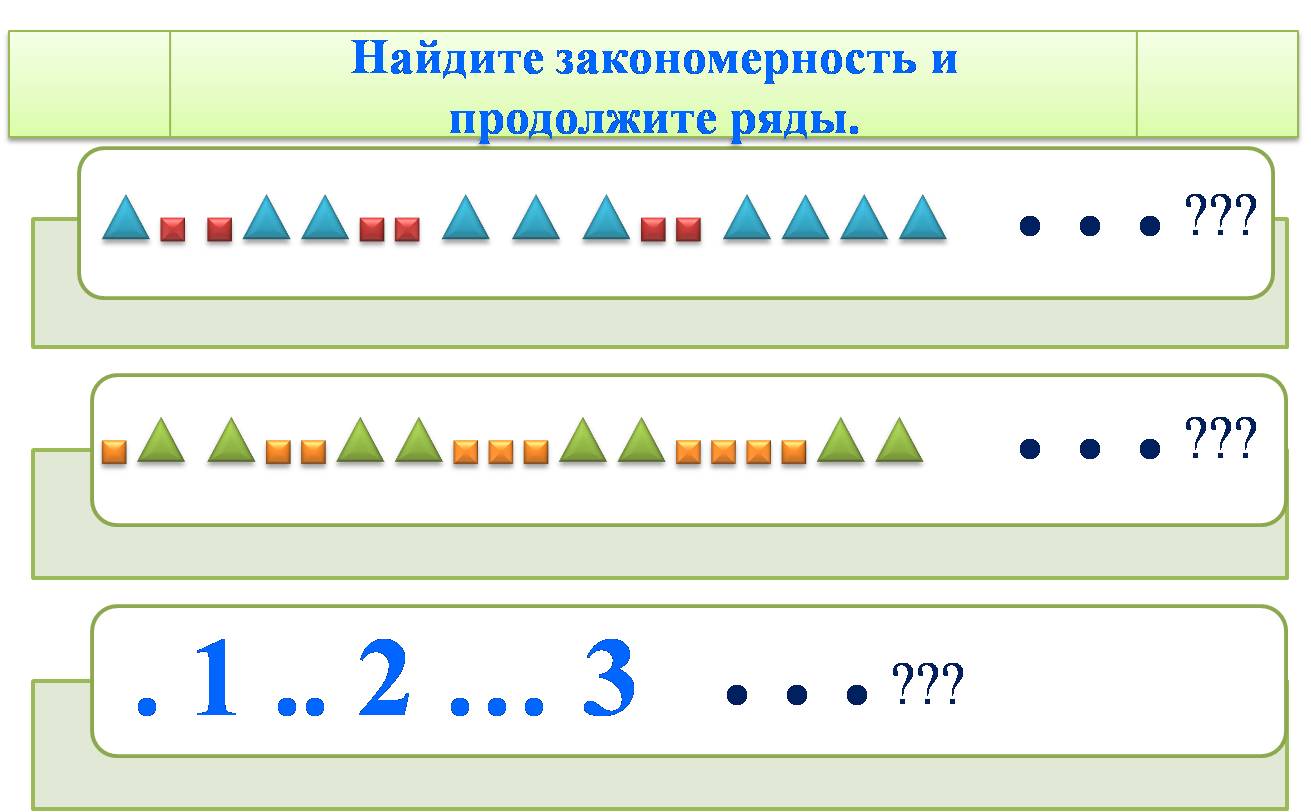
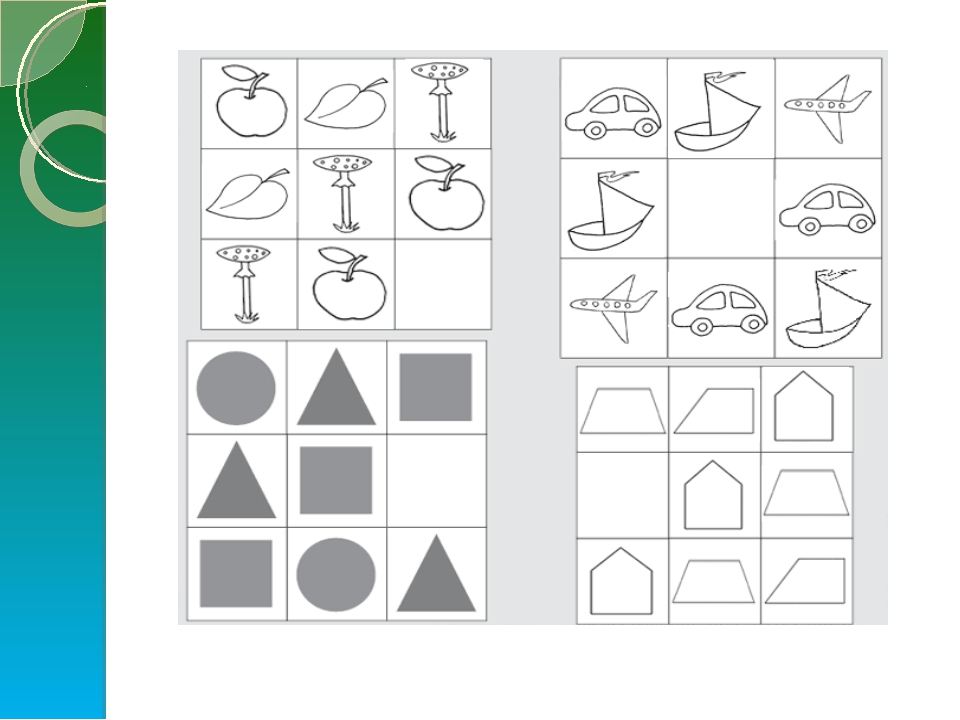
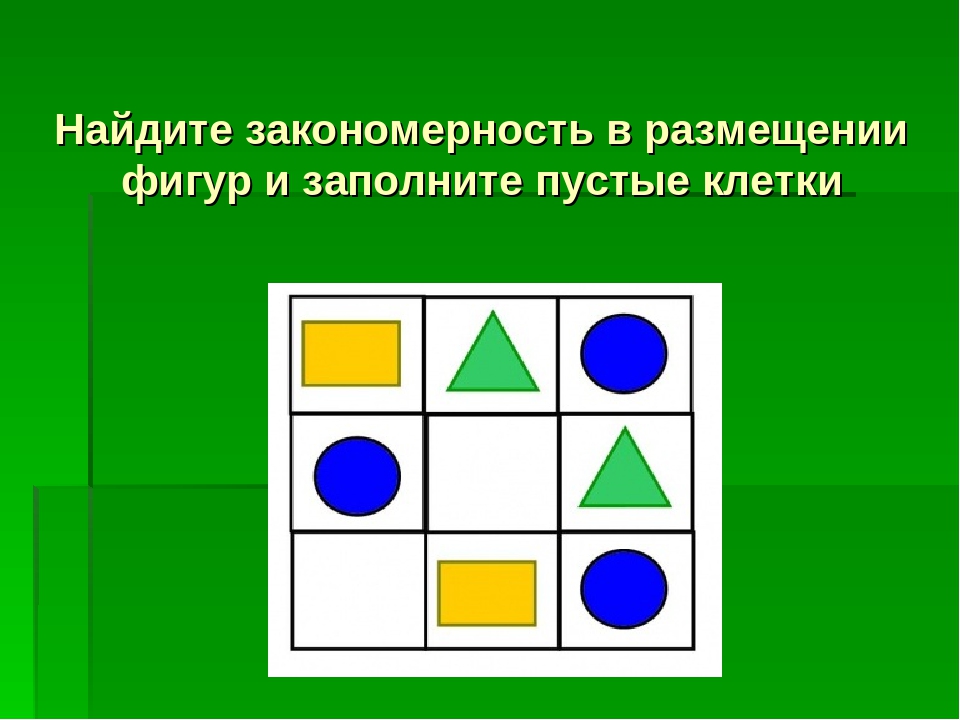
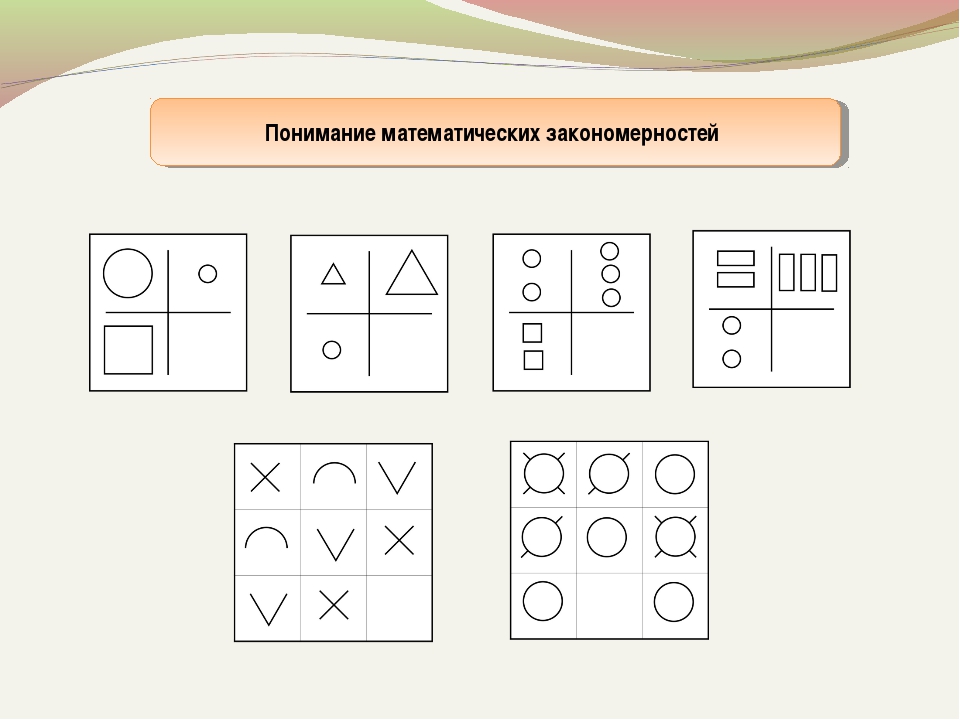
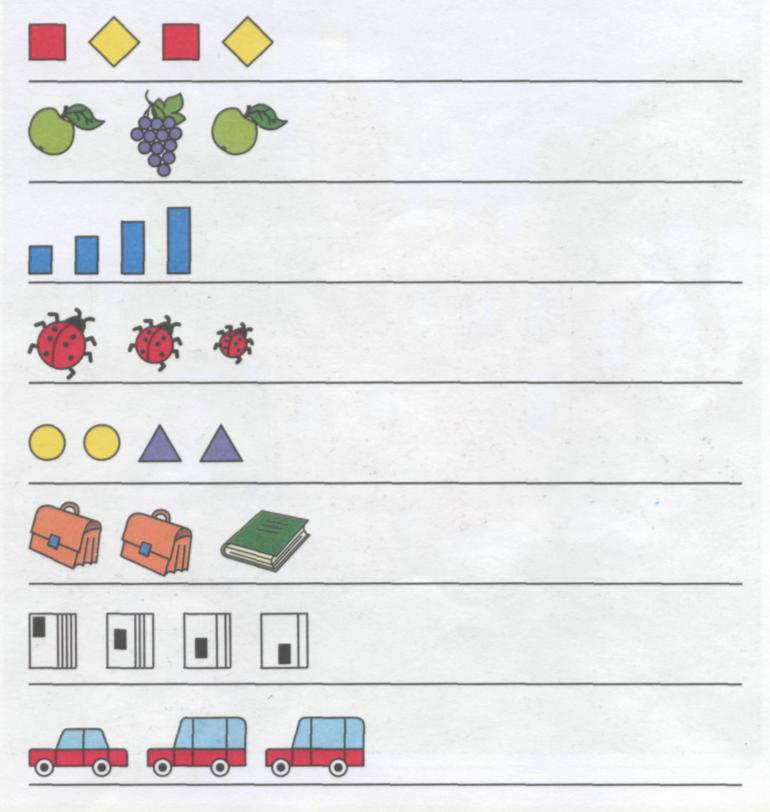

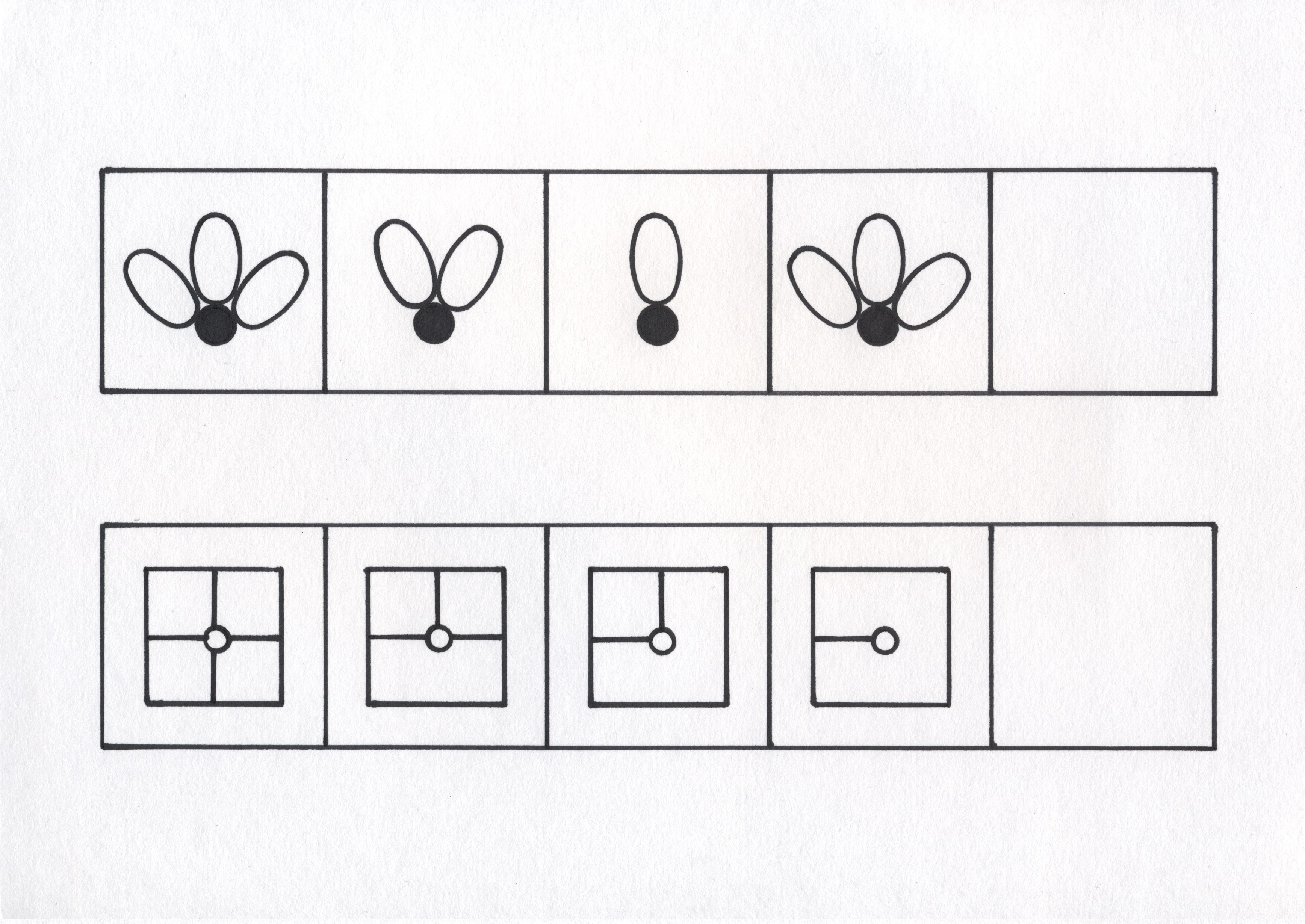

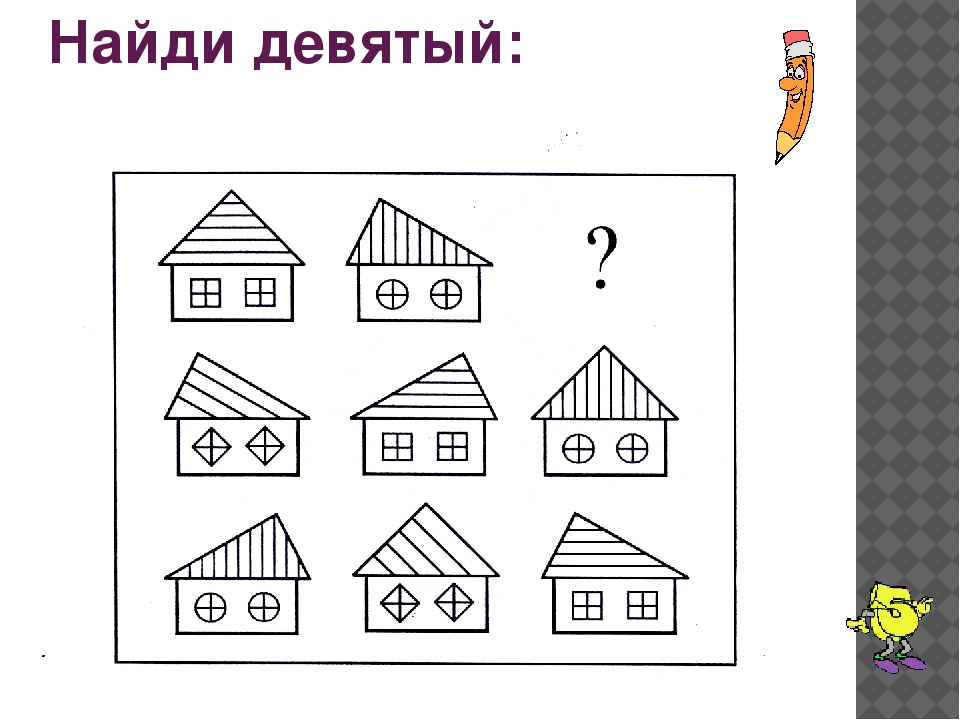
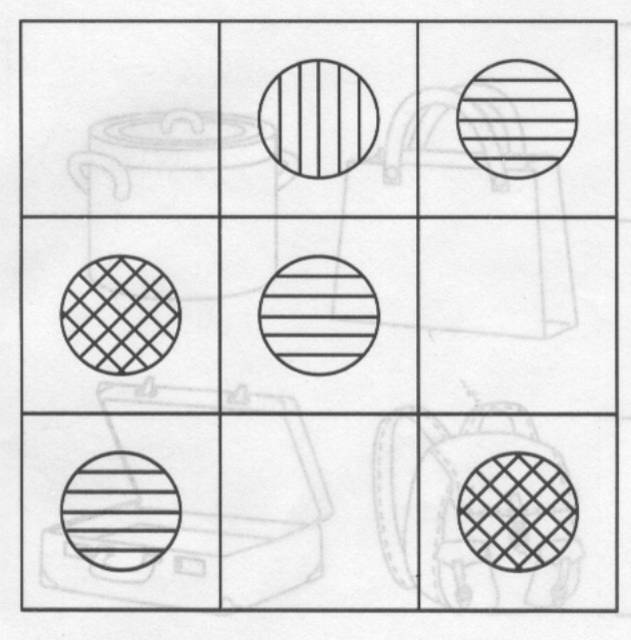 Вера не с лукошком. Что взяла с собой каждая девочка?
Вера не с лукошком. Что взяла с собой каждая девочка?
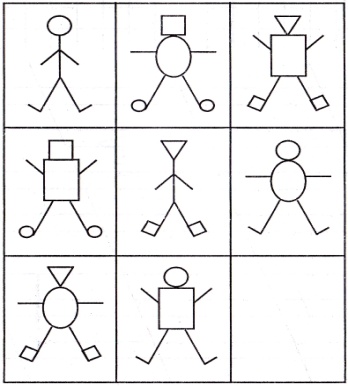


 Вера не с лукошком. Что взяла с собой каждая девочка?
Вера не с лукошком. Что взяла с собой каждая девочка?
