МКОУ «Юстинская средняя общеобразовательная школа»
Конкурс «От исследования – к научному поиску».
Секция – Естественно-научная.
Исследовательская работа по математике
на тему:
«Золотая пропорция»
Работу выполнила: ученица 8 класса,
Лиджи-Гаряева Эвелина.
Руководитель: учитель математики, почетный работник общего образования РФ
Амулангова В.А.
п.Юста, 2013г.
Краткая аннотация.
Цель работы: поиск закономерностей «золотой пропорции» в различных областях неживой и живой природы и в моем окружении.
Методы и приемы исследования: наблюдения, сбор данных, расчеты, математическая обработка полученных результатов.
В данной работе рассмотрены способы нахождения «Золотого сечения», изложены примеры, взятые из областей науки и искусства, в которых отражается эта пропорция: архитектура, живопись, скульптура, природа. В своей работе я хотела продемонстрировать красоту и широту « Золотого сечения» в реальной жизни. Я поняла, что мир математики приоткрыл мне одну из удивительных тайн, которую я постаралась раскрыть в своей работе.
. Выводы: «Золотая пропорция проявляет себя как в мире живой природы, так и в нашем окружении.
Содержание
стр
Введение ………………………..………………………………………….……..3
Основная часть
1. «Золотые» фигуры и тела..……………….…………………………………..5
2. Загадки древних строений
2.1 Египетские пирамиды……..……………….……………….…….…………….5
2.2 Парфенон в Афинах……………………………………………………………6
3. Проявление «золотой пропорции» и ее образующих в науке
3.1 Научные открытия……………………………………………..….…………..6
4. «Золотая пропорция» в моем окружении
4.1 «Золотая пропорция» в растениях……………………………………………7
4.2 «Золотой прямоугольник»……………………………………………………8
4.3 «Золотая» пропорция в анатомии человеческого тела……………………….9
Заключение………………………………..…………………………….……………12
Список используемой литературы………………………………………………..13
Введение
«Геометрия обладает двумя великими сокровищами.
Первое – это теорема Пифагора, второе – деления отрезка
в крайнем и среднем отношении».
Иоганн Кеплер.
Изучая различную научную литературу, я пришла к выводу, что «золотое сечение» перестало быть сокровищем одной лишь геометрии.
Все это побудило меня исследовать «золотую пропорцию» как универсальную мировую константу.
Предмет исследования: «золотая пропорция».
Цель исследования: поиск закономерностей «золотой пропорции» в различных областях неживой и живой природы и в моем окружении.
В ходе исследования сформировались задачи:
1.Изучить необходимую литературу по данной теме;
2.Определить и рассмотреть использование «золотой пропорции» в неживой и живой природе, ее применение в современном мире;
3.Выявить и изучить проявления «золотой пропорции» и ее производных в моем окружении.
Гипотеза: если «золотая пропорция» универсальная мировая константа, то она встречается в мире живой и неживой природы.
Значимость работы заключается в том, что в процессе работы была изучена научно-популярная литература по данной теме, а также выявлено несколько видов «золотой пропорции» – «золотая спираль», «числа Фибоначчи», «золотая» симметрия.
Апробация работы состоит в применении «золотой пропорции» на уроках математики, биологии, физики, мировой художественной культуры, а также во внеклассных мероприятиях и при проведении предметных недель.
Слово «пропорция» в переводе с латинского означает «соразмерность», «определенное отношение частей между собой». Учение об отношениях и пропорциях особо успешно развивалось в четвертом веке до нашей эры в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремеслами.
Из «Начал» Евклида к нам пришла геометрическая задача, называемая задачей «о делении отрезка в крайнем и среднем отношении». Существует бесконечное множество разбиения отрезка (рис 1) на две части, и лишь единственный способ разбиения такой, что отношение всего отрезка к его большей части равно отношению большей части к его меньшей части
рис 1.
Обозначим длину всего отрезка через 1, а длину его большей части за x, тогда длина меньшей части будет 1 – x. Составим пропорцию согласно приведенному определению:
откуда: 1 – x = х2.
корни уравнения являются иррациональными числами:
Длина отрезка выражается положительным числом, поэтому из двух корней следует выбрать второй. Число обозначается буквой в честь древнегреческого скульптора Фидия, в творениях которого оно встречается многократно. Число
– иррациональное, с восемью десятичными знаками оно записывается так:
φ ≈0,61803398… .
Вокруг этого числа, называемым числом Фибоначчи, создан романтический ореол таинственности и чуть ли не мистического поклонения. Еще его называют «золотым сечением», или «золотой пропорцией».
Приложения «золотого сечения» изучают в математике, физике, ботанике, философии, биологии, медицине, компьютерной науке.
К.Птолемей, александрийский астроном, математик и географ рассчитал, что рост человека правильного телосложения естественно делится в «золотом» отношении. Древние скульпторы использовали этот факт как критерий гармонии и канон красоты. «Золотое сечение» наблюдается в шрифтах и бытовых предметах.
Большинство греческих памятников архитектуры, непревзойденная «Джоконда», картины Рафаэля, Шишкина, Васильева, этюды Шопена, музыка Бетховена, Чайковского, стихи Вознесенского – не полный перечень выдающихся произведений искусства, насыщенных чудесной гармонией «золотого сечения».
1. «Золотые» фигуры и тела
Диагонали «пентагона» (пятиугольника) ABCDE (рис 2) образуют пятиугольную звезду. Точки пересечения диагоналей всегда являются точками «золотого сечения».
рис 2.
Таким образом:
Бесконечная повторяемость одной и той же геометрической фигуры вызывает эстетическое чувство ритма и гармонии.
2. Загадки древних построек
2.1 Египетские пирамиды
Правильная четырехугольная пирамида (рис 3) является одной из хорошо изученных геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление вверх. Отношение поверхности граней к площади основания также равно «золотой» пропорции. Гениальные создатели пирамиды Хеопса стремились поразить далеких потомков глубиной своих знаний, и они достигли этого. Следует лишь удивляться высокому знанию и искусству древних математиков и архитекторов Египта, которые смогли воплотить в пирамиде две иррациональные величины – π и Ф – со столь поразительной точностью, оперируя исходными отношениями целых чисел – стороной основания и высотой пирамиды.
рис 3.
2.2 Парфенон в Афинах
Рассмотрим один из знаменитейших произведений древнегреческой архитектуры – Парфенон в Афинах (рис 4). Длина его архитрава – 31,2 м, высота здания от основания до верхней точки – 19,6 м. Эти две цифры – ширина и длина – удовлетворяют пропорции золотого деления. Если высоту Парфенона разбить на части по пропорции золотого деления, то окажется, что все получающиеся при этом точки обозначены характерными выступами фасада.
Произведения готической архитектуры также удовлетворяют приведенному принципу.
рис 4.
Вывод:
В пирамидах Хеопса древние египтяне воплотили две иррациональные величины – π и Ф, оперируя исходными отношениями целых чисел – стороной основания и высотой пирамиды.
3. Проявление «Золотой пропорции» в науке
3.1 Научные открытия
Благодаря «золотой пропорции» были сделаны открытия:
– обнаружен пояс астероидов между Марсом и Юпитером;
– точка компенсации струны (возбуждение струны в точке, делящей ее в отношении «золотого сечения», не вызовет колебаний);
– на летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с «золотой пропорцией».
4. «Золотая пропорция» в моем окружении
4.1 «Золотая пропорция» в растениях.
Мною было проведено исследование, цель которого – выяснить, на примере домашних растений, каким образом золотая пропорция присутствует в растительном мире. Результаты этого исследования оформлены в приведенной таблице 1.
На каждом из рассмотренных растений я исследовала по 10 побегов. В первом столбце приведены названия растений; во втором и третьем – распространение правила золотой пропорции на побегах (на какое количество побегов из 10 распространено правило, а на какое – нет); в четвертом и пятом столбцах – соотношение количества побегов, на которые распространено правило золотой пропорции, и побегов, на которые не распространено, в процентах (%).
Таблица 1.
|
Название |
Наличие золотой пропорции |
Соотношение в % |
||
|
Есть |
Нет |
Есть |
Нет |
|
|
Традесканция |
8 |
2 |
80% |
20% |
|
Фикус |
7 |
3 |
70% |
30% |
|
Яблоня |
6 |
4 |
60% |
40% |
Результаты моего исследования показали, что золотая пропорция действительно существует. Она распространена в природе, причем более 2/3 растений подчинены ей.
А мы снова и снова убеждаемся в том, что все в природе подчинено единому плану, единым законам – и раскрыть и объяснить эти законы и есть главная задача человеческой науки. Я думаю, что мы не раз еще обнаружим в природе интересные математические отношения. Надо только уметь их наблюдать.
4.2 «Золотой прямоугольник»
Прямоугольник, стороны которого находятся в золотом отношении, иногда называются золотым прямоугольником (рис 5). Золотой прямоугольник обладает многими интересными свойствами. Если, например, от золотого прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник меньших размеров. Если этот процесс продолжить, то получим так называемые вращающие квадраты, и весь прямоугольник оказывается составленным из этих квадратов. Если соединить противоположные вершины квадратов плавной кривой, то получим кривую, называемую «золотой спиралью».
Где встречается «золотая спираль» в природе? Паук плетет паутину тоже спиралеобразно (рис 6). Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается также по спирали. По спирали закручены раковины многих моллюсков, улиток (рис 7). Спирально закручиваются усики растений, рога архаров (рис 8) По спирали происходит рост ткани в стволах деревьев.
Мною были проведены эксперименты на тему «Золотая пропорция и восприятие». Респонденты отдали предпочтение книге, имеющей форму, близкую к «золотому прямоугольнику», оставляя без внимания другие книги, имеющие форму вытянутого прямоугольника и форму, близкую к квадратной. И участники эксперимента предпочитали садиться на свободную лавочку в том месте, точка которого соответствовала пропорции «золотого отрезка». Также среди учащихся 5-11классов и учителей было проведено исследование «Визитная карточка». Нужно было выбрать наиболее привлекательную визитную карточку. Визитки были разной формы: квадратная, удлиненная прямоугольная и форма близкая к «золотому прямоугольнику». Из таблицы 2 видно, что из 38 опрошенных учителей и учащихся, 27 выбрали визитную карточку близкую к «золотому прямоугольнику». Это объясняется тем, что бесконечное повторение одних и тех же геометрических фигур вызывает у нас неосознанное эстетическое чувство гармонии и красоты.
рис 5. рис 6. рис 7.
рис 8.
Таблица 2.
|
Таблица |
Количество испытуемых |
«золотой прямоугольник» |
квадрат |
Вытянутый прямоугольник |
|
Учителя. |
13 |
11 (84%) |
1 (8%) |
1 (8%) |
|
Учащиеся 5 -11классов. |
25 |
16 (64%) |
2 / 8% |
7 (28%) |
|
Всего: |
38 |
27 (71%) |
3 /(8%) |
8 (21%) |
4.3 «Золотая» пропорция в анатомии человека
То, что части красиво сложенного человеческого тела находятся в определенной пропорции, знает каждый: недаром мы говорим о пропорционально сложенной фигуре.
Но далеко не всем известно, что здесь имеет место золотое сечение. Лучшим доказательство того, что древние ваятели руководствовались данным принципом в своем творчестве, являются античные статуи. Идеально сложенное человеческое тело полностью отвечает этому принципу. Если высоту великолепно сложенной фигуры разделить в крайнем и среднем отношении, то линия раздела окажется на высоте талии (рис 9). Особенно хорошо удовлетворяет этой пропорции мужская фигура, и художники давно знают, что, вопреки общему мнению, мужчины сложены красивее, чем женщины.
рис 9.
Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотого сечения. Самая главная книга всех современных архитекторов справочник Э.Нойферта “Строительное проектирование” содержит основные расчеты параметров туловища человека, заключающие в себе золотую пропорцию.
Немецкий профессор Цейзинг в середине 18 столетия проделал огромную работу: он измерил более 2000 тел и высказал предположение, что золотое сечение выражает среднестатистический закон: деление тела точкой пупа – один из основных показателей золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. Чтобы проверить гармоничность в строении (телосложении) учащихся нашей школы, мною были произведены некоторые измерения: рост, высота от стопы до пупочной линии, от пупочной линии макушки.
Работая над проектом, я решила провести эксперимент. Мне стало интересно – встречается ли гармоническая пропорция тела у современных людей? В эксперименте участвовали учащиеся 5-11 классов. Для этого мне нужно было узнать их рост – как целое(с), длину от ступни до талии – как большую часть(b), и длину от талии до темечка, как меньшую часть(а). Перед тем, как провести эксперимент, я составила таблицу с нужными мне для расчёта величинами. Теперь я могу провести измерения. Для этого мне нужно знать формулу «золотой» пропорции и способ её применения. В нашем случае формула «золотого сечения» выглядит так: a:b=b:с.
Таблица 3
|
Таблица |
Рост (с) |
От стопы до пупочной линии (b) |
От пупочной линии до макушки (a) |
«Золотая пропорция» |
||
|
b / с |
a / b |
|||||
|
Девушки: №1. |
161 |
102 |
59 |
0, 63 |
0,57 |
|
|
№2 |
162 |
100 |
62 |
0,62 |
0.,62 |
|
|
№3 |
165 |
100 |
65 |
0,61 |
0,65 |
|
|
№4 |
167 |
102 |
65 |
0,61 |
0,64 |
|
|
№5 |
169 |
104 |
65 |
0,62 |
0,62 |
|
|
Юноши №6 |
165 |
102 |
63 |
0,62 |
0,62 |
|
|
№7 |
182 |
105 |
77 |
0,58 |
0,73 |
|
|
№8 |
177 |
109 |
67 |
0,62 |
0,62 |
|
|
№9 |
183 |
110 |
73 |
0,61 |
0,66 |
|
|
№10 |
180 |
112,5 |
67,5 |
0,62 |
0,6 |
В процессе расчёта выяснилось, что у некоторых участников эксперимента фигуры оказалась приближены к стандартам «золотой» пропорции, потому что их отношение большей части к целому равно отношению меньшей части к большей. И это отношение равно 0,618, как того и требует пропорция. У других участников эксперимента соотношения пропорций не соответствовало стандарту «золотой» пропорции. Это не значит, что они не соответствуют общепризнанным канонам пропорций человеческого тела. Просто для «золотого сечения» их пропорции не подходят. И теперь я смело могу утверждать, что меня окружают люди с «божественной» пропорцией тела. Но это встречается не у всех. Параметры тела у всех людей разные. Это зависит от наследственности, среды обитания, условий проживания, особенностей трудовой деятельности.
Выводы:
Бесконечное повторение одних и тех же геометрических фигур, основанное на «золотом сечении», вызывает у нас неосознанное эстетическое чувство гармонии и красоты. Поэтому многие предметы прямоугольной формы зачастую имеют форму «золотого прямоугольника»: книги, визитные карточки. Точка деления отрезка в «золотом отношении» подсознательно притягивает наше внимание.
Рост человека правильного телосложения естественно делится в «золотом» отношении. 60 % испытуемых учащихся 5-11 классов моей школы подтвердили гармонию красоты своего тела.
Нам в своей жизни необходимо стремиться к созданию гармонии красоты не только в архитектуре, живописи, своего тела, но и в поведении, учении и познавательности.
Заключение.
Значение золотого сечения в современной науке очень велико. В данной работе рассмотрены способы нахождения «Золотого сечения», изложены примеры, взятые из областей науки и искусства, в которых отражается эта пропорция: архитектура, живопись, скульптура, природа. В своей работе я хотела продемонстрировать красоту и широту « Золотого сечения» в реальной жизни. Я поняла, что мир математики приоткрыл мне одну из удивительных тайн, которую я постаралась раскрыть в своей работе, кроме того, эти вопросы выходят за рамки школьного курса, они способствуют совершенствованию и развитию важнейших математических умений. Я собираюсь продолжать свои исследования и дальше, и искать еще более интересные и удивительные факты. Но изучая закон золотого сечения важно помнить, что он не является обязательным во всем, что мы встречаем в природе, а символизирует идеал построения. Небольшие несоответствия идеалу – это то, что делает наш мир таким разнообразным.
«Золотая пропорция» действительно является универсальной мировой константой.
В ходе работы гипотеза о том, что «золотая пропорция» уникальна, универсальна, является мировой константой, нашла свое подтверждение.
Список используемой литературы:
- Справочник руководителя сельской школы.
- Журнал «Математика», 2008
- Петров В.М., Прянишников Н.Е. «Формулы прекрасных пропорций».
- Пидоу Д. «Геометрия и искусство».
- Прохоров А.И. «Золотая спираль».
- www.sotvoreniye.ru/articles/golden_ratio2.php
- sapr.mgsu.ru/biblio/arxitekt/zolsech/zolsech2.htm
https://ria.ru/20221116/sechenie-1832065968.html
Гармония во всем: что такое золотое сечение и способы его применения
Золотое сечение: что это такое, пропорции, принцип, применение в архитектуре и строительстве
Гармония во всем: что такое золотое сечение и способы его применения
“Божественная гармония” или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке,… РИА Новости, 16.11.2022
2022-11-16T21:08
2022-11-16T21:08
2022-11-16T21:08
общество
европа
греция
ле корбюзье (шарль-эдуар жаннере-гри)
леонардо да винчи
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_0:318:3076:2048_1920x0_80_0_0_74519bda270895480ff99027b7b160ec.jpg
МОСКВА, 16 ноя — РИА Новости. “Божественная гармония” или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.Золотое сечение”Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе”, – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.ИсторияПо словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.”Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся”, – отмечает Максим Господинко.Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе “божественной пропорцией” (лат. “Divina Proportione”, итал. “Proporzione Divina”).По мнению Сергея Дементьева, “божественная пропорция” (“золотое сечение”) как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).Пионеры Возрождения Пачоли и Леонардо да Винчи (“Тайная вечеря” и “Мона Лиза” вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в “Началах” Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении (“ἄκρος καὶ μέσος λόγος”), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в “Десяти книгах об архитектуре” (лат. “De architectura libri decem”) о применении математики к искусству архитектуры.Пропорции золотого сеченияО том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.”Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция”, – поясняет он. К слову, она равна всегда 1,618, и это так называемое число “фи” обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.”Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности”, – говорит Ренат Мансуров.Золотое сечение в математикеИтальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.”Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число – это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.”, – поясняет Ренат Мансуров.0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.Правило золотого сеченияНа практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.Метод золотого сечения”Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр”, – поясняет Ренат Мансуров.Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.Где можно увидеть золотое сечениеЕсли разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.ПриродаСвою точку зрения озвучил Максим Господинко.”У растения есть важная задача – наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача – на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению “фи”, – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет”.По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. “Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи””, – отмечает специалист.ЧеловекПропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:ИскусствоМножество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.”Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы – пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать”, – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.Примеры использования в живописи.Примеры использования золотого сечения в дизайне логотипов.Применение золотого сеченияПримеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.По мнению эксперта, теория золотого сечения и “божественных пропорций” довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. “То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно”, – говорит Ренат Мансуров.Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. “Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия”, – советует Ренат Мансуров.Второе золотое сечениеВторое золотое сечение вытекает из основного сечения и дает отношение 44: 56.Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в “серебряном сечении”, если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок – один к одному. “Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 – крест. Каждой задаче – свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным”, – говорит Максим Господинко.Мифы о золотом сечении”Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы”.
https://ria.ru/20210121/litso-1593906541.html
https://radiosputnik.ria.ru/20220201/piramida-1769426771.html
https://ria.ru/20181111/1532496249.html
европа
греция
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2022
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e6/0b/10/1832031636_345:0:3076:2048_1920x0_80_0_0_d15c886e20acd2d1355969b43de06ca8.jpg
РИА Новости
internet-group@rian.ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
общество, европа, греция, ле корбюзье (шарль-эдуар жаннере-гри), леонардо да винчи
Общество, Европа, Греция, Ле Корбюзье (Шарль-Эдуар Жаннере-Гри), Леонардо да Винчи
- Золотое сечение
- История
- Пропорции золотого сечения
- Золотое сечение в математике
- Правило золотого сечения
- Метод золотого сечения
- Где можно увидеть золотое сечение
- Природа
- Человек
- Искусство
- Применение золотого сечения
- Второе золотое сечение
- Мифы о золотом сечении
МОСКВА, 16 ноя — РИА Новости. “Божественная гармония” или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве. Что такое ряд чисел Фибоначчи, принцип расчета и метод построения на основе пропорций – в материале РИА Новости.
Золотое сечение
“Определенные пропорции повсеместно используются в дизайне и архитектуре, фотографии и очень часто наблюдаются в естественной природе”, – говорит Ренат Мансуров, профессиональный фотограф, фотохудожник, лауреат и участник международных фотоконкурсов.
История
«
“Первым про золотое сечение писал еще Евклид в “Началах”, которые в свое время были вторые по популярности после Библии. Людям свойственно искать закономерности везде, даже там где их нет, поэтому число “фи” всегда было темой для религиозных спекуляций. Леонардо да Винчи, например, считал, что золотое сечение является выражением божественной сущности Троицы”, – комментирует Максим Господинко, диджитал-художник, дизайнер, основатель Spoils.
По словам эксперта, про эту пропорцию писал Ян Чихольд, использовал Малевич, Монферран построил по ней Исаакиевский собор.
“Но, как мне кажется, острое желание привязать всё мироздание к одному закону больше говорит о людях прошлого, чем о самом мире. Ум человека плохо переносит множественность, неточность моделей и просто хаос. Из этой особенности и происходит когнитивное “удобство”, когда порядок и закономерность всё-таки находятся”, – отмечает Максим Господинко.
«
“Впервые термин “золотое сечение” (“goldener Schnitt”) употребил в эпоху резкого роста европейской секуляризации в примечании ко второму изданию своей “Чистой элементарной математики” в 1835 году доктор философии Мартин Ом. Термин был известен ранее (из текста следует, что Ом не сам его придумал), и в дальнейшем быстро распространился в европейской литературе”, – поясняет Сергей Дементьев, эксперт сервиса meta-luxury недвижимости “Душа объекта”.
Эксперт отмечает, что до Ома это соотношение благодаря трактату монаха францисканца Луки Пачоли, изданному в соавторстве с Леонардо да Винчи, с 1509 года именовали в Европе “божественной пропорцией” (лат. “Divina Proportione”, итал. “Proporzione Divina”).
По мнению Сергея Дементьева, “божественная пропорция” (“золотое сечение”) как известная концепция красоты (еще древнегреческий скульптор Поликлет сформировал альтернативные правила красоты, а в 20-м веке модернист архитектор Ле Корбюзье разработал собственную систему пропорционирования) обязана своему появлению упадку веросознания: Эпоха Возрождения в Европе – именно историческая попытка Ренессанса веросознания в новых его формах через умозрение и затем деятельное воплощение в культуре (художественное творчество, архитектура, строительство, парковый, ландшафтный и интерьерный дизайн и т.д.).
Пионеры Возрождения Пачоли и Леонардо да Винчи (“Тайная вечеря” и “Мона Лиза” вписаны в геометрические фигуры) обратили свое внимание на античность, где еще в “Началах” Евклид (ок. 300 лет до нашей эры) говорил о делении отрезка в крайнем и среднем отношении (“ἄκρος καὶ μέσος λόγος”), полагая, что на числах построено все мироздание, на идеи Витрувия (ок. 80-70 гг. до нашей эры — после 13 г. до нашей эры), изложенные в “Десяти книгах об архитектуре” (лат. “De architectura libri decem”) о применении математики к искусству архитектуры.
Пропорции золотого сечения
О том, как высчитывать золотые пропорции, рассказал эксперт в сфере фотографии Ренат Мансуров.
“Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция”, – поясняет он. К слову, она равна всегда 1,618, и это так называемое число “фи” обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.
Ренат Мансуров отмечает, что в правильном прямоугольнике соотношение сторон соответствует золотому сечению.
“Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности”, – говорит Ренат Мансуров.
Золотое сечение в математике
Итальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.
“Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число – это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.”, – поясняет Ренат Мансуров.
0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.
А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.
Правило золотого сечения
На практике золотое сечение представляет собой пропорцию, соотношение сторон прямоугольника, отрезков определенной длины, других геометрических форм или сопряженных размерных характеристик реальных объектов.
Метод золотого сечения
“Если построить прямоугольник, используя метод, указанный выше, и встроить в этот прямоугольник линии, используя числа золотого сечения, то получится разграничение прямоугольника несколькими линиями. И если говорить о композиции, то размещая объекты на линиях или их пересечениях, можно максимально выделить эти объекты как смысловые центры, и наоборот, чем дальше от этих точек, тем труднее будет улавливать смысловой центр”, – поясняет Ренат Мансуров.
Если же совместить спираль Фибоначчи и эту сетку, то получится практически инструкция по использованию золотого сечения в фотографии, живописи и дизайне.
Где можно увидеть золотое сечение
Если разделить обычное куриное яйцо мысленно пополам в самой широкой его части, то получатся правильные золотые пропорции. Пропорции здания Парфенона в Греции, спирали раковин, пропорции тела человека, спиральные галактики и растения, и еще много всего вокруг.
Природа
«
По словам Рената Мансурова, примеров этих золотых чисел и спиралей найти в природе можно множество. “Распределение семян подсолнуха, спиральные раковины, спиральные галактики, соотношения пропорций человеческого тела, и например, если внимательно посмотреть на нераскрытую еловую шишку или ананас с торца, то можно увидеть эти спирали”, – отмечает эксперт.
Свою точку зрения озвучил Максим Господинко.
“У растения есть важная задача – наиболее оптимально расположить свои листья или лепестки, для того чтобы уловить больше солнечного света или просто уместить больше семян. В некоторых случаях есть возможность делать это только по плотной спирали (ананас, еловая шишка, подсолнечник). Кажется, что перед таким растением стоит сложная математическая задача – на какой угол сдвинуть следующую семечку или лепесток, но на самом деле вопрос лишь в том, насколько сильное создается отталкивание от уже существующего элемента.
И так складывается, что угол отклонения от предыдущего листка действительно очень близок к отношению “фи”, – комментирует эксперт. – Ни одно рациональное отношение не подходит, потому что при повороте под такими углами возникают колонны-лучи с большими дырами, а как мы знаем, семена подсолнечника уложены красивыми спиралями, число которых как раз соответствует числам из ряда Фибоначчи и дыр там никаких нет”.
По словам Максима Господинко, ряд Фибоначчи можно легко образовать, взяв ноль и единицу, а каждое последующее за ними получить из суммы двух предыдущих. “Моделировать растение конечно не умеет, насколько мне известно, и не знает количества рядов спиралей, а усилие отталкивания следующего элемента регулируется поколениями и естественным отбором, но в итоге приходит именно к “фи””, – отмечает специалист.

Названы знаменитости с идеальными пропорциями лица
Человек
Пропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:
- от плеч до макушки к размеру головы = 1:1.618
- от подбородка до верхней губы и от нее до носа = 1:1.618
- от пупка до макушки к отрезку от плеч до макушки = 1:1.618
- от пупка до колен и от колен до ступней = 1:1.618
Искусство

Пирамида Хеопса – единственное сохранившееся классическое чудо света
Множество произведений искусства и архитектурных шедевров сделаны по принципам золотого сечения. Египетские и пирамиды Майя, греческий Парфенон и так далее. Картины известных художников тоже выполнены с учетом правил золотого сечения.
Прослеживаются такие пропорции и в музыкальных произведениях Шуберта, Моцарта, Баха, Шопена и прочих.
“Для дизайнера и художника вопрос о золотом сечении стоит лишь в разрезе более широкой темы – пропорционирования. Не каждый использует этот инструмент, хоть и должен, но часто амбициозный художник, схватившись за “божественную истину”, начинает транслировать лишь её, упуская суть художественного высказывания, передачу образа. Пропорция – лишь инструмент и, очевидно, инструмент не должен идти вперёд задачи. Если образ не понят художником, его невозможно передать”, – говорит Максим Господинко. Но тем не менее, переоценить важность этой пропорции сложно. Часто чувствительный художник сам интуитивно может расположить элементы в соответствии с “фи”, также оно является достаточно простым инструментом, чтобы создать изящную композицию даже в самых простых вещах.
Примеры использования в живописи.
© Public DomainКартина Леонардо Да Винчи “Мона Лиза”

Картина Леонардо Да Винчи “Мона Лиза”
1 из 2
Репродукция картины “Девочка на шаре” 1905 г. работы Пабло Пикассо, выставленная в Государственном музее изобразительных искусств им. А.С. Пушкина.
2 из 2
Картина Леонардо Да Винчи “Мона Лиза”
1 из 2
Репродукция картины “Девочка на шаре” 1905 г. работы Пабло Пикассо, выставленная в Государственном музее изобразительных искусств им. А.С. Пушкина.
2 из 2
Примеры использования золотого сечения в дизайне логотипов.

Логотип социальной сети Twitter на экранах мобильного телефона и компьютера.
1 из 2

Логотип компании Apple на стене фирменного магазине на 5-й авеню в Нью-Йорке.
2 из 2
Логотип социальной сети Twitter на экранах мобильного телефона и компьютера.
1 из 2
Логотип компании Apple на стене фирменного магазине на 5-й авеню в Нью-Йорке.
2 из 2
Применение золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений и создании проекта дома, в современном дизайне интерьера при планировании и зонировании пространства, расстановки мебели и даже цветовом оформлении, а также в ландшафтном дизайне при выкладке закрученных дорожек, расположении растений на клумбах и других элементов.
Так, к примеру, при строительстве квартир и домов отношение самой большой комнаты к площади всей квартиры равно как 0,62 к 1, меньшее помещение делают с таким же соотношением к площади большей комнаты. Так, кухня – к меньшей комнате, прихожая к кухне, санузел к прихожей, а балкон – к санузлу.
Кроме того, с помощью золотого сечения подбирают и цветовое оформление. В интерьере применяют соотношение 10-30-60, основанное на золотом сечении. В пространстве используют три основных цвета: первый – доминирующий, охватывает 60% комнаты (стены и пол). Второй оттенок составляет 30% – мебель. И третий, 10%, приходится на декор.
«
“Существует множество вариантов золотого сечения. Но все они, так или иначе, основаны на числах Фибоначчи. Какие то из них популярны, какие то не очень, но о чем мы говорим сегодня, это то, что выработалось за последние столетия – это явно золотой стандарт, – говорит Ренат Мансуров. – Конечно, нужно понимать, что творчество остается творчеством и отходить от стандарта не возбраняется, но и совсем идти наперекор этим пропорциям не стоит”.
По мнению эксперта, теория золотого сечения и “божественных пропорций” довольно популярна, но наука не стоит на месте, и сейчас активно исследуются теории восприятия с научной точки зрения. “То, что работает на практике не одно столетие, однозначно должно напоминать каждый раз о том, что эти пропорции проверены временем и сотнями тысяч творческих людей: фотографы, художники, дизайнеры и архитекторы каждый день работают и используют золотые пропорции в своей работе.

Реальная Вавилонская башня и первая пирамида: самые старые строения в мире
Высчитывать миллиметры и микроны в надежде сделать ваше творчество золотым, наверное, не стоит, но и забывать о приятных для глаза пропорциях наверняка не нужно”, – говорит Ренат Мансуров.
Как это делать правильно, каждый решает самостоятельно, существует множество приемов композиции и работы с психологией восприятия, которые вместе могут улучшить работу в разы. “Учитесь правильно и не останавливайтесь в изучении художественных и композиционных приемов, и ваше творчество будет сиять оригинальностью и легкостью восприятия”, – советует Ренат Мансуров.
Второе золотое сечение
Второе золотое сечение вытекает из основного сечения и дает отношение 44: 56.
Максим Господинко отмечает, что золотое сечение – не единственная пропорция, приятная глазу человека, есть “серебряное сечение”. Две величины находятся в “серебряном сечении”, если отношение суммы меньшей и удвоенной большей величины к большей то же самое, что и отношение большей величины к меньшей. Также можно отметить, что порядок разлинованной в клетку тетради приятнее полного хаоса чистого листа (если не брать пропорцию самого его формата за порядок).
По словам эксперта, пропорция тетрадки в клетку ничем не хуже золотого сечения, но действие на человека она оказывает иное, как будто организуя простейший порядок – один к одному. “Если бы мы использовали такой поворот угла в подсолнухе, то получили бы одну линию семян, в случае с 1/4 – крест. Каждой задаче – свое решение. В случае с растениями им нужно как раз самое иррациональное число. Примечательно, что именно такое число и прослыло божественным”, – говорит Максим Господинко.
Мифы о золотом сечении
“Можно спекулировать на тему того, что где-то в глубине восприятия человека лежит именно закономерность ряда Фибоначчи, вероятно, где-то мы так же решали геометрическую задачу поворота на нужный угол по спирали, может быть, всё живое, так или иначе помнит этот опыт. Но чтобы не очаровываться золотым сечением чрезмерно, можно обратить внимание на любовь человека к зигзагам и орнаментам. Далеко не обязательно строить бабушкин ковёр по “фи”, чтобы на него было приятнее смотреть, чем на голую стену, – считает Максим Господинко. – Оказывается, этот вид визуального комфорта обусловлен строением визуального кортекса человеческого мозга, и такие орнаменты, как мы можем увидеть в традиционных культурах, ложатся в него как недостающий кусочек удобного паззла вместо хаотичного визуального потока внешней среды. Резной наличник лучше голых ставень. Кружева лучше минимализма. Природа лучше асфальта. Потому что экономят ресурсы человека, показывая привычные и близкие формы”.
Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.

Содержание
Экскурс в историю: кто придумал золотое сечение
Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:
- маленький отрезок – это сын;
- большой – отец;
- весь отрезок – это святой дух.
Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.
Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.
Божественная пропорция: что создано природой
Обратимся к природе, которая является безусловной и стремится к идеальному. В любом, созданном процессе, можно наблюдать эту магическую пропорцию 62:38. Придя к выводу, что гармоничное восприятие заложено в человеке от природы, ученые назвали это соотношение «Божественная пропорция».
Архимед выразил ее в спирали, повторяющей очертания раковины моллюска, подметив однажды ее идеальные формы. Божественная пропорция в архитектуре выражена с помощью сопоставления различных элементов здания и приведения их к одному целому, гармоничному для восприятия.
Действительно, обычно притягивает взгляд либо совершенство, либо уродство. И то и другое имеет одни корни. Совершенство – созданный по системе золотой пропорции идеал, и неважно, искусственный или природный источник использовался в его создании. Уродство же, напротив, привлекает полным несоответствием гармонии, что вынуждает подсознательно искать в нем заложенные природой прекрасные пропорции. И, если постараться, их можно найти. Этот феномен будоражит мозг, заставляя искать спокойной геометрии во всем.
Идеальные здания
В мире большое количество зданий, строений, памятников и произведений искусств, которые могут стать символом гармонии, заложенной природой. Идеальные золотые, божественные пропорции в архитектуре примеры сооружений показывают однозначно. Здания настолько гармоничны, что не возникает ни малейшего чувства дискомфорта при взгляде на них. Приведем несколько примеров.
Невероятной красоты Успенский собор Киево-Печерской лавры построен по принципу божественной пропорции. Стиль барокко гармонично сочетается с белоснежными стенами и золотыми куполами собора.

Еще пример — Петровский путевой дворец, созданный по проекту архитектора Матвея Казакова. Величественное сооружение было построено по приказу Екатерины II. Внутренний двор, два крыла и само здание подчиняется божественной пропорции.
Тадж-Махал… Дворец, единственный в своем роде памятник великой любви. Император Великих Моголов Шах Джахан подарил его своей покойной жене. Легенда о Тадж-Махале по-восточному красива и печальна.
Монументальные здания, с богатым художественным оформлением, занимающие не одну сотню метров, казалось бы, должны подавлять своими размерами и мощью. Тем не менее они радуют глаз, заставляют восхищаться и возвращаться к ним снова и снова.
Пропорции востока
Восток – мир, созданный по законам природы. Все, что относится к созданным произведениям искусства, четко придерживаются определенных правил, не отступая ни на шаг. Геометрия – конек восточного искусства. Знаменитый Тадж-Махал – индийский дворец из белого мрамора – имеет совершенные пропорции.
Убранство богатых домов, дворцов стран Востока также подчинено божественной пропорции. Арки, имеющие тройной поднимающийся свод, расположение окон, дверей и фасады главного дворцового входа – наглядно демонстрируют мастерство зодчих и художников. Сознательное или подсознательное использование пропорции в архитектуре и искусстве восточными мастерами, создало неповторимый восточный стиль, который отличается своей самобытностью и стремлением к природной гармонии.

Стили в архитектуре и интерьере
Использование пропорции в архитектуре и искусстве разных времен и народов привело к тому, что каждая последующая эпоха, беря основные элементы одного стиля, рождала свое неповторимое направление в искусстве. Золотое сечение наблюдается во всех достойных сооружениях своего времени, несмотря на то, что внешний вид элементов сильно разнится.
Греция
Страна, которая обладает богатым наследием архитектурных памятников, может дать много ответов на вопросы о золотом сечении. Пропорции в архитектуре Греции стремятся к идеальным. Одним из ярких примеров является храм Афины – Парфенон. Сооружение практически не имеет прямых линий, и соответствует золотому сечению, а пропорции скалы у его подножия также относятся к божественным.
Скульптуры и бюсты, созданные древнегреческими мастерами, имеют совершенные пропорции. Греческое искусство дает возможность понять, что человек, как творение божье, является идеально пропорциональной фигурой.
Викторианская эпоха
Английский Викторианский стиль опирается на учение о золотой пропорции. Стремление к уравновешенности и симметрии, использование четких линий в соотношениях тяжеловесности цвета и легкости форм предметов. Пропорции архитектуры в Средние века заимствуются для возведения сооружений и зданий в более позднее время. Фасады зданий, имеющие божественную пропорцию, стали распространены и в Викторианскую эпоху с ее стремлением к гармонии и статичности.
Неоготика XIX века
Этот стиль продолжает древние готические направления и предшествует Викторианской эпохе. Пропорции в архитектуре Неоготики 19 века подарили и своим последователям мрачные сводчатые, уходящие ввысь здания, которые повторяют такие же заостренные проемы окон и дверей. Расположение башен, порталов и сводов подвержено четкому сухому ритму числа 1,68…

Неоготика, соблюдая традиции готической архитектуры, все же становится менее темной. В ней, соблюдая божественные пропорции, соединяются разные стили и направления архитектуры, при этом сохраняя общую тематическую направленность. Сочетания круглых окон с уходящими вверх стрельчатыми сводами и башнями также подвержены золотому сечению, что составляет гармоничное восприятие всего сооружения в целом.
Золотая пропорция и религия
Большинство храмов, церквей, других религиозных строений имеют в основе своей золотое сечение. Божественные пропорции в архитектуре этих зданий можно объяснить и с теософской точки зрения. Монах Лука Пачоли в 1509 году усмотрел в геометрии гармонию, которую объяснил так: если целый отрезок будет принят как Святой дух, то отрезок поменьше – это Отец, а самый маленький – это Сын. Таким образом, в очередной раз подчеркивается влияния природной гармонии на восприятие мира человеком.
Принцип расчета и построения золотого сечения
Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.
Как определить число золотого сечения
С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:
- 0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
- если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.
Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.

Ряд Фибоначчи в церкви Покрова на Нерли
Как рассчитать золотое сечение на простейшем примере
Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.
Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.
Как построить золотое сечение на примере прямоугольника и спирали
Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:
- нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
- над ними разместить квадрат со стороной 2;
- слева гармонично помещается квадрат с гранью 3;
- ниже – квадрат со стороной 5;
- справа пространство займет квадрат с гранью 8;
- площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
- если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
- если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.
Принцип золотого сечения в прямоугольнике

Построение золотой спирали из прямоугольника
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Ничего особенного, но взгляд не оторвать. Знаете почему?
Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.

Деление отрезка на участки с идеальным соотношением
Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Витрувианский человек Леонардо
Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.
Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.

С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.
Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.
Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.
Исследования золотого сечения в 16-19 веках
Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.
В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.
Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.
Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.

Золотое сечение Фибоначчи. Божественная мера красоты
Давайте выясним, что общего между древнеегипетскими пирамидами, картиной Леонардо да Винчи «Мона Лиза», подсолнухом, улиткой, сосновой шишкой и пальцами человека? Ответ на этот вопрос сокрыт в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (род. ок. 1170 — умер после 1228), итальянский математик.
Давайте выясним, что общего между древнеегипетскими пирамидами, картиной Леонардо да Винчи «Мона Лиза», подсолнухом, улиткой, сосновой шишкой и пальцами человека?

Ответ на этот вопрос сокрыт в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (род. ок. 1170 — умер после 1228), итальянский математик. Путешествуя по Востоку, познакомился с достижениями арабской математики; способствовал передаче их на Запад.
После его открытия числа эти так и стали называться именем известного математика. Удивительная суть последовательности чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.
Итак, числа, образующие последовательность:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
называются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи.
В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то пpевосходящая, то не достигающая его. (Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично)
Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряда… Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)
Итак, Золотая пропорция = 1 : 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
Тело человека и золотое сечение

Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону Золотой пропорции.
Самая главная книга всех современных архитекторов справочник Э.Нойферта «Строительное проектирование» содержит основные расчеты параметров туловища человека, заключающие в себе золотую пропорцию.
Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы:
M/m=1,618
Первый пример золотого сечения в строении тела человека:
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.
Кроме этого есть и еще несколько основных золотых пропорции нашего тела:
- расстояние от кончиков пальцев до запястья до локтя равно 1:1.618;
- расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618;
- расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618;
- расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618;
- расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618;
- расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;
- расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618:

Золотое сечение в чертах лица человека как критерий совершенной красоты.
В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.
К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.
На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:
- Высота лица / ширина лица;
- Центральная точка соединения губ до основания носа / длина носа;
- Высота лица / расстояние от кончика подбородка до центральной точки соединения губ;
- Ширина рта / ширина носа;
- Ширина носа / расстояние между ноздрями;
- Расстояние между зрачками / расстояние между бровями.
Рука человека
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.
- Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца);
- Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения;
- У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи:
Золотая пропорция в строении легких человека
Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.
Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.
- Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.
Золотое сечение в архитектуре
Множество построек древности, которые сохранились до сих пор, служат подтверждением тому, что архитекторы из эпохи средневековья были знакомы с гармоническим правилом. Очень хорошо заметно стремление соблюсти гармоническую пропорцию при сооружении церквей, значимых общественных зданий, резиденций королевских особ.

К примеру, собор Парижской Богоматери возведен таким образом, что многие из его участков соотносится с правилом золотого сечения. Можно найти немало произведений архитектуры 18 века, которые были построены в согласии с этим правилом. Правило применяли и многие русские архитекторы. Среди них был и М. Казаков, который создавал проекты усадеб и жилых зданий. Он проектировал здание сената и Голицынскую больницу.
Естественно, дома с таким отношением частей возводили и до открытия правила золотого сечения. Например, к таким зданиям относится церковь Покрова на Нерли. Красота здания приобретает еще большую загадочность, если учесть, что здание покровской церкви было возведено в XVIII веке. Однако современный вид постройка приобрела после реставрации.

В трудах о золотом сечении упоминается, что в архитектуре восприятие объектов зависит от того, кто наблюдает. Пропорции, образованные при помощи золотого сечения, дают максимально спокойное соотношение частей строения относительно друг друга.
Ярким представителем из ряда строений, соответствующих универсальному правилу, является памятник архитектуры Парфенон, возведенный еще в пятом веке до н. э. Парфенон устроен с восьмью колоннами по меньшим фасадам и с семнадцатью – по большим. Храм возведен из благородного мрамора. Благодаря этому использование раскраски ограничено. Высота строения относится к его длине 0,618. Если разделить Парфенон по пропорциям золотого сечения, получатся определенные выступы фасада.
Все эти сооружения имеют одно сходство – гармоничность сочетания форм и отменное качество строительства. Это объясняется использованием гармонического правила.
Использование золотого сечения в дизайне
Принципы использования универсальной пропорции все чаще используют при строительстве частных домов. Особое внимание уделяется соблюдению оптимальных пропорций конструкции. Немало внимания уделяют правильному распределению внимания внутри дома.
Современная интерпретация золотого сечения уже не относится лишь к правилам геометрии и формы. Сегодня принципу гармонических пропорций подчиняются не только размеры деталей фасада, площадь комнат или длины фронтонов, но и цветовая палитра, используемая при создании интерьера.

Соорудить гармоничное строение на модульном основании гораздо проще. Многие отделения и помещения в этом случае выполняются как отдельные блоки. Они проектируются в строгом соответствии с гармоническим правилом. Возвести здание как набор отдельных модулей, значительной проще, чем создавать единую коробку.
Многие фирмы, занимающиеся сооружением загородных домов, при создании проекта соблюдают гармоническое правило. Это позволяет создать у клиентов впечатление, что конструкция здания детально проработана. Такие дома обычно описывают, как наиболее гармоничные и комфортные в использовании. При оптимальном выборе площадей комнат жильцы психологически ощущают успокоение.

Если дом возведен без учета гармонических пропорций, можно создать планировку, которая будет по соотношению размеров стен приближена к показателю 1:1,61. Для этого в комнатах устанавливают дополнительные перегородки, или переставляют предметы мебели.
Аналогично меняют габариты дверей и окон таким образом, чтобы проем имел ширину, показатель которой меньше значения высоты в 1,61 раза.
Сложнее подбирать цветовые решения. В этом случае можно соблюдать упрощенное значение золотого сечения – 2/3. Основным цветовым фоном следует занять 60% пространства комнаты. Оттеняющий оттенок занимает 30% помещения. Оставшаяся площадь поверхностей закрашивается близкими друг к другу тонами, усиливающими восприятие выбранного цвета.

Внутренние стены комнат делят горизонтальной полосой. Ее располагают в 70 см от пола. Высота мебели должна находиться в гармоническом соотношении с высотой стен. Это правило относится и к распределению длин. К примеру, диван должен иметь габариты, которые бы оказались не меньше 2/3 длины простенка. Площадь помещения, которая занята предметами мебели, тоже должна иметь определенное значение. Она относится к общей площади всего помещения как 1:1,61.
Золотая пропорция сложно применима на практике ввиду наличия всего одного числа. Именно поэтому. Проектирую гармоничные строения, пользуются рядом чисел Фибоначчи. Благодаря этому обеспечивается разнообразие вариантов форм и пропорций деталей строения. Ряд чисел Фибоначчи также носит название золотого. Все значения строго соответствуют определенной математической зависимости.

Кроме ряда Фибоначчи, в современной архитектуре применяют и другой метод проектирования – принцип, заложенный французским архитектором Ле Корбюзье. При выборе этого способа отправной единицей измерения выступает рост владельца дома. Исходя из этого показателя рассчитывают размеры здания и внутренних помещений. Благодаря этому подходу дом получается не только гармоничным, но и приобретает индивидуальность.
Любой интерьер приобретет более завершенный вид, если в нем использовать карнизы. При использовании универсальных пропорций можно вычислить его размер. Оптимальными показателями являются 22,5, 14 и 8,5 см. Устанавливать карниз следует по правилам золотого сечения. Маленькая сторона декоративного элемента должна относиться к большей так, как относится к сложенным значениям двух сторон. Если большая сторона будет равна 14 см, то маленькую стоит сделать 8,5 см.
Придать помещению уюта можно путем деления стеновых поверхностей при помощи гипсовых зеркал. Если стена поделена бордюром, от оставшейся большей части стены следует отнять высоту карнизной планки. Для создания зеркала оптимальной длины от бордюра и карниза следует отступить одинаковое расстояние.

Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

Правило треугольника в садовом дизайне
От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.

Пример подбора цвета по правилам правильной пропорциональности
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Пропорциональность — важная вещь
Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Важность золотого сечения для человека
Архитектура древних построек и средневековых домов довольно интересна и для дизайнеров современности. Это объясняется такими причинами:
- Благодаря оригинальному оформлению домов можно не допустить надоевших штампов. Каждое такое здание является архитектурным шедевром.
- Массовое применение правила для украшения скульптур и статуй.
- Благодаря соблюдению гармонических пропорций взгляд притягивается к более важным деталям.

Важно! При создании проекта постройки и создании внешнего облика архитекторы средневековья применяли универсальные пропорции, опираясь на закономерности человеческого восприятия.
Сегодня психологи пришли к выводу, что принцип золотого сечения – не что иное, как человеческая реакция на определенное соотношение размеров и форм. В одном эксперименте группе испытуемых предложили согнуть бумажный лист таким образом, чтобы стороны получились с оптимальными пропорциями. В 85 результатах из 100 люди сгибали лист практически в точном соответствии с гармоническим правилом.

Как утверждают современные ученые, показатели золотого сечения относятся скорее к сфере психологии, нежели характеризуют закономерности физического мира. Это объясняет, почему к нему проявляется такой интерес со стороны мистификаторов. Однако при построении объектов согласно этому правилу человек воспринимает их более комфортно.
Применение золотого сечения в кибернетике и технике
Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.
Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.
Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.
Современные исследования теории о золотой пропорции
Начиная с середины 20 века, интерес к проблемам и влиянию закономерностей золотых пропорций на жизнь человека, резко возрастает, причем со стороны многих ученых различных профессий: математиков, исследователей этноса, биологов, философов, медицинских работников, экономистов, музыкантов и др.
В США с 1970-хгодов начинает выпускаться журнал The Fibonacci Quarterly, где публикуются работы на эту тему. В прессе появляются работы, в которых обобщенные правила золотого сечения и ряда Фибоначчи используют в различных отраслях знаний. Например, для кодирования информации, химических исследований, биологических и т.д.

Все это подтверждает выводы древних и современных ученых о том, что золотая пропорция многосторонне связана с фундаментальными вопросами науки и проявляется в симметрии многих творений и явлений окружающего нас мира.
Наблюдения за природой и попытки раскрыть тайны ее прекрасных созданий принесли немало открытый. Одно из них — золотое сечение. Это некоторая закономерность, которой подчиняется все, что мы называем красивым. Люди, животные, цветы, здания, галактики…
Содержание статьи
- 1 Что такое золотое сечение и как его понимать
- 2 Как построить прямоугольник с идеальными пропорциями
- 3 Как разделить отрезок по правилу золотого сечения
- 4 Идеальный треугольник и пентаграмма
- 5 Применение в строительстве
- 6 Золотое соотношение во внутреннем оформлении
- 7 Золотое сечение в ландшафтном дизайне
Что такое золотое сечение и как его понимать
Часто мы сталкиваемся с домами, предметами, строениями, растениями, которые нас чем-то завораживают. Люди издавна пытались понять, почему одно нам кажется красивым, другое нет, искали закономерности. И вроде нашли. Это некоторое соотношение частей, которое назвали золотым сечением.
О том, кто и когда придумал золотое сечение никто не знает точно. Кто-то приписывает открытие Пифагору, но первое упоминание нашли еще в «Началах» Евклида, а жил он в 3 веке до нашей эры. Так что находка явно давняя. Именно по этому принципу построены древнегреческие и римские храмы. Конечно, это могут быть совпадения, но очень уж странные и очень их много. Так что, скорее всего, они были в курсе идеальных пропорций.

Совершенно точно то, что Леонардо да Винчи искал подтверждение этому принципу в строении человеческого тела. И, что самое интересное, нашел. Те лица и тела, которые кажутся нам красивыми, имеют пропорции, которые как раз и подчиняются закону золотого сечения.
Формальное определение звучит и просто, и сложно. Его связывают с двумя разными по размеру отрезками. Звучит этот принцип примерно так: если отрезок разделить на две неравные части, то это деление будет пропорциональным, если большая часть отрезка относится к целому так же, как и меньшая часть к большему. Будет понятнее, если посмотреть на иллюстрацию и формулу.

На рисунке целый отрезок разделен так, что если а разделить на b, получим 1,1618, та же цифра получается, если целый отрезок разделить на большую часть — a. Это число и есть воплощением идеальной пропорции. Теперь, если посмотрите на картинку с Парфеноном, пропорции этого строения также подчиняются указанному соотношению.
Ту же закономерность можно представить в виде процентов. Может, кому-то так проще. Для того, чтобы деление целого было пропорциональным, части должны составлять 62% и 38%. Возможно, так будет проще запомнить.

Эту закономерность развил дальше математик Фибоначчи. Он разработал числовую последовательность, элементы которой, начиная с девятого, подчиняются тому же закону. Графическое изображение этой последовательности — спираль. Если присмотреться, и в природе, и в архитектуре, и в человеческом теле пропорции красоты присутствуют.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.

Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).

Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как разделить отрезок по правилу золотого сечения
Это умение пригодится, например, при создании проекта дома, планировки, при разработке дизайна квартиры, расстановке мебели и т.д. Точно также может понадобиться при планировке участка, клумб, высадке растений и т.д. В общем, применяться может практически везде.

Итак, порядок деления отрезка по правилу золотого сечения:
- Берем отрезок, делим его пополам.
- Из одного из концов восстанавливаем перпендикуляр (прямая под углом 90°), который длиной равен половине отрезка. На рисунке это отрезок BC.
- Полученную точку C соединяем прямой с другим концом отрезка (A).
- На отрезке AC ставим точку D. Она находится на расстоянии, равном длине отрезка BС. Проще всего это сделать при помощи циркуля, но можно и линейкой.
- Замеряем длину отрезка AD (снова циркулем, либо линейкой). Такую же длину откладываем на отрезке AB. Получаем точку E.
- Теперь, если измерить длины отрезков AE и EB и разделить их, получим то самое заветное число — 1,62.

Пару раз повторив процедуру, вы научитесь делать все буквально за считанные минуты. Если же вам надо, например, определить высоту окна, его форму, также можно воспользоваться данными пропорциями. По тому же принципу можно определять местоположение всех архитектурных элементов, их размеры. При планировании уже имеющихся объектов, деление проще проводить при помощи процентного соотношения. Тут уже либо считаете в уме, либо используете калькулятор.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
https://youtu.be/c3SVIQBXMnA
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.

Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно. Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Золотое соотношение во внутреннем оформлении
Что еще дает золотое сечение кроме визуального наслаждения? Психологи говорят, что в интерьере, созданном по этому правилу человек чувствует себя более комфортно. Это, конечно, субъективно, но можно попробовать. Итак, вот как интерпретируют правило золотого сечения в дизайне интерьеров:
- Если вы собираетесь разделить комнату на зоны, воспользуйтесь правилом. Это значит, что одна из частей должна быть около 62%, вторая — 38%.
- Площадь, занятая предметами мебели, не должна быть больше чем 2/3.
- При подборе мебели руководствуемся правилом: каждый средний предмет по габаритам относится к крупным так же, как маленький к средним.
- При выборе цвета придерживайтесь примерно тех же правил:
- Основной цвет составляет порядка 2/3, все дополнительные и акцентный — 1/3. Цвета выбирают сочетающиеся по определенным правилам.
- Второй вариант: 60% — основной цвет, 30% дополнительные и 10% — это акцентные.

Пример подбора цвета по правилам правильной пропорциональности
- При использовании горизонтального деления стены (панели), высоту панели можно брать 1/3 или 2/3 от общей высоты комнаты. Но при этом мебель подбирается пропорциональной по высоте, а не по длине.
Относительно мебели правило кажется непонятным, но это только на первый взгляд. Например, подбираем группу отдыха. Крупный предмет в этом случае — диван или софа. Средний — журнальный или кофейный столик, кресла. Мелкие — аксессуары. Так вот, размеры журнального столика не должны быть больше длинной стороны дивана, кресла — не больше его короткой стороны. Аксессуары по размерам не больше размеров столика или кресел. В идеале, они соотносятся с ними как 62% и 38%.

Почему не указывается точное соотношение? Потому что, во-первых, найти такие предметы нереально. Во-вторых, золотое сечение — это не только 62% и 38%. Это еще и последовательность Фибоначчи, следование которой также делает оформление гармоничным. Есть люди, у которых следование этой последовательности является «встроенной функцией». Им не надо считать, они выбирают основываясь на чутье и интуиции. Но если проанализировать их выбор, пропорции будут близки к идеальным. Вот так.
Золотое сечение в ландшафтном дизайне
При создании ландшафта на участке, принцип идеальных пропорций применяют, называя его правилом треугольника. В композиции должна быть одна доминанта, остальные ее составляющие лишь подчеркивают, оттеняют ее. Например, на участке есть большое дерево и вы хотите его обыграть. Оно и будет центром композиции — доминантой. Нанесите его на план, расчертите клумбу или рокарий, альпинарий — то, что хотите сделать.

От главенствующего растения или камня, под прямым углом проведите две линии. На этих линиях надо будет высадить более низкие растения. Причем второе по высоте не должно быть выше чем 2/3 от высоты основного объекта. Третий объект — не выше чем 1/3. Дополняют композицию еще более низкорослыми насаждениями. Это коротко о том, как применять золотое сечение в планировке посадок.
Но это не все. Растения надо подбирать по цветам — сочетание зелени разных оттенков, вкрапления цветов и декоративно-лиственных растений — все подчиняется тому же закону. Доминирующий оттенок составляет порядка 60%, дополнительные цвета — 30%, акценты — 10 %. Это если говорить о правилах подбора в одной группе. Но также надо согласовывать и весь план целиком — по размерам, высоте, цветам.
Скачать: |pdf| |doc|


Шкруднев Фёдор Дмитриевич
В своих работах Фёдор Дмитриевич обращает внимание на феномен золотого сечения, который был незаслуженно забыт современной наукой. Однако в изучении природных объектов, развивающихся по законам золотого сечения и симметрии, по-прежнему скрывается источник новых научных идей и открытий.
***
Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией.
Великий русский кристаллограф Г. В. Вульф (1863–1925) считал золотое сечение одним из проявлений симметрии.
Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии. Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.
Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи. Он много путешествовал по Востоку, познакомил Европу с арабскими цифрами. В 1202 г. вышел в свет его математический труд «Книга об абаке» (счётной доске), в котором были собраны все известные на то время задачи.
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.
Особенность последовательности чисел состоит в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13+ 21 = 34 и т. д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34:55=0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – даёт непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до без(с)конечности, когда меньший отрезок так относится к большему, как больший ко всему.
Например, длина каждого сустава пальца соотносится с длиной следующего сустава по пропорции Ф. Такое же соотношение проявляется во всех пальцах рук и ног. Эта связь как-то необычна, потому что один палец длиннее другого без всякой видимой закономерности, но это всё не случайно, как не случайно всё в теле человека. Расстояния на пальцах, отмеченные от А до В до С до D до Е, все соотносятся друг с другом по пропорции Ф, равно как и фаланги пальцев от F до G до H.
Взгляните на этот скелет лягушки (Рис. 1.) и посмотрите, как каждая косточка соответствует модели пропорции Ф точно так, как и в теле человека (Рис. 2.).
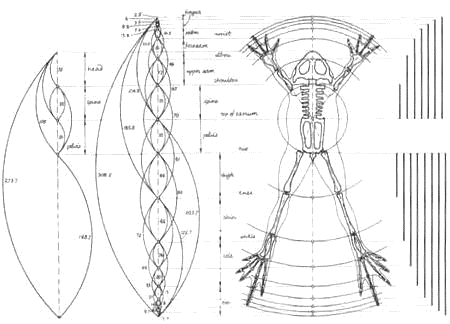
Рис. 1. Пропорция Ф
в скелете лягушки

Рис. 2. Пропорция Ф
в частях тела человека
Принципы формообразования в природе
Всё, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах: рост вверх или расстилание по поверхности земли и закручивание по спирали.
Раковина закручена по спирали. Если её развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали (Рис. 3.) очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал её и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение её шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике. Еще Гёте подчеркивал тенденцию природы к спиральности, называя спираль «кривой жизни». Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно.

Рис. 3. Спираль – одна из самых
распространенных форм в природе
Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т. д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филлотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетёт паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью.
Золотая спираль тесно связана с циклами. Современная наука о хаосе изучает простые циклические операции с обратной связью и порождённые ими фрактальные формы, неизвестные ранее.

Рис. 4. Фракталы Мандельброта
Рисунок показывает известный ряд Мандельброта (Рис. 4.) – страницу из словаря без(c)конечности индивидуальных паттернов, называемых юлианскими рядами. Некоторые учёные связывают формулу Мандельброта с генетическим кодом клеточных ядер. Последовательное увеличение сечений раскрывает изумительные по своей художественной сложности фракталы. И тут тоже присутствуют логарифмические спирали! Это тем более важно, что и ряд Мандельброта, и юлианские ряды не являются изобретением человеческого разума. Они возникают из области первообразов Платона. Как сказал Р. Пенроуз, «они подобны горе Эверест».
Среди придорожных трав растёт ничем, казалось бы, непримечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток (Рис. 5.). Тут же расположился первый листок.
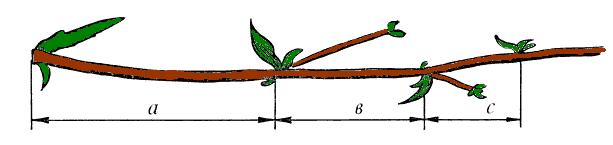
Рис. 5. Пропорции «золотого сечения»
у растений
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок ещё меньшего размера и снова выброс.
Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т. д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определённые пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
У многих бабочек соотношение размеров грудной и брюшной частей тела отвечает золотой пропорции (Рис. 6.). Сложив крылья, ночная бабочка образует правильный равносторонний треугольник. Но стоит развести крылья, и вы увидите тот же принцип членения тела на 2, 3, 5, 8. Стрекоза также создана по законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

Рис. 6. Закономерности «золотой» пропорции
проявляются в пропорциях насекомых
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина её хвоста так относится к длине остального тела, как 62 к 38.
Иначе говоря, и в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого. Большой интерес представляет исследование форм птичьих яиц (Рис. 7.). Их всевозможные формы колеблются между двумя крайними типами: один из них может быть вписан в прямоугольник золотого сечения, другой в прямоугольник с модулем 1,272 (квадратный корень золотой пропорции).
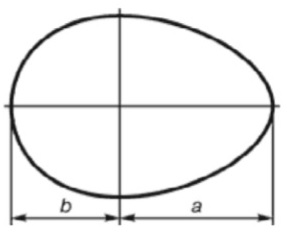
Рис. 7. «Золотое сечение»
присутствует и в форме яйца
Такие формы птичьих яиц не являются случайными, поскольку в настоящее время установлено, что форме яиц, описываемых отношением золотого сечения, отвечают более высокие прочностные характеристики оболочки яйца.
Бивни слонов и вымерших мамонтов, когти львов, и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль. В живой природе широко распространены формы, основанные на «пентагональной» симметрии (морские звёзды, морские ежи, цветы).
Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда, без исключений, построены по совершенной чёткой формуле золотого сечения.
В микромире трёхмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трёхмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов – вирус Адено (Рис. 8.). Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы, и из этих углов простираются шипообразные структуры.
Рис. 8. Вирус Адено
Впервые золотое сечение в строении вирусов обнаружили в 1950-хх годах ученые из Лондонского Биркбекского Колледжа А. Клуг и Д. Каспар. Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino.
Возникает вопрос: каким образом вирусы образуют столь сложные трёхмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А. Клюг даёт такой комментарий: «Доктор Каспар и я показали, что для сферической оболочки вируса самой оптимальной формой является симметрия типа формы икосаэдра. Такой порядок сводит к минимуму число связующих элементов… Большая часть геодезических полусферических кубов Букминстера Фуллера построены по аналогичному геометрическому принципу. Монтаж таких кубов требует чрезвычайно точной и подробной схемы-разъяснения, тогда как бессознательные вирусы сами сооружают себе столь сложную оболочку из эластичных, гибких белковых клеточных единиц».
Рис. 9. Сложная структура фуллерена
из белковых молекул
Комментарий А. Клюга ещё раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который учёные классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует чёткий замысел и осуществлён разумный проект. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру, проектами, созданными гениальным архитектором Букминстером Фуллером.
Трёхмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.
Радиолярии формируют своё тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр, причём из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.
Великий Гёте, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввёл в научный обиход термин морфология. Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.
Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
Тело человека и золотое сечение
Все кости человека выдержаны в пропорции золотого сечения. Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными (Рис. 10.).
Если принять центром человеческого тела точку пупа, а расстояние между ступнёй человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1,618:
• расстояние от уровня плеча до макушки головы и размера головы равно 1 : 1,618;
• расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1 : 1 ,618;
• расстояние точки пупа до коленей и от коленей до ступней равно 1 : 1,618;
• расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1 : 1,618;
• собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора;
• расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1 : 1,618;
• расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1 : 1,618.
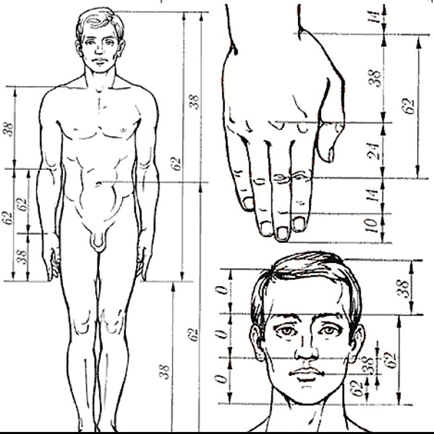
Рис. 10. Тело человека
и золотое сечение
Высота лица/ширина лица:
• центральная точка соединения губ до основания носа/длина носа;
• высота лица/расстояние от кончика подбородка до центральной точки соединения губ;
• ширина рта/ширина носа;
• ширина носа/расстояние между ноздрями;
• расстояние между зрачками/расстояние между бровями.
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдёте в нём формулу золотого сечения.
Каждый палец нашей руки состоит из трёх фаланг. Сумма длины двух первых фаланг пальца в соотношении со всей длиной пальца и даёт число золотого сечения (за исключением большого пальца). Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.
У человека две руки, пальцы на каждой руке состоят из трёх фаланг (за исключением большого пальца). На каждой руке имеется по пять пальцев, то есть всего 10, но за исключением двух фаланговых больших пальцев только восемь пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 – есть числа последовательности Фибоначчи.
Также следует отметить тот факт, что у большинства людей расстояние между концами расставленных рук равно росту.
Истины золотого сечения внутри нас и в нашем пространстве. Особенность бронхов, составляющих лёгкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче. Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причём соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1 : 1,618.
Во внутреннем ухе человека имеется орган Cochlea («Улитка») (Рис. 11.), который исполняет функцию передачи звуковой вибрации. Эта костевидная структура наполнена жидкостью и также сотворена в форме улитки, содержащую в себе стабильную логарифмическую форму спирали =73°43’.
Рис. 11. Орган Cochlea
во внутреннем ухе человека
Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке сердца в момент его сжатия (систолы). В артериях во время систолы желудочков сердца кровяное давление достигает максимальной величины, равной 115–125 мм ртутного столбца у молодого, здорового человека.
В момент расслабления сердечной мышцы (диастола) давление уменьшается до 70–80 мм рт. ст. Отношение максимального (систолического) к минимальному (диастолическому) давлению равно в среднем 1,6, то есть близко к золотой пропорции.
Если взять за единицу среднее давление крови в аорте, то систолическое давление крови в аорте составляет 0,382, а диастолическое 0,618, то есть их отношение соответствует золотой пропорции. Это означает, что работа сердца в отношении временных циклов и изменения давления крови оптимизированы по одному и тому же принципу закону золотой пропорции.
Молекула ДНК состоит из двух вертикально переплетённых между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем – одна стомиллионная доля сантиметра). Так вот 21 и 34 – это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины, и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1 : 1,618.
Рис. 12. Схематичный участок спирали ДНК
Оптимальные физические параметры
внешней среды
Известно, что максимальная громкость звука, которая вызывает болевые ощущения, равна 130 децибелам. Если разделить этот интервал золотой пропорцией 1,618, то получим 80 децибел, которые характерны для громкости человеческого крика. Если теперь 80 децибел разделить золотой пропорцией, то получим 50 децибел, что соответствует громкости человеческой речи. Наконец, если разделить 50 децибел квадратом золотой пропорции 2,618, то получим 20 децибел, что соответствует шёпоту человека. Таким образом, все характерные параметры громкости звука взаимосвязаны через золотую пропорцию.
При температуре 18–200°C интервал влажности 40–60 % считается оптимальным. Границы оптимального диапазона влажности могут быть получены, если абсолютную влажность 100% дважды разделить золотым сечением:100/2,618 = 38,2 % (нижняя граница); 100/1,618 = 61,8 % (верхняя граница).
При давлении воздуха 0,5 МПа у человека возникают неприятные ощущения, ухудшается его физическая и психологическая деятельность. При давлении 0,3–0,35 МПа разрешается только кратковременная работа, а при давлении 0,2 МПа разрешается работать не более 8 мин. Все эти характерные параметры связаны между собой золотой пропорцией: 0,5/1,618 = 0,31 МПа; 0,5/2,618 = 0,19 МПа.
Граничными параметрами температуры наружного воздуха, в пределах которых возможно нормальное существование (а, главное, стало возможным происхождение) человека является диапазон температур от 0 до +(57–58)°С. Очевидно, по первой границе пояснений можно не приводить.
Разделим указанный диапазон положительных температур золотым сечением. При этом получим две границы (обе границы являются характерными для организма человека температурами): первая соответствует температуре, вторая граница соответствует максимально возможной температуре наружного воздуха для организма человека.
Золотое сечение
и восприятие изображения
О способности зрительного анализатора человека выделять объекты, построенные по алгоритму золотого сечения, как красивые, привлекательные и гармоничные, известно давно. Золотое сечение даёт ощущение наиболее совершенного единого целого. Формат многих книг соответствует золотому сечению. Оно выбирается для окон, живописных полотен и конвертов, марок, визиток. Человек может ничего не знать о числе Ф, но в строении предметов, а также в последовательности событий он подсознательно находит элементы золотой пропорции.
Проводились исследования, в которых испытуемым предлагалось выбирать и копировать прямоугольники различных пропорций. На выбор предлагалось три прямоугольника: квадрат (40 : 40 мм), прямоугольник «золотого сечения» с отношением сторон 1 : 1,62 (31 : 50 мм) и прямоугольник с удлиненными пропорциями 1 : 2,31 (26 : 60 мм).
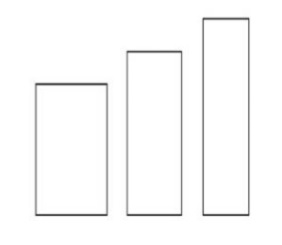
Рис. 13. Исследование восприятия «золотого сечения»
на примере прямоугольников разных пропорций
При выборе прямоугольников в обычном состоянии в 1/2 случаев предпочтение отдается квадрату. Правое полушарие предпочитает золотое сечение и отвергает вытянутый прямоугольник. Наоборот, левое полушарие тяготеет к удлиненным пропорциям и отвергает золотое сечение.
При копировании этих прямоугольников наблюдалось следующее: когда активно правое полушарие – пропорции в копиях выдерживались наиболее точно; при активности левого полушария – пропорции всех прямоугольников искажались, прямоугольники вытягивались (квадрат срисовывался как прямоугольник с отношением сторон 1 : 1,2; пропорции вытянутого прямоугольника резко увеличивались и достигали 1 : 2,8). Наиболее сильно искажались пропорции «золотого» прямоугольника; его пропорции в копиях становились пропорциями прямоугольника 1 : 2,08.
При рисовании собственных рисунков преобладают пропорции, близкие к золотому сечению, и вытянутые. В среднем пропорции составляют 1 : 2, при этом правое полушарие отдает предпочтение пропорциям золотого сечения, левое полушарие отходит от пропорций золотого сечения и вытягивает рисунок.
А теперь нарисуйте несколько прямоугольников, измерьте их стороны и найдите соотношение сторон. Какое полушарие у вас преобладает?
Золотое сечение и космос
Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда нашел закономерность и порядок в расстояниях между планетами солнечной системы.
Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Сосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти И. Тициуса в начале XIX в. Ряд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты – свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.
Две Золотых Спирали галактики совместимы со Звездой Давида (Рис. 14).
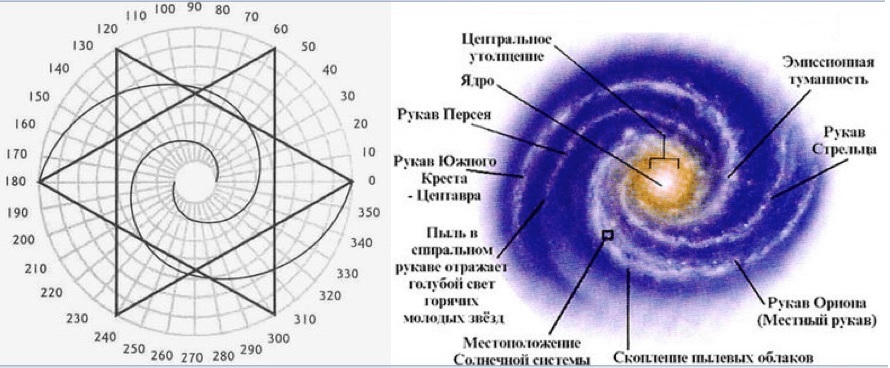
Рис. 14. Галактика в форме спирали,
соответствующей формуле золотого сечения
Обратите внимание на звёзды, выходящие из галактики по белой спирали. Точно на 1 800 от одной из спиралей выходит другая развёртывающаяся спираль… Долгое время астрономы просто считали, что всё, что там есть – это то, что мы видим; если что-то видимо, то оно существует. Они либо совершенно не замечали невидимой части Реальности, либо они не считали её важной. Но невидимая сторона нашей Реальности в действительности значительно больше видимой стороны и, вероятно, важнее… Иными словами, видимая часть Реальности значительно меньше, нежели один процент от целого – почти ничто. На самом деле, наш настоящий дом – невидимая вселенная…
Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения. В спирали нашей галактики лежит коэффициент золотого сечения.
Заключение
Природа, понимаемая как весь мир в многообразии его форм, состоит, как бы, из двух частей: живой и неживой природы. Для творений неживой природы характерна высокая устойчивость, слабая изменчивость, если судить в масштабах человеческой жизни. Человек рождается, живёт, стареет, умирает, а гранитные горы остаются такими же и планеты вращаются вокруг Солнца также, как и во времена Пифагора.
Мир живой природы предстает перед нами совсем иным – подвижным, изменчивым и удивительно разнообразным. Жизнь демонстрирует нам фантастический карнавал разнообразия и неповторимости творческих комбинаций! Мир неживой природы – это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир природы – это прежде всего мир гармонии, в которой действует «закон золотого сечения».
В современном мире наука приобретает особое значение, в связи с усилением воздействия человека на природу. Важными задачами на современном этапе являются поиск новых путей сосуществования человека и природы, изучение философских, социальных, экономических, образовательных и других проблем, стоящих перед обществом.
В данной работе было рассмотрено влияние свойств «золотого сечения» на живую и не живую природу, на исторический ход развития истории человечества и планеты в целом. Анализируя всё вышеизложенное можно ещё раз подивиться грандиозности процесса познания мира, открытием всё новых его закономерностей и сделать вывод:
Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.
Можно ожидать, что законы развития различных систем природы, законы роста не очень разнообразны и прослеживаются в самых различных образованьях. В этом и проявляется единство природы. Идея такого единства, основанная на проявлении одних и тех же закономерностей в разнородных явлениях природы, сохранила свою актуальность от Пифагора до наших дней.
| Октябрь 2019 г. | Ф. Д. Шкруднев |
Комментарий
Cтатья: «Золотое сечение и симметрия»
Размещена в Журнале «De Lapide Philosophorum»
Номер выпуска: № IV (020)
Дата выпуска: Октябрь, 2019 г.
Страница расположения статьи в журнале: 34 стр.
http://www.trinitas.ru/rus/doc/0001/005d/2355-dlp.pdf
В разделе IN BREVI
Журнала «De Lapide Philosophorum»
(Кратко изложена информация об авторе)
Фёдор Дмитриевич Шкруднев – офицер-подводник, профессиональный военный, жизнь которого неразрывно связана с Военно-морским флотом и служением Отчизне. Проходил службу на Северном флоте в разных должностях, с 1985 по 1988 год нес службу командиром крейсерской атомной подводной лодки К–369 11 флотилии атомных подводных лодок Северного флота. В 1991 году окончил Военно-морскую академию им. А. Кузнецова. Капитан первого ранга в запасе.
Награждён орденом «За службу Родине» III степени, медалями «За безупречную службу» I, II, III степеней, орденом Дружбы, международным орденом Святого Константина Великого.
Трудился в Администрации Президента РСФСР, полномочным представителем Президента РФ в Ленинградской области.
Член Военного Совета Северо-Западного пограничного округа, действительный член Санкт-Петербургской Инженерной Академии.
В феврале 1999 года основал общественно-политическое движение «Новый Союз». В марте 1999 года встретился с Президентом Республики Беларусь А. Г. Лукашенко и получил публичную поддержку движению «Новый Союз» по объединению Республики Беларусь и России в Союзное государство.
В 2002 году создал Русское Научно – Техническое Общество, в настоящее время является Председателем Президиума Общества.
***
Полностью статья «Золотое сечение»
Размещена на сайте автора: www.shkrudnev.com
