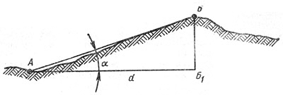
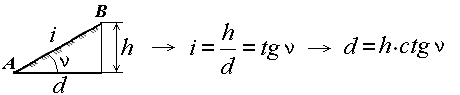Рельеф земной поверхности, его изображение. Крутизна ската. График заложений.
Совокупность
неровностей земной поверхности
называют рельефом. Рельеф
играет значительную роль в деятельности
человека. Его учитывают при проектировании
строительства, преобразуют в формы,
удобные для эксплуатации сооружения.
Правильное освоение и использование
территорий невозможно без учета рельефа.
На
топографических картах и планах рельеф
изображают горизонталями. Горизонталь —
это линия, соединяющая точки земной
поверхности с одинаковыми высотами. Понятие
о горизонтали можно получить, если
представить себе местность, затопленную
до заданной высоты. Береговая линия в
этом случае будет горизонталью. Изменяя
уровень воды (высоту уровенной
поверхности), получим горизонтали с
различными высотами.
Чтобы
правильно изобразить рельеф необходимо
знать его основные формы.
Крутизна
скатов.
О
крутизне ската можно судить по величине
заложений на карте. Чем меньше заложение
(расстояние между горизонталями), тем
круче скат. На рис. 12, а заложение
do больше d0,
поэтому скат первой линии круче.
Для
характеристики крутизны ската на
местности используют угол наклона u
(рис. 12.б). Чем больше угол наклона, тем
круче скат. Другой характеристикой
крутизны служит уклон.
Уклоном линии местности называют
отношение превышения к горизонтальному
проложению i=h/d=tgu. Из формулы следует,
что уклон безразмерная величина. Его
выражают в процентах % (сотых долях) или
в промилле %0 (тысячных
долях).
График
заложения предназначен для определения
крутизны скатов. TgV=h/d; d=h/tgv; h-высота
сечения
-
Высота
сечения рельефа на картах различных
маштабов.
Высота
сечения рельефа –
это разность высот двух смежных секущих
поверхностей (заданное расстояние между
секущими плоскостями).
На
карте она выражается разностью высот
двух смежных горизонталей. В пределах
листа карты высота сечения рельефа, как
правило, является постоянной. Высота
сечения может быть определена на
топографических картах как разность
высот между двумя соседними горизонталями.
На карте заложение можно определить
как расстояние между двумя смежными по
скату горизонталями (то есть расстояние
между двумя соседними горизонталями
является заложением).
Направление ската определяется как
перпендикуляр горизонтали, лежащей в
плоскости ската. Заложение всегда меньше
ската. Чем меньше заложение, тем больше
крутизна ската. Высота сечения на
топографической карте в данном масштабе
постоянна. При увеличении заложения
угол х уменьшается.
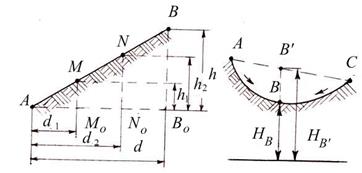
На
рисунке 2 показан вертикальный разрез
(профиль) ската. Через точки М, N, О
проведены уровенные поверхности на
расстоянии друг от друга, равном высоте
сечения h. Пересекая поверхность ската,
они образуют кривые линии, ортогональные
проекции которых в виде трех горизонталей
показаны в нижней части рисунка.
Рисунок
2. – Профиль ската:
h – высота сечения
рельефа; а – заложение горизонталей; α
– крутизна ската
Таблица
1. – Высота сечения рельефа в зависимостиот
характера местности
|
Местность |
Высота |
||||
|
1:25 000 |
1:50 000 |
1:100 000 |
1:200 000 |
1:500 000 |
|
|
Плоскоравнинная |
2,5 |
10 |
20 |
20 |
50 |
|
Плоскоравнинная |
5 |
10 |
20 |
20 |
50 |
|
Равнинная |
5 |
10 |
20 |
20 |
50 |
|
Предгорная |
5 |
10 |
20 |
40 |
100 |
|
Высокогорная |
10 |
20 |
40 |
40 |
100 |
Основная
высота сечения рельефа для карты масштаба
1:1 000 000 устанавливается в соответствии
с высотными поясами по следующей шкале:
от 100 м ниже уровня моря до 400 м над уровнем
моря – 50 м, от 400 до 1000 м – 100 м, выше 1000 м
– 200 м.
-
Проведение
(итерполирование) горизонталей.
Интерполяция
горизонталей — это проведение между
заданными на карте точками горизонталей
с одинаковыми высотами.
Интерполяцию
можно осуществить несколькими способами:
-
Визуально
(на глаз) -
Аналитический
(прямо пропорционально) -
Графический
(с помощью палетки)
Разберем
подробнее последний пункт.
Палетка представляет
собой систему параллельных линий
(масштабную сетку), проведенных на кальке
на равном расстоянии друг от друга
(обычно 2…5 мм). Выполняется интерполяция
в такой последовательности. Точки,
отметки уровней которых подлежат
интерполяции, соединяют вспомогательной
прямой линией(после
окончания работы линия может быть
стерта). Палетка накладывается
на одну из точек таким
образом, чтобы отметка на палетке и
отметка точки совпадали. Эта точка
фиксируется путем
прокола булавкой. Далее палетка
поворачивается вокруг
булавки до тех пор, пока отметка второй
точки не совпадет с отметкой на палетке. На
пересечении отрезка,
соединяющего точки с масштабной сеткой
палетки, находят искомые
точки.
-
Решение
задач по карте с горизонталями.(вопрос
большой)
Определение
крутизны ската. Крутизна ската
характеризуется углом наклона v, который
образует линия местности, напримерАВ,
с горизонтальной плоскостью Р (рис.
4.6).
Из
прямоугольного треугольника ABB’ следует:
tgν
= h/α, (4.1)
где h –
высота сечения рельефа, α – заложение.
Зная
тангенс, по таблицам значений
тригонометрических функций находят
значение угла наклона.
Крутизну
ската характеризуют также уклоном i
i =
tgα. (4.2)
Уклон
линии выражается в процентах или промилле
(‰), т. е. тысячных долях единицы.
Пример. Определить
угол наклона и уклон ската местности
между горизонталями на плане масштаба
1:1000, если заложение равно 20 мм, высота
сечения рельефа h = 1,0м.
На
местности заложению будет соответствовать
длина отрезка, равная ab = 20 мм ×
1000 = 20000 мм = 20 м. По формулам (4.1) и (4.2) tgν
= i = 1/20 = 0,05, откуда i = 5% = 50‰, a
ν = 2,9°.
Как
правило, при работе с картой или планом
угол наклона либо уклон ската определяют,
пользуясь графиками (рис. 4.7, а, б),
называемыми масштабами (или
шкалами) заложений.
Для
этого с плана раствором циркуля берут
заложение между двумя горизонталями
по данному скату, затем по графику
находят то место, где расстояние между
кривой и горизонтальной прямой равно
этому заложению. Для найденной таким
образом ординаты
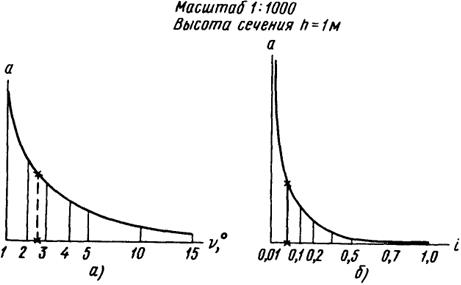
Рис.
4.7. Графики заложений к плану масштаба
1:1000 при высоте сечения рельефаh = 1
м:
а – для углов наклона, б –
уклонов
33

Рис.
4.8. Схемы а…г для определения
отметок точек по горизонталям
прочитывают
значение ν или i по горизонтальной
прямой (на приведенных графиках отмечено
звездочками: ν = 2,9°, i = 0,05 = 5%).
Определение
отметок точек местности. Если точка
расположена на горизонтали, ее отметка
равна отметке горизонтали. Когда точка
находится между горизонталями с разными
высотами, ее отметка определяется
интерполированием (нахождением
промежуточных значении величин) на глаз
между отметками этих горизонталей.
Интерполирование
заключается в определении коэффициента
пропорциональности расстояния d от
определяемой точки до меньшей по значению
горизонтали к величине заложения а,
т. е. отношения d/a, и умножения его на
значение высоты сечения рельефа h.
Пример. Отметка hk (рис.
4.8, а) точки К, расположенной между
горизонталями с отметками 150 м и 152,5 м,
равна HK = HМ.Г. + (d/a)h = 150 м +
0,4 + 0,25 = 151 м.
Если
определяемая точка расположена между
одноименными горизонталями – на седловине
(рис. 4.8, б) или внутри замкнутой
горизонтали на холме или котловине
(рис, 27, в, г), ее отметку можно определить
лишь приближенно, считая, что ее отметка
больше или меньше высоты этой горизонтали
на 0,5h. Например, на рисунке для седловины
отметка точки К равна 138,8, для холма
– 128,8 м, для котловины – 126,2 м.
Проведение
на карте линии заданного предельного
уклона (рис. 4.9). Между заданными на
карте точками А и В требуется
провести кратчайшую линию так, чтобы
ни один отрезок не имел уклона больше
заданного предельного iпред.
Проще
всего задача решается с помощью масштаба
заложения для уклонов. Взяв по нему
раствором циркуля заложение aпред,
соответствующее предельному уклону,
засекают последовательно точки 1…7 –
все горизонтали от точки А до
точки В. Если раствор циркуля меньше
расстояния между горизонталями, линию
проводят по кратчайшему направлению.
Соединив все точки, получают линию с
заданным предельным уклоном.

Рис.
4.9. Схема проведения на карте линии
заданного предельного уклона
34

Рис.
4.10. Схемы построения профиля по заданному
направлению
Если
нет масштаба заложений, заложение апред можно
подсчитать по формуле aпред = h/(iпредM,
где М – знаменатель числового
масштаба карты.
Построение
профиля местности по заданному на карте
направлению. Рассмотрим построение
профиля на конкретном примере (рис.
4.10). Пусть требуется построить профиль
местности по линии АВ. Для этого
линию АВ переносят в масштабе
карты на бумагу и отмечают на ней точки 1,
2, 4, 5, 7, 9, в которых она пересекает
горизонтали, а также характерные точки
рельефа (3, 6, 8). Линия АВ служит
основанием профиля. Взятые с карты
отметки точек откладывают на перпендикулярах
(ординатах) к основанию профиля в
масштабе, в 10 раз превышающем горизонтальный
масштаб. Полученные точки соединяют
плавной линией. Обычно ординаты профиля
уменьшают на одну и ту же величину, т.
е. строят профиль не от нуля высот, а
от условного горизонта УГ (на рис.
29 за условный горизонт принята высота,
равная 100 м).
С
помощью профиля можно установить
взаимную видимость между двумя точками,
для чего их нужно соединить прямой
линией. Если построить профили из одной
точки по нескольким направлениям, можно
нанести на карту или план участки
местности, не видимые с этой точки. Такие
участки называют полями невидимости.
Вычисление
объемов (рис. 4.11). По карте с горизонталями
можно вычислить объемы горы и котловины,
изображаемых системой горизонталей,
замыкающихся в пределах небольшой
площадки. Для этого формы рельефа делят
на части, ограниченные двумя соседними
горизонталями.

Рис.
4.11. Схема определения объема по карте
с горизонталями
Каждую
такую часть можно приближенно принять
за усеченный конус, объем которого
равен Vi = (1/2)(Si + Si+j)hсеч,
где Si и Si+1 – площади, ограниченные
на карте нижней и верхней горизонталями,
являющимися основаниями усеченного
конуса, hсеч – высота сечения
рельефа, i = 1, 2, …, k – текущий
номер усеченного конуса.
Площади S измеряют
планиметром (механическим или электронным).
Приближенно
площадь участка можно определить, деля
его на ряд правильных математических
фигур (трапеций, треугольников и т. п.)
и суммируя по площади. Объем VB самой
верхней части вычисляют как объем
конуса, площадь основания которого
равна SB а высота h – разности
отметок верхней точки t и горизонтали,
ограничивающей основание конуса: VB =
(SB/3)h.
Если
отметка точки t на карте не подписана,
то принимают h = hсеч/2.
Полный
объем вычисляют как сумму объемов
отдельных частей: V = V1 + V2 +
… + Vk + VB, где k – число частей.
-
Маштабы
(численный,линейный,нормальный
поперечный,) переходный поперечный
Точность маштаба карты.
На
рис. 3.1,а показаны линейные масштабы,
представляющие собой шкалы, разделенные
на равные отрезки, называемые основанием
масштаба; отрезки принимаются равными
1, 2 или 2,5 см, что должно соответствовать
круглому числу метров на местности (5,
10, 20, 50, 100, 200 м и т.д.). Первые слева основания
делятся на равные части. Подпись 0
ставится справа первого основания.
Остальные штрихи, обозначающие концы
оснований, надписываются в соответствии
с принятым численным масштабом плана.
Изображенные линейные масштабы построены
по численным масштабам 1:50000 и 1:100000.
Основание линейного масштаба в первом
случае равно 2 см, во втором – 1 см.
Наименьшие деления левых оснований при
подписанном значении 1000 м (1 км)
соответственно равны 500 м и 100 м.
При
пользовании линейным масштабом измеряемое
на плане расстояние берут в раствор
измерителя, затем одну из игл устанавливают
на штрих одного из оснований таким
образом, чтобы вторая игла располагалась
внутри крайнего левого основания.
Десятые доли наименьшего деления
оценивают на глаз.
Для
того, чтобы избежать оценки делений на
глаз и таким образом повысить точность
измерения и построения отрезков на
картах и планах, применяют номограмму,
построенную на основаниях линейного
масштаба и использующую метод
пропорционального клина. Такая номограмма
называется графическим масштабом длин
или поперечным масштабом (рис. 3.1,б).

численного, именованного и линейного
масштабов на картах (а) и поперечный
масштаб (б)
Рис.
3.1
На
рис. 3.1,б показан нормальный поперечный
масштаб с основанием 2 см. Если принять
численный масштаб 1:5000, то для удобства
пользования поперечным масштабом его
необходимо подписать. В данном случае
вдоль линии оснований и вправо и влево
от нуля – 100, 200, 300 и 400 м. Для определения
по этому масштабу длины линий берут в
раствор измерителя соответствующее
расстояние на плане, затем одну из игл
измерителя ставят на таком перпендикуляре,
чтобы вторая игла размещалась на
наклонной линии первого основания, при
этом обе иглы измерителя должны лежать
на одной горизонтальной линии.
Масштаб
плана выбирают в соответствии с размерами
объекта в натуре и руководствуются
точностью масштаба таким образом, чтобы
размеры объекта были на плане в 5-10 раз
больше 0,1 мм (разрешающая способность
человеческого глаза 0,1 мм). Например,
если отдельные детали строительных
объектов на площадке горного предприятия
имеют размеры порядка 1 м, то для их
отображения на плане возможен масштаб
1:2000 – 1:1000.
-
Способы
измерения площадей.
форм
применяются следующие способы определения
площадей: графический,
механический
и аналитический.
Графический
способцелесообразно
применять, когда измеряемый участок
имеет
более или менее правильную форму и
ограничен прямыми линиями. Такими
участками
обычно являются те, форма которых
определилась деятельностью
человека
(например, сельскохозяйственные угодия,
территории населенных пунктов
или
их частей, полосы отвода транспортных
магистралей и т.п.). Палетками выгодно
измерять
площади небольших участков, имеющих на
карте размеры не более 4-5
см2,
а также узкие, сильно вытянутые участки
(например, долины рек, полосы
отвода
транспортных магистралей и т.п.).
Механический
способнаходит
широкое применение при определении
площадей,
имеющих произвольную, часто весьма
неправильную конфигурацию,
таких,
например, как водосборные бассейны,
леса, болотные комплексы, рудные
поля
и т.п.
Аналитический
способопределения
площадей контуров и участков требует
измерений
линий и углов на местности. Его
целесообразно применять, если площадь
надо
получить с повышенной точностью и не
дожидаясь составления плана (карты).
Наиболее
точный – аналитический способ, так как
на точность определения
площади
при этом способе влияют только погрешности
измерений на местности, в
то
время как при графическом и механическом
способах, помимо погрешностей
измерений
на местности, влияют и погрешности:
составления плана (карты),
определения
площадей по плану и деформация бумаги.
Полярный
планиметр.
Планиметрами называются приборы для
измерения площадей. Наиболее распространён
полярный планиметр (рис. 4.11). Он состоит
из двух рычагов – полюсного 1 и обводного
4, соединяемых шарниром 8. Полюс планиметра
(массивный цилиндр 2 с иглой, втыкаемой
в бумагу) в процессе измерения площади
остается неподвижным. На конце длинного
плеча обводного рычага укреплен шпиль
3 (или лупа с маркой в виде креста в ее
центре), которым обводят контур измеряемой
площади. На коротком плече обводного
рычага крепится каретка с мерным
колесиком 6, опирающимся на поверхность
бумаги, и счетным механизмом. Когда
обводной шпиль 3 (или марка) перемещается
по линии контура перпендикулярно рычагу,
мерное колесико 6 катится по бумаге. При
перемещении обводного шпиля по направлению
рычага колесико скользит по бумаге, не
вращаясь. При перемещении шпиля в иных
направлениях происходит и вращение, и
скольжение. Суммарное число оборотов
колесика, накопленное при обводке шпилем
контура, пропорционально площади,
ограниченной контуром.
-
Графический
способ измерения площадей, (ответ в
вопросе 53) -
Аналитический
способ измерения площадей (ответ в
вопросе 53) -
Механический
способ измерения площадей(ответ в
вопросе 53) -
Поверки
и юстировка планиметра.
Перед
началом обмера проверяют правильность
работы механизмов планиметра. Счетное
колесо должно свободно вращаться на
своей оси и не задевать верньер. Барабан
счетного колеса расположен достаточно
близко к верньеру, но не касается его.
Ось счетного колеса также должна свободно
(без трения) вращаться.
-
Общие
сведения об измерениях.
-
Задачи
теории ошибок.Виды ошибок измерений.
Измерения
в геодезии рассматриваются с двух точек
зрения: количественной, выражающей
числовое значение измеренной величины,
и качественной, характеризующей ее
точность. Из практики известно, что даже
при самой тщательной и аккуратной работе
многократные (повторные) измерения не
дают одинаковых результатов. Это
указывает на то, что получаемые результаты
не являются точным значением измеряемой
величины, а несколько отклоняются от
него. Значение отклонения характеризует
точность измерений.
_При
геодезических измерениях неизбежны
ошибки. Эти ошибки
бывают грубые, систематические и случайные.
-
Грубые
ошибки.
К грубым
ошибкам относятся
просчеты в измерениях по причине
невнимательности наблюдателя или
неисправности прибора, и они полностью
должны быть исключены. Это достигается
путем повторного измерения.
-
Систематические
ошибки.
__Систематические
ошибки происходят
от неизвестного источника, имеют
определенный знак и величину и их можно
учесть при измерениях и вычислениях.
-
Случайные
ошибки .Свойства случайных ошибок.
лучайные
ошибки обусловлены разными причинами
и полностью исключить их из измерений
нельзя. Поэтому возникают две задачи:
как из результатов измерений получить
наиболее точную величину и как оценить
точность полученных результатов
измерений. Эти задачи решаются с помощью
теории ошибок измерений. _______
_______В
основу теории ошибок положены
следующие свойства
случайных ошибок:
_______1.
Малые
ошибки встречаются чаще, а большие
реже.
_______2.
Ошибки
не превышают известного предела.
_______3.
Положительные
и отрицательные ошибки, одинаковые по
абсолютной величине, одинаково часто
встречаются.
_______4.
Сумма
ошибок, деленная на число измерений,
стремится к нулю при большом числе
измерений.
_______По
источнику происхождения различают:
ошибки приборов, внешние и личные. Ошибки
приборов обусловлены
их несовершенством, например погрешность
угла, измеренного теодолитом, неточным
приведением в вертикальное положение
оси его вращения.
_______Внешние
ошибки происходят
из-за влияния внешней среды, в которой
протекают измерения, например погрешность
в отсчете по нивелирной рейке из-за
изменения температуры воздуха на пути
светового луча (рефракция) или нагрева
нивелира солнечными лучами.
_______Личные
ошибки связаны
с особенностями наблюдателя, например,
разные наблюдатели по-разному наводят
зрительную трубу на визирную цель. Так
как грубые погрешности должны быть
исключены из результатов измерений, а
систематические исключены или ослаблены
до минимально допустимого предела, то
проектирование измерений с необходимой
точностью и оценку результатов выполненных
измерений производят, основываясь на
свойствах случайных погрешностей.
-
Среднее
арифметическое значение измеренной
величины и его свойства.
Если
одна величина измерена n раз
и получены результаты: l1,
l2,
l3,
l4,
l5,
l6,…..,
ln,
то
_______Величина x называется арифметической
срединой или
вероятнейшим значением измеренной
величины. Разности между каждым измерением
и арифметической срединой называют
вероятнейшими ошибками измерений:
Или
в общем виде получим:
Тогда
[v] = 0.
-
Критерии
точности результатов измерений. (вопрос
большой)
-
Средняя
квадратиическая ошибка,вычисления по
формуле Гаусса, и ее преимущества по
сравнению с другими критериями точности
результатов измерений.
Для
правильного использования результатов
измерений необходимо знать, с какой
точностью, т. е. с какой степенью близости
к истинному значению измеряемой величины,
они получены. Характеристикой точности
отдельного измерения в теории ошибок
служит предложенная Гауссом средняя
квадратическая ошибка m,
вычисляемая по формуле

где п –
число измерений данной величины.
Эта
формула применима для случаев, когда
известно истинное значение измеряемой
величины. Такие случаи в практике
встречаются редко. В то же время из
измерений можно получить результат,
наиболее близкий к истинному значению,-
арифметическую средину. Для этого случая
средняя квадратическая ошибка одного
измерения подсчитывается по формуле
Бесселя

где
δ – отклонения отдельных значений
измеренной величины от арифметической
средины, называемые вероятнейшими ошибками,
причем [δ]=0.
Точность
арифметической средины, естественно,
будет выше точности отдельного измерения.
Ее средняя квадратическая ошибкаМ определяется
по формуле
М = m/√n(5.4)
где т –
средняя квадратическая ошибка одного
измерения, вычисляемая по формуле (5.2)
или (5.3).
Часто
в практике для контроля и повышения
точности определяемую величину измеряют
дважды – в прямом и обратном направлениях,
например, длину линий, превышения между
точками. Из двух полученных значений
за окончательное принимается среднее
из них. В этом случае средняя квадратическая
ошибка одного измерения подсчитывается
по формуле

а
средний результат из двух измерений –
по формуле
39

где d –
разность двукратно измеренных величин, п –
число разностей (двойных измерений).
В
соответствии с первым свойством случайных
ошибок для абсолютной величины случайной
ошибки при данных условиях измерений
существует допустимый предел,
называемый предельной ошибкой.
В строительных нормах предельная ошибка
называетсядопускаемым
отклонением.
-
Предельная
ошибка. Средняя ошибка v.Вероятная
ошибка r.
После
проведения отбора для определения
возможных границ генеральных характеристик
рассчитываются средняя и предельная
ошибки выборки.
Эти
два вида ошибок связаны следующим
соотношением:
Δ=tμ,
где
Δ – предельная ошибка выборки;
μ
– средняя ошибка выборки;
t –
коэффициент доверия, определяемый в
зависимости от уровня вероятности р.
Величина
средней ошибки выборки рассчитывается
дифференцированно в зависимости от
способа отбора и процедуры выборки.
Так, при случайном повторном отборе
средняя ошибка определяется по формуле:
µ
= s / √n
где:
s
– выборочное (или генеральное) среднее
квадратическое отклонение;
n
– объем выборочной совокупности.
Расчет
средней и предельной ошибок выборки
позволяет определить возможные пределы,
в которых будут находиться характеристики
генеральной совокупности. Например,
для выборочной средней такие пределы
устанавливаются на основе следующих
соотношений:
Формулу
подписать: Х с волной сверху – треугольник
и внизу подстрочное Х с волной Меньше
либо равно Х с волной Меньше либо равно
Х с волной плюс такой дже треугольник
с подстрочным Х с волной
где
х и ~ – генеральная и выборочная средняя
соответственно; х
–
предельная ошибка выборочной средней.
-
Относительная
ошибка.
Относительной ошибкой
называется отношение абсолютной
погрешности к значению самой измеренной
величины. Относительная ошибка выражается
в виде простой дроби, числитель которой
– единица, а знаменатель – число, округленное
до двух-трех значащих цифр с нулями.
Например, относительная средняя
квадратическая ошибка измерения линии
длиной l =
110 м при ml =
2 см равна ml/l=
1/5500, а относительная предельная ошибка
при ∆пред =
3m∆пред/l =
1/1800.
-
Средняя
квадратическая ошибка функций
непосредственно измеренных величин.
Если
мы имеем функцию суммы или разности
двух независимых величин
(18)
то
квадрат средней квадратической ошибки
функции выразится формулой:
(19)
При тх =
ту =
т
(20)
Пример.
Линия на плане масштаба 1:5000 измерена
по частям. Одна часть длиной 600,5 м, вторая
часть длиной 400,0 м. Найти средние
квадратические ошибки суммы и разности
этих длин и соответствующие им
относительные ошибки.
Ответ.
Средняя квадратическая_ошибка суммы и
разности двух длин будет тг =0,7
м, где т = 0,5-точность масштаба. Относительные
ошибки суммы и разности длин соответственно
равны
0,7/1000,5=1/1
400 и 0,7/200,5=1/300
Если
функция имеет вид
(21)
то
(22)
т.
е. квадрат средней квадратической ошибки
алгебраической суммы аргументов равен
сумме квадратов средних квадратиче-ских
ошибок слагаемых.
Если
m1 =
m2 =
m3 =
.. .
= mп=
m. то
формула (22) примет вид
(23)
т.
е. средняя квадратическая ошибка
алгебраической суммы (разности) измеренных
с одинаковой точностью величин в √п раз
больше средней квадратческой ошибки
одного слагаемого.
Пример.
В шестиугольнике каждый угол измерен
с одинаковой точностью 0,5′, средняя
квадратическая ошибка суммы всех
измеренных углов будет
(24)
то
(27)
-
Частные
случаи вычисления средних квадратических
ошибок рассмотренных функцый(будет
четыре вопроса по четырем рассмотренным
функциям).
Оценить
точность каких-либо измерений – это
значит определить на основе полученных
результатов сравнимые числовые
(количественные) характеристики,
выражающие качественную сторону самих
измерений и условий их проведения.
Количественные характеристики измерений
или критерии оценки точности измерений
устанавливаются теорией вероятности
и теорией ошибок (в частности, способом
наименьших квадратов). Согласно этим
теориям оценка точности результатов
измерений производится только по
случайным ошибкам. Показателями точности
измерений могут служить:
–
средняя квадратическая ошибка измерений;
–
относительная ошибка измерений;
–
предельная ошибка измерений.
Понятие
средней квадратичной ошибки введено
Гауссом, и в настоящее время она принята
в качестве основной характеристики
точности измерений в геодезии.
Средней
квадратичной ошибкой называется среднее
квадратичное значение из суммы квадратов
ошибок отдельных измерений. Для ее
вычисления используют либо истинные
ошибки измерений, либо уклонения
результатов измерений от среднего
арифметического.
Обозначим
истинное значение измеряемой величины
через X, результат измерения через li.
Истинными
ошибками измерений Δi называются
разности результатов измерений и
истинных значений, т. е.
Δi =
li –
X.
В
этом случае среднюю квадратичную ошибку
m отдельного результата вычисляют по
формуле
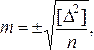
где
n – количество равноточных измерений.
Однако
в большинстве случаев практики, если
не считать редких случаев специальных
исследований, истинное значение
измеряемой величины и, следовательно,
истинные ошибки остаются неизвестными.
В этих случаях для нахождения окончательного
значения измеряемой величины и оценки
точности результатов измерений используют
принцип среднего арифметического.
Пусть l1,
l2,
…. ln результаты n равноточных
измерений одной и той же величины. Тогда
частное
называется
средним арифметическим из измеренных
значений этой величины.
Разность
каждого отдельного результата измерения
и среднего арифметического значения
называется уклонением результатов
измерений от среднего арифметического
и обозначается буквой v:
vi = li – .
-
Средняя
квадратическая ошибка среднего
арифметического значения измеренной
величины.
Точность
арифметической средины, естественно,
будет выше точности отдельного измерения.
Ее средняя квадратическая ошибкаМ определяется
по формуле
М = m/√n(5.4)
где т –
средняя квадратическая ошибка одного
измерения, вычисляемая по формуле
-
Формула
Бесселя.
-
Обработка
ряда равноточных измерений.
1.
Вычисляют среднее арифметическое L
.
2.
Вычисляют поправки к vi результатам
измерений
(i =
1, 2, …, n)
Контролем
правильности вычислений служит сумма
поправок, которая должна быть близка к
нулю.
3.
Вычисляют среднюю квадратическую
погрешность одного измерения по формуле
Бесселя:
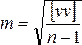
Значение m вычисляют
с двумя-тремя значащими цифрами.
4.
Вычисляют среднюю квадратическую
погрешность среднего арифметического
.
-
Принцип
измерения горизантального и вертикального
углов.
Рис.
8.1. Принцип измерения горизонтального
угла
Расположим
над вершиной измеряемого угла параллельно
горизонтальной плоскости градуированный
круг, центр которого совмещен с точкой
отвесной линии Вв (рис. 8.1). Тогда
угол b – измеряемый горизонтальный угол.
Деления на круге подписаны по ходу
часовой стрелки, а и с – отсчеты по
градуированной окружности круга,
горизонтальный угол b = а – с.
-
Конструктивная
схема теодолита.
(лекция
теод
-
Отчетные
устройства в теодолитах. -
Классификация
теодолитов по точности.
теодолит
предназначен для измерения горизонтальных
и вертикальных углов для измерения
расстояний для измерения ориентирных
углов. Приборы у которых горизонтальные
и вертикальные круги выполнены из
высокоточного стекла относятся к
оптическим теодолитам. По точности
теодолиты подразделяются:
1)
высокоточные Т-1
2)
точные Т2 и Т5
3)
технические Т15, Т30
4)
учебные Т60
Цифра
после буквы означает среднеквадратичную
погрешность измерения угла в секунду
полным приёмом. По устройству теодолиты
подразделяют на прямые и обратные. С
цилиндрическим уровнем и с компенсатором-
это устройство внутри прибора позволяющее
автоматически приводить ось прибора в
отвесное положение.
-
Уровни.
-
Цилиндрический
уровень. -
Круглый
уровень. -
Устройство
зрительной трубы. -
Зрительная
труба с внешним фокусированием.
Оптика
простейших зрительных труб состоит из
двух собирательных линз: объектива (1),
направленного на предмет, и окуляра (2).
Изображение всегда получается при
прохождении лучей через объектив,
действительным, обратным и уменьшенным.
Чтобы увеличить его, в трубу вводят
окуляр, действующий как лупа. Получаем
мнимое, увеличенное изображение.
Рис.
44. Зрительная труба: 1 – объектив; 2 –
окуляр; 3 – фокусирующая линза; 4 – сетка
нитей; 5 – кремальерный винт (кольцо)
Так
как при визировании на разные расстояния
изображение будет перемещаться, то для
получения ясного изображения необходимо,
чтобы окуляр мог перемещаться относительно
объектива вдоль оси трубы.
Новейшие
геодезические трубы снабжаются трубой
постоянной длины, в которой объектив и
сетка нитей закреплена в одной оправе.
Фокусирование производится при
помощи фокусирующей
линзы (3)
– рассеивающего стекла, перемещающегося
в трубе между объективом и сеткой
нити (4)
при вращении особого кремальерного
винта или
кольца (5), охватывающего зрительную
трубу около её окуляра.
-
Увеличение
зрительной трубы и способы его
определения. -
Поле
зрения зрительной трубы и способы
определения угла поля зрения зрительной
трубы. -
Эквивалентное
фокусное расстояние системы двух линз. -
Схема
зрительной трубы с внутренним
фокуссированием. Установка зрительной
трубы для наблюдений. Параллакс сетки
нитей. (См.лекции и лабараторные занятия).
используют
для наведения на марки и другие визирные
цели и для отсчитывания по рейкам.
Современные зрительные трубы являются
сложными оптико-механическими устройствами
и как минимум состоят из объектива,
окуляра, фокусирующей линзы и сетки
нитей. Как правило, они дают увеличенное
обратное изображение. Однако изготавливают
трубы, дающие прямое изображение, для
чего между окуляром и объективом помещают
оборачивающие системы, формирующие
совместно с окуляром прямое изображение.
1.67.
Схемы зрительной трубы с внутренним
фокусированием: а — устройство; б —
сетка нитей; в — ход лучей; 1 — объектив;
2 — головка фокусирующего устройства;
3 — фокусирующая линза; 4 — исправительные
винты сетки; 5 — стеклянная пластинка
сетки; 6 — окуляр
-
Исследования
теодолита.(Вопрос большой и будет разбит
на отдельные вопросы,см. лекции и
лабараторные занятия). -
Поверки
и юстировка теодолита.( Вопрос большой
и будет разбит на отдельные вопросы,см.
лекции и лабараторные занятия). -
Ошибки
влияющие на точность измерения
горизонтальных углов.(вопрос большой
будет разделен на отдельные вопросы).
-
Иструментальные
ошибки. -
Влияние
коллимационной ошибки на отсчет по
лимбу и на величину измеряемого угла. -
Влияние
угла наклона оси на врашения зрительной
трубы на отсчет по лимбу и на величину
измеренного угла. -
Влияние
эксцентриситета алидады горизонтального
круга на отсчет на лимба и на величину
измеренного угла. -
Влияние
рена шкалового микроскопа горизонтального
круга на отсчет по лимбу -
Влияние
внешних условий. (Вопрос большой и будет
разбит на отдельные вопросы) . -
Ошибка
редукции. -
Ошибка
центрирования. -
Влияние
ошибок за боковую рефракцию. -
Ошибка
собственно измерения угла.Точность
измерения горизонтального угла. -
Измерение
горизонтального угла теодолитом.Контроль
измерения угла. -
Устройство
вертикального угла. -
Определение
места нуля и измерение вертикальных
углов.Поверка постоянства место нуля
и пиведение его к нулю. -
Непосредственное
измерение расстояний.( Вопрос большой
и будет разбит на отдельные вопросы) -
Мерные
ленты и рулетки.Компарирование мерных
приборов.Закрепление и обозначение
пунктов -
Вешение
линий.Измерение длины линий мерной
лентой(рулеткой) и контроль
измерений.Приведение к горизонту длины
линии и точности измерений. -
Измерение
расстоний оптическими
дальномерами.(классификация дальномеров) -
Нитяный
дальномер у зрительной трубе с внешним
фокусированием -
Нитяный
дальномер у зрительной трубе с внутренним
фокусированием -
Определение
поправки «Р» для различных расстояний. -
Измерение
расстояний нитяным дальномером.
Приведение к горизонту расстоний
,измеренных нитяным дальномером.(См.конспект) -
Точность
измерения расстояний нитяным
дальномером(источники ошибок,точность
контроль меры по ослаблению влияния
источников ошибок.)
22
Содержание
- Высота сечения рельефа, заложение, уклон и их взаимосвязь
- Изображение рельефа способом горизонталей, высота сечения рельефа, заложение ската, уклоны и крутизна ската.
- Горизонтали и их свойства. Способы построения горизонталей
- По отметкам точек
- Способы построения горизонталей по отметкам точек.
- Решение инженерных задач по планам и картам
- Определение площадей по картам и планам
Высота сечения рельефа, заложение, уклон и их взаимосвязь
Билет 7.
Общие понятия о геодезических измерениях. Виды измерений
Вид геодезических измерений – классификационная категория геодезических измерений, выделяемая по признаку измеряемой геодезической величины.
Различают следующие виды геодезических измерений:
Угловые (геодезические) измерения – вид геодезических измерений, в которых измеряемой геодезической величиной являются горизонтальные и (или) вертикальные углы (зенитные расстояния).
Линейные (геодезические) измерения – вид геодезических измерений, в которых измеряемой геодезической величиной являются длины сторон геодезических сетей (расстояния или их разности).
Геодезические измерения превышений – вид линейных геодезических измерений, в которых измеряемой геодезической вели-чиной являются разности высот пунктов (точек).
Гироскопические измерения (гироскопическое ориентирование) – вид угловых геодезических измерений, в которых измеряемой геодезической величи-ной являются азимуты направлений, определенные с помощью гироскопических приборов.
Геодезические измерения координат (координатные измерения) – вид геодезических измерений, в которых измеряемой геодезической величиной являет-ся положение геодезических пунктов относительно исходных пунктов в заданной отсчетной системе.
Разность высот смежных горизонталей называется высотой сечения рельефа и обозначается буквой h. Высота сечения рельефа в пределах плана или карты строго постоянна. Её выбор зависит от характера рельефа, масштаба и назначения карты или плана. Для определения высоты сечения рельефа иногда пользуются формулой
h = 0,2 мм · М,
где М – знаменатель масштаба.
Такая высота сечения рельефа называется нормальной.
— Расстояние между соседними горизонталями на плане или карте называется заложением ската или склона. Заложение есть любое расстояние между соседними горизонталями, оно характеризует крутизну ската местности и обозначается d.
Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона ската ν. Чем больше угол наклона, тем круче скат.
-Другой характеристикой крутизны служит уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует, что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промиллях (‰).Если угол наклона ската до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками.
Эти характеристики связаны формулой
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.009 сек. —>
Источник
Изображение рельефа способом горизонталей, высота сечения рельефа, заложение ската, уклоны и крутизна ската.
Высота сечения рельефа– расстояние h между соседними секущими плоскостями.
Крутизна ската –расстояние между горизонталями в плане.
Заложение ската – это заложение, нормальное к горизонталям и являющее кратчайшим.
Уклоны– отношение высоты сечение рельефа к заложению.

В геодезии на топографических картах рельеф изображают в виде совокупности 2-х способов: способ горизонталей указанием отметок высот характерных точек местности. рассмотрим сущность, Q – часть уровенной поверхности. Проведем плоскость Р||Q. Плоскость Р рассечет участок земной поверхности. Отвесными линиями спроектируем след и получим горизонтальную проекцию следа сечения. «а» и «b» — проекции А и B. Затем построим вторую секущую плоскость на расстоянии h. По аналогии рассмотрим след сечения и спроектируем его на плоскость Q. Если мы хотим получить изображение горизонтальных проекций следов сечения на ограниченной плоскости, то их следует уменьшить. Уменьшенное изображение следов сечения мы видим на топ. Карте в виде коричневых линий. Эти линии – горизонтали. h принято называть «высота сечения рельефа»(расстояние между секущими плоскостями). Эта величина постоянна для данного листа карты. Н может быть вычислена по формуле hсеч=0.2мм∙М. М — знаменатель численного масштаба карты. 0,2мм – наименьшее деление нормального поперечного масштаба – минимальный отрезок, когда две горизонтали мы видим раздельно.
Дата добавления: 2015-02-16 ; просмотров: 18 | Нарушение авторских прав
Источник
Горизонтали и их свойства. Способы построения горизонталей



По отметкам точек
Рельефом называют совокупность неровностей земной поверхности. Знание рельефа местности необходимо при проектировании и строительстве железных и автомобильных дорог, осушительных и оросительных систем, промышленных предприятий и т. д. Существует несколько способов изображения рельефа на топографических картах и планах. Наиболее старый способ – это изображение рельефа штрихами, наносимым на карту по особой шкале.
Рельеф местности может быть также изображен подписями отметок ряда точек или отмывкой красками различного тона. Однако наилучшим способом оказалось изображать рельеф горизонталями в сочетании с некоторыми условными знаками и подписями отметок характерных точек. Горизонталь – это линия, соединяющая точки земной поверхности с одинаковыми высотами.
Чтобы правильно изобразить рельеф, необходимо знать его основные формы.
Существует пять основных форм рельефа (рисунок 3.5):
— возвышенность (рисунок 3.5, а);
— котловина (рисунок 3.5, б);
— хребет (рисунок 3.5, в);
— лощина (рисунок 3.5, г);
— седловина (рисунок 3.5, д).
На рисунке 3.5 эти формы рельефа показаны в разрезе. Рассмотрим сущность изображения рельефа горизонталями. На рисунке 3.5, а показана возвышенность (холм, гора), наивысшую точку которой называют вершиной, низ – подошвой, а боковые поверхности – скатами. Для изображения возвышенности горизонталями представим себе, что эту возвышенность пересекают ряд равноотстоящих друг от друга плоскостей, параллельных основной уровенной поверхности. Линии пересечения этими плоскостями земной поверхности и будут являться горизонталями. Спроектировав их отвесными линиями на плоскость, получим на ней изображение возвышенности.
Для наглядности некоторые горизонтали подписывают, кроме того у них ставят черточки-бергштрихи, показывающие направление ската местности.
Расстояние между двумя соседними секущими плоскостями называют высотой сечения рельефа h. На картах и планах высота сечения рельефа характеризуется разностью высот двух смежных горизонталей. Например, на рисунке 3.5, а высота сечения рельефа h = 5 м.
Расстояние между горизонталями на плане или карте называется заложением. На рисунке 3.5, а заложение d = АС. Зависимость между высотой сечения рельефа h, заложением d, углом наклона υ, уклоном i и линии местности АВ можно получить из треугольника АВС (рисунок 3.5, а):
i = h / d = tg υ. (3.6)
Уклон и угол наклона линии местности являются основными характеристиками крутизны скатов. Чем больше угол наклона, тем круче скат местности. Из формулы (3.6) следует, что чем меньше заложение d или чем чаще горизонтали на плане, тем скат местности круче.
Изображение горизонталями котловины, лощины, хребта и седловины показано на рисунке 3.5. Котловина (впадина) – замкнутое углубление поверхности (см. рисунок 3.5, б). Самую низкую часть впадины называют дном, боковые поверхности – скатами, а линию слияния с окружающей местностью – бровкой.
Рисунок 3.5 – Основные формы рельефа
Хребет – вытянутая в одном направлении возвышенность с двумя скатами (см. рисунок 3.5, в). Линию встречи скатов в верхней части называют водоразделом (водораздельной линией).
Лощина – вытянутое в одном направлении понижение с двумя скатами (рисунок 3.5 г). Линию встречи скатов в нижней их части называют водосливом или тальвегом (водосливной линией).
Седловина – понижение между двумя возвышенностями (см. рисунок 3.5 д). Наиболее низкую точку между возвышенностями называют перевалом.
Бергштрихи на картах и планах обычно показывают по водораздельным и водосливным линиям. Подписи на горизонталях делают так, чтобы основание числа показывало направление ската. Горизонтали вычерчивают коричневым цветом. Каждую десятую или пятую из них вычерчивают утолщенной линией.
Из сущности горизонталей вытекают их свойства:
— горизонталь – это замкнутая кривая линия, все точки на которой имеют одинаковую высоту, кратную высоте сечения рельефа;
— горизонтали на плане не могут раздваиваться и обрываться; если горизонталь не замыкается в пределах плана, она замыкается за его пределом;
— горизонтали не должны пересекаться между собой, так как они получаются пересечением земной поверхности плоскостями, лежащими на разных высотах;
— чем чаще горизонтали на плане, тем уклон местности больше, или чем меньше заложение, тем скат круче;
— водораздельные и водосливные линии и направления максимального уклона горизонтали пересекают под прямым углом.
Высота сечения рельефа устанавливается в зависимости от масштаба плана и характера рельефа местности так, чтобы горизонтали не сливались между собой. В Республике Беларусь приняты следующие высоты сечения рельефа при масштабах съемки:
| 1:500 – h = 0,25; 0,5 м; 1:1000 – h = 0,25; 0,5; 1 м; 1:2000 – h = 0,5; 1; 2 м; | 1:5000 – h = 0,5; 1; 2; 5 м; 1:10000 – h = 1; 2,5; 5 м. |
Для более полного изображения и удобства чтения рельефа на картах и планах подписывают отметки характерных точек рельефа (вершин холмов, дна котловин, перевалов и т. д.). Например, на рисунке 3.5, б подписана отметка дна котловины 98,7 м.
Способы построения горизонталей по отметкам точек.
Для проведения горизонталей на плане нужно нанести характерные точки, снятые на местности, и выписать их высоты. Те точки, между которыми земная поверхность не имеет переломов, т. е. имеет постоянный уклон, соединить линиями. Далее на каждой линии интерполированием находят точки пересечения ее горизонталями и отмечают высоты этих горизонталей.
Соединив затем плавными кривыми линиями точки с одинаковыми высотами, получают изображение рельефа местности на плане. Таким образом, задача построения горизонталей на плане в основном сводится к умению находить проекции точек пересечения горизонталями линий, отметки концов которых известны, при этом высота сечения рельефа должна быть уже установлена. Эта задача называется интерполированием горизонталей, т. е. нахождением промежуточных значений высот горизонталей по отметкам точек. Интерполирование можно производить аналитическим или графическим способом.
Аналитический способ. По известным высотам точек А и В и расстоянию d между ними (рисунок 3.6, а) необходимо найти величины расстояний d1 и d2 от точки А до точек М0 и N0 c отметками Нм и HN, равными отметкам горизонталей.
Рисунок 3.6 – Аналитический способ интерполирования
Из подобия треугольников АВВО, АММО и ANNO находим:
На плане откладывают отрезки d1 и d2 и получают точки MO и NO, у которых подписывают их отметки. Следует отметить, что интерполирование горизонталей проводят только по линиям с равномерным скатом. На рисунке 3.6, б показан случай неправильной интерполяции между точками А и С с неравномерным скатом местности. Как видно из рисунка, вместо действительного положения точки В будет получена точка В ‘ и соответственно вместо НВ будет получена неверная высота НВ ‘ .
Графический способ. Интерполирование этим способом выполняют с помощью миллиметровой или прозрачной бумаги. При наличии миллиметровой бумаги ее прикладывают к линии плана АВ. По отметкам концов АВ строят профиль этой линии. Проектируя затем на линию плана точки пересечения линии профиля с линиями миллиметровой бумаги, принятыми за секущие плоскости, получают искомые точки М и N.
При наличии прозрачной бумаги (восковки, кальки), на ней предварительно наносят ряд равноотстоящих друг от друга параллельных линий, которым придают отметки секущих плоскостей. Восковку накладывают на план так, чтобы конечные точки линии плана заняли положение, соответствующее их отметкам между линиями восковки (рисунок 3.7). Далее точки пересечения линии плана с линиями восковки перекалывают на план. Это и будут искомые точки на плане.
Решение инженерных задач по планам и картам
Современные топографические карты и планы дают богатый и разносторонний материал о той местности, которая на них изображена условными знаками. Зная условные знаки, при изучении карты можно получить необходимые данные о населенных пунктах, гидрографии, растительности, дорожной сети, рельефе и других объектах. Кроме того, при помощи карты можно решать ряд инженерных задач: определять географические и прямоугольные координаты точек, измерять дирекционные углы и азимуты направлений, определять высоты точек, уклоны заданных линий, водосборные площади бассейнов, строить профили земной поверхности, производить трассирование и т. д.
Рассмотрим решение этих задач более подробно .
1. Прямоугольные координаты точек на карте определяют от линии координатной (километровой) сетки, абсциссы и ординаты которых подписываются в общегосударственной системе координат.
2. На картах подписываются также широты и долготы точек пересечения параллелей и меридианов, ограничивающих данный лист. Кроме того, на обрамляющих карту рамках вычерчиваются одноминутные деления широты и долготы. Соединяя точки одноименных делений северной и южной сторон рамок, а также западной и восточной, получим на карте сетку меридианов и параллелей, пользуясь которой, можно определить широту и долготу любой точки карты.
3. Дирекционный угол или азимут линии можно измерить транспортиром непосредственно на карте, как угол между направлением линии километровой сетки или истинного меридиана и направлением заданной линии. Обычно на полях карты всегда дается для данного листа сближение меридианов и склонение магнитной стрелки, используя которые, по формулам (2.3) – (2.4) можно вычислить все углы ориентирования.
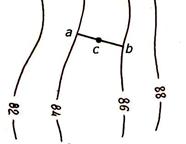
4. Высоту (отметку) любой точки, например С (рисунок 3.8, а), можно определить, если через нее провести линию ab по кратчайшему расстоянию между горизонталями.
Из подобия треугольников abb1 и acc1, учитывая, что h – высота сечения рельефа, d – заложение (рисунок 3.8, б), получим cc1 = ac bb1 / ab или Δh = Δd h /d. (3.7)
Отметка точки НС будет равна отметки точки a плюс величина Δh:
|
|
 б) б) |
Рисунок 3.8 – Определение отметки точки
В формуле (3.7) величины d и Δd измеряют на плане, а высота сечения рельефа известна на плане или карте.
5. Определяют уклон линии. Уклоном линии называется тангенс угла наклона этой линии или отношение высоты сечения рельефа к заложению (рисунок 3.8, б):
i = tg υ = h / d. (3.8)
Для определения уклона можно воспользоваться формулой (3.6) или (3.8). Из формул следует, что уклон – безразмерная величина. Его выражают в процентах (% – сотых долях) или в промилях (‰ – тысячных долях). Для определения угла наклона линии (крутизны ската) υ из формулы (3.8) можно получить:
υ = arctg i = arctg (h / d). (3.9)
Угол наклона можно также определить графически с помощью графика заложений, который обычно приведен под южной рамкой карты. При отсутствии графика заложений его можно построить. Для этого на горизонтальной прямой АВ от точки А откладывают равные отрезки произвольной величины (рисунок 3.9). Из точек отложения к прямой АВ восстанавливают перпендикуляры. Используя формулу (3.8), определяют заложение:
d = h / tg υ = h / i, (3.10)
где h – высота сечения рельефа
Подставляя в формулу (3.10) величины υ, равные 1, 2, 3 о и т. д., последовательно получают заложение для каждого из углов наклона υ и откладывают их на перпендикулярах в масштабе плана или карты. Полученные на перпендикулярах точки соединяют плавной кривой линией, а внизу подписывают углы наклона.
Для определения угла наклона по графику заложений с помощью циркуля-измерителя измеряют величину заложения на плане (ab) и прикладывают раствор измерителя к графику заложений так, чтобы одна игла измерителя находилась на основании графика, а вторая располагалась параллельно вертикальным линиям графика, и перемещают измеритель по горизонтальной линии основания вправо или влево до совпадения верхней иглы с кривой графика. По росписи графика заложений отсчитывают крутизну ската. Например, на рисунке 3.9 при заложении ab крутизна ската υ = 1,4 о . По графику заложений можно решать и обратную задачу, т. е. по заданной крутизне ската определять величину заложения на плане.
6. Для построения по заданному направлению АВ на плане профиля линии местности при помощи полоски бумаги линия с плана переносится на миллиметровую бумагу с отметками всех точек пересечения линии с горизонталями. Далее в заданном вертикальном масштабе по вертикальным линиям откладывают отметки точек, и все вершины перпендикуляров соединяют прямыми линиями. Получают профиль местности по заданному направлению (рисунок 3.10).
7. Для проведения на карте или плане линии заданного уклона по графику заложений или, исходя из формулы (3.10), определяют величину заложения соответствующего уклона. Затем циркулем-измерителем откладывают это заложение в масштабе плана и, начиная от первой горизонтали, пересекающей линию, последовательно засекают смежные горизонтали. Полученная ломаная линия будет иметь заданный уклон (рисунок 3.11).
Рисунок 3.10 – Продольный профиль
8. Водосборные площади по картам и планам определяют для вычисления расхода воды с бассейнов при строительстве плотин, мостов, труб и т. п. Водосборной площадью или бассейном водотока называют ту площадь, с которой поверхностные воды после дождя или таяния снега по условиям рельефа местности и его геологического строения стекают в данный водоток. Границами водосборной площади служат водораздельные линии и линии наибольшего ската. На карте или плане сначала намечают границы водосборной площади до створа строящегося сооружения, а затем при помощи планиметра или палетки определяют площадь в пределах установленной границы (рисунок 3.12).
Решение практических задач на планах и картах подробно изложено в учебно-методических пособиях по выполнению расчетно-графических и лабораторных работ по геодезии.
Определение площадей по картам и планам
При решении многих вопросов, связанных с использованием земельной территории, необходимо знать площади тех или иных участков. Площади участков могут быть определены или по результатам обмера участка в натуре или по планам и картам.
Существует три основных способа определения площадей:
— графический, когда площадь вычисляется по данным, взятым графически с плана или карты;
— аналитический, когда площадь вычисляют непосредственно по результатам полевых измерений или по их функциям – координатам вершин участка;
— механический, когда площадь определяется по плану при помощи специальных приборов, называемых планиметрами.
Часто эти способы применяются комбинированно. Например, общая площадь участка определяется аналитическим способом, а площадь внутренних контуров – графическим или механическим. Рассмотрим каждый из вышеуказанных способов более подробно.
Графический способ определения площадей. Сущность этого способа состоит в том, что данный участок на плане разбивают прямыми линиями на ряд простейших геометрических фигур (обычно треугольники, реже – прямоугольники, квадраты или трапеции) и с помощью циркуля-измерителя и масштабной линейки определяют в каждой фигуре размеры тех элементов, которые необходимы для вычисления площади фигуры.
Вычислив по известным формулам геометрии площади фигур и взяв их сумму, находят общую площадь участка. Ошибка определения площади графическим способом равна примерно 1:100 – 1:200 от величины вычисляемой площади. Для повышения точности определения площадей этим способом следует пользоваться планами наиболее крупного масштаба, а также использовать, где это возможно, данные измерений в натуре.
Площади криволинейных контуров удобно определять при помощи палеток. Палетка (рисунок 3.13) представляет собой сетку квадратов, нанесенную на восковке или прозрачной целлулоидной пластинке. Стороны квадратов могут быть от 2 до 10 мм. Пользование палеткой видно из рисунка 3.13. Для определения площади палетку накладывают на контур и считают число квадратов, поместившихся внутри контура.
Доли неполных квадратов при этом оценивают на глаз. Зная в масштабе плана площадь одного квадрата, умножением на число квадратов находят общую площадь контура. Точность определения площадей палеткой несколько ниже, описанного выше графического способа. Главная ошибка при этом происходит от оценки частей неполных квадратов на глаз. Более высокую точность дают палетки с меньшей стороной квадрата.
Аналитический способ определения площадей. Исходными данными для вычисления площадей данным способом служат координаты вершин многоугольника.
Пусть требуется вычислить площадь полигона 1-2-3-4 (рисунок 3.14), координаты вершин которого известны: 1 (X1, Y1); 2 (Х2, Y2); 3 (Х3, Y3); 4 (Х4, Y4). Из рисунка 3.14 видно, что площадь Р данного четырехугольника представляет собой алгебраическую сумму и разность площадей трапеции:
Раскрыв скобки, выполнив сокращение и приведение подобных членов, получим:
или в общем виде для n-угольника можно записать
Подобным образом из уравнения (3.11) после преобразований можно получить:

Согласно формулам (3.12) и (3.13) двойная площадь многоугольника равна сумме произведений всех абсцисс на разность ординат последующей и предыдущей вершин, или сумме произведений всех ординат на разность абсцисс предыдущей и последующих вершин.
Следует иметь ввиду, что сумма всех разностей абсцисс (или ординат) от первой до последней точки должна равняться нулю. Это свойство используется для контроля вычисления разностей в формулах (3.12) и (3.13). Погрешность вычисления площадей аналитическим способом не превышает 1:1000 вычисляемой площади.
Механический способ определения площадей. Определение площадей механическим способом производится при помощи планиметров. Наибольшее распространение получил полярный планиметр (рисунок 3.15), состоящий из полюсного и обводного рычагов.
Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом – штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм (рисунок 3.15), состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета.
Червячная передача устроена так, что одному обороту колеса соответствует поворот циферблата на одно деление. Рядом с колесом находится верньер, по которому отсчитывают десятые доли делений колеса или тысячные доли его оборота.
Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья – по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру. Например, отсчет на рисунке 3.15 составит 3215.
При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Р при полюсе вне фигуры вычисляют по формуле
а при полюсе внутри фигуры –
где С – цена деления планиметра;
g – постоянное число планиметра.
Перед работой планиметр необходимо поверить и определить его цену деления и постоянное число.
При проверке планиметра должны быть проверено выполнение следующих условий:
— счетное колесо планиметра должно свободно вращаться на оси без трений и колебаний. Выполнение этого условия достигается регулировкой подшипников оси колеса при помощи исправительных винтов.
— плоскость ободка счетного колеса должна быть перпендикулярна к оси обводного рычага. Для проверки этого условия обводят одну и ту же фигуру при двух положениях планиметра, когда счетный механизм находится слева и справа от фигуры. Если расхождение между разностями отсчетов в обоих случаях не превышает 2-3 делений планиметра, то условие выполнено. В противном случае площадь следует определять при двух положениях планиметра и брать среднее из результатов.
Цену деления планиметра определяют многократными обводами двух-трех квадратов координатной сетки плана или карты при двух положениях планиметра, помещая полюс вне фигуры.
Тогда цена деления будет равна известной площади обводимой фигуры Р, деленной на среднюю разность отсчетов:
После определения цены деления планиметра находят его постоянное число. Для этого обводят планиметром большой квадрат координатной сетки с известной площадью при полюсе внутри фигуры.
Постоянное число планиметра:
При передвижении счетного механизма вдоль обводного рычага изменяется его длина и соответственно изменяется цена деления и постоянное число планиметра. Длина обводного рычага точно фиксируется по шкале с делениями, нанесенными на рычаге.
При определении площадей планиметром необходимо соблюдать следующие правила:
— план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;
— положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;
— обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;
— для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.
Точность определения площадей планиметром зависит от формы и размера обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10–30 см 2 ) ошибка определения площади планиметром не превышает 1:200 величины площади.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник
Скачать с Depositfiles
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Горно-геологический факультет
Кафедра геоинформатики и геодезии
Отчёт
По курсу «Геодезия»
По лабораторной работе №6
Тема: «Определение крутизны ската по графику заложения. Проектирование линий заданного уклона»
Выполнила:
Ст. гр. ГКЗ-11
Проверил:
Асс. каф.
Шморгун Е. И.
Донецк 2011
Определение крутизны ската по графику заложений
Крутизной ската называется угол наклона ската к горизонтальной плоскости. Чем больше угол, тем круче скат. Величина угла наклона ската ν вычисляется по формуле:
ν = arctg
где 

Заложением называется расстояние на карте между двумя соседними горизонталями; чем круче скат, тем меньше заложение.
Чтобы избежать расчетов при определении крутизны скатов по карет, на практике часто пользуются специальными графиками, называемыми графиками заложений. График заложений представляет собой график функции d=h*ctgν, абсциссами которого являются значения углов наклона, начиная с 0°30′, а ординатами – значения заложений, соответствующих этим углам наклона и выраженных в масштабе карты.
Для определения крутизны ската раствором циркуля берут с карты соответствующее значение и переносят его на график заложений так, чтобы отрезок АВ оказался параллельным вертикальным линиям графика, а одна ножка циркуля располагалась на горизонтальной линии графика, другая ножка – на кривой заложений.
Значение крутизны ската определяют, пользуясь оцифровкой горизонтальной шкалы графика.
Крутизна ската ν = ° ‘
Проектирование линии заданного уклона.
При проектировании автомобильных и железных дорог, каналов, различных инженерных коммуникаций возникает задача построения на карте трассы будущего сооружения с заданным уклоном.
Пусть на карте масштаба 1:10 000 требуется наметить трассу автомобильной дороги между точками Т1 и Т2, чтобы уклон ее на всем протяжении не превышал
і=0,06. Высота сечения рельефа на карте h=2,5 м.
Для решения задачи рассчитывают величину заложения, соответствующую заданному уклону і=0,06 и высоте сечения рельефа на карте h=2,5 м:
d= 

затем выражают заложение в масштабе карты:



Величину заложения 
Построение трассы между точками Т1 и Т2 осуществляется следующим образом. Раствором циркуля, равным заложению 
Во многих случаях рельеф местности позволяет наметить не один, а несколько вариантов трассы, из которых выбирается наиболее приемлемый по технико-экономическим соображениям. Так, например, из двух вариантов трассы, проведенной примерно в одинаковых условиях, будет выбран вариант с меньшей длиной проектируемой трассы.
При построении линии трассы на карте может оказаться, что из какой-либо точки трассы раствор циркуля не достигает следующей горизонтали, т.е. рассчитанное заложение 
Скачать с Depositfiles
ОПРЕДЕЛЕНИЕ КРУТИЗНЫ СКАТОВ
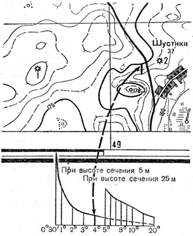
Наиболее распространенный способ определения крутизны скатов — по шкале заложений, помещаемой в южной части листа карты. Этот способ заключается в том, что для нахождения крутизны ската на каком-либо участке дороги с помощью полоски бумаги или циркуля измеряют расстояние между горизонталями, проходящими через те точки, крутизна ската между которыми определяется. Отмеченное на полоске бумаги или же обозначенное раствором циркуля расстояние (на рис. 20 оно обозначено утолщенной полоской) переносят на шкалу заложений.
Тогда у основания шкалы можно прочитать величину крутизны ската. Так, на нашем рисунке крутизна ската между двумя смежными горизонталями, отмеченными черточкой, оказалась равной 4°.
После определения крутизны ската по карте можно решить, учитывая возможности своих средств передвижения, условия погоды и время года, преодолим или нет данный участок местности, лежащий на маршруте движения.
Для точного определения крутизны ската существует формула
| h | |||
| tg α | = | —— | |
| d |
где а — угол в градусах, обозначающий критузну ската;
h — относительное превышение точек, расположенных на скате, крутизна которого определяется;
d — расстояние между точками, снятое с карты.
В приведенной формуле величины h и d должны быть в одних и тех же единицах измерения (обычно в метрах).
Определение крутизны ската между точками А и Б по разности их абсолютных высот
Пример. Требуется определить крутизну ската по дороге между пунктами А и Б, имеющимися на карте. На рисунке положение точек А и Б карты изображено в виде проекции на вертикальную плоскость, рассекающую скат.
Решение. По горизонталям (отметкам) карты определяем абсолютные высоты точек А и Б. Пусть они соответственно равны 110 и 230 м. Расстояние между ними (АБ1 = d), измеренное по карте, оказалось равным 600 м. Превышение между точками А и Б будет равно h= 230-110=120 м. Тогда , откуда (по специальной таблице значений тангенсов углов) находим крутизну ската а = 11,5°.
Высота сечения рельефа это расстояние между двумя смежными основными горизонталями по высоте. Высоту сечения рельефа подписывают на каждом листе карты под ее масштабом. Крутизна скатов высот определяется на карте по шкале заложений и глазомерно.
Определение абсолютных высот и взаимного превышения точек на местности, горизонтали высот, направление, форма и крутизна скатов, порядок их определения на карте по шкале заложений и глазомерно.
На топографических картах приняты следующие высоты сечения, указанные в таблице ниже.
Высоты точек местности и высот на карте определяются по горизонталям. Используя имеющиеся на них отметки высот. Если точка находится на горизонтали, то ее абсолютная высота равна высоте горизонтали (над уровнем моря). Если точка расположена между горизонталями, то ее абсолютная высота равна высоте нижней горизонтали плюс превышение точки (определяется интерполированием) над этой горизонталью.
Кроме горизонталей высоты, отметки подписываются на возвышенностях, контурных точках и урезах воды. Если горизонталей высот с подписанными высотами в каком-либо месте карты нет, то их высоты легко определить, отталкиваясь от высоты ближайшей к ним контурной точки.
Относительное превышение (относительная высота).
Это превышение одной точки местности над другой. Определяется по разности абсолютных высот точек. При расположении точек на одном скате, относительное превышение можно определить по числу промежутков между основными горизонталями, умноженному на высоту сечения.
Точность определения высот точек, отметки которых не подписаны на карте, равна 0,3-0,5 высоты сечения. Относительные превышения дна оврагов, выемок, ям или вершин курганов, насыпей определяются с учетом подписей, стоящих рядом с условными знаками.
Направление, форма и крутизна скатов, порядок их определения.
Скат — наклонная поверхность форм рельефа. Основные элементы ската:
— Крутизна — угол наклона ската в горизонтальной плоскости.
— Высота — превышение высшей точки над низшей.
— Заложение — проекция ската на горизонтальную плоскость.
— Перегиб ската — линия плоского изменения крутизны ската от крутого к пологому и наоборот.
Направление ската по карте определяется:
— По расположению водоемов — понижение в сторону водоема.
— По горизонталям, имеющим бергштрихер — штрих направлен в сторону понижения.
— Отметкам высот — понижение в сторону меньшей отметки.
— По подписи отметок горизонталей — основание цифр направлено в сторону понижения.
Изучая по карте конфигурацию горизонталей в совокупности с направлением ската, можно легко определить типовые формы рельефа.
Формы ската высот:
— Ровный — горизонтали располагаются на равных расстояниях одна от другой.
— Выпуклый — расстояния между горизонталями вниз по скату уменьшаются.
— Вогнутый — расстояния между горизонталями вниз по скату увеличиваются.
— Волнистый (ступенчатый) — наблюдается чередование уменьшения и увеличения расстояний между горизонталями на всем протяжении ската.
По положению относительно своих подразделений и противника (преступников) различают передний скат, понижающийся в сторону противника и обратный скат, понижающийся в сторону тыла своих подразделений.
Способы определения крутизны ската.
Крутизну ската высот можно определить на карте по шкале заложений. На местности — глазомерно.
Определение крутизны ската высот по шкале заложений.
Для определения крутизны ската по шкале заложений необходимо:
— Отмерить циркулем-измерителем, линейкой или полоской бумаги отрезок между двумя смежными основными горизонталями.
— Приложить полученный отрезок к шкале эаложений таким образом, чтобы он поместился строго между верхней кривой и нижней прямой линиями шкалы заложений.
— Прочитать число градусов у основания шкалы.
Заложением 3 называется расстояние на карте между двумя соседними горизонталями. Чем круче скат, тем меньше заложение.
Измерение крутизны ската высот по шкале заложений.
На отдельных топографических картах рядом со шкалой заложений, соответствующей высоте сечения может быть дана шкала заложений, соответствующая пятикратному сечению. Это делается для того, чтобы повысить точность определения крутизны скатов высот на участках местности с большим углом наклона. В этом случае измеряется расстояние между пятью основными горизонталями и прикладывается к соответствующей шкале заложений.
Определение крутизны ската высот глазомерно.
Глазомерным способом определения крутизны ската следует пользоваться в том случае, если есть определенный опыт данной работы. При этом достаточно оценить в миллиметрах заложение (промежуток между основными горизонталями) и определить крутизну ската по формуле;
КС = 12/заложение.
Этот способ применим при высоте сечения на картах масштаба: 1 : 25000 — 5 м, 1 : 50000 — 10 м. 1 : 100000 — 20 м, 1 : 200000 — 40 м. Общее правило для приближенного определения крутизны ската глазомерным способом: определяемая крутизна во столько раз больше (меньше) одного градуса, во сколько раз его заложение между смежными основными горизонталями меньше (больше) 1 см.
Например, на топографической карте масштаба 1 : 50 000 с высотой сечения 10 метров крутизна ската будет примерно равна. При заложении ската 0,5 см — 2 градуса, при заложении ската 2 см — 0,5 градуса.
По материалам книги «Справочник по военной топографии».