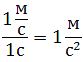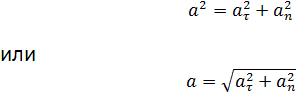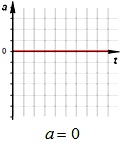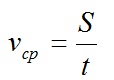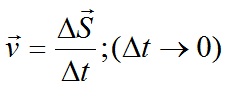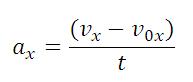Как найти замедленное ускорение

Как найти ускорение — определение и формулы расчета в физике

Содержание:

• Что такое ускорение
  • Единица измерения
• Как рассчитать ускорение: формулы
  • Для прямолинейного движения
  • Для равноускоренного движения
  • Для равнозамедленного движения
  • Нахождение ускорения через массу и силу
• Мгновенное ускорение
• Максимальное ускорение
• Среднее ускорение
• Проекция ускорения

Что такое ускорение

Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.

Единица измерения

В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

(a;=;frac{mathrm V}t)

(a;=;frac{2S}{t^2})

(a;=;frac{V^2}{2S})

Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V₀ и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

(overrightarrow a=frac{overrightarrow F}m)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})

Максимальное ускорение

(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось (х):

(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.

Текст с ошибкой:

Расскажите, что не так

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

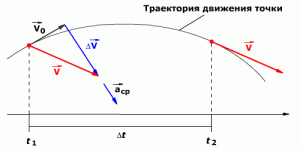
Среднее ускорение

Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

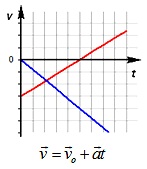
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости 

Если скорость тела по модулю уменьшается, то есть

v2 < v1

то направление вектора ускорения противоположно направлению вектора скорости  Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

Виды движения (равномерное, равноускоренное) и их графическое описание

По форме траектории движение делится на криволинейное (траектория движения тела кривая линия) и прямолинейное (траектория движения тела прямая линия).

При движении тела по прямолинейной траектории модуль вектора перемещения всегда совпадает с пройденным путём. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути

Равномерное прямолинейное движение.

Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Уравнение равномерного движения (перемещение тела при равномерном движении):

 S=v_х·t

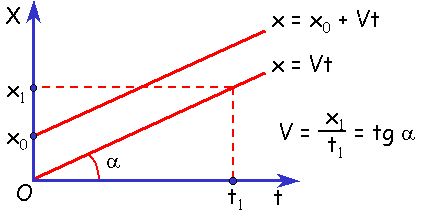
Уравнение координаты тела:

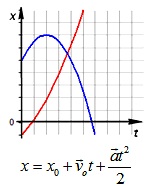
х=х₀+v_х·t

Обозначения:

х– координата движущегося тела

х₀ – начальная координата движущегося тела

v_ср-Средняя скорость равномерного прямолинейного движения

v_х — Скорость равномерного прямолинейного движения

S — Перемещение тела (расстояние, на которое передвинулось тело)

t — Промежуток времени перемещения (время)

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

v(t) – изменение скорости со временем

S(t) – изменение перемещения (пути) со временем

a(t) – изменение ускорения со временем

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно (v=const), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) – прямая линия, параллельная оси времени.

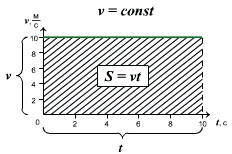
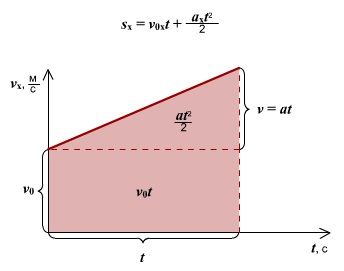
Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

Зависимость перемещения от времени. График s(t) – наклонная линия:

Зависимость координаты от времени. График х(t) – наклонная линия:

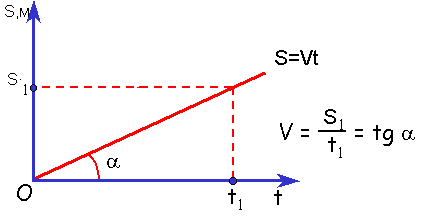
Из графика видно, что проекция скорости равна:

v_х=S/t=tga

Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t) и x(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

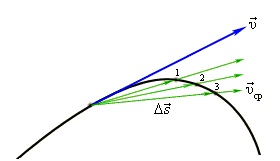
Средняя скорость движения равна отношению всего пути, пройденного материальной точкой  к промежутку времени, за который этот путь пройден.

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называют равноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

Обозначения:

v_х — конечная скорость тела при равноускоренном движении по прямой

v_0х — начальная скорость тела

a — ускорение тела

t — время движения тела

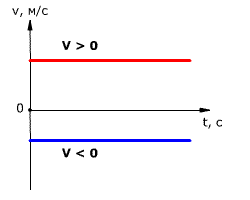
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [м/с²].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения:

Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

Обозначения:

— Перемещение тела при равноускоренном движении по прямой

— Начальная скорость тела

— Скорость тела при равноускоренном движении по прямой

— Ускорение тела

— Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

– если известны начальная, конечная скорости движения и ускорение.

– если известны начальная, конечная скорости движения и время всего движения

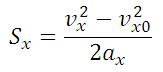
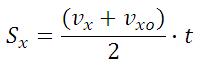
Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

v(t) – изменение скорости со временем

S(t) – изменение перемещения (пути) со временем

a(t) – изменение ускорения со временем

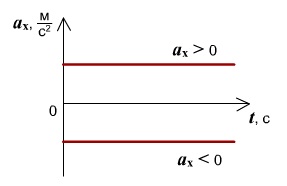
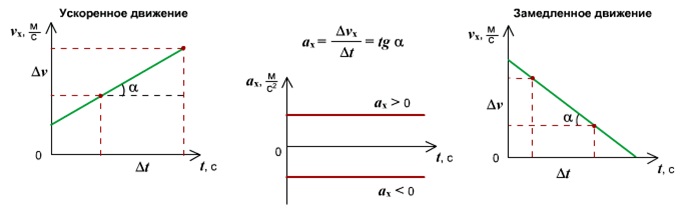
Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости .

Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.

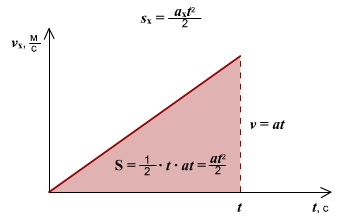
Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

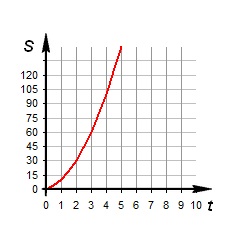
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратичной зависимости

В координатах зависимость имеет вид .

Графиком является ветка параболы.

Расширения для Joomla

Прямолинейное
движение. В
случае, если
траекто­рией является прямая линия,
радиус кривизны беско­нечен

нормальное ускорение равно нулю
.
При этом полное ускорение будет совпадать
с касательным:

и
.

Поскольку в этом
случае скорость всегда направлена по
одной и той же линии, то мы можем сделать
вывод о физическом смысле касательного
ускорения: касательное
ускорение характеризует изменение
модуля скорости.

Равномерное
движение. Равномерным
называется
такое движение точки, при котором модуль
скорости все время остается постоянным:
.
Тогда

и полное ускорение совпадает с нормальным:
.

Поскольку в этом
случае не изменяется модуль ско­рости,
мы можем сделать вывод о физическом
смысле нормального ускорения: нормальное
ускорение характе­ризует изменение
направления скорости.

При равномерном
движении
_.
Интегрируя
последнее равенство, легко получить
уравне­ние равномерного движения:
.

Это уравнение
определяет величину дуговой коорди­наты
в любой момент времени. Для определения
прой­денного точкой пути σ
следует
интегрировать модуль скорости:
.
При равномерном движении
.

Равномерное и
прямолинейное движение. В этом
слу­чае равны нулю и касательное, и
нормальное, и полное ускорения:

,
а скорость точки будет постоянна как
вектор:.

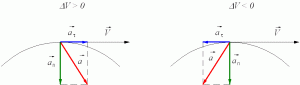
Ускоренное и
замедленное движение. Ускоряется
или замедляется движение точки, т. е.
увеличивается или уменьшается модуль
ее скорости, можно определить по знакам
величин проекций вектора скорости и
вектора ускорения на касательную.

Легко убедиться
в том, что если знаки одинаковы и,
следовательно, произведение этих
проекций положитель­но (
> 0) , то движение
точки ускоренное, а если зна­ки разные
и их произведение отрицательно

(
< 0) – движение замедленное.

Рис.

На рис. показаны
векторы скорости и ускорений для случаев
ускоренного (а) и замедленного (б)
движе­ний
точки.

Проекция a_v
ускорения
на направление вектора скоро­сти
может быть равна проекции ускорения на
касательную

( при

> 0) ,
или противоположна ей по знаку ( при

< 0), т.е.
.

Если ввести в
рассмотрение угол α (рис. ) между
скоростью и полным ускорением, то можно
записать про­екцию a_v
в виде

В числителе
последней формулы образовалось ска­лярное
произведение векторов


_и
,
которое можно расписать через их
проекции, и тогда получается

По знаку этой
проекции можно сразу установить, является
движение точки ускоренным или замедленным.
Поскольку

,
то:

,

эта формула будет
использоваться для вычисления
каса­тельного ускорения при координатном
способе задания движения точки.

Равнопеременное
движение. Равнопеременным
назы­вается
такое движение точки, при котором модуль
каса­тельного ускорения все время
остается постоянным:
.
Оно бывает равноускоренным
и равнозамедленным.

Дважды интегрируя
равенство

легко получить выражения для скорости
и дуговой коорди­наты, т. е. уравнения
равнопеременного движения:

,

Где


и

начальные значения величин


и

2010-03-23 20:26

Если мгновенная скорость движущегося тела растет, то движение называют ускоренным, если мгновенная скорость уменьшается, то движение называют замедленным.

Скорость в различных неравномерных движениях изменяется по разному. Например, товарный поезд, отходя от станции, движется ускоренно; на перегоне — то ускоренно, то равномерно, то замедленно; подходя к станции, он движется замедленно. Пассажирский поезд также движется неравномерно, но его скорость изменяется быстрее, чем у товарного поезда. Скорость пули в канале ствола винтовки возрастает от нуля до сотен метров в секунду за несколько тысячных долей секунды; при попадании в препятствие скорость пули уменьшается до нуля также очень быстро. При взлете ракеты ее скорость растет сначала медленно, а потом все быстрее.

Среди разнообразных ускоренных движений встречаются движения, в которых мгновенная скорость за любые равные промежутки времени увеличивается на одну и ту же величину. Такие движения называют равноускоренными. Шарик, начинающий скатываться по наклонной плоскости или начинающий свободно падать на Землю, движется равноускоренно. Заметим, что равноускоренный характер этого движения нарушается трением и сопротивлением воздуха, которые пока учитывать не будем.

Чем больше угол наклона плоскости, тем быстрее растет скорость скатывающегося по ней шарика. Еще быстрее растет скорость свободно падающего шарика (примерно на 10 м/с за каждую секунду). Для равноускоренного движения можно количественно охарактеризовать изменение скорости с течением времени, вводя новую физическую величину — ускорение.

В случае равноускоренного движения ускорением называют отношение приращения скорости к промежутку времени, за который это приращение произошло:

(text{ускорение} = {text{приращение скорости} over text{промежуток времени}})

Ускорение будем обозначать буквой

. Сравнивая с соответственным выражением из § 9, можно сказать, что ускорение есть скорость изменения скорости.

Пусть в момент времени

 скорость была

, а в момент

 она стала равной

, так что за время

 приращение скорости составляет

. Значит, ускорение

(16.1)

Из определения равноускоренного движения следует, что эта формула даст одно и то же ускорение, какой бы промежуток времени

 ни выбрать. Отсюда видно также, что при равноускоренном движении ускорение численно равно приращению скорости за единицу времени. В СИ единица ускорения есть метр на секунду в квадрате (м/с²), т. е. метр в секунду за секунду.

Если путь и время измерены в других единицах, то и для ускорения надо принимать соответственные единицы измерения. В каких бы единицах ни выражать путь и время, в обозначении единицы ускорения в числителе стоит единица длины, а в знаменателе — квадрат единицы времени. Правило перехода к другим единицам длины и времени для ускорения аналогично правилу для скоростей (§11). Например,

(1 см/с^2=36 м/мин^2)

Если движение не является равноускоренным, то можно ввести, пользуясь той же формулой (16.1), понятие среднего ускорения. Оно охарактеризует изменение скорости за определенный промежуток времени на пройденном за этот промежуток времени участке пути. На отдельных же отрезках этого участка среднее ускорение может иметь разные значения (ср. со сказанным в § 14).

Если выбирать такие малые промежутки времени, что в пределах каждого из них среднее ускорение остается практически неизменным, то оно будет характеризовать изменение скорости на любой части этого промежутка. Найденное таким образом ускорение называют мгновенным ускорением (обычно слово «мгновенное» опускают, ср. § 15). При равноускоренном движении мгновенное ускорение постоянно и равно среднему ускорению за любой промежуток времени.