Сосредоточенные и распределенные заряды
Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.
Сосредоточенный заряд
Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.
Рис. 1. Точечный заряд
Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.
Распределенные заряды
Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.
Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.
Примечание: Плотности отрицательных зарядов записывают со знаком «минус».
Формула линейной плотности заряда
Рис. 2. Заряд распределен по длинному тонкому телу
[ large boxed {tau = frac{q}{L} } ]
( large q left(text{Кл} right) ) – заряд;
( large L left(text{м} right) ) – длина, по которой распределен заряд;
( large tau left(frac{text{Кл}}{text{м}} right) ) – линейная плотность заряда;
Формула поверхностной плотности заряда
Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.
Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).
Рис. 3. Заряд распределен по плоской поверхности
[ large boxed {sigma = frac{q}{S} } ]
( large S left(text{м}^{2} right) ) – площадь, по которой распределен заряд;
( large sigma left(frac{text{Кл}}{text{м}^{2}} right) ) – поверхностная плотность заряда;
Формула объемной плотности заряда
Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.
Рис. 4. Заряд распределен по объему тела
[ large boxed {rho = frac{q}{V} } ]
( large V left(text{м}^{3} right) ) – объем, по которому распределен заряд;
( large rho left(frac{text{Кл}}{text{м}^{3}} right) ) – объемная плотность заряда;
Примечание:
Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.
Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.
Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.
Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.
Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.
Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.
Оценка статьи:
Загрузка…
Поверхностная плотность заряда
Напряженность электрического поля зависит от величины заряда и конфигурации заряженного тела.
Поверхностная плотность заряда — есть отношение заряда к площади заряженной поверхности.
Единица СИ поверхностной плотности заряда:
[ [σ] = frac{кулон}{квадратный enspace метр} = frac{Кл}{м^2} ]
Если
| σ | поверхностная плотность заряда, | Кулон/метр2 |
|---|---|---|
| Q | заряд поверхности проводника, | Кулон |
| S | площадь поверхности проводника, | метр2 |
то
[ σ = frac{Q}{S} ]
Вычислить, найти поверхностную плотность заряда по формуле (2)
Наличие зарядов приводит к возникновению сил, которые в свою очередь действуют на заряды, помещенные в электрическое поле. Причина и следствие здесь взаимно переплетаются.
Если
| σ | поверхностная плотность заряда, | Кулон/метр2 |
|---|---|---|
| E | напряженность электрического поля, | Вольт/метр |
| ε0 | электрическая постоянная, 8.85·10-12 | Кулон/(Вольт · метр) |
то
[ σ = ε_0 · E ]
Вычислить, найти поверхностную плотность заряда через напряженность электрического поля по формуле (3)
Поверхностная плотность заряда |
стр. 626 |
|---|
Ученик
(188),
закрыт
10 лет назад
Татьяна Полтавцева
Профи
(833)
10 лет назад
Обозначим: n – концентрация свободных заряженных частиц в про воднике, v – скорость их поступательного движения, q – заряд одной частицы, тогда I = qnvS. ( Физика – 10, “Законы постоянного тока”, стр. 270).
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2016 года; проверки требуют 15 правок.
| Плотность заряда (линейная, поверхностная, объемная) |
|
|---|---|
 |
|
| Размерность | L−1TI, L−2TI, L−3TI |
| Единицы измерения | |
| СИ | Кл/м, Кл/м2, Кл/м3 |
| Примечания | |
| скалярная величина |
Пло́тность заря́да — количество электрического заряда, приходящееся на единицу длины, площади или объёма. Таким образом определяются линейная, поверхностная и объёмная плотности заряда, которые в системе СИ измеряются в кулонах на метр (Кл/м), в кулонах на квадратный метр (Кл/м²) и в кулонах на кубический метр (Кл/м³), соответственно. В отличие от плотности вещества, плотность заряда может принимать не только положительные, но и отрицательные значения, поскольку существуют заряды обоих знаков.
Плотность заряда в классической физике[править | править код]
Линейная, поверхностная и объёмная плотности электрического заряда обычно задаются функциями 
, 
и 
, соответственно, где 
— радиус-вектор. Зная эти функции, можно определить полный заряд:
-
,- ,
- .
Плотность заряда в квантовой механике[править | править код]
В квантовой механике плотность заряда, например электрона в атоме, связана с волновой функцией 
через соотношение
-
- ,
где 
— заряд электрона. При этом волновая функция должна иметь нормировку:
-
- .
Определение плотности заряда через δ-функцию[править | править код]
Иногда требуется записать объёмную плотность заряда для системы из точечных зарядов 
(
). Это может быть сделано с использованием δ-функции:
-
- ,
где сумма берётся по всем имеющимся зарядам, а 
— радиус-вектор заряда .[1]
Полный заряд, находящийся во всём пространстве, равен интегралу 
по всему пространству. Можно написать этот интеграл в четырёхмерном виде:
-
- ,
где интегрирование производится по всей четырёхмерной гиперплоскости, перпендикулярной к оси x0 (очевидно, что это и означает интегрирование по всему трёхмерному пространству). 
— 4-вектор плотности тока.
Плотность заряда в формулах электродинамики[править | править код]
Объёмная плотность заряда в явном виде фигурирует в одном из уравнений Максвелла: (
). Кроме того, она входит в уравнение непрерывности 
.
Поверхностная плотность заряда входит в граничные условия для нормальных компонент электрической индукции на стыке двух сред: 
.
Плотность заряда в любом варианте (объёмная, поверхностная, линейная) может использоваться при вычислении напряжённости электрического поля или потенциала путём интегрирования закона Кулона
- ,
где элемент заряда 
записывается как 
, 
или 
в зависимости от конкретной задачи.
См. также[править | править код]
- Плотность тока
Примечания[править | править код]
- ↑ Ландау Л.Д., Лифшиц Е.М. Теория Поля, Том 2 из 10.. — 8 издание. — ФИЗМАТЛИТ, 2003. — С. 104. — 531 с. — ISBN 5-9221-0056-4.
Литература[править | править код]
- Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..
- САВЕЛЬЕВ И. В. Основы теоретической физики: Учеб. руководство: Для вузов. В 2 т. Т. 1. Механика и электродинамика.— 2-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1991.— 496 с. ISBN 5-02-014455-X (Т. 1)
Роман Алексеевич Лалетин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В случае равновесного распределения заряды проводника распределяются в тонком поверхностном слое. Так, например, если проводнику сообщить отрицательный заряд, то из-за наличия сил отталкивания элементов этого заряда они рассредоточатся по всей поверхности проводника.
Исследование при помощи пробной пластинки
Для того чтобы на опыте исследовать, как распределяются заряды на внешней поверхности проводника используют так называемую пробную пластинку. Эта пластинка настолько мала, что при соприкосновении с проводником ее можно рассматривать как часть поверхности проводника. Если эту пластинку приложить к заряженному проводнику, то часть заряда ($triangle q$) перейдет на нее и величина этого заряда будет равна заряду, который находился на поверхности проводника по площади равной площади пластинки ($triangle S$).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Тогда величина равная:
[sigma=frac{triangle q}{triangle S}(1)]
называется поверхностной плотностью распределения заряда в данной точке.
Разряжая пробную пластинку через электрометр можно судить о величине поверхностной плотности заряда. Так, например, если зарядить проводящий шар, то можно увидеть, с помощью вышеприведенного метода, что в состоянии равновесия поверхностная плотность заряда на шаре одна и та же во всех его точках. То есть заряд по поверхности шара распределяется равномерно. Для проводников более сложной формы распределение заряда сложнее.
Поверхностная плотность проводника
Поверхность любого проводника является эквипотенциальной, но в общем случае плотность распределения заряда может очень сильно отличаться в разных точках. Поверхностная плотность распределения заряда зависит от кривизны поверхности. В разделе, который был посвящен описанию состояния проводников в электростатическом поле, мы установили, что напряженность поля около поверхности проводника перпендикулярна поверхности проводника в любой его точке и равна по модулю:
[E=frac{sigma}{varepsilon {varepsilon }_0} left(2right),]
где ${varepsilon }_0$ — электрическая постоянная, $varepsilon $ — диэлектрическая проницаемость среды. Следовательно,
[sigma=Evarepsilon {varepsilon }_0 left(3right).]
Чем больше кривизна поверхности тем, тем больше напряженность поля. Следовательно, на выступах плотность заряда особенно велика. Вблизи углублений в проводнике эквипотенциальные поверхности расположены реже. Следовательно, напряженность поля и плотность зарядов в этих местах меньше. Плотность зарядов при заданном потенциале проводника определяется кривизной поверхности. Она растет с увеличением выпуклости и убывает с увеличением вогнутости. Особенно большая плотность заряда на остриях проводников. Так, напряженность поля на острие может быть настолько велика, что может возникать ионизация молекул газа, который окружает проводник. Ионы газа противоположного знака заряда (относительно заряда проводника) притягиваются к проводнику, нейтрализуют его заряд. Ионы того же знака отталкиваются от проводника, «тянут» за собой нейтральные молекулы газа. Такое явление называют электрическим ветром. Заряд проводника уменьшается в результате процесса нейтрализации, он как бы стекает с острия. Такое явление называют истечением заряда с острия.
Мы уже говорили, что когда мы вносим проводник в электрическое поле, происходит разделение положительных зарядов (ядер) и отрицательных (электронов). Такое явление носит название электростатической индукции. Заряды, которые появляются в результате, называют индуцированными. Индуцированные заряды создают дополнительное электрическое поле.
«Распределение заряда по поверхности проводника» 👇
Поле индуцированных зарядов направлено в сторону противоположную направлению внешнего поля. Поэтому заряды, которые накапливаются на проводнике, ослабляют внешнее поле.
Перераспределение зарядов идет, пока не выполнены условия равновесия зарядов для проводников. Такие как: равенство нулю напряженности поля везде внутри проводника и перпендикулярность вектора напряженности заряженной поверхности проводника. Если в проводнике есть полость, то при равновесном распределении индуцированного заряда поле внутри полости равно нулю. На этом явлении основана электростатическая защита. Если какой-либо прибор хотят защитить от воздействия внешних полей, его окружают проводящим экраном. В таком случае внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами. Такой может быть не обязательно сплошным, но и в виде густой сетки.
Пример 1
Задание: Бесконечно длинная нить, заряженная с линейной плотностью $tau $, расположена перпендикулярно бесконечно большой проводящей плоскости. Расстояние от нити до плоскости $l$. Если продолжить нить до пересечения с плоскостью, то в месте пересечения получим некоторую точку А. Составьте формулу зависимости поверхностной плотности $sigma left(rright) $индуцированных зарядов на плоскости от расстояния до точки А.
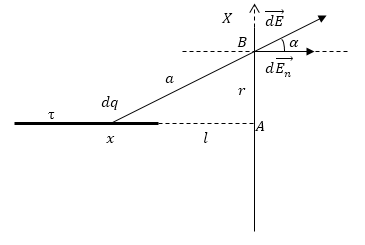
Рис. 1
Решение:
Рассмотрим некоторую точку В на плоскости. Бесконечно длинная заряженная нить в точке В создает электростатическое поле, в поле находится проводящая плоскость, на плоскости образуются индуцированные заряды, которые в свою очередь создают поле, которое ослабляет внешнее поле нити. Нормальная составляющая поля плоскости (индуцированных зарядов) в точке В будет равна нормальной составляющей поля нити в этой же точке, если система находится в равновесии. Выделим на нити элементарный заряд ($dq=tau dx, где dx-элементарный кусочек нити $), найдем в точке В напряжённость, создаваемую этим зарядом ($dE$):
[dE=frac{tau dx}{4pi {varepsilon }_0varepsilon a^2}left(1.1right).]
Найдем нормальную составляющую элемента напряженности поля нити в точке В:
[dE_n=dEcosalpha =frac{tau dxcosalpha }{4pi {varepsilon }_0varepsilon a^2}left(1.2right),]
где $cosalpha $ выразим как:
[cosalpha =frac{x}{a}left(1.3right).]
Выразим расстояние $a$ по теореме Пифагора как:
[a=sqrt{r^2+x^2} left(1.4right).]
Подставим (1.3) и (1.4) в (1.2), получим:
[dE_n=frac{tau dx}{4pi {varepsilon }_0varepsilon a^2}frac{x}{a}=frac{tau xdx}{4pi {varepsilon }_0varepsilon {left(r^2+x^2right)}^{{3}/{2}}}left(1.5right).]
Найдем интеграл от (1.5) где пределы интегрирования от $l (расстояние до ближайшего конца нити от плоскости) до infty $:
[E_n=intlimits^{infty }_l{frac{tau xdx}{4pi {varepsilon }_0varepsilon {left(r^2+x^2right)}^{{3}/{2}}}}=frac{tau }{4pi {varepsilon }_0varepsilon }intlimits^{infty }_l{frac{xdx}{{left(r^2+x^2right)}^{{3}/{2}}}}=frac{tau }{4pi {varepsilon }_0varepsilon }cdot frac{1}{{left(r^2+x^2right)}^{{1}/{2}}}left(1.6right).]
С другой стороны, мы знаем, что поле равномерно заряженной плоскости равно:
[E=frac{sigma}{2varepsilon {varepsilon }_0} left(1.7right).]
Приравняем (1.6) и (1.7), выразим поверхностную плотность заряда:
[frac{1}{2}cdot frac{sigma}{varepsilon {varepsilon }_0}=frac{tau }{4pi {varepsilon }_0varepsilon }cdot frac{1}{{left(r^2+x^2right)}^{{1}/{2}}}to sigma=frac{tau }{2cdot pi {left(r^2+x^2right)}^{{1}/{2}}}.]
Ответ: $sigma=frac{tau }{2cdot pi {left(r^2+x^2right)}^{{1}/{2}}}.$
Пример 2
Задание: Рассчитайте поверхностную плотность заряда, который создается около поверхности Земли, если напряженность поля Земли равна 200$ frac{В}{м}$.
Решение:
Будем считать, что диэлектрическая проводимость воздуха $varepsilon =1$ как у вакуума. За основу решения задачи примем формулу для расчёта напряженности заряженного проводника:
[E=frac{sigma}{varepsilon {varepsilon }_0}left(2.1right).]
Выразим поверхностную плотность заряда, получим:
[sigma=E{varepsilon }_0varepsilon left(2.2right),]
где электрическая постоянная нам известна и равна в СИ ${varepsilon }_0=8,85cdot {10}^{-12}frac{Ф}{м}.$
Проведем вычисления:
[sigma=200cdot 8,85cdot {10}^{-12}=1,77cdot {10}^{-9}frac{Кл}{м^2}.]
Ответ: Поверхностная плотность распределения заряда поверхности Земли равна $1,77cdot {10}^{-9}frac{Кл}{м^2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
