Задача 1 (закон сохранения электрического заряда и закон Кулона)
Два одинаковых шарика обладают зарядами 8 нКл и -4 нКл. Шарики приводят в соприкосновение и разводят на прежние места. Как изменилась сила взаимодействия этих зарядов (заряженных шариков)?
Дано: ;
Найти: ,
– кулоновская после взаимодействия шариков;
– кулоновская сила, которая была до соприкосновения шариков.
Решение
Переводим данные в систему СИ:
Система из двух шариков замкнутая, следовательно, сумма зарядов, входящих в эту систему, остаётся величиной постоянной (закон сохранения электрического заряда):
Так как шарики одинаковые, то при соприкосновении заряд перераспределится и заряды шариков будут одинаковыми ():
Запишем кулоновскую силу до взаимодействия зарядов (шариков):
Кулоновская сила после взаимодействия зарядов (шариков):
Отношение этих сил равно:
Ответ:
Задача 2 (закон Кулона, динамика)
На тонкой шёлковой нити подвешен шарик, масса которого – 2 г. Этот шарик обладает зарядом 2 нКл. На какое расстояние надо поднести к данному шарику другой шарик, заряд которого 5 нКл, чтобы натяжение нити уменьшилось в два раза?
Дано: ;
;
;
(T – первоначальная сила натяжения,
– сила натяжения после того, как поднесли другой шарик).
Найти: r
Решение
Переводим данные в систему СИ:
1. Укажем силы, действующие на шарик при отсутствии внешнего электрического поля (см. рис. 1):
- сила натяжения –
;
- сила тяжести –
.
Эти силы направлены в разные стороны. Согласно первому закону Ньютона:
(шарик находится в состоянии покоя)
Рис. 1. Иллюстрация к задаче
Сила натяжения совпадает по направлению с выбранной осью OY, сила тяжести направлена против оси OY:
2. Второй шарик подносим к первому снизу, как показано на рисунке 2 (шарики обладают положительными зарядами, поэтому сила электрического действия () будет уменьшать силу натяжения нити (
)).
Рис. 2. Иллюстрация к задаче
Относительно оси OY запишем выражение:
Так как , а
:
Электрическая сила () является кулоновской силой, поэтому:
Из данного выражения найдём искомое значение r – расстояние между зарядами (шариками):
;
– для вакуума
м
Ответ:
Задача 3 (напряжённость электрического поля)
Капля масла, масса которой , находится в электрическом поле во взвешенном состоянии. Напряжённость электрического поля равна 100 Н/Кл. Необходимо определить заряд капли масла.
Дано: ;
Найти:
Решение
Переводим данные в систему СИ:
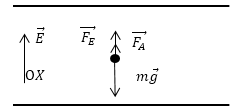
На рисунке 3 изображена капля, находящаяся в однородном электрическом поле (между положительно заряженной плоскостью (внизу) и отрицательно заряженной плоскостью (вверху)).
Капля будет находиться в состоянии покоя, если сила тяжести, действующая на неё, и сила электрического действия () (то есть кулоновская сила, которая действует на заряд, сосредоточенный на капле) обеспечивают ей равновесие.
Рис. 3. Иллюстрация к задаче
Согласно направлению векторов действующих сил и выбранной оси OY:
Напряжённость электрического поля равна отношению электрической силы к заряду, помещённому в это поле:
Так как , то:
Из полученного выражения найдём заряд капли масла:
Ответ:
Список литературы
- Мякишев Г. Я., Буховцев Б. Б., Сотский Н. Н. Физика: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2008.
- Касьянов В. А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. – М.: Дрофа, 2000.
- Рымкевич А. П. Физика. Задачник. 10–11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.
- Генденштейн Л. Э., Дик Ю. И. Физика. 10 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (базовый уровень) – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «distant.phys.msu.ru» (Источник)
- Интернет-портал «phyzika.ru» (Источник)
- Интернет-портал «bambookes.ru» (Источник)
Домашнее задание
- Сформулируйте закон Кулона.
- Стр. 89: № 685–687; стр. 91: № 703, 704. Рымкевич А. П. Физика. Задачник. 10–11 кл. (Источник).
- Какая сила действует на заряд 12 нКл, помещенный в точку, в которой напряженность электрического поля равна 2 кВ/м?
- Найти напряженность поля заряда 36 нКл в точках, удаленных от заряда на 9 см и 18 см.
- На каком расстоянии друг от друга заряды 1 мкКл и 10 нКл взаимодействуют с силой 9 мН?
Физика > Опыт Милликена
В чем заключается опыт Милликена – эксперимент с масляной каплей. Читайте детальное описание опыта и выводы, уравнения, заряд электрона, предельная скорость.
В 1911 году при помощи заряженных капелек масла Роберт Милликен смог сформировать заряд электрона.
Задача обучения
- Разобраться в отличии реального заряда электрона и созданного Милликеном.
Основные пункты
- В эксперименте участвовали ионизирующие капли масла. Попав в воздух, они балансируют силой тяжести с силой электрического поля.
- Милликен не смог напрямую подсчитать количество электронов в каждой масляной капле, но выявил общий знаменатель – 1.5924 (17) х 10-19 С (заряд электрона).
- Полученное значение отличается от принятого на 1% – 1.602176487 (40) х 10-19 С.
Термины
- Электрическое поле – участок вокруг заряженной частички или между двумя напряжениями.
- Напряжение – количество электростатического потенциала между двумя точками в пространстве.
- Предельная скорость – скорость, с которой объект в свободном падении останавливает ускорение вниз, потому что сила тяжести равна и противоположна сопротивлению.
Эксперимент с масляной каплей
Это одно из наиболее значимых исследований в истории физической науки. За его осуществление принялись Роберт Милликен и Харви Флетчер в 1911 году. Они хотели определить заряд одного электрона.
Для этого Милликен использовал распылитель для создания тумана крошечных масляных капель в камере, где было отверстие. Некоторые капли проваливались в дыру и камеру, где ученые вычисляли финальную скорость и массу
Далее Милликен обнажил капли до рентгеновских лучей, ионизирующих молекулы в воздухе и заставляющих электроны прикрепляться к масляным каплям. Это привело к заряду. Верх и низ камеры подключались к батарее, а разность потенциалов представляла электрическое поле.
Милликену удалось уравновесить силу тяжести и силу электрического поля, из-за чего масляные капли оказались подвершенными в воздухе.
В устройстве есть параллельная пара горизонтальных металлических пластин. В пространстве между ними формируется равномерное электрическое поле. Кольцо обладает тремя отверстиями для подвески и одним для наблюдения в микроскоп. В камеру распыляется специальное масло, где капли электрически заряжаются. Капли поступают в пространство между пластинами и могут управляться через изменение напряжения на пластинах
Далее Милликен определил заряд частиц, подвешенных в воздухе. Он предполагал, что сила тяжести приравнивается к силе электрического поля:
q⋅E = m⋅g
q = m⋅g/E
Он располагал массой масляных капель и ускорением силы тяжести (9.81 м/с2), а также энергией рентгеновских лучей, благодаря чему и вычислил заряд.
Заряд каждой капли оставался загадкой, поэтому Милликен скорректировал силу рентгеновских лучей, ионизирующих воздух, а также вычислил остальные значения. В каждом случае заряд достигал 1.5924 (17) х 10-19 С. Результаты были очень точными и отличались всего на 1% от того, что используется сейчас – 1.602176487 (40) х 10-19 С.
Этот эксперимент был крайне важным для определения заряда электрона и доказательства существования частичек, меньше атома.
Фотография установки Милликена. Большой контейнер с моторным маслом обеспечивает постоянную температуру во внутренних камерах. Вверху слева находится распылитель, внизу слева — телескоп для наблюдения[1]. Также для наблюдения можно использовать три окна. Справа сверху находится электрический провод, идущий от батареи
Опыт Милликена, или эксперимент с каплей масла, — важный эксперимент по определению электрического заряда электрона. Он назван в честь американского физика Роберта Эндрюса Милликена, который провёл этот опыт совместно со свим коллегой и соотечествеником Харви Флетчером[en] в 1909 году[2][3]. Милликен усовершенствовал его в 1913 году[4] и в 1923 году получил Нобелевскую премию по физике за работы по определению элементарного электрического заряда и по фотоэлектрическому эффекту.
Опыт, по сути, состоял в создании капель масла с помощью распылителя и в наблюдении за их поведением в электрическом поле. Некоторые из капель были электрически заряжены в результате захвата ионов после облучения воздуха рентгеновским излучением, и можно было управлять их вертикальным движением, задавая соответствующее значение электрического поля. Измеряя напряженность электрического поля, необходимого для противодействия силе тяжести, и зная массу капель, которую можно вычислить, измеряя скорость их свободного падения в воздухе, Милликен заметил, что значения электрических зарядов капель всегда были целыми числами, кратными фиксированной величине, которая стала отождествляться с элементарным зарядом. Полученное значение составило e = −1,5924(17) × 10−19 Кл, что всего на 0,62 % ниже принятого в настоящее время значения e = −1,602… × 10−19 Кл[5].
Предпосылки[править | править код]
В 1896 году британский физик Джозеф Джон Томсон провёл серию экспериментов, которые показали, что катодные лучи на самом деле являются отдельными частицами, а не волнами, атомами или молекулами, как считалось ранее. Томсон сделал оценки отношения заряда электрона к его массе и показал, что оно не зависело от материала катода[6][7].
Роберт Эндрюс Милликен (1923 год)
Как только отношение заряда и массы было определено, проблема, которую требовалось решить, стала очевидной: определить массу и заряд электрона отдельно. Первая попытка определения заряда электрона принадлежит английскому физику Джону Сили Таунсенду, ученику Дж. Дж. Томсона, который опубликовал свой результат в 1897 году. Его эксперимент состоял в измерении двух величин: полного заряда облака водяного пара, образовавшегося при расширении ионизированного газа, и количества капель в облаке. Основная гипотеза состояла в том, что каждая капля конденсируется на одном ионе. Таким образом, деление общего заряда на количество капель (равное количеству ионов) должно было дать значение заряда одной из них. Значение, полученное Таунсендом, в два раза отличается от принятого в настоящее время значения[8].
Этот метод был модифицирован самим Дж. Дж. Томсоном и английским физиком Гарольдом Уилсоном[en] (1874—1964). Уилсон добавил металлические пластины ниже и выше облака капель, чтобы их можно было заряжать электрически и создавать однородное вертикальное электрическое поле в пространстве, занимаемом облаком. Скорость падения облака измерялась в зависимости от электрического поля, и он смог вычислить величину заряда из уравнения для силы, предполагая справедливость закона Стокса[9].
Американский физик Роберт Э. Милликен заинтересовался проблемой определения заряда электрона во время годичного пребывания в Европе в 1895 году. В октябре он посетил в Берлине серию лекций Макса Планка по теоретической физике о катодных лучах. Вернувшись в США в 1896 году, он работал ассистентом Альберта Абрахама Майкельсона в Чикагском университете. В следующем году Дж. Дж. Томсон определил корпускулярную природу катодных лучей. В 1906 году Милликен решил усовершенствовать метод Уилсона, используя более мощные батареи с напряжением до 4000 В, для создания более интенсивного электрического поля между пластинами, разделёнными 5 мм промежутком. Работая со своим докторантом Луи Бегеманом[ca] (1865—1958), они получили более точные значения (Бегеман приводит значение для заряда электрона −1,557 · 10−19 Кл в своей докторской диссертации)[10][11].
Эксперимент[править | править код]
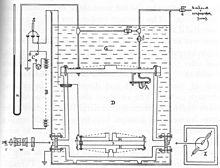
Схема устройства. A — распылитель, B — электрическая батарея, C — переключатели, D — распылительная камера, G — ёмкость с моторным маслом, M и N — пластины конденсатора, между которыми создаётся электрическое поле, X — источник рентгеновских лучей, g — два окна, m — манометр, a — телескоп, а w и d — вода и раствор хлорида меди (II) для поглощения рентгеновских лучей на выходе
В 1909 году Харви Флетчер[en] (1884—1981) стал докторантом Милликена, который предложил ему подготовить эксперимент по определению заряда электрона в качестве темы работы. По словам Флетчера, заметив, что капли воды испаряются менее чем за две секунды, он предложил использовать другие вещества, обладающие меньшим испарением, — ртуть или масло. Милликен не был согласен с аргументами, но так как это была докторская диссертация Флетчера, он позволил докторанту использовать эту идею. С этого момента Флетчер разработал новую камеру для проведения измерений с маслом того же типа, которое используется для смазки в часах[12]. Сам Милликен в своей автобиографии вспоминает, что идея использовать масло пришла к нему в сентябре 1909 года[1].
По окончании эксперимента Флетчер написал статью, которую Милликен и он должны были опубликовать, но Милликен хотел стать единственным автором, хотя и сослаться на Флетчера как соавтора. Также правила Чикагского университета не позволяли статьям, подписанным более чем одним автором, быть частью докторской диссертации одного из них. Таким образом, Флетчеру пришлось изменить свою диссертацию и представить работу о броуновском движении, в то время как Милликен остался единственным автором опыта с каплей масла[2][13][14][15][16]. В основной статье фамилия Флетчера упомянута несколько раз, Милликен описывает эксперимент, используя местоимение «мы»[17].
Устройство[править | править код]
Устройство для опыта с каплями масла состояло из трёх камер. В большой камере находились две другие меньшего размера, и было залито 40 л моторного масла для поддержания постоянной температуры внутри установки с колебаниями всего 0,02 °C. Самая внутренняя камера состояла из двух круглых латунных пластин диаметром 22 см, расположенных горизонтально друг над другом на расстоянии 1,6 см друг от друга. В верхней пластине было небольшое отверстие в центре, и она была заряжена положительно (+); нижняя не имела отверстий и была заряжена отрицательно (−). Между этими пластинами создавалось однородное электрическое поле, направленное вниз или вверх, с напряженностью от 3000 до 8000 В/см. Пластины были разделены тремя небольшими кусками изолятора (эбонита), а всё пространство закрыто эбонитовой лентой снаружи[18]. В этой полосе эбонита было три стеклянных окна квадратной формы по 1,5 см с каждой стороны, расположенных под углом 0°, 165° и 180°. Узкий луч света, создаваемый дуговой лампой, проникал через первое окно и выходил через противоположное. 165º окно использовалось для наблюдения с помощью маленького телескопа, расположенного на удалении 61 см от внутренней части камеры[3].
Распылитель, подобный тем, что используется во флаконах для духов[12], создавал маленькие капли масла выше второй камеры, содержащей описанную выше камеру. Капли падали под действием гравитации, и некоторые из них проходили через маленькое игольное отверстие в верхней пластине. Освещение было устроено так, что капля виделась как сияющая[18]. Во время наблюдения за падением капли между пластинами отверстие закрывалось для предотвращения потоков воздуха. В качестве источника излучения использовались рентгеновские лучи или радий (испускающие β-лучи и γ-лучи). Излучение проходило через окно для освещения, что позволяло ионизировать молекулы воздуха (азот или кислород), а ионы, катионы или электроны поглощались каплей масла[3][18].
Схема устройства, использованного в опыте Милликена
Используемая техника[править | править код]
Падение капель масла в воздухе определяется законом Стокса, то есть скорость падения, 



Когда воздух ионизируется, капли поглощают электроны. В отсутствие электрического поля они продолжают падать с той же скоростью, поскольку массы электронов очень малы. Включая электрическое поле между пластинами, падение капли можно остановить, в этом случае уравняв силу тяжести и электростатическую силу, или, если напряженность электрического поля ещё больше увеличится, то можно заставить капли двигаться вверх. Движение вверх, опять же по закону Стокса, представляет собой движение с постоянной скоростью. Одну и ту же каплю можно поднимать и опускать до тех пор, пока она не коснётся одной из пластин, поэтому для одной и той же капли можно провести серию измерений[3][18].
Одним из основных моментов исследования Милликена является то, что капли были заряжены неопределенным количеством электронов, которое он не мог знать заранее. С помощью своих измерений он получал значения различных электрических зарядов, 


Расчёты с каплями[править | править код]
На тело, подчиняющееся закону Стокса, действуют две силы: гравитационная и лобового сопротивления. В тот момент, когда обе силы уравниваются, ускорение тела становится равным нулю, а его скорость — постоянной
Силы, возникающие при подъёме капли масла под действием электрического поля
Милликен использовал закон Стокса, чтобы связать установившуюся скорость падения: 



где 

Милликен внёс поправку в это уравнение, потому что его капли были очень маленькими, и соответствующее трение меньше, чем заданное по этому законом, поскольку в течение некоторого времени капли из-за своих малых размеров падают в вакууме. Уравнение Стокса верно для сфер размером более 0,1 см. Исправленная Милликеном формула принимает вид
Капли масла, наблюдаемые в телескопе
Движение капли вверх и вниз
при 

В отсутствие электрического поля капля падает в результате действия гравитационного поля Земли, и замедляется под действием силы трения Стокса 









и установившаяся скорость капли 
Выделение константы 
Электрический заряд капли 


В случае падения без электрического поля и без учёта поправки к закону Стокса, сделанной Милликеном для упрощения этой демонстрации, можно получить массу капли 




Массу капли 





Чтобы рассчитать массу 
Теперь следует использовать формулу нагрузки 
Упрощая, получается формула, которая даёт нагрузку на основе известных значений, измеримых в эксперименте[2]
Некоторые из значений эксперимента Милликена: вязкость воздуха 





Величина элементарного заряда e[править | править код]
В выражении заряда Милликен также использовал соображение, что капля масла находится в воздухе, поэтому она испытывает восходящую тягу из-за принципа Архимеда, силы которого учитываются в кажущемся весе
Таким образом получается формула, данная Милликеном, при замене плотности 

Значение, полученное в первоначальных экспериментах, проведённых Милликеном и Флетчером в 1911 году, составляло e = 4 891 × 10 −10 Фр = 1,631×10−19 Кл[3], что соответствует разнице в 4,8 % от принятого в настоящее время значения. С усовершенствованиями, внесёнными Милликеном позже, в 1913 году он достиг значения e = 4,774 ± 0,009 · 10−10 Фр = 1,592 ± 0,003·10−19 Кл[4], всего лишь на 0,62 % ниже принятого в настоящее время значения e = 1,602 176 634⋅10-19 Кл[23].
Последствия[править | править код]
Слева направо: В. Нернст, А. Эйнштейн, М. Планк, Р. А. Милликен и М. фон Лауэ в 1931 году
Экспериментальные данные Милликена 1912 года. Значения, опубликованные в 1913 году, и отброшенные значения
Весной 1910 года началась так называемая «электронная битва» между Милликеном и физиком Венского университета Феликсом Эренхафтом[en] (1879—1952). В том же году Эренхафт опубликовал[24] измерения элементарного заряда, выполненные с помощью эксперимента, аналогичного Милликену, но с использованием металлических частиц, и объявившего о существовании всего распределения зарядов меньше, чем заряд электрона. В последующие годы он со студентами продолжал публиковать статьи, указывающие на существование зарядов меньших, чем у электрона, которые они назвали субэлектронами. Это привело к тому, что вопрос о существовании субэлектронов стоял на повестке дня некоторых из самых известных физиков того времени (Макса Планка, Жана Перрена, Альберта Эйнштейна, Арнольда Зоммерфельда, Макса Борна и Эрвина Шрёдингера). Чтобы подкрепить свои результаты, Милликен улучшил эксперимент и провёл новые, более точные измерения, которые подтвердили, что заряд электрона является элементарным зарядом, опубликовав новую статью в 1913 году, в которой он также рассчитал постоянную Авогадро[4]. В 1916 году он опубликовал обширную статью, в которой подробно описал ряд ошибок в экспериментальной методике, использованной Эренхафтом[25]. Научное сообщество в значительной степени встало на сторону Милликена (Э. Варбург, Г. Рубенс, В. Вин, Ж. Перрен и А. Эйнштейн уже сделали это на Сольвеевской конференции 1911 года) и его регулярно номинировали на Нобелевскую премию по физике с 1916 года до присуждения в 1923 году за его работы по определению элементарного электрического заряда и фотоэффект[26].
Некоторое противоречие в исходных данных Милликена нашёл историк Джеральд Холтон (1978), который указал, что учёный записал в свой журнал больше измерений, чем включил в свой окончательный анализ. Холтон предположил, что эти точки данных не были включены в большой набор капель масла, измеренных в его экспериментах, без видимой причины. Это утверждение было оспорено Алланом Франклином[en], экспериментатором по физике высоких энергий и философом науки из Университета Колорадо[27]. В лабораторных журналах Милликена было обнаружено, что, несмотря на указание в его статье 1913 года, что все капли, которые он изучал в течение девяти недель эксперимента, были перечислены (с 13 февраля по 16 апреля 1912 года), всего 58, но количество капель, которые он измерил оказалось около 100. Милликен не включил данные о 25 каплях, из-за прерванного эксперимента до его завершения, ещё 17 не использовал, потому что считал, что в его измерениях были ошибки: капли слишком большие, засорение манометра пузырьком воздуха, конвекционные помехи, ошибки секундомера или неисправность форсунки (распылителя). С другой стороны, Эренгафт, следуя наиболее ортодоксальному научному методу, представил все свои результаты, и нельзя было сделать вывод, что заряд электрона наименьший в природе. Изучение лабораторных журналов Милликена, на рубеже XX века, зародило подозрение в манипулировании данными[14][28][18]. Однако тщательный анализ неопубликованных данных показывает, что Милликен ни в коем случае не исключал данные с намерением манипулировать результатами. Многие из неопубликованных данных, если их использовать, дадут тот же результат, что и опубликованные. Дэвид Гудштейн[en] исследовал оригинальные подробные записные книжки, которые вёл Милликен, и пришёл к выводу, что Милликен прямо заявляет в отчётах, что он включил только капли, прошедшие «полную серию наблюдений», и не исключил ни одной капли из этой группы полных измерений[29][30]. Впрочем, некоторые исследователи критикуют Милликена за многочисленные арифметические ошибки в статье[18].
Эксперимент Милликена как пример психологических эффектов в научной методологии[править | править код]
В приветственной речи, произнесённой в Калифорнийском технологическом институте в 1974 году (и перепечатанной в книге «Вы, конечно, шутите, мистер Фейнман!» в 1985 году, а также в книге «Удовольствие от открытия вещей»[en] в 1999 году), физик Ричард Фейнман отметил[31][32]:
Мы немало научились на собственном опыте, о том, как бороться с некоторыми способами, которыми мы сами себя обманываем. Один пример: Милликен измерил заряд электрона в эксперименте с падающими каплями масла и получил ответ, который, как мы теперь знаем, не совсем правильный. Он немного неточен потому, что Милликен использовал неверное значение вязкости воздуха. Интересно взглянуть на историю измерений заряда электрона после Милликена. Если вы изобразите их как функцию времени, вы обнаружите, что одно немного больше, чем у Милликена, следующее — немного больше прошлого, а следующий за ним — немного больше последнего, пока, наконец, они не успокоились, остановившись на числе, которое ещё больше.
Почему сразу не было открыто, что новое число больше? Учёные стыдятся этой истории, потому что очевидно, что люди вели себя следующим образом: когда они получали число, которое было заметно больше, чем у Милликена, они думали, что что-то не так — и начинали искать и находили причину почему что-то может быть не так. Когда они получили число, близкое к значению Милликена, они не столь усердствовали. И поэтому они удаляли числа, которые слишком сильно отличались, и делали другие подобные вещи …
We have learned a lot from experience about how to handle some of the ways we fool ourselves. One example: Millikan measured the charge on an electron by an experiment with falling oil drops, and got an answer which we now know not to be quite right. It’s a little bit off because he had the incorrect value for the viscosity of air. It’s interesting to look at the history of measurements of the charge of an electron, after Millikan. If you plot them as a function of time, you find that one is a little bit bigger than Millikan’s, and the next one’s a little bit bigger than that, and the next one’s a little bit bigger than that, until finally they settle down to a number which is higher.
Why didn’t they discover the new number was higher right away? It’s a thing that scientists are ashamed of—this history—because it’s apparent that people did things like this: When they got a number that was too high above Millikan’s, they thought something must be wrong—and they would look for and find a reason why something might be wrong. When they got a number close to Millikan’s value they didn’t look so hard. And so they eliminated the numbers that were too far off, and did other things like that …
По состоянию на май 2019 года размер элементарного заряда определён как точная величина, равная e = −1,602 176 634⋅10−19 Кл[23]. До этого с 2014 года принятым значением было[33] (−1,6021766208 ± (98))⋅10−19 Кл, где (98) указывало неопределённость двух последних десятичных знаков. В своей Нобелевской лекции Милликен привёл своё значение для заряда электрона (−4,774 ± (5))⋅10−10 Фр, что равняется (−1,5924 ± (17))⋅10−19 Кл[5].
Проведя рентгеновские эксперименты, Эрик Беклин в 1928 году обнаружил большее значение элементарного заряда, (4,793 ± 0,015)⋅10-10 статКл или (1,5987 ± 0,005)⋅10-19 Кл, что находится в пределах неопределённости точного значения. Раймонд Бирдж, проводя обзор физических констант в 1929 году, заявил: «Исследование Беклина представляет собой новаторскую работу, и вполне вероятно, что как таковое оно содержит различные неожиданные источники систематических ошибок. Если [ … это …] взвешено в соответствии с очевидной вероятной ошибкой […], средневзвешенное значение всё равно будет подозрительно высоким […] автор, наконец, решил отказаться от значения Беклина и использовал взвешенное среднее оставшихся двух значений». Бирдж усреднил результат Милликена и другой, менее точный рентгеновский эксперимент, который совпал с результатом Милликена[34] .
Последовательные рентгеновские эксперименты продолжали давать высокие результаты, и предположения об ошибках были исключены экспериментально. Стен фон Фризен[en] измерил значение с помощью нового метода дифракции электронов, и переделанный эксперимент с каплей масла дали высокие цифры. К 1937 году стало «совершенно очевидно», что значение Милликена больше не может быть правильным, и установленное значение стало (4,800 ± 0,005)⋅10-10 статКл или (1,6011 ± 0,0017)⋅10-19 Кл[35].
Примечания[править | править код]
- ↑ 1 2 Perry, 2007, p. 57.
- ↑ 1 2 3 Millikan, R. A. (30 setembre 1910). “The Isolation of an Ion, A Precision Measurement of Its Charge, and the Correction of Stokes’s Law”. Science. 32 (822): 436—448. Архивировано из оригинала 2021-04-20. Дата обращения 2021-04-20.
- ↑ 1 2 3 4 5 6 Millikan, R. A. (Abril 1911). “The Isolation of an Ion, a Precision Measurement of its Charge, and the Correction of Stokes’s Law” (PDF). Phys. Rev. 32 (4): 349—397. DOI:10.1103/PhysRevSeriesI.32.349. Архивировано (PDF) из оригинала 2019-07-13. Дата обращения 2021-04-20.
- ↑ 1 2 3 Millikan, R. A. (1 agost 1913). “On the Elementary Electrical Charge and the Avogadro Constant”. Phys. Rev. 2 (2): 109—143. DOI:10.1103/PhysRev.2.109.
- ↑ 1 2 Robert Millikan. APS Physics. Дата обращения: 26 апреля 2016. Архивировано 24 апреля 2021 года.
- ↑ Thomson, J. J. (1897). “Cathode Rays”. Philosophical Magazine. 44: 293—316. Архивировано из оригинала 2019-08-30. Дата обращения 2021-04-20.
- ↑ Serway, R.; Moses, C.; Moyer, C. Modern Physics (англ.). — 3rd ed. — Thomson Brooks Cole, 2005. — P. 108. — 682 p. — ISBN 0534493394.
- ↑ Townsend, J.S (1897). “On Electricity in Gases and the Formation of Clouds in Charged Gases”. Proc. Cambridge Phil. Soc. 9: 244—258.
- ↑ Thomson, G. P. (1965). “Harold Albert Wilson 1874-1964”. Biographical Memoirs of Fellows of the Royal Society. 11: 186—201. DOI:10.1098/rsbm.1965.0013.
- ↑ Millikan, R. A. (1908). “On the Charge Carried by the Negative Ion of an Ionized Gas” (PDF). Phys. Rev. 26: 197—198. Архивировано (PDF) из оригинала 2018-11-04. Дата обращения 2021-04-20.
- ↑ Perry, 2007, p. 56.
- ↑ 1 2 Schirber, M. (20 gener 2012). “Landmarks – Millikan Measures the Electron’s Charge”. Physics. 9: 9. DOI:10.1103/Physics.5.9.
- ↑ Fletcher, H. (1982). “My work with Millikan on the oildrop experiment” (PDF). Phys. Today. 35 (6): 43—47. DOI:10.1063/1.2915126. Архивировано из оригинала (PDF) 2014-10-12. Дата обращения 2021-04-20.
- ↑ 1 2 Trocchio, Federico Di. Las mentiras de la ciencia: porqué y cómo engañan los científicos?. — Grupo Anaya Comercial, 1998. — 469 с. — ISBN 8420639885.
- ↑ Perry, 2007, p. 58—59.
- ↑ Radioactivity, 2016, p. 186.
- ↑ Perry, 2007, p. 59.
- ↑ 1 2 3 4 5 6 7 8 9 10 Tutubalin et al., 2016.
- ↑ Tutubalin, Valeriy; Barabasheva, Yulia; Devyatkova, Galina; Uger Elena. The Millikan experiment from the point of view of mathematical statistics = Измерения Милликеном заряда электрона и математическая статистика // Вопросы Истории Естествознания и Техники. — 2016. — Т. 37. — С. 233—250.
- ↑ 1 2 3 Serway, Moses & Moyer, 2005, p. 118.
- ↑ Serway, Moses & Moyer, 2005, p. 115.
- ↑ Radioactivity, 2016, p. 184.
- ↑ 1 2 9th edition of the SI Brochure. BIPM (2019). Дата обращения: 20 мая 2019. Архивировано 19 апреля 2021 года.
- ↑ Ehrenhaft, F. (1910). “Über die Messung von Elektrizitätsmengen, die kleiner zu sein scheinen als die Ladung des einwertigen Wasserstoffions oder Elektrons und von dessen Vielfachen abweichen”. Kais. Akad. Wiss. Wien, Sitzber. math.-nat. Kl. (IIa) S. 119: 815—867.
- ↑ Millikan, R. A. (1916). “The existence of a subelectron?” (PDF). Physical Review. 8: 595—625. Архивировано (PDF) из оригинала 2020-09-23. Дата обращения 2021-04-20.
- ↑ The Nobel Prize in Physics 1923. Nobelprize.org. Nobel Media AB 2014. Дата обращения: Dimecres, 6 gener 2015. Архивировано 29 июля 2018 года.
- ↑ Franklin, A. (1997). “Millikan’s Oil-Drop Experiments”. The Chemical Educator. 2 (1): 1&ndash, 14. DOI:10.1007/s00897970102a.
- ↑ Niaz, Mansoor. Innovating Science Teacher Education: A History and Philosophy of Science Perspective. — Routledge, 2010. — 240 с. — ISBN 9781136941955.
- ↑ Goodstein, D. (2000). “In defense of Robert Andrews Millikan” (PDF). Engineering and Science. Pasadena, California: Caltech Office of Public Relations. 63 (4): 30&ndash, 38. Архивировано (PDF) из оригинала 2021-04-29. Дата обращения 2021-04-25.
- ↑ Goodstein, David (2001). “In Defense of Robert Andrews Millikan”. American Scientist. 89 (1): 54. Bibcode:2001AmSci..89…54G. DOI:10.1511/2001.1.54.
- ↑ Cargo Cult Science. California Institute of Technology. Дата обращения: 22 февраля 2018. Архивировано 17 апреля 2021 года. (adapted from the 1974 California Institute of Technology Архивная копия от 25 апреля 2021 на Wayback Machine commencement address), Donald Simanek’s Pages Архивная копия от 5 июня 2021 на Wayback Machine, Lock Haven University Архивная копия от 24 апреля 2021 на Wayback Machine, rev. December 2017.
- ↑ Feynman, Richard Phillips. “Surely you’re joking, Mr. Feynman!”: adventures of a curious character / Richard Phillips Feynman, Ralph Leighton, Edward Hutchings. — New York : W. W. Norton & Company, 1997-04-01. — P. 342. — ISBN 978-0-393-31604-9. Архивная копия от 1 января 2014 на Wayback Machine
- ↑ 2014 CODATA Values: Older values of the constants. The NIST Reference on Constants, Units, and Uncertainty. NIST (25 июня 2015). Дата обращения: 19 августа 2019. Архивировано 16 июня 2019 года.
- ↑ Birge, Raymond T. (1 July 1929). “Probable Values of the General Physical Constants”. Reviews of Modern Physics. 1 (1): 1—73. Bibcode:1929RvMP….1….1B. DOI:10.1103/revmodphys.1.1.
- ↑ von Friesen, Sten (June 1937). “On the values of fundamental atomic constants”. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 160 (902): 424—440. Bibcode:1937RSPSA.160..424V. DOI:10.1098/rspa.1937.0118.
Ссылки[править | править код]
- Simulation of the oil drop experiment (requires JavaScript) Архивная копия от 25 февраля 2021 на Wayback Machine
- Thomsen, Marshall, «Good to the Last Drop». Millikan Stories as «Canned» Pedagogy. Eastern Michigan University.
- CSR/TSGC Team, «Quark search experiment Архивная копия от 11 марта 2007 на Wayback Machine». The University of Texas at Austin.
- Engeness, T. E., «The Millikan Oil Drop Experiment Архивная копия от 10 июня 2007 на Wayback Machine». 25 April 2005.
- Millikan R. A. (1913). “On the elementary electrical charge and the Avogadro constant” (PDF). Physical Review. Series II. 2 (2): 109&ndash, 143. Bibcode:1913PhRv….2..109M. DOI:10.1103/PhysRev.2.109. Архивировано (PDF) из оригинала 2013-09-27. Дата обращения 2013-01-10. Paper by Millikan discussing modifications to his original experiment to improve its accuracy.
- Hudspeth, Paul (2000). “A search for free quarks in the micro gravity environment of the International Space Station”. AIP Conference Proceedings. 504: 715—722. Bibcode:2000AIPC..504..715H. DOI:10.1063/1.1302567. A variation of this experiment has been suggested for the International Space Station.
- Perry, Michael F. (2007). “Remembering the oil-drop experiment” (PDF). Physics Today. 60 (5): 56—60. Bibcode:2007PhT….60e..56P. DOI:10.1063/1.2743125. Архивировано (PDF) из оригинала 2016-03-03. Дата обращения 2021-04-20.
- L’Annunziata, Michael F. Radioactivity. Introduction and History, from the Quantum to Quarks (англ.). — 2nd ed.. — Elsevier, 2016. — 932 p. — ISBN 0444634967.
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Confused by the Question (oil drop charge)
-
Thread starter
linuxux -
Start date
Mar 14, 2007 -
-
Tags -
Charge
Confused
Drop
-
- Mar 14, 2007
- #1
the givens were oil drop mass: 2.6 x 10^15 kg, plate separation = .005 m ,potential difference between plate = 270 V , and it also says the lower plate is at a lower potential.
to determine E, i used E = v / d , where v is voltage, and d is plate separation, then i used the above equation to determine q.
Answers and Replies
- Mar 15, 2007
- #2
- Mar 15, 2007
- #3
When i divide this number by the charge of an electron , [tex]e=1.60cdot10^{-19}[/tex] , i get 2.93 !
What went wrong?
- Mar 15, 2007
- #4
- Mar 15, 2007
- #5
- Mar 15, 2007
- #6
- Mar 15, 2007
- #7
- Mar 16, 2007
- #8
I don’t know about the excess electrons sorry.
Suggested for: Confused by the Question (oil drop charge)
- Apr 20, 2022
- Apr 13, 2023
- Sep 24, 2022
- Apr 8, 2023
- Dec 13, 2020
- Jul 19, 2022
- Mar 26, 2023
- May 15, 2022
- Feb 9, 2023
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Электрический заряд
В соответствии с современными представлениями атомы всех тел построены из электрически заряженных частиц. Относительно легких электронов и довольно тяжелых положительно заряженных атомных ядер. В целом тела электрически нейтральны, так как суммарный отрицательный заряд электронов равен суммарному положительному заряду атомных ядер данного тела. Отрицательный заряд электрона равен (так как к этой величине прибегают довольно часто, то заряд электрона часто имеет свое обозначение $q_e$ или $e$) $e=1,6cdot {10}^{-16}Кл$ (в системе СИ) или $e=4,8cdot {10}^{-10}$ абсолютных электростатических единиц электричества (в СГСЭ). Положительные заряды атомных ядер равны по модулю целым, кратным элементарному заряду (так еще называют заряд электрона), то есть заряд ядра: $q=ne$, где $n$- целое число. Масса электрона равна $m_e=9.1cdot {10}^{-31}кг$. Самым лёгким ядром является ядро атома водорода, которое именуется протоном. Его масса равна $m_p=1.67cdot {10}^{-27}кг$. Размеры атомных ядер, электронов малы по сравнению с расстояниями между ними в атомах и молекулах, что позволяет во многих случаях считать их материальными точками, которые имеют массу и электрический заряд.
Мысль о дискретности электрического заряда была высказана уже Б. Франклином в 1752 г. Экспериментом она подтверждена Фарадеем, при исследовании законов электролиза. Однако окончательный вывод о дискретности электрического заряда был сделан Г.Л. Гельмгольцем и Д. Стонеем в 1881 г. Количественное значение элементарного заряда было вычислено на основании законов электролиза. Прямое экспериментальное измерение элементарного заряда было сделано Р.Э. Милликеном в 1909 г. Были предприняты поиски дробных зарядов, но они дали отрицательный результат. Сделаем вывод, на сегодняшний момент установлено, что дробных зарядов в свободном состоянии не существует.
Независимость количественного значения элементарного заряда от скорости доказывается фактом нейтральности атомов. Электроны в атоме движутся значительно быстрее протонов (это следствие различая масс). В том случае, если бы заряд зависел от скорости, то нейтральность атомов нарушалась. Инвариантность заряда относительно скорости — одно из экспериментальных обоснований теории электричества.
«Электрический заряд. Закон его сохранения» 👇
В большинстве макроскопических явлений участвует очень большое количество электрических зарядов, в таком случае их дискретность значения не имеет, и в большинстве случаев можно считать, что заряд как бы непрерывно распределён в пространстве.
Объемная плотность распределения
Объемной плотностью распределения зарядов называют отношение:
где $triangle Q$- полный заряд, находящийся в объеме $triangle V$, $e_i$ — элементарный заряд, $triangle V$ — малый объем, но не бесконечно малый в математическом смысле, он характеризуется координатой точки внутри него. Это значит, что можно записать: $rho =rho left(x,y,zright).$ При определении объемной плотности $rho $ можно рассматривать как функцию, а заряд считать непрерывно распределенным, тогда можно записать, что:
где $dV$- дифференциал объема.
Концентрацией зарядов (n) называют отношение:
где ∆n — количество зарядов в объеме $triangle V$.
Поверхностной плотностью заряда ($sigma$) называется соотношение:
где $triangle S$- малая площадь поверхности, $triangle Q$ — заряд, находящийся на поверхности $triangle S$. Полный заряд поверхности, при условии равномерного распределения заряда по ней, можно найти как:
где $dS$ — дифференциал площади поверхности.
Закон сохранения заряда
Закон сохранения заряда приведем в двух формах. Одна из них следующая. Она исходит из двух фактов:
- Электрон и протон — материальные частицы с бесконечным временем жизни, их заряды инвариантны и не зависят от скорости. В такой трактовке, закон сохранение — следствие неуничтожимой носителей заряда.
- Кроме протонов и электронов существуют другие заряженные элементарные частицы. Все они рождаются, порождают другие частицы, участвуют в процессах взаимных превращений, но какими бы ни были превращения, суммарный заряд частиц до равен суммарному заряду после взаимопревращений.
Таким образом, закон сохранения заряда может быть сформулирован следующим образом:
Заряд сохраняется при всех процессах и движениях носителей зарядов.
Здесь надо отметить, что имея некоторую самостоятельность, заряд не может существовать отдельно от его носителя – материи.
Закон сохранения заряда можно записать в интегральной форме. Изменение заряда в некотором объеме V может произойти только в результате втекания или вытекания заряда через замкнутую поверхность $S$, которая ограничивает объем $V$. Или в математическом виде:
где сила тока, протекающая через замкнутую поверхность S равна интегралу по этой поверхности:
где $overrightarrow{j}cdot doverrightarrow{S}=jdScos(widehat{overrightarrow{j}cdot doverrightarrow{S}})$, j — плотность тока $overrightarrow{j}=frac{1}{triangle V}sumlimits_{triangle V}{e_i{overrightarrow{v}}_i}$, ${overrightarrow{v}}_i$ — скорость элементарного заряда, $doverrightarrow{S}$ направлен по внешней нормали к поверхности.
$frac{partial }{partial t}intnolimits_V{rho dV}$- скорость изменения заряда в объеме. Знак минус в формуле (6) указывает на то, что если положительный заряд внутри объема уменьшатся, то плотность тока направлена из объема $V$.
Дифференциальная форма закона сохранения заряда (оно же уравнение непрерывности) имеет вид:
Напомним, что $divoverrightarrow{j}=frac{partial j_x}{partial x}+frac{partial j_y}{partial y}+frac{partial j_z}{partial z}$.
Пример 1
Схема опытов Милликена изображена на рис. 1. Маленькие заряженные шарообразные частицы (капельки масла) движутся в воздухе при наличии однородного электрического поля $overrightarrow{E}.$ На частицу действуют следующие силы: силы тяжести ($ {rho }_{ch}>{rho }_{vozd}, плотность частицы left( {rho }_{ch}right), плотность воздуха ({rho }_{vozd})$), сила вязкого трения, электростатическая сила, сила Архимеда. Сила вязкого трения пропорциональна скорости, следовательно, при постоянной скорости частицы сумма действующих на частицу сил равна нулю. Все силы, помимо электрической измерялись экспериментально при движении частицы в отсутствии электрического поля. Исследовав движение частицы в поле, Милликен нашел силу $qoverrightarrow{E}.$ Это позволило вычислить заряд частицы, так как напряженность поля известна. Изменяя напряженность поля можно добиться, чтобы заряженная частица находилась в покое.
Задание: В электростатическое поле впрыскивают заряженную каплю масла (плотность масла считать известной, равной ${rho }_{ch}$) радиуса R. Напряжённость поля (E) подбирают такой, чтобы капля масла оставалась неподвижной. Капля находится в воздухе, плотность воздуха ${rho }_{vozd}$. Определите заряд капли.
Решение:
Рис. 1
Если скорость частицы равна нулю, то сила вязкого трения также равна нулю.
Запишем второй закон Ньютона для заряженной капельки масла, если мы знаем, что частица неподвижна:
[moverrightarrow{g}+overrightarrow{F_A}+overrightarrow{F_E}=0left(1.1right).]
Направим ось ОX вдоль поля, запишем проекцию уравнения (1.1) на эту ось:
[F_A+F_E-mg=0 left(1.2right),]
где $F_A$ сила Архимеда, которая равна:
[F_A=с_{vozd}Vg=с_{vozd}frac{4}{3}pi R^3g left(1.3right),]
$R$ — радиус капли масла.
$F_E$ — электростатическая сила, действующая на заряженную каплю со стороны поля:
[F_E=qE left(1.4right),]
где $q$ — заряд капли масла, $E$ — напряженность электростатического поля.
$mg$- сила тяжести, действующая на каплю, ее можно выразить через плотность масла:
[mg=с_{ch}frac{4}{3} pi R^3g left(1.5right).]
Подставим выражения (1.3) — (1.5) в уравнение (1.2), получим:
[{rho }_{vozd}frac{4}{3}pi R^3g +qE-{rho }_{ch}gfrac{4}{3}pi R^3=0 left(1.6right).]
Выразим из (1.6) заряд капли:
[q=frac{{rho }_{ch}gfrac{4}{3}pi R^3-{rho }_{vozd}frac{4}{3}pi R^3g}{E}=frac{frac{4}{3}{pi R^3(rho }_{ch}-{rho }_{vozd})g}{E}]
Ответ: Заряд капли масла должен быть $q=frac{frac{4}{3}{pi R^3(rho }_{ch}-{rho }_{vozd})g}{E}$.
Пример 2
Задание: Два одинаковых металлических шарика имею заряды $q_1$ и $q_2$ одинаковые по знаку. Их соединили, а за тем развели. Чему будут равны заряды каждого из шариков после разъединения.
Решение:
Основа для решения — закон сохранения заряда, запишем его для нашего случая:
[q_1+q_2={q’}_1+{q’}_2 left(2.1right).]
Так как шарики одинаковые можем записать, что суммарный заряд шариков $q_1+q_2$ разделится поровну между ними, то есть:
[{q’}_1=frac{q_1+q_2}{2}, {q’}_2=frac{q_1+q_2}{2}.]
Ответ: Заряд каждого шарика станет равен q=$frac{q_1+q_2}{2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме