Как найти заряд конденсатора если известно напряжение

Как найти напряжение и заряд на каждом из конденсаторов.

UptoLike

Конденсаторы емкостями ( = 2) мкФ, ( = 15) мкФ и ( = 10) мкФ соединены последовательно и находятся под напряжением (U = 850) В. Определить напряжение и заряд на каждом из конденсаторов.

ОПРЕДЕЛЕНИЯ

количественная характеристика, показывающая степень возможного участия тела в электромагнитных взаимодействиях

устройство, предназначенное для получения нужных величин электрической ёмкости и способное накапливать и отдавать (перераспределять) электрические заряды

разность потенциалов между двумя точками электрической цепи; на участке цепи, не содержащей электродвижущую силу, равно произведению силы тока на сопротивление участка

Дополнительные материалы

Как определить напряжение на обкладках конденсаторов.

Конденсаторы емкостью ( = 5) мкФ и ( = 10) мкФ заряжены до напряжений ( = 60) В и ( = 100) В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.

Как определить на сколько изменится емкость батареи.

Два одинаковых плоских воздушных конденсатора емкостью (C = 100) пФ каждый соединены в батарею последовательно. Определить, на сколько изменится емкость (C) батареи, если пространство между пластинами одного из конденсаторов заполнить парафином.

Источник

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

2. Емкость плоского конденсатора

C = ε a ⋅ S d = ε r ⋅ ε 0 ⋅ S d ,

S – поверхность каждой пластины конденсатора;

ε_r – диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4 π ⋅ с 2 ⋅ 10 − 7 ≈ 8,85418782 ⋅ 10 − 12 Ф м – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C = C 1 + C 2 + . + C n = ∑ k = 1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 + . + 1 C n = ∑ k = 1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 = U ⋅ C 2 C 1 + C 2 ; U 2 = U ⋅ C 1 C 1 + C 2 .

5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

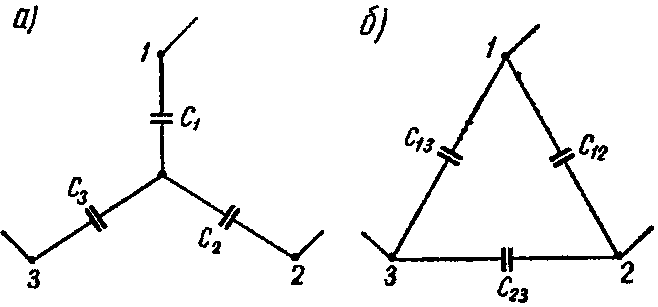
осуществляется по формулам:

6. Энергия электростатического поля конденсатора:

W = C ⋅ U 2 2 = Q ⋅ U 2 = Q 2 2 C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k = 1 n E k = ∑ k = 1 n U C k = ∑ k = 1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

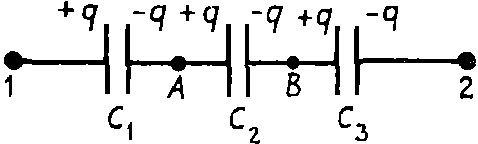
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость – это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ – φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 = ( φ 1 − φ A ) + ( φ A − φ B ) + ( φ B − φ 2 ) = U 1 A + U A B + U B 2 .

Воспользовавшись формулой напряжения на конденсаторе

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 + . + 1 C n = ∑ k = 1 n 1 C k .

Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

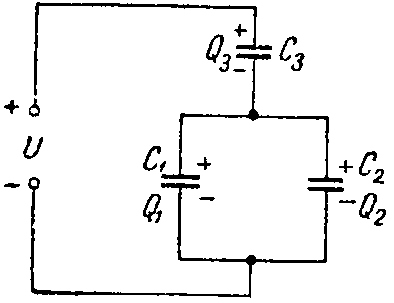
Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

эквивалентная емкость всей цепи равна

C = C 12 ⋅ C 3 C 12 + C 3 = 200 ⋅ 300 500 = 120 м к Ф .

Заряд на эквивалентной емкости

Q = C·U = 120·10 –6 ·240 = 288·10 –4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10 –4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288 ⋅ 10 − 4 300 ⋅ 10 − 6 = 96 В .

Напряжение на конденсаторах C₁ и C₂ равно

их заряды имеют следующие значения

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72 ⋅ 10 − 4 ⋅ 144 2 ≈ 0,52 Д ж ; W 2 = Q 2 ⋅ U 2 2 = 216 ⋅ 10 − 4 ⋅ 144 2 ≈ 1,56 Д ж ; W 3 = Q 3 ⋅ U 3 2 = 288 ⋅ 10 − 4 ⋅ 96 2 ≈ 1,38 Д ж .

Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см 2 , имеет диэлектрик, состоящий из слюды (ε_r₁ = 6) толщиною d₁ = 0,3 мм и стекла (ε_r₂ = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

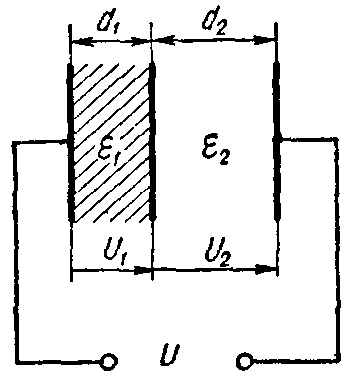
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C = C 1 ⋅ C 2 C 1 + C 2 = ε a 1 ⋅ S d 1 ⋅ ε a 2 ⋅ S d 2 ε a 1 ⋅ S d 1 + ε a 2 ⋅ S d 2 = ε a 1 ⋅ ε a 2 ⋅ S ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 .

C = ε 0 ⋅ ε r 1 ⋅ ε r 2 ⋅ S ε r 1 ⋅ d 2 + ε r 2 ⋅ d 1 = 8,85 ⋅ 10 − 12 ⋅ 6 ⋅ 7 ⋅ 12 ⋅ 10 − 4 6 ⋅ 0,4 ⋅ 10 − 3 + 7 ⋅ 0,3 ⋅ 10 − 3 = 99 ⋅ 10 − 12 Ф .

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C ⋅ U п р ε a 1 ⋅ S d 1 = ε a 2 ⋅ d 1 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U п р ; U 2 = Q C 2 = C ⋅ U п р ε a 2 ⋅ S d 2 = ε a 1 ⋅ d 2 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U п р .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a 2 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U ′ п р ; E 2 = U 2 d 2 = ε a 1 ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ⋅ U ″ п р .

Здесь U’_np – общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»_np – общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ п р = E 1 ⋅ ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ε a 2 = 49,5 к В ; U ″ п р = E 2 ⋅ ε a 1 ⋅ d 2 + ε a 2 ⋅ d 1 ε a 1 = 27,0 к В .

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см 2 . Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅ S d 1 ⋅ U 2 2 ,

где С₁ – емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из

где C₂ – емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅ S d 2 ⋅ U 2 2 2 = ε 0 ⋅ S 10 d 1 ⋅ ( 10 U ) 2 2 = 10 ⋅ ε 0 ⋅ S d 1 ⋅ U 2 2 = 10 ⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 = 9 ⋅ W 1 = 9 ⋅ ε 0 ⋅ S d 1 ⋅ U 2 2 = 2,86 ⋅ 10 − 7 Д ж .

Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅ U = 20 ⋅ 10 − 6 30 ⋅ 10 − 6 + 20 ⋅ 10 − 6 ⋅ 20 = 8 В ; U 2 = U − U 1 = 20 − 8 = 12 В .

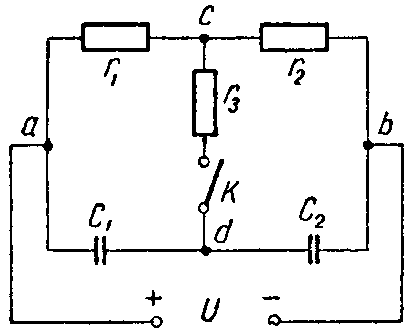
Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I = U r 1 + r 2 = 20 500 = 0,04 А ,

а через сопротивление r₃ ток не протекает.

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

Аналогично напряжение на втором конденсаторе равно

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

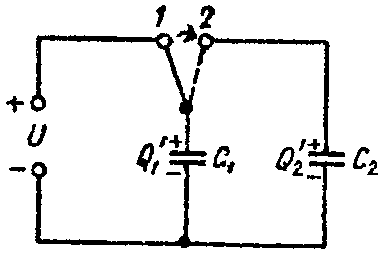
Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

По второму закону Кирхгофа имеем

0 = U C 1 − U C 2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

Q ′ 1 5 ⋅ 10 − 6 − Q ′ 2 120 ⋅ 10 − 6 = 0. ( 2 )

Решая уравнения (1) и (2), найдем

Напряжение на зажимах конденсаторов станет равным

U C 1 = Q ′ 1 C 1 = U C 2 = Q ′ 2 C 2 = 5 ⋅ 10 − 6 5 ⋅ 10 − 6 = 1 В .

Энергия обоих конденсаторов будет равна

W = C 1 ⋅ U C 1 2 2 + C 2 ⋅ U C 2 2 2 = 62,5 ⋅ 10 − 6 Д ж .

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W н а ч = C 1 ⋅ U 2 = 5 ⋅ 10 − 6 ⋅ 25 2 2 = 1562,5 ⋅ 10 − 6 Д ж .

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10 –6 – 62,5·10 –6 = 1500·10 –6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

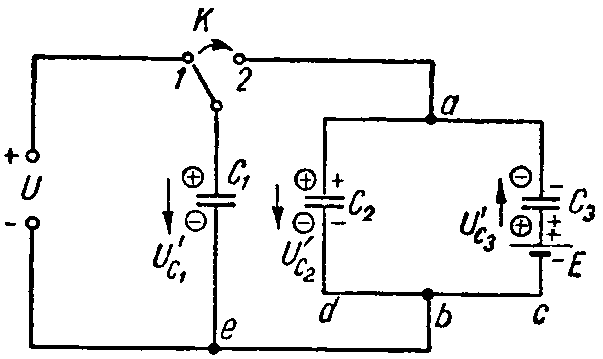
Рубильник находится в положении 1. Заряд конденсатора C₁ равен

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E = U C 2 + U C 3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅ E = 30 ⋅ 10 − 6 ⋅ 60 ⋅ 10 − 6 90 ⋅ 10 − 6 ⋅ 50 = 1 ⋅ 10 − 3 К л .

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

0 = U ′ C 1 − U ′ C 2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

E = U ′ C 2 − U ′ C 3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) – (3), после подстановки числовых значений величин, примут вид

Решая совместно уравнения (4) – (6), получим

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C 1 = Q ′ 1 C 1 = 0,33 ⋅ 10 − 3 10 ⋅ 10 6 = 33 В ; U C 2 = Q ′ 2 C 2 = 0,99 ⋅ 10 − 3 30 ⋅ 10 6 = 33 В ; U C 3 = Q ′ 3 C 3 = 1,02 ⋅ 10 − 3 60 ⋅ 10 6 = 17 В .

Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

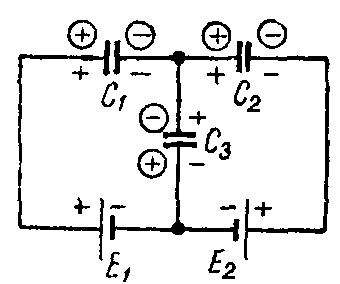
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 = 0 ; E 1 = U C 1 − U C 3 = Q 1 C 1 − Q 3 C 3 ; E 2 = − U C 2 − U C 3 = − Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ – противоположна выбранной.

Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

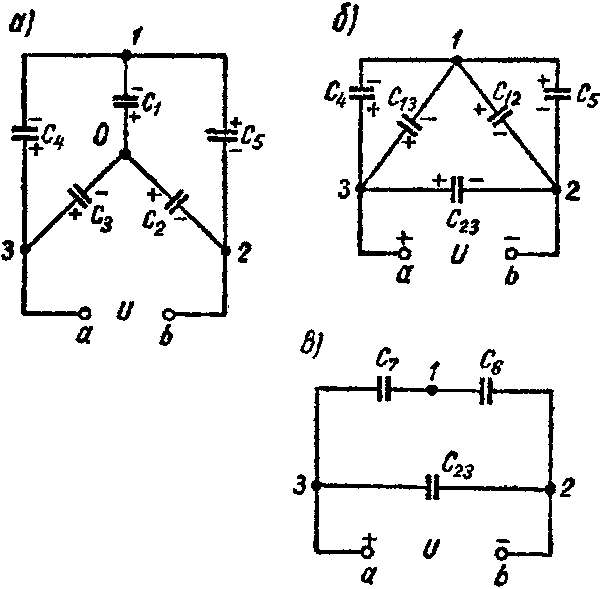
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 = 0,6 м к Ф ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 = 1,0 м к Ф ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 = 1,5 м к Ф .

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C a b = C 23 + C 6 ⋅ C 7 C 6 + C 7 = 2,7 м к Ф .

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅ U = 6 В .

Таково же напряжение и на конденсаторах C₄ и C₁₃

Напряжение на конденсаторе C₆ равно

По закону сохранения электричества для узла 1 схем 8, а и б имеем

а напряжение на конденсаторе, емкостью C₁ составляет

Далее находим напряжения и заряды на остальных конденсаторах

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 = 0 ; ( 3 )

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 = 0 ; ( 4 )

Система уравнений (1) – (5) – содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

E 1 = U C 1 + U C 4 − U C 3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

E 2 = U C 5 − U C 3 + U C 2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

0 = U C 4 − U C 5 − U C 6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

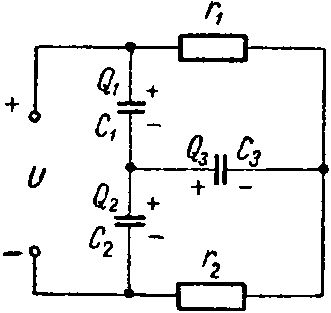
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Через сопротивления протекает ток

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 = 0 ; U = U C 1 + U C 2 = Q 1 C 1 + Q 2 C 2 ; I ⋅ r 1 = U C 1 + U C 3 = Q 1 C 1 + Q 3 C 3 ,

Q 1 = Q 2 + Q 3 ; 45 = Q 1 6 ⋅ 10 − 6 + Q 2 2 ⋅ 10 − 6 ; 25 = Q 1 6 ⋅ 10 − 6 + Q 3 3 ⋅ 10 − 6 .

Решив эту систему уравнений, найдем, что

Цепи с конденсаторами, Конденсатор в цепи постоянного тока, Расчет цепи конденсаторов, параллельное соединение конденсаторов, последовательное соединение конденсаторов

Источник

Как найти заряд конденсатора

В технике и задачах по физике иногда требуется найти заряд конденсатора. Непосредственное измерение заряда конденсатора – задача довольно трудоемкая. Поэтому на практике используются более доступные способы нахождения заряда конденсатора.

Вам понадобится

конденсатор, вольтметр

Инструкция

Чтобы найти заряд конденсатора, подключенного к источнику постоянного напряжения, умножьте емкость конденсатора на величину напряжения, т.е. воспользуйтесь формулой:
Q=UC, где:
Q – заряд конденсатора, в кулонах,
U – напряжение источника напряжения, в вольтах,
С – емкость конденсатора, в фарадах.
Учтите, что вышеприведенная формула определяет величину заряда полностью заряженного конденсатора. Но так как зарядка конденсатора происходит достаточно быстро, то на практике пользуются именно этой закономерностью.

Напряжение источника питания можно измерить вольтметром. Для этого переключите его в режим измерения постоянного напряжения и подключите клеммы прибора к источнику напряжения. Запишите показания прибора в вольтах.

Узнать емкость конденсатора можно прочитав маркировку на его корпусе. Учтите, что единица емкости фарада (Ф)– очень большая, поэтому на практике используется редко. Для обозначения емкости конденсаторов используются более мелкие единицы. Это микрофарада (мкФ), равная одной миллионной фарады и пикофарада (пФ), равная одной миллионной микрофарады.
1 мкФ=10-6 Ф, 1 пФ = 10-12 Ф.
Иногда используется и промежуточная единица емкости – нанофарада, равная одной миллиардной части фарады.
1 нФ = 10-9 Ф.

Если конденсатор малогабаритный, то его емкость указывается с помощью условных обозначений.
Внимательно прочтите маркировку конденсатора, обратив внимание на его цвет.Если на конденсаторе указаны всего две цифры, то это его емкость в пикофарадах.
Так, например, надпись «60» будет означать емкость 60 пФ.

Если на конденсаторе указана одна прописная латинская буква или цифра, то найдите в нижеприведенной таблице соответствующее числовое значениеA 1.0 I 1.8 R 3.3 Y 5.6
B 1.1 J 2.0 S 3.6 Z 6.2
C 1.2 K 2.2 T 3.9 3 6.8
D 1.3 L 2.4 V 4.3 4 7.5
E 1.5 N 2.7 W 4.7 7 8.2
H 1.6 O 3.0 X 5.1 9 9.1и, в зависимости от цвета конденсатора, умножьте его на соответствующий множитель:Оранжевый – 1
Черный – 10
Зеленый – 100
Голубой – 1.000
Фиолетовый – 10.000
Красный – 100.000Например:
H на оранжевом конденсаторе – 1,6 * 1 = 1,6 пФ
E на зеленом конденсаторе – 1,5 * 100 = 150 пФ
9 на голубом конденсаторе – 9,1 * 1000 = 9100 пФ

Если на конденсаторе обнаружится надпись, состоящая из одной заглавной латинской буквы и стоящей рядом цифры, то найдите в нижеприведенной таблице соответствующее (этой букве) числовое значение и умножьте его на 10 в той степени, которая указана после буквы.A 10 G 18 N 33 U 56
B 11 H 20 P 36 V 62
C 12 J 22 Q 39 W 68
D 13 K 24 R 43 X 75
E 15 L 27 S 47 Y 82
F 16 M 30 T 51 Z 91Например:
B1 – 11 * (10) = 110 пФ
F3 – 16 * (10*10*10) = 16 000 пФ=16нФ=0,016 мкФ

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .

5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

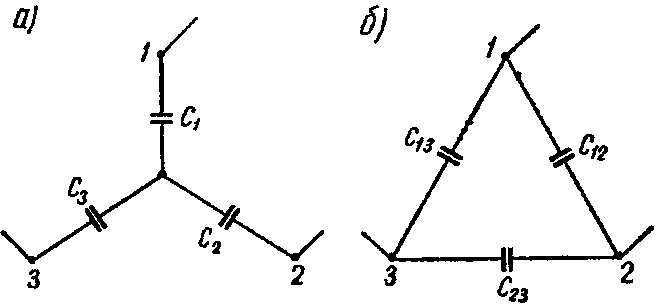
Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

ΣQ=Σ Q ′ .

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

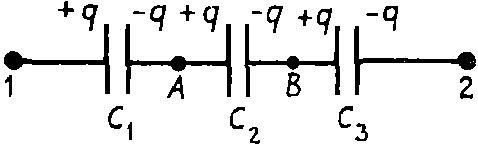
Рис. 1

Решение

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

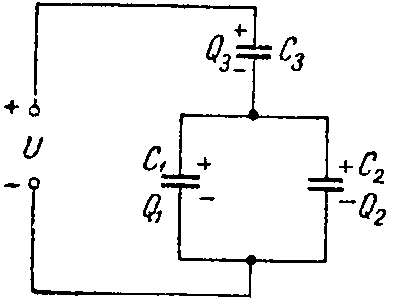
Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.

Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r₁ = 6) толщиною d₁ = 0,3 мм и стекла (ε_r₂ = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

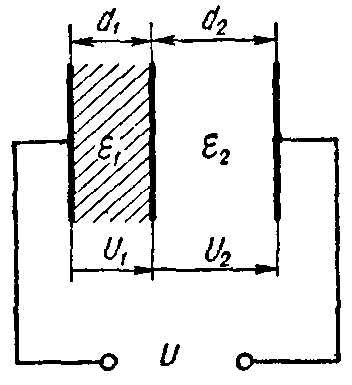
Рис. 3

Решение

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a₁ = ε_r₁·ε₀ и ε_a₂ = ε_r₂·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.

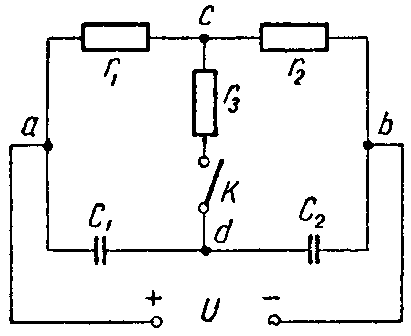
Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04 А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C₁ = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C₂ = I·r₂ = 0,04·400 = 16 В.

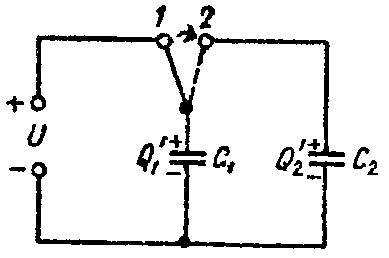
Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

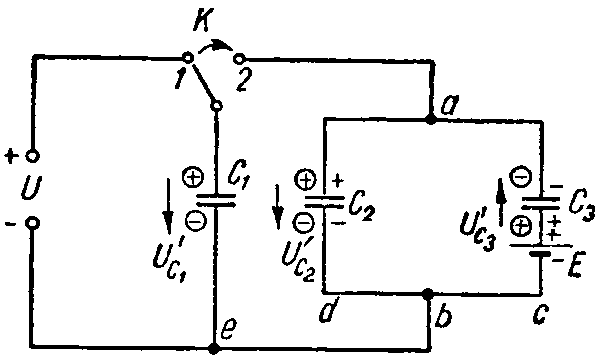
Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.

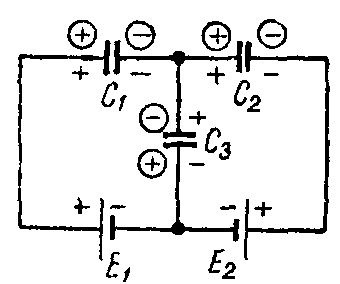
Рис. 7

Решение

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

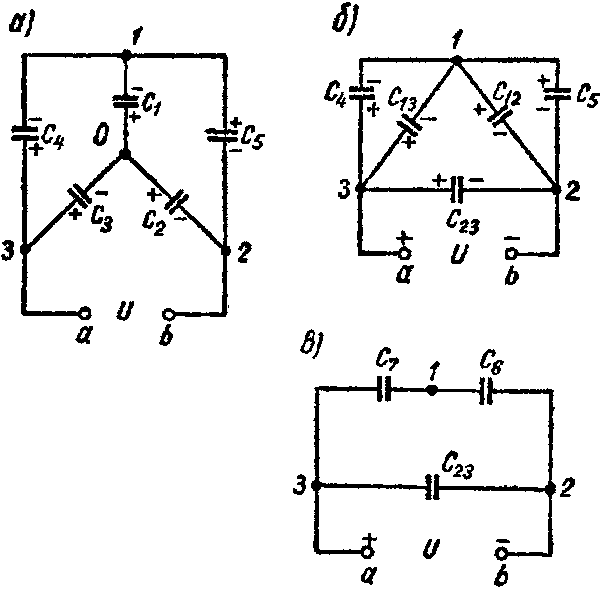
Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол. Фото на Купчинской 32 – Ксерокс распечатка документов Купчино. юристы по земельным вопросам в Севастополе – адреса.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6 В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8 В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U. (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

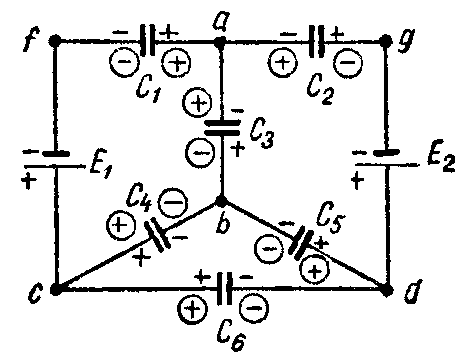
Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

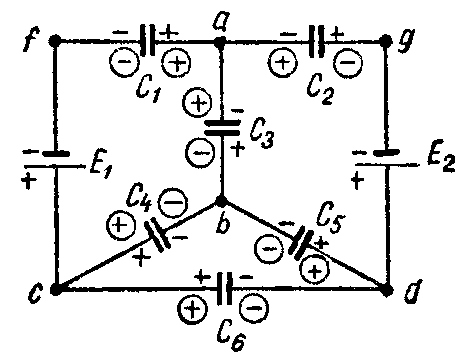
Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

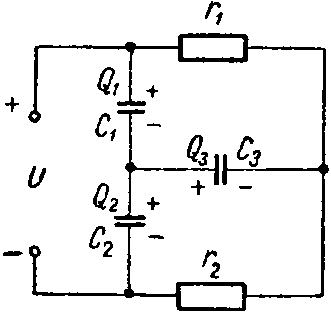
Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05 А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии

Источник

Конденсаторы в электрических цепях постоянного тока

Для учащихся (для лучшего понимания физики).

Вспомним основное из предыдущей статьи.

Плоский конденсатор представляет собой устройство, состоящее из двух металлических пластин (обкладок), между которыми находится диэлектрик.

На практике конденсаторы нашли очень широкое применение благодаря их способности накапливать на обкладках значительные электрические заряды. При этом между обкладками возникает разность потенциалов (напряжение).

Конденсаторы характеризуются электрической ёмкостью С:

Ёмкость конденсатора численно равна отношению заряда на одной из обкладок к напряжению между обкладками

или

ёмкость конденсатора численно равна заряду, который надо сообщить обкладке конденсатора, чтобы повысить напряжение между обкладками на единицу напряжения.

Надо помнить, что заряд конденсатора и его напряжение зависят друг от друга, а ёмкость конденсатора не зависит ни от заряда, ни от напряжения, она только численно равна их отношению.

Ёмкость плоского конденсатора зависит лишь от его размеров (от площади пластин, расстояния между ними) и от диэлектрической проницаемости среды между обкладками:

Заряжаются конденсаторы от источников постоянного тока (см. статью “Зарядка конденсатора. Зарядный и разрядный ток проводимости”

На рисунке ниже показана электрическая цепь, состоящая из источника постоянного напряжения, конденсатора и сопротивления:

В момент замыкания ключа К возникший в цепи ток (рисунок справа) имеет максимальное значение, так как разность потенциалов между полюсом источника и обкладкой конденсатора (она не была заряжена) максимальна.

По мере роста заряда на обкладке ток в цепи уменьшается, обращаясь в нуль в момент, когда напряжение на конденсаторе станет равным напряжению на клеммах источника:

Если заряженный конденсатор отключить от источника (следующий рисунок) и замкнуть его обкладки через сопротивление, то по цепи пойдёт разрядный ток, направленный в сторону обратную зарядному току.

Ниже на одном рисунке показаны кривые зависимости зарядного и разрядного тока от времени, из которого видно, что и зарядный, и разрядный токи имеют максимальные значения в моменты замыкания цепей.

При разрядке конденсатор является источником электрической энергии, отдаваемой во внешнюю цепь.

Чтобы энергия конденсаторов постоянно пополнялась, их включают в электрические цепи, содержащие источники постоянного тока. Такие цепи называют ещё конденсаторными цепями.

Дальше рассмотрим некоторые задачи на расчёт таких цепей. Расчёт сводится, как правило, к нахождению заряда конденсаторов или напряжения на конденсаторах.

Задача.

При решении задач на конденсаторные цепи можно кроме способов, применённых при решении рассмотренных выше задач, пользоваться первым, вторым, третьим и четвёртым правилами.

Сейчас на примере качественного решения следующей задачи рассмотрим перечисленные правила.

Задача

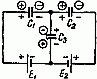
Найти заряд каждого конденсатора в изображённой на рисунке цепи, если известны ЭДС источников постоянного тока и ёмкости конденсаторов.

Сначала подумаем, какие обкладки конденсаторов заряжены положительно, а какие – отрицательно.

Левая обкладка первого конденсатора и правая обкладка третьего конденсатора заряжены отрицательно, так как они соединены с отрицательными полюсами источников. По этой же причине верхняя обкладка второго конденсатора заряжена положительно. Другие обкладки конденсаторов имеют противоположные знаки.

Первое правило

Если в цепи есть точки, в которых сходятся провода обкладок конденсаторов, не соединённых с источником, то их общий заряд равен нулю.

В нашей задаче такой точкой является точка В.

Второе правило

В цепи находим точки равного потенциала и соединяем их в узлы. Потенциал одного из узлов принимаем за нуль. Заряд каждого конденсатора выражаем через его ёмкость и разность потенциалов (напряжение).

Наша цепь содержит два узла А и В. Примем потенциал узла В за нуль.

Третье правило

Для любого замкнутого контура в конденсаторной цепи алгебраическая сумма ЭДС, входящих в контур, равна алгебраической сумме напряжений на конденсаторах в контурах.

В статье “Как найти заряды конденсаторов в цепи …” всё это проделано для нашей задачи и получен ответ.

Все четыре правила расчёта конденсаторных цепей подробно с примерами рассмотрены в статье Занятии 54 и следующих за ней четырёх статьях.

Итак, пользуясь изложенными здесь методами и правилами можно решать сложные задачи на расчёт цепей постоянного тока, содержащих конденсаторы.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.

Для школьников предлагаются подборки материала по темам:

!. Механика. Кинематика. Равномерное прямолинейное движение.

2. Равнопеременное прямолинейное движение.

Предыдущая запись: Ёмкость уединённого проводника. Ёмкость конденсатора. Почему диэлектрик повышает ёмкость конденсатора?

Следующая запись: Явление электростатической индукции в задачах.

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .

Источник

Конденсатор .

Конденсатор это устройство, способное накапливать электрический заряд.

Конденсатор также называют электрической емкостью.

Конденсатор имеет два электрических контакта.

На этой схеме конденсатор подключен к источнику питания(батарейке):

Сверху источник питания, снизу конденсатор.

Конденсатор на схеме обозначается буквой (C )

Любой конденсатор обладает емкостью ( C )

Емкость конденсатора измеряется в фарадах [Ф]

1 фарад это довольно большая величина, обычно емкость конденсаторов намного меньше
одного фарада.

Обычно емкости конденсаторов даны в:

Микрофарадах ( ( 1 мкФ= 10^{-6} Ф ) )

Нанофарадах ( ( 1 нФ =10^{-9} Ф ) )

Пикофарадах ( (1 пФ= 10^{-12} Ф ) )

Чем больше емкость конденсатора , тем больший заряд он может накопить.

( q=CU )

(q)- заряд конденсатора

(U) – напряжение на конденсаторе

Задача 1.

Найти заряд

конденсатора, если напряжение на нем составляет (U=100 Вольт ), а его

емкость (C=0,0001 Ф . )