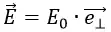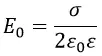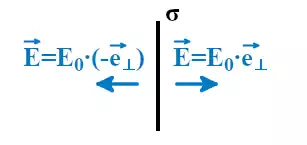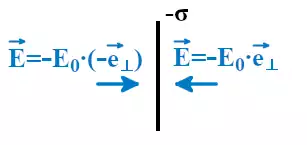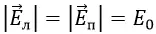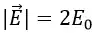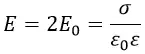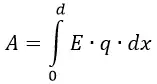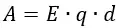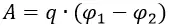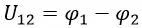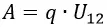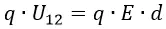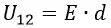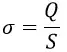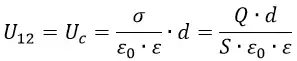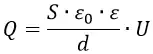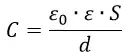Как найти заряд конденсатора по площади

Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются 👍 В первую очередь, рассмотрим устройство и принцип работы, а затем плавно перейдем к основным свойствам и характеристикам – заряду, энергии и, конечно же, емкости конденсатора.

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

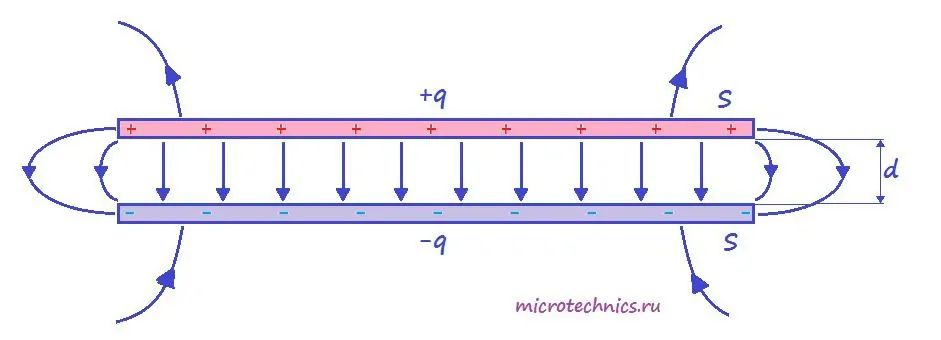
Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

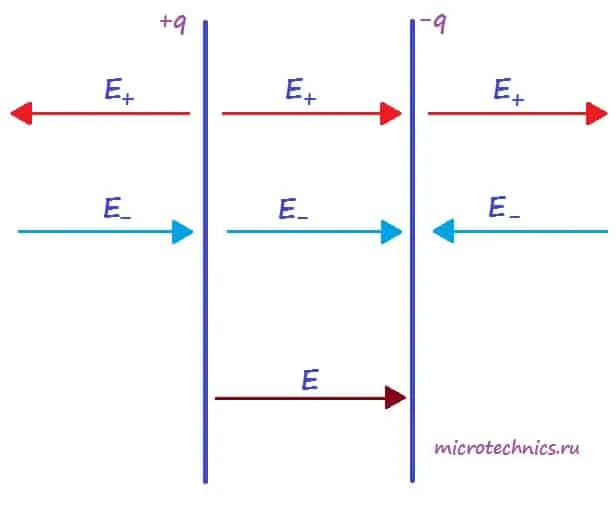
Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E_{пл} = frac{sigma}{2varepsilon_0thinspacevarepsilon}

Здесь sigma– это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

Соответственно, вне конденсатора (слева и справа от обкладок) поля пластин компенсируют друг друга и результирующая напряженность равна 0.

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

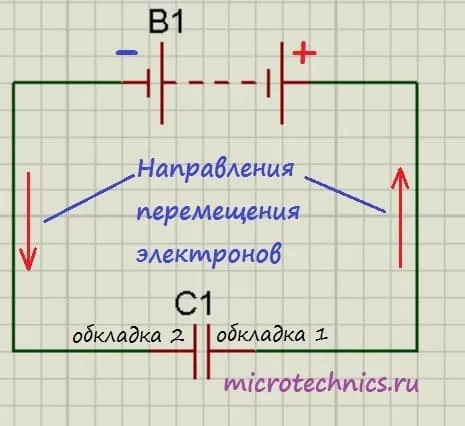
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной.

Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Именно так происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию. Как видите, здесь нет ничего сложного.

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда q одного из проводников к разности потенциалов между проводниками:

C = frac{q}{Deltavarphi} = frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является неимоверно большой, поэтому чаще всего используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

U = Ed = frac{qd}{varepsilon_0thinspacevarepsilon S}

Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:

C = frac{qvarepsilon_0thinspacevarepsilon S}{qd} = frac{varepsilon_0thinspacevarepsilon S}{d}

Если в качестве диэлектрика выступает воздух, то во всех формулах можно подставить varepsilon = 1. Для запасенной же энергии конденсатора справедливы следующие выражения:

W = frac{CU^2}{2} = frac{qU}{2} = frac{q^2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, резюмируем – сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку.

Конденсатор – радиоэлектронный прибор, способный накапливать и отдавать заряд. Как правило, на его корпусе дается информация о его емкости, но иногда требуется самому рассчитать этот номинал.

Конденсаторами могут выступать и проводники, они также обладают определенной емкостью. Для расчета существует несколько формул емкости конденсатора, их и рассмотрим.

В чем измеряется емкость конденсатора

Что такое заряд еще проходят в школе, когда эбонитовую палочку натирают о шерстяную ткань и подносят к маленьким кусочкам бумаги.

Под действием электромагнитных сил бумага прилипает к палочке. Подобный заряд накапливается в конденсаторе. Но для начала познакомимся с самим конденсатором.

Простейшим конденсатором являются две металлические пластины, разделенные диэлектриком. От качества диэлектрика зависит, как долго энергия заряженного конденсатора может сохраняться.

На этих пластинах, они еще называются обкладками, накапливается разноименный заряд. Как это происходит?

Электрический заряд, а в случае с металлами это электроны, способен перемещаться под действием электродвижущей силы (э. д. с.).

Подключая металлические пластинки к источнику тока, мы получаем замкнутую цепь, но разделенную диэлектриком. Электростатическое поле проходит этот диэлектрик, замыкая цепь, а электроны, дойдя до препятствия, останавливаются и скапливаются.

Полная статья на блоге “Электрик в доме”:

Получается, на одной обкладке наблюдается избыток электронов, и эта пластина имеет отрицательный знак, а на другой пластине электронов недостает настолько же, знак на этой обкладке, конечно же, будет положительным.

Вот теперь нужна для определения емкости конденсатора формула, определяющая, какой заряд способен разместится на конкретном конденсаторе.

В качестве единицы измерения в международной системе (СИ) емкость определяется в Фарадах.

Много это или мало – емкость в 1Ф? Чтобы конденсатор обладал емкостью в 1Ф, он должен содержать в себе заряд в 1К (кулон) и при этом напряжение между обкладками должно равняться 1 вольту.

Интересно. Что такое заряд в 1 кулон? Если два предмета, каждый из которых имеет заряд в один кулон разместить в вакууме на расстоянии один метр, то сила притяжения между ними будет равна силе притяжения землей тела массой в один миллион тонн.

Как и любая буквальная емкость один и тот же конденсатор может вмещать разное количество заряда.

Рассмотрим пример.

• В трехлитровую банку входит три литра воздуха. Его хватит для дыхания, допустим, на 3 минуты. Но если воздух закачать под каким-то давлением, то емкость так и останется три литра, однако дышать можно будет дольше. Так устроен акваланг для ныряльщиков. Получается, количество воздуха в банке зависит от давления, которое в ней создается. Точно так же есть некая зависимость между различными силами, влияющими на емкость.

Формула емкости плоского конденсатора

Прежде чем узнать, по какой формуле вычисляется емкость плоского конденсатора, рассмотрим формулу для одиночного проводника. Она имеет вид:

• где Q – заряд,
• φ – потенциал.

Как видно емкость конденсатора, формула которого здесь приведена, будет тем больше, чем больший заряд способен накапливаться на нем при незначительном потенциале. Чтобы легче это было понять, рассмотрим получившие широкое распространение плоские конденсаторы разных размеров.

Для получения качественного конденсатора важны любые мелочи:

1. ровная поверхность каждой обкладки;
2. обе пластинки по всей площади должны располагаться на одинаковом расстоянии;
3. размеры обкладок должны быть строго идентичными;
4. от качества диэлектрика, расположенного между пластинками, будет зависеть ток утечки;
5. емкость напрямую зависит от расстояния между обкладками, чем оно меньше, тем больше емкость.

Теперь обратимся к плоскому конденсатору. Формула определения емкости конденсатора несколько отличается от приведенной выше:

• где S – площадь одной обкладки,
• εr – диэлектрическая проницаемость диэлектрика,
• ε0 – электрическая постоянная,
• d – расстояние между обкладками.

Электрическая постоянная выражается числом 8,854187817×10-12.

Внимание! Эта формула справедлива только тогда, когда расстояние между пластинами намного меньше их площади.

Попробуем разобраться с каждой переменной подробнее. Площадь измеряется в м2, точнее, приводится к этой величине. А вот проницаемость диэлектрика может обозначаться по-разному.

В России это εr (также означает относительная проницаемость), в англоязычной литературе встречается εa (также означает абсолютная проницаемость), а то может и вовсе использоваться без индекса, просто ε. О том, что здесь используется диэлектрическая проницаемость диэлектрика можно понять из контекста.

Дальше идет ε0. Это уже вычисленное значение, измеряемое в Ф/м. Последняя переменная – d. Измеренное расстояние также приводится к метру. Емкость конденсатора, формула которого сейчас рассматривается, показывает сильную зависимость от расстояния обкладок. Поэтому стараются это расстояние по возможности сокращать. Почему этот показатель так важен?

Идеальными условиями для получения наибольшей емкости – это отсутствие промежутка между обкладками, чего, конечно, добиться невозможно. Чем ближе находятся разноименные заряды, тем сильнее сила притяжения, но здесь возникает компромисс.

При уменьшении толщины диэлектрика, а именно он разделяет разноименные заряды, возникает вероятность его пробоя из-за разности потенциалов на обкладках. С другой стороны, как уже говорилось, при увеличении напряжения увеличивается количество зарядов. Вот и приходится выбирать между емкостью и рабочим напряжением конденсатора.

Есть другая формула для плоского переменного конденсатора:

Здесь диэлектрическая проницаемость обозначена буквой ε, π = 22/7 ≈ 3,142857142857143, d – толщина диэлектрика. Формула предназначена для конденсатора, состоящего из нескольких пластин.

Допустимая толщина диэлектрика d также зависит от εr, чем выше коэффициент, тем тоньше можно использовать диэлектрик, тем большую емкость будет иметь конденсатор. Это был самый сложный материал, дальше будет легче.

Формула емкости цилиндрического конденсатора

Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой.

Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:

Здесь видим несколько новых переменных:

• l – высота цилиндра;
• R1 и R2 – радиус первого и второго (внешнего) цилиндров;
• ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.

Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).

Из нее видно, что все расстояния нужно приводить к метру.

Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.

Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.

Формула емкости сферического конденсатора

Последнее что осталось разобрать – формулу определения емкости конденсатора, состоящего из двух сфер. Причем одна сфера находится внутри другой. Формула имеет следующий вид:

Из приведенных переменных здесь все знакомо. Стоит обратить внимание лишь на сам конденсатор.

Кроме своей необычной формы у него есть свои особенности: внутри малой сферы никакого заряда нет, он образуется на внешней части малой сферы и внутренней части большого шара. Также заряд отсутствует и на внешней стороне внешней сферы.

Так же как и все другие конденсаторы, сферы разделены диэлектриком. Толщина и качество диэлектрика оказывают такое же влияние на емкость, как в случае с другими конденсаторами.

После того как были рассмотрены формулы, стоит испробовать их на практике. Рассмотрим, как найти емкость конденсатора каждого вида.

Примеры решения задач

Начнем с плоского конденсатора. Формула для этого вида:

Допустим, у нас есть следующие значения:

• в качестве диэлектрика возьмем слюду толщиной 0,02 мм, ε = 6;
• конденсатор квадратный со сторонами в 7 мм.

Определяем площадь пластин: 7×7 = 49 мм2.

Приводим к единой системе: 4,9×10-5 = 0,000049 м2. Толщина диэлектрика 0,02×10-5 = 0,00002 м. Электрическая постоянная 8,854187817×10-12.

Подставляем в формулу и высчитываем числитель: 6×8,854187817×10-12 ×4,9×10-5, сокращаем и решаем 6×49×8,854187817×10-17 = 2,603131218198×10-14.

Делим на толщину диэлектрика: 2,603131218198×10 / 2×10 = 1301,565609099×10 = 1,301565609099×10. Шесть нулей – это тысячи или приставка «микро», получается округлено 1,3 мкФ.

Возможно, при вычислении была допущена ошибка, но это не экзамен по математике. Важно понять сам метод вычисления.

Формула для цилиндрического конденсатора:

Выбираем значения:

• l = 1 см;
• R1 = 0,25 мм;
• R2 = 0,26 мм;
• ε = 2.

Подгоняем под единую систему: l – 1 см = 1×10-2 = 0,01 м; R1 – 0,25 мм = 0,0025 м; R2 – 0,26 мм = 0,0026 м.

Подставляем значения в числитель: 2×3,142857142857143×8,854187817×10-12×2×0,01 1,11×10-12. Находим знаменатель: 0,26:0,25 = 1,04.

Находим натуральный логарифм, он равен примерно 0,39. Числитель делим на знаменатель: 1,11×10-12/0,39 = 2,85×10-12.

Число с 12 нулями это приставка «пико», получаем 2,85 пФ.

Формула для сферического конденсатора:

Выбираем значения:

• ε= 4;
• r1= 5 см;
• r2= 5,01 см.

Снова все подгоняем: 5 см = 0,05 м; 5,01 см = 0,0501 м. Заполняем числитель. 4×3,142857142857143×4×8,854187817×10-12×0,05×0,0501 1,11×10-12 Вычисляем знаменатель: 0,0501 – 0,05 = 0,01. Производим деление: 1,11×10-12×0,01 = 1,11×10-10. Снова получили пикофарады, а именно 1,11 пФ.

Интересные статьи на канале:

Статья заинтересовала? Лайк, подписка, комментарий!

Друзья ПОДПИСЫВАЙТЕСЬ Дзен на канал, а также заходите на блог https://electricvdome.ru 👍!

#конденсатор #емкость #формула

В статье поле плоской пластины была выведена формула напряжённости электрического поля бесконечной плоской пластины. Если эту пластину рассмотреть в разрезе и ввести понятие поверхностной плотности заряда σ, то согласно указанной статьи в любой точке пространства напряжённость электрического поля направлена перпендикулярно плоскости пластины и по величине равно:

E₀ здесь жёстко определяется поверхностной плотностью заряда σ:

где σ – поверхностная плотность заряда;
ε₀ – диэлектрическая проницаемость для вакуума;
ε – относительная диэлектрическая проницаемость для вещества, которая для вакуума равна 1.

Формулы показывают, что величина напряжённости электрического поля плоской пластины, имеющей бесконечные размеры, не зависит от расстояния до неё.

Если σ положительная, то напряжённость электрического поля будет направлена от пластины и поле отталкивает положительные заряды.

Если σ отрицательная, то напряжённость электрического поля направлена к пластине и поле притягивает положительные заряды.

Плоским конденсатором будем называть пару параллельных плоских пластин с плотностью заряда одинаковой по модулю, но противоположной по знаку.

Расчёт и вывод формулы ёмкости плоского конденсатора

Напряжённость электрического поля конденсатора

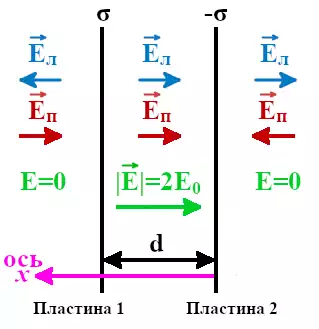
Для расчёта плоского конденсатора расположим две пластины бесконечных размеров параллельно друг другу на некотором расстоянии d. Пусть одна пластина будет иметь поверхностную плотность заряда σ, а другая -σ. По модулю величины поверхностных плотностей зарядов будут равны. В такой ситуации общее поле плоского конденсатора по принципу суперпозиции равно сумме полей.

Обозначим напряжённости электрического поля от левой пластины плоского конденсатора как E_л, при этом положительные заряды будут отталкиваться от пластины.

Напряжённость электрического поля от правой пластины плоского конденсатора обозначим как E_п, при этом поле пластины будет притягивать к себе положительные заряды.

При равной плотности заряда напряжённость поля во всех точках пространства и от левой, и от правой пластин конденсатора будут равны по модулю. Это приведёт к тому, что слева и справа от пары пластин поля взаимно компенсируются и их сумма будет равна нулю. При этом поля между пластинами плоского конденсатора будут складываться.

где E₀ – напряжённость поля при положительной σ.

Суммарная напряжённость электрического поля плоского конденсатора будет направлена от пластины с положительной σ к пластине с отрицательной σ.

Электрическая энергия плоского конденсатора отсутствует вне его пластин и вся накоплена в пространстве между пластинами.

Работа по перемещению заряда

Для перемещения заряда от отрицательно заряженной пластины в направлении к положительно заряженной придётся совершить работу против электрической силы:

При вычислении этой работы видно, что величина заряда q и напряжённость поля E постоянны, поэтому формула примет вид:

В электрическом поле можно ввести понятие потенциала ϕ и выразить работу по перемещению заряда в точку 2 из точки 1 через разность потенциалов ϕ₁-ϕ₂.

Напряжение между пластинами плоского конденсатора

Разность электрических потенциалов между двумя точками называют напряжением и обозначают U₁₂:

Таким образом, сравнивая две формулы для работы мы получим:

В реальном конденсаторе площадь пластин ограничена по естественным причинам, поэтому, как правило, мы не имеем возможности знать плотность заряда, а знаем только заряд пластины. В этом случае плотность заряда σ мы можем вычислить по формуле:

где Q – заряд пластины;
S – площадь пластины.

Если пластины плоского конденсатора находятся достаточно близко друг к другу, то краевыми эффектами можно пренебречь и считать, что поле внутри конденсатора реальных размеров подобно полю внутри конденсатора с пластинами бесконечных размеров.

В таком случае имеем следующее выражение:

Напряжение между пластинами пропорционально полному заряду этих пластин:

Электрическая ёмкость плоского конденсатора

Коэффициент пропорциональности между зарядом на обкладках плоского конденсатора и напряжением между ними носит название ёмкости плоского конденсатора и обозначается буквой C:

Подробности венецианская штукатурка для внутренней отделки цена на сайте.

Конденсатор. Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

(1)

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля имеем:

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

или

(4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

(5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

(6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

(7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

(8)

Соответственно, напряжение на конденсаторе:

(9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

(10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где — напряжённость поля первой обкладки:

Следовательно,

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:

(11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

где

Это можно переписать следующим образом:

где

(12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

(13)

(14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

к оглавлению ▴

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

Но — объём конденсатора. Получаем:

(15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

(16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

(17)

(18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.