Для учащихся (для лучшего понимания физики).
Вспомним основное из предыдущей статьи.
Плоский конденсатор представляет собой устройство, состоящее из двух металлических пластин (обкладок), между которыми находится диэлектрик.
На практике конденсаторы нашли очень широкое применение благодаря их способности накапливать на обкладках значительные электрические заряды. При этом между обкладками возникает разность потенциалов (напряжение).
Конденсаторы характеризуются электрической ёмкостью С:
Ёмкость конденсатора численно равна отношению заряда на одной из обкладок к напряжению между обкладками
или
ёмкость конденсатора численно равна заряду, который надо сообщить обкладке конденсатора, чтобы повысить напряжение между обкладками на единицу напряжения.
Надо помнить, что заряд конденсатора и его напряжение зависят друг от друга, а ёмкость конденсатора не зависит ни от заряда, ни от напряжения, она только численно равна их отношению.
Ёмкость плоского конденсатора зависит лишь от его размеров (от площади пластин, расстояния между ними) и от диэлектрической проницаемости среды между обкладками:
Заряжаются конденсаторы от источников постоянного тока (см. статью “Зарядка конденсатора. Зарядный и разрядный ток проводимости”
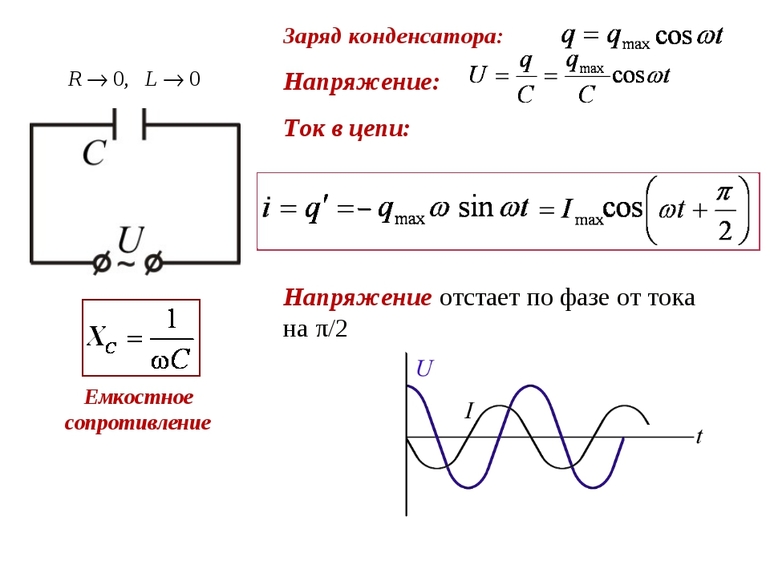
На рисунке ниже показана электрическая цепь, состоящая из источника постоянного напряжения, конденсатора и сопротивления:
В момент замыкания ключа К возникший в цепи ток (рисунок справа) имеет максимальное значение, так как разность потенциалов между полюсом источника и обкладкой конденсатора (она не была заряжена) максимальна.
По мере роста заряда на обкладке ток в цепи уменьшается, обращаясь в нуль в момент, когда напряжение на конденсаторе станет равным напряжению на клеммах источника:
Если заряженный конденсатор отключить от источника (следующий рисунок) и замкнуть его обкладки через сопротивление, то по цепи пойдёт разрядный ток, направленный в сторону обратную зарядному току.
Ниже на одном рисунке показаны кривые зависимости зарядного и разрядного тока от времени, из которого видно, что и зарядный, и разрядный токи имеют максимальные значения в моменты замыкания цепей.
При разрядке конденсатор является источником электрической энергии, отдаваемой во внешнюю цепь.
Чтобы энергия конденсаторов постоянно пополнялась, их включают в электрические цепи, содержащие источники постоянного тока. Такие цепи называют ещё конденсаторными цепями.
Дальше рассмотрим некоторые задачи на расчёт таких цепей. Расчёт сводится, как правило, к нахождению заряда конденсаторов или напряжения на конденсаторах.
Задача.
При решении задач на конденсаторные цепи можно кроме способов, применённых при решении рассмотренных выше задач, пользоваться первым, вторым, третьим и четвёртым правилами.
Сейчас на примере качественного решения следующей задачи рассмотрим перечисленные правила.
Задача
Найти заряд каждого конденсатора в изображённой на рисунке цепи, если известны ЭДС источников постоянного тока и ёмкости конденсаторов.
Сначала подумаем, какие обкладки конденсаторов заряжены положительно, а какие – отрицательно.
Левая обкладка первого конденсатора и правая обкладка третьего конденсатора заряжены отрицательно, так как они соединены с отрицательными полюсами источников. По этой же причине верхняя обкладка второго конденсатора заряжена положительно. Другие обкладки конденсаторов имеют противоположные знаки.
Первое правило
Если в цепи есть точки, в которых сходятся провода обкладок конденсаторов, не соединённых с источником, то их общий заряд равен нулю.
В нашей задаче такой точкой является точка В.
Второе правило
В цепи находим точки равного потенциала и соединяем их в узлы. Потенциал одного из узлов принимаем за нуль. Заряд каждого конденсатора выражаем через его ёмкость и разность потенциалов (напряжение).
Наша цепь содержит два узла А и В. Примем потенциал узла В за нуль.
Третье правило
Для любого замкнутого контура в конденсаторной цепи алгебраическая сумма ЭДС, входящих в контур, равна алгебраической сумме напряжений на конденсаторах в контурах.
В статье “Как найти заряды конденсаторов в цепи …” всё это проделано для нашей задачи и получен ответ.
Все четыре правила расчёта конденсаторных цепей подробно с примерами рассмотрены в статье Занятии 54 и следующих за ней четырёх статьях.
Итак, пользуясь изложенными здесь методами и правилами можно решать сложные задачи на расчёт цепей постоянного тока, содержащих конденсаторы.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Для школьников предлагаются подборки материала по темам:
!. Механика. Кинематика. Равномерное прямолинейное движение.
2. Равнопеременное прямолинейное движение.
Предыдущая запись: Ёмкость уединённого проводника. Ёмкость конденсатора. Почему диэлектрик повышает ёмкость конденсатора?
Следующая запись: Явление электростатической индукции в задачах.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Как найти заряд конденсатора
В технике и задачах по физике иногда требуется найти заряд конденсатора. Непосредственное измерение заряда конденсатора – задача довольно трудоемкая. Поэтому на практике используются более доступные способы нахождения заряда конденсатора.

Вам понадобится
- конденсатор, вольтметр
Инструкция
Чтобы найти заряд конденсатора, подключенного к источнику постоянного напряжения, умножьте емкость конденсатора на величину напряжения, т.е. воспользуйтесь формулой:
Q=UC, где:
Q – заряд конденсатора, в кулонах,
U – напряжение источника напряжения, в вольтах,
С – емкость конденсатора, в фарадах.
Учтите, что вышеприведенная формула определяет величину заряда полностью заряженного конденсатора. Но так как зарядка конденсатора происходит достаточно быстро, то на практике пользуются именно этой закономерностью.
Напряжение источника питания можно измерить вольтметром. Для этого переключите его в режим измерения постоянного напряжения и подключите клеммы прибора к источнику напряжения. Запишите показания прибора в вольтах.
Узнать емкость конденсатора можно прочитав маркировку на его корпусе. Учтите, что единица емкости фарада (Ф)– очень большая, поэтому на практике используется редко. Для обозначения емкости конденсаторов используются более мелкие единицы. Это микрофарада (мкФ), равная одной миллионной фарады и пикофарада (пФ), равная одной миллионной микрофарады.
1 мкФ=10-6 Ф, 1 пФ = 10-12 Ф.
Иногда используется и промежуточная единица емкости – нанофарада, равная одной миллиардной части фарады.
1 нФ = 10-9 Ф.
Если конденсатор малогабаритный, то его емкость указывается с помощью условных обозначений.
Внимательно прочтите маркировку конденсатора, обратив внимание на его цвет.Если на конденсаторе указаны всего две цифры, то это его емкость в пикофарадах.
Так, например, надпись «60» будет означать емкость 60 пФ.
Если на конденсаторе указана одна прописная латинская буква или цифра, то найдите в нижеприведенной таблице соответствующее числовое значениеA 1.0 I 1.8 R 3.3 Y 5.6
B 1.1 J 2.0 S 3.6 Z 6.2
C 1.2 K 2.2 T 3.9 3 6.8
D 1.3 L 2.4 V 4.3 4 7.5
E 1.5 N 2.7 W 4.7 7 8.2
H 1.6 O 3.0 X 5.1 9 9.1и, в зависимости от цвета конденсатора, умножьте его на соответствующий множитель:Оранжевый – 1
Черный – 10
Зеленый – 100
Голубой – 1.000
Фиолетовый – 10.000
Красный – 100.000Например:
H на оранжевом конденсаторе – 1,6 * 1 = 1,6 пФ
E на зеленом конденсаторе – 1,5 * 100 = 150 пФ
9 на голубом конденсаторе – 9,1 * 1000 = 9100 пФ
Если на конденсаторе обнаружится надпись, состоящая из одной заглавной латинской буквы и стоящей рядом цифры, то найдите в нижеприведенной таблице соответствующее (этой букве) числовое значение и умножьте его на 10 в той степени, которая указана после буквы.A 10 G 18 N 33 U 56
B 11 H 20 P 36 V 62
C 12 J 22 Q 39 W 68
D 13 K 24 R 43 X 75
E 15 L 27 S 47 Y 82
F 16 M 30 T 51 Z 91Например:
B1 – 11 * (10) = 110 пФ
F3 – 16 * (10*10*10) = 16 000 пФ=16нФ=0,016 мкФ
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Конденсатором называется система, состоящая из двух проводников, расположенных достаточно близко друг от друга. Проводники называют обкладками конденсатора. Если на обкладки конденсатора поместить равные по модулю и противоположные по знаку заряды, то разность потенциалов (напряжение) между обкладками будет пропорциональна заряду обкладок, т. е. отношение заряда к напряжению не будет зависеть от заряда. На основании этого утверждения, которое приводим без доказательства, вводится понятие электроёмкости (ёмкости конденсатора).
Ёмкостью конденсатора называется отношение заряда $$ Q$$ одной из обкладок к разности потенциалов $$ U$$ между этой обкладкой и соседней:
| $$ C={displaystyle frac{Q}{U}}$$. | (10.1) |
Если взят заряд на положительно заряженной обкладке, то $$ Q>0, U>0$$ и получится $$ C>0$$. Если заряд взят на отрицательной обкладке, то Q<0, U<0Q<0,;U<0 и опять будет $$ C>0$$. Итак, из определения ёмкости следует, что ёмкость величина положительная. В системе СИ ёмкость измеряется в фарадах: `1″Ф”=1` Кл/В.
Требование близости обкладок друг к другу связано с тем, что для независимости $$ C$$ от $$ Q$$ в (10.1) нужно, чтобы поле от зарядов на обкладках было сосредоточено практически полностью между обкладками, т. е. все силовые линии, начинающиеся на одной обкладке, заканчивались только на другой и не уходили на окружающие тела. В этом случае окружающие тела не будут влиять на ёмкость конденсатора.
Можно вывести, что ёмкость плоского конденсатора
| $$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d}}$$. | (10.2) |
Здесь $$ S$$ – площадь обкладок, $$ d$$ – расстояние между ними, $$ varepsilon $$ – диэлектрическая проницаемость диэлектрика между обкладками.
При последовательном соединении изначально не заряженных конденсаторов с ёмкостями $$ {C}_{1}, {C}_{2}, …$$, общий заряд равен заряду каждого конденсатора, общее напряжение равно сумме напряжений на отдельных конденсаторах, общая ёмкость определяется из формулы: $$ {displaystyle frac{1}{C}}={displaystyle frac{1}{{C}_{1}}}+{displaystyle frac{1}{{C}_{2}}}+…$$
Полезно помнить формулу для частного случая последовательного соединения двух конденсаторов: $$ C={displaystyle frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}}$$.
Для последовательно соединённых n одинаковых конденсаторов ёмкостью $$ {C}_{1}$$ каждый $$ C={C}_{1}/n.$$
Если последовательно соединены предварительно заряженные конденсаторы, то применение перечисленных выше свойств и формул может привести к неправильному результату!
При параллельном соединении конденсаторов с емкостями $$ {C}_{1,} {C}_{2}, …$$ общий заряд равен сумме зарядов отдельных конденсаторов, общее напряжение равно напряжению на каждом, общая ёмкость равна сумме ёмкостей:
$$ C={C}_{1}+{C}_{2}+…$$
 |
| Рис. 10.1 |
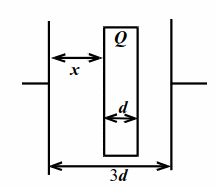
В плоский конденсатор параллельно его обкладкам вставлена пластина из диэлектрика с диэлектрической проницаемостью $$ varepsilon $$ (рис. 10.1). Площадь обкладок конденсатора и пластины $$ S$$, толщина пластины $$ d$$, расстояние между обкладками $$ 3d$$. Найти ёмкость такого конденсатора.
Пусть расстояние от пластины до левой обкладки конденсатора $$ x$$. Наклеим мысленно на обе стороны пластины тонкую проводящую и незаряженную фольгу. От этого ничего не изменится. Обе фольги можно рассматривать как своеобразные провода, соединяющие три последовательно соединённых конденсатора с расстояниями $$ x$$, $$ d$$ и $$ 2d-x$$. Для общей ёмкости $$ C$$:
$$ {displaystyle frac{1}{C}}={displaystyle frac{x}{{varepsilon }_{0}S}}+{displaystyle frac{d}{varepsilon {varepsilon }_{0}S}}+{displaystyle frac{2d-x}{{varepsilon }_{0}S}}$$.
Окончательно $$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d(2varepsilon +1)}}.$$ Заметим, что не заданная в условии величина $$ x$$ «исчезла» в процессе решения.
 |
| Рис. 10.2 |
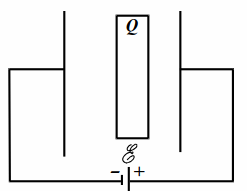
В плоский конденсатор ёмкостью $$ C$$ вставлена параллельно обкладкам плоская проводящая пластина с зарядом $$ Q$$ (рис. 10.2). Конденсатор подсоединён к источнику с ЭДС $$ mathcal{E}$$. Площади пластины и обкладок конденсатора равны. Толщина пластины равна расстоянию от неё до правой обкладки и составляет четверть от расстояния между обкладками. Найти заряд конденсатора.
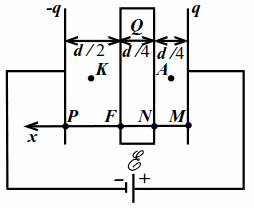
Пусть $$ d$$ – расстояние между обкладками, $$ S$$ – их площадь. Пусть $$ q$$ заряд правой обкладки. Тогда заряд левой будет $$ -q$$, т. к. заряд в значительных количествах не может накапливаться на соединительных проводах и в источнике. Направим ось $$ x$$ влево (рис. 10.3).
 |
| Рис. 10.3 |
Заметим, что поле внутри пластины отсутствует и разность потенциалов $$ {varphi }_{N}-{varphi }_{F}$$ между точками $$ N$$ и $$ F$$ равна нулю. Кроме того, заряды на поверхностях пластины создают вне пластины такое же поле, как и заряд $$ Q$$, если бы его расположить на любой из двух поверхностей пластины. Это легко показать отдельно.
Разность потенциалов $$ {varphi }_{M}-{varphi }_{P}$$ между точками $$ M$$ и $$ P$$ равна $$ mathcal{E}$$. Поэтому
$$ ({varphi }_{M}-{varphi }_{N})+({varphi }_{N}-{varphi }_{F})+({varphi }_{F}-{varphi }_{P})=mathcal{E}$$.
У нас $$ {varphi }_{M}-{varphi }_{N}={E}_{A}{displaystyle frac{d}{4}}, {varphi }_{N}-{varphi }_{F}=0, {varphi }_{F}-{varphi }_{P}={E}_{K}{displaystyle frac{d}{2}}$$.
Здесь – $$ {E}_{A}$$ и $$ {E}_{K}$$ – проекции напряжённости результирующего поля на ось `x`. По принципу суперпозиции полей
$$ {E}_{A}={displaystyle frac{q}{2{varepsilon }_{0}S}}-{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q-Qright)$$,
$$ {E}_{K}={displaystyle frac{q}{2{varepsilon }_{0}S}}+{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q+Qright)$$.
Подставляя выражения для $$ {E}_{A}$$, $$ {E}_{K}$$ и разностей потенциалов в первое
уравнение, получим после упрощений $$ 6q+Q=8mathcal{E}{displaystyle frac{{varepsilon }_{0}S}{d}}$$.
Так как $$ {displaystyle frac{{varepsilon }_{0}S}{d}}=C$$, то $$ q=(8Cmathcal{E}-Q)/6$$.
Следует заметить, что знак найденного заряда правой обкладки зависит от соотношения заданных в условии задачи величин.
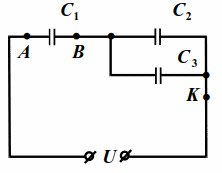 |
| Рис. 10.4 |
На схему (рис. 10.4) подано напряжение `U=24` В. Ёмкости конденсаторов `C_1=1` мкФ, $$ {C}_{2}=2$$ мкФ, $$ {C}_{3}=3$$ мкФ. Найти напряжения на конденсаторах.
В задачах, где есть схемы с конденсаторами, обычно предполагается, что схемы собраны из первоначально незаряженных конденсаторов.
Ёмкость между точками $$ B$$ и $$ K$$:
$$ {C}_{BK}={C}_{2}+{C}_{3}=5$$ мкФ.
Общая емкость: $$ {C}_{AK}={displaystyle frac{{C}_{1}{C}_{BK}}{{C}_{1}+{C}_{BK}}}={displaystyle frac{5}{6}}$$ мкФ.
Общий заряд всей батареи конденсаторов $$ {q}_{AK}={C}_{AK}U=20·{10}^{-6 }mathrm{Кл}.$$
Так как заряд $$ {q}_{1}$$ конденсатора $$ {C}_{1}$$ равен заряду батареи, то напряжение на этом конденсаторе $$ {U}_{1}={q}_{1}/{C}_{1}={q}_{AK}/{C}_{1}=20$$ В. Напряжения на конденсаторах $$ {C}_{2}$$ и $$ {C}_{3}$$ равны напряжению между точками $$ B$$ и $$ K$$ и в сумме с $$ {U}_{1}$$ дают $$ U$$.
Поэтому $$ {U}_{2}={U}_{3}={U}_{BK}=U-{U}_{1}=4$$ В.
Приведённая в задаче схема негромоздкая, и ответ легко получить в общем виде:
$$ {U}_{1}={displaystyle frac{{C}_{2}+{C}_{3}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=20$$ B,
$$ U2=U3={displaystyle frac{{C}_{1}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=4$$ B.

Общие сведения
Слово «конденсатор» переводится с латинского как «сгущение». Поэтому устройство, позволяющее получить однородное электрическое поле, и было названо эти термином. В физике существует чёткое определение такого прибора. Согласно ему, конденсатором называется система из двух плоских проводников расстояние между которыми гораздо меньше их размеров. Первым таким устройством стала «Лейденская банка».
В 1745 году голландец Питерван Мушенбрук и его ученик Кюнеус в городе Лейдене собрали прибор в форме банки предназначенный для хранения и накапливания зарядов. Устройство содержало следующие компоненты:
- стеклянный цилиндр;
- внешнюю и внутреннюю оболочки;
- деревянную пробку;
- проволочный проводник.
Оболочки покрывали сосуд примерно на две трети и были выполнены из листового олова. Через пробку обеспечивающую герметичность банки проходил металлический стержень. Касаясь подводника заряженным телом, учёный передавал заряды в ёмкость. При соприкосновении электроны перемещались на проводник и накапливались на электроде. В итоге одна обкладка конденсатора заряжалась положительно, а другая — отрицательно.

Как оказалось, такая конструкция была способна накапливать запас электричества. Изобретение первого конденсатора привело к более глубокому изучению природы электричества. С его помощью стало возможным разобраться в поведении диэлектриков и проводников, понять механизм разделения зарядов.
С физической точки зрения, в устройстве проходят следующие процессы. Две разделённые пластины заряжаются частицами с разным знаком. Вектор напряжённости положительно заряженного проводника направлен от него во все стороны. При этом силовые линии, которые создаются между обкладками не зависят от расстояния, одинаковые по модулю и направлению. Поэтому с внешней стороны отрицательной пластины создаётся такое же поле, но с линиями входящими в неё.
Так как заряды на электродах одинаковые, то напряжённость поля внутри обкладок равняется E = E1 * E2 = 2E1 = 2E2. Снаружи силовые линии направлены друг на друга, поэтому суммарное значение энергии за пластинами равняется нулю.
Таким образом, конденсатор не только позволяет создавать внутри него однородное поле, но и блокировать его снаружи. Следовательно, такое устройство может набрать довольно высокое значение заряда.
Электрическая ёмкость
Способность устройства накапливать заряд прежде всего зависит от его ёмкости. Найти её величину можно разделив заряд, сосредоточенный на пластинах, на разность потенциалов между ними: C = q / U. Полученный результат измеряется в фарадах [F]. Так, ёмкость в 1 фарад будет равняться значению заряда в 1 кулон создавшему напряжение на выводах конденсатора 1 вольт. Кулон — это довольно большая величина. Поэтому на практике при различных расчётах приходится иметь дело с микрофарадами (µF), нанофарадами (nF) и пикофарадами (pF).

После создания «Лейденской банки» учёные провели ряд экспериментов, направленных на увеличение количества запасаемой энергии устройством. Так было обнаружено, что если между обкладками конденсатора поместить диэлектрик, то он не только предотвращает замыкание проводников, но и влияет на ёмкость.
Пусть имеется устройство пластины которого имеют площадь S. Между обкладками размещён непроводник тока, характеризующийся диэлектрической проницаемостью ε. Это коэффициент, показывающий во сколько раз напряжённость в однородном поле меньше чем создаваемое значение теми же зарядами в вакууме.
Можно предположить, что положительный заряд будет скапливаться на левой пластине, а отрицательный на правой. Чтобы найти ёмкость конденсатора нужно воспользоваться следующей последовательностью действий:
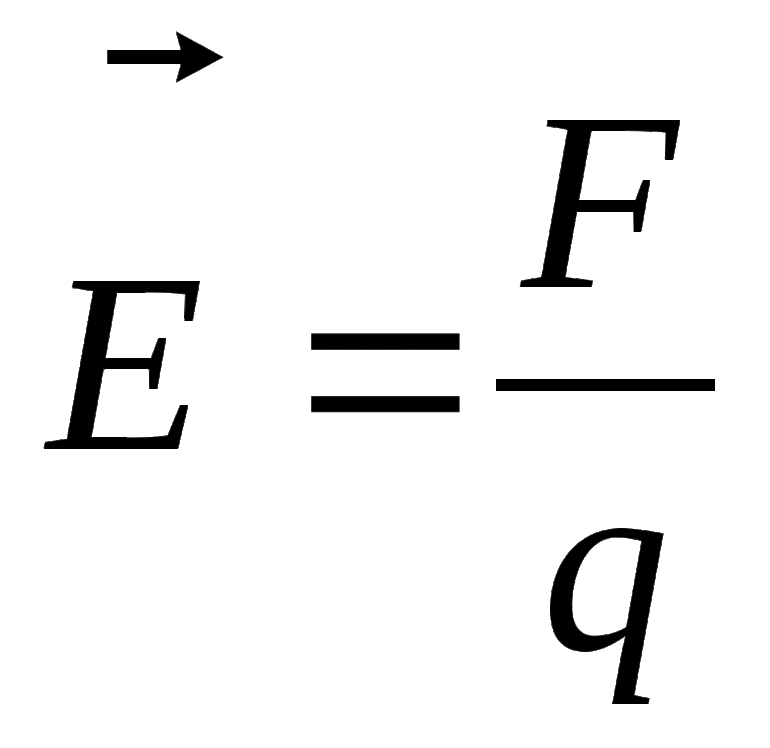
- Найти напряжённость поля в середине устройства. Для этого каждую обкладку нужно представить, как бесконечно однородно заряженную плоскость. Тогда: E1 = σ / (2 * ε * ε0). Так как поля внутри складываются, то расчётная формула примет вид: E = σ / (ε * ε0).
- Определить поверхностную плотность зарядов. Это величина, показывающая чему равняется отношение заряда к площади, по которой он распределён: σ = q / S.
- Выразить напряжение между пластинами через заряд. Между обкладками поле однородное. Значит, напряжение можно найти умножением напряжённости на расстояние: U = E * d. Тогда, пользуясь полученными формулами для E и σ, можно записать: U = (q * d) / (ε * ε0 * S).
- Вычислить электрическую ёмкость, подставив выражения в формулу: C = q / U. В результате получится: C = (ε * ε0 * S) / d.
Таким образом, чем больше площадь пластин, тем выше ёмкость конденсатора. Отсюда следует, что будет больше накоплен заряд. При этом его величина зависит и от расстояния между пластинами. Если d уменьшается, то ёмкость увеличивается.
Энергия устройства
Зарядить конденсатор мгновенно невозможно. Для этого процесса требуется определённое время. Это явление используется в радиотехнике. Так, с помощью конденсатора сглаживаются импульсные всплески. В первом приближении конденсатор похож на аккумулятор. Но при этом он отличается от него принципом накопления энергии, ёмкостью и скоростью заряда разряда. При подключении источника питания к выводам обкладок устройства конденсатор накапливает на них заряд.~

Работу устройства можно объяснить по аналогии с протеканием воды. Пусть имеется сосуд с жидкостью площадью поперечного сечения S. По сути, это эквивалент ёмкости. Тогда вода это будет заряд, а высота водяного столба — напряжение. Получается, что энергия — это произведение зарядов на высоту. Но если аккумулятор можно представить как сосуд, в котором имеется тонкий шланг (вывод) и по которому вытекает вода (заряд), то в конденсаторе его диаметр трубки будет равен размеру всей банки. То есть устройство может мгновенно отдать весь накопленный заряд.
При подаче напряжения на обкладки происходит электризация диэлектрика. В результате происходит смещение и на пластины передаётся энергия. На одной из них возникнет избыток электронов, и она условно зарядится отрицательно, а на второй недостаток — проводник станет положительным. Поэтому в формуле, определяющей заряд на обкладках конденсатора, большое значение имеет диэлектрическая проницаемость непроводящего ток вещества.
Между обкладками возникает сила. Величина действующей со стороны первой равняется F = ε1 * q, а со стороны второй F = ε2 * q. Таким образом, можно записать: F = ε1 * q = ε2 * q = E / 2 * q. При увеличении расстояние между обкладками от нулевого до d, будет выполняться работа: A = F * d. Она направлена на преодоление силы взаимодействия между заряженными проводниками.
То есть: A = E / 2 * q * d. Исходя из того, что ε = U/d будет верно записать: А = 1 / 2 q * U. Значит, механическая работа A в соответствии с законом сохранения энергии будет равна количеству зарядов, запасённых в электрическом поле конденсатора: Wэ = C * U2 / 2.
Следует отметить, что при подаче переменного сигнала внутри диэлектрика происходит постоянная смена знаков заряда. В итоге происходит нагревание, что приводит конденсатор к выходу из строя. Характеризуется это явление тангенсом угла диэлектрических потерь. Определяется он как отношение затраченной мощности к реактивной.
Заряд и разряд
Процесс зарядки конденсатора не может быть мгновенным. Его время зависит от силы тока и электроёмкости. При подключении источника питания на одном проводнике собираются электроны, а на другом — остаются протоны. Так как между обкладками находится диэлектрик, то заряженные частицы не могут перейти на противоположную сторону. Но вместе с тем, электроны поступают от источника напряжения на пластины, поэтому ток в цепи всё же есть.
В начале периода зарядки разность потенциалов между обкладками равняется нулю. Как только на пластины переходят заряженные частицы, возникает напряжение. Происходит это из-за диэлектрика, который не даёт притягивающимся друг к другу зарядам перейти на другую сторону. В момент заряда конденсатора на его обкладках много свободного места. Электрический ток в этот момент не встречает сопротивления, и его величина достигает максимального значения. По мере разделения заряженных частиц сила тока снижается. Это происходит до тех пор, пока не исчезнет свободное место на обкладках конденсатора.

То время, которое проходит между начальным состоянием и полного заряда, называют переходным периодом заряда конденсатора. В его конце прекращается рост напряжения, и оно становится равным значению, выдаваемому источником питания. Если нарисовать зависимости тока и напряжения заряда от времени на графике, то можно будет увидеть, что их изменения проходят зеркально по отношению друг к другу.
Формула, по которой можно рассчитать, как происходит заряд конденсатора выглядит так: I = C * V / t, где:
- I — сила тока;
- С — ёмкость конденсатора;
- V / t — изменение напряжения за время.
Как только источник питания будет отключён, то вся энергия, запасённая конденсатором, будет отдана в нагрузку. Фактически устройство само на этом моменте превращается в источник питания. Электроны из-за силы притяжения существующей между разноимёнными частицами, начнут перемещаться в сторону положительно заряженной обкладки.
В начальный момент подключения нагрузки, напряжение на конденсаторе равно тому, что выдавал источник питания.
Но в тот момент, когда в цепи появится ток, конденсатор начнёт отдавать энергию, а напряжение на его выводах станет падать. Следовательно, сила тока тоже снизится. При этом время зарядки и разрядки конденсатора определяется двумя параметрами — ёмкостью и сопротивлением цепи.
как рассчитать заряд конденсатора?
Знаток
(450),
закрыт
3 года назад
Дополнен 12 лет назад
Период электромагнитных колебаний в идеальном колеб. контуре состоящем их конденсатора и катушки индук. Равен 6,3мкс. Амплитуда колебаний силы тока (Им) =5мА. в момент времени т сила тока в катушке равна 3мА .найти заряд конд-ра в этот момент
григорий иванушкин
Ученик
(43)
12 лет назад
Имеем последовательно соединённые конденсаторы разной ёмкости С1, С2 заряженные на разные напряжения U1, U2.
Как расчитать общее напряжение U и общий заряд Q этих конденсаторов?
Используемые ф-лы:
W = C*U^2/2
W = Q^2/2C
C= C1*C2/(C1+C2)
Q=C*U
Если заряд последовательно соединённых конденсаторов происходит от одного источника, то:
U1= U*C2/(C1+C2).
Q1 = Q2
Rasha
Оракул
(53579)
12 лет назад
“Александр R9AAA Прокудин
Q=C*U – емкость в фарадах умножить на напряжение в вольтах”
так как там колебания, U это мгновенное напряжение на конденсаторе которое вычисли сама
