Еще в древности было известно, что наэлектризованные тела взаимодействуют. Силу взаимодействия двух небольших заряженных шариков с помощью крутильных весов впервые измерил Шарль Кулон. Он сформулировал закон, который позже назвали его именем.
Так же, было выяснено, что сила, с которой два заряда притягиваются, или отталкиваются, зависит не только от самих зарядов, но и от вещества, в котором эти заряды находятся.
Опыт Кулона
Кулон нашел способ измерить взаимное действие двух зарядов. Для этого он использовал крутильные весы.
Ему не пришлось применять дополнительную особо чувствительную аппаратуру. Потому, что взаимное действие зарядов имело достаточную для наблюдения интенсивность.
Примечание: Опыт Кулона похож на опыт Кавендиша, который экспериментально определил гравитационную постоянную G.
Устройство крутильных весов
Такие весы (рис. 1) содержат перекладину — тонкий стеклянный стержень, расположенный горизонтально. Он подвешен на тонкой вертикально натянутой упругой проволоке.
На одном конце стержня находится небольшой металлический шарик. К другому концу прикреплен груз, который используется, как противовес.
Еще один металлический шарик, прикрепленный ко второй палочке из стекла, можно располагать неподалеку от первого шарика. Для этого в верхней крышке корпуса весов проделано отверстие.

Рис. 1. Устройство крутильных весов, использованных Кулоном для обнаружения силы взаимодействия зарядов
Если наэлектризовать шарики, они начнут взаимодействовать. А прикрепленная к проволоке перекладина, на которой находится один из шариков, будет поворачиваться на некоторый угол.
На корпусе весов на уровне палочки располагается шкала с делениями. Угол поворота связан с силой взаимного действия шариков. Чем больше угол поворота, тем больше сила, с которой шарики действуют друг на друга.
Чтобы сдвинувшийся шарик вернуть в первоначальное положение, нужно закрутить проволоку на некоторый угол. Так, чтобы сила упругости скомпенсировала силу взаимодействия шариков.
Для закручивания проволоки в верхней части весов есть рычажок. Рядом с ним расположен диск, а на нем – еще одна угловая шкала с делениями.
По нижней шкале определяют точку, в которую необходимо вернуть шарик. Верхней шкалой пользуются, чтобы установить угол, на который нужно рычажком закрутить проволоку.
С помощью крутильных весов Шарль Кулон выяснил, как именно сила взаимного действия зависит от величины зарядов и расстояния между зарядами.
В те годы единиц для измерения заряда не было. Поэтому ему пришлось изменять заряд одного шарика с помощью метода половинного деления.
Когда он касался заряженным шариком второго такого же шарика, заряды между ними распределялись поровну. Таким способом, можно было уменьшать заряд одного из шариков, участвующих в опыте, в 2, 4, 8, 16 и т. д. раз.
Так опытным путем Кулон получил закон, формула которого очень похожа на закон всемирного тяготения.
В память о его заслугах, силу взаимодействия зарядов называют Кулоновской силой.
Закон Кулона для зарядов в вакууме
Рассмотрим два точечных заряда, которые находятся в вакууме (рис. 2).

Рис. 2. Два положительных заряда q и Q, расположенных в вакууме на расстоянии r, отталкиваются. Силы отталкивания направлены вдоль прямой, соединяющей заряды
На рисунке 2 сила (large F_{Q} ) – это сила, с которой положительный заряд Q отталкивает второй положительный заряд q. А сила (large F_{q} ) принадлежит заряду q, с такой силой он отталкивает заряд Q.
Примечание: Точечный заряд – это заряженное тело, размером и формой которого можно пренебречь.
Силы взаимодействия зарядов, по третьему закону Ньютона, равны по величине и направлены противоположно. Поэтому, для удобства можно ввести обозначение:
[large F_{q} = F_{Q} = F]
Для силы взаимодействия зарядов в вакууме Шарль Кулон сформулировал закон так:
Два точечных заряда в вакууме,
взаимодействуют с силой
прямо пропорциональной
произведению величин зарядов
и обратно пропорциональной
квадрату расстояния между ними.
Формула для этого закона на языке математики запишется так:
[large boxed { F = k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;
(|q| left( text{Кл}right) ) – величина первого заряда;
(|Q| left( text{Кл}right) ) – величина второго заряда;
(r left( text{м}right) ) – расстояние между двумя точечными зарядами;
(k ) – постоянная величина, коэффициент в системе СИ;
Сила – это вектор. Две главные характеристики вектора – его длина и направление.
Формула позволяет найти одну из характеристик вектора F — модуль (длину) вектора.
Чтобы определить вторую характеристику вектора F – его направление, нужно воспользоваться правилом: Мысленно соединить два неподвижных точечных заряда прямой линией. Сила, с которой они взаимодействуют, будет направлена вдоль этой прямой линии.
Сила Кулона – это центральная сила, так как она направлена вдоль прямой, соединяющей центры тел.
Примечание: Еще один пример центральной силы — сила тяжести.
Что такое коэффициент k с точки зрения физики
Постоянная величина (k ), входящая в формулу силы взаимодействия зарядов, имеет такой физический смысл:
(k ) — это сила, с которой отталкиваются два положительных точечных заряда по 1 Кл каждый, когда расстояние между ними равно 1 метру.
Значение постоянной k равно девяти миллиардам!
[large boxed { k = 9cdot 10^{9} left( H cdot frac{text{м}^{2}}{text{Кл}^{2}}right) } ]
Это значит, что заряды взаимодействуют с большими силами.

Рис. 3. Коэффициент k в формуле взаимодействия зарядов
Константу k можно вычислить опытным путем, расположив два известных заряда (не обязательно по 1 Кулону каждый) на удобном для измерений расстоянии (не обязательно 1 метр) и измерив силу из взаимного действия.
Нужно подставить известные величины зарядов, расстояние между ними и измеренную силу в такую формулу:
[large boxed { k = frac {F cdot r^{2}}{|q| cdot |Q|} } ]
Величина k связана с электрической постоянной (varepsilon) такой формулой:
[large boxed { k = frac{1}{4pi cdot varepsilon_{0}} } ]
Поэтому дробь из правой части этой формулы можно встретить в различных справочниках физики, где она заменяет коэффициент k.
Закон Кулона для зарядов в веществе
Если два точечных заряда находятся в веществе, то сила их взаимного действия будет меньше, чем в вакууме. Для зарядов в веществе закон Кулона выглядит так:
[large boxed { F = frac{1}{varepsilon} cdot k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила взаимодействия зарядов в веществе;
(|q| ; |Q| left( text{Кл}right) ) – величины зарядов;
(r left( text{м}right) ) – расстояние между зарядами;
( k = 9cdot 10^{9} ) – постоянная величина;
( varepsilon ) – диэлектрическая проницаемость вещества, для разных веществ различается, ее можно найти в справочнике физики;

Рис. 4. Два заряда -q и +Q, расположенные в вакууме на расстоянии r, притягиваются сильнее, нежели те же заряды, расположенные на таком же расстоянии в диэлектрике
Силы, с которыми заряды действуют друг на друга в веществе, отличаются от сил взаимодействия в вакууме в ( varepsilon ) раз:
[large boxed { F_{text{(в диэлектрике)}} = frac{1}{varepsilon} cdot F_{text{(в вакууме)}} } ]
Примечание: Читайте отдельную статью, рассказывающую, что такое диэлектрическая проницаемость и электрическая постоянная.
Электростатика: элементы учебной физики
Продолжение. См. № 17,
18/07
В.В.МАЙЕР,
Гоу ВПО ГГПИ им. В.Г.Короленко, г. Глазов,
Республика Удмуртия
varaksina_ei@list.ru
Электростатика: элементы учебной
физики
Лекция 3. ВЗАИМОДЕЙСТВИЕ
ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
Закон взаимодействия электрических
зарядов установлен Ш.Кулоном в 1785 г. Это
фундаментальный закон электростатики,
экспериментальное обоснование справедливости
которого при изучении физики в школе совершенно
необходимо. Разумеется, не нужно стремиться к
излишней точности опытов, – это только усложнит
экспериментальную установку и мало что добавит к
убедительности обоснования закона Кулона. Лучше
всего использовать такие эксперименты, которые
каждый школьник сможет поставить у себя дома.
То, что это возможно, проверено нами
непосредственно в школе. Один из выпускников
Глазовского пединститута во время
педагогической практики поставил перед
десятиклассниками задачу изготовить простейшие
электростатические динамометры и
экспериментально проверить закон Кулона дома.
Весь класс с большим интересом провёл
соответствующие исследования. У каждого
школьника получился свой прибор и свои
результаты эксперимента, но все они в пределах
погрешности подтвердили справедливость закона
Кулона.
При изучении закона Кулона особое
внимание следует обратить на формирование
понятий точечного заряда и бесконечности. В
теории всё просто: нет школьника, который,
представляя себе точку, не сумел бы представить,
что к тому же она имеет массу или заряд. Плохо то,
что многие школьники убеждены в реальном
существовании материальных точек и точечных
зарядов. Примерно так же дело обстоит и с
бесконечностью. Утверждая, что заряды
взаимодействуют на любом как угодно большом
расстоянии между ними, мы формируем у школьников
представление об унылом плоском мире, в котором
длятся и длятся, никогда не кончаясь,
электрические и другие поля. В действительности
реальная бесконечность всегда конечна.
Поэтому экспериментальное
обоснование закона Кулона должно сформировать у
учащихся соответствующие теории и эксперименту
понятия точечности заряда и бесконечно большого
расстояния между зарядами. Это формирование
наиболее успешно произойдёт в процессе
самостоятельных экспериментальных исследований
учащихся.
3.1. Опыты Кулона. Разберёмся в
физической сущности опытов Кулона.
Использовавшаяся учёным экспериментальная
установка схематически изображена на рисунке.
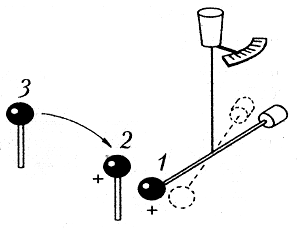
Главным её элементом являются
крутильные весы. Это лёгкое коромысло на тонкой
упругой нити. Верхний конец нити прикреплён к
втулке, снабжённой указателем и шкалой. К нижнему
концу нити прикреплено коромысло из диэлектрика,
на одном конце которого находится лёгкий
проводящий шарик 1, а на другом — противовес.
Два точно таких же шарика 2 и 3 укреплены
на изолирующих подставках. Возле коромысла
имеется вторая шкала, непосредственным
измерением по которой можно убедиться, что угол
закручивания нити пропорционален силе,
действующей на шарик.
Основной опыт Кулона заключался в
следующем. Он зарядил шарик 2 и прикоснулся им к
шарику 1. Заряды распределились на шариках
поровну, и шарики, получив одноимённые заряды
некоторой величины q, оттолкнулись друг от
друга и разошлись на расстояние r. При этом
нить закрутилась на некоторый угол ![]() , пропорциональный силе
, пропорциональный силе
электрического отталкивания f.
За втулку Кулон поворачивал верхний
конец нити в противоположном направлении так,
чтобы расстояние между шариками уменьшалось в 2,
3, 4, … раза, и обнаружил, что угол закручивания
нити, а следовательно, сила, увеличивались
соответственно в 4, 9, 16, … раз. Отсюда он сделал
вывод, что сила взаимодействия заряженных
шариков обратно пропорциональна квадрату
расстояния между ними: f ~ 1/r2.
Прикоснувшись к шарику 2
незаряженным шариком 3, Кулон уменьшил заряд
шарика 2 в два раза. Повторяя описанный опыт,
он обнаружил, что сила взаимодействия
уменьшилась в два раза и осталась обратно
пропорциональной квадрату расстояния между
зарядами. Разрядив шарик 3 и вновь
коснувшись им шарика 2, он уменьшил заряд
последнего в 4 раза по сравнению с
первоначальным, и т.д. Из этой серии опытов Кулон
заключил, что сила взаимодействия
пропорциональна произведению зарядов тел: f ~ q1q2.
Наконец, Кулон заметил, что если
расстояние между заряженными шариками мало, то
наблюдаются отступления от обнаруженных
закономерностей. Отсюда следует, что в
формулировке закона взаимодействия заряженные
тела должны считаться небольшими, в пределе –
точечными.
3.2. Закон Кулона.
Проанализировав результаты описанных серий
опытов, мы приходим к выводу, что получено
экспериментальное доказательство
справедливости закона Кулона: сила
взаимодействия двух точечных зарядов
пропорциональна произведению этих зарядов и
обратно пропорциональна квадрату расстояния
между ними:
![]()
(3.1)
На самом деле точечных зарядов,
конечно, не существует, как не существует и
заряженных точек. Требование точечности зарядов
означает, что заряженные тела имеют размеры,
много меньшие расстояния между ними.
В системе единиц СИ коэффициент
пропорциональности в законе Кулона
![]()
Впоследствии мы убедимся, что
коэффициент k удобно записывать в виде
![]()
(3.2)
а закон Кулона – в виде:
![]()
(3.3)
Величина
![]()
называется электрической
постоянной.
В этой системе единиц заряд 1 Кл можно
было бы определить как такой, который
взаимодействует с равным себе и удалённым на
расстояние 1 м зарядом с силой 9 • 109 Н.
Однако в системе СИ в качестве основной
используют не единицу заряда, а единицу силы
электрического тока ампер, которая вводится
на основе магнитного взаимодействия движущихся
зарядов. Поэтому единица заряда является
производной от ампера: кулон – электрический
заряд, проходящий через поперечное сечение
проводника за 1 с при силе тока через проводник 1
А.
Разумеется, грубые опыты Кулона и те их
варианты, которые мы можем повторить, не в
состоянии убедительно свидетельствовать в
пользу справедливости закона Кулона. Но из
закона Кулона можно получить следствия, которые
допускают гораздо более точную
экспериментальную проверку. Сейчас нет никаких
сомнений в том, что закон Кулона для силы
взаимодействия электрических зарядов
справедлив с высокой степенью точности.
3.3. Взаимодействие зарядов в среде.
Нетрудно представить, что крутильные весы
можно изготовить так, что они будут допускать
измерение кулоновской силы в различных газах и
жидкостях. Силу взаимодействия зарядов в
принципе можно измерить также в твёрдых телах.
Эксперименты показали, что закон Кулона
выполняется и в диэлектриках, но сила
кулоновского взаимодействия в них в e раз меньше,
чем в вакууме:
![]()
(3.4)
Величина ![]() = fвак /f получила
= fвак /f получила
название диэлектрической проницаемости среды.
Диэлектрическая проницаемость среды
– это физическая величина, показывающая, во
сколько раз сила взаимодействия зарядов в среде
меньше силы их взаимодействия в вакууме.
Исследование 3.1. Доказательность
опытов Кулона
Информация. В одном из своих
опытов Кулон получил следующие результаты.
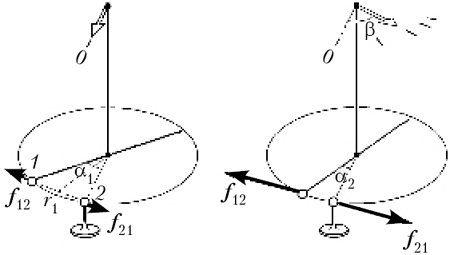
После соприкосновения шарика 1 на
коромысле с заряженным шариком 2 коромысло
повернулось на угол ![]() 1 = 24° (левый рисунок). Чтобы угол
1 = 24° (левый рисунок). Чтобы угол
между двумя шариками уменьшился в два раза и стал
равен ![]() 2 = 12°,
2 = 12°,
верхний конец нити крутильных весов пришлось
повернуть на угол ![]() = 84° (правый рисунок).
= 84° (правый рисунок).
Задание. Покажите, что эти
экспериментальные результаты подтверждают
закон Кулона.
Вариант выполнения.
Первоначальный угол закручивания нити ![]() 1 = 24°. Если
1 = 24°. Если
плечо коромысла равно d, то расстояние между
шариками в этом случае r1 = 2d(sin![]() 1/2). Когда угол
1/2). Когда угол
поворота коромысла уменьшился в два раза,
расстояние между шариками стало равно r2
= 2d(sin![]() 2/2).
2/2).
Отношение этих расстояний:
![]()
Но сила взаимодействия
пропорциональна углу закручивания нити
крутильных весов. В первом случае этот угол был
равен ![]() 1 = 24°,
1 = 24°,
а во втором ![]()
Отношение углов ![]()
Таково же отношение соответствующих кулоновских
сил. Таким образом, экспериментальные данные
Кулона показывают, что сила взаимодействия между
двумя зарядами обратно пропорциональна квадрату
расстояния между ними.
Исследование 3.2.
Экспериментальное обоснование закона Кулона
Задание. Разработайте доступную
конструкцию крутильных весов, соберите
экспериментальную установку и на опыте
убедитесь в справедливости закона Кулона.
Вариант выполнения.
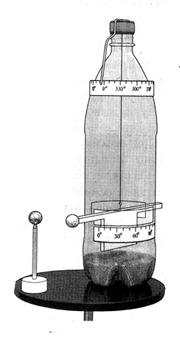
Одна из наиболее доступных
экспериментальных установок изображена на
фотографии. Нить крутильных весов представляет
собой медную проволоку диаметром около 0,1 мм и
длиной 200 мм (можно использовать и тонкую леску).
Один конец её проходит через расположенные рядом
отверстия в крышке пластиковой бутылки и
закреплён скруткой. Второй конец проволоки также
скруткой закреплён в ушке канцелярской булавки,
которая вставлена в центр коромысла крутильных
весов. Коромысло специальной формы вырезано
острым ножом из тонкого листа пенопласта. Длина
собственно коромысла составляет примерно 200 мм.
Нижняя часть коромысла размером 40 ![]() 70 мм выполняет функцию
70 мм выполняет функцию
демпфера, увеличивающего затухание крутильных
колебаний. На одном конце коромысла деревянной
шпилькой, сделанной из спички, закреплён шарик
диаметром 1–2 см, вырезанный из пенопласта и
покрытый тонкой алюминиевой фольгой. В качестве
штатива можно взять пластиковую бутылку, в
стенке которой для коромысла диаметрально
противоположно вырезаны два прямоугольных
отверстия. Чтобы прибор был устойчив, на дно
бутылки насыпают немного речного песка или
кладут чтонибудь тяжёлое. Коромысло
уравновешивают противовесом (например, втыкают в
свободный конец канцелярские булавки). На
бутылку скотчем наклеивают две шкалы: снизу,
возле прорези для коромысла, и сверху, возле
крышки. К крышке прикрепляют проволочный
указатель.
Пьезоэлектрическим источником или
иным способом зарядите второй шарик,
расположенный на изолированной подставке.
Прикоснитесь этим шариком к шарику на крутильных
весах. При этом шарики одинаковых размеров
приобретут равные одноимённые заряды,
оттолкнутся, и коромысло с шариком повернётся на
некоторый угол ![]() ,
,
величину которого определите по нижней шкале.
Поворачивайте крышку, к которой прикреплён
верхний конец нити, в противоположном
направлении до тех пор, пока угол поворота
коромысла a не уменьшится вдвое. По верхней шкале
определите угол поворота ![]() крышки. Тогда угол закручивания нити
крышки. Тогда угол закручивания нити
составит ![]() (см.
(см.
исследование 3.1).
Найдите отношение этого угла ![]() к
к
первоначальному углу закручивания нити ![]() . Если оно окажется
. Если оно окажется
близким к 4, значит, опыт доказывает, что сила
взаимодействия двух заряженных шариков обратно
пропорциональна квадрату расстояния между ними.
Самостоятельно убедитесь, что она
пропорциональна произведению зарядов шариков.
Исследование 3.3.
Экспериментальное подтверждение следствия
закона Кулона
Информация. Справедливость
закона Кулона подтверждена многочисленными
экспериментами и не вызывает сомнений. Однако,
если нужно не просто заучить этот закон, а
глубоко вникнуть в его сущность, обосновывающий
его учебный эксперимент совершенно необходим.
Вовсе не обязательно, чтобы эксперимент
подтверждал закон напрямую, во многих случаях
предпочтительнее опосредованное обоснование
теоретического положения. Нередко прямое
экспериментальное обоснование вообще
невозможно. Тогда из предполагаемого закона
выводят следствия и, если они выдерживают
экспериментальную проверку, делают заключение о
справедливости закона.
Проблема. Все школьные задачи на
взаимодействие зарядов решаются на основе
закона Кулона, значит, они являются следствиями
этого закона. Нельзя ли использовать для
подтверждения закона Кулона имеющуюся во всех
школьных учебниках задачу об отталкивании двух
висящих на нитях одинаково заряженных шариков?
Задание.
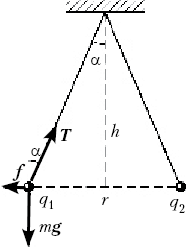
Пусть два одинаковых проводящих
шарика подвешены в одной точке на нитях
одинаковой длины. При сообщении им одноимённых
зарядов q1 и q2 шарики,
отталкиваясь, расходятся на расстояние r
друг от друга так, что прямая, по которой
действуют кулоновские силы, оказывается на
расстоянии h от точки подвеса. Найдите связь
между расстояниями r и h. Используя
решение этой задачи, разработайте и поставьте
эксперимент, подтверждающий справедливость
закона Кулона.
Вариант выполнения. Вначале решим
предложенную задачу. На шарик действуют сила
тяжести mg, кулоновская сила f
и сила натяжения нити T, модули
которых связаны соотношениями:
f = Tsin![]() ; mg = Tcos
; mg = Tcos![]()
Отсюда сила отталкивания шариков:
![]()
Подставляя выражение для кулоновской
силы, получаем ![]()
Отсюда:
![]()
(3.5)
Таким образом, связь между
расстояниями r и h найдена. Теперь
обратимся к эксперименту.
Если в эксперименте электрические
заряды шариков остаются неизменными, то
предыдущую формулу удобно переписать в виде
![]()
(3.6)
Если неизменны расстояние h и
заряд одного из шариков, например, q2
= const, то решение задачи можно представить в
виде:
![]()
(3.7)
Очевидно, все привёденные здесь
выражения являются следствиями закона Кулона
(3.1). Подтвердив их справедливость, мы тем самым
получим экспериментальное обоснование закона
Кулона.
Пенопластовые шарики диаметром
примерно 1 см покройте тонкой алюминиевой
фольгой. Шарики подвесьте на тонких нейлоновых
нитях длиной 20–40 см так, чтобы они
соприкасались. Параллельно нитям закрепите в
горизонтальном положении гладкий стержень из
диэлектрика (например, стеклянную трубку). Нити
должны слегка касаться стержня, тогда удастся
избежать их скручивания и длительных колебаний
шариков. За шариками на расстоянии примерно 10 см
поставьте белый экран с миллиметровой шкалой.
Осветите шарики небольшой лампой так, чтобы на
экране можно было определять расстояние r’
между центрами их теней.
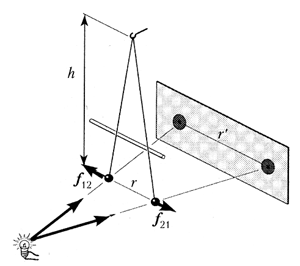
Соприкасающиеся шарики зарядите от
наэлектризованной палочки или
пьезоэлектрического источника. Шарики
оттолкнутся друг от друга. Линейкой измерьте
расстояние h от линии взаимодействия
шариков до точки подвеса и по шкале на экране
измерьте расстояние r’ между центрами теней
шариков. Пальцами сведите нити вместе ниже точки
подвеса и измерьте новые значения тех же
расстояний. Повторите опыт в третий раз.
Найдите значения отношений r’3/h
для всех трёх измерений и убедитесь, что в
пределах ошибок они одинаковы. Таким образом,
опыт подтверждает справедливость формулы (3.1).
Отсюда следует, что сила Кулона обратно
пропорциональна квадрату расстояния между
заряженными телами.
Для доказательства того, что
кулоновская сила пропорциональна произведению
зарядов, достаточно при неизменном подвесе
изменять заряд одного из шариков прикосновением
к нему незаряженным шариком того же размера.
Пусть это будет первый шарик.
Измерьте расстояние r’ между
тенями шариков для некоторого заряда q1
одного из них. Уменьшите заряд этого шарика в два
раза (до значения q1/2) и измерьте новое
расстояние между шариками. Повторите опыт в
третий раз для заряда q1/4. Для
полученных значений найдите отношения r’ 3/q1,
подставляя в них вместо q1 числа 1; 0,5;
0,25, и убедитесь, что в пределах ошибок опыта они
совпадают. Таким образом, эксперимент подтвердил
справедливость следствия (3.7) из закона Кулона.
Очевидно, отсюда следует, что сила Кулона
пропорциональна произведению взаимодействующих
зарядов.
Вы полностью разобрались в
эксперименте, если поняли, почему необходимо
измерять не непосредственно расстояние r
между шариками, а расстояние r’ между их
тенями, и почему в вычислениях это
обстоятельство не учитывается. Советуем вместо
пенопластовых шариков, покрытых фольгой,
попробовать скатанные из алюминиевой фольги
шарики диаметром 2–4 мм. Получится ли
эксперимент, если проводящие шарики заменить
гильзами из алюминиевой фольги?
Исследование 3.4.
Электростатический динамометр
Информация. Крутильными весами
(исследование 3.2) неудобно измерять силу, с
которой взаимодействуют электрически
заряженные тела. Необходим простой и
чувствительный прибор, позволяющий делать это в
учебных экспериментах. Вспомним электрометр: в
нём стрелка отклоняется на весьма большие углы
даже при сравнительно небольших зарядах.
Обеспечивается это тем, что центр масс стрелки
находится возле оси её вращения, несколько ниже
неё.
Проблема. Нельзя ли принцип
действия стрелочного электрометра использовать
для создания чувствительного
электростатического динамометра?
Задание.
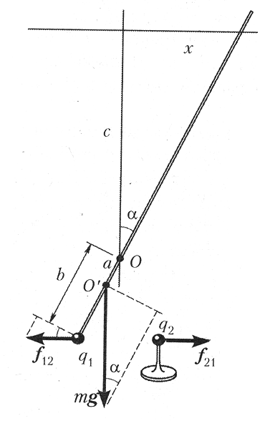
Представьте, что на нижнем конце
стержня из диэлектрика закреплён проводящий
шарик. Общая масса системы m, центр масс
находится в точке О’, а ось вращения
расположена на расстоянии а от центра масс
системы и на расстоянии b от шарика в точке О.
На расстоянии с от оси вращения,
перпендикулярно начальному положению стержня,
расположена шкала, по которой отсчитывается
смещение х верхней части стержня. Шарику
сообщили некоторый заряд, и к нему подносят
другой заряженный шарик так, что отрезок,
соединяющий их центры, остаётся горизонтальным.
Докажите, что прибор, построенный в соответствии
с изложенной идеей, позволяет измерить силу
кулоновского взаимодействия между заряженными
шариками. Разработайте конструкцию, изготовьте и
исследуйте электростатический динамометр.
Вариант выполнения. Вначале решим
задачу, сформулированную в задании. На подвижную
систему действуют только две силы: кулоновская
f = f12 и
сила тяжести mg. Стержень окажется в
равновесии, если сумма моментов этих сил
относительно оси вращения равна нулю: fcos![]() • b – mgsin
• b – mgsin![]() • a = 0.
• a = 0.
Отсюда: ![]()
Но tg ![]() = x/c, следовательно,
= x/c, следовательно,
![]()
(3.8)
Значит, кулоновская сила f,
действующая на шарик, может быть измерена по
величине отрезка х.
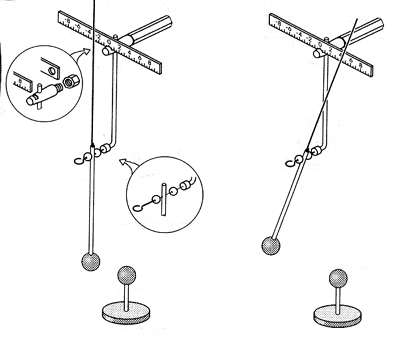
Простейший электростатический
динамометр без особых затруднений вы сможете
собрать из подручных материалов: полиэтиленовой
трубки (чистый стержень от шариковой ручки),
отрезка медной проволоки, канцелярской булавки,
пенопласта, алюминиевой фольги, пластмассовой
крышки и т.п.
Очевидно, чувствительность прибора
тем больше, чем, при прочих равных условиях,
меньше расстояние от центра масс подвижной
системы до её оси вращения. Один из наших
приборов имел параметры: а = 5 мм, b = 55 мм, с
= 100 мм, m = 0,94 г.
Исследование 3.5.
Электростатическое взаимодействие заряженных
шаров
Информация. Закон Кулона
сформулирован для точечных зарядов, хотя сам
Кулон экспериментировал, разумеется, не с
заряженными точками, которых в природе не
существует, а с шарами конечных размеров. Принято
считать заряженные тела точечными, если их
размеры существенно меньше расстояния между
ними. Для неточечных зарядов закон Кулона не
выполняется. Наиболее ярко свидетельствует об
этом явление, при котором уменьшение расстояния
между одноимённо заряженными шарами разных
размеров приводит к тому, что взаимное
отталкивание шаров сменяется их притяжением.
Проблема. Каково в реальности
соотношение между размерами заряженных шаров и
расстоянием между ними, при котором шары можно
считать точечными зарядами?
Задание. Используя
электростатический динамометр, детально
исследуйте зависимость силы кулоновского
взаимодействия двух зарядов от расстояния между
ними.
Вариант выполнения.
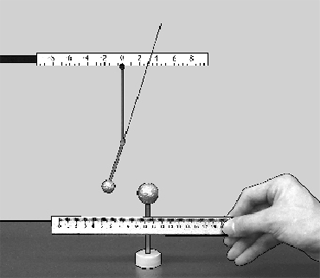
На изолирующей стойке закрепите шарик
из пенопласта, обёрнутый алюминиевой фольгой.
Зарядите его от пьезоэлектрического источника,
одноимённым зарядом зарядите пробный шарик на
стержне электростатического динамометра.
Пробный заряд находится бесконечно
далеко от исследуемого, если электростатический
динамометр не фиксирует силы
электростатического взаимодействия между
зарядами. В эксперименте удобно
электростатический динамометр оставить
неподвижным, а перемещать исследуемый заряд.
Постепенно приближайте заряженный
шарик на изолирующей подставке к шарику
электростатического динамометра так, чтобы
соединяющий центры шариков отрезок оставался
горизонтальным. В таблицу записывайте значения
расстояния между зарядами и соответствующие им
значения силы электростатического
взаимодействия. Удобно расстояние измерять в
сантиметрах, а силу – в условных единицах, в
которых отградуирована шкала динамометра.
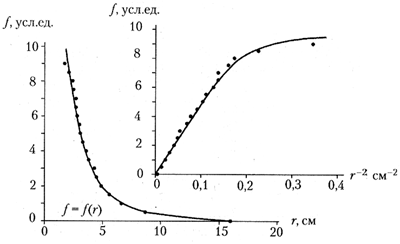
По получившимся данным постройте
график зависимости силы от расстояния (левый
рисунок). Ещё раз убедитесь, что сила
электростатического взаимодействия обратно
пропорциональна квадрату расстояния между
зарядами, для чего постройте график зависимости
силы от величины, обратной квадрату расстояния
(правый рисунок): получается прямая линия.
Обратите внимание: при небольших расстояниях
между заряженными шариками сила взаимодействия
меньше, чем это требует закон Кулона. Объясните
это явление.
Исследование 3.6. Определение
зарядов шаров
Информация. В учебных
экспериментах по электростатике, как правило,
определяют знак заряда, но не его величину.
Объясняется это тем, что соответствующих
измерительных приборов в учебной лаборатории
просто не существует. Однако принципиально важно
непосредственное определение заряда без
использования каких бы то ни было
электроизмерительных приборов. В этом случае вся
электростатика сразу приобретает надёжную
экспериментальную основу.
Проблема. Возможно ли в доступном
учебном эксперименте количественно оценить
электрический заряд на теле, образующийся при
электризации?
Задание. Используя
электростатический динамометр, определите
заряды, которые несут взаимодействующие тела.
Вариант выполнения. Для
одинаковых зарядов q1 = q2 = q
из закона Кулона (3.1) имеем
![]()
(3.9)
Силу f вычислим, измерив параметры
электростатического динамометра (см.
исследование 3.4). Один из наших приборов имел
параметры: а = 5 • 10–3 м, b
= 55 • 10–3 м, с = 100 • 10–3 м, m
= 0,94 • 10–3 кг. Тогда:
![]()
(3.10)
где х — смещение по шкале
указателя динамометра, в метрах.
Это, в частности, даёт основание на
графиках зависимости модуля кулоновской силы f
от расстояния r и от величины 1/r2,
обратной квадрату расстояния, рядом с условными
единицами силы поставить абсолютные их значения
в миллиньютонах. Теперь для произвольного
значения расстояния r по левому графику
можно определить соответствующее значение силы f
и, подставив эти значения в формулу ![]() вычислить заряды q
вычислить заряды q
взаимодействующих шаров.
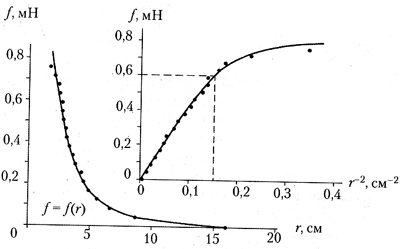
Можно воспользоваться и правым
графиком, по которому квадрат заряда
определяется через тангенс угла наклона
прямолинейной части графика к горизонтальной
оси:
![]()
Отсюда искомый заряд q =
6,6 • 10–9 Кл.
Наконец, проще всего, именно пользуясь
электростатическим динамометром, измерить
отклонение его стрелки х и соответствующее
расстояние r между центрами одинаковых и
одинаково заряженных шариков, а затем по формуле
(3.10) вычислить силу взаимодействия между
шариками, и по формуле (3.9) – заряд каждого из
шариков.
Вопросы и задания для самоконтроля
1. В чём суть опытов Кулона? Какова их
точность? Нужно ли в школе стремиться к точному
подтверждению закона Кулона?
2. Сформулируйте закон Кулона. Что
понимается под точечными зарядами?
Литература
Демонстрационный эксперимент по
физике в старших классах средней школы. Т. 2.
Электричество. Оптика. Физика атома: Под ред.
А.А.Покровского — М.: Просвещение, 1972.
Жакин С.П. Крутильные весы в
демонстрационном эксперименте. – Физика в школе,
2003, № 7, с. 44–46.
Роджерс Э. Физика для
любознательных. Т. 3. Электричество и
магнетизм. Атомы и ядра.— М.: Мир, 1971.
Суербаев А.Х., Клюев П.Н.
Физический эксперимент по демонстрации закона
Кулона: В сб. «Проблемы учебного физического
эксперимента. Сборник научных трудов», вып.
11. – М.: ИОСО РАО, 2001, с. 58–59.
Шахмаев Н.М., Каменецкий С.Е.
Демонстрационные опыты по электродинамике. — М.:
Просвещение, 1973.
Продолжение в № 20/07
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.

История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).

У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10-9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1º. Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r2

Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 — 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 1018 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10-12 Кл2/Н∙м2. Выполнив несложные вычисления, мы находим: k = 9×109 H*м2 / Кл2. В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).

Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Использованная литература:
- Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004.
- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов.
- Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм.
Видео по теме
Электризация и электрический заряд
Определения
Электростатика — раздел физики, изучающий неподвижные заряды.
Электризация — процесс, в результате которого тело приобретает электрический заряд. Если тело начиняет притягивать к себе другие тела, то говорят, что оно наэлектризовано, или приобрело электрический заряд.
Электрический заряд — физическая величина, определяющая способность тел участвовать в электромагнитных взаимодействиях.
Электрический заряд обозначается как q. Единица измерения — Кулон (Кл).
В природе существуют два вида зарядов, которые условно назвали положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные притягиваются.
Закон сохранения зарядаАлгебраическая сумма зарядов в замкнутой системе сохраняется:
∑qi=const.
Замкнутая система в электростатике — такая система, которая не обменивается зарядами с окружающей средой.
Экспериментально доказано, что заряды можно делить, но до определенного предела. Носитель наименьшего электрического заряда — электрон. Он заряжен отрицательно.
Заряд электрона:
qe=−1,6·10−19 Кл
Масса электрона:
me=9,1·10−31 кг
Модуль любого заряда кратен заряду электрона:
q=Nqe
N — избыток электронов.
В процессе электризации от одного тела к другому передаются только электроны. Если у тела избыток электронов, то оно заряжено отрицательно, а если недостаток, то — положительно.
Внимание! Заряженные тела притягивают к себе нейтральные тела и тела с противоположным зарядом. Отталкивание наблюдается только между одноименно заряженными телами.
Пример №1. На двух одинаковых металлических шарах находятся положительный заряд 7 нКл и отрицательный заряд 1 нКл. Каким станет заряд на каждом шаре при соприкосновении шаров?
После того, как шары соприкоснутся, заряд на них выровняется. Так как большим зарядом обладает положительно заряженный шар, то оба шара в итоге будут заряжены положительно:
(7 – 1)/2 нКл = 3 нКл
Каждый шар будет иметь положительный заряд, равный 3 нКл.
Закон Кулона
Закон Кулона — основной закон электростатики, который был открыт экспериментально в 1785 году.
Закон Кулона
Два неподвижных точечных заряда в вакууме взаимодействуют друг с другом с силой, прямо пропорциональной квадрату расстояния между ними:
FK=k|q1||q2|r2
FK — сила, с которой взаимодействуют два точечных заряда (кулоновская сила, или сила Кулона). |q1| (Кл) и |q2| (Кл) — модули зарядов, r (м) — расстояние между зарядами, k — коэффициент пропорциональности, который численно равен силе взаимодействия между двумя точечными зарядами по 1 Кл, находящимися на расстоянии 1 м друг от друга:
k=14πε0=9·109 Н·м2/Кл2
ε0 — электрическая постоянная равная, 8,85∙10–12 Кл2/(Н∙м2).
Закон Кулона в среде
FK=k|q1||q2|εr2
ε — диэлектрическая проницаемость. Это табличная величина, которая показывает, во сколько раз электрическое взаимодействие в среде уменьшается по сравнению с вакуумом.
Направление силы Кулона
Направление силы Кулона зависит от знаков зарядов. На рисунке ее прикладывают к центру заряженного тела.
Подсказки к задачам
Подсказка №1
При соприкосновении одинаковых проводящих шариков, один из которых заряжен, заряд между шариками делится поровну:
q′
1=q′2=q2
Подсказка №2
При соприкосновении одинаковых проводящих шаров заряды складываются с учетом знаков и делятся поровну. Модули зарядом двух шариков:
q′1=q′2=|q1±q2|2
Пример №2. Два маленьких одинаковых металлических шарика заряжены положительными зарядами q и 5q и находятся на некотором расстоянии друг от друга. Шарики привели в соприкосновении и раздвинули на прежнее расстояние. Как изменилась сила взаимодействия шариков?
Изначально сила Кулона была равна:
FK1=kq5qr2=5kq2r2
Когда шарики коснулись, заряд каждого из них стал равен:
q′=5q+q2=3q
После того, как шарики раздвинули на прежнее расстояние, сила взаимодействия между ними стала равна:
FK2=k3q3qr2=9kq2r2
Поделим вторую силы на первую и получим:
FK2FK1=9kq2r2·r25kq2=95=1,8
Следовательно, после всех манипуляций сила взаимодействия между двумя заряженными шариками увеличилась в 1,8 раз.
Задание EF17493
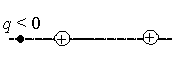 Точечный отрицательный заряд q помещён слева от неподвижных положительно заряженных шариков (см. рисунок). Куда направлена равнодействующая кулоновских сил, действующих на заряд q?
Точечный отрицательный заряд q помещён слева от неподвижных положительно заряженных шариков (см. рисунок). Куда направлена равнодействующая кулоновских сил, действующих на заряд q?
а) вверх
б) вниз
в) вправо
г) влево
Алгоритм решения
- Вспомнить, как взаимодействуют разноименные заряды.
- Установить взаимодействие заряда с каждым из шариков.
- Выяснить, куда будет направлена равнодействующая сила, действующая на заряд со стороны заряженных шариков.
Решение
Отрицательные и положительные заряды притягиваются. Следовательно, каждый из положительно заряженных шариков притягивает отрицательный заряд q к себе — каждая из сил (FK1 и FK2) будет направлена вправо. Поэтому их равнодействующая FK тоже будет направлена вправо.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17545
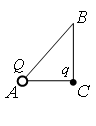 В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
а) 0,36
б) 0,60
в) 0,75
г) 1,67
Алгоритм решения
1.Записать исходные данные.
3.Применить закон Кулона для данного случая.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Сила, с которой заряд Q действует на точечный заряд q, помещенный в вершину С: FKC = 2,5∙10–8 Н.
• Сила, с которой заряд Q действует на точечный заряд q, помещенный в вершину В: FKB = 9∙10–9 Н.
Запишем закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона для 1 и 2 случая:
FKC=k|q||Q|AC2
FKB=k|q||Q|AB2
По условию задачи нужно найти соотношение сторон треугольника АС к ВC. Для этого выразим известные стороны треугольника из формул выше:
AC=√k|q||Q|FKC
AB=√k|q||Q|FKB
Сторону ВС можно выразить с помощью теоремы Пифагора (АВС — прямоугольный треугольник, так как угол С является прямым):
BC=√AB2−AC2=√k|q||Q|FKB−k|q||Q|FKC=√k|q||Q|(FKC−FKB)FKBFKC
Отсюда:
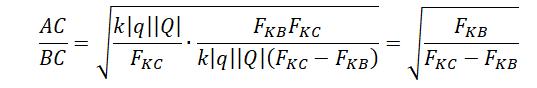
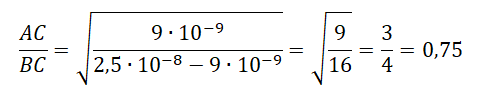
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17737
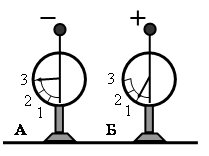 На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных знаков. Если их шары соединить проволокой, то показания обоих электрометров
На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных знаков. Если их шары соединить проволокой, то показания обоих электрометров
Ответ:
а) не изменятся
б) станут равными 1
в) станут равными 2
г) станут равными 0
Алгоритм решения
1.Записать показания электрометров.
2.Установить, что произойдет, если их соединить проволокой.
3.Вычислить показания электрометров после их соединения.
Решение
Запишем показания электрометров:
• Слева электрометр показывает отрицательный заряд q1, равный «3».
• Справа электрометр показывает положительный заряд q2, равный «1».
Когда электрометры соединятся проволокой, избыточный отрицательный заряд в виде электронов частично переместится из левого электрометра в правый электрометр так, что показания приборов выровняются. Они будут показывать:
q=|−q1+q2|2=22=1
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.6k

Закон Кулона
Закон сохранения электрического заряда
Напряженность
Принцип суперпозиции
Электрическое поле
Потенциал электростатического поля
Разность потенциалов
Теория
Совсем чуть−чуть.
Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:
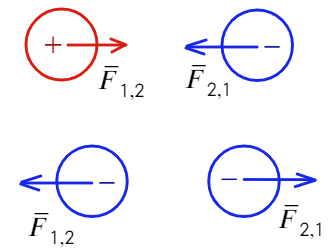
Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.
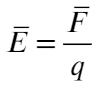
Напряженность НЕ зависит от величины заряда, помещенного в поле!
Задачи
Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.
Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:
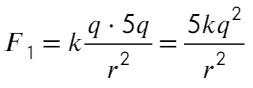
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:
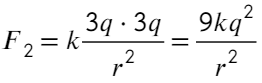
Отношение получится таким:
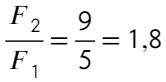
Ответ: 1,8
Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.
Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).
А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:
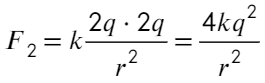
Отношение:
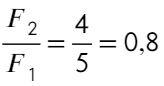
Ответ: 0,8
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?
В начальный момент времени на шарик действуют две силы:
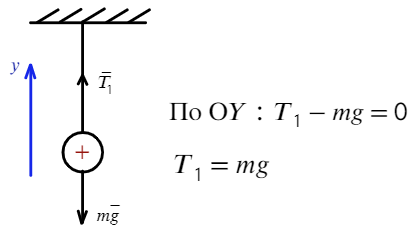 а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
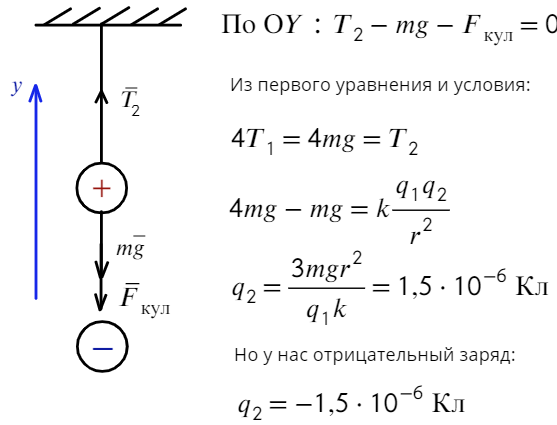 б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
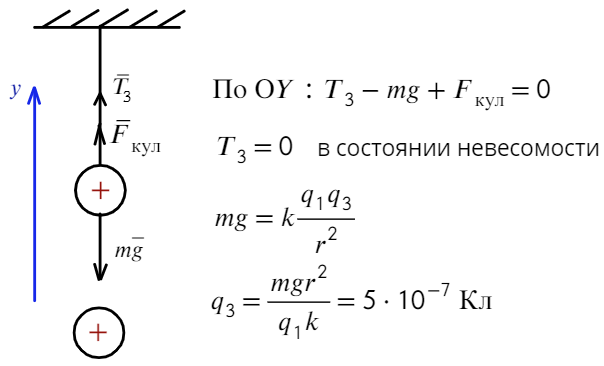 Ответ: −1,5 мкКл, 500 нКл.
Ответ: −1,5 мкКл, 500 нКл.
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.
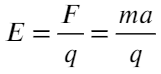
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.
Найдем ускорение электрона в электрическом поле:
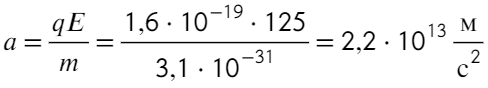
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:
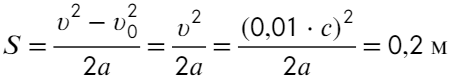
Ответ: 0,2 м
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?
Для начала разберемся, какие силы действуют на заряд:
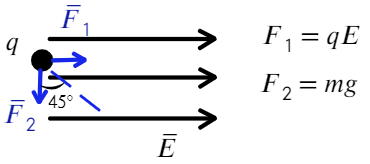
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:
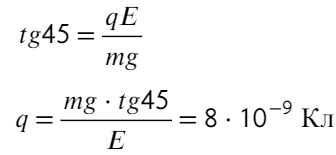
Ответ: 8×10⁻⁹ Кл
Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)
Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:
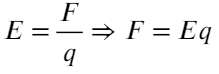
Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:
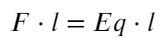
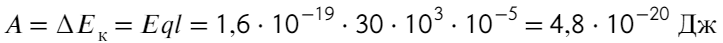
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹
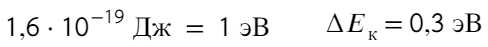
Ответ: 0,3 эВ
Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.
Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).
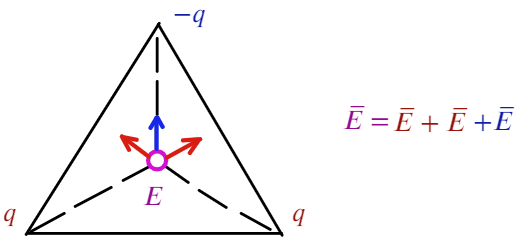
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:
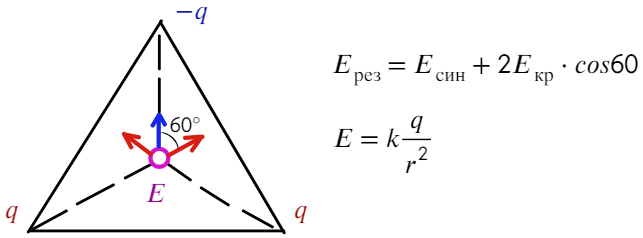
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:
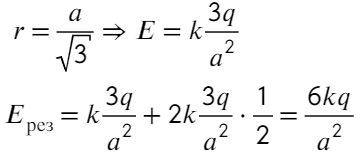
Ответ: 6kq/a²
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)
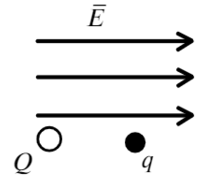
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.
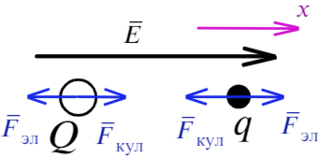
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:
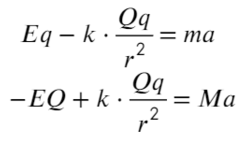
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.
Разделим одно уравнение на другое и выразим массу:
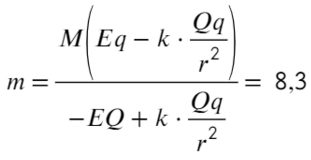
Ответ: 8,3 гр.
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)
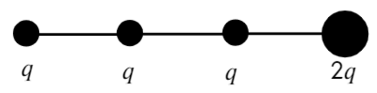
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:
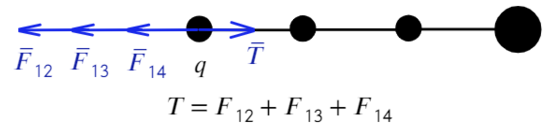
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:
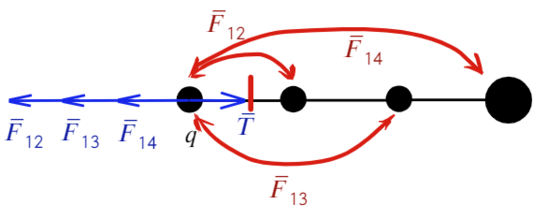
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:
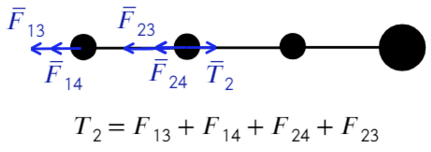
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:
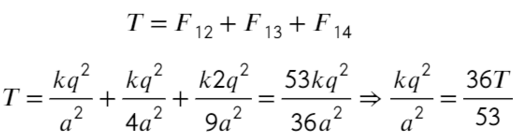
Второе уравнение с подстановкой выражения из первого:
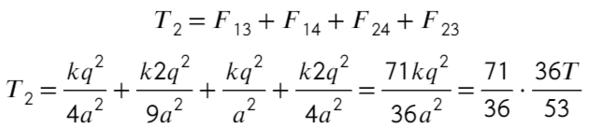
Ответ: 71T/53
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)
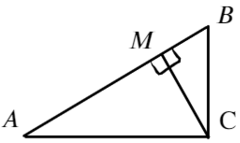
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:
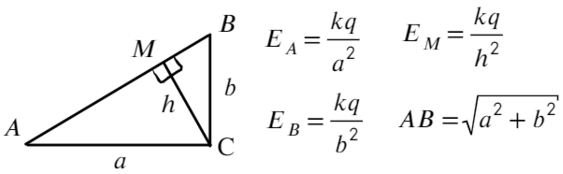
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:
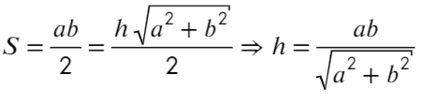
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:
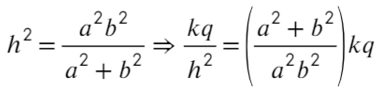
Выразим a² и b² через напряженность:
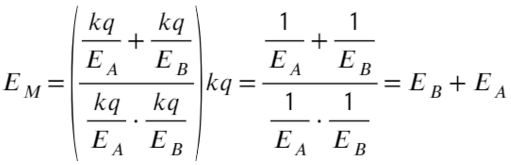
Ответ: Ea+Eb
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)
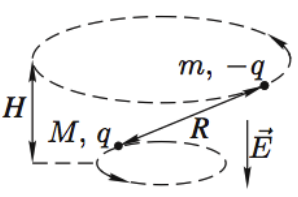 Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
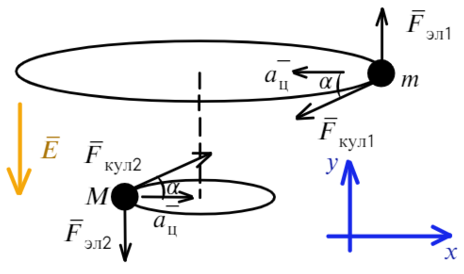
Запишем уравнения по осям на верхнюю частицу:
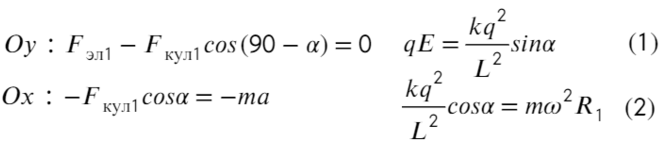
На нижнюю частицу:
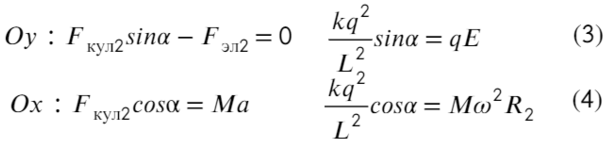
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.
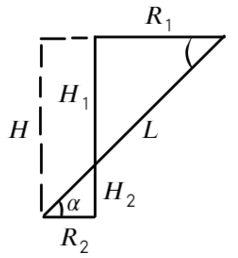
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:
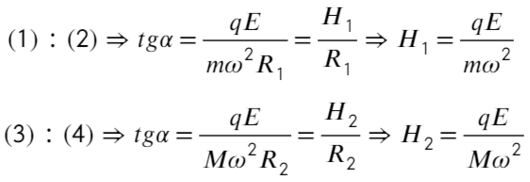
Сложим два уравнения, чтобы найти расстояние между плоскостями:
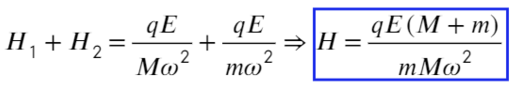
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:
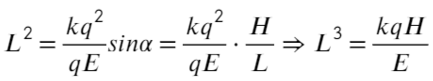
Вместо Н подставим то, что мы нашли:
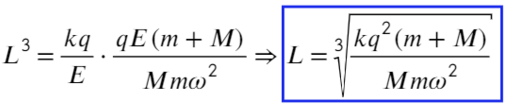
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)
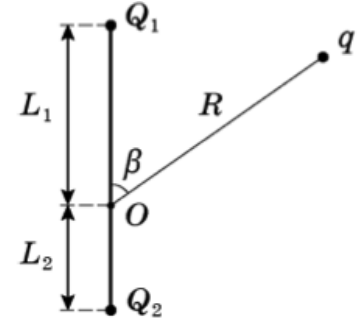
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:
 Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
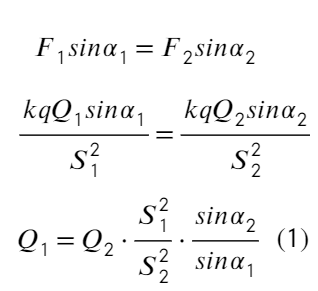
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:
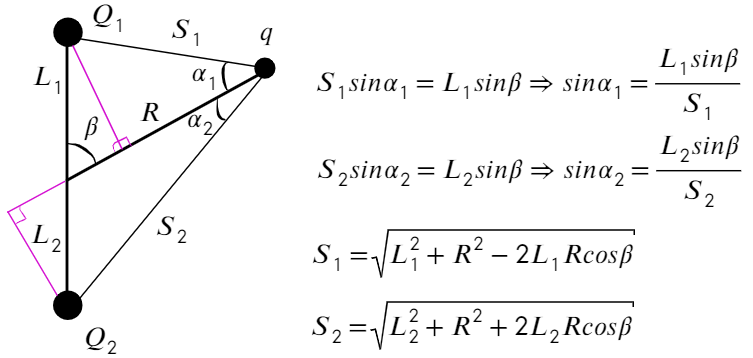
Подставим в ур-ие (1):
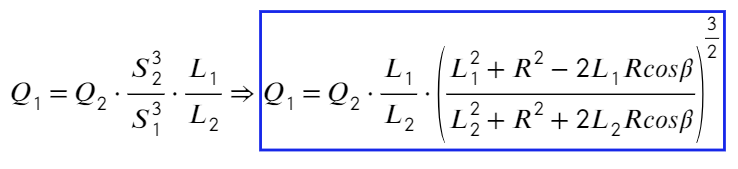
В качестве закрепления материала решите несколько похожих задач с ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
