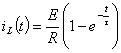Как найти заряд на катушке

Подобный термин применяется обычно для определения элемента цепи. Индуктивность является характеристикой эффекта самоиндукции. Это физическое явление было открыто Майклом Фарадеем.

Понятие индуктивности

Индуктивность необходима для составления характеристики магнитных свойств электрической цепи. Индуктивность можно определить в качестве коэффициента пропорциональности между магнитным потоком, который находится в замкнутом контуре и электрическим током. Причем сам магнитный поток создается непосредственно текущим током, который проходит через поверхность контура.

Индуктивность связывают с дополнительными показателями:

• размером контура;
• значением магнитной проницаемости окружающей среды;
• формой.

Величина в системе измерений СИ обозначается латинской буквой $L$ (генри).

$L = frac{NF}{I}$, где:

• $F$ – магнитный поток,
• $I$ – это ток в контуре.

Самоиндукция

Исходя из указанной формулы, можно сказать, что индуктивность контура будет зависеть от его размеров, формы, а также магнитных свойств окружающей среды. При течении электрического тока в замкнутом контуре возникает магнитное поле, которое постоянно изменяется. Такой процесс порождает через некоторое время возникновение электродвижущей силы.

«Заряд индуктивности электрической цепи» 👇

Самоиндукция не позволяет току в контуре изменяться. При обнаружении явления самоиндукции можно использовать иной способ подключения и применения электрической цепи. В этом случае готовят цепь с включенным резистором и катушкой с железным сердечником. Также подключают последовательно и электрические лампы. В подобной ситуации сопротивление резистора будет иметь идентичные показатели с сопротивлением катушки на постоянном токе. В итоге получается яркое горение электрических осветительных приборов.

Самоиндукция широко используется в настоящее время в электротехнике.

Наиболее простой формулой для нахождения индуктивности является:

$L = frac{F}{I}$

При помощи индуктивности выражают иные величины, в том числе электродвижущую силу самоиндукции. Для этого принято использовать следующее написание формулы:

$Ei = -frac{LdI}{dt}$

Такая формула дает ответ о численном равенстве индукции с электродвижущей силой. Она должна возникать при изменении силы тока в контуре на 1 амперметр за секунду времени.

$W = frac{L I^{2}}{2}$ – формула переменной индуктивности, которая позволяет найти энергию магнитного поля ($W$).

Катушка индуктивности

Намотанная медная изолированная со всех сторон металлическая проволока является катушкой индуктивности. В качестве изоляционного материала обычно используют:

• различные ткани;
• лаки;
• проводные изоляции.

Величина магнитного потока лежит в зависимости от площади цилиндра. При увеличении тока в катушке магнитное поле также будет увеличиваться. При подаче электрического тока на катушку возникает напряжение, которое действует в противоположном направлении напряжению тока. Однако подобное напряжение может внезапно исчезнуть и быть нестабильным. В этом состоит явление электродвижущей силы самоиндукции. При подаче напряжения на катушку электрической цепи сила тока изменит свое значение до определенного числа.

По закону Ома напряжение в этот момент времени также изменит показатели, так как $I = frac{U}{R}$. Величина $I$ – сила тока, $U$ – напряжение, $R$ – сопротивление катушки.

В катушке обнаруживается еще одна особенность. Электродвижущая сила прибавляется к напряжению, если разомкнуть электрическую цепь. Тогда сила тока в катушке индуктивности изменит свои показания немедленно.

В настоящее время используют катушки двух основных видов:

• с магнитным наконечником;
• с железной сердцевиной.

Сердечники эффективно увеличивают уровень индуктивности. Также катушки принято различать по внешнему виду и внутреннему строению. Индивидуальные параметры катушек влияют на индуктивность заряда электрической цепи.

Индуктивность для однослойной и многослойной катушки определяется разными способами.

Индуктивность соленоида

Для поиска индуктивности в соленоиде применяют следующую формулу:

$L= mu0n^{2} V$, где вводятся дополнительные показатели в виде магнитной проницаемости вакуума $mu0$, количества совершенных витков $n^{2}$, а также объема тела соленоида $V$.

Для расчета индуктивности соленоида также используют величину площади поперечного сечения соленоида и его длину.

Магнитное поле, созданное внутри катушки, направлено вдоль оси, поэтому при расчете индуктивности при постоянном и переменном токе используется формула $B= mu0nI$.

При вычислении индуктивности, когда ток движется по соленоиду и возникает запас энергии в катушке, используется формула следующего вида:

$E = frac{LI^2}{2}$

Электродвижущая сила в этом случае возникает при изменении тока в соленоиде. Переменное магнитное поле появляется в момент начала работы на переменном токе. Направление силы притяжения может меняться или быть в неизменном виде.

Направление силы меняется при использовании соленоида в качестве электромагнита. Если якорь сделан из магнитомягкого материала, то направление неизменно.

Соленоид на переменном токе обладает комплексным сопротивлением, которое состоит из сопротивления обмотки, а также ее индуктивности.

При использовании соленоидов на переменном токе сила зависит от строения сердечника и корпуса. Соленоиды иного типа применяются в качестве индукторов для нагрева в тигельных печах.

При определении индуктивность катушки в колебательных контурах электрической цепи, применяется формула:

$XL = WL$, где $XL$ – показатель реактивного сопротивления катушки, а $W$ – круговая частота.

Рассмотрим схему цепи, в
которой до коммутации протекал ток I от
источника постоянного напряжения Е
(рисунок 2.19). При этом
в магнитном поле катушки индуктивности
была запасена энергия 
LI²/2.
После коммутации катушка оказывается
включенной на сопротивление R, и запасенная
энергия рассеивается на резисторе.

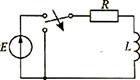
Рисунок 2.19

Дифференциальное уравнение
для такой цепи буде следующим

Выделять из системы одно
уравнение путем преобразований
относительно одного неизвестного не
требуется. Решение находится в виде

,

где 
i_L(∞)
= 0, так как рано или поздно вся энергия
катушки рассеивается резистором. Корень
характеристического уравнения

 Обратите
внимание на то, что p_k
< 0 (в случае комплексных корней

Re{р_k}
< 0), так как свободные составляющие
определяются по схеме без источников
и всегда затухают со временем. Из закона
коммутации следует i_L(+0)
= i_L
(-0).  В
то же время 
i_L(+0)
= i_L(∞)+A,
поэтому A
= i_L
(-0). До коммутации по
цепи протекал ток I
= E/R ,
значит, i_L
(-0) =  E/R . Итак,
решение получено

.

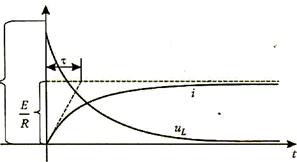
График этой функции
представлен на рисунок 2.20.

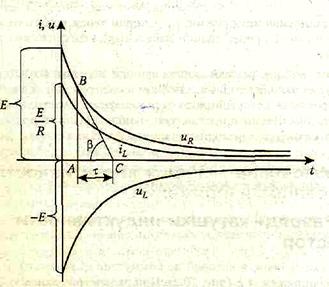
Рисунок 2.20

Напряжение на резисторе
повторяет форму кривой тока

.

 Напряжение на катушке
индуктивности уравновешивается
напряжением на резисторе u_L(t)
= u_R(t)
(второй закон Кирхгофа). Его можно
определить и из математической модели
элемента

;

 . До коммутации
u_L(t)
= 0 ,
затем при t
= 0 оно скачком изменяется так, что
u_L(t)
= -E 
и по экспоненте падает до нуля. Обычно
вместо р
вычисляется постоянная времени 

,

имеющая размерность времени, и ответ
записывают в виде

.

2.4.2 Включение катушки
индуктивности на постоянное напряжение

Рассмотрим схему цепи, в
которой коммутация заключается во
включении цепочки RL на постоянное
напряжение (рисунок 2.5).

Рисунок 2.21

Для нее дифференциальное
уравнение будет следующим  

Преобразовывать систему
уравнений не требуется. Получим решение
дифференциального уравнения

.

  Окончательное решение
для тока

.

Напряжение на катушке 

 показывает, что в момент
включения напряжение источника
уравновешивается напряжением на
индуктивности, так как ток в этот момент
равен нулю и падение напряжения на
резисторе отсутствует (рисунок 2.22).

Рисунок
2.22

3 Описание объекта измерения

В задании на лабораторную
работу предоставлен только один параметр
катушки – индуктивность. Для составления
электрической схемы проведения испытаний
не хватает еще одного параметра –
сопротивления потерь. Этот параметр
состоит из потерь в токопроводе, потерь
в сердечнике, экране и диэлектрических
потерь. Сопротивление потерь сильно
зависит от частоты, на которой работает
катушка.

Процесс коммутации, который мы будем
использовать при проведении
экспериментальных работ, предполагает
воздействие на катушку широкополосного
высокочастотного сигнала. Однако этот
процесс длится очень маленький промежуток
времени Δt → 0 и может
не учитываться. Основные экспериментальные
результаты получаются в результате
наблюдения за осциллограммами в более
широком интервале времен от нуля до t
_max и, следовательно,
на более низких частотах.

На низких частотах основной вклад в
сопротивление потерь вносит сопротивление
токопровода, а еще на более низких
частотаx сопротивление
потерь фактически равно сопротивлению
провода обмотки постоянному току. Этот
параметр приводится в таблице 3.1.

В задании для лабораторной работы с
целью удобства проведения арифметических
расчетов представлены округленные
значения индуктивности. В отчете же
значение ESR нужно выбирать
для номинального значения, ближайшего
к указанному в задании. Например, для
75 мкГн значение ESR будет
0,67 Ом как для номинального значения 68
мкГн. С учетом того, что согласно таблице
1 допуск на ESR составляет
± 40 %, то, с целью упрощения арифметических
расчетов, значение этого параметра
можно округлять до одной значащей цифры,
например, с 0,67 до 0,7 Ом.

Таблица 3.1 – Основные параметры некоторых
катушек индуктивности фирмы Murata,
Япония

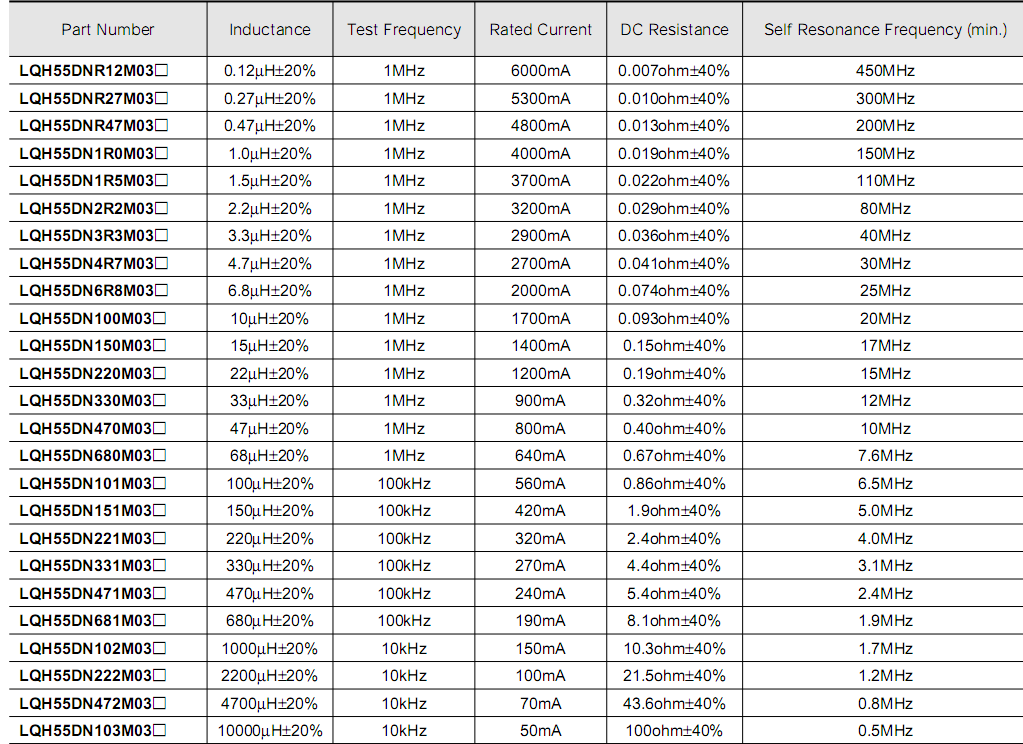
Приведенные в таблице 3.1 катушки
выпускаются массово и активно используются
в современных электронных средствах.
Эти катушки предназначены для монтажа
на поверхность (ПМИ – поверхностно
монтируемые изделия с использованием
русскоязычной терминологии) или в
английской терминологии SMD
– Surface Mount
Devices.

На рисунке 3.1 показан внешний вид и
габаритные размеры катушек такого типа.

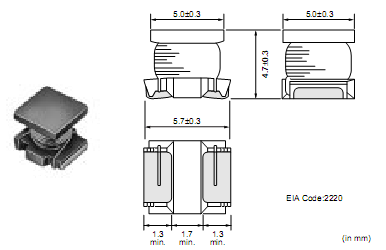
Рисунок
3.1 – Внешний вид и габаритные размеры
катушек серии LQH55D
(2220 Size)

Размер 2220 означает
произведение 22 × 20 в сотых долях дюйма.
1 дюйм – это 25,4 мм.

В таблице 3.1
наименование столбцов означает:

– Part Number – полное
условное обозначение (ПУО) в КД или
запись при заказе;

– Inductance –
индуктивность;

– Test Frequency – тестовая
частота;

– Rated Current –
максимально допустимый ток;

– DC Resistance –
сопротивление постоянному току;

– Self Resonance Frequency
(min.) – минимальное значение собственной
резонансной частоты катушки.

Полное условное
обозначение (Part Number) представлено в
виде кода LQH55DN1R0M03К. Для расшифровки
этого кода на сайте производителя
имеются специальные таблицы, одна из
которых представлена на рисунке 3.2.

После расшифровки
получаем следующую информацию. Катушка,
предназначенная для монтажа на поверхность
LQ с проволочной обмоткой на сердечнике
из феррита H с размерами (55)
5,7 × 5,0 мм, которые она занимает на
печатной плате, используемая как
дроссель D, с функцией стандартного типа
N, номинальным значением 1R0 индуктивности
1 мкГн, допуском M ± 20 %, стандартного типа
0, с выводами 3, покрытыми оловом,
упакованная в блистерную ленту с
выдавленным посадочным местом и свернутую
в спираль диаметром 330 мм К.

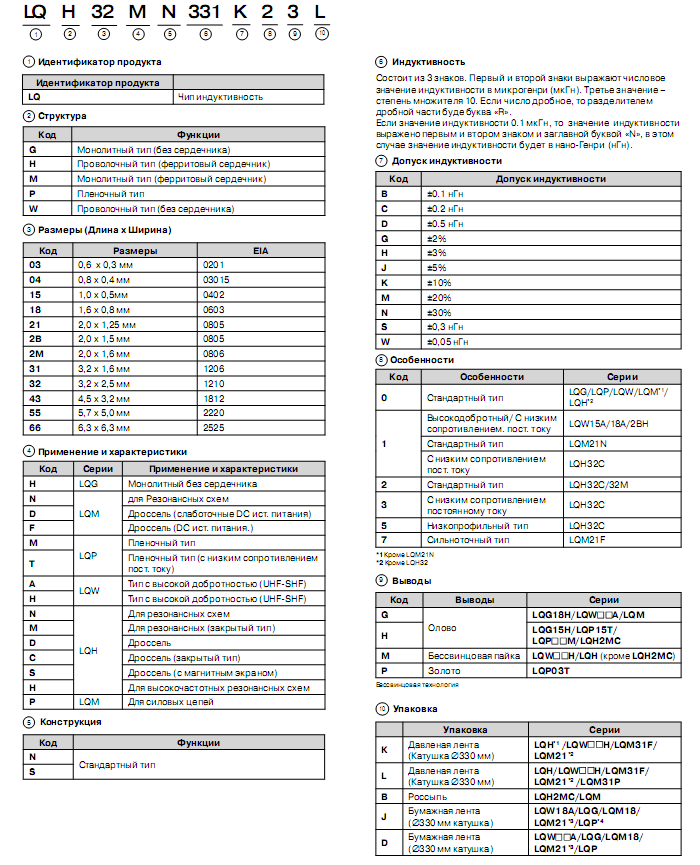
Рисунок 3.2 – Таблицы для расшифровки
кода полного
условного обозначения (Part Number)
катушек для монтажа на поверхность
фирмы Murata, Япония

Соседние файлы в папке ЛР МиКЭС 2020

• #
• #
• #
• #
• #
• #
• #
• #
• #

Условие задачи:

В замкнутую накоротко катушку из медной проволоки вводят магнит, создающий внутри ее поле 0,01 Тл. Определите заряд, протекающий при этом через катушку. Радиус витка катушки 10 см, площадь поперечного сечения проволоки 0,1 мм².

Задача №8.4.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(B=0,01) Тл, (r=10) см, (S_{сеч}=0,1) мм², (q-?)

Решение задачи:

Итак, в замкнутую накоротко катушку вводят магнит. Понятно, что из-за изменения магнитного потока в ней будет возникать ЭДС индукции. Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока. Поэтому:

[{{rm E}_i} = frac{{Delta Phi }}{{Delta t}};;;;(1)]

Заметим, что формулу (1) можно использовать только при равномерном изменении магнитного потока (условно мы примем изменение именно таким). Так как площадь (S), охватываемая катушкой, не изменяется, то изменение магнитного потока (Delta Phi) следует искать по формуле ((N) – число витков в катушке):

[Delta Phi = NDelta BS]

Если принять начальное значение индукции магнитного поля равным нулю (например, если катушка вначале находилась достаточно далеко), то изменение значения индукции магнитного поля (Delta B) равно (B), поэтому:

[Delta Phi = NBS]

Таким образом, формула (1) примет вид (также избавимся от знака изменения времени, он здесь не нужен):

[{{rm E}_i} = frac{{NBS}}{t};;;;(2)]

С другой стороны, из закона Ома следует, что (заметим, что в нашем случае ток будет постоянным):

[{{rm E}_i} = IR;;;;(3)]

В этой формуле (I) – сила тока в катушке, (R) – сопротивление катушки.

Приравняем (2) и (3), тогда:

[frac{{NBS}}{t} = IR]

Домножим обе части уравнения на время (t):

[NBS = ItR]

Произведение силы тока (I) на время (t) даёт искомый протекший через катушку заряд (q), значит:

[NBS = qR]

[q = frac{{NBS}}{R};;;;(4)]

Площадь (S), охватываемую катушкой, легко найти по формуле (учитывая, что катушка – круглая):

[S = pi {r^2};;;;(5)]

Сопротивление медной катушки (R) радиуса (r), состоящей из (N) витков (удельное электрическое сопротивление меди (rho) равно 17 нОм·м), можно найти по формуле:

[R = N rho frac{{2pi r}}{{{S_{сеч}}}};;;;(6)]

Подставим (5) и (6) в (4):

[q = frac{{NB cdot pi {r^2} cdot {S_{сеч}}}}{{N rho cdot 2pi r}}]

[q = frac{{B{S_{сеч}}r}}{{2rho }}]

Задача решена в общем виде, посчитаем численный ответ:

[q = frac{{0,01 cdot 0,1 cdot {{10}^{ – 6}} cdot 0,1}}{{2 cdot 17 cdot {{10}^{ – 9}}}} = 2,94 cdot {10^{ – 3}};Кл = 2,94;мКл]

Ответ: 2,94 мКл.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.4.2 Магнитный поток, пронизывающий контур проводника, равномерно изменился на 0,5 Вб
8.4.4 Магнитный поток в контуре проводника за 0,2 с изменился на 1,2 Вб. Какова ЭДС
8.4.5 Магнитный поток через контур изменяется от 6 до 14 Вб за 20 с. Определите абсолютную

Как найти заряд конденсатора в тот момент, когда энергия электрического поля конденсатора и энергия магнитного опля катушки становятся одинаковыми?