Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.
Потенциальные и непотенциальные силы в электродинамике
Все силы можно разделить на потенциальные и непотенциальные.
Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.
Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))
Энергия системы заряженных тел
Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.
Изменение потенциальной энергии заряда в однородном электрическом поле
Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).

Рис. (1). Перемещение заряда в однородном поле
Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.
Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б – vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б – vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:
(A=-E_Б). ((5))
Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))
Энергия взаимодействия точечных зарядов
Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.
Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).

Рис. (2). Перемещение заряда в поле точечного заряда
Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.
В таком случае работа электрического поля на дуге (СБ) будет нулевой:
(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))
поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:
(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)
(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))
Энергия системы (n) точечных зарядов
Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.
Свойство линий напряжённости электрического поля
Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).

Рис. (3). Замкнутая линия электрического поля
Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).
Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.
Источники:
Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.
Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.
Рис. 3. Замкнутая линия электрического поля. © ЯКласс.

Положительная энергия – это один из видов энергии человека и окружающей его среды. Она дает нам силу, активность, хорошее настроение, высокую работоспособность, здоровье и удачу в общении с людьми. Чем больше у человека положительной энергии, тем он успешнее, бодрее, здоровее. От него исходит позитив и хорошие эмоции. У него прекрасные отношения с коллегами, друзьями, соседями. Он не ноет и не жалуется на свою жизнь – он ей просто наслаждается и получает удовольствие!
Заряд положительной энергией – это как заряд силами. Он просто жизненно необходим каждому человеку. Если Вы вдруг почувствовали, что жизнь стала скучной, у Вас все валится из рук, появились проблемы со здоровьем и общением с людьми, то Ваш диагноз ясен. Это острая нехватка положительной энергии! Шутки шутками, а ведь ее дефицит действительно снижает качество жизни.
А как наполнить себя положительной энергией?
Для начала необходимо обратиться к своему внутреннему «Я» и выяснить, чего ему не хватает, какие проблемы его тревожат. Иногда, прислушавшись к себе, можно найти ответы на все вопросы, найти правильное решение, услышать подсказку.
Затем необходимо выяснить, куда уходит Ваша драгоценная положительная энергия. Возможно, Вы давно не были в отпуске, Вы сильно устали. Или Вас тревожит какое-то заболевание. Последнее, кстати, является и причиной, и следствием отсутствия положительной энергии. Стоит пересмотреть и свое окружение. Никто ли не доставляет Вам хлопот, проблем, расстройства в последнее время? Если такой человек есть, то смело прерывайте с ним какие бы то ни было контакты. Иначе он будет продолжаться пользоваться Вашей положительной энергией.

- Как заряжаться положительной энергией с помощью природных сил, природных источников? Как известно, природа – это живая сила. Только ей мы обязаны всем, что имеем. Поэтому она, как мать, всегда примет и поможет. Во-первых, больше времени проводите на свежем воздухе! Причем делайте это не по дороге в ближайший магазин. Лучше всего будет выйти на прогулку в парк, погулять с собакой. На выходные, если есть такая возможность, выбирайтесь за город. А, если Ваше мини-путешествие будет на велосипеде, то это и для здоровья будет полезно! В этом случае Вас будет заряжать положительной энергией и Солнце, и воздух. Во-вторых, почаще купайтесь. Конечно, летом для этого возможностей гораздо больше. Но и в холодное время года можно, например, записаться в бассейн. Вода – это мощный источник положительной энергии.
- Как зарядить себя положительной энергией с помощью творчества? Найдите себе занятие по душе. Это может быть что угодно: рисование, танцы, вышивка, шитье, сбор моделей самолетов или танков (для мужчин). Занимаясь своим хобби, представляйте, как все плохое уходит от Вас, а хорошее приходит. Дополнительной подзарядкой для Вас станет преподнесение плодов своего творчества (картины, расшитого полотенца) родным и близким.
- Зарядиться положительной энергией можно и при общении с другими людьми. Но, разумеется, что эти люди должны быть Вам дороги. Иногда откровенный разговор по душам с мамой или веселые беседы с лучшим другом могут стать Вашим спасением. Каждый из нас ощущал, как порой бывает легко и тепло на душе после общения с кем-либо. Это достигается за счет Ваших светлых чувств к человеку: за счет любви, преданности, дружбы. Ведь они так важны и так необходимы каждому.
- Еще один способ – это полезные и добрые дела. Помогите бездомным, которые живут неподалеку от Вас, навестите престарелых одиноких родственников. Конечно, если эти порывы будут идти от души, от сердца. Иначе никакой положительной энергии Вы не получите.
- Если есть такая возможность, то общайтесь с детьми: со своими или с детишками своих друзей, родных. Такой контакт – это невероятно приятный, веселый и полезный способ зарядиться позитивом. Дети всегда отдают взрослым свою взрывную энергию. Она находится у них в избытке. Вы сами сможете на несколько минут оказаться в детстве, дурачась и играя вместе с ними.
- Иногда положительная энергия человека может перестать циркулировать по организму из-за так называемых мышечных блоков. Ведь энергетические потоки находятся в нашем теле, нашей физической оболочке. Поэтому полезным станут такие процедуры и занятия, как массаж, йога, дыхательная гимнастика, упражнения. Возьмите за правило делать зарядку каждое утро, начните бегать или заниматься дома. А еще лучше приобрести абонемент на профессиональные тренировки. Это и для фигуры полезно, и для своего энергетического состояния. Сюда же можно отнести спа-процедуры, баню и сауну. Релакс, снятие мышечного напряжения помогут Вам вновь наполниться положительной энергией.
- Побольше времени проводите с любимым человеком. Проявляйте свои нежные чувства. И дело тут не только в сексе. Объятья, поцелуи, совместные прогулки – это лучше всяких психологов и психотерапевтов. Доказано, что любящие и влюбленные люди живут дольше, более успешны и позитивны. Ведь между двумя близкими людьми циркулирует мощнейший поток положительной энергии. Но, если у Вас пока нет такого человека, то не бойтесь влюбляться! Возможно, Вы вскоре встретите свою вторую половинку.
- Положительная энергия может прийти к человеку и при его культурно-духовном самосовершенствовании и развитии. Возьмите в библиотеке хорошую книгу, послушайте классическую музыку. Те, кто верит в Бога, могут сходить в церковь на воскресную службу.

Теперь Вы знаете, как зарядиться положительной энергией! И Вам остается только действовать! Вот увидите, что скоро в жизни все изменится в лучшую сторону!
Как быстро зарядиться энергией и остановить бег мыслей.
Электрический потенциал
Публикации по материалам Д. Джанколи. “Физика в двух томах” 1984 г. Том 2.
Электрический потенциал и потенциальная энергия
Понятие энергии исключительно полезно для решения задач механики. Прежде всего энергия сохраняется и поэтому служит важной характеристикой явлений природы. Используя представления об энергии, многие задачи удается решить, не имея детальных сведений о силах или в случае, когда применение законов Ньютона потребовало бы сложных вычислений.
Энергетическим подходом можно воспользоваться и при изучении электрических явлений, и здесь он оказывается чрезвычайно полезным: позволяет не только обобщить закон сохранения энергии, но и в новом аспекте увидеть электрические явления, а также служит средством более просто находить решения, чем путем рассмотрения сил и электрических полей.
Потенциальную энергию можно определить лишь для консервативных сил; работа такой силы по перемещению частицы между двумя точками не зависит от выбранного пути.
Легко видеть, что электростатическая сила является консервативной: сила, с которой один точечный заряд действует на другой, определяется законом Кулона: F = kQ1Q2 /r 2 ; здесь та же обратно пропорциональная зависимость от квадрата
расстояния, что и в законе всемирного тяготения: F = Gm1m2 /r 2. Такие силы консервативны. Сила, действующая на выбранный заряд со стороны любого распределения зарядов, может быть записана в виде суммы кулоновских сил; следовательно, и сила, создаваемая произвольным распределением зарядов, консервативна. А это позволяет ввести потенциальную энергию электростатического
поля.
Разность потенциальных энергий точечного заряда q в двух различных точках электрического поля можно определить как работу, совершаемую внешними силами по перемещению заряда (против действия электрической силы) из одной точки в другую. Это равносильно определению изменения потенциальной энергии заряда в поле как взятой с обратным знаком работы, совершаемой самим полем по перемещению заряда из одной точки в другую.
Рассмотрим для примера электрическое поле между двумя пластинами с равным по величине и противоположным по знаку зарядом. Пусть размеры пластин велики по сравнению с расстоянием между ними, и поэтому поле между пластинами можно считать однородным (рис. 24.1).

Поместим в точку а вблизи положительно заряженной пластины точечный положительный заряд q.
Электрическая сила, действующая на заряд, будет стремиться переместить его к отрицательной пластине (в точку b), совершая работу по переносу заряда. Под действием силы заряд приобретет ускорение и его кинетическая энергия возрастет; при этом потенциальная энергия уменьшится на величину работы, совершенной электрической силой по перемещению заряда из точки a в точку b. Согласно закону сохранения энергии, потенциальная энергия заряда в электрическом поле перейдет в кинетическую энергию, но полная энергия останется неизменной. Заметим, что положительный заряд q обладает наибольшей потенциальной энергией U вблизи положительной пластины (в этой точке его способность совершать работу над другим телом или системой максимальна). Для отрицательного заряда справедливо обратное: его потенциальная энергия будет максимальна вблизи отрицательной пластины.
Напряженность электрического поля мы определяли как силу, действующую на единичный заряд; аналогично удобно ввести электрический потенциал (или просто потенциал, если это не вызывает недоразумений) как потенциальную энергию единичного заряда.
Электрический потенциал обозначается символом V; итак, если в некоторой точке a точечный заряд q обладает
потенциальной энергией Ua, то электрический потенциал в этой точке равен Va = Ua /q.
Реально мы измеряем только изменение потенциальной энергии. Соответственно фактически можно измерить лишь разность потенциалов между
двумя точками (например, точками a и b на рис. 24.1). Если работа электрических сил по перемещению заряда от
точки a в точку b есть Wba (а разность потенциальных
энергий соответственно равна этой величине с обратным
знаком), то для разности потенциалов можно написать

Единицей электрического потенциала (и разности потенциалов) является джоуль на кулон (Дж/Кл); этой единице присвоено наименование вольт (В) в честь Алессандро Вольты (1745-1827) (он известен как изобретатель электрической батареи); 1 В = 1 Дж/Кл. Заметим, что,
согласно данному определению, положительно заряженная пластина на рис. 24.1 имеет более высокий потенциал, чем отрицательная. Таким образом, положительно заряженное тело будет стремиться перейти из точки с более высоким потенциалом в точку с более низким
потенциалом, отрицательно заряженное тело – наоборот. Разность потенциалов часто называют электрическим напряжением.
Потенциал в данной точке Va зависит от выбора «нуля» потенциала; как и в случае потенциальной энергии,
нулевой уровень может выбираться произвольно, поскольку измерить можно лишь изменение потенциальной энергии (разность потенциалов). Часто за нулевой принимают потенциал земли или проводника, соединенного с землей, и остальные значения потенциалов отсчитывают относительно «земли». (Например, говоря, что потенциал в какой-то точке равен 50 В, имеют в виду, что разность потенциалов между этой точкой и землей равна 50 В.) В иных случаях, как мы увидим, удобно считать нулевым потенциал на бесконечности.
Поскольку электрический потенциал определяется как потенциальная энергия единичного заряда, изменение потенциальной энергии заряда q при перемещении его из точки a в точку b равно
ΔU = Ub – Ua = qVba
Другими словами, когда заряд q перемещается между точками с разностью потенциалов Vba, его потенциальная
энергия изменяется на величину qVba. Если, например, разность потенциалов между пластинами на рис. 24.1 составляет 6 В, то заряд 1 Кл, перемещенный (внешней силой) из точки b в точку a, увеличит свою потенциальную энергию на (1 Кл) (6 В) = 6 Дж. (Перемещаясь же из a в b, он потеряет потенциальную энергию 6 Дж.)
Аналогично энергия заряда 2 Кл увеличится на 12 Дж и т. п. Таким образом, электрический потенциал служит мерой изменения потенциальной энергии электрического заряда в данной ситуации. А поскольку потенциальная энергия – это способность совершать работу, электрический потенциал служит мерой той работы, которую может совершить данный заряд. Количество работы зависит как от разности потенциалов, так и от величины заряда.
Чтобы лучше понять смысл электрического потенциала, проведем аналогию с гравитационным полем. Пусть камень падает с вершины скалы. Чем выше скала, тем большей потенциальной энергией обладает камень и тем больше будет его кинетическая энергия, когда он долетит до подножия скалы. Величина кинетической энергии и соответственно работа, которую может совершить камень, зависят от высоты скалы и от массы камня. Точно так же и в электрическом поле изменение потенциальной энергии (и работа, которую можно совершить) зависит от разности потенциалов (эквивалентной высоте скалы) и заряда (эквивалентного массе).
Используемые на практике источники электроэнергии – батареи, электрогенераторы – создают определенную разность потенциалов. Количество энергии, отбираемой от источника, зависит от величины переносимого заряда.
Рассмотрим, например, автомобильную фару, соединенную с аккумулятором, разность потенциалов на зажимах которого равна 12 В. Количество энергии, преобразуемой фарой в свет (и, конечно, в тепло), пропорционально заряду, протекшему через фару, что в свою очередь
зависит от того, как долго включена фара. Если за некоторое время через фару прошел заряд 5,0 Кл, то
преобразованная фарой энергия составит (5,0 Кл)*(12,0 В) = 60 Дж. Если оставить фару включенной вдвое дольше, то через нее пройдет заряд 10,0 Кл, и количество преобразованной энергии составит (10,0 Кл)*(12,0 В) = 120 Дж.
Эффекты, обусловленные тем или иным распределением зарядов, можно описать как с помощью напряженности электрического поля, так и через электрический потенциал. Между напряженностью поля и потенциалом существует тесная связь. Рассмотрим вначале эту связь для случая однородного электрического поля, например поля между пластинами на рис. 24.1 с разностью потенциалов Vba. Работа электрического поля по перемещению положительного заряда q из точки a в точку b равна
W = – qVba
Обратим внимание на то, что величина Vba = Vb – Va отрицательна (Vba < 0), так как потенциал в точке a выше, чем в точке b (и положителен по отношению к потенциалу в точке b). Поэтому совершаемая полем работа положительна.
С другой стороны, работа равна произведению силы на перемещение, а сила, действующая на заряд q,
есть F = qE, где Е – напряженность однородного электрического поля между пластинами. Таким образом,
W = Fd = qEd
где d – расстояние между точками a и b (вдоль силовой линии).
Приравняв эти выражения для работы, получим
– qVba = qEd
или
Vb – Va = Vba = – Ed (поле E однородно).
Знак минус в правой части указывает просто на то, что Va Vb , т.е. потенциал положительной пластины выше,
чем отрицательной, как мы уже говорили. Положительные заряды стремятся двигаться из области с высоким потенциалом в область с низким потенциалом. Отсюда можно найти Е:
Е = – Vba /d .
Из последнего равенства видно, что напряженность электрического поля можно измерять как в вольтах на метр (В/м), так и в ньютонах на кулон (Н/Кл). Эти единицы эквивалентны между собой: 1 Н/Кл = 1 Н·м/Кл·м = 1 Дж/Кл·м = 1 В/м.
Чтобы перейти к общему случаю неоднородного электрического поля, вспомним соотношение между силой F и потенциальной энергией U, обусловленной этой силой. Разность потенциальных энергий в двух точках пространства a и b определится формулой

где dl – бесконечно малое перемещение, а интеграл берется вдоль произвольной траектории между точками a и b. В
случае электрического поля нас больше интересует разность не потенциальных энергий, а потенциалов:
Vba = Vb – Va = (Ub – Ua )/q
Напряженность электрического поля Е в любой точке пространства определяется отношением силы к заряду: Е = F/q.
Подставляя эти два равенства в формулу, получим

Это и есть общее соотношение, связывающее напряженность электрического поля с разностью потенциалов.
Когда поле однородно, например, на рис. 24.1 вдоль траектории, параллельной силовым линиям, от точки a у положительной
пластины до точки b у отрицательной пластины (поскольку направления E и dl всюду совпадают) имеем

где d – расстояние вдоль силовой линии между точками a и b. И вновь знак минус в правой части свидетельствует
лишь о том, что на рис. 24.1 Va > Vb .
Продолжение следует. Коротко о следующей публикации:
Эквипотенциальные поверхности.
Электрический потенциал можно представить графически, изображая эквипотенциальные линии или в трех измерениях – эквипотенциальные поверхности.
Альтернативные статьи:
Электрический ток,
Закон Ома.
Замечания и предложения принимаются и приветствуются!
III. Основы электродинамики
Тестирование онлайн
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.



Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.


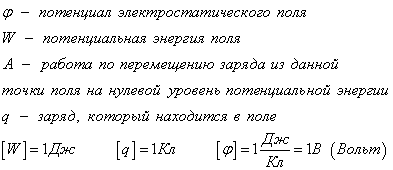
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.
Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.


Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
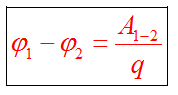
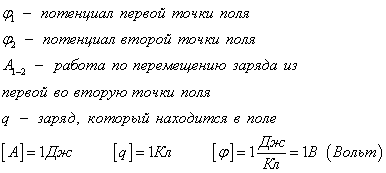
Эту формулу можно представить в ином виде


Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
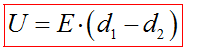

От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
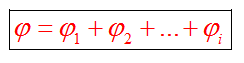
Как определить знак потенциала
Зависимость напряженности и потенциала от расстояния
Напряжение в природе
Энергия взаимодействия зарядов*
Потенциальная энергия заряженного тела в однородном электростатическом поле
- Подробности
- Обновлено 13.08.2018 18:35
- Просмотров: 730
«Физика – 10 класс»
Вспомните из курса механики определение потенциальной энергии в поле силы тяжести.
Какие силы действуют на точечный заряд в электростатическом поле?
Какое поле называется однородным?
Заряженные тела притягивают или отталкивают друг друга. При перемещении заряженных тел, например листочков электроскопа, действующие на них силы совершают работу. Из механики известно, что система, способная совершить работу благодаря взаимодействию тел друг с другом, обладает потенциальной энергией. Значит, система заряженных тел обладает потенциальной энергией, называемой электростатической или электрической.
Понятие потенциальной энергии самое сложное в электростатике. Вспомните, как нелегко было представить себе, что такое потенциальная энергия в механике. Силу мы ощущаем непосредственно, а потенциальную энергию нет. На пятом этаже дома потенциальная энергия нашего тела больше, чем на первом. Но мы это никак не воспринимаем. Различие становится понятным, если вспомнить, что при подъёме вверх пришлось совершить работу, а также если представить себе, что произойдёт при падении с пятого этажа.
Энергия взаимодействия электронов с ядром в атоме и энергия взаимодействия атомов друг с другом в молекулах (химическая энергия) — это в основном электрическая энергия.
С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом. При перемещении заряда действующая на него со стороны поля сила совершает работу. (В дальнейшем для краткости будем говорить просто о работе поля.) Поэтому можно утверждать, что заряженное тело в электрическом поле обладает энергией. Найдём потенциальную энергию заряда в однородном электрическом поле.

Работа при перемещении заряда в однородном электростатическом поле.
Однородное поле создают, например, большие параллельные металлические пластины, имеющие заряды противоположного знака. Это поле действует
на заряд q с постоянной силой  = q
= q , подобно тому как Земля действует с постоянной силой
, подобно тому как Земля действует с постоянной силой  = m
= m на камень вблизи её поверхности.
на камень вблизи её поверхности.
Пусть пластины расположены вертикально (рис. 14.31), левая пластина В заряжена отрицательно, а правая — положительно. Вычислим работу, совершаемую полем при перемещении положительного заряда q из точки 1, находящейся на расстоянии d1 от левой пластины, в точку 2, расположенную на расстоянии d2 от неё. Точки 1 и 2 лежат на одной силовой линии.
Электрическое поле при перемещении заряда совершит положительную работу:
А = qE(d1 – d2) = qEΔd. (14.12)
Работа по перемещению заряда в электрическом поле не зависит от формы траектории, подобно тому как не зависит от формы траектории работа силы тяжести.

Докажем это непосредственным расчётом.
Пусть перемещение заряда происходит по кривой (рис. 14.32). Разобьём эту кривую на малые перемещения. Сила, действующая на заряд, остаётся постоянной (поле однородно), а угол а между направлением силы и направлением перемещения будет изменяться. Работа на малом перемещении Δ равна ΔА = qElΔ
равна ΔА = qElΔ lcosa. Очевидно, что |Δ
lcosa. Очевидно, что |Δ |cosa = Δd — проекция малого перемещения на горизонтальное направление. Суммируя работы на малых перемещениях, получаем А = qEd.
|cosa = Δd — проекция малого перемещения на горизонтальное направление. Суммируя работы на малых перемещениях, получаем А = qEd.
С помощью аналогичных рассуждений можно вывести формулу для работы кулоновской силы при перемещении заряда q0 из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q. При этом должно быть учтено, что сила  зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение
зависит от расстояния до точечного заряда q. Для работы кулоновской силы в поле точечного заряда q справедливо выражение

Мы видим, что работа зависит только от положения начальной (r1) и конечной (r2) точек траектории и не зависит от формы траектории.
Электростатическая сила, действующая на заряды, является так же, как и силы тяжести, тяготения и упругости, консервативной силой.
Потенциальная энергия.
Поскольку работа электростатической силы не зависит от формы траектории точки её приложения, сила является консервативной, и её работа согласно формуле (5.22) равна изменению потенциальной энергии, взятому с противоположным знаком:
А = -(Wп2 – Wп1) = -ΔWп. (14.13)
Сравнивая полученное выражение (14.12) с общим определением потенциальной энергии (14.13), видим, что ΔWп = Wп2 – Wп1 = -qEd. Считаем, что в точке 2 потенциальная энергия равна нулю. Тогда потенциальная энергия заряда в однородном электростатическом поле равна:
Wп = qEd, (14.14)
где d — расстояние от точки 2 до любой точки, находящейся с точкой 2 на одной силовой линии.
Теперь получим формулу для потенциальной энергии заряда, находящегося в поле точечного заряда. Изменение потенциальной энергии заряда q0 при перемещении из точки 1 в точку 2 в неоднородном поле неподвижного точечного заряда q равно работе консервативной силы, взятой с обратным знаком:

Если считать, что в бесконечно удалённой точке потенциальная энергия равна нулю (при r2 → ∞ Wп2 — 0), то потенциальная энергия заряда q0 в некоторой точке, находящейся на расстоянии r от точечного заряда q, создающего поле:  Потенциальная энергия прямо пропорциональна заряду q0, внесённому в поле.
Потенциальная энергия прямо пропорциональна заряду q0, внесённому в поле.
Отметим, что формула (14.14) подобна формуле Wп = mgh для потенциальной энергии тела. Но заряд q в отличие от массы может быть как положительным, так и отрицательным.
Если поле совершает положительную работу, то потенциальная энергия заряженного тела при его свободном перемещении в поле в точку 2 уменьшается: ΔWп < 0. Одновременно согласно закону сохранения энергии растёт его кинетическая энергия. И наоборот, если работа отрицательна (например, при свободном движении положительно заряженной частицы в направлении, противоположном направлению вектора напряжённости поля Е; это движение подобно движению камня, брошенного вверх), то ΔWп > 0. Потенциальная энергия растёт, а кинетическая энергия уменьшается; частица тормозится.
На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю:
A= -ΔWп = -(Wп1 – Wп1) = 0.
Это — свойство полей консервативных сил.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика – Физика, учебник для 10 класса – Класс!ная физика
Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
